A novel background field removal method for MRI using projection onto dipole fields (PDF)

Abstract

For optimal image quality in susceptibility-weighted imaging and accurate quantification of susceptibility, it is necessary to isolate the local field generated by local magnetic sources (such as iron) from the background field that arises from imperfect shimming and variations in magnetic susceptibility of surrounding tissues (including air). Previous background removal techniques have limited effectiveness depending on the accuracy of model assumptions or information input. In this article, we report an observation that the magnetic field for a dipole outside a given region of interest (ROI) is approximately orthogonal to the magnetic field of a dipole inside the ROI. Accordingly, we propose a nonparametric background field removal technique based on projection onto dipole fields (PDF). In this PDF technique, the background field inside an ROI is decomposed into a field originating from dipoles outside the ROI using the projection theorem in Hilbert space. This novel PDF background removal technique was validated on a numerical simulation and a phantom experiment and was applied in human brain imaging, demonstrating substantial improvement in background field removal compared with the commonly used high-pass filtering method.

INTRODUCTION

The magnetic susceptibility of biomaterials generates a local magnetic field and provides a very important contrast mechanism in MRI, such as T₂^*-weighted imaging, susceptibility-weighted imaging (SWI) (1) and quantitative susceptibility mapping (QSM) (2–8). Recently, it has been reported that accurate QSM can be generated by combining information from magnitude and phase images (3). For appropriate phase masking in SWI and accurate susceptibility quantification in QSM (9), it is necessary to separate the local field in a given region of interest (ROI) from the background field. This background field arises from various sources, including imperfect shimming and magnetic susceptibility sources outside the ROI (both inside and outside the imaging volume). For example, in brain imaging, the air–tissue interfaces near the skull and various air cavities induce a strong background field variation extending deep into the brain. The background field is superimposed onto the local fields generated by venous blood, iron deposition and calcifications, impeding clear visualization of the local details in SWI and introducing errors in QSM.

Current background removal techniques assume that the local and background fields in a space spanned by the Fourier basis (10) or polynomial functions are separable (2,11,12), or require a priori knowledge of the spatial distribution of all background susceptibility sources (13,14). The assumption of the separability between local and background fields in a certain space is often violated, leading to erroneous estimation of local fields, and the results depend on the choice of the basis functions (11). In practice, the knowledge of the background susceptibility source surrounding a given ROI is often not fully available or sufficiently accurate, particularly when there are significant variations in susceptibility outside the imaging field of view (FOV), leading to a substantial residual background field that requires additional attention (13). A reliable background field removal method is the use of reference scans, in which an identical object but with the susceptibility sources removed is scanned to measure the reference background field (2,7). However, it is impractical or impossible to perform a reference scan in many in vivo situations.

Recently, we have described a method that effectively fits the background field to the field generated by dipole sources outside a certain ROI (3). This method was further confirmed by another group (15). In this article, we provide a detailed description and justification of this new approach to background field removal, which we term here the ‘projection onto dipole fields’ (PDF) method. We observe that the inner product of the field of a background dipole outside the ROI and the field of a local dipole inside the ROI is almost zero in the ROI, except for local dipoles near the boundary. This observation forms the foundation for the PDF method to differentiate the local and background fields. The performance of the PDF method was validated in a numerical simulation and a phantom experiment, and was applied to human brain MRI.

THEORY: APPROXIMATE DIPOLE FIELD ORTHOGONALITY AND PROJECTION THEOREM

For a given ROI, the local field f_L is defined as the magnetic field generated by the susceptibility distribution χ_L inside an ROI M, and the background field f_B is defined as the magnetic field generated by the susceptibility distribution χ_B in the region M̅, which is outside the ROI and inside a sufficiently large FOV. It should be noted that the background field extends into the ROI, just as the local field extends outside the ROI. For human MRI, tissue susceptibility satisfies |χ| ≪1, making the magnetic fields generated by human tissue susceptibility variation orders of magnitudes smaller than the main field. Taking this into account, the total magnetic field is written as:

$$\mathbf{f}={\mathbf{f}}_L+{\mathbf{f}}_B=\mathrm{d}\otimes [{\mathbf{\chi }}_L+{\mathbf{\chi }}_{\mathrm{B}}]$$ [1]

Here, the symbol ⊗ denotes convolution and d is the unit dipole field, which is the magnetic field created by a unit dipole at the origin with the Lorentz sphere correction (6,16,17).

Our proposed PDF method is to project the total field measured in the ROI onto the subspace spanned by all the background unit dipole fields. This was inspired by the projection theorem in Hilbert space (18), which we review briefly here. Let T be an inner product space spanned by all unit dipole responses {d_r|r ∈ M ∪ M̅}, where d_r denotes the magnetic field induced by a unit dipole located at r. Hence, the total field f ∈ T. The inner product between any f₁, f₂ ∈ T is defined as the sum of element-wise multiplication between f₁ and f₂ inside the ROI only. Following Equation [1], the background field component f_B is formed of basis functions {d_rB|r_B ∈ M̅}, which represent fields created by background unit dipoles. The subspace spanned by all the background unit dipole fields is then denoted as B. Similarly, the basis functions of the local field component f_L are {d_rL|r_L ∈ M} and the subspace spanned by all the local unit dipole fields is denoted as L. According to the projection theorem (18), argminf_B∈B‖f − f_B‖₂ has a unique value ${\mathbf{f}}_B^{*}$, and $\mathbf{f}-{\mathbf{f}}_B^{*}$ is orthogonal to B; if L⊥B, f − f_B=f_L is orthogonal to B, and so ${\mathbf{f}}_B^{*}$ obtained by the minimization is exactly f_B, the true background field. Therefore, we propose the PDF method that estimates the background field as:

$$\text{argmin}{\mathbf{\chi }}_{B\in \overline{M}}{\Vert \mathrm{f}\mathrm{d}\otimes {\mathbf{\chi }}_B\Vert }_2$$ [2]

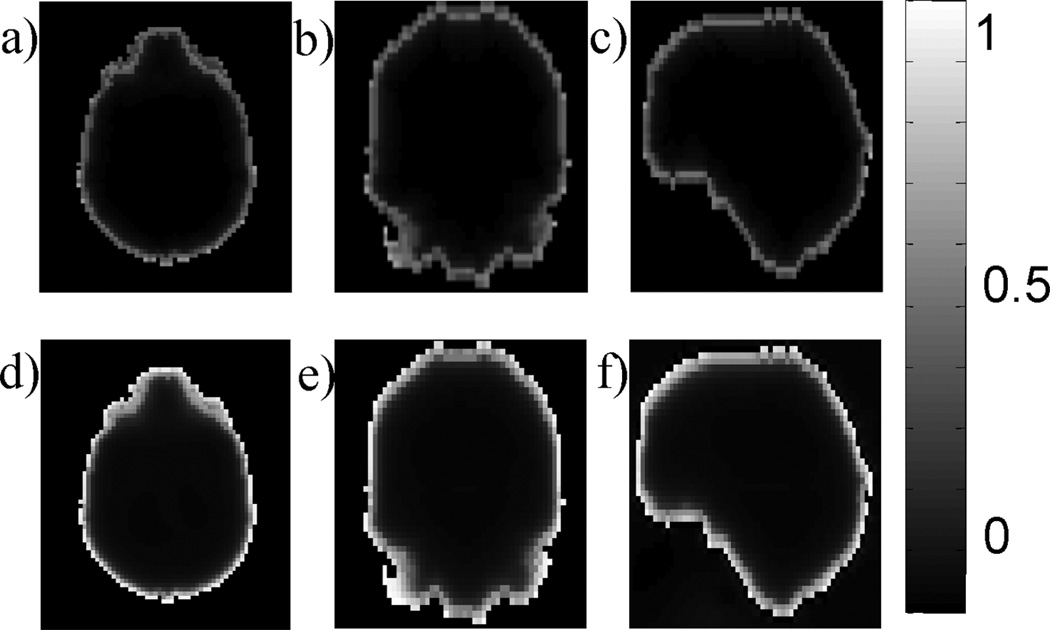
To justify the use of the projection theorem for removal of the background field in MRI, we evaluated the orthogonality assumption using a typical brain ROI segmented from an actual brain scan (detailed in the following in vivo brain scan section). Orthogonality requires that, for each given local unit dipole field, its inner product with any possible background unit dipole field is zero. Accordingly, we evaluated the correlation quantity c(r_L), defined as the maximum absolute normalized inner product between a given local field induced by a unit dipole at r_L ∈ M and any possible background unit dipole field:

$$0\le c({\mathit{r}}_L)={\text{max}}_{{\mathit{r}}_B\in \overline{M}}|<{\mathbf{d}}_{{\mathit{r}}_{\mathrm{L}}},{\mathbf{d}}_{{\mathit{r}}_{\mathbf{B}}}>/({\Vert {\mathbf{d}}_{{\mathit{r}}_{\mathrm{L}}}\Vert }_2\times {\Vert {\mathbf{d}}_{{\mathit{r}}_{\mathrm{B}}}\Vert }_2)|\le 1$$ [3]

This maximum absolute normalized inner product c(r_L) is almost zero [c(r_L) ≪ 0.1], except for locations within five voxels from the boundary, as demonstrated in the realistic brain ROI (Fig. 1a–c). Therefore, the orthogonality between the background field subspace and the local field subspace may be considered a good approximation.

Figure 1.

Approximate orthogonality between dipole fields. For each local dipole inside the region of interest (ROI), the maximum absolute normalized inner product between its field and any background unit dipole field is plotted in axial (a), coronal (b) and sagittal (c) sections of a typical ROI in human brain MRI (same as in Fig. 4 with the resolution reduced to a 80 × 60 × 46 matrix for practical computing time). The inner product values are close to zero at most voxels, except for those near the boundary. The relative error (see text for definition) for each local dipole is shown in the axial (d), coronal (e) and sagittal (f) sections.

Error analysis

The approximate orthogonality does not guarantee that the local field will be perfectly recovered by the PDF method, but it does predict that large maximum absolute normalized inner products are likely to lead to greater errors in the estimated local field. To demonstrate the spatial dependence of error, the PDF method was performed on a simulated total field consisting of a single local unit dipole field d_rL, r ∈ M and a zero background field to generate an estimated background field f^*_b,rL. The true background field is zero and, therefore, the PDF method should ideally not remove any part of the local field. Any residual f^*_b,rL represents an error in the background field estimated by the PDF method, which is quantified by calculating the ratio between the norms of the error (f^*_b,rL − 0) and d_rL over the ROI: E(r_L) = ‖f^*_b,rL‖₂/‖d_rL‖₂. This relative error is visualized for every voxel r inside the ROI in Fig. 1d–f. It is observed that the error is low (E < 0.1) for dipoles located at most of the voxels in the ROI, and increases for dipoles near the boundary of the ROI.

METHODS AND MATERIALS

PDF algorithm implementation

The computation of the total field f from MR phase data was based on phase data from multiple echo data (2), followed by a magnitude image-guided unwrapping algorithm (19). To correct for a large background field from potentially poor shimming, zeroth and first-order spherical harmonic terms in the field expansion were estimated and removed from the measured total field using a weighted least-square minimization (2,11). The corrected total field f was then used in all the following background removal methods.

We accounted for spatial variations of noise in the MR field maps by adding a weight to Equation [2] to normalize the noise to a normal distribution N(0,1). The weight w was derived from magnitude images across multiple echoes (5). The resulting minimization becomes:

$${{\mathbf{\chi }}_B}^{*}={\text{argmin}}_{\mathbf{\chi }B}{\Vert \mathbf{w}(\mathbf{f}-\mathbf{d}\otimes {\mathbf{\chi }}_B)\Vert }_2$$ [4]

where the norm ‖·‖₂ in Equation [4] is again calculated only over the ROI M, which may be defined using image segmentation, and the dot symbol indicates point-wise multiplication between vectors.

We let N be the number of voxels in the MR image dataset, and expressed the measured total field f and the total susceptibility distribution χ as N × 1 column vectors. Let I be an N × N identity matrix and M an N × N diagonal matrix, where the diagonal elements are equal to unity when they correspond to voxels inside the ROI and are equal to zero otherwise. Then, the background susceptibility was written as χ_B=(I−M) χ. D denotes an N × N matrix representing the convolution with the unit dipole field d, and W denotes an N × N diagonal matrix formed by placing the weighting w on the diagonal. With this notation, the minimizer in Equation [4] was found by solving (18):

$$\mathbf{M}\mathbf{W}\mathbf{D}(\mathbf{I}-\mathbf{M})\mathbf{\chi }=\mathbf{M}\mathbf{W}\mathbf{f}$$ [5]

In a typical high-resolution three-dimensional brain MRI dataset with N > 10⁶ voxels, D has more than 10¹² elements, which is impossible to explicitly form and store in computer memory. Therefore, a conjugate gradient (CG) algorithm was used in which the convolution is efficiently calculated in the Fourier domain (13,14,20,21). The forward system on the left-hand side of Equation [5] was made positive semi-definite by applying the Hermitian conjugate of the matrix A = MWD(I−M) to both sides of Equation [5] (22):

$${\mathbf{A}}^H\mathbf{A}\mathbf{\chi }={\mathrm{A}}^H\mathbf{\beta }$$ [6]

where β = MWf. The CG iteration was stopped when the norm of the residual was smaller than 50% of the expected noise level ‖ A^HMu‖₂, where u was a column vector containing ones. Once χ had been estimated, the background field was calculated as:

$${{\mathbf{f}}_B}^{*}=\mathbf{D}{{\mathbf{\chi }}_B}^{*}=\mathbf{D}(\mathbf{I}-\mathbf{M}){\mathbf{\chi }}^{*}$$ [7]

and was subtracted from the measured total field f to estimate the local field ${\mathbf{f}}_L^{*}$.

Comparison with high-pass filtering (HPF)

In this study, the PDF method was compared with the HPF method that has been commonly used in the literature. In HPF, a three-dimensional Hann window low-pass filter with a kernel size of 32 × 32 × 32 was applied to the complex MRI data when one echo was used (10). When multiple echoes were acquired, the low-pass filter was applied to a reconstructed complex MRI dataset formed by setting the magnitude equal to that of the first echo and the phase equal to the unwrapped total field normalized to [−π,π). The background field was estimated from the phase of the resulting low-pass-filtered complex image. All the algorithms were implemented on a personal computer with Intel^® Core™ i7 CPU, 6-GB memory using MATLAB (2009a) code (MathWorks, Natick, MA, USA).

Validation of background field removal methods

The reference scan method (2,7) can be used to estimate the local field without any algorithmic bias in both numerical simulation and phantom experiments, and served as the gold standard for the evaluation of any background field removal method, including the proposed PDF method.

Numerical simulation

An ellipsoid whose radii were 40, 40 and 54 voxels was created in a 160 × 160 × 160 matrix to imitate the shape of a head. Five smaller ellipsoids were created inside the head-shaped ellipsoid to simulate mastoid cavities, ethmoid and maxillary sinuses. The radii of these ellipsoids ranged from 10 to 15 voxels. Three cylinders with a radius of two voxels and a length of 20 voxels were created to simulate veins and were placed inside the head-shaped ellipsoid along the x, y and z directions, respectively. A sphere with a radius of five voxels was created in the mid-brain to mimic a hemorrhage. Complex MRI data were simulated from this geometry. A uniform intensity of 100 was assigned to the ‘head’ region, and the ‘air’ cavities were assigned a value of zero. Susceptibility in the ‘head’ region was chosen to be the zero reference, the susceptibility of ‘air’ was 9.4 ppm (2), the vessels were 0.3 ppm (9) and the hemorrhage was 1.2 ppm (3). The total field was calculated using a forward calculation (14,20,21). The reference background field was obtained by repeating the total field calculation in the same numerical phantom, but with the vessels and hemorrhage removed. The phase image was calculated from the total field by assuming TE = 30 ms and a scanner field strength B₀ equal to 1.5 T. Zero-mean Gaussian white noise with a standard deviation of unity was added to both the real and imaginary parts of the complex images independently. Noise was not added to the reference scan. Finally, an 80 × 80 × 80 volume in the upper middle part was cropped from the 160 × 160 × 160 matrix to emulate a prescribed FOV that narrowly encompasses the brain (Fig. 2a–d). The 80 × 80 × 80 matrix was then used for subsequent simulations. The total field, the reference background field and the reference local field (obtained by subtracting the reference background field from the total field) are shown in Fig. 2a–c. An ROI M was chosen as the ‘air-free’ region (white regions in Fig. 2d) and M̅ was the ‘air’ region (black regions in Fig. 2d). Estimated background fields were then calculated using both techniques, and subtracted from the total field to generate the estimated local fields. For quantitative comparison, relative errors of the background field were calculated to assess the goodness of the background removal. Relative errors were calculated by taking the norm of the difference between the estimated background field and the reference background field, and then normalized by the norm of the reference background field. The norms were calculated inside the ROI only. The attenuation of the local field as a result of the background removal processes was calculated as one minus the ratio between the norm of the estimated local field and the norm of the reference local field. The norms were calculated inside a manually defined rectangular volume comprising the susceptibility sources of interest to capture the local attenuation of the local field, whilst ignoring the amplification elsewhere, e.g. near the boundary of the ROI.

Figure 2.

Validation in numerical simulation. The numerical brain phantom is shown in a prescribed field of view (FOV) in coronal view with the simulated total field (a), the corresponding reference background field (b), the reference local field with annotated hemorrhage (H) and veins (V) (c) and the defined region of interest (ROI) (white area) (d). The projection onto dipole fields (PDF) method was used to estimate the background susceptibility distribution (e). The PDF-estimated background field (f), the PDF-estimated local field (g) and the corresponding difference from the reference (h) showed substantial improvement over the high-pass filtering (HPF) method (i, j and k, corresponding to HPF-estimated background field, HPF-estimated local field and difference from the reference, respectively). The relative errors were 23.51% and 3.21% for the HPF and PDF methods, respectively. The black box in (a) indicates the region in which the attenuation of the local field was measured.

Phantom MRI experiment

A cylindrical water phantom (diameter, 10 cm; height, 8.5 cm) was constructed. Three vials (diameter, 1.2 cm; height, 6 cm) with 1% concentrated gadolinium (Gd; Magnevist, Berlex Laboratories, Wayne, NJ, USA) were placed vertically in the water container to mimic three vessels. A waterproof plastic air box (2.5 × 2.5 × 1.5 cm³) was glued to the bottom of the water container to imitate an air cavity. The phantoms were scanned on a 1.5-T clinical MRI scanner (General Electric Excite HD; GE Healthcare, Waukesha, WI, USA) using a 5-in surface coil for signal reception. A dedicated three-dimensional gradient-echo sequence was designed to sample at different TEs in an interleaved manner. The scanning parameters were as follows: FOV, 15 × 15 × 10 cm³; matrix size, 150 × 150 × 100; bandwidth, ±62.50 kHz; TR = 30 ms; flip angle, 30°. Four TEs (1.7, 2.2, 4.2 and 14.2 ms) were used to achieve a balance between the precision of the estimated total field and the total scan time. After this scan had been completed, the three vials were removed from the water phantom. The scan was repeated with identical imaging parameters to acquire a reference background field. The scanner gradient shimming was kept constant between the two scans. The background air region without MR signal was segmented as M̅ (background black region in Fig. 3d), and the rest was denoted as M. Noise was estimated from M̅. Similar to the numerical simulation, estimated background fields were compared qualitatively and quantitatively with the reference background field.

Figure 3.

Validation in phantom MRI. Acquired three-dimensional data are shown in a coronal section with the total field (a), the corresponding reference background field (b), the reference local field (c) and the magnitude image (d) [with the large circular disk as the region of interest (ROI)]. The projection onto dipole fields (PDF) method was used to estimate the background susceptibility distribution (e). The PDF-estimated background field (f), the PDF-estimated local field (g) and the corresponding difference from the reference (h) showed substantial improvement over the high-pass filtering (HPF) method (i, j and k, corresponding to HPF-estimated background field, HPF-estimated local field and the difference from the reference, respectively). The relative errors were 18.36% and 5.53% for the HPF and PDF methods, respectively. The black box in (a) indicates the region in which the attenuation of the local field was measured.

In vivo brain scan

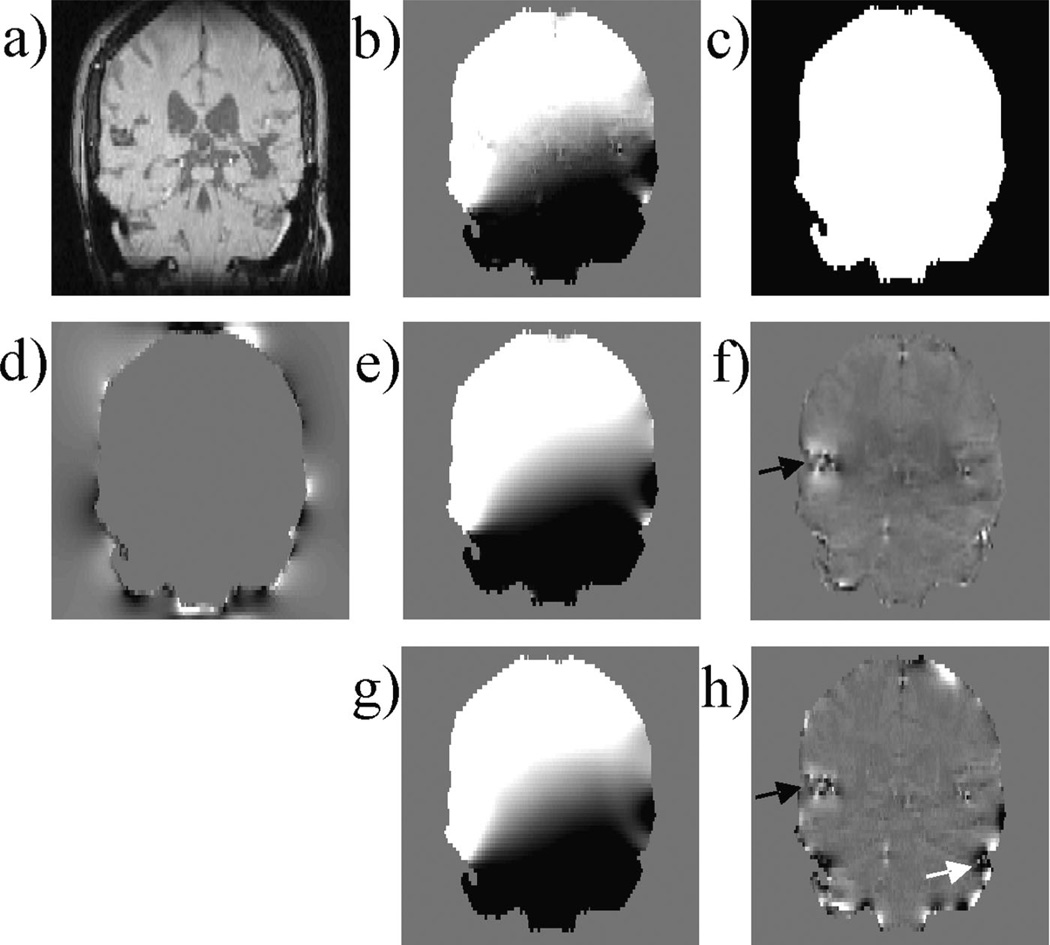
This study was approved by our Institutional Review Board. In vivo MRI was performed on 15 patients with histories of hemorrhagic stroke on a 3-T clinical MRI scanner (General Electric Excite HD; GE Healthcare). Standardized data acquisition and data processing were performed on all patients in the following manner. Data were acquired using an eight-channel head coil and a multiple echo spoiled gradient-echo sequence with three-dimensional flow compensation. The imaging parameters were as follows: TE = 3.5, 7, 10.5, 14, 17.5, 21 ms; TR = 40 ms; slice thickness, 2 mm; flip angle, 15°; number of slices, 70 axially through the brain. The imaging matrix was 240 × 180 × 70, with a pixel bandwidth of 520 Hz per pixel and a FOV of 24 × 18 × 14 cm³. The phase images were used to fit the total field. The brain region was segmented and denoted as the ROI M, and the remaining regions in the imaging volume were considered to comprise M̅. Estimated background fields were obtained and removed using both techniques. The three-dimensional brain data was reformatted to coronal sections for inspection. To quantitatively assess the improvement of the PDF method, field contrasts were calculated from PDF and HPF processed field maps. Rectangular volumes immediately superior to the hemorrhages and volumes on the right of the hemorrhages were drawn, and the differences between the mean values insides these two regions were calculated. These two regions fall inside two lobes of the dipole field that have opposite sign. The resulting contrast measurements were compared between the HPF and PDF methods over the 15 patients using a two-tailed paired t-test with a significance level p of 0.01.

RESULTS

The results of the numerical simulation are shown in Fig. 2. The PDF method successfully removed the background field, leaving the local fields from ‘veins’ and ‘hemorrhage’ intact, leading to the distinct dipole pattern in the local field (Fig. 2g). There was little discernible visual difference between the local field estimated by the PDF method and the reference local field (Fig. 2h). In contrast, HPF left substantial residual background field in regions close to the ‘ethmoid sinus’ and ‘mastoid cavities’ (Fig. 2j), and removed indiscriminately the slowly varying component of the field induced by the ‘hemorrhage’ (Fig. 2i, k, arrows). The relative errors between the estimated and reference background fields were 23.51% and 3.21% for the HPF and PDF methods, respectively, and the attenuations of the local fields were 41.1% and 1.2%, respectively. The CG algorithm of the PDF method converged with 10 iterations in 0.7 s.

The results for the phantom experiment are shown in Fig. 3. The estimated background field by the PDF method was in good agreement with the reference background field (Fig. 3h), whereas the estimated background field by the HPF method contained a substantial amount of the local field (Fig. 3i, k, arrow). The relative errors between the estimated and reference background fields were 18.36% and 5.53% for the HPF and PDF methods, respectively, and the attenuations of the local fields were 43.0% and 3.2%, respectively. The CG algorithm of the PDF method converged with 43 iterations in 17.0 s.

Hemorrhages were found in all patients, with an example illustrated in Fig. 4. Compared with the estimated local field by the PDF method (Fig. 4f ), the estimated local field by the HPF method contained substantially more field variation at the periphery of the brain ROI, which might be interpreted as high-spatial-frequency residual background field because of the air–tissue interface (Fig. 4h, white arrow). The local fields arising from the hemorrhagic lesion estimated by the PDF method were stronger than those estimated by the HPF method (black arrows), resulting in a better contrast in the field maps between the hemorrhage and the surrounding tissue by the PDF method. Quantitatively, the PDF-processed image showed higher field contrast than the HPF-processed image for each of the 15 cases (21 ± 8Hz versus 12 ± 5 Hz, p < 0.001).

Figure 4.

Patient brain imaging. Acquired three-dimensional data are shown in a coronal section with the magnitude image (a), the total field (b) and the region of interest (ROI) (white region) (c). (d) Estimated background susceptibility distribution using the projection onto dipole fields (PDF) method. (e, f) Background and local fields estimated by the PDF method. (g, h) Background and local fields estimated by the high-pass filtering (HPF) method. The estimated local field generated by the PDF method provides better depiction of the hemorrhage (black arrows), with a higher visual contrast between the hemorrhage and the surrounding tissue and with less artifacts (white arrow).

DISCUSSION

Our preliminary data demonstrate that this nonparametric background removal technique, PDF, is successful in removing the background field, whilst allowing an accurate estimation of the local field. Compared with the HPF method, the PDF method estimates the background fields with smaller errors and results in less attenuation of the local field with respect to the reference scan method in a numerical simulation and a phantom experiment. The PDF method provides superior local field maps for in vivo brain imaging with less artifacts near tissue–air boundaries and more contrast in local fields induced from different brain structures.

The HPF method performs background removal using the Fourier basis. The HPF method does not distinguish the source of the slowly varying components of the total field, either from the background or from the ROI. Hence, HPF suffers when there are overlaps between the Fourier spectra of the background and local fields. In general, the background field may contain high-spatial-frequency components and the local field may contain low-spatial-frequency components. Consequently, the HPF method may fail to remove the high-spatial-frequency components of the background field near air–tissue boundaries in brain imaging (Fig. 4h, white arrow), and may erroneously remove the low-spatial-frequency components of the local field (as demonstrated in Fig. 3i, where the uniform local field inside the vials and the slowly varying local fields outside the vials were removed). Therefore, the HPF method might not be suitable for the visualization of local fields of large brain structures, such as basal ganglia or hemorrhage, and brain structures near the brain ROI boundary. In addition, it has also been convincingly demonstrated that the results of the HPF method depend on the choice of the kernel size (10,11,15). An increase in the kernel size can improve the removal of the unwanted background field, but at the cost of attenuating the local field.

The advantage of the PDF method over the HPF method lies in the fact that there is substantial separation in the dipole field representations of the background and local fields, as measured by their approximate orthogonality (Fig. 1). According to the dipole equation (17), the strength of a dipole field decays on the order of r³, where r is the distance to the dipole, so that the impact of the dipole is strong within its immediate vicinity and diminishes rapidly. Hence, if a local and a background dipole are far away in space, their spatial overlap, as measured by the normalized inner product, is very small. The separation between local and background fields may be fundamentally explained by the Maxwell equation, which states that the field generated by the background dipoles is a harmonic function inside the ROI, but the field generated by the local dipoles is nonharmonic (23). Therefore, the background and local fields may be separable in an ideal harmonic function space. In the PDF method, the estimated background field generated by background dipoles is guaranteed to be a harmonic function. In comparison, the estimated background field by the HPF method may violate the harmonic condition. Recently, Schweser et al. (24) presented a background removal technique that exploits the mean value property of harmonic functions. A full comparison between this method and the proposed PDF method is beyond the scope of this article, but is the subject of ongoing research. The projection of the measured field on to a subspace generated by dipoles was also used by Wharton et al. (15), where 300 dipoles were manually positioned around the ROI.

This approximate orthogonality property provides a reasonable separability between the background and local fields, as demonstrated in the experimental results reported here. The PDF method’s applicability to general MRI may be confirmed by evaluating the correlation quantity (Equation [3]) for a desired ROI shape numerically. This separability holds very well for the interior of the ROI (Fig. 1), making it very useful for brain imaging, where most of the strong susceptibility sources caused by brain iron deposits tend to be located deeper inside the brain. The PDF method also performed better than the HPF method (Figs 2h, k, 3h, k, 4f, h) near the ROI boundary, where the PDF performance may be further improved by means such as dilating the ROI by a few voxels to convert voxels near the original ROI boundary into interior points of the enlarged ROI.

Because a given magnetic field may arise from many susceptibility distributions as a result of the nontrivial null space of the dipole kernel convolution (25), the intermediate background susceptibility distribution estimated during the PDF process may not correspond to the actual susceptibility distribution outside the ROI (Figs 2e, 3e, 4d). However, this does not affect the final calculation of the background field, which is our sole concern here. For instance, the Fourier aliasing in Fig. 2e (visible as the two white regions near the top of the FOV) is not a problem: its presence effectively modeled the background field at the bottom of the FOV that was, in reality, caused by susceptibility sources further below the FOV.

CONCLUSION

In this study, we have proposed a nonparametric technique that removes the background field from the measured total field in an ROI by projecting the total field inside the ROI to the fields generated by dipoles outside the ROI. This novel PDF method was validated in a numerical simulation and phantom study, and was demonstrated to be applicable for in vivo human brain imaging.

Abbreviations used

CG

conjugate gradient

FOV

field of view

HPF

high-pass filtering

PDF

projection onto dipole fields

QSM

quantitative susceptibility mapping

ROI

region of interest

SWI

susceptibility-weighted imaging