Revision surgery is overestimated in hip replacement

Abstract

Objectives

The Kaplan-Meier estimation is widely used in orthopedics to calculate the probability of revision surgery. Using data from a long-term follow-up study, we aimed to assess the amount of bias introduced by the Kaplan-Meier estimator in a competing risk setting.

Methods

We describe both the Kaplan-Meier estimator and the competing risk model, and explain why the competing risk model is a more appropriate approach to estimate the probability of revision surgery when patients die in a hip revision surgery cohort. In our study, a total of 62 acetabular revisions were performed. After a mean of 25 years, no patients were lost to follow-up, 13 patients had undergone revision surgery and 33 patients died of causes unrelated to their hip.

Results

The Kaplan-Meier estimator overestimates the probability of revision surgery in our example by 3%, 11%, 28%, 32% and 60% at five, ten, 15, 20 and 25 years, respectively. As the cumulative incidence of the competing event increases over time, as does the amount of bias.

Conclusions

Ignoring competing risks leads to biased estimations of the probability of revision surgery. In order to guide choosing the appropriate statistical analysis in future clinical studies, we propose a flowchart.

Article focus

• A comparison of statistical approaches to estimate the probability of revision surgery in hip replacements

Key messages

• The Kaplan-Meier estimator will overestimate the probability of revision surgery when competing risks are present

• When estimating the probability of revision surgery, the incidence of any competing events that have occurred must be assessed. If so, a competing risk approach would give a more accurate estimate of the probability of revision surgery

Strengths and limitations

• Strength: the comparison of statistical approaches allows a direct estimation of the amount of bias, which is introduced by disregarding competing events

• Limitation: the amount of bias depends on the cumulative incidence of the competing event

Introduction

One of the most important outcome measures in orthopaedic surgery is the time to a certain event. In joint replacement surgery, for instance, the time to revision surgery is seen as the most important determinant of the clinical success of any prosthesis. Techniques from the field of survival analysis, such as the Kaplan-Meier estimator,¹ have been used to estimate time to revision surgery since the 1980s.^2,3 The time from implantation of a prosthesis until a specified event of interest is used in survival analyses. An important advantage of survival analyses is that these techniques allow analyses with “censored data”, i.e. data concerning patients for which revision surgery has not yet taken place within the study period.¹ If the endpoint of interest has not yet occurred at the end of the observation window, the event time is censored. The probability of revision surgery can be estimated with the Kaplan-Meier estimator at any specific point in time.

At first glance, the Kaplan-Meier estimator seems ideal for orthopaedics since analyses can be performed before revision surgery has occurred in all patients. However, this method makes a number of assumptions.^4,5 The Kaplan-Meier estimator is specifically developed for studies with a single time to a certain event, which in turn is able to be censored. The assumption of independence of the time to time to event and the censoring distributions is of critical importance. The probability of the event of interest is estimated by assuming that patients whose time is censored have the same probability of revision at any later time. When estimating the time to revision surgery, often more types of events play a role, which may prevent the event of interest from occurring. For instance, revision of an implant may be unobservable because the patient dies. In this particular case, death is a competing event, which poses a competing risk – a risk that may be high, especially in studies with long-term follow-up.

The Kaplan-Meier method of censoring patients who experience a competing event is not ideal when the estimation of the probability of the event of interest is the goal, since this implicitly assumes that the event of interest still could occur after the time point at which censoring occurred.^6-8 If a patient does experience a competing event, the event of interest can no longer occur: therefore the potential contribution to the estimate from this patient should become zero. The probability of the event of interest must be estimated by taking into account the probability of the competing events; ignoring the competing risks leads to a biased estimation of the probability of the event of interest (see Appendix 1 of the Supplementary Material for more technical details).^5,9-11

In this study we compare the Kaplan-Meier estimator with the cumulative incidence estimator in a competing risk setting and show how the level of bias introduced by violating critical assumptions of the Kaplan-Meier estimator. We propose a simple algorithm to help select the appropriate data analysis technique to estimate the probability of revision surgery in future studies. In order to illustrate these statistical methods, developed by Kaplan and Meier¹ and Bernoulli,^10,11 we used data from a previous cohort of acetabular revision patients.¹²

Materials and Methods

In our published cohort study, 62 acetabular revisions were performed in 58 patients between January 1979 and March 1986, at the Radboud University Medical Center in Nijmegen, The Netherlands.¹² There were 13 men and 45 women with a mean age at revision of 59.2 years (23 to 82). Revision was undertaken using impacted morsellised bone grafts and a cemented acetabular component in all cases. They were followed prospectively with yearly clinical and radiological assessments.

Competing risks versus Kaplan-Meier

Competing risks are applied to situations where more than one competing endpoints are possible. Their competing in that one event will preclude the other occurring. In our situation there are two different endpoints: revision surgery and death. The occurrence of death prevents the occurrence of the event of interest, namely revision surgery. The competing risks model can be represented as an initial state (alive after initial revision surgery) and two different competing endpoints: revision surgery and death. We are interested in the probability of revision surgery (event of interest) in the presence of the competing event of death – which clearly prevents the occurrence of revision.

The Kaplan-Meier estimator is often used to estimate this probability. However, in this model the competing cause endpoints (i.e., death) are treated as censored observations. If a patient has experienced death, he or she has zero probability of experiencing the event of interest, and this must be considered in the model.

The cumulative incidence estimator is used to estimate the probability of each competing event. The cumulative incidence function of cause k is defined as the probability of failing from cause k before time t. Here we are interested in the cumulative incidence function of revision surgery in the presence of death.

Statistical analysis

All analyses concerning competing risks models have been performed using the mstate library^13,14 in R.¹⁵ For technical details concerning the software, see de Wreede et al.^13,14

Results

At a mean of 23 years (20 to 25) after surgery, no patients were lost to follow-up. A total of 13 hips in 12 patients had undergone revision surgery, and 30 patients (33 hips) had died of causes unrelated to their hip surgery (Table I).

Table I.

Details of the 62 consecutive acetabular revisions

	Acetabular revisions	Patients
Total	62	58
Lost to follow-up	0	0
Died without further surgery	33	30
Revisions	13	12
Septic loosening	2
Aseptic loosening	8
Mismatch during femoral revision	1
Wear	2

The estimated survival rates with revision surgery as the endpoint obtained by applying the Kaplan-Meier method at five, ten, 15, 20 and 25 years were, respectively, 98% (95% confidence interval (CI) 95 to 100), 93% (95% CI 86 to 99), 81% (95% CI 67 to 95), 75% (95% CI 57 to 93) and 66% (95% CI 49 to 83).

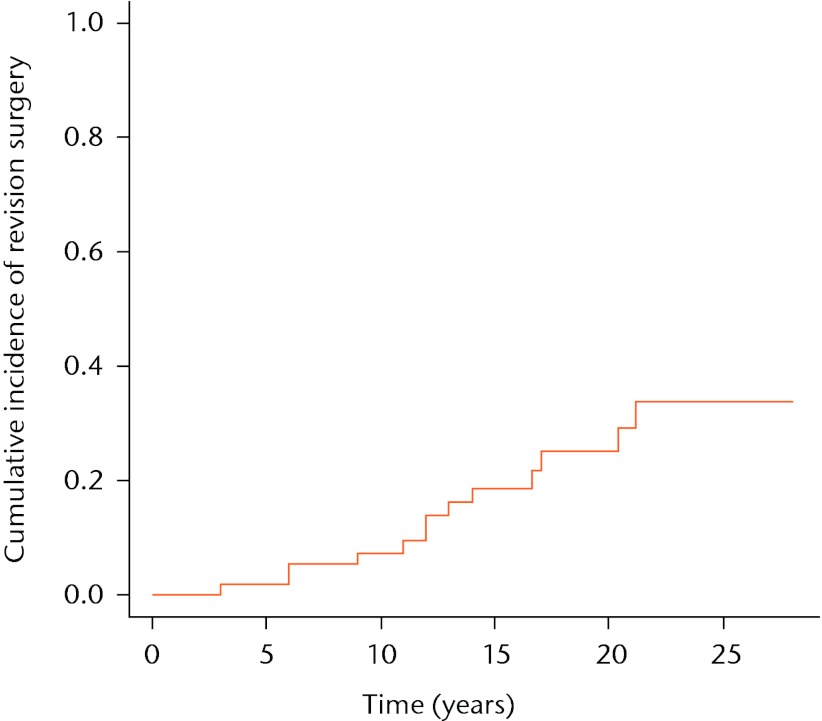
The estimated risk of revision surgery (1 – estimated survival of the implant) obtained with the Kaplan-Meier estimator, is shown in Figure 1. These estimated risks of revision surgery were therefore 2%, 7%, 19%, 25% and 34% at five, ten, 15, 20 and 25 years, respectively.

Fig. 1.

Kaplan-Meier curve showing the cumulative incidence of revision surgery. The risk of revision surgery in the Kaplan-Meier approach can be represented as: risk at time t = 1 – survival at time t.

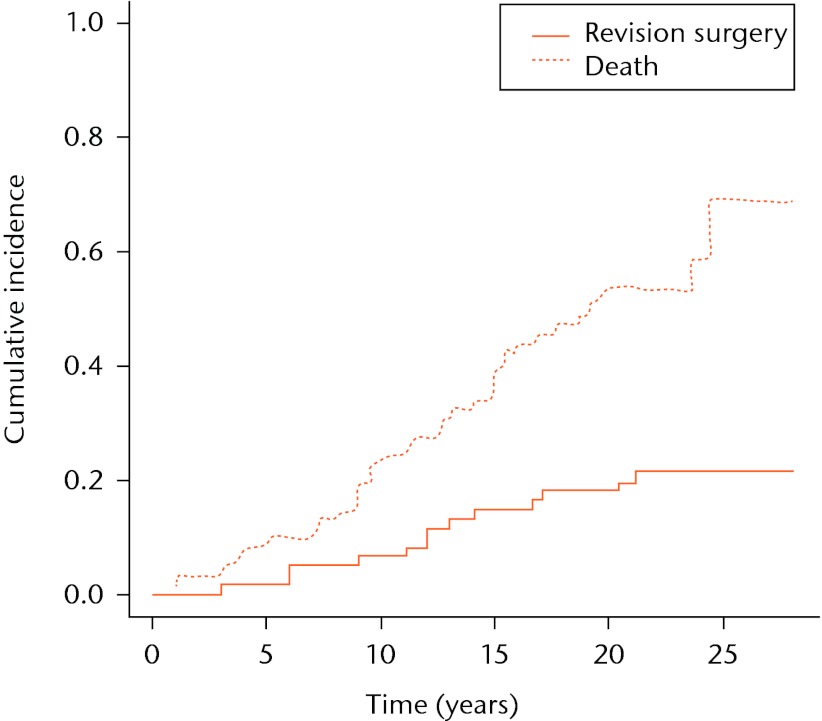
The cumulative incidence estimators for both competing events, i.e. revision surgery and death, are shown in Figure 2. The cumulative incidence estimator of revision surgery by the competing risks method at five, ten, 15, 20 and 25 years is 2%, 6%, 15%, 18% and 21%, respectively. The cumulative incidence of death represents the probability of dying before revision surgery. If death occurs first, the observation will not be considered censored in the competing risk approach (in contrast to the Kaplan-Meier approach), but it will contribute to the competing event of death.

Fig. 2.

Cumulative incidence of implant failure and death in a competing risk setting. The graphs represent the cumulative incidence of death and revision surgery in a competing risk setting.

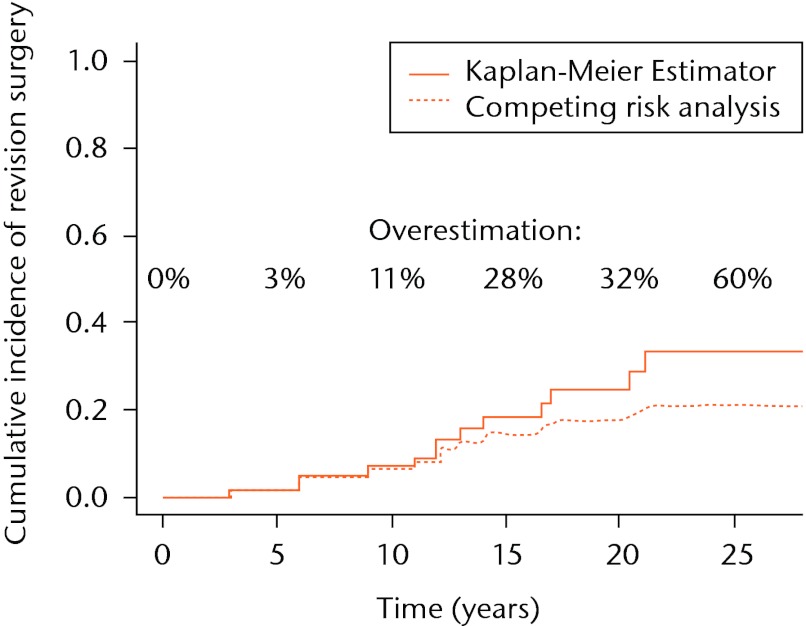
In the dataset described above, the Kaplan-Meier model can be seen to overestimate the probability of revision surgery by 3%, 11%, 28%, 32% and 60% at five, ten, 15, 20 and 25 years, respectively (Fig. 3).

Fig. 3.

Comparison of cumulative incidence of revision surgery estimated with the Kaplan-Meier estimator and the competing risks method. The discrepancy between the lines represents the bias, which is introduced by erroneous usage of the Kaplan-Meier estimator.

Discussion

In the current orthopaedic literature, the Kaplan-Meier estimator is an accepted standard in estimating the probability of revision surgery in cohort studies of any type of joint replacement. In the absence of competing risks, this method is valid. However, in the presence of competing risks, the Kaplan-Meier estimator overestimates the probability of revision surgery. In our example, the probability of revision surgery is overestimated by 60% at a follow-up of 25 years. In the Kaplan-Meier approach failures from the competing causes are treated as censored observations. Individuals who will never be revised because they have died, are censored and thus treated as if they still could be revised. In other words, the Kaplan-Meier estimator allows patients to be revised after they have died. Clearly, this results in an incorrect or biased estimate of the actual probability of revision surgery at that specific time point.

When competing risks are absent (i.e., the competing event death has not occurred), the Kaplan-Meier estimator gives a valid estimation of the probability of revision surgery. However, in our example involving a long follow-up, competing events such as death do occur frequently. Also, it can be seen from our dataset that the first patient died as early as one year after surgery (Fig. 2). By five years after the initial surgery, a total of six patients had died, compared with only one patient who had undergone revision surgery, resulting in a 3% overestimation of the probability of revision surgery (Fig. 3). In other words, the hazard of the competing events is considerable, leading to an overestimation of the revision surgery probability, even at mid-term follow-up.

In this paper a competing risks model has been applied to a cohort where only two competing events are present. However, in other clinical situations, more competing events can occur. Consider estimating the probability of revision surgery due to a specific event, for instance the probability of revision surgery due to recurrent dislocations. In this situation, there are three competing events: revision surgery for recurrent dislocations, revision surgery for any other reason and death of a patient. The competing risk model can easily be extended to deal with another competing event.

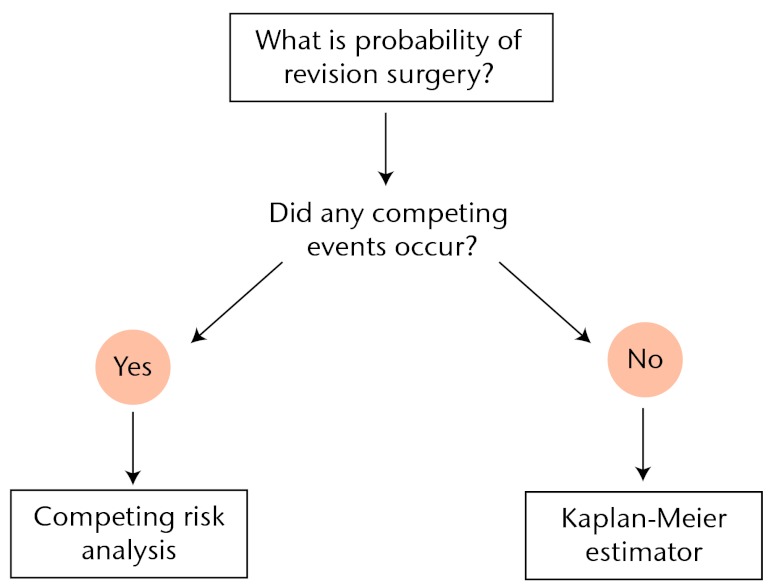
From a statistical point of view, competing risk analysis should be used whenever competing risks are present. In order to aid in deciding which analysis should be used to estimate the probability of revision surgery in future clinical studies, we propose a simple algorithm (Fig. 4). Every clinical study that investigates the probability of revision surgery should address the occurrence of competing events. When no competing events have occurred, the Kaplan-Meier estimator of revision surgery will be valid. However, whenever any competing event occurs, the Kaplan-Meier estimator will introduce bias. The resulting bias is greater when the “competition” is heavier, i.e. when the hazard of the competing events is larger. See Appendix 2 of the Supplementary Material for a concise summary of necessary variables to perform a competing risk analysis.

Fig. 4.

Algorithm detailing the appropriate data analysis technique to estimate the probability of revision surgery. The possibility and actual occurrence of competing events should be assessed in order to determine the appropriate data analysis technique.

Recently, minimal clinically important differences (MCIDs) have gained attention in the literature.^16-18 Using MCIDs, patients can be classified as responders or non-responders to a particular therapy. Theoretically, one could investigate the time to a MCID after joint replacement, using MCIDs in health-related quality of life (HRQoL). However, contrary to the occurrence of revision surgery or the first occurrence of a complication,¹⁹ which can be assessed over a time period, whether or not a patient has attained a MCID in HRQoL is typically measured using a questionnaire at a specific point in time. Neither the Kaplan-Meier estimator nor a competing risk model is an appropriate approach, unless the assessment of the occurrence of an MCID is repeated at small time intervals. The competing risk analysis can be performed using the mstate library^13,14 in R.¹⁵ R and the mstate package are both freely available at The R Project for Statistical Computing and The Comprehensive R Archive Network.

Funding Statement

None declared