Nonparametric Bayes Modeling of Multivariate Categorical Data

Abstract

Modeling of multivariate unordered categorical (nominal) data is a challenging problem, particularly in high dimensions and cases in which one wishes to avoid strong assumptions about the dependence structure. Commonly used approaches rely on the incorporation of latent Gaussian random variables or parametric latent class models. The goal of this article is to develop a nonparametric Bayes approach, which defines a prior with full support on the space of distributions for multiple unordered categorical variables. This support condition ensures that we are not restricting the dependence structure a priori. We show this can be accomplished through a Dirichlet process mixture of product multinomial distributions, which is also a convenient form for posterior computation. Methods for nonparametric testing of violations of independence are proposed, and the methods are applied to model positional dependence within transcription factor binding motifs.

1. INTRODUCTION

Our goal is to develop methods for Bayesian nonparametric modeling of multivariate unordered categorical data. The application that motivated this work is the modeling of dependence of nucleotides within a transcription factor binding motif, which is a short DNA sequence involved in gene regulation. Let x_i = (x_i1, …, x_ip)′ denote a sequence of nucleotides within positions 1, …, p of a known motif of interest. We let x_ij ∈ {1, …, d_j}, for d_j = d = 4, with values 1, 2, 3, 4 corresponding to the A, C, G, T nucleotides, respectively. In the motif application, the most common model for x_i is the product-multinomial distribution, which characterizes the elements of x_i as independent draws from multinomial distributions having a position-specific weight matrix (Lawrence and Reilly 1990; Liu 1994; Liu, Neuwald, and Lawrence 1995). However, experimental data suggest independence is often violated (Bulyk, Johnson, and Church 2002; Tomovic and Oakeley 2007).

Barash et al. (2003) proposed using a Bayesian network (BN). Unless p is small, the number of possible BNs is so large that it is only feasible to visit a small proportion of the models. Even computationally expensive search algorithms can miss the best models. In large model spaces, there are typically many BNs that are consistent with the data, so the best BN according to any criteria is very unlikely to be the true model. In addition, the selected BN will be sensitive to the criteria chosen for inclusion of an edge, and there is a tendency for overfitting in large networks due to the massive number of potential edges. For a recent article developing an efficient recursive method for BN search, refer to Xie and Geng (2008). Zhou and Liu (2004) noted that the Barash et al. (2003) approach is very time consuming to implement and is subject to problems in prior choice and overfitting, motivating a simpler model based on pairs of correlated positions. Nikolajewa et al. (2007) focused on tree-augmented BNs to reduce computational time and problems with poor performance of BNs in small datasets.

Ideally, it would be possible to accommodate the fact that we have no idea what the true dependence structure is, while favoring a sparse structure that allows efficient computation without facing problems with overfitting. The dependence is of substantial interest biologically, and more realistic models of variability within motifs open the door for improved approaches for motif discovery. With this motivation in mind, our goal is to develop a nonparametric Bayes approach to allow the distribution of multiple unordered categorical variables to be unknown. We show that mixtures of product multinomial distributions have full support, with Dirichlet process (DP) (Ferguson 1973, 1974) mixtures providing a convenient and flexible framework. For posterior computation, we can rely on efficient and simple-to-implement methods developed for conjugate DP mixture models. Hence, we bypass the complexities involved in building a Bayes network for unordered categorical data without inducing any restrictions, while also favoring a sparse formulation of the heterogeneity structure. A formal test of lack of fit for the product multinomial model against a nonparametric alternative can be constructed directly from the Gibbs sampling output.

Although our initial motivation was the motif application, our methodology provides a general approach for nonparametric Bayes modeling of multivariate unordered categorical data. The current literature on parametric models focuses primarily on underlying continuous variable specifications. For example, the multinomial probit model (Ashford and Sowden 1970; Ochi and Prentice 1984; Chib and Greenberg 1998) incorporates a latent multivariate Gaussian random variable, which is linked to the categorical observations through thresholding. Zhang, Boscardin, and Belin (2008) developed a Bayes approach to posterior computation for the multivariate multinomial probit model. Such models are quite flexible, but also tend to be difficult to implement due to the need to estimate a correlation matrix in underlying variables that have a complex relationship with the measured outcomes. An alternative approach is to use a finite mixture model. Such an approach has historically been referred to as latent structure analysis (Lazarsfeld and Henry 1968), though the term latent class modeling is more commonly used in recent years. Refer to Formann (2007) for a recent article applying latent class modeling to multivariate categorical data with missing values.

The nonparametric Bayes literature on multivariate unordered categorical data analysis for more than two categories is essentially nonexistent. A number of articles have focused on nonparametric Bayes methods for multiple binary outcomes (Quintana and Newton 2000; Hoff 2005; Jara, Garcia-Zattera, and Lesaffre 2007). In addition, Kottas, Müller, and Quintana (2005) propose a nonparametric Bayes modification of the multivariate probit model for ordinal data, with the normal distribution on the underlying variables replaced with a Dirichlet process mixture (DPM) of normals. Ansari and Iyengar (2006) proposed a semiparametric Bayes approach to repeated unordered categorical choice data, again following the approach of using DPMs to relax normality assumptions on latent variables. Quintana (1998) instead considered a nonparametric Bayes approach to assess homogeneity in contingency tables having fixed right marginals. His approach borrowed information across the rows of the contingency table by assuming the row vectors of probabilities are drawn from a common distribution, which is assigned a DP prior. This approach is appropriate for univariate unordered categorical data collected for subjects in different groups.

Section 2 describes the proposed nonparametric Bayes mixture model, providing theoretical support. Section 3 describes a simple approach for posterior computation and goodness-of-fit testing. Section 4 contains a simulation study. Section 5 applies the method to assess dependence within the p53 motif, and Section 6 contains a discussion.

2. PRODUCT MULTINOMIAL MIXTURE MODELS

2.1 Latent Structure Analysis and Properties

We focus initially on the case in which p = 2, so that data for subject i consist of a pair of categorical variables, x_i = (x_i1,x_i2)′, resulting in a d₁ × d₂ contingency table with cell (c₁, c₂) containing the count ${\sum }_{i=1}^{n}1(x_{i1}=c_1,x_{i2}=c_2)$, for c₁ = 1, …, d₁ and c₂ = 1, …, d₂. Our focus is on sparse non-parametric modeling of the cell probabilities, π = {πc_1c2} with πc_1c2 = Pr(x_i1 = c₁, x_i2 = c₂).

One simple and parsimonious model for π can be obtained by assuming $Pr(x_{i1}=c_1)={\psi }_{c_1}^{(1)}$ and $Pr(x_{i2}=c_2)={\psi }_{c_2}^{(2)}$ with x_i1 and x_i2 independent. In this case, we obtain ${\pi }_{c_1{c}_2}={\psi }_{c_1}^{(1)}{\psi }_{c_2}^{(2)}$, so that instead of d₁d₂ − 1 free parameters characterizing π in the saturated case, we have d₁ + d₂ − 2 free parameters. In practice, this model may be overly simple, motivating latent structure analysis (Lazarsfeld and Henry 1968; Goodman 1974), which instead relies on the finite mixture specification

$$Pr(x_{i1}=c_1,x_{i2}=c_2)={\pi }_{c_1{c}_2}=\sum _{h=1}^k{\nu }_h{\psi }_{{hc}_1}^{(1)}{\psi }_{{hc}_2}^{(2)},$$ (1)

where ν = (ν₁, …, ν_k)′ is a vector of mixture probabilities, z_i ∈ {1, …, k} denotes a latent class index, $Pr(x_{i1}=c_1\mid z_i=h)={\psi }_{{hc}_1}^{(1)}$ is the probability of x_i1 = c₁ in class h, $Pr(x_{i2}=c_2\mid z_i=h)={\psi }_{{hc}_2}^{(2)}$ is the probability of x_i2 = c₂ in class h, and x_i1 and x_i2 are assumed to be conditionally independent given z_i.

There is a rich literature focusing on issues in latent structure modeling, including identifiability of the ν and $\mathit{\psi }={\{{\mathit{\psi }}_h\}}_{h=1}^k$ parameters, methods for selection of k, extensions to multiple group settings, etc. However, our goal is to build Bayesian non-parametric models that favor sparse formulations, while including all joint distributions for x_i1 and x_i2 in the support of the prior. With this goal in mind, it is important to verify the following theorem in order for formulation (1) to be sufficiently flexible.

Theorem 1

Any π ∈ Π_d1d2 can be characterized as in (1) for some k, with Π_d1d2 containing all d₁ × d₂ probability matrices with elements 0 ≤ π_c1c2 ≤ 1 and ${\sum }_{c_1=1}^{d_1}{\sum }_{c_2=1}^{d_2}{\pi }_{c_1{c}_2}=1$.

It follows from Theorem 1 that the joint distribution of two categorical random variables can always be expressed as a finite mixture of product-multinomial distributions. Good (1969) previously noted the similarity between the singular value decomposition (SVD) and the latent structure model without providing a proof that any probability matrix, π, can be decomposed using formulation (1). Gilula (1979) instead used the SVD to provide conditions for identifying the distribution of latent variables inducing dependence in two categorical variables.

Focusing on the generalization to the multivariate case, let

$$\mathit{\pi }=\{{\pi }_{c_1{c}_2\cdots c_p},c_j=1,\dots ,d_j,j=1,\dots ,p\}\in {\mathrm{\Pi }}_{d_1\cdots d_p}$$

denote a higher order tensor, with Π_d1···dp denoting the set of all probability tensors of size d₁ × d₂ × · · · × d_p, where probability tensors have nonnegative elements and

$${\left|\right|\mathit{\pi }\left|\right|}_1=\sum _{c_1=1}^{d_1}\cdots \sum _{c_p=1}^{d_p}\mid {\pi }_{c_1{c}_2\cdots c_p}\mid =1.$$

Using a tensor generalization of the matrix SVD (Kolda 2001), one can let

$$\mathit{\pi }=\sum _{h=1}^k{\lambda }_h{\mathbf{U}}_h,{\mathbf{U}}_h={\mathbf{u}}_h^{(1)}\otimes {\mathbf{u}}_h^{(2)}\otimes \cdots \otimes {\mathbf{u}}_h^{(p)},$$ (2)

where λ₁ ≥ · · · ≥ λ_k > 0, U_h is a decomposed tensor, ${\mathbf{u}}_h^{(j)}\in {\mathfrak{R}}^{d_j}$, and ⊗ denotes the outer product, so that ${\pi }_{c_1\cdots c_p}={\sum }_{h=1}^k{\lambda }_h{\prod }_{j=1}^p{u}_{{hc}_j}^{(j)}$. If k is chosen to correspond to the minimum value such that π can be expressed as in (2), one obtains a rank decomposition. Rank decompositions are not necessarily unique, but uniqueness is not necessary for our purposes in developing a Bayesian nonparametric procedure.

Corollary 1

For any π ∈ Π_{d1··· dp} decomposed as in (2), we can obtain an equivalent decomposition

$$\mathit{\pi }=\sum _{h=1}^k{\nu }_h{\mathrm{\Psi }}_h,{\mathrm{\Psi }}_h={\mathit{\psi }}_h^{(1)}\otimes {\mathit{\psi }}_h^{(2)}\otimes \cdots \otimes {\mathit{\psi }}_h^{(p)},$$

where ν = (ν₁, …, ν_k)′ is a probability vector, Ψ_h ∈ Π_{d1··· dp}, and ${\mathit{\psi }}_h^{(j)}$ is a d_j × 1 probability vector, for h = 1, …, k and j = 1, …, p.

From Corollary 1 it is clear that any multivariate categorical data distribution can be expressed as a latent structure model,

$$Pr(x_{i1}=c_1,\dots ,x_{ip}=c_p)=x_{c_1\cdots c_p}=\sum _{h=1}^k{\nu }_h\prod _{j=1}^p{\psi }_{{hc}_j}^{(j)},$$ (3)

where ν is a vector of component probabilities, z_i ∈ {1, …, k} is a latent class index, x_i = (x_i1, …, x_ip)′ are conditionally independent given z_i and $Pr(x_{ij}=c_j\mid z_i=h)={\psi }_{{hc}_j}^{(j)}$ is the probability of x_ij = c_j given allocation of individual i to class h.

2.2 Infinite Mixture of Product Multinomials

Although any multivariate categorical data distribution can be expressed as in (3) for a sufficiently large k, a number of practical issues arise in the implementation. Firstly, it is not straightforward to obtain a well-justified approach for estimation of k. Because the data are often very sparse with most of the cells in the d₁ × · · · × d_p contingency table being empty, a unique maximum likelihood estimate of the parameters in (3) often does not exist even when a modest k is chosen. Such problems may lead one to choose a very small k, which may be in-sufficiently large to provide an adequate approximation to the true multivariate distribution. Hence, inferences on the dependence structure in the observations may be severely biased.

These issues provide motivation for a Bayesian nonparametric approach, which avoids selection of a single finite k, allowing the number of components that are occupied by individuals in the sample to grow with sample size, while also allowing model averaging over the posterior distribution for the number of components. Such model averaging is preferable to approaches that conduct inferences conditional on a selected k, and hence ignore the (often substantial) uncertainty in estimation of k.

We propose to induce a prior, π ~ P, through the following specification

$$\begin{array}{l}\mathit{\pi }=\sum _{h=1}^{\infty }{\nu }_h{\mathrm{\Psi }}_h,{\mathrm{\Psi }}_h={\mathit{\psi }}_h^{(1)}\otimes \cdots \otimes {\mathit{\psi }}_h^{(p)},\\ {\mathit{\psi }}_h^{(j)}~P_{0j},\text{independently}\text{for}j=1,\dots ,p,h=1,\dots ,\infty ,\\ \mathit{\nu }~Q,\end{array}$$ (4)

where P_0j is a probability measure on the d_j-dimensional probability simplex, 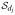, and Q is a probability measure on the countably infinite probability simplex, 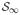. For example, P_0j may correspond to a Dirichlet measure, while Q corresponds to a Dirichlet process or more broadly to a GEM or Poisson–Dirichlet measure. In the Dirichlet process case, the stick-breaking representation of Sethuraman (1994) implies that ν_h = V_h Π_l<h (1 − V_l) with V_h ~ beta(1, α) independently for h = 1, …, ∞, where α > 0 is a precision parameter characterizing Q. For small values of α, ν_h decreases towards zero rapidly with increases in the index h, so that the prior favors a sparse representation with most of the weight on few components. By choosing a hyperprior for α, one can allow the data to inform about an appropriate degree of sparsity, with the intrinsic Bayes penalty for model complexity protecting against overfitting.

From Section 2.1, it is clear that any π⁰ ∈ Π_d1···dp can be characterized using the infinite mixture representation in the first line of (4). However, in placing prior distributions on the components characterizing (4), it is not immediately clear that this flexibility is maintained. Certainly, this is not true for any choice of P₀ = P₀₁ ⊗ · · · ⊗ P_0p and Q. For this reason, it is necessary to place conditions on P₀ and Q so that P has full support on Π_d1···dp with respect to some appropriate topology.

Theorem 2

Letting 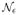(π⁰) = {π : ||π − π⁰||₁ < ε} denote an L₁ neighborhood around an arbitrary π⁰ ∈ Π_d1···dp, the probability P{ 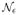(π⁰)} > 0 for any ε > 0 under the following conditions:

1. $P_{0j}\{{\mathcal{N}}_{\epsilon }({\mathit{\psi }}_0^{(j)})\}>0$ for any ${\mathit{\psi }}_0^{(j)}\in {\mathcal{S}}_{d_j}$ and ε > 0, j = 1, …, p;

2. Q{ 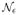(ν₀)} > 0 for any ε > 0 and ν₀ ∈ 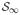such that ν_0h = 0 for h > r with r the (finite) maximum possible rank of π.

For P_0j chosen as a finite Dirichlet and Q a Dirichlet process, it is straightforward to verify that the conditions of Theorem 2 are satisfied, so the resulting prior P has L₁ support on Π_d1···dp. Because there are finitely many parameters in π, this condition is sufficient for posterior consistency, with

$$\underset{n\to \infty }{lim}Pr\{\mathit{\pi }\in {\mathcal{N}}_{\epsilon }({\mathit{\pi }}^0)\mid \mathbf{X}\}\to 1\text{for}\text{any}\epsilon >0,$$

where π⁰ is the true value of π, x_i = (x_i1, …, x_ip)′ is the data for subject i, and X = {x₁, …, x_n} is the data for all n subjects.

3. POSTERIOR COMPUTATION

3.1 Slice Sampling Algorithm

In the special case in which P_0j are finite Dirichlet and Q is a Dirichlet process, posterior computation under prior (4) can proceed via a simple-to-implement and efficient Gibbs sampling algorithm, which modifies the slice sampling approach of Walker (2007). To clarify, the model can be expressed in the following hierarchical form in this case:

$$\begin{array}{l}{x}_{ij}~\text{Multinomial}\left(\{1,\dots ,d_j\},{\psi }_{z_{i}1}^{(j)},\dots ,{\psi }_{z_i{d}_j}^{(j)}\right),\\ z_i~\sum _{h=1}^{\infty }{V}_h\prod _{l<h}(1-V_l){\delta }_h,V_h~\text{beta}(1,\alpha ),\\ {\mathit{\psi }}_h^{(j)}~\text{Dorichlet}(a_{j1},\dots ,a_{{jc}_j}),\end{array}$$ (5)

where the x_ij’s are sampled independently conditional on the latent class z_i and the stick-breaking random variables V = {V_h} and probability vectors $\mathit{\psi }=\{{\mathit{\psi }}_h^{(j)}\}$ are mutually independent. We introduce a vector of latent variables, u = (u₁, …, u_n)′, and define the joint likelihood of u and X given V and ψ as

$$\prod _{i=1}^n\left\{\sum _{h=1}^{\infty }1(u_i<{\nu }_h)\prod _{j=1}^p\prod _{l=1}^{d_j}{({\psi }_{hl}^{(j)})}^{1(x_{ij}=l)}\right\},$$ (6)

where ν_h = V_h Π_l<h(1 − V_l), for h = 1, …, ∞. In marginalizing out u, it is clear that (6) is consistent with (5). The augmented joint posterior distribution is proportional to the prior on V, ψ and α multiplied by the augmented data likelihood (6). Conditional posterior distributions for each of the unknowns can be derived using standard algebra, and a data augmentation Gibbs sampler is then used for posterior computation.

This Gibbs sampler iterates through the following sampling steps:

1. Update u_i, for i = 1, …, n, by sampling from the conditional posterior, Uniform(0, ν_zi).

2. For h = 1, …, k^*, with k^* = max{z₁, …, z_n}, update ${\mathit{\psi }}_h^{(j)}$ from the full conditional posterior distribution obtained in updating the Dirichlet prior with the likelihood of the jth response for subjects in component h,

   $$\text{Dirichlet}\left(a_{j1}+\sum _{i:z_i=h}1(x_{ij}=1),\dots ,a_{{jd}_j}+\sum _{i:z_i=h}1(x_{ij}=d_j)\right).$$
3. For h = 1, …, k^*, sample V_h from the full conditional posterior, which is beta(1, α) truncated to fall into the interval

   $$\left[\underset{i:z_i=h}{max}\left\{\frac{u_i}{{\prod }_{l<h}(1-V_l)}\right\},1-\underset{i:z_i>h}{max}\left\{\frac{u_i}{V_{z_i}{\prod }_{l<z_i,l\ne h}(1-V_l)}\right\}\right].$$
4. To update z_i, for i = 1, …, n, sample from the multinomial full conditional with

   $$Pr(z_i=h\mid \cdots )=\frac{1(h\in A_i){\prod }_{j=1}^p{\psi }_{{hx}_{ij}}^{(j)}}{{\sum }_{l\in A_i}{\prod }_{j=1}^p{\psi }_{l{x}_{ij}}^{(j)}},$$

   where A_i = {h : ν_h > u_i}. To identify the elements in A₁, …, A_n, first update V_h, for h = 1, …, k̃, where k̃ is the smallest value satisfying ${\sum }_{h=1}^{\stackrel{\sim }{k}}{\nu }_h>1-min\{u_1,\dots ,u_n\}$.

5. Finally, assuming a gamma(a_α, b_α) hyperprior for α, with the gamma parameterized to have mean a_α/b_α and variance $a_{\alpha }/b_{\alpha }^2$, the conditional posterior is

   $$\text{gamma}\left(a_{\alpha }+k^{\ast },b_{\alpha }-\sum _{h=1}^{k^{\ast }}log(1-V_h)\right).$$

These steps are quite similar to those presented in Walker (2007), though he considered Dirichlet process mixtures of normals. Each step involves sampling from a standard distribution, so should be very simple and efficient to implement. Note that in using the slice sampler we avoid the need to approximate (4) through truncation, and only update those components that are needed. This is conceptually related to the retrospective sampling approach of Papaspiliopoulos and Roberts (2008), though the slice sampler is simpler to implement. One can potentially gain efficiency while maintaining simple sampling steps by combining the slice sampler with the retrospective sampler using the approach described by Papaspiliopoulos (2008). Such an algorithm is similar to our proposed algorithm, but updates the V_hs from a beta conditional posterior distribution obtained in marginalizing out the latent variables u.

3.2 Testing and Inferences

It is often of interest to test for independence of the elements of x_i = (x_i1, …, x_ip)′. For example, in the transcription factor binding motif application, there has been considerable debate in the literature regarding the appropriateness of the independence assumption implicit in the product multinomial model. Under our proposed formulation, the null hypothesis of independence is nested within a nonparametric alternative that accommodates a sequence of models of increasing complexity including the saturated model. In particular, the independence model corresponds to H₀ : ν₁ = 1. As noted in Berger and Sellke (1987), interval null hypotheses are often preferred to point null hypotheses. Motivated by this reasoning and by computational considerations, we focus instead on the interval null H₀ : ν^* > 1 − ε, with ν^* = max{ν_h, h = 1, …, k^*} and ε a prespecified small positive constant. In particular, ε is chosen to permit deviations from independence that are so small as to be nonsignificant in the subject matter area. We find that ε = 0.05 provides a good default value based on simulations from the prior in a variety of cases. For very small ε, the interval null provides an approximation to the point null.

Under the prior proposed in Section 3.1, the probability allocated to H₀ is approximately

$$Pr({\nu }_1>1-\epsilon )={\int }_{1-\epsilon }^1{\int }_0^{\infty }\alpha {(1-V_1)}^{\alpha -1}\frac{b_{\alpha }^{a_{\alpha }}}{\mathrm{\Gamma }(a_{\alpha })}{\alpha }^{a_{\alpha }-1}exp(-b_{\alpha }\alpha )d\alpha d{V}_1$$

which can easily be calculated numerically. From this expression, it is clear that the hyperparameters a_α and b_α control the prior probability allocated to H₀. In order to assign approximately equal probabilities to H₀ and H₁, one should choose values of a_α, b_α to produce Pr(H₀) ≈ 0.5. Noting that a_α + b_α is often interpreted as a prior sample size, we recommend letting a_α + b_α = 1/2 as a default corresponding to a vague prior. As ν₁ is a parameter in each of the models under consideration, it is acceptable to choose a vague prior. We then choose a_α = 1/4 to obtain Pr(H₀ : ν^* > 1 − ε) ≈ 0.5. To complete a default prior specification, we let a_j1 = · · · = a_jcj = 1, for j = 1, …, p, which corresponds to choosing uniform priors for the category probabilities in each class for each outcome type.

To conduct a Bayesian test of independence, we can rely on the Bayes factor in favor of the alternative hypothesis, which corresponds to

$$\text{BF}=\frac{Pr(H_1\mid \mathbf{X})/Pr(H_1)}{Pr(H_0\mid \mathbf{X})/Pr(H_0)},$$ (7)

which can easily be estimated based on the output of the Gibbs sampler proposed in Section 3.1, with $\widehat{Pr}(H_1\mid \mathbf{X})$ equal to the proportion of samples for which ν^* ≤ 1 − ε and $\widehat{Pr}(H_0\mid \mathbf{X})=1-\widehat{Pr}(H_1\mid \mathbf{X})$. The performance of the Bayes factor-based test is assessed in a simulation study in Section 4.

In addition to testing for independence, it may be of interest to estimate the marginal distribution for each x_ij and to conduct inferences on the dependence structure in the different elements of x_i. To obtain approximate draws from the posterior distribution for π_jl = Pr(x_ij = l), which can be used to obtain point and interval estimates, we suggest using the approximation

$${\pi }_{jl}\approx \sum _{h=1}^{k^{\ast }}{\nu }_h{\psi }_{hl}^{(j)},$$

where k^* is the maximum class index. Clearly, unless the sample size is quite small, the error in this approximation is neglible, with $1-{\sum }_{h=1}^{k^{\ast }}{\nu }_h$ providing an easily calculated upper bound on this error. In small samples, one can obtain an approximation that is as accurate as desired by drawing ν_h’s and ${\mathit{\psi }}_h^{(j)}$ for h = k^* + 1, …, k_m, with k_m chosen so that the error bound is below a prespecified constant. This idea is conceptually related to that proposed by Muliere and Tardella (1998).

To conduct inferences on the dependence between x_ij and x_ij′ for all j, j′ ∈ {1, …, p}, it is necessary to first choose a measure of association for two nominal variables. Most of the symmetric measures of association that are commonly used are based on the Pearson χ², with various adjustments proposed to attempt to remove the dependence on sample and table size. For example, Cramer’s $V=\sqrt{{\chi }^2/n(k-1)}$, with k = min{d_j, d_j′}, is a commonly used measure that ranges from 0 to 1. From a Bayesian perspective, the measure of association should not depend on the data directly, but should be a function of the parameters characterizing the multivariate distribution. Hence, we recommend

$${\rho }_{{jj}^{\prime }}^2=\frac{1}{min\{d_j,d_{j^{\prime }}\}-1}\sum _{c_j=1}^{d_j}\sum _{c_{j^{\prime }}=1}^{d_{j^{\prime }}}\frac{{({\pi }_{c_j{c}_{j^{\prime }}}-{\overline{\psi }}_{c_j}^{(j)}{\overline{\psi }}_{c_{j^{\prime }}}^{(j^{\prime })})}^2}{{\overline{\psi }}_{c_j}^{(j)}{\overline{\psi }}_{c_{j^{\prime }}}^{(j^{\prime })}},\text{with}{\overline{\psi }}_l^{(j)}=\sum _{h=1}^{k^{\ast }}{\nu }_h{\psi }_{hl}^{(j)},$$ (8)

where ρ_jj′ is a model-based version of Cramer’s V and ranges from 0 to 1, with ρ_jj′ ≈ 0 when x_ij and x_ij′ are independent.

Our Bayesian approach has the nice feature that we can estimate the posterior distribution of ρ_jj′ for all j, j′ pairs based on the output of the Gibbs sampler from Section 3.1. To conduct inference on the dependence structure between each of the pairs, we recommend reporting a p × p association matrix, with the elements corresponding to posterior means for each ρ_jj′. In addition, we can calculate posterior probabilities and Bayes factors for local null hypotheses, H_1jj′ : ρ_jj′ > ε from the Gibbs output.

Using posterior probabilities of H_1jj′ for each j, j′ pair as a basis for inferences on the dependence structure has substantial advantages over model selection-based approaches. In particular, in a standard Bayesian network analysis, one would estimate a directed acyclic graph (DAG) characterizing the dependence structure in the elements of x_i. Unless p is small, this estimation involves a massive-dimensional model selection problem, as the number of possible DAGs is enormous. In very large model spaces, the available data are typically consistent with a large number of different models, and it is extremely unlikely that the estimated DAG will correspond to the true model.

Although we focus on testing of global dependence and dependence between pairs of variables, since these are the hypotheses most often of interest, our approach can be adapted for comparing competing dependence structure models. For example, one may have two or more alternative graphical models of dependence representing different biological hypotheses. In this case, it is likely that none of the graphical models in the list of those being compared is exactly true. In this setting, one can represent the true model using our proposed Dirichlet process mixture of product multinomial models. The graphical model is then selected that produces a predictive distribution closest to that for the nonparametric model in KL distance using the methods of Walker and Gutiérrez-Peña (2007).

4. SIMULATION STUDIES

To assess the performance of the proposed approach, we conducted a simulation study. Simulated data consisted of A, C, G, T nucleotides (d_j = d = 4) at p = 20 positions for n = 100 sequences. We considered two simulation scenarios, generating the nucleotides (1) independently, and (2) assuming dependence in locations 2, 4, 12, and 14. One mechanism by which positional dependence can be induced is the existence of multiple subpopulations, with each subpopulation having different A, C, G, T probabilities at certain locations. Within a subpopulation, nucleotides are positionally independent. However, marginalizing out the latent subpopulation indicator, one obtains dependence in those locations that have different nucleotide frequencies across the subpopulations. The presence of such sub-populations is biologically motivated, with different subpopulations potentially having a different combination of dominant (i.e., high probability) nucleotides at certain locations. Presumably there is more than one combination that can lead to a functioning motif, so that different working combinations can arise through evolution in isolated groups of individuals. We assumed 80% of individuals fall into the first subpopulation, with the remaining individuals in a second subpopulation. Nucleotides were generated from a discrete uniform except at locations 2, 4, 12, and 14. For these locations, we used a product multinomial, with the probabilities of A, C, G, or T differing between the subpopulations in case 2 but not in case 1.

For each case, we generate 100 simulated datasets, analyzing each separately using the default prior of Section 3.2 and the Gibbs sampler of Section 3.1 run for 100,000 iterations with a 20,000 iteration burn-in. Mixing and convergence rates were good based on examination of trace plots. We also implemented the Bayes network search method of Xie and Geng (2008) for comparison, using a threshold of 0.05 on the p-values for inclusion of an edge.

For simulation case 1 (no positional dependence, H₀ is true), we obtained good results, with the estimated values of ρ_jj′ close to zero for each j, j′ pair and all of the simulation replicates. Figure 1(a) provides a histogram showing the estimated posterior probabilities of H₁ across the 100 simulated datasets using ε = 0.10. The method appropriately assigns a value close to zero to Pr(H₁|data) when H₀ is true in most cases, with only 1/100 having an estimated Pr(H₁|data)>0.5. In contrast, the Xie and Geng (2008) approach badly over-fit the data, including dependence in 26.7 pairs of variables on average (range = [5, 171] out of 190 possible). These results improved somewhat using a threshold of 0.01 for inclusion of an edge, but the average number of false positives was still 3.5 (range = [0, 25]).

Figure 1.

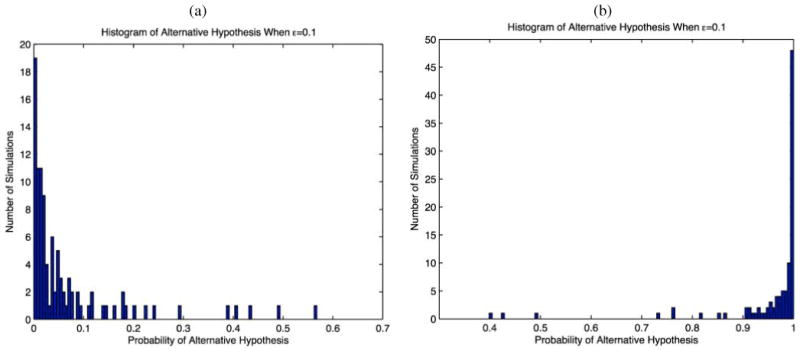
Histograms of estimated posterior probabilities of H₁ in each of the 100 simulations under (a) case 1 (no positional dependence—H₀ is true) and (b) case 2 (positional dependence—H₁ is true).

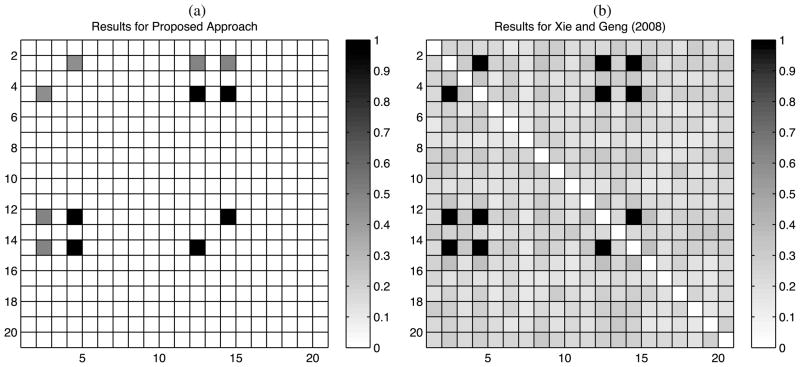
Figure 1(b) provides results in simulation case 2. The posterior probability assigned to H₁ was close to one in the majority of the simulations. The left panel of Figure 2 shows the proportions of simulations having Pr(H_1jj′|X) > 0.95. These proportions are 0/100 for all position pairs that are truly uncorrelated and ranged from 53/100 to 97/100 for position pairs that were dependent. The right panel of Figure 2 shows results for the Xie and Geng (2008) approach, plotting the proportion of simulations in which each position pair is flagged as correlated. The Xie and Geng (2008) approach had slightly higher power, but a substantially higher Type I error rate. Their method detected 5.7 of the 6 truly dependent pairs of variables on average (range = [3, 6]), while also reporting 36.7 false positives on average (range = [10, 105]). For a threshold of 0.01 for edge inclusion, the average number of true and false positives detected were 5.36 and 5.6, respectively.

Figure 2.

Results of simulation case 2—percentages of simulations for which (a) Pr(H_1jj′|X)>0.95, and (b) the Xie and Geng (2008) method estimated an association between positions j, j′. The true model has dependence in positions 2, 4, 12, and 14.

The relatively poor performance of the Xie and Geng (2008) method does not reflect on their approach for BN search, but instead on the general drawbacks of relying on model selection in very large model spaces. For comparison, we conducted a simple frequentist alternative, which avoids BN search by focusing on pairwise testing, while adjusting for multiplicity. In particular, we implemented separate chi-square tests for each position pair, flagging those positions having p-values below the Benjamini and Hochberg (1995) threshold to maintain a false discovery rate ≤ 0.05. We find that dependence in (4, 12) and (12, 14) is detected in all of the simulations, but dependence in positions (2, 4), (2, 12), (2, 14), and (4, 14) was missed in all 100 simulations.

Hence, based on these simulations, the proposed Bayesian nonparametric approach has better performance than Bayes network-based methods and frequentist pairwise testing. In addition to bypassing the difficulties involved in graphical model search, our approach has the conceptual advantage of providing a weight of evidence that two variables are correlated accounting for uncertainty in the dependence in other variables and automatically adjusting for dependence in the different hypothesis tests. Accounting for dependence in hypotheses induces an automatic Bayes adjustment for multiple testing, as discussed in the setting of simpler parametric models by Scott and Berger (2006).

5. APPLICATION TO MODELING POSITIONAL DEPENDENCE WITHIN MOTIFS

We applied the method to data for the p53 transcription factor binding motif. The data consisted of A, C, G, T nucleotides (d_j = d = 4) with p = 20 positions for n = 574 sequences obtained from 542 high-confidence p53 binding loci identified by ChIP-PET experiments (Wei et al. 2006). The p53 tumor suppressor is a sequence-specific DNA binding transcription factor. It regulates the expression of genes involved in a variety of cellular functions, including cell-cycle arrest, DNA repair, and apoptosis (Vogelstein, Lane, and Levine 2000). Hence, p53 provides a natural starting application for our methodology for flexibly characterizing and testing for positional dependence within gene sequences.

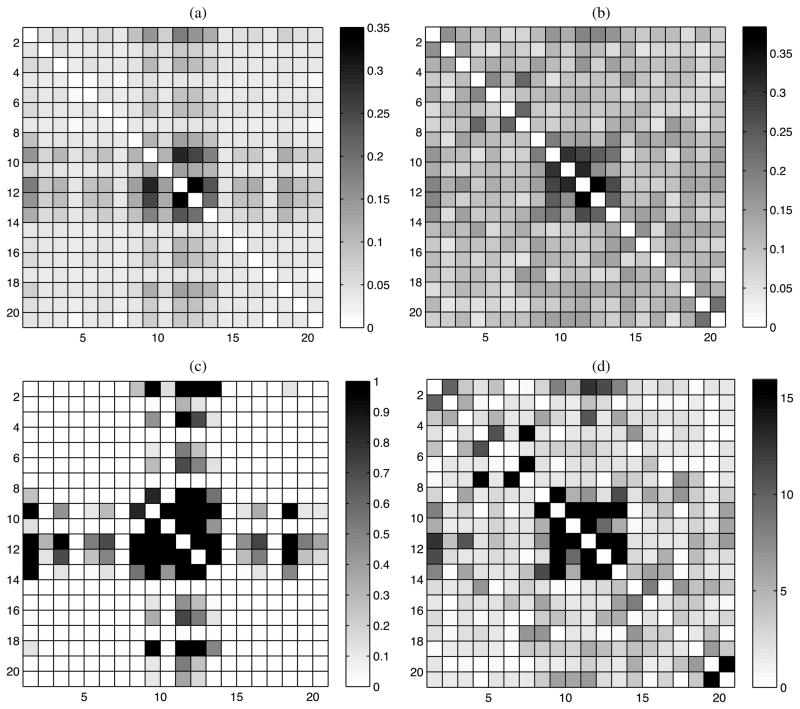
We applied the same approach implemented in the simulation study examples. The null hypothesis test for p53 data gave that $\widehat{Pr}(H_0\mid \mathbf{X})=1-\widehat{Pr}(H_1\mid \mathbf{X})=0.00$, with $\widehat{Pr}(H_1\mid \mathbf{X})$ equal to the proportion of samples from which max{ν_h|h = 1,2, …, k^*} ≤ 1 − ε, where ε is set to be 0.10 (identical results were obtained for 0.01 and 0.05). To estimate the pairwise positional dependence structure, we used the ρ_jj′ correlation measure defined in expression (8). Figure 3(a) shows the posterior means of ρ_jj′ for each pair j, j′ ∈ {1, …, 20}, while Figure 3(b) shows the frequentist Cramer’s V estimates applied separately to each pair of locations. Our estimates are consistent with the Cramer’s V estimates in that we assign relatively high correlations to similar pairs of locations. However, as expected in using our Bayes sparseness-favor approach, the smaller correlations are shrunk closer to zero.

Figure 3.

Results for p53 data. (a) Posterior mean of ρ_jj. (b) Pairwise Cramer’s V values. (c) Pairwise posterior probabilities, Pr(H_1jj′|X). (d) − log₁₀ p-values from pairwise χ² tests.

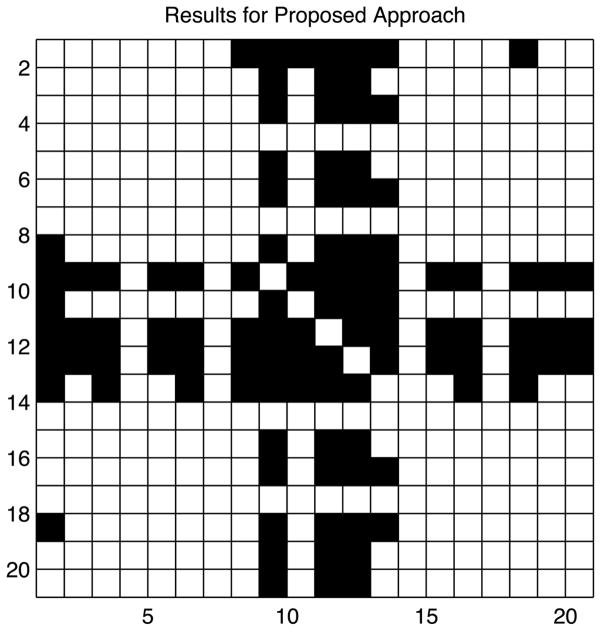
Figure 3(c) shows the estimated posterior probabilities of H_1jj′ : ρ_jj′ > 0.1, while Figure 3(d) shows − log₁₀ p-values from pairwise χ² tests. Given that − log₁₀ 0.05 = 1.3, it is apparent in examining Figure 3(d) that there is a large number of very small p-values. In fact, choosing those position pairs that satisfy the Benjamini and Hochberg (1995) threshold to maintain a false discovery rate (FDR) ≤ 0.05, we obtain 126 pairs, with a large number flagged even for FDR ≤ 0.01. The Xie and Geng (2008) approach selected all 190 pairs as dependent when using a p-value threshold of 0.05 or 0.01 for edge inclusion. In contrast, our Bayesian procedure selects only 16 pairs of positions having Pr(H_1jj′|X) > 0.95. The pairs of positions selected by our method are shown in Figure 4. Given the much lower Type I error rate of our Bayes nonparametric approach in the simulation study, we expect our results are closer to the truth.

Figure 4.

Pairs of positions flagged as dependent for the p53 data using the proposed Bayesian nonparametric approach with Pr(H_1jj′|X) > 0.95.

6. DISCUSSION

This article has proposed a Bayesian nonparametric approach for inference in sparse contingency tables constructed for multivariate nominal data. We focused in particular on Dirichlet process mixtures of product multinomial models, which can be shown to be highly flexible and computationally convenient. In fact, we find the proposed Gibbs sampler for posterior computation to be quite efficient, which is promising in terms of scaling up the approach to deal with several problems that are of substantial interest. The first is flexible modeling of dependence in large numbers of single nucleotide polymorphisms. As long as the dependence structure can be characterized using a sparse mixture, with most of the weight on few components in the latent structure decomposition, then scaling up to much larger p should be straightforward. In addition to inferences on dependence across the genome, one important application is to accommodating missing genotype data, which is straightforward within the proposed framework. In fact, following the argument of Formann (2007), one can even allow violations of the missing at random assumption.

A common focus of statistical analyses of sequence data is searching for new motifs in long nucleotide sequences, with such searches attempting to identify words (sequences of nucleotides) that are conserved across sequences collected for different subjects. Most search algorithms make the assumption of independence across the positions within a motif. However, the Gibbs sampling approach of Liu, Neuwald, and Lawrence (1995) can potentially be modified to allow dependence through our proposed approach, so that one can allow for dependence in searching for motifs. Jensen and Liu (2008) recently used a Dirichlet process-based approach for clustering of different transcription factor binding motifs allowing for different lengths.

Another interesting extension of our proposed approach would be to include predictors, w_i = (w_i1, …, w_iq)′, that potentially impact the joint distribution of x_i. This can be accomplished in a sparse manner by allowing the weights to be predictor dependent, so that ν_h is replaced by ν_ih = ν_h(w_i). A predictor-dependent stick-breaking process, which generalizes the Dirichlet process, can then be defined for these weight functions. For example, the kernel stick-breaking process of Dunson and Park (2008) can be used directly.

APPENDIX A: PROOF OF THEOREM 1

To prove Theorem 1, first note that the singular value decomposition (SVD) expresses π as

$$\mathit{\pi }=\sum _{h=1}^k{\lambda }_h{\mathit{\xi }}_h{\mathit{\kappa }}_h^{\prime },$$ (A.1)

where λ_h ≥ 0 are singular values, ${\lambda }_1^2\ge \cdots \ge {\lambda }_k^2>0$ are the nonzero eigenvalues of the matrix ππ′, ξ_h is a d₁ × 1 vector, κ_h is a d₂ × 1 vector, and $\mathit{\xi }={\{{\mathit{\xi }}_h\}}_{h=1}^k$ and $\mathit{\kappa }={\{{\mathit{\kappa }}_h\}}_{h=1}^k$ are orthonormal bases for the spaces spanned by the rows of ππ′ and π′π, respectively. The SVD decomposition in (A.1) is unique up to multiplication of ξ_h and κ_h by −1. As A = ππ′ is nonnegative, the rows of A (A′) can be expressed as linear combinations of nonnegative orthonormal bases ξ(κ). We remove sign ambiguity in (A.1) by restricting ξ and κ to be nonnegative. The spectral radius of the positive definite matrix A is defined as $\rho (\mathbf{A})={max}_h\{{\lambda }_h^2\}$. It is known that ρ(A) ≤ ||A||, where ||·|| denotes an induced norm, such as ${\left|\right|\mathbf{A}\left|\right|}_1={max}_{1\le j\le d_1}{\sum }_{i=1}^{d_1}\mid a_{ij}\mid$. Because the elements of π are nonnegative probabilities summing to one, it is clear that ${\sum }_{i=1}^{d_1}\mid a_{ij}\mid \le 1$ for all j, so that ρ(A) ≤ 1. From the Perron–Frobenius theorem, ${\lambda }_1^2=\rho (\mathbf{A})$, and hence 0 < λ_h ≤ 1 for h = 1, …, k.

Using the known restrictions on ${\{{\lambda }_h\}}_{h=1}^k$, ξ and κ, we can equivalently express (A.1) as

$$\mathit{\pi }=\sum _{h=1}^k{\lambda }_h{\mathit{\xi }}_h{\mathit{\kappa }}_h^{\prime }=\sum _{h=1}^k{\stackrel{\sim }{\lambda }}_h{\stackrel{\sim }{\mathit{\xi }}}_h{\stackrel{\sim }{\mathit{\kappa }}}_h^{\prime },$$ (A.2)

where ξ_h = c_ξ,h ξ̃_h, $c_{\xi ,h}={\sum }_{j=1}^{d_1}{\xi }_{hj}$, κ_h = c_κ,h κ̃_h, $c_{\kappa ,h}={\sum }_{j=1}^{d_2}{\kappa }_{hj}$, and λ̃_h = c_ξ,hc_κ,hλ_h. In the reparameterization, ξ̃_h and κ̃_h are probability vectors, with the elements in ${\stackrel{\sim }{\mathit{\xi }}}_h{\stackrel{\sim }{\mathit{\kappa }}}_h^{\prime }$ summing to one. Because the elements of π sum to one, it is straightforward to show that ${\sum }_{h=1}^k{c}_{\xi ,h}{c}_{\kappa ,h}{\lambda }_h=1$, and hence λ̃ = (λ̃₁, …, λ̃_k)′ is a probability, vector. Noting that (1) can be expressed as $\mathit{\pi }={\sum }_{h=1}^k{\nu }_h{\mathit{\psi }}_h^{(1)}{{\mathit{\psi }}_h^{(2)}}^{\prime }$, Theorem 1 follows directly.

APPENDIX B: PROOF OF COROLLARY 1

The approach used in proving Theorem 1 can be applied directly after showing that expression (2) holds under the constraints (i) 0 < λ_h ≤ 1 for h = 1, …, k; and (ii) the elements of ${\mathbf{u}}_h^{(j)}$ are nonnegative for h = 1, …, k and j = 1, …, p. Letting π_[jj′] denote the d_j × d_j′ matrix containing Pr(x_ij = c_j, x_ij′ = c_j′) in element c_j, c_j′, it follows from (2) that

$${\mathit{\pi }}_{[{jj}^{\prime }]}=\sum _{h=1}^k{\lambda }_h{\mathbf{u}}_h^{(j)}\otimes {\mathbf{u}}_h^{(j^{\prime })},j,j^{\prime }\in \{1,\dots ,p\},$$

where the rows of ${\mathit{\pi }}_{[{jj}^{\prime }]}{\mathit{\pi }}_{[{jj}^{\prime }]}^{\prime }$ can be expressed as linear combinations of ${\{{\mathbf{u}}_h^{(j)}\}}_{h=1}^k$. Hence, ${\{{\mathbf{u}}_h^{(j)}\}}_{h=1}^k$ forms a basis for the union of the row spaces of ${\mathit{\pi }}_{[j1]}{\mathit{\pi }}_{[j1]}^{\prime },\dots ,{\mathit{\pi }}_{[jp]}{\mathit{\pi }}_{[jp]}^{\prime }$. Because π is a nonnegative tensor, the rows of ${\mathit{\pi }}_{[{jj}^{\prime }]}{\mathit{\pi }}_{[{jj}^{\prime }]}^{\prime }$ are nonnegative and can be expressed as linear combinations of nonnegative vectors having positive weights. Hence one can choose each of the ${\mathbf{u}}_h^{(j)}$ vectors to be nonnegative, which satisfies property (ii). Because (2) is not uniquely defined in that λ_hU_h can be replaced by λ_hCC⁻¹U_h for any C ∈ ℜ⁺, the restriction 0 < λ_h ≤ 1 can be included trivially.

APPENDIX C: PROOF OF THEOREM 2

Using Corollary 1, π⁰ can be expressed as

$${\mathit{\pi }}^0=\sum _{h=1}^{\infty }{\nu }_{0h}{\mathrm{\Psi }}_{0h},{\mathrm{\Psi }}_{0h}={\mathit{\psi }}_{0h}^{(1)}\otimes \cdots \otimes {\mathit{\psi }}_{0h}^{(p)},$$

where ν₀ = (ν₀₁, …, ν_0k0, 0, …, 0)′, k₀ is the rank of the tensor, π⁰, ν_0h = 0 for h = k₀ + 1, …, ∞, and ${\mathit{\psi }}_{0h}^{(1)},\dots ,{\mathit{\psi }}_{0h}^{(p)}$ are probability vectors with respective dimensions d₁, …, d_p. The L₁ distance between π⁰ and an arbitrary π ∈ Π_d1···dp can be defined as

$${\left|\right|\mathit{\pi }-{\mathit{\pi }}^0\left|\right|}_1=\sum _{c_1=1}^{d_1}\cdots \sum _{c_p=1}^{d_p}\sum _{h=1}^{\infty }\left|{\nu }_h\prod _{j=1}^p{\psi }_{{hc}_j}^{(j)}-{\nu }_{0h}\prod _{j=1}^p{\psi }_{0{hc}_j}^{(j)}\right|,$$ (C.1)

which is a function of the probability vectors characterizing the tensor SVD decompositions. Holding π⁰ fixed, the probability allocated to 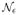_ε (π⁰)can then be defined as

$$\int 1({\left|\right|\mathit{\pi }-{\mathit{\pi }}^0\left|\right|}_1<\epsilon )dQ(\mathit{\nu })\prod _{h=1}^{\infty }\prod _{j=1}^p{dP}_{0j}({\mathit{\psi }}_h^{(j)}).$$ (C.2)

For any ε >0, it is straightforward to show that there exist infinitely many values ε̃ >0 and ε^* > 0 such that

$${\left|\right|\mathit{\nu }-{\mathit{\nu }}_0\left|\right|}_1<\stackrel{\sim }{\epsilon }\text{and}{\Vert {\mathit{\psi }}_h^{(j)}-{\mathit{\psi }}_{0h}^{(j)}\Vert }_1<{\epsilon }^{\ast }\forall h,j$$

implies that ||π − π⁰||₁ < ε. Hence, to show that (C.2) is strictly positive, it suffices to show

$$Pr({\left|\right|\mathit{\nu }-{\mathit{\nu }}_0\left|\right|}_1<\stackrel{\sim }{\epsilon },{\Vert {\mathit{\psi }}_h^{(j)}-{\mathit{\psi }}_{0h}^{(j)}\Vert }_1<{\epsilon }^{\ast },h=1,\dots ,\infty ,j=1,\dots ,p)>0,$$

which follows directly from conditions (i) and (ii) of the Theorem 2 due to independence.