The relationship between EQ-5D, HAQ and pain in patients with rheumatoid arthritis

Abstract

Objective. This study aims to provide robust estimates of EQ-5D as a function of the HAQ and pain in patients with RA.

Method. Repeated observations were made of patients diagnosed with RA in a US observational cohort (n = 100 398 observations) who provided data on HAQ, pain on a visual analogue scale and the EQ-5D questionnaire. We used a bespoke statistical method based on mixture modelling to appropriately reflect the characteristics of the EQ-5D instrument and to compare this with results from standard multiple regression.

Results. EQ-5D can be predicted from summary HAQ and pain scores. We identify four different classes of respondents who differ in terms of disease severity. Unlike the multiple regression, the mixture model exhibits very good fit to the data and does not suffer from problems of bias or predict values outside the feasible range.

Conclusion. It is appropriate to model the relationship between HAQ and EQ-5D but only if suitable statistical methods are applied. Linear models underestimate the quality-adjusted life year benefits, and therefore the cost-effectiveness, of therapies. The bespoke mixture model approach outlined here overcomes this problem. The addition of pain as an explanatory variable greatly improves the estimates. Reimbursement agencies rely on these types of analyses when formulating policy on the use of new drug therapies. Clinicians as well as economists should be concerned with these issues.

Introduction

Economic evaluation of health care technologies is now a technique in widespread use across most developed health care systems and a key aid to decision makers. It provides a rational framework to consider both the cost and benefits of treatments that compete for scarce health care resources. In RA, the advent of high-cost biologic drugs has been a particular driver for the large number of such cost-effectiveness analyses. In many jurisdictions, decision makers wish to have health benefits of treatments expressed in terms of quality-adjusted life years (QALYs) so that comparisons across diverse disease areas can be made using a common metric. The QALY attaches weight to each year of survival to adjust for its perceived quality. A year in full health is scored as 1 and death is 0. These serve as the points around which all intermediate health states are valued.

In order for the health benefits of a therapy to be estimated in terms of QALYs gained, it is usual for an appropriate outcome measurement tool to be administered to patients as part of the clinical trial. Several off-the-shelf instruments are available, including the EQ-5D [1], SF-6D [2] (a derivative of the SF-36) and the Health Utilities Index [3]. Each of these instruments comprises questions that ask patients to indicate their health on a range of dimensions. Pre-existing scores on the QALY scale calculated from the general populations of several different countries are then available to attach to those health states.

However, in RA, many of the pivotal trials for new therapies have failed to include such preference-based instruments. In this situation, analysts have attempted to estimate the relationship between clinical outcome measures that are included in trials (predominantly the HAQ) and preference-based measures via statistical modelling [4–8]. These are almost all simple linear regression models, which is problematic because this kind of statistical model has been shown to fit badly to the data and thereby undervalue treatment benefits. This is evident from numerous studies in varying disease settings [9] and in RA populations when using either the HAQ summary score [10] or the individual components of HAQ [4, 11] as predictors. In these cases, the statistical model underestimates utility values for those patients with little or no functional disability, but overestimates the utility score for those with poor function.

This linking of clinical and economic outcome measures has been referred to as mapping and has been subject to substantial controversy. The OMERACT Economics Group recognized this and reported that mapping should be better explored [12]. Scott et al. [13] go so far as to suggest that economic evaluations should not be based on HAQ transformed to EQ-5D.

We have previously developed a new statistical approach to modelling EQ-5D [14]. Using a small dataset from an early RA cohort, we demonstrated the appropriateness of the method using HAQ and pain to estimate EQ-5D scores. This article refines the method and applies it to a much larger dataset to provide definitive results. While this article concentrates on the UK EQ-5D tariff, the issues are relevant to EQ-5D using scores from other countries’ populations or for other health utility-based instruments. Overall, we aim to estimate EQ-5D as a function of HAQ and pain. The issue is not just of importance to health economists but directly influences the availability of drug and other therapies. In England and Wales, for example, every single appraisal of biologic therapies undertaken by the National Institute for Health and Clinical Excellence (NICE) and their broader guidelines on the management of RA have relied in part on estimating such a relationship.

Patients and methods

Data were provided by the US National Data Bank for Rheumatic Diseases (NDB). The NDB is a not-for-profit rheumatic disease research databank in which patients completed detailed self-report questionnaires at 6-month intervals [15]. Patients signed informed consent forms before being enrolled in the NDB. The consent form was approved by the Via Christie Institutional Review Board. Eligible patients in this study were those with RA who had completed a biannual survey for events occurring between 1 July 2002 and 22 November 2010.

At each assessment, demographic variables were recorded, including sex, age, ethnic origin, education level, current marital status, medical history and total family income. Patients also complete the HAQ Disability Index, including pain on a visual analogue scale (VAS) scored from 0 to 100 and EQ-5D, amongst other items. UK EQ-5D tariff values were used. Summary statistics for the sample are provided in Table 1.

Table 1.

Descriptive statistics of RA patients from NDB by observation (n = 100 398)

Characteristic	Value
Female, n (%)	79 639 (79.3)
RA duration (years)	17.17 (11.07)
Age (years)	62.82 (12.24)
Pain	35.32 (26.76)
HAQ	1.00 (0.73)
EQ-5D	0.66 (0.27)

All values are mean (s.d.) unless indicated oterwise.

A total of 103 867 observations were included in the total dataset from 16 011 patients; 3469 observations had missing data and were not included in the statistical models. The size of the dataset dwarfs that which is typical of most mapping studies. Patients spanned the full range of HAQ, pain and EQ-5D values. Nevertheless, very few observations were observed in the most extreme HAQ health state. A total of 1244 observations (1.2%) from 528 patients had an HAQ exceeding 2.5, and just 152 observations (0.15%) from 64 patients had an HAQ of 3.

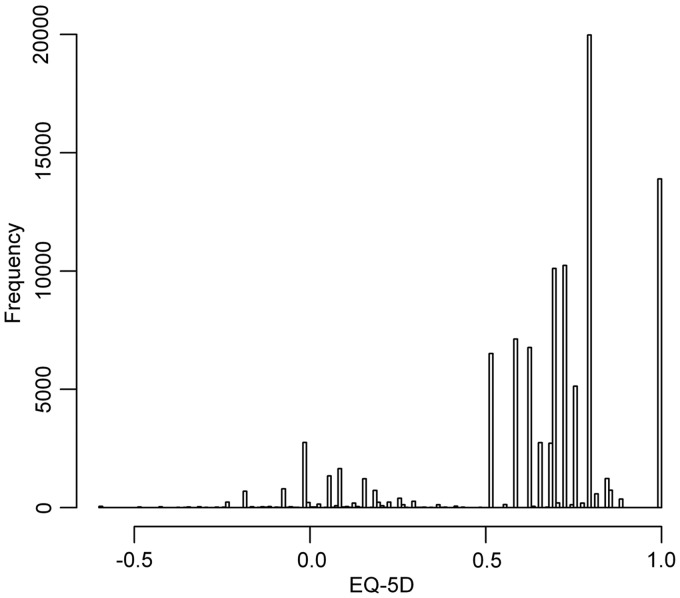
The histogram in Fig. 1 displays the key features typical of EQ-5D. First, there is a substantial mass of observations at 1. There are 13 891 observations (14%) at full health. Second, there is a gap between these observations and those for any level of impairment, as is imposed by the method for calculating EQ-5D tariff scores. There are then at least two more separate components to the distribution with models around 0 and 0.75. There is a very large mass of observations around 0.8. There are 50 observations in the so-called Pits state (i.e. 33333), the worst state that can be described by the EQ-5D descriptive system. These are the features of EQ-5D that raise statistical challenges and result in the poor performance of standard approaches.

Fig. 1.

Distribution of EQ-5D scores from the NDB cohort.

Statistical methods

We aim to estimate the relationship between EQ-5D, HAQ and pain on a scale of 0 to 100. Standard multiple regression models are in widespread use for modelling EQ-5D but such models are rarely suitable when the distribution of the variable of interest is complicated. It is clearly not appropriate in this situation, given the bounded and multimodal nature of the distribution (Fig. 1), and has been shown to perform poorly for this very reason. A linear regression model was included here solely to confirm this. Instead, we apply the general framework for estimating EQ-5D from Hernández et al. [14], which combines bespoke distributions in a mixture model. Full details are provided elsewhere [14], however, the key details of the two main elements of the approach are provided here.

First, mixture models are formed from a number of different component distributions or classes that are combined to form a new distribution: essentially, instead of estimating a single statistical model, a mixture model is based on simultaneously estimating as many separate models (or classes) as the analyst requests. The overall estimate of EQ-5D, predicted from any set of HAQ, pain and age values, is a weighted function of these individual components. The precise weights can also be based on different explanatory variables. We chose this mixture approach because it offers an extremely flexible and convenient manner in which complex distributions (such as EQ-5D) can be analysed [16]. So, while each of the individual components can be based on standard statistical assumptions, when these are combined together they can form extremely non-standard distributions, as is clearly required in this setting.

The analyst must exercise judgement in determining the appropriate number of components. Adding an additional component will always improve the extent to which the model fits the actual data but it also loses generalizability. We therefore used measures that compare models in terms of fit but include a penalty for having more components (Bayesian information criteria) as well as subjective judgements as to whether adding an additional class captured a large or small amount of the data and whether this was at the extremes of poor/good health, where even small improvements can be particularly important. We considered models that had between three and six separate components.

The second novel feature of the analysis is that, in this case, instead of basing each separate class of the mixture on a standard normal distribution, we based it instead on a distribution specific to the characteristics of EQ-5D, namely, limited above at full health (1), below at −0.594 and adjusted to reflect the gap in feasible values between 1 and 0.883.

Explanatory variables may enter the model in two ways: either as predictors of the relationship with EQ-5D within each of the individual classes, as in standard regression, or as predictors of component membership. We compared several different variants of using the explanatory variables in these two ways and identified the best performing approach.

Patients are followed every 6 months in the NDB. Therefore each individual contributes multiple assessments and these are likely to be correlated with each other. All the models presented here reflect this correlation using random effects terms. We compare the different statistical models using a number of different measures that are commonly used to assess how well the predictions from the model fit the actual data: Akaike’s and Bayesian information criteria (AIC/BIC), mean absolute error (MAE) and root mean squared error (RMSE).

Many RA cost-effectiveness analyses are performed by simulating many hypothetical, individual patients [7, 17]. By tracking these patients over a long time period, and simulating their course of disease both with and without the health technology that is the subject of the analysis, an assessment of the difference in costs and benefits can be made. In this situation, the cost-effectiveness analyst requires our statistical models to estimate EQ-5D scores for these individuals. This is different from the average EQ-5D score. To reflect this use of the model results, we simulated a set of 100 modelled EQ-5D scores for each of the patients in the NDB dataset. This further illustrated differences between the observed data and the results generated by the linear regression and the mixture model approaches.

Results

A four-class mixture model was selected as the optimal model. Explanatory variables enter the model in two ways. First, within each class, EQ-5D is predicted by HAQ and HAQ², pain, age and age². Second, the probability of any patient’s observation being in each of the four classes is based on HAQ, pain and pain². The optimal linear regression model included HAQ and HAQ², pain, age and age². However, this model suffered very poor fit particularly at the extremes of good health and poor health.

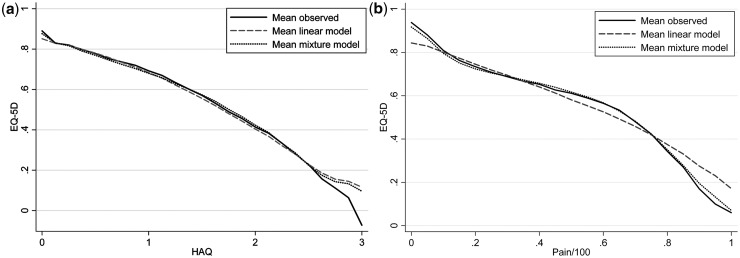
The mixture model vastly outperformed the linear model in terms of summary fit measures. AIC and BIC were both lower (indicating better fit) for the mixture model and there was a 9.6% improvement in MAE and a 3.4% improvement in RMSE. Importantly, the improvement in fit was greatest at the extremes of very poor and very good health. For those patients with an HAQ either between 0 and 1 or between 2 and 3, MAE improved by more than 11%. At pain scores of 0, the MAE reduces from 0.13 to 0.08, a 35% improvement. At pain scores exceeding 95, the MAE reduces from 0.23 to 0.18, a 22% improvement. These features are evident in Fig. 2, which plots the mean EQ-5D versus (a) HAQ and (b) pain for the observed data, the linear regression model and the preferred mixture model. Results for this model are reported in Table 2.

Fig. 2.

Mean observed and predicted values for linear and mixture models: (a) HAQ vs EQ-5D and (b) pain vs EQ-5D.

Table 2.

Results from the four-class mixture model

	Variable	Parameter	Robust s.e.	t-value	P-value
Explanatory variables within class 1	HAQ	−0.0898	0.0027	−32.9151	0.0000
	HAQ2	0.0005	0.0009	0.5892	0.5557
	Pain/100	−0.0580	0.0023	−25.4275	0.0000
	Age/10m	0.0049	0.0005	10.1656	0.0000
	Age/10m2	0.0003	0.0002	1.2111	0.2258
Explanatory variables within class 2	HAQ	0.0544	0.0301	1.8043	0.0712
	HAQ2	−0.0509	0.0100	−5.1027	0.0000
	Pain/100	−0.3841	0.0225	−17.0781	0.0000
	Age/10m	0.0291	0.0035	8.2411	0.0000
	Age/10m2	0.0023	0.0017	1.3532	0.1760
Explanatory variables within class 3	HAQ	−0.1415	0.0076	−18.5781	0.0000
	HAQ2	0.0155	0.0027	5.7871	0.0000
	Pain/100	−0.0839	0.0089	−9.3978	0.0000
	Age/10m	0.0037	0.0012	3.2078	0.0013
	Age/10m2	0.0007	0.0006	1.1702	0.2419
Explanatory variables within class 4	HAQ	−0.1958	0.0811	−2.4137	0.0158
	HAQ2	0.0347	0.0246	1.4097	0.1586
	Pain/100	−0.0127	0.0693	−0.1839	0.8541
	Age/10m	−0.0043	0.0058	−0.7417	0.4583
	Age/10m2	0.0002	0.0021	0.1106	0.9119
Variances for each class	Variance 1	0.0025	0.0001	48.7842	0.0000
	Variance 2	0.0240	0.0016	14.8595	0.0000
	Variance 3	0.0022	0.0002	10.2405	0.0000
	Variance 4	0.0044	0.0042	1.0374	0.2995
Random effects terms	Intercept 1	0.8141	0.0013	629.4830	0.0000
	Intercept 2	0.4266	0.0164	25.9934	0.0000
	Intercept 3	0.3297	0.0081	40.6365	0.0000
	Intercept 4	1.0220	0.0327	31.2430	0.0000
	Male	−0.0265	0.0013	−20.9092	0.0000
Random effects	Variance	0.0026	0.0001	46.2489	0.0000
Explanatory variables explaining the probability of class membershipa	Intercept 1	−1.2746	0.0637	−20.0245	0.0000
	HAQ	0.2420	0.4424	0.5471	0.5843
	Pain/100	23.4673	0.5897	39.7970	0.0000
	Pain/1002	−21.5513	0.6707	−32.1307	0.0000
	Intercept 2	−6.6310	0.2597	−25.5366	0.0000
	HAQ	2.1936	0.4234	5.1808	0.0000
	Pain/100	18.3719	1.2220	15.0337	0.0000
	Pain/1002	−13.8001	0.8071	−17.0981	0.0000
	Intercept 3	−7.4768	0.2988	−25.0242	0.0000
	HAQ	1.0517	0.4344	2.4209	0.0155
	Pain/100	25.3396	1.1359	22.3075	0.0000
	Pain/1002	−16.9622	0.7624	−22.2473	0.0000

^aThese probabilities are computed using class 4 as the reference.

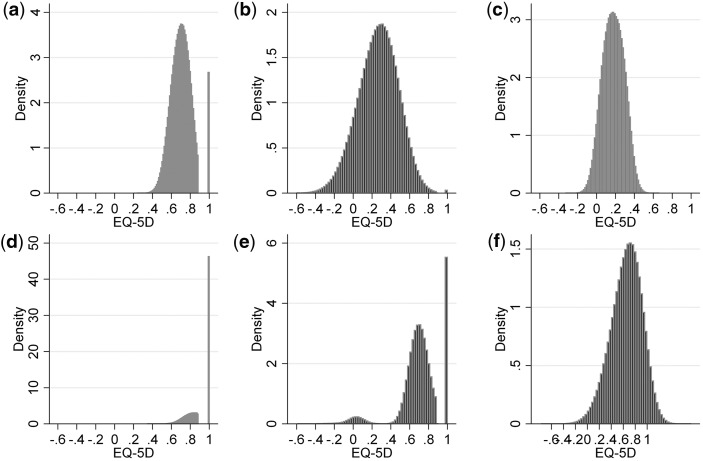
The first class is by far the largest, with a mean probability of class membership of 0.73. In this class, HAQ and pain are negatively related to EQ-5D (P = 0.000) (Table 2). HAQ² is not significant. A positive relationship with age and age² is demonstrated but in the case of age² this is not statistically significant (P = 0.230). The average characteristics of those patients most likely to be in this class are very similar to those of the average overall dataset. Notably, these are less severely affected patients with a mean HAQ of approximately 1, EQ-5D of 0.67 and disease duration of 17 years. Fig. 3a illustrates that this component of the model has a peak around 0.7 that coincides with that of the observed data in Fig. 1. This component also contributes to the mass of data at EQ-5D equal to 1, but does not contribute significantly to the lower end of the distribution.

Fig. 3.

Distribution of simulated values from the four-component mixture and linear models: (a)–(d) for each component individually, (e) four-class combined and (f) linear model.

The mean probability of an observation being in the second class is 0.05, making it the smallest class. This component of the model has a large spread, including both those patients in the most severe EQ-5D health states and those in full health (Fig. 3b). The coefficients on HAQ and HAQ² indicate that EQ-5D decreases, by increasing amounts, as HAQ worsens. The impact of pain on EQ-5D in this group is the most pronounced of all the classes. In those patients most likely to be assigned to this group, the mean HAQ is almost 2.76 (s.d. 0.23), EQ-5D is 0.33 (s.d. 0.32), but pain is relatively mild at 10.3 (s.d. 11.2). Patients most likely to be in this group have an average RA duration in excess of 31 years.

Fig. 3c shows that the fourth component is centred around EQ-5D of 0.2 and accounts in part for the second element of the bi-modal EQ-5D distribution. Seven per cent of patients are most likely to be assigned to this component. HAQ is negatively associated with EQ-5D and is much greater in magnitude than the positive coefficient on HAQ². Pain is also negatively associated with EQ-5D. This is a class made up of patients with poor functional status. The mean HAQ is 2.03 (s.d. 0.44). These patients also have the most severe average pain score for any of the four groups at 87.8 (s.d. 7.4).

The fourth class shows no statistically significant relationship between EQ-5D and either age or pain. HAQ is negatively related to EQ-5D (P < 0.05). HAQ² is not statistically significant. This group of 14% of the dataset is made up of patients with mild or no symptoms. The mean HAQ is 0.15 (s.d. 0.27), pain is 2.3 (s.d. 2.5) and EQ-5D is 0.93 (s.d. 0.11). Fig. 3d illustrates how this element of the model contributes predominantly to the mass of values at EQ-5D equal to 1.

Fig. 3e shows that the key features of the EQ-5D data distribution (Fig. 1) are replicated by the bespoke mixture model: a mass of observations at 1, a gap to the next set of feasible values, tri-modal and does not predict values outside the feasible range either at the top or the bottom. The linear regression model has none of these features (Fig. 3f).

Discussion

Cost-effectiveness analyses of treatments for patients with RA frequently estimate health benefits in terms of QALYs by estimating the relationship between preference-based outcome measures like EQ-5D and clinical outcome measures like HAQ. However, the statistical models used to do this tend to be relatively simplistic and do not account for the many idiosyncrasies of the EQ-5D instrument and valuation system. For this reason, such approaches result in systematically biased estimates that undervalue the benefits of treatments. Unsurprisingly, this has led to criticism from the rheumatology community since the methods used to estimate these relationships are not merely of academic interest, but form critical components of the analyses that reimbursement authorities across the world rely on in reaching funding decisions [13]. These features are not limited to the UK version of the EQ-5D and many are present in other quality-of-life instruments used to estimate QALYs such as the SF-6D [2] and the Health Utilities Index [3]. Indeed, comparisons of linear models using several of these instruments have been performed in RA using data from the NDB [10].

This study uses a very large dataset to refine a flexible statistical approach that was designed specifically to address such shortcomings.

Results show that the preferred four-component model does indeed overcome the problems of poor fit associated with simplistic techniques. Fit is substantially better at the extremes of the distribution and there is no evidence of the systematic undervaluation of the benefits of treatment. Where economic models estimate benefits over a very long time period, these differences will have a large additive effect year after year over a patient’s lifetime, which could be of critical importance in informing policy makers. For example, many current estimates of biologic therapies place them right at the boundary of what decision makers consider to be cost effective. Even marginal changes in the values that inform these estimates are therefore going to be of direct importance to clinicians and their patients.

Furthermore, the model is not capable of predicting values that lie outside the feasible range (−0.561 to 1). Simple approaches generate such nonsensical estimates particularly when they are used to simulate individual patients and when the parameter uncertainty in the estimates is reflected in cost-effectiveness models. The covariance matrix that would allow analysts to perform such analyses with this model is available online (Supplementary Data, available at Rheumatology Online).

Many cost-effectiveness analyses focus on changes in HAQ due to treatment. This study demonstrates that better estimates of the benefits of treatments in terms of QALYs will be gained if HAQ and pain are simultaneously considered. This is neither new [10, 14] nor surprising when one considers that pain is one of the five domains in the EQ-5D instrument and contributes the greatest weight to the summary score. Yet this finding implies that economists will need to consider the decision models they use and how meta-analysis methods can capture treatment benefits appropriately.

The mixture model approach that has been reported here was implemented because it offers a flexible framework for complex distributions like EQ-5D. However, it also opens the potential for the consideration of patient subgroups: the relationship between HAQ and pain to EQ-5D is very different within the four components of the model. In some instances, pain is particularly important and in others it is HAQ that is critical. The patients who are likely to form these groups are also very different in terms of age, duration and severity of disease. These implications require further investigation. It is also worth noting that in the previous implementation of this modelling approach in RA, the preferred model comprised three components. The addition of a fourth class here improved fit at the bottom end of the EQ-5D distribution. Data at this extreme of poor health were lacking in the study by Hernández et al. [14]. This issue is diminished but not eliminated by using the NDB. The only place where the mixture model does not fit extremely well is where the HAQ exceeds 2.5. While a better model fit would be achieved by fitting a greater number of classes to the mixture, this would be at the expense of generalizability. The validity of observations from patients at such extreme levels of functional impairment may also be questionable and for this reason we propose the four-class model.

More recent clinical trials of newer biologic agents are increasingly incorporating preference-based outcome measures. However, while it has often been claimed that direct health utility assessment is preferable to using indirect mapping methods [4, 9], this is not necessarily the case. Here we have a dataset comprising in excess of 100 000 observations across the full spectrum of functional disability and pain combined with an appropriate method to relate these measures to EQ-5D. On the other hand, clinical studies, particularly trials, have limited patient variability and follow-up. Economic evaluations therefore extrapolate well beyond these clinical studies, often over the entire patient lifetime, to accurately capture the impact of treatment on long-term costs and health benefits. Our approach offers a means by which such extrapolations can be undertaken.

Furthermore, even if new trials include measures like EQ-5D, the entirety of the evidence base remains relevant, including studies of older treatments as comparators. Hence, given that such estimates will be critical to reimbursement decisions for some time to come, it is of vital importance for patients and their physicians that treatment benefits are appropriately valued. The results reported here can be used in future economic evaluations.

Disclosure statement: The authors have declared no conflicts of interest.

Supplementary data

Supplementary data are available at Rheumatology Online.