High-Dimensional Structured Feature Screening Using Binary Markov Random Fields

Abstract

Feature screening is a useful feature selection approach for high-dimensional data when the goal is to identify all the features relevant to the response variable. However, common feature screening methods do not take into account the correlation structure of the covariate space. We propose the concept of a feature relevance network, a binary Markov random field to represent the relevance of each individual feature by potentials on the nodes, and represent the correlation structure by potentials on the edges. By performing inference on the feature relevance network, we can accordingly select relevant features. Our algorithm does not yield sparsity, which is different from the particular popular family of feature selection approaches based on penalized least squares or penalized pseudo-likelihood. We give one concrete algorithm under this framework and show its superior performance over common feature selection methods in terms of prediction error and recovery of the truly relevant features on real-world data and synthetic data.

1 Introduction

The dimensionality of machine learning problems keeps increasing, and feature selection becomes a necessary procedure in many applications, resulting in improved performance, greater efficiency and better interpretability (Guyon & Elisseeff, 2003). However, feature selection in many applications becomes more and more challenging due to both the increasing number of features and the complex correlation structure among the features. For instance, in genome-wide association studies (GWAS), researchers are interested in identifying all relevant genetic makers (single-nucleotide polymorphisms, or SNPs) among millions of candidates with hundreds or thousands of samples. Usually the truly relevant markers are rare and only weakly associated with the response variable. A screening feature selection procedure is usually the only method computationally feasible because of the high dimension, but it is typically unreliable and suffers from high false positive rate. On the other hand, the features are usually correlated with one another. For example in GWAS, most SNPs are highly correlated with one or more nearby SNPs, with squared Pearson correlation coefficients well above 0.8. In the next paragraph, we give a toy example showing that taking into account the correlation between features can be beneficial.

Suppose that our measured features are correlated because they are all influenced by some hidden variable. This is often the case in GWAS, where our features are markers that are easy to measure, but the actual underlying causal genetic variation is not measured. Suppose that our data are generated from the Bayesian network in Figure 1(a). All variables are binary. Hidden variables are denoted by H₁ and H₂. H₁ is weakly associated with the class variable. H₂ is not associated. Both H₁ and H₂ have a probability of 0.5 of being 1. Observed variables A and B are associated with H₁. Observed variables C and D are associated with H₂. We label the arc from H₁ to A with a 0.8 to denote that A is 0 with probability 0.8 when H₁ is 0, and A is 1 with probability 0.8 when H₁ is 1. Under the distribution, the probability that A and the class variable take the same value is 0.8×0.6+(1−0.8)×(1−0.6) = 0.56, and it is the same for B. The probability that H₂ takes the same value with the class variable is 0.5. C and D take the same value with the class variable with probability 0.5 respectively. The probability that A and B take the same value is 0.68, and it is the same for C and D. Suppose that there are more nonassociated hidden variables than associated ones and we generate a small sample set from this distribution specified by the Bayesian network. There will be some nonassociated variables (i.e. C) that appear to be as promising as associated features (i.e. B) if we only look at the sample-based probability of agreement with the class variable. Suppose that C appears as promising as A and B, with a probability of 0.56 agreement with the class variable. In Figure 1(b), the number on the dotted edges stands for the sample-based probability of agreement with the class variable. Since D is expected to show agreement with C with probability 0.68, we expect the sample-based probability of agreement between D and the class variable to be 0.56×0.68+(1−0.56)×(1−0.68) = 0.52. If we are using any screening method to evaluate the features, it will rank A, B and C equally high. However in this case, we should make use of the information that C is more likely to be a false positive because its highly correlated feature D does not appear as relevant as does A's (B's) highly-correlated feature. Therefore, we seek a way of taking into account the correlation structure in this manner during the procedure of feature selection.

Figure 1.

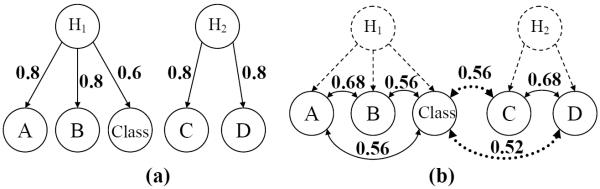
One Bayesian network example.

Markov random fields provide a natural way of representing the relevance of each feature and the correlation structure among the features. The relevance of each feature is represented as a node that takes the values in {0, 1}. The correlation structure among the features is captured as the potentials on the edges. We can regard the feature selection problem in the original covariate space as an inference problem on this binary Markov random field which is called a feature relevance network. Section 2 gives a precise description of the feature relevance network and introduces one feature selection algorithm. Sections 3 and 4 evaluate the algorithm on synthetic data and real-world data respectively. We finally conclude in Section 5.

2 Method

2.1 Feature Relevance Network

Suppose that we have a supervised learning problem with d features and n samples (d ⪢ n). A feature relevance network (FRN) is a binary Markov random field on a random vector X = (X₁, …, X_d) ∈ {0, 1}^d described by undirected graph G(V, E) with the node set V and the edge set E. The relevance of feature_i is represented by the state of node_i in V. X_i = 1 represents that feature_i is relevant to the response variable whereas X_i = 0 represents that feature_i is not relevant. Correlation between X_i and X_j is denoted by an edge connecting node_i and node_j in E. The potential on node_i, ϕ(X_i), depicts the relative probability that feature_i is relevant to the response variable when feature_i is analyzed individually. The potential on the edge connecting node_i and node_j, ψ(X_i, X_j), depicts the relative joint probability that feature_i and feature_j are relevant to the response variable jointly. For a given FRN, the probability of a given relevance state x = (x₁, …, x_d) is

$$\begin{array}{cc}\hfill P\left(\mathrm{x}\right)& =\frac{1}{Z}\prod _{i=1}^{\mid V\mid }\varphi \left(x_i\right)\prod _{(i,j)\in E}\psi (x_i,x_j)\hfill \\ \hfill & =\frac{1}{Z}\exp \left\{\sum _{i=1}^{\mid V\mid }\log \varphi \left(x_i\right)+\sum _{(i,j)\in E}\log \psi (x_i,x_j)\right\},\hfill \end{array}$$ (1)

where Z is a normalization constant, and |V| = d.

Performing feature selection with an FRN involves a construction step and an inference step. To construct an FRN, one needs set ϕ(X_i) for i = 1, …, |V| and ψ(X_i, X_j) for (i, j) ∈ E. Section 2.2 continues to discuss the construction step in detail. In the second step, one has to find the most probable state (maximum a posterior, or MAP) of the FRN, and the features can be selected according to its MAP state. For a binary pairwise Markov random field, finding the MAP state is equivalent to an energy function minimization problem (Boykov et al., 2001) which can be exactly solved by a graph cut algorithm (Kolmogorov & Zabih, 2004). Section 2.3 discusses the inference step in detail.

2.2 The Construction Step

In the construction step, we set the potential functions ϕ(X_i) and ψ(X_i, X_j). Suppose that we are using hypothesis testing to evaluate the relevance of each individual feature, and we observe the test statistic S = (S₁, …, S_d). We assume that S_i's are independent given X. Suppose that the probability density function of S_i given X_i = 0 is f₀, and the density of S_i given X_i = 1 is f₁. If f₀ and f₁ are Gaussian, the model is essentially a coupled mixture of Gaussians model(Wainwright & Jordan, 2006). Here we give one concrete example. Suppose that we are trying to identify whether a binary feature_i is relevant to the binary response variable Y ∈ {0, 1} with empirical counts from data shown in Table 1.

Table 1.

Empirical counts at feature_i with a binary response variable Y.

	featurei = 0	featurei = 1	Total
Y = 1	u 0	u 1	u
Y = 0	u 0	v 1	v
Total	n 0	n 1	n

If we use a two-proportion z-test to test the relevance of feature_i with Y, the test statistic is

$$S_i=\frac{u_1∕u-v_1∕v}{\sqrt{u_0{u}_1∕u^3+v_0{v}_1∕v^3}}.$$ (2)

S_i|X_i = 0 is approximately standard normally distributed. S_i|X_i = 1 is approximately normally distributed with variance 1 and some nonzero mean δ_i. Many GWAS applications employ logistic regression followed by a likelihood ratio test to identify associated SNPs. We call this testing procedure LRLR. In this situation, S_i|X_i = 0 has an asymptotic χ² distribution with 2 degrees of freedom and S_i|X_i = 1 has an asymptotic non-central χ² distribution with 2 degrees of freedom. We give the details in the supplementary material.

In the FRN, we only connect a pair of nodes if their corresponding features are correlated. After specifying the structure of the FRN, we have a parameter learning problem in the Markov random field. The parameters include ϕ(X_i) for i = 1, …, |V| and ψ(X_i,X_j) for (i, j) ∈ E. We claim learning all these parameters is extremely difficult and practically unrealistic for three reasons. First, learning parameters is difficult by nature in undirected graphical models due to the global normalization constant Z (Wainwright et al., 2003; Welling & Sutton, 2005). Second, there are too many parameters to estimate. Last but not least, X is latent and we only have one training sample which is S. Therefore, we propose a compromise solution as follows. Although this solution looks arbitrary, it can be easily applied in practice and has an interpretation given in formula (9).

The way of setting ψ(X_i, X_j) comes from the observation that the chance that X_i and X_j agree increases as the magnitude of the correlation between feature_i and feature_j increases. Therefore, if we can estimate the Pearson correlation coefficient r_ij between feature_i and feature_j, we set

$$\psi (X_i,X_j)=e^{\lambda \mid r_{\mathit{ij}}\mid I(X_i=X_j)},$$ (3)

where λ (λ > 0) is a tradeoff parameter and I(X_i = X_j) is an indicator variable that indicates whether X_i and X_j take the same value.

The way of setting ϕ(X_i) is as follows. We set

$$\varphi \left(X_i\right)=e^{\mid X_i-q_i\mid },$$ (4)

where q_i = 1 − p_i and p_i = P(feature_i is relevant). With hypothesis testing in (2), we usually set p_i to be 1 if the absolute value of the test statistic is greater than or equal to some threshold ξ and 0 if otherwise. We call the p_i (from such a “hard” method using some threshold) $p_i^H$, namely

$$p_i^H=\{\begin{array}{cc}1,\hfill & \mathit{if}\mid S_i\mid \ge \xi ,\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}\phantom{\}}$$

We can also set p_i by Bayes' rule if we know f₁ and f₀. We call it $p_i^B$.

$$p_i^B=\frac{1}{\alpha f_0\left(s_i\right)+1},$$ (5)

where

$$\alpha =\frac{P(X_i=0)}{f_1\left(s_i\right)P(X_i=1)}.$$ (6)

However in most of the cases, the parameter δ_i in f₁ is unknown to us. In the two-proportion z-test in (2), δ_i refers to the mean parameter in f₁ which is Gaussian. In LRLR, δ_i refers to the non-centrality parameter in f₁ which is non-central χ². We can use its data-driven version ${\delta }_i^{\ast }$. This step has a flattening effect on calculating p_i because it assumes the values of the test statistic for relevant features are uniformly distributed. Therefore, we introduce an adaptive procedure for calculating p_i by

$$p_i=\gamma p_i^H+(1-\gamma )p_i^B,$$ (7)

where 0 ≤ γ ≤ 1. We choose ξ in $p_i^H$ to be the test statistic that makes $p_i^B$ be 0.5 in (5). Eventually, we have three parameters in the construction step, namely λ, γ and α. In practice, one can tune the three parameters from cross-validation.

2.3 The Inference Step

For a given FRN, we need to find the most probable state which maximizes the posterior probability of (1) so as to select the relevant features. Finding the MAP state of the Markov random field specified by (1) is equivalent to minimizing its corresponding energy function E, which is defined as

$$E\left(\mathrm{x}\right)=-\sum _{i=1}^{\mid V\mid }\log \varphi \left(x_i\right)-\sum _{(i,j)\in E}\log \psi (x_i,x_j).$$ (8)

As long as −log ψ(X_i, X_j) is submodular, the energy minimizing problem can be exactly solved by the graph-cut algorithm on a weighted directed graph F(V′,E′) (Kolmogorov & Zabih, 2004) in polynomial time. If ϕ(X_i) and ψ(X_i, X_j) are set as formula (4) and formula (3), the optimization problem is

$$\underset{x}{\min }\left\{\sum _{i=1}^{\mid V\mid }\mid x_i-p_i\mid +\lambda \sum _{i,j=1}^{\mid V\mid }I(x_i\ne x_j)\mid r_{\mathit{ij}}\mid \right\},$$ (9)

which can be interpreted as seeking a state of the FRN with two different goals. The first goal is that the MAP state is close to the relevance of the features when evaluated individually, which is implied by the first term. The second goal is that strongly correlated features arrive at the same state, which is implied by the second term. We can run a max-flow-min-cut algorithm, such as the push-relabel algorithm (Goldberg & Tarjan, 1986) or the augmenting path algorithm (Ford & Fulkerson, 1958), to find the minimum-weight cut of this directed graph; a cut is a set of edges whose removal eliminates all paths between the source and sink nodes. Finally, after we cut the graph, every feature node is either connected to the source node or connected to the sink node. We select the features that are connected with the source node.

2.4 Related Methods

A variety of feature selection algorithms appear in both the statistics and machine learning communities, such as FCBF (Yu & Liu, 2004), Relief (Kira & Rendell, 1992), DISR (Meyer et al., 2008), MRMR (Peng et al., 2005), “cat” score (Zuber & Strimmer, 2009) and CAR score (Zuber & Strimmer, 2011). Variables can be selected within SVM (Guyon et al., 2002; Zhang et al., 2006; Ye et al., 2011). With the rapid increase of feature size, some approaches focus on high-dimensional or ultrahigh-dimensional feature selection (Wasserman & Roeder, 2009; Fan et al., 2009). One particular popular family of approaches is based on penalized least squares or penalized pseudo-likelihood. Specific algorithms include but are not restricted to LASSO (Tibshirani, 1996), SCAD (Fan & Li, 2001), Lars (Efron et al., 2004), Dantzig selector(Candés & Tao, 2007), elastic net (Zou & Hastie, 2005), adaptive elastic net (Zou & Zhang, 2009), Bayesian lasso (Hans, 2009), pairwise elastic net (Lorbert et al., 2010), exclusive Lasso (Zhou et al., 2010) and regularization for nonlinear variable selection (Rosasco et al., 2010). Several recent algorithms also take into account the structure in the covariate space, such as group lasso (Yuan & Lin, 2006), fused lasso with a chain structure (Tibshirani & Saunders, 2005), overlapping group lasso (Jenatton et al., 2009; Jacob et al., 2009), graph lasso (Jacob et al., 2009), group Dantzig selector (Liu et al., 2010) and EigenNet (Qi & Yan, 2011). However, most of the penalized least squares or penalized pseudo-likelihood feature selection methods are to find a minimal feature subset optimal for regression or classification, which is termed the minimal-optimal problem (Nilsson et al., 2007). However in this paper, the goal of feature screening is to identify all the features relevant to the response variable which is termed the all-relevant problem (Nilsson et al., 2007). The hidden Markov random field model in our FRN has also been used in other problems, such as image segmentation (Celeux et al., 2003) and gene clustering (Vignes & Forbes, 2009).

3 Simulation Experiments

In this section, we generate synthetic data and compare the FRN-based feature selection algorithm with other feature selection algorithms. We generate binary classification samples with an equal number (n) of positive samples and negative samples. In order to generate correlated features, we introduce h hidden Bernoulli random variables H₁,…,H_h. For each hidden variable H_i, we generate m observable Bernoulli random variables X_ij (j = 1, …, m), where X_ij takes the same value as H_i with a probability t_i. We set the first πh hidden variables to be the true associated hidden variables and accordingly we have πhm true associated observable features, where π is the prior probability of association. For associated hidden variable H_i, we set P(H_i = 1) to be uniformly distributed on the interval [0.01,0.5]. We also set the relative risk, defined as follows,

$$\mathit{rr}=\frac{P(\text{positive}\mid H_i=1)}{P(\text{positive}\mid H_i=0)}.$$ (10)

For each nonassociated hidden variable H_i we also set P(H_i = 1) to be uniformly distributed on the interval [0.01,0.5]; this stays the same for the positive samples and negative samples.

One baseline feature screening method is the two-proportion z-test which is given in formula (2). We rank the features with the P-values from the tests. The other baseline feature selection method is the elastic net (in the R package “glmnet”). Unlike other penalized least squares or penalized pseudo-likelihood feature selection methods, the elastic net approach does not select a sparse subset of features and is usually good at recovery of all the relevant features. For the elastic net penalty, we set α to be 0.5, and we use a series of 20 values for λ. For our FRN-energy minimizing algorithm, we exactly follow formula (5), formula (6) and formula (7). We choose a series of 20 values for α, and set γ to be 0, and λ to be 1. Since we have the ground truth of which features are relevant to the response variable, we can compare the ROC curves and the precision-recall curves for feature capture (i.e., we treat associated features as positives).

For the first set of experiments, we set n = 500, h = 1000, m = 5, t_i uniformly distributed on the interval (0.8, 1.0), π = {0.025, 0.05}, and rr = {1.1, 1.2, 1.3}. Because we have 2 values for π and 3 values for the relative risk rr, we run the simulation a total of 6 times for different combinations of the two parameters. The results are shown in Figure 2 and Figure 3. When the relative risk is 1.1, it is difficult for all three algorithms to recover the relevant features. When the relative risk is 1.2 or 1.3, our FRN algorithm outperforms the two baseline algorithms. The prior of association π does not make too much difference for the ROC curves. However for the precision-recall curves, when π is larger, the precision will be higher for the same recall value in the same parameter configuration.

Figure 2.

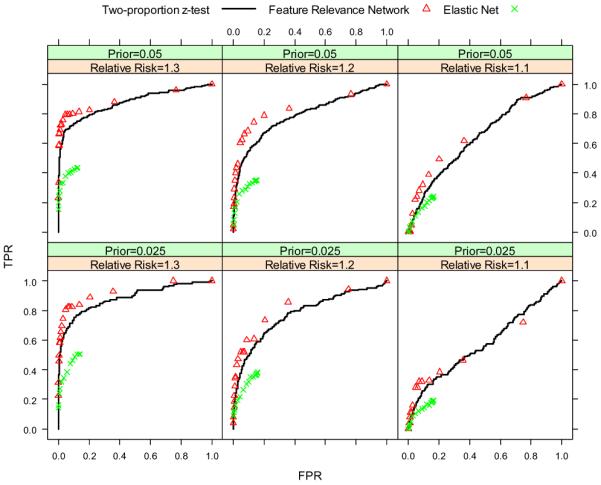
ROC curves of two-proportion z-test, FRN and elastic net for different prior probabilities and different relative risks.

Figure 3.

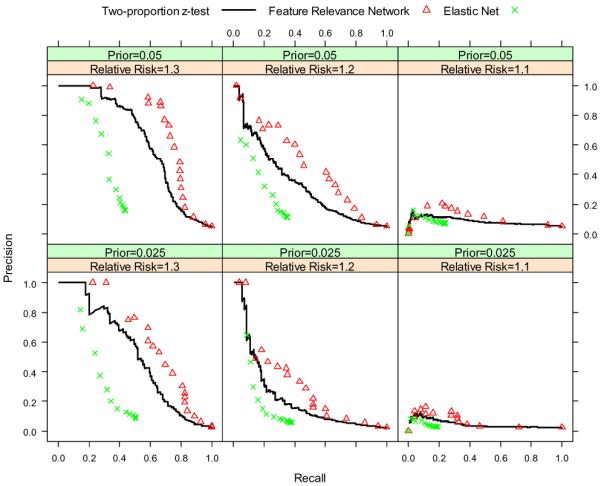
Precision-recall curves of two-proportion z-test, FRN and elastic net for different prior probabilities and different relative risks.

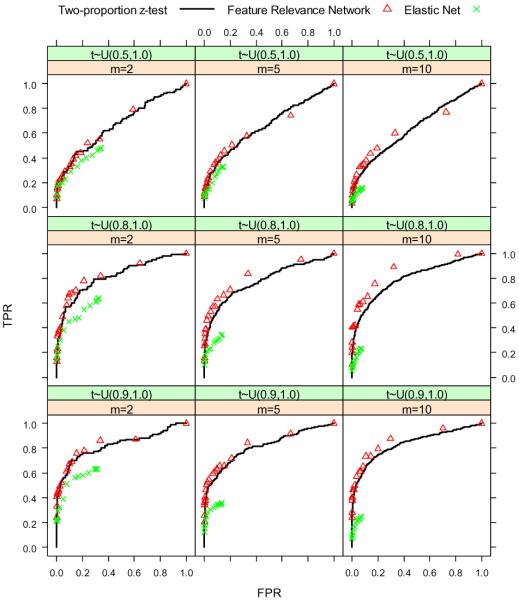
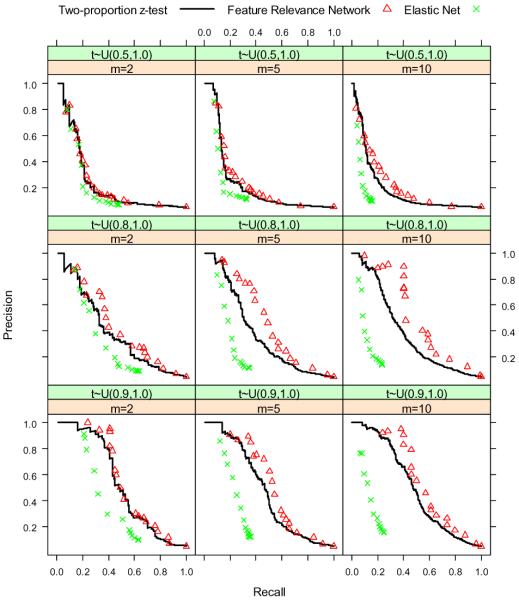
For the second set of experiments, we set n = 500, h = 1000, π = 0.05, rr uniformly distributed on the interval (1.1, 1.3), m = {2, 5, 10}, and t_i uniformly distributed on the interval (τ, 1.0) where τ = {0.5, 0.8, 0.9}. Because we have 3 values for m and 3 choices for t_i, we run the simulation a total of 9 times for different combinations of the two parameters. The results are shown in Figure 4 and Figure 5. When the features have a lot of highly correlated neighbors, the FRN approach shows an advantage over the ordinary screening method and the elastic net. However, when the features do not have a lot of neighbors or when the neighbors are not highly correlated, the FRN does not help a lot.

Figure 4.

ROC curves of two-proportion z-test, FRN and elastic net when we choose different correlation structures of covariates.

Figure 5.

Precision-recall curves of two-proportion z-test, FRN and elastic net when we choose different correlation structures of covariates.

4 Real-world Application: A Genome-wide Association Study on Breast Cancer

4.1 Background

A genome-wide association study analyzes genetic variation across the entire human genome, searching for variations that are associated with a given heritable disease or trait. The GWAS dataset on breast cancer for our experiment comes from NCI's Cancer Genetics Markers of Susceptibility website (http://cgems.cancer.gov/data/). We name this dataset CGEMS data. It includes 528, 173 SNPs as features for 1, 145 patients and 1, 142 controls. Details about the data can be found in the original study (Hunter et al., 2007). This GWAS also exhibits weak-association, and the relative risk of the several identified SNPs are between 1.07 and 1.26 (Pharoah et al., 2008). The reasons for weak association are that (i) it is estimated that genetics only accounts for about 27% of breast cancer risk and the rest is caused by environment (Lichtenstein et al., 2000) and (ii) breast cancer and many other diseases are polygenic, namely the genetic component is spread over multiple genes. Therefore, given equal numbers of breast cancer patients and controls without breast cancer, the highest predictive accuracy we might reasonably expect from genetic features alone is about 63.5%, obtainable by correctly predicting the controls and correctly recognizing 27% of the cancer cases based on genetics. If we select SNPs which are already identified to be associated with breast cancer by other studies (for example, one study (Pharoah et al., 2008) uses a much larger dataset which includes 4,398 cases and 4,316 controls, and confirms results on 21,860 cases and 22,578 controls), we get a set of 19 SNPs (the closest feature set we have the ground truth for this task). Using these 19 SNPs as input to leading classification algorithms, such as support vector machines, results in at most a 55% predictive accuracy.

4.2 Experiments on CGEMS Data

Since we do not know which SNPs are truly associated, we are unable to evaluate the recovery of the truly relevant features as what we do in Section 3. Instead, we compare the performance of supervised learning when coupled with the feature selection algorithms. The baseline feature selection methods include (i) logistic regression with likelihood ratio test (LRLR), (ii) FCBF (Yu & Liu, 2004), (iii) Relief (Kira & Rendell, 1992) and (iv) lasso penalized logistic regression (LassoLR) (Wu et al., 2009). Because SVMs have been shown to perform particularly well on high-dimensional data such as genetic data (Wei et al., 2009), we employ it as our machine learning algorithm to test the performance of feature selection methods. All the experiments are run in a stratified 10-fold cross-validation fashion, using the same folds for each approach, and each feature selection method is paired with a linear SVM. For running the SVM, we convert the SNP value AA into 1, AB into 0, and BB into −1 where A stands for the common allele at this locus and B stands for the rare allele. For each fold, the entire training process (feature selection and supervised learning) is repeated using only the training data in that fold before predictions are made on the test set of that fold, to ensure a fair evaluation. For all feature selection approaches, we tune the parameters in a nested cross-validation fashion. In each training-testing experiment of the 10-fold cross-validation, we have 9 folds for training and 1 fold for testing. On the 9 folds of training data, we carry out a 9-fold cross-validation (8 folds for training and 1 fold for tuning) to select the best parameters. Since we have almost equal numbers of cases and controls, we use accuracy to measure the classification performance for both inner and outer cross-validation.

We build the FRN based on LRLR. Namely, we follow the calculation of p_i in Section 2.2. Then we exactly use formula (4) and formula (3) to set the ϕ(X_i) and ψ(X_i, X_j). α in (5) and (6) essentially determines the threshold of the mapping function which maps the test statistic to the association probability p_i. Our tuning considers 5 values of α, namely 500, 1000, 1500, 2500, and 5000. γ in (7) determines the slope of the mapping function. We considers 5 values of γ, namely 0.0, 0.25, 0.5, 0.75, and 1.0. λ in (9) is the tradeo parameter between fitness and smoothness. Our tuning considers 4 values of λ, namely 0.25, 0.5, 0.75, and 1.0. Usually if there are multiple parameters to tune in supervised learning, one might use grid search. However, since we will have in total 100 parameter configurations if we grid-search them, it might overfit the parameters. Instead, we tune the parameters one by one. We first tune α based on the average performance over the different γ and λ values. With the best α value, we then tune γ based on the average performance over different λ values. Finally we tune λ with the selected α and γ configuration. The computation for correlation between features can result in high run-time and space requirements if the number of features is large. General push-relabel algorithms and augmenting-path algorithms both have O(|V|²|E|) time complexity. Owing to these two reasons, it is necessary to remove a portion of irrelevant SNPs in the first step to reduce the complexity when applying the FRN-based feature selection algorithm to this GWAS data. Therefore, in the experiments on the GWAS data we only keep the top k SNPs based on the individual relevance measurements. Tuning k may lead to better performance. Since we already have three parameters to tune for the energy minimizing algorithm, we fix k at 50, 000. For the baseline algorithms, there is one parameter f, the number of features to select for supervised learning. We tune it with 20 values, namely 50, 100, 150, …, and 1000.

As listed in Table 2, linear SVM's average accuracy is 53.08% when the FRN algorithm is used. When LRLR, FCBF, Relief and LassoLR are used, linear SVM's average accuracies are 50.64%, 51.68%, 50.90% and 48.75% respectively. We perform a significance test on the 10 accuracies from the 10-fold cross-validation using a two-sided paired t-test. The FRN algorithm significantly outperforms the logistic regression with likelihood ratio test algorithm and the lasso penalized logistic regression algorithm at 0.05 level.

Table 2.

The classification accuracy (%) of linear SVM coupled with different feature selection methods, logistic regression with likelihood ratio test (LRLR), FCBF, Relief, lasso penalized logistic regression (LassoLR) and feature relevance network (FRN) followed by the P-values from significance test (two-sided paired t-test) comparing the baseline algorithms with FRN.

Alg	LRLR	FCBF	Relief	LassoLR	FRN
Ace	50.64	51.68	50.90	48.75	53.08
P	0.021	0.367	0.069	0.007	–

4.3 Validating Findings on Marshfield Data

The Personalized Medicine Research Project (McCarty et al., 2005), sponsored by Marshfield Clinic, was used as the sampling frame to identify 162 breast cancer cases and 162 controls. The project was reviewed and approved by the Marshfield Clinic IRB. Subjects were selected using clinical data from the Marshfield Clinic Cancer Registry and Data Warehouse. Cases were defined as women having a confirmed diagnosis of breast cancer. Both the cases and controls had to have at least one mammogram within 12 months prior to having a biopsy. The subjects also had DNA samples that were genotyped using the Illumina HumanHap660 array, as part of the eMERGE (electronic MEdical Records and Genomics) network (McCarty et al., 2011). In total 522, 204 SNPs have been genotyped after the quality assurance step. Despite the difference in genotyping chips and the different quality assurance process, 493, 932 SNPs also appear in the CGEMS breast cancer data. Due to the small sample size, it is undesirable to repeat the same experiment procedure in Section 4.2 on Marshfield data. However, we can use it to validate the results from the experiment on the CGEMS data. We apply FRN and LRLR on CGEMS data, and compare the log odds-ratio of the selected SNPs by the two approaches on Marshfield data. The CGEMS dataset was also used by another study (Wu et al., 2010). They proposed a novel multi-SNP test approach logistic kernel-machine test (LKM-test) and demonstrated that it outperformed individual-SNP analysis method and other state-of-the-art multi-SNP test approaches such as the genomic-similarity-based test (Wessel & Schork, 2006) and the kernel-based test (Mukhopadhyay et al., 2010). Based on the CGEMS data, LKM-test identified 10 SNP sets (genes) to be associated with breast cancer. The 10 SNP sets include 195 SNPs. We set FRN to select the same number of relevant SNPs on the CGEMS data, and we compare the SNPs identified by LKM-test and the SNPs identified by FRN on a different real-world GWAS dataset on breast cancer so as to compare the performance of LKM-test and FRN.

We run FRN and LRLR on the entire CGEMS dataset and validate the selected SNPs on Marshfield data. For FRN, we tune the parameters from the 10-fold cross validation similarly. The selected parameters for FRN are α = 1000, γ = 0.5, and λ = 0.75. In total, FRN selected 428 SNPs from the CGEMS data; 393 of them appear in the Marshfield data. We pick the top 423 SNPs selected by LRLR which also result in 393 overlapped SNPs with Marshfield data. On Marshfield data we compare the log odds-ratio of the 393 SNPs selected by FRN and the 393 SNPs selected by LRLR via the quantile-quantile plot (Q-Q plot) which is given in Figure 6(a). On the CGEMS data the LKM-test selected 195 SNPs, 178 of which appear in Marshfield data. To ensure a fair comparison, we pick the 194 of the 428 SNPs selected by FRN using their individual P-values, which also yields 178 SNPs in Marsh-field data. We also compare the log odds-ratio of the 178 SNPs selected by FRN and the 178 SNPs selected by LKM-test via Q-Q plot, which is given in Figure 6(b). If the log odds-ratios of the SNPs selected by two different methods are from the same distribution, the points should lay on the 45 degree line (the red straight lines in the plots) in the Q-Q plot. However in both of the two plots we observe obvious discrepancies at the tails. When comparing the log odds-ratio on a different cohort, the top SNPs picked up by FRN appear to be much more relevant to the disease than the top SNPs selected by either LRLR or LKM-test.

Figure 6.

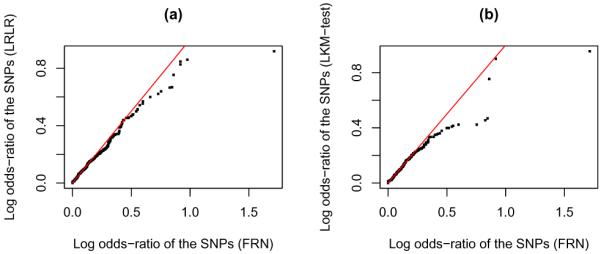
Q-Q plots for (a) comparing log odds-ratio of the SNPs selected by FRN and the SNPs selected by LRLR and (b) comparing log odds-ratio of the SNPs selected by FRN and the SNPs selected by LKM-test. The selection of SNPs is done on CGEMS data. The log odds-ratio is calculated on Marshfield data.

5 Discussion

We propose the feature relevance network as a further step for feature screening which takes into account the correlation structure among features. For simulations in Section 3, it took a few hours to finish all runs on a single CPU. For results in Section 4, we finished, including tuning parameters, in two weeks in a parallel computing environment (~ 20 CPUs). Besides the computation burden, another drawback is that our algorithm only returns the selected variables according to the MAP state. It doesn't provide P-values or other measures for each variable. In this paper, the correlation structure among the features is pairwise, which is represented as edges in an undirected graph. However, there are also other types of correlation structure which one might want to provide as prior knowledge, such as the features coming from groups (may or may not overlap), chain structures or tree structures. Representing all these types of correlation structure with the help of Markov random fields will be one important direction for future research.

In this paper, the goal of feature screening is to identify all the features relevant to the response variable, which is termed the all-relevant problem (Nilsson et al., 2007), although we also compare the prediction performance of supervised learning due to the lack of the ground truth in the real-world GWAS application in Section 4. In some other applications, the goal of feature selection is to find a minimal feature subset optimal for classification or regression, which is termed the minimal-optimal problem (Nilsson et al., 2007). We do not address the minimal-optimal problem at all in the present paper. For solving the minimal-optimal problem in high-dimensional structured covariate space, many approaches have been well-studied under the lasso framework (Tibshirani, 1996). Specific algorithms include but are not restricted to group lasso (Yuan & Lin, 2006), fused lasso with a chain structure (Tibshirani & Saunders, 2005), overlapping group lasso (Jenatton et al., 2009; Jacob et al., 2009), graph lasso (Jacob et al., 2009) and group Dantzig selector (Liu et al., 2010).