Adaptive trials in paediatric development: dealing with heterogeneity and uncertainty in pharmacokinetic differences in children

Abstract

AIMS

To assess whether an adaptive design in early clinical trials based on the paradigm of variable dosing and controlled exposure can provide better dosing recommendations compared with the standard fixed dose approach.

METHODS

In a clinical trial simulation setting, a paediatric study was simulated using a pharmacokinetic model previously developed for abacavir. Plasma concentrations following the current recommended dose (8 mg kg⁻¹) were taken at standard sampling times, exposures (AUC) were calculated and doses individually adapted to reach the target exposure (i.e. effective exposure in adults). A second round of simulations followed with the adapted doses, and the resulting concentrations were fitted again with the same model. Exposure distributions in both conditions (i.e. fixed dose and controlled exposure) were compared with the target exposure.

RESULTS

The AUC distribution after the current dose resulted in a median exposure of 6.43 mg h l⁻¹ (90th percentile 3.13–10.67 mg h l⁻¹). A total of 61 of 128 subjects showed AUC values either too low or to high compared with the target exposure. After dose adjustment, the median exposure was 6.94 mg h l⁻¹ (5.57–8.25 mg h l⁻¹), and only 14 subjects deviated from the target range.

CONCLUSIONS

Adaptive randomization can be used to optimize dosing regimens in early paediatric clinical trials. The randomization of patients to target exposure rather than dose increases the probability of demonstrating efficacy (i.e. study power) compared with dose-controlled trials. Furthermore, it contributes to further understanding of the role of dose on the total heterogeneity in clinical response.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• In children, differences in treatment response may be influenced by the effect of developmental changes and maturation on drug disposition, which lead to ambiguous relationships between dose and exposure.

• Initial estimation of the paediatric dose is obtained by extrapolation. However, no consensus on dose selection methodologies has been reached so far.

• The paradigm compound used in this investigation is abacavir, a nucleoside reverse transcriptase inhibitor used to treat human immunodeficiency virus infection. The recommended paediatric dose is 8 mg kg⁻¹ twice daily up to a maximum of 300 mg twice daily.

WHAT THIS STUDY ADDS

• The use of adaptive rather than fixed dose protocols enables the accurate selection of the paediatric dose.

• Adaptive procedures ensure shrinkage of the observed exposure distribution around the target range irrespective of study size.

• Modelling and simulation techniques provides the basis for the systematic evaluation of the implications of dose selection in a paediatric clinical trial.

Introduction

The efficacy of a pharmacological intervention is usually described by a function that relates the effect with the dose; however, drug concentration and exposure (e.g. the area under the concentration vs. time curve (AUC)) are known to be better descriptors of the pharmacological effect. Nevertheless, fixed dose protocols are considered best practice in the assessment of efficacy in clinical trials, which often results in (an unnecessarily) large variability in response. This issue is particularly important in paediatric pharmacology, where differences in treatment response may be influenced by the effect of developmental changes and maturation on drug disposition, which lead to ambiguous relationships between dose and exposure. In this case, the interpretation of efficacy and safety findings may be inconclusive without pharmacokinetic data. This confounding effect ultimately impairs the selection of an appropriate dose range for children [1]. Unfortunately, it has been shown that the doses proposed in early clinical development propagate into clinical practice, irrespective of further considerations about the need for a different dosing recommendation during the course of development [2].

The use of model-based approaches for the characterization of pharmacokinetics in children has been recommended by regulatory agencies and clinical pharmacologists as a tool for overcoming some of the challenges associated with dose selection and dose rationale for paediatric indications [3–7]. In a recent publication, however, we have shown that limitations exist in the approach when extrapolations are required from one population to another, in particular when using data from adults to support dose selection across different age groups in the paediatric population [8, 9]. Such limitations require that careful consideration be given to dose selection during drug development when study populations may be staggered by age and an initial estimation of the paediatric dose must be obtained by extrapolation.

Based on the afore-mentioned factors, we can state that a model-based approach for the assessment of pharmacokinetics in children is necessary but not sufficient. The use of a model-based (parametric) approach, whether mechanistic or not, must consider model uncertainty and eventual misspecification. In these circumstances, the learning-confirming paradigm proposed by Sheiner becomes essential [10]. These concepts should be reflected in the experimental design used to support the estimation of the parameters of interest. In brief, it must be clear that uncertainty plays as important a role as heterogeneity. These two factors are interrelated and cannot be addressed by rigid experimental designs.

Here we propose the introduction of a randomized concentration-controlled trial (RCCT) design as framework for the implementation of experimental protocols in early clinical development. Using abacavir, a powerful nucleoside analogue reverse transcriptase inhibitor [11], as a paradigm compound, we illustrate the principles of RCCT based on a comprehensive simulation exercise that takes into account uncertainty in parameter distributions. An adaptive design is proposed that makes use of a pharmacokinetic model built using sparse paediatric and dense adult data. This scenario reflects the situation where a formal trial is performed after the drug has been clinically used in children in an off-label manner, and therefore some paediatric pharmacokinetic data are already available to support model building.

In contrast to a randomized dose-controlled trial (RDCT), where patients are randomly assigned to a predefined fixed dose, in a RCCT the patients are randomly assigned to a predefined drug exposure range or value, i.e. the nominal dose is allowed to vary between patients in a treatment arm. During the study, each patient's dose is adjusted so as to bring drug exposure to the prespecified randomization range or value [12]. This adjustment is normally made using an algorithm, the complexity of which may depend on the compound being studied, the population and the objectives of the study [13]. If well designed, these procedures allow control of different sources of variability in drug absorption, distribution and elimination. These features represent an appealing option for paediatric clinical trials. Unfortunately, the main criticism of the use of this approach is often related to the increased workload these protocols require compared with the standard designs [14, 15]. Based on clinical trial simulation concepts, we illustrate that the advantages may outweigh the practical challenges for the implementation of this approach during the evaluation of novel compounds.

Methods

Rationale for the target exposure

In a bridging exercise, the objective is to ensure comparable exposure between the reference and target populations. In addition, assumptions must be made about the similarities in disease progression and pharmacokinetic–pharmacodynamic relationships in both populations. Although a debate is still ongoing in paediatric human immunodeficiency virus research about the clinical relevance of differences in immunological response in children [16], pharmacokinetic–pharmacodynamic relationship and disease progression have been considered comparable for the purposes of our analysis.

In the case of abacavir, the target exposure is most probably determined by the intracellular concentrations of its anabolite, carbovir triphosphate, which are believed to be associated with the pharmacodynamic effect. Given that the exact relationship between the abacavir and carbovir triphosphate concentrations is not fully understood, we have considered AUC as the most suitable measure of exposure. In adults, the median exposure observed showing efficacy is 6.02 mg h l⁻¹[17]; to warrant an effective exposure to more than half of the paediatric patients, an AUC calculated over an interval of 12 hours (AUC_0–12) of 7 mg h l⁻¹ was set as the target exposure for the purposes of the present analysis. For practical and computational reasons, a single reference value has been selected, but a range or interval may also be considered in prospective studies.

Pharmacokinetic model

The pharmacokinetics of abacavir in children has been previously described according to a one-compartment model with first-order absorption and first-order elimination processes [8]. Given the availability of adult data (n= 111), the analysis also demonstrated how prior information can be introduced into the estimation procedures during model building. In the final model, bodyweight was identified as a covariate on clearance (CL) and volume of distribution (V). The covariate effect was characterized by an exponential relationship, as follows:

1

where θ_i is the individual parameter (CL or V), θ is the population parameter, BW_i is the individual body weight and EXP is the allometric exponent. Details of the model building and validation procedures can be found in [8].

Clinical trial simulation

Simulations of an RCCT were performed according to an adaptive protocol design, in which patients are expected to reach the target exposure in steady-state conditions. Protocol procedures include monitoring of drug concentrations at predefined intervals after the beginning of therapy. Based on the observed exposure at these intervals, if necessary, the total dose is adjusted using model parameter estimates, as determined by the nonlinear mixed-effects modelling. An overview of the protocol procedures and adaptation rules is presented in Figure 1.

Figure 1.

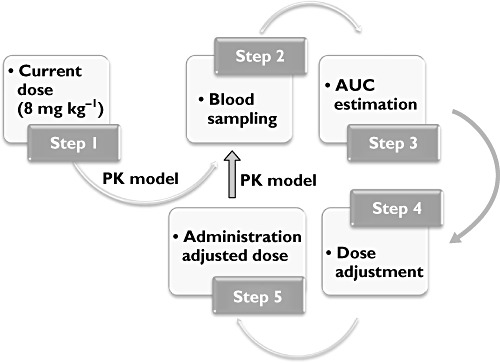
Diagram depicting protocol procedures and adaptation rules. The loop on the right-hand side (steps 2–5) can be virtually repeated at will. Abbreviations: AUC, area under the concentration vs. time curve; PK, pharmacokinetics

Study population

A paediatric population with a broad range of weights and ages was simulated. Age distribution included children and adolescents from 2 to 17 years old. Weight distributions were calculated according to the growth charts from the National Center for Health Statistics (http://www.cdc.gov/growthcharts/cdc_charts.htm). To ensure appropriate assessment of the covariate effect and prevent the potential confounders due to imbalance in the population, a total of 128 subjects were simulated, with the objective of obtaining eight patients per year of age. Scenarios with imbalanced stratification and smaller cohorts of patients can also be considered for the purpose of a clinical trial simulation; however, an evaluation of the impact of different protocol designs was beyond the scope of our investigation.

Dosing regimen and adjustment criteria

Patients are initially given a dose of 8 mg kg⁻¹ up to a maximum of 300 mg, i.e. the recommended twice daily dose of abacavir in adults. Using a sparse blood-sampling schedule and nonlinear mixed-effects modelling, individual predictions of AUC can be obtained at each monitoring step. Based on these estimates, individual doses are subsequently adjusted with the objective of reaching the target exposure. In our example, a third monitoring step has also been implemented to confirm the expected results and to allow further dose titration if necessary. Given that abacavir shows linear pharmacokinetics at therapeutic levels, individual doses can be adjusted according to the following formula:

2

Equation 2 aims at adjusting the dose depending on the measured AUC after first dose, according to the proportion, first dose:individual AUC = adjusted dose:target AUC.

Sampling scheme

The number of plasma samples used in the simulations reflects the number of samples in the original paediatric trial, i.e. seven samples per patient, at 1, 2, 3, 4, 6, 8 and 12 h.

Simulation and dose adaptation procedures

Individual concentration data were simulated at predefined sampling times. The simulated concentration vs. time profiles were subsequently analysed using the pharmacokinetic model described above. This procedure allowed individual pharmacokinetic parameters to be estimated for each patient. The dose adjustment required to achieve the predefined target exposure was based on individual parameter estimates and consisted in up- or down-titration relative to the starting dose. Finally, to explore whether clustering of exposures around the target range would improve the precision of parameter estimates, the simulated concentration vs. time data were analysed again following the adaptive step.

Pharmacokinetic parameter estimation

The stochastic approximation expectation maximization (SAEM) [18] method in NONMEM VII (release 1) [19] was used to fit the data. The pharmacokinetic parameters obtained after the first and second adaptation procedures were compared with the values initially used to simulate the concentration vs. time profiles. In addition, the precision of model parameters was assessed by means of a nonparametric bootstrap procedure. Five hundred bootstrap samples were generated by resampling with replacement. These results were used to evaluate model stability and to obtain reliable confidence intervals for the parameter estimates. Each model was fitted repeatedly to the replicate bootstrap samples using the standard options in Perl-speaks-NONMEM (PsN) [20]. The estimates of parameters obtained from bootstrapping were compared with those obtained from the original data set.

Area under the concentration vs. time curve and target exposure

The distribution of AUC_0–12 values observed after the first and the second adaptation procedures where calculated according to the trapezoidal rule and compared with each other. Based on this distribution, we assessed the number of individuals showing an exposure to abacavir < 6.02 mg h l⁻¹. This figure represents the proportion of individuals theoretically underexposed to abacavir and therefore reflects those patients treated with the wrong dose. Given that no clear information is available about the relationship between exposure to abacavir and toxicity, an arbitrary threshold of 10 mg h l⁻¹ was selected to indicate the level beyond which patients would potentially be overexposed. The proportion of patients trespassing this threshold was also calculated.

Finally, to demonstrate the clinical implications of the adaptive procedures in a paediatric protocol, we simulated a trial with the same 14 patients who were available for model building in the original pharmacokinetic analysis [8]. Concentration vs. time profiles were simulated following administration of doses individually adapted to reach the proposed target exposure. The distribution of AUC_0–12 values obtained in the original trial was then compared with the distribution observed following dose adjustment procedures. All calculations included in the statistical and graphical analysis were performed in R [21].

Results

The AUC distribution after the initial dose level (8 mg kg⁻¹) resulted in a median exposure of 6.43 mg h l⁻¹ and 90th percentile ranging between 3.13 and 10.67 mg h l⁻¹. Fifty-one subjects, out of a cohort of 128 patients, showed AUC values below the effective exposure (6.02 mg h l⁻¹), whereas 10 of 128 reached an AUC higher than the arbitrary safety threshold of 10 mg h l⁻¹. In total, this means that 61 patients (48%) received a dose that was either too low or too high. After the dose adjustment as defined by the adaptation procedures, the median exposure reached 6.94 mg h l⁻¹, with 90th percentile ranging between 5.57 and 8.25 mg h l⁻¹. Only 14 subjects appeared to remain below the target exposure, whilst no one showed values higher than 10 mg h l⁻¹. The second adaptation step resulted in no changes to the median exposure, which remained the same (6.94 mg h l⁻¹), with 90% confidence intervals ranging between 5.75 and 8.37 mg h l⁻¹. Despite the dose adjustment, on this occasion 14 subjects were still showing AUC levels lower than desired, whilst two subjects exceeded the safety threshold. The AUC distributions obtained after the initial dose and the consecutive dose adjustments are graphically summarized in Figure 2.

Figure 2.

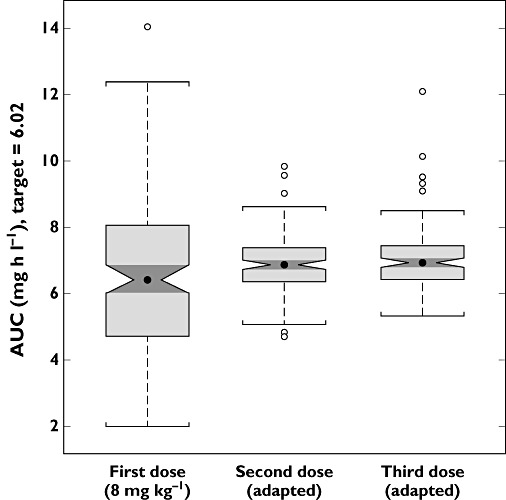
Whisker plots of the distribution of exposures obtained with the different dosing protocols. Clinical trial simulation scenarios included 128 children

A summary of the implications of fixed dose vs. adaptative protocols on the proportion of patients achieving a predefined target exposure is presented in Table 1.

Table 1.

Implications of fixed dose vs. adaptative protocols on the proportion of patients achieving a predefined target exposure, based on a trial with n= 128 subjects

	Initial dose	First dose adjustment	Second dose adjustment
Patients underdosed (AUC < 6.02 mg h l−1)	51	14	14
Patients overdosed (AUC > 10.00 mg h l−1)	10	0	2
Total patients with inappropriate exposure	61 (48%)	14 (11%)	16 (12%)

In this example, 11% of the patients do not reach effective exposure despite dose-adjustment procedures. These results suggest that the heterogeneity of the population (i.e. width of the parameter distribution) may play a more important role than accuracy and precision (i.e. uncertainty) in parameter estimates. Abbreviation: AUC, area under the concentration vs. time curve.

An example of the individual concentration vs. time course profiles for patients below and above the effective exposure is shown in Figure 3, including the corresponding profiles obtained after the adaptation steps.

Figure 3.

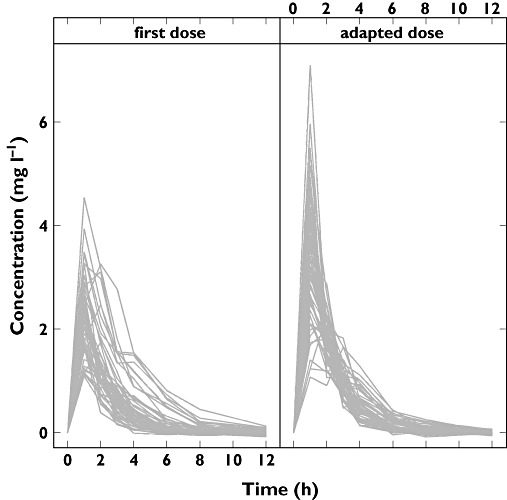
Concentration profiles of subjects receiving a suboptimal dose as starting dose (either too low or too high; left panel) and the corresponding profiles after dose adjustment (right panel)

In addition to the target exposure, a comparison was performed of the precision and accuracy of model parameter estimates obtained from data generated according to a fixed dose protocol vs. adaptive procedures in an RCCT. In the pharmacokinetic analysis performed after the first dose level (8 mg kg⁻¹), the parameter estimates all fell around 5% of the true value (the value used to simulate the concentration profiles), with exception of the absorption rate constant (K_A) (+17.6%) and the allometric exponent on V (−10.1%). After the first adaptation of the doses, the accuracy of the parameter estimates was very similar to the previous one. In this case, all estimates were found to vary around 5% of the true parameter value, with the exception of V (−9.8%) and the allometric exponent on V (−20.2%). The precision of the parameter estimates was also similar in both protocols, although the RCCT generally showed lower coefficients of variation. A summary of the pharmacokinetic parameters obtained according to the fixed and adaptive protocol design is shown in Table 2.

Table 2.

Estimates of pharmacokinetic parameters for abacavir

Parameter	Model parameters from Cella et al. [8]	Parameter re-estimation after the initial dose		Parameter re-estimation after the adapted dose
		Mean	Bootstrap mean (%CV)	Mean	Bootstrap mean (%CV)
Fixed effects
CL (l h−1)	40.6	41.5	41.2 (5.2)	42.3	42.0 (4.5)
V (l)	69.1	65.5	65.3 (5.5)	62.3	62.2 (4.3)
KA (h−1)	3.58	4.21	4.34 (16)	3.67	3.86 (16)
Exponent on CL	0.722	0.761	0.761 (7.0)	0.745	0.744 (6.2)
Exponent on V	0.810	0.728	0.726 (7.2)	0.646	0.646 (7.0)
Interindividual variability (%)
CL	27	26	25 (17)	25	25 (15)
V	11	19	19 (24)	17	16 (20)
KA	98	101	101 (24)	99	101 (21)
F	37	39	47 (33)	34	35 (30)
Residual error (%)
ε	3.6	3.7	3.7 (10)	3.7	3.7 (10)

It is evident from the re-estimation procedures based on a fixed-dose protocol (middle columns) that although precise and accurate, pharmacokinetic parameter estimation alone does not guarantee that patients achieve the desired target exposure. In contrast, parameter estimates from simulated data according to an adaptive protocol yielded the expected target exposure with comparable accuracy and precision (right columns). In both cases, all bootstrapped data sets resulted in successful minimization of the objective function. CL, clearance; V, volume of distribution; K_A, absorption rate constant; F, bioavailability; ε, proportional residual error; %CV, coefficient of variation.

Finally, the simulation of a trial including the original 14 children in whom the current dosing regimen was used (8 mg kg⁻¹) yielded a median exposure of 5.0 mg h l⁻¹, with 90th percentile varying between 2.96 and 9.08 mg h l⁻¹. Ten of the 14 patients showed an AUC lower than the effective exposure, whilst one had an AUC value higher than the arbitrary safety threshold. Based on these findings, it seems that 79% of the patients were administered with a suboptimal dose. In contrast, in the adaptive protocol the median exposure rises to 6.97 mg h l⁻¹ (90th percentile 6.38–12.81 mg h l⁻¹), with no patients showing exposure levels below the effective AUC and two of them being above the safety threshold. The AUC distributions observed after each design are depicted in Figure 4.

Figure 4.

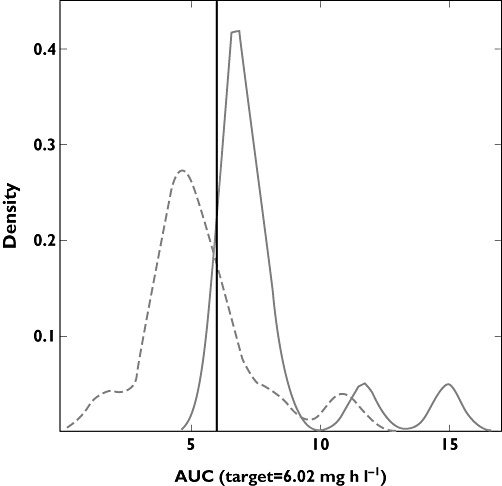
Density plots of the exposure distribution obtained from the original 14 children after the current dose (8 mg kg⁻¹; dashed line) and the simulated exposure distribution of the same patients after dose adjustment (continuous line)

Discussion

In contrast to common practice in paediatric drug development, the recent introduction of the paediatric legislation in the European Union imposes prospective assessment of pharmacokinetics, pharmacodynamics, safety and efficacy of drugs prior to their approval and therapeutic use [22].

Thus far, despite the feasibility and potential advantages of model-based approaches to the design and analysis of early paediatric trials, issues such as dose selection, dose rationale and study design for paediatric indications continue to be addressed in an empirical manner. In fact, some reluctance in the use of pharmacostatistical methods (e.g. nonlinear mixed-effects modelling) may result from a lack of understanding of quantitative clinical pharmacology. The possibility of applying modelling and simulation as a tool to evaluate relevant clinical questions is simply beyond the working knowledge of most paediatricians and drug developers. In contrast, there are some key conceptual issues with regard to the use of model-based approaches that are more of a scientific and statistical nature. The former refers to the predictive value of models when extrapolations are made from one population to another, given that the role of developmental growth and maturation processes varies considerably from birth to adolescence [23]. The latter refers to the assumptions regarding population heterogeneity (i.e. parameter distributions), parameter–covariate correlations and model performance (i.e. accuracy and precision of estimates) when dealing with different groups, phenotypes or clinical conditions [24]. From a statistical perspective, this means that model uncertainty and eventual misspecification must be taken into account. These considerations are vital for the use of modelling and simulation as a basis for the dose rationale and overall study design in paediatric drug development.

In the present investigation, we have demonstrated that some of the potential scientific and statistical limitations of hierarchical modelling can be addressed by a learning-confirming paradigm. The use of adaptive rather than fixed dose protocols enables the accurate selection of the paediatric dose. More specifically, an RCCT design was proposed as a framework for clinical protocols in early clinical development. Even though consensus about the advantages of RCCT over the RDCT has not been reached in terms of precision and bias reduction in parameter estimates [25, 26], Monte Carlo methods suggest that the RCCT is more efficient (in terms of sample size) than the more traditional dose-controlled trials, yielding higher statistical power [27]. In fact, our clinical trial simulations reveal how abacavir exposure differs between subjects when fixed doses are used compared with protocols in which a target exposure is predefined. Furthermore, our results show that despite comparable AUC values in children and adults (6.43 mg h l⁻¹ in children vs. 6.02 mg h l⁻¹ in adults), linear scaling of the dose according to bodyweight resulted in a very wide distribution of AUC values, with nearly half of the subjects lying outside the target range.

Although one could question whether a different dosing regimen would have shrunk the observed AUC distribution, the adaptation procedures did clearly affect the resulting exposure. After dose adjustment, AUC values clustered around the median value of 6.94 mg h l⁻¹, showing a much narrower distribution. The proportion of patients with suboptimal dosing was reduced to 11%, with no patients showing exposure above the safety threshold. As anticipated for abacavir, the second adaptation step did not produce significant changes to the observed exposure distribution. However, the possibility of multiple adaptive steps is relevant when pharmacokinetics is known to be affected by metabolic induction or time-dependent inhibition [28–31].

In addition to identifying the most appropriate dose for children and supporting the rationale for pharmacokinetic bridging studies, we have previously hypothesized that this design would also yield an increase in the statistical power of the study, allowing for a potential reduction in the number of patients, as well as in the sampling frequency. Indeed, applying the same methodology to 14 children, who were included in the original clinical trials used to develop the pharmacokinetic model, yielded comparable results. Adaptive procedures allow shrinkage of the observed exposure distribution around the target range irrespective of population size. From a clinical perspective, this means fewer patients will be potentially under- or overdosed.

Another statistical aspect addressed by our investigation was the gain in precision and accuracy of parameter estimates [13], suggesting superiority of RCCT over fixed dose protocols. The accuracy of estimates of pharmacokinetic parameters for abacavir was comparable across protocols (i.e. fixed vs. adaptive dose), whilst parameter precision appeared to be only slightly higher after dose adjustment, as indicated by the coefficients of variation obtained by bootstrapping.

Finally, it should be noted that the use of simulation scenarios allowed systematic evaluation of the implications of dose selection in a clinical trial. Irrespective of the primary objective of a clinical protocol (i.e. pharmacokinetic bridging or efficacy), one needs to understand that the larger the heterogeneity in the target population the larger the proportion of subjects deviating from the central tendency (e.g. median, mean or target range). It is evident from our results that fixed dose protocols lead to a considerable proportion of patients beyond a desirable target range. In adult populations, this dispersion is often a reflection of the underlying biological processes and can be expressed as random effects (i.e. interindividual variability) in parameters such as clearance and volume of distribution. In contrast, in paediatric populations, variability arises from additional time-varying factors due to developmental growth and maturation processes. Depending on the experimental protocol design (e.g. treatment duration, dose level), these time-varying factors are further confounded by the disease condition or demographic characteristics (e.g. ethnic differences). As such, they cannot be disregarded and must be captured either as fixed or random effects in a model. However, accurate model selection and characterization of parameter–covariate correlations may not be achieved based solely on inferential (extrapolation) methods. Confirmatory evidence (data) from the population of interest is also required, which may not be available at the beginning of a clinical development programme with novel compounds.

It can be concluded that defining the dose rationale for children based on extrapolation or interpolation procedures is unlikely to ensure an optimal dosing regimen at the individual patient level. Adaptive procedures are required to cope with model uncertainty (i.e. model misspecification), discriminating it from the uncertainty in parameter estimates (i.e. heterogeneity). The availability of such data in early clinical development allows formal assessment of dose and dosing regimen requirements for a fixed dose protocol, which can then be used in subsequent confirmatory trials. Despite the challenges associated with the implementation of adaptive protocols, the advantages of a RCCT largely exceed the practical drawbacks attributed to it, i.e. it ensures the child's right to receive the right dose.

Competing Interests

There are no competing interests to declare.