Effect of mismatched place-of-stimulation on the salience of binaural cues in conditions that simulate bilateral cochlear-implant listening

Abstract

Although bilateral cochlear implantation has the potential to improve sound localization and speech understanding in noise, obstacles exist in presenting maximally useful binaural information to bilateral cochlear-implant (CI) users. One obstacle is that electrode arrays may differ in cochlear position by several millimeters, thereby stimulating different neural populations. Effects of interaural frequency mismatch on binaural processing were studied in normal-hearing (NH) listeners using band-limited pulse trains, thereby avoiding confounding factors that may occur in CI users. In experiment 1, binaural image fusion was measured to capture perceptual number, location, and compactness. Subjects heard a single, compact image on 73% of the trials. In experiment 2, intracranial image location was measured for different interaural time differences (ITDs) and interaural level differences (ILDs). For larger mismatch, locations perceptually shifted towards the ear with the higher carrier frequency. In experiment 3, ITD and ILD just-noticeable differences (JNDs) were measured. JNDs increased with decreasing bandwidth and increasing mismatch, but were always measurable up to 3 mm of mismatch. If binaural-hearing mechanisms are similar between NH and CI subjects, these results may explain reduced sensitivity of ITDs and ILDs in CI users. Large mismatches may lead to distorted spatial maps and reduced binaural image fusion.

INTRODUCTION

Although cochlear implants (CIs) were originally designed for unilateral implantation, bilateral implantation of CIs is becoming more prevalent. Bilateral CIs may have the potential to yield large improvements in sound localization and signal detection in noisy environments compared to unilateral CIs. Nonetheless, the ability to utilize binaural information in bilateral CIs remains much poorer than that of listeners with normal hearing (NH) (e.g, Litovsky et al., 2009; Loizou et al., 2009; Majdak et al., 2011). There are many reasons that bilateral CI users do not perform as well as NH subjects when tested on binaural tasks: hearing history, possible cochlear damage during implantation, physical limitations of stimulating the cochlea electrically, compromised encoding of acoustic information in a CI compared to NH, and anatomical placement of the electrode arrays in the two cochleae.

Present day multi-electrode CIs are controlled by sound processors that subdivide the spectrum of an incoming sound into frequency channels with bandpass filters. The typical frequency range of the bandpass filters covers frequencies most important to the understanding of speech, from about 0.2 to 8 kHz. For each channel, the envelope is extracted and used to modulate electrical pulse trains at a pre-assigned electrode. It is reasonable to assume that there exists a frequency-to-place of stimulation mismatch because insertion depths are generally shallow. For a 35-mm cochlea, typical insertions depths range from 20 to 30 mm (Ketten et al., 1998; Gstoettner et al., 1999). For bilateral CI users, the insertion depth of the electrode array into the scala tympani has the potential to differ greatly between the ears, because the corresponding electrodes that encode approximately the same frequency range may not stimulate the same cochlear place in both ears. It is unclear how well a surgeon is able to match insertion depths across the ears during simultaneous bilateral implantation; such control is probably more difficult to maintain during sequential implantation without the help of x-rays and/or CT scans. Therefore, there is a high probability that bilateral CI users experience interaural frequency mismatch on the order of several millimeters, where binaural information that is meant to be presented at the same tonotopic locations across the two ears is presented at different tonotopic locations.

Most psychophysical studies in bilateral CI subjects attempt to eliminate interaural frequency mismatch by using a pair of electrodes that are matched in pitch (Long et al., 2003). The necessity of interaurally matched frequency inputs is consistent with many current physiological models of the binaural system that compute interaural time differences (ITDs) and interaural level differences (ILDs). One common model assumes that ITDs are processed in a coincidence matrix with matched frequency inputs (Jeffress, 1948). If the interaural frequency mismatch is sufficiently small, the excitation pattern for an acoustic input or spread of excitation for an electrical input would still provide neural firing in an overlapping region with matched frequency inputs, thus mostly preserving the overall timing information but having a lower average neural firing rate. Monopolar electrical stimulation, the typical stimulation mode of many present day CIs, produces large regions of excitation (e.g., Nelson et al., 2008). Hence, the large spread of current in electrical stimulation would provide some amelioration of the need to find perfectly interaurally frequency-matched inputs to achieve maximum binaural sensitivity.

There have been some investigations into the effects of interaural frequency mismatch in bilateral CI users. A number of studies have tested binaural sensitivity using research processors that control stimulation in each ear at the level of a single electrode and can provide bilaterally synchronized pulses. Long et al. (2003) reported that pitch-matched electrodes were more likely to show interaural sensitivity in a bilateral CI subject and that there was a monotonic decrease in sensitivity when the electrode pairs used for stimulation moved away from the pitch-matched pair. Eddington et al. (2002) showed a similar trend, but related ITD sensitivity to the subjective impression of how well the auditory image was fused, thus creating a unitary sound that is heard at a single location within the head. Better ITD sensitivity was observed when listeners perceived auditory images that were more fused or compact than when the images were unfused or diffuse. van Hoesel and Clark (1997) reported that 3 to 6 mm of mismatch was necessary to degrade ITD just-noticeable differences (JNDs). Poon et al. (2009) reported that the interaural frequency mismatch required to increase ITD JNDs by a factor of 2 was 3.4 mm on average for four subjects. Through clinical processors, Laback et al. (2004) found pitch-matched electrodes by using sine tones with a frequency at that of an electrode analysis band. ILD JNDs for different types of signals were increased from 2.9 dB for pitch-matched electrode pairs to 10.3 dB for pairs that were almost at opposite ends of the electrode array.

Other studies have examined interaural frequency mismatch in NH subjects. Both Henning (1974) and Nuetzel and Hafter (1981) measured ITD JNDs of SAM tones with low envelope modulation rates (<350 Hz) and high-frequency carriers (>1500 Hz). They found that ITD JNDs increased with increasing interaural frequency mismatch of the carriers. Brown and Yost (2011) used noise that was high-pass filtered with asymmetric cutoffs between the ears, which might be considered a form of interaural frequency mismatch in the center frequency of the noise bands. For stimuli with frequencies less than 1500 Hz and an otherwise interaurally coherent band with an ITD, performance was degraded (i.e., ITD JNDs were increased). Blanks et al. (2007) used stimuli with a 4-kHz center frequency (CF) and found that subjects could detect either static or dynamic ITDs encoded in the envelopes of SAM tones for interaural frequency mismatches up to 2–3 octaves. These results were consistent with physiological recordings in inferior colliculus (IC) neurons of unanaesthetized rabbits measured in the same study. Blanks et al. (2008) studied ITD discrimination using transposed tones (van de Par and Kohlrausch, 1997) while varying interaural frequency mismatch and overall level, and found that ITD JNDs increased with increasing mismatch and decreasing level. They also restricted the stimulus spectrum of the transposed tones to 512-Hz and found that ITD JNDs increased when the spectrum was restricted. They interpreted these results as evidence that ITDs can be discriminated when the stimulus carriers had interaural frequency mismatch, as long as there was a region of excitation that overlapped between the ears.

Although there have been many studies on interaural frequency mismatch and ITD sensitivity in NH subjects, there are relatively fewer examining interaural frequency mismatch and ILD sensitivity. In one study by Francart and Wouters (2007), ILD JNDs were measured for 1/3-octave narrowband noise stimuli that were interaurally uncorrelated at center frequencies of 250, 500, 1000, and 4000 Hz. As occurs for ITDs, ILD JNDs increased with increasing mismatch.

Despite the numerous studies on interaural frequency mismatch in CI and NH subjects, drawing comparisons between the two subject groups is difficult. One attempt at comparison was made by Poon et al. (2009). The interaural frequency mismatch required to increase ITD JNDs by a factor of 2 for bilateral CI subjects was five times greater than the ITD JNDs collected by Nuetzel and Hafter (1981) in NH subjects listening to sinusoidally amplitude modulated (SAM) tones, with a high-frequency carrier (>1500 Hz) but a low modulation rate (∼100 Hz). However, it is not clear that such a comparison is ideal. One factor that limits comparisons is the vast difference in the bandwidth (BW) of the stimuli and the resulting area of neural excitation. In CI research, it has been shown that spread of excitation for a single electrode is quite large for monopolar stimulation, with a spatial BW of approximately 4.6 mm (Nelson et al., 2008). If the frequency-to-place map of Greenwood (1990) is used as a reference, then depending on the anatomical place of stimulation, the current spread can translate into a BW from 0.7 kHz (1-kHz CF) to 12.7 kHz (20-kHz CF). However, many of the NH acoustic studies with interaural frequency mismatch have used SAM tones, which results in a spectrum that has a BW that is twice the modulation frequency. For the aforementioned studies, modulation frequencies were between 100 and 600 Hz, thus resulting in BWs of 200–1200 Hz. Transposed tones have a larger BW than SAM tones, however, the BW remains constant in Hz with interaural frequency mismatch. In contrast for CIs, the spatial BW remains constant in mm with interaural frequency mismatch. More realistic acoustic simulations of CI stimulation should account for the spatial BW in mm.

Although the problem of attempting to keep the spatial BW constant in mm can be somewhat resolved through the use of narrowband noise stimuli with BWs measured in octaves, a new problem is introduced. It is difficult to precisely control the interaural correlation of narrowband noises with interaural frequency mismatch, thus using uncorrelated noise stimuli in the two ears may be a reasonable solution (see Francart and Wouters, 2007). However, binaurally uncorrelated noise is perceptually diffuse (i.e., has a larger perceived auditory source width), whereas correlated noise is perceptually compact (i.e., has a smaller perceived auditory source width) (Blauert and Lindemann, 1986; Whitmer et al., 2012). In fact, studies have shown that post-lingually deafened bilateral CI users listening to constant-amplitude pulse trains with ITDs or ILDs often report a compact auditory image, rather than a diffuse image, for reasonably pitch-matched electrode pairs (van Hoesel and Clark, 1997; Eddington et al., 2002; Long et al., 2003; Litovsky et al., 2010).

A solution that solves these two problems in NH acoustic simulation of CI stimulation is to use bandpass-filtered pulse trains. As discussed above, keeping the spatial BW constant is problematic, but this can be controlled by changing the temporal shape of the pulses as CF changes. The problem that image compactness is compromised can be solved by modulating tonal carriers instead of noise. Several studies have used bandpass-filtered pulse trains to simulate CI performance in psychophysical tasks involving speech understanding (Bingabr et al., 2008), pitch perception (Carlyon et al., 2008), correlation change detection (Goupell, 2012), and sound localization (Laback et al., 2004; Goupell et al., 2010).

It seems likely that binaural image fusion would be best for a pitch-matched pair of electrodes (simulated or real), where there is the greatest likelihood of regions of excitation that have generally overlapping range of characteristic frequencies. However, it is unclear how interaural frequency mismatch affects binaural image fusion using stimuli with such a large BW. Furthermore, to fully understand the effects of interaural frequency mismatch, a careful investigation using several different binaural tasks is necessary. The purpose of these experiments was to examine the effect of interaural frequency mismatch on subjective and objective measures of ITD and ILD processing using acoustic stimuli that better model the direct electrical stimulation from a single pair of electrodes. This was done by using pulse trains with a much wider spectrum than would occur for SAM tones, transposed tones, or 1/3-octave narrowband noises, which have been used in previous NH experiments. We kept the BW of our stimuli constant in mm (i.e., the spatial BW), rather than the BW in Hz, and used tonal carriers that yielded mostly perceptually compact auditory images. With these stimuli, we examined the effect of interaural frequency mismatch in three different tasks: binaural image fusion, lateralization, and left-right discrimination. We predicted that binaural image fusion would decrease and the number of auditory images would increase for increasing interaural frequency mismatch because several reports demonstrate poor image fusion for interaurally frequency mismatched electrode pairs in bilateral CIs (van Hoesel and Clark, 1997; Eddington et al., 2002; Long et al., 2003; Litovsky et al., 2010). We also predicted that the ability of subjects to lateralize sounds and discriminate interaural differences would decrease with increasing interaural frequency mismatch because of the assumption that the central binaural processor depends on frequency-matched inputs in order to perform binaural comparisons with fidelity (Jeffress, 1948). However, they would be able to tolerate much larger interaural frequency mismatches compared to the previous studies with NH subjects because of the relatively large BW of our stimuli, which are more like the electrical stimulation that occurs with a CI.

EXPERIMENT 1: BINAURAL IMAGE FUSION

Motivation

The motivation behind the binaural image fusion experiment followed the logic of the fusion scale developed by Eddington et al. (2002), who used this scale to provide guidance in selecting interaural electrode pairs that would provide binaural sensitivity. Since then it has become more commonly accepted to find interaurally pitch-matched electrodes, rather than rely on fusion (e.g., Long et al., 2003; Laback et al., 2007; van Hoesel, 2008; Litovsky et al., 2010). However, unlike previous work, the present experiment was aimed at understanding how interaural frequency mismatch changes the (1) number, (2) location(s), and (3) compactness of auditory images in our CI simulations. These three measures are fundamentally important when it comes to interpreting lateralization and discrimination data.

Eddington et al. used a numerical scale from 0 to 5, and instructed subjects to rank the perceived “binaural image fusion” of a 300-ms, 200-pulses-per-second (pps) constant-amplitude pulse train presented to the two ears at a comfortable level. On this scale, response categories were defined as: 0 = two different auditory images, one at each ear; 1 = the same auditory image, at two different points; 1.5 = the same auditory image, at two different regions; 2 = diffuse auditory image, fills head with two concentrated regions; 3 = diffuse auditory image, fills head; 4 = diffuse auditory image, fills head with one concentrated region; 5 = one punctuate auditory image. Preliminary testing in our lab found it was necessary to expand this scale in order to record the number, location(s), and compactness of auditory images. Responses could thus be categorized into one of three major groups, with sub-groups in each category, as follows: (1) one auditory image (on the left, in the center, on the right), (2) multiple auditory images (left strong, right weak; equally strong; left weak, right strong; three images), and (3) diffuse auditory image(s) (no concentration, one concentration, two concentrations). Although these categories may not have encompassed every possible perception reported by subjects, they cover the vast majority of perceptions reported in pilot tests. The design of the experiment was such that the number of possibilities was not too many to make the task exceedingly complicated for the subjects. We found that ten categories may have been initially complicated for some subjects, but after a short explanation of the interface and some task familiarization, subjects were comfortable with the experiment.

Subjects and equipment

Twenty subjects, ranging in age from 18 to 38 years were tested in this experiment. All subjects had pure tone thresholds at or below 20 dB HL octave interval frequencies between 250 and 8000 Hz. Also, for each subject, the thresholds between the two ears differed by less than 10 dB at any tested frequency. They consented to participation in the study and were paid an hourly wage. Some subjects had extensive previous experience in binaural hearing experiments. Two subjects were authors.

Stimuli were generated on a personal computer in matlab (the Mathworks; Massachusetts). A Tucker-Davis Technologies System 3 (RP2.1, PA5, and HB7; Florida) delivered the stimuli to ear-insert headphones (ER2, Etymotic; Illinois) that were deeply inserted. ER2 headphones were used because of the relatively flat frequency response between 4 and 20 kHz, which was the frequency range of the stimuli used in these experiments. This provided a better simulation of CI processing because the resonances of the outer ear were bypassed, which also occurs for the behind-the-ear microphones of CI users. The tests were performed in a single-walled sound booth (Acoustic Systems; Texas).

Stimuli

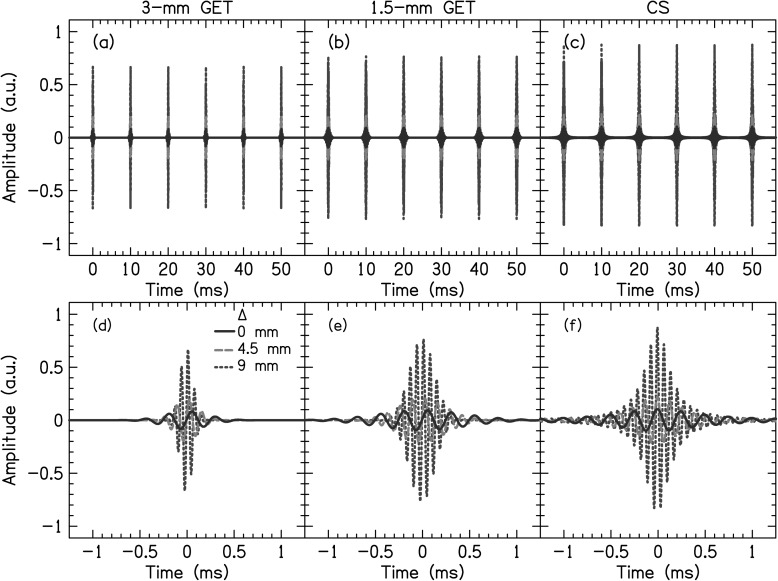
Stimuli were acoustic pulse trains (PTs) presented at 100 pps. The pulses had one of three different temporal shapes, shown in Fig. 1. The first was a relatively temporally narrow Gaussian-enveloped tone (GET) pulse [Figs. 1a, 1d], the second was a relatively temporally wide GET pulse [Figs. 1b, 1e], and the third was a non-Gaussian-shaped pulse [Figs. 1c, 1f]. The GET pulses when presented in a PT had greater than 99% modulation depth whereas the non-Gaussian-shaped PTs did not. The reasons to use different types of pulse trains were to simulate different amounts of current spread and to validate them as appropriate CI simulations.

Figure 1.

(Color online) Right-channel waveforms for the different types of PTs for different values of interaural frequency mismatch Δ (i.e., at different center frequencies).

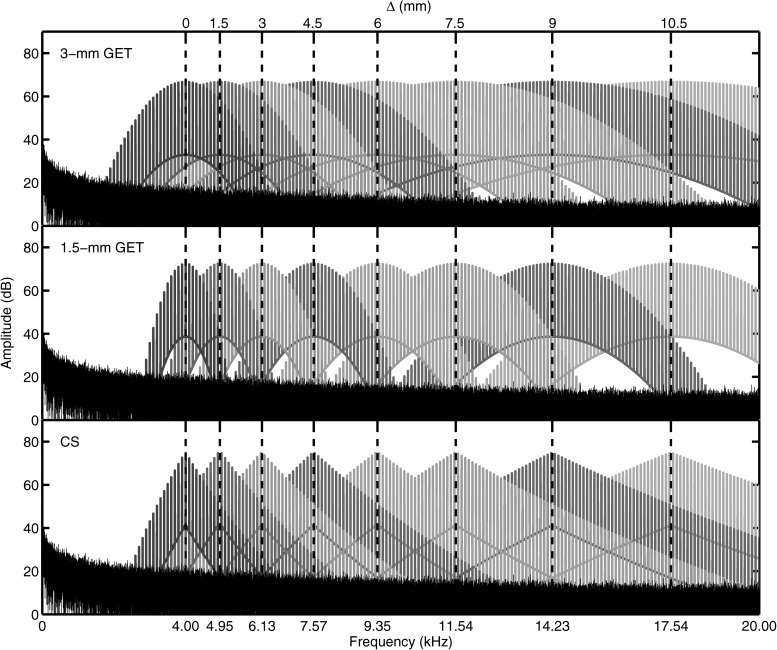
Figure 2 shows the spectra of the PTs. The temporally narrow PTs had a Gaussian-shaped spectral envelope with a 3-mm, −3-dB spatial BW, to be called 3-mm PTs. The temporally wide PT had a Gaussian-shaped spectral envelope with a 1.5-mm BW, to be called 1.5-mm PTs. The spatial BWs for the GET PTs were determined by using Greenwood's place-to-frequency mapping function (Greenwood, 1990), calculating the frequencies associated with 1.5 or 0.75 mm above and below the CF for the 3-mm or 1.5-mm PTs, respectively. GET PTs have previously been used in a number of experiments simulating CI electrical stimulation (e.g., Goupell et al., 2010; Goupell, 2012). The third type of PT had a triangular spectrum designed to simulate current spread (CS) from monopolar stimulation from an intracochlear electrode (Bingabr et al., 2008). This was done by using 2048-order finite impulse response filters designed in matlab using the fir2 command. The frequency response of the filters had bandpass characteristics with slopes that approximated the decay of current and took into account the difference between the dynamic range of CI and NH subjects. In this paper, we modeled a 3.75 dB/mm current decay rate and assumed a dynamic range of 30 and 65 dB for CI and NH subjects, respectively.

Figure 2.

(Color online) Spectra of different types of PTs. The spectrum of the pink masking noise, used in experiments 2 and 3, is also shown.

Interaural frequency mismatch between the CFs of the left and right channels, denoted by the symbol Δ, was introduced in simulated mm and was the independent variable in this experiment. The physical stimuli had zero ITD and ILD. Mismatches of Δ = 0, ±1.5, ±3, ±4.5, ±6, ±7.5, ±9, and ±10.5 mm were tested. For Δ = 0 mm, the CF of both channels was 4 kHz. Positive values of Δ changed the CF of the right channel to a frequency higher than 4 kHz; negative values of Δ changed the CF of the left channel to a frequency higher than 4 kHz. The CFs of the right and left channels are reported in Table TABLE I.. All three types of PTs with a 4-kHz CF were presented at an A-weighted sound pressure level (SPL-A) of 70 dB. To best control the characteristics of the physical stimuli like the overlapping spectral region between the two ears, the maximum of the spectral envelope remained constant for each condition (see Fig. 2), which meant that the PTs with a CF greater than 4 kHz were not presented at 70 dB SPL-A. Other types of level normalization across conditions were also considered, but were deemed suboptimal compared to controlling the physical stimuli. It was not clear to us that normalization by measuring equal sound pressure levels or equal loudness for different values of Δ would add any more control to the experiment. Note that Blanks et al. (2008) also used spectral peak normalization in their study with interaural frequency mismatch. The levels for each pulse train are reported in Table TABLE I..1

TABLE I.

Center frequencies (CFs) for each ear with different interaural frequency mismatches (Δ). Positive values of Δ increased the CF in the right ear and negative values of Δ increased the CF in the left ear. Levels for the right channel for the three different types of stimuli (3-mm PT, 1.5-mm PT, and CS) are also reported.

	CF (kHz)		Level (dB SPL-A)
Δ (mm)	Left	Right	3-mm PT	1.5-mm PT	CS
−10.5	17.54	4
−9	14.23	4
−7.5	11.54	4
−6	9.35	4
−4.5	7.57	4
−3	6.13	4
−1.5	4.95	4
0	4	4	70.0	70.0	70.0
1.5	4	4.95	70.4	70.6	71.3
3	4	6.13	66.7	64.7	64.5
4.5	4	7.57	60.9	58.1	58.0
6	4	9.35	54.4	51.4	51.1
7.5	4	11.54	48.5	45.8	45.3
9	4	14.23	45.4	42.8	41.6
10.5	4	17.54	43.2	41.2	39.8

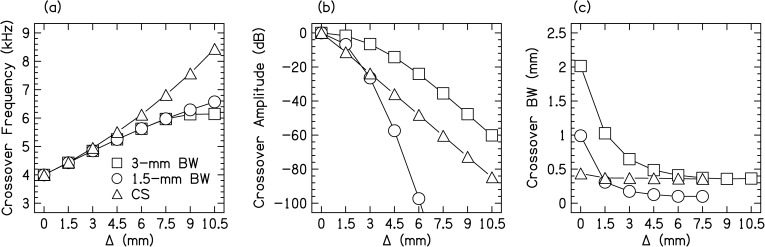
To further characterize the stimuli in ways that might be important to the salience of binaural cues in our experiments, the frequency, amplitude, and BW of the region where the PTs overlap (called the crossover region) are shown in Fig. 3. Figure 3a shows the crossover frequency, the maximum point where the spectral envelope had the same level across the ears, which increased with increasing Δ. The crossover frequency was essentially the same for the two GET PTs, but the CS PT had systematically larger crossover frequencies for values of Δ > 4.5 mm because of the asymmetric filter shape of the CS PT. Figure 3b shows the crossover amplitude, the amplitude of the spectral envelopes at the crossover frequency, which decreased with increasing Δ. It was the largest for the 3-mm PT and smallest for the 1.5-mm PT for Δ > 3 mm. Figure 3c shows the crossover BW, the BW of the overlapping spectral region measured 3-dB down from the crossover amplitude. The crossover BW decreased for increasing Δ. It was largest for the 3-mm PT. For Δ > 7.5 mm, the crossover BW could not be measured for the 1.5-mm and the CS PTs assuming the crossover region was audible. With these calculations, it was possible to relate the amount of binaural image fusion and salience of interaural differences for the different types of PTs and different values of Δ to the stimulus properties.

Figure 3.

Stimulus properties for the different types of PTs. (a) Crossover frequency as function of interaural mismatch (Δ). (b) Crossover amplitude as function of Δ. (c) Crossover BW as function of Δ.

Procedure

Subjects listened to a PT and categorized the sound using one of the ten possible response categories. Subjects initiated each trial by pressing a button. Subjects were allowed to repeat any stimulus as many times as necessary. Before the main experiment, subjects were familiarized with the experimental screen. In addition, they were told that the task was subjective and that they were not required to use all available responses. They then performed a short familiarization block of 30 trials using the 3-mm PTs, which contained Δ = 0, ±1.5, ±3, ±4.5, ±6, ±7.5, ±9, and ±10.5 mm. During testing each subject completed 6 blocks of trials, 2 blocks of each of the three filter types, presented in random order. Each block contained 10 trials of each of the possible Δ's, for a total of 150 trials per block. Therefore, there were 900 total test trials per subject in this experiment. The experiment took approximately two hours per subject.

Results

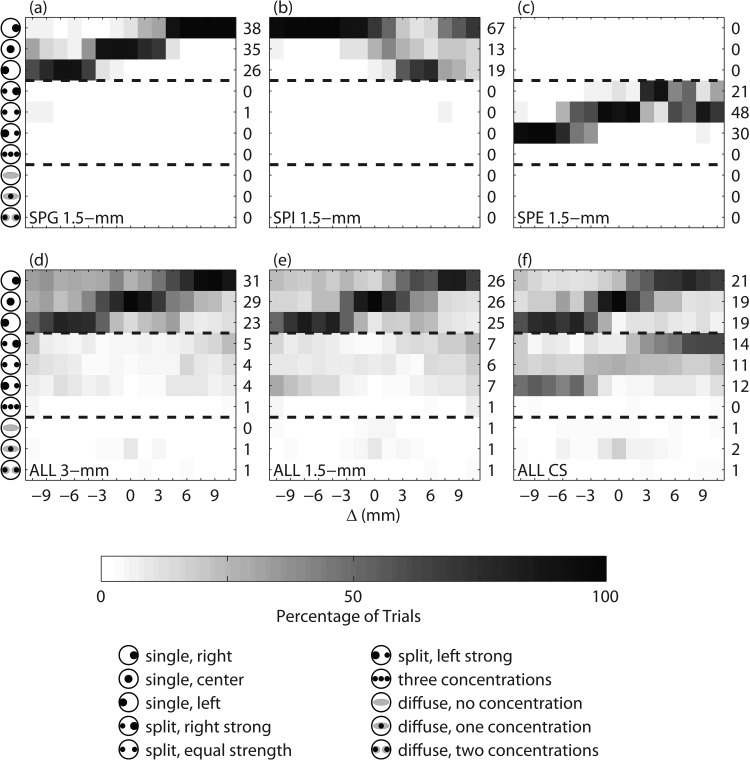
The results for the binaural image fusion task are shown in Fig. 4, the top row showing data for three sample subjects and the bottom row showing data of all the subjects. The icons on the left of each panel show the response options in the forced choice task, which denote combinations of number, location, and compactness of the auditory images (see Sec. 2A). The numbers on the right of each panel show the percentage of responses for each category. Figure 4a shows an example of a subject with 99% of responses as a single auditory image for the 1.5-mm PTs. Note that for the same subject, the condition with Δ = 0 mm resulted in the auditory image being mostly in the center of the head. As Δ increased, the subject increasingly responded that the auditory image was right of center. Likewise, as Δ decreased, the subject increasingly responded that the auditory image was left of center. Figure 4b shows the response pattern for subject SPI for the 1.5-mm PTs, which has the opposite pattern to that seen in Fig. 4a. In general, more subjects (12 of 20 subjects) had response patterns that looked like Fig. 4a than 4(b) (1 of 20 subjects). Figure 4c shows the response pattern for subject SPE for the 1.5-mm PTs; this subject responded with two auditory images for all of the trials (5 of 20 subjects had a similar response pattern). The stronger auditory image was on the right for positive Δ and on the left for negative Δ, similar to the single-image pattern seen in Fig. 4a.

Figure 4.

(Color online) Subjective fusion results as a function of interaural mismatch (Δ). Each row in each panel represents a different categorical perception; the iconic representation of these categories are shown on the left side of the plot. The first three rows represent single image categories. The next four rows represent categories with two or three compact images. The last three rows represent categories with diffuse auditory image(s). Panels (a)–(c) show examples of individual subject responses. Panels (d)–(f) show the responses of all twenty subjects for the 3-mm, 1.5-mm, and CS PTs.

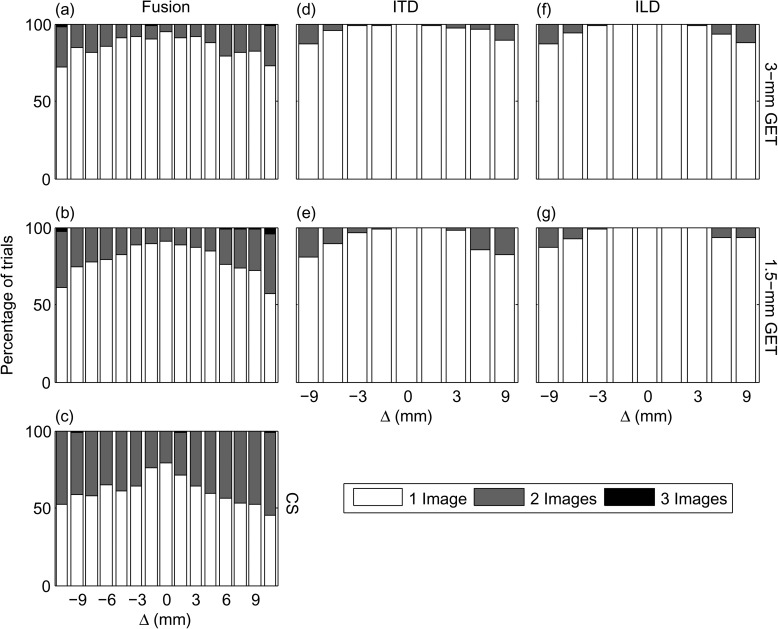
The second row shows the collective responses for all 20 subjects for each PT type. Figure 4d shows the response pattern for the 3-mm PT. Like Fig. 4a, for Δ = 0 mm, the majority of responses (83%) were a single image and of these only 29% were in the center of the head. The majority of responses indicated that one image was perceived to the right of center as Δ increased and one image was perceived to the left of center as Δ decreased. There was little difference between the 3-mm and 1.5-mm PTs when comparing Figs. 4d, 4e, except that the number of single images decreased from 83 to 77 %. A similar response pattern was seen for the CS PT in Fig. 4f, however, the number of single-image responses decreased to 59%.

The percentage of one, two, or three image responses are shown in Figs. 5a, 5b, 5c. A majority of responses were a single image. There was an increasing percentage of two-image responses as the magnitude of Δ increased and as the BW decreased from 3-mm PTs to 1.5-mm PTs to the CS PTs. Three-image responses almost never occurred.

Figure 5.

(Color online) Percentage of responses with one, two, or three auditory images in experiments 1 and 2.

Discussion

The results in Figs. 45a, 5b, 5c show that subjects mostly perceived a single auditory image for the 3-mm and 1.5-mm PTs. This sound was perceived in the center of the head for Δ = 0 mm and became lateralized to the ear with the higher CF when Δ ≠ 0 mm. Consistent with predictions from the stimulus attributes in Fig. 3, more multiple auditory images were heard as the BW decreased. Subjects heard the largest percentage of multiple auditory images for the CS stimuli. Since post-lingually deafened CI subjects who show sensitivity to ITDs and ILDs often report single auditory images in a similar task (Kan et al., 2011), this may indicate a weakness in the CS stimuli as a CI simulation. Perceptually, subjects reported that the CS stimuli sounded very tonal, which is likely due to the sharpness of the amplitude spectrum shown in Fig. 2. Comparing the spectra in Fig. 2, the 1.5-mm PTs have approximately the same BW as the CS PTs, however, they have the advantage of deeper modulation depth (see Fig. 1) and a less tonal perception. The CS PTs were therefore omitted from the subsequent experiments because we concluded that the 1.5-mm PTs provided a better CI simulation with approximately the same BW.

EXPERIMENT 2: LATERALIZATION

Experiment 1 showed that subjects often perceived non-centered auditory images if there was interaural frequency mismatch. The next experiment was aimed at investigating the effect of interaural frequency mismatch on perceived image location(s) and number of auditory images, now with ITDs and ILDs imposed on the stimuli.

Methods

All 20 subjects from experiment 1 participated in experiment 2. The equipment and stimulus generation was the same as in experiment 1.

The 3- and 1.5-mm PTs from experiment 1 were presented over headphones with various ITDs (0, ±100, ±200, ±400, or ±800 μs) or ILDs (0, ±1.5, ±3, ±6, or ±9 dB). Positive ITDs were defined to be leading in the right ear; negative ITDs were defined to be leading in the left ear. Positive ILDs were defined to have a higher level in the right ear; negative ILDs were defined to have a higher level in the left ear. ITDs and ILDs were imposed by applying half of the magnitude of the change to each ear. Mismatches of Δ = 0, ±1.5, ±3, ±6, and ±9 mm were tested. Subjects were split into four groups of five subjects each. Groups 1 and 3 listened to 3-mm PTs and groups 2 and 4 listened to 1.5-mm PTs. In order to mask possible distortion products, particularly the intermodulation distortion product at 100 Hz (Wiegrebe and Patterson, 1999), dichotic pink noise was presented along with the PTs for groups 3 and 4. Because of the wide spectrum of some of the pulse trains, a broadband masker was used so that each condition would experience approximately the same interference from the masker. The spectrum of the pink noise can be seen in Fig. 2. The pink noise had a level of 30 dB SPL-A, began 250 ms before the PT, and ended 250 ms after.

In performing the lateralization task, subjects were presented with a computer interface containing an image of a head. Subjects initiated each trial by pressing a button. After hearing the stimulus, they selected the number of sound sources they heard (one, two, or three) and then selected the intracranial lateral position or lateralization of each source by clicking on slider bars imposed on the head. The bars allowed subjects to report only the lateral position of the auditory images. Subjects were instructed to respond with the most salient, strongest, or loudest source on the topmost bar if they heard multiple auditory images. The responses were translated to a numerical scale (Yost, 1981), where the left ear is −10, center is 0, and the right ear is +10. Like experiment 1, subjects were allowed to repeat any stimulus and they ended each trial with a button press.

Before data collection, subjects were familiarized with the testing interface. In the main experiment, they completed five blocks of stimuli with ITDs followed by five blocks of stimuli with ILDs. Each block contained two trials of each of the possible combinations of Δ and ITD or ILD, for a total of 162 trials per block. With 10 repetitions per condition, the total number of trials was 1620 (9 Δ's × 9 ITDs × 10 repetitions + 9 Δ's × 9 ILDs × 10 repetitions). The experiment took approximately six hours per subject.

Results

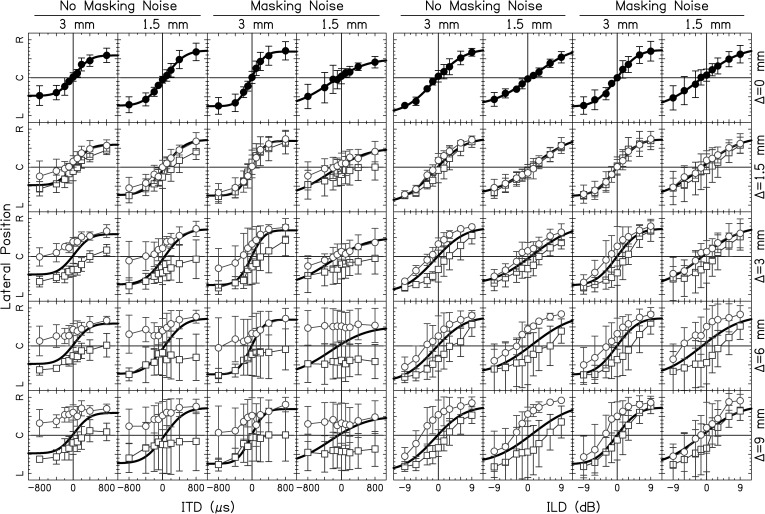
The average intracranial locations of the first/strongest auditory image are shown in Fig. 6. Two analyses of variance (ANOVAs) were performed on the perceived lateral position (on the scale of −10 to 10) with factors BW, Δ, Noise, and ITD or ILD. The top row of Fig. 6 shows the conditions with Δ = 0 mm. In each condition, independent of BW and whether masking noise was absent or present, subjects perceived negative ITDs to the left and positive ITDs to the right [main effect ITD: F(8,1296) = 82.7, p < 0.0001]. Likewise, subjects perceived negative ILDs to the left and positive ILDs to the right [main effect ILD: F(8,1296) = 311.0, p < 0.0001].

Figure 6.

(Color online) Lateralization data for ITDs (left four columns) and ILDs (right four columns) for different BWs. The vertical axis shows the response lateralization over the range of left ear (L) to center (C) to right ear (R). The top row shows conditions with Δ = 0 mm. Data points represent the average over the average response from each subject and errors bars shown ±1 standard deviation from the average. Mismatched conditions are plotted in the bottom four rows. Circles represent +Δ's; squares represent –Δ's. The solid line is the fit from the Δ = 0 mm condition.

The Δ = 0 mm data from the first row of Fig. 6 were fit with a function that had the form

$$y=A\left[1+\text{erf}\left(\frac{x-{\mu }_X}{\sqrt{2}\sigma }\right)\right]-{\mu }_Y,$$ (1)

where x was the ITD or ILD values, and A, σ, ${\mu }_X$, and ${\mu }_Y$ were the variables optimized to fit the data. Each fit described more that 99% of the variance in the data. These fits were copied on the panels for conditions with Δ ≠ 0 mm to observe the deviation in the perceived lateralization from the Δ = 0 mm conditions.

For each column in Fig. 6, as Δ increased (circles), lateralization curves shifted to the left and as Δ decreased (squares), lateralization curves shifted to the right for both ITD [main effect Δ: F(8,1296) = 132.8, p < 0.0001] and ILD [main effect Δ: F(8,1296) = 75.6, p < 0.0001]. This can easily be seen by comparing the circles and squares to the solid fit lines. Post hoc tests showed significant differences in Δ at the 0.05 level for most conditions (see Table TABLE II.).

TABLE II.

Post hoc tests between different values of Δ from experiment 2 for ITD and ILD lateralization. The asterisks represent a significant difference at the p = 0.05 level.

ITD	−9	−6	−3	−1.5	0	1.5	3	6	9
−9	—			*	*	*	*	*	*
−6	—	—		*	*	*	*	*	*
−3	—	—	—	*	*	*	*	*	*
−1.5	—	—	—	—		*	*	*	*
0	—	—	—	—	—		*	*	*
1.5	—	—	—	—	—	—	*	*	*
3	—	—	—	—	—	—	—	*	*
6	—	—	—	—	—	—	—	—
9	—	—	—	—	—	—	—	—	—
ILD	−9	−6	−3	−1.5	0	1.5	3	6	9
−9	—			*	*	*	*	*	*
−6	—	—		*	*	*	*	*	*
−3	—	—	—	*	*	*	*	*	*
−1.5	—	—	—	—			*	*	*
0	—	—	—	—	—		*	*	*
1.5	—	—	—	—	—	—	*	*	*
3	—	—	—	—	—	—	—	*	*
6	—	—	—	—	—	—	—	—
9	—	—	—	—	—	—	—	—	—

For ITDs, many curves did not cross the perceived midline (marked “C”) as Δ increased or decreased from 0 mm. In fact for Δ = 9 mm, there was a very little to no change in laterality as ITD was varied [interaction Δ × ITD: F(64,1296) = 1.88, p < 0.0001]. This is in contrast to the data for ILDs where all of the lateralization curves crossed the perceived midline [interaction Δ × ILD: F(64,1296) = 1.94, n.s.]

The extent of the lateralization (i.e., range used in lateral position responses) was generally smaller as BW decreased for ITD [main effect BW: F(1,1296) = 10.8, p = 0.001; interaction BW × ITD: F(8,1296) = 5.35, p < 0.0001] and lateralization was affected by an interaction between BW and Δ [interaction BW × Δ: F(8,1296) = 2.62, p = 0.007; interaction BW × Δ × ITD: F(64,1296) = 2.72, n.s.].2 Likewise, the extent of the lateralization was generally smaller as BW decreased for ILD [main effect BW: F(1,1296) = 0.97, n.s.; interaction BW × ILD: F(8,1296) = 4.40, p < 0.0001] and lateralization curves were affected by an interaction between BW and Δ [interaction BW × Δ: F(8,1296) = 2.02, p = 0.042; interaction BW × Δ × ILD: F(64,1296) = 0.31, n.s.].

Lateralization of ITDs was minimally affected by the addition of low-frequency masking noise [main effect Noise: F(1,1296) = 2.11, n.s.], although there were some significant interactions [interaction Δ × Noise: F(8,1296) = 2.22, p = 0.024; BW × Noise × ITD: F(8,1296) = 5.79, p < 0.0001]. Lateralization curves of ILD were significantly affected by the addition of low-frequency masking noise [main effect Noise: F(1,1296) = 5.46, p = 0.020] and a significant interaction [Δ × Noise: F(8,1296) = 2.37, p = 0.016]. All interactions not mentioned were not significant.

The number of auditory images for each condition in the lateralization task is shown in Figs. 5d, 5e, 5f, 5g. The number of multiple images increased with Δ for both the ITD and ILD lateralization, which is consistent with the data from the binaural image fusion experiment shown in Figs. 5a, 5b, 5c. For ITD lateralization, there was a relatively larger difference in the number of multiple images across the two BWs. For ILD lateralization, there was little difference in the number of multiple images across the two BWs.

Discussion

Experiment 2 was aimed at understanding where auditory images were heard for different amounts of mismatch and how many were perceived. Results showed that subjects heard a single fused auditory image for a majority of conditions. There were more multiple auditory images as the magnitude of Δ increased [Figs. 5d, 5e, 5f, 5g]. There were more multiple auditory image responses for the 1.5-mm PTs compared to the 3-mm PTs, which is consistent with the fusion data from experiment 1. Generally, there were less multiple auditory image responses in the lateralization task compared to the binaural image fusion task, which might have occurred because subjects attended less to the number of auditory images heard and more to the location of the auditory images.

Subjects perceived a change in lateral position as a function of ITD and ILD for most conditions tested as shown in Fig. 6. However, lateralization of the auditory image (or strongest auditory image if multiple images occurred) deviated from the Δ = 0 mm condition as shown by difference in data points compared to the fit lines in Fig. 5. The deviation was more pronounced as the magnitude of Δ increased. In other words, the “typical” intracranial auditory map of space (Δ = 0 mm) became more distorted as the simulated electrode pair became more mismatched.

The distortion of the intracranial auditory map of space was more pronounced for ITDs compared to ILDs. For magnitudes of Δ ≥ 6 mm, an ITD of –800 μs produced responses on the right side of the head (i.e., lateralization curves were located entirely on one side of the head). This implies that the maximum ITD that can be physically produced by the average human head would not allow for correct determination of the side that a sound source was located. For the 1.5-mm PTs, lateralization curves were essentially flat as a function of ITD. In contrast, ILD lateralization curves did cross the perceived midline for all of the Δ's tested. The robust encoding of ILDs may be a reason why present bilateral CI users who experience interaural frequency mismatch because of different electrode array insertion depths can localize sound sources better than unilateral CI users.

One consistent trend is that Δ ≠ 0-mm lateralization curves follow the Δ = 0-mm lateralization curves even if there is a deviation from those curves, and very rarely does the Δ ≠ 0-mm data cross the Δ = 0-mm curves. All of the lateralization curves were shifted to the left for positive Δ's (right ear higher in frequency) and right for negative Δ's (left ear higher in frequency) confirmed by the significant effect of Δ. This shift means that a majority of the responses were lateralized to the same side as the ear that had a carrier higher in frequency.

A comparison of significant factors for the ITD and ILD lateralization data show that BW is significant for ITD lateralization but not ILD lateralization. This is in agreement with the conclusion of Blanks et al. (2008) that neural processing of ITDs needs an overlapping area of excitation between the two ears. In Fig. 3b, the crossover amplitude for a Δ = 6 mm produces a level of –24 dB and –48 dB for the 3-mm and 1.5-mm PTs, respectively. Thus, the Δ = 6-mm and 1.5-mm PTs have too small a crossover BW and amplitude to produce a change in lateralization with ITD. The fact that ILDs can be lateralized for any Δ are consistent with the discrimination results from Francart and Wouters (2007). Logically, since the data shown that it is not necessary for ILDs to have an overlapping area of excitation between the two ears like ITDs to produce change in lateralization suggests a different neural mechanism for encoding location with ILDs (Hartmann and Constan, 2002).

Low-frequency masking noise was included to mask distortion products that could be used by NH subjects to perform the task. Since the distortion products would not be present in CI subjects, masking the distortion products would ultimately allow the fairest comparison between NH and CI subjects. The main effect of masking noise did not significantly affect the ITD lateralization curves, but did affect the ILD lateralization curves. However, both ITD and ILD lateralization curves were affected by significant interactions with the noise. We expected larger effects of masking noise on ITD lateralization because of possible binaural interference (Heller and Richards, 2010). Since we found a larger effect on ILD lateralization, the difference of our stimuli compared to those in Heller and Richards and the small subject group sizes may have contributed to this discrepancy.

Since interaural frequency mismatch produces a non-centered auditory image for stimuli with zero ITD and ILD, this may produce larger ITD and ILD JNDs as Δ is increased. It has been previously shown that interaural discrimination sensitivity worsens if the auditory image reference position is not centered (Yost, 1974; Yost and Dye, 1988). The effect of a non-centered reference position on measuring ITD and ILD JNDs as a function of mismatch was tested in the following experiment.

EXPERIMENT 3: DISCRIMINATION

Methods

In order to disambiguate the effect of Δ from the effect of auditory image reference position in ITD and ILD discrimination, a left-right discrimination experiment was performed using a two-interval, two-alternative forced-choice procedure. Each interval contained a 500-ms PT. An ITD or ILD was presented in the first interval in the left or right direction and in the opposite direction in the second interval. Stimuli in both intervals contained the same value of Δ (0, 1.5, 4, 6, or 9 mm; only positive values were tested in this experiment) and had the same BW (3 or 1.5 mm). There was a 500-ms inter-interval duration. The pink masking noise used in experiment 2 was presented throughout each trial, beginning 250 ms before the first stimulus and ending 250 ms after the second. Subjects initiated each trial by pressing a play button and were instructed to respond with the direction that the auditory image moved from the first interval to the second.

Each run consisted of five tracks, one for each of the value of Δ tested. Within a run, either ITD or ILD was adjusted adaptively. A two-down, one-up staircase procedure was used, and the last six of ten turnarounds were averaged to determine the JND for each track. ITDs were scaled by a factor of 3 for the first two turnarounds, 2 for the next two, then $\sqrt{2}$ for the remainder of the track. ILDs were changed by 2 dB for the first two turnarounds, 1 dB for the next two, and then 0.5 dB for the remainder of the track. For the ILD conditions, 10 dB of diotic level roving was applied to each interval. The magnitudes of the initial starting values for the staircases were 400 or 2500 μs for ITDs and 5 or 20 dB for ILDs.3 Staircases were not allowed to adapt to a value above the starting values. A track was ended if a listener provided four incorrect answers at the largest possible ITD or ILD. These JNDs were considered immeasurable and set to a value of 2500 μs for ITD tracks (25 of 600 ITD tracks were immeasurable; there were no ILD tracks that were immeasurable).

In order to determine if a centered image would result in improved interaural discrimination for mismatched conditions, corrections using ILDs were obtained for each subject at each value of Δ and type of PT. The stimuli were the same as those used in the experiment 2 with the masking noise. To find the ILD correction, subjects performed a two-alternative forced choice task where the subject responded to whether they heard the sound on the right or left. The ILD presented was adjusted adaptively with a one-up, one-down method; a response of “right” shifted the ILD towards the left (i.e., a negative ILD) was imposed and vice versa. The ILDs of the last six of eight turnarounds were averaged to determine the ILD necessary to center the image for each track. The step size for the first two turnarounds of each track was 2 and 0.5 dB for the remainder of the track. There were ten total tracks, two for each of the five Δ's tested in this experiment. One track began with an ILD of +15 dB and the second began with an ILD of –15 dB. All ten tracks were interleaved and the trials from each track were selected in a random order. At the end of the task the two ILDs for each condition were averaged to determine the ILD needed to center the auditory image. This task took approximately 30 min.

In the main experiment, there were a total of eight conditions [2 BWs × (ITD or ILD) × (not centered or centered) = 8]. Each subject completed three runs of each condition, each run took 15–20 min, and testing was administered in four two-hour testing sessions.

Results

The results of the experiment are shown in Fig. 7. Separate repeated-measures ANOVAs with factors BW, centering, and Δ were performed on the ITD and ILD discrimination data; the results are reported in Table TABLE III.. For the significant p-values in Table TABLE III., the level of significance is 0.01 after Box–Geisser–Greenhouse Epsilon correction.

Figure 7.

Discrimination ITD and ILD JNDs as a function of Δ. Symbols show the average over subjects and runs, and the error bars represent ±1 standard deviation from the average. For ITD discrimination, JNDs that could not be measured were set to 2500 μs in calculation of the average and standard deviation. Squares show 3-mm PTs and circles show 1.5-mm PTs. Open symbols show JNDs using the correction procedure to ensure a centered reference position and closed symbols show JNDs when this procedure was not used.

TABLE III.

Results from the repeated-measures ANOVA performed on the discrimination data. The factors were the bandwidth (BW), if centering was applied (Cent.), and the amount of interaural mismatch (Δ). The degrees of freedom (df), F statistic, p value, and partial Ω² are reported for each factor and interaction.

Condition	Factor	df	F	p	Ω2
ITD	BW	1	14.2	0.005 a	0.59
	Cent.	1	2.28	0.17	0.12
	Δ	4	14.7	< 0.0001 a	0.60
	BW × Cent.	1	2.51	0.15	0.14
	BW × Δ	4	10.7	< 0.0001 a	0.52
	Cent. × Δ	4	1.15	0.35	0.02
	BW × Cent. × Δ	4	1.21	0.32	0.02
ILD	BW	1	21.5	0.0012 a	0.70
	Cent.	1	0.30	0.60	−0.08
	Δ	4	55.0	< 0.0001 a	0.82
	BW × Cent.	1	0.94	0.36	−0.01
	BW × Δ	4	0.60	0.66	−0.05
	Cent. × Δ	4	0.88	0.49	−0.01
	BW × Cent. × Δ	4	0.14	0.96	−0.11

^aSignificant p-values.

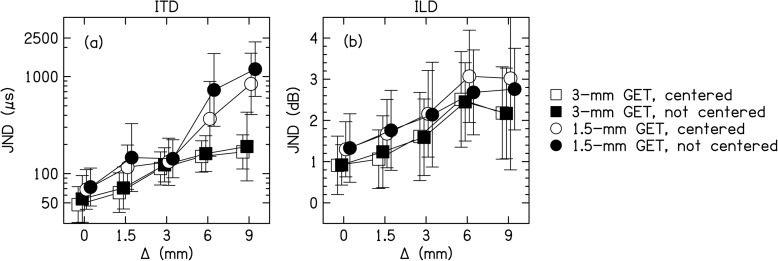
Figure 7a shows that ITD JNDs significantly increased (worsened) with increasing Δ. The JNDs were significantly lower for the 3-mm PTs compared to the 1.5-mm PTs. On average for the 3-mm PTs, the ITD JNDs were about 50 μs for Δ = 0 mm and 110 μs for Δ = 9.5 mm. Also, the ITD JNDs were higher for the 1.5-mm PTs for Δ ≥ 6 mm, shown by the significant interaction of BW × Δ. The interaction resulted from several immeasurable ITD JNDs for these conditions (25 out of 120), which were set to a value of 2500 μs. Bonferroni-corrected pairwise comparisons showed that significant differences (p < 0.005) occurred between conditions with Δ = 0 and 9.5 mm, Δ = 1.5 and 9.5 mm, and Δ = 3 and 9.5 mm.

Figure 7b shows that, similar to the effects seen with ITDs, ILD JNDs significantly increased with increasing Δ. Also similar to ITD JNDs, the ILD JNDs were significantly lower for the 3-mm PTs compared to the 1.5-mm PT. On average for the 3-mm PTs, the ILD JNDs were about 1 dB for Δ = 0 mm and 2 dB for Δ = 9.5 mm. Unlike the ITD JNDs, the interaction between BW × Δ was not significant, which we attribute to subjects always being able to perform the ILD discrimination task for all the conditions tested. In fact, ILD JNDs plateau slightly for increasing Δ; the difference between Δ = 6 and 9 mm is not significant in a Bonferroni-corrected pairwise comparison (p = 0.45). All other combinations of Δ were different (p < 0.005) with the exceptions that Δ = 0 and 1.5 mm, and Δ = 1.5 and 3 mm.

Discussion

In this experiment, we measured the effects of interaural frequency mismatch (Δ), BW, and whether the reference location of the auditory image was centered on ITD and ILD JNDs. We predicted that a non-centered reference location, as measured in experiment 2, was a potentially confounding variable when measuring the effect of Δ on ITD and ILD JNDs. As Δ increased, performance generally worsened, as seen by the fact that ITD and ILD JNDs significantly increased. This finding is generally consistent with previous measurements of interaural frequency mismatch (e.g., Francart and Wouters, 2007; Blanks et al., 2008). For Δ's of 6 or 9 mm, the ITDs JNDs became increasing immeasurable whereas the ILDs JNDs reached a plateau. Again, it seems that an overlapping region of excitation is necessary to perceive changes in location for ITDs but not for ILDs. The effects in the discrimination data can also be compared to the effects in the lateralization data from experiment 2. There was also a significant effect of Δ in experiment 2 for both ITDs and ILDs. Because the ITD lateralization curves for Δ's of 6 or 9 mm in experiment 2 were flat (Fig. 5), this provides an explanation for the fact that many ITD JNDs were immeasurable in experiment 3. In other words, the discrimination experiment ideally tested subjects' ability to discriminate between two intracranial locations; however, some conditions could not provide a change in intracranial location, even for the largest ITDs. There was less of an effect for ILD lateralization, suggesting that ILDs are more robust to interaural frequency mismatch (i.e., perception of ILDs do not necessarily need overlapping areas of excitation).

There was a significant effect of BW for both ITD and ILD discrimination, where the larger BW stimuli yielded smaller JNDs. For ITDs, this is consistent with the significant effect of BW in experiment 2. However, for ILDs, this is inconsistent with the lack of significant effect of BW in experiment 2. It may be that it is not entirely valid to compare the lateralization task, where subjects were asked to report the lateral position of an auditory image for a large range of ITDs and ILDs, to the discrimination task, where subjects simply made a two-alternative forced choice decision based on perceived changes in relatively small ITDs and ILDs.

The main goal of this experiment was to determine if a non-centered reference position, as occurs when signals are mismatched, affects ITD and ILD JNDs. Contrary to expectation, correcting for a non-centered reference position did not significantly change JNDs either by main effect or interaction with another factor.4 Centered images have been shown to produce smaller ITD and ILD JNDs (Yost, 1974; Yost and Dye, 1988). It was hypothesized that centering the reference position as Δ increased (see Fig. 5) would allow subjects to discriminate smaller ITDs and ILDs. The lack of improved JNDs for the centered reference position could have several reasons. The first reason is that the centering procedure might not have adequately determined the centered auditory image for each condition. We were unable to use individual lateralization curves because not all of the subjects in experiment 3 participated in experiment 2 (collecting the data for new subjects would not have been pragmatic). We piloted many centering methods and used the method that provided the most consistent data in a reasonable amount of time. In one method, we tried using the average offset from the lateralization curves from experiment 2. However, many subjects reported that this type of correction produced non-centered auditory images. In another method, we let subjects manually center stimuli by using an interface that applied ILDs to a stimulus. However, the results from this method were highly variable if subjects performed this type of centering multiple times. In another method, which was the one we utilized, we performed the adaptive method described above. This method provided relatively stable offsets in a reasonable amount of time. The second reason why the centering did not affect ITD and ILD JNDs is that centering may only change JNDs for matched carriers but not for mismatched carriers. The third reason is that the offsets may have been too small to see a significant effect of centering.

GENERAL DISCUSSION

Experimental findings

One of the major arguments for providing bilateral CIs to people with bilateral profound deafness is to improve spatial hearing, including segregation of speech from noise and sound localization in the horizontal plane. The change in perceived sound location in the horizontal plane is mediated by perceptually usable ITDs and ILDs. However, bilateral CI users do not localize as well as NH listeners. One of the contributing factors to the disruption of binaural hearing may be interaural frequency mismatch in bilateral cochlear implantation. In these experiments, we attempted to create a more complete picture of the perceptual consequences of sounds that carry ITD and ILD cues when interaural frequency mismatch is imposed. The mismatch in this study was parametrically imposed on the carrier signals of modulated waveforms. Three different experiments were performed in order to measure three distinct aspects of perception: binaural image fusion, lateralization, and interaural difference discrimination. The signals were 100-pps acoustic pulse trains that had a constant spatial BW (in mm) as would occur in electrical stimulation.

In experiment 1, subjects reported their subjective impression of the sounds (number, location, and compactness of images) with interaural frequency mismatch and zero ITD and ILD. A majority of the responses were of a single auditory image (73%) located on the side of the head with the higher-frequency carrier (see Fig. 3). A minority of responses had multiple (24%) or diffuse (3%) auditory images. The number of multiple auditory image responses increased with increasing interaural frequency mismatch and decreasing BW (see Fig. 5). To our knowledge, there is no existing literature that has quantified the number of perceived auditory images in this way, although numerous reports suggest that multiple perceived images can occur in a variety of binaural stimuli (e.g., Hafter and Jeffress, 1968; Blauert and Lindemann, 1986).

In experiment 2, subjects reported the lateral position of auditory images in the presence of a range of ITDs or ILDs with different interaural frequency mismatches. As interaural frequency mismatch increased, the range of responses for ITD conditions became smaller. For a 9-mm mismatch and 1.5-mm BW PTs, the range of ITDs produced a very small change in lateral position (see Fig. 6). This result is consistent with models of ITD encoding that necessitate interaurally correlated inputs at similar characteristic frequencies across the ears. It appears that encoding of ITDs to produce changes in lateral position diminishes with increased interaural frequency mismatch but less so for ILDs. This result may be thought of similarly to the diminished ability to lateralize ITDs but not ILDs as a signal becomes more interaurally decorrelated (Rakerd and Hartmann, 2010).

We found that subjects lateralized a majority of the sounds to the side of the higher-frequency carrier in experiment 2, consistent with the results of experiment 1. There could be several reasons for this finding. One is that an additional ITD besides the one in the waveform delay could be imposed upon the neural coding of the signal because of the difference in the cochlear traveling wave path lengths (Shamma et al., 1989; Strelcyk and Dau, 2009). Another is that since the temporal shape of the pulses changed for different carrier frequencies, the signal with the sharper attack imposed an additional ITD to the higher-frequency carrier (see Fig. 1). The change in temporal shape also affects the duration of the pulses, depending on how it is measured or more importantly neurally encoded. Lastly, our choice of using spectral peak normalization could have introduced an effective ILD for stimuli that we had defined as having zero physical ILD. Our normalization choice was to best control the physical properties of the stimuli. Note that the overall levels for the higher-frequency stimuli are actually much lower than the level for the 4-kHz carrier (Table TABLE I.), which is a counter-argument that lateralization was biased to the ear with the higher-frequency carrier because it was louder. Admittedly, it is likely that a complex interaction of binaural and monaural processing occurred for our stimuli that had different spectra between the ears, which may have produced unwanted lateralization of the auditory image. However, it is beyond the scope of this paper to begin to develop a model that addresses the interaction of monaural loudness, binaural loudness, and perceived lateralization. Whatever the reason or combination of reasons, the consistent lateralization offset with mismatch could have impaired ITD and ILD discrimination performance because the auditory images with zero physical ITD and ILD were not centered.

In experiment 3, we measured ITD and ILD discrimination performance as a function of interaural frequency mismatch. For matched carriers, we measured ITD JNDs (using the arithmetic mean and a two-down, one-up staircase) in the range of 10 to 110 μs for a 3-mm BW and 20 to 120 μs for 1.5-mm BW GET PTs presented at 70 dB SPL-A. These ITD JNDs can be compared to those in Blanks et al. (2008) who used transposed tones presented at 30, 50, and 70 dB compared to a tone with an equivalent peak amplitude (i.e., spectral peak normalization). For the 70-dB stimuli (the level most comparable to our stimuli), they measured ITD JNDs (using the geometric mean and a three-down, one-up staircase) in the range of 30 to 50 μs, thus consistent with our measurements. As interaural frequency mismatch increased, so did ITD JNDs. In our study, a 9-mm mismatch (approximately a 10-kHz difference in CF) and 1.5-mm BW PT degraded performance to the point where ITD JNDs were immeasurable for many subjects. In Blanks et al. (2008), ITD JNDs for a 1600-Hz frequency separation were immeasurable for two of three subjects at 70 dB. Our subjects could tolerate larger mismatches compared to the subjects in Blanks et al. because of the much larger BW of our stimuli.

Regarding ILDs, for matched carriers we measured ILD JNDs in the range of 0.3–2.2 dB for a 3-mm BW and 0.4–2.4 dB for 1.5-mm BW GET PTs. These ILD JNDs can be compared to those in Francart and Wouters (2007) who used uncorrelated 1/3-octave noise bands with a 4-kHz center frequency before mismatch. Their ILD JNDs were in the range of 1–2 dB, thus consistent with our measurements. As interaural frequency mismatch increased, so did ILD JNDs. In our study, ILD JNDs for a 9-mm mismatch and 1.5-mm BW PT were in the range of 1–7 dB, and increased by about 1.5 dB on average compared to the matched condition. Notably, unlike the ITD conditions, there were no conditions in which ILD JNDs were immeasurable. In Francart and Wouters (2007), the ILD JNDs increased by 1.5 dB for a 1 octave shift. Given that large mismatches compared to the BW of the stimuli were used in both studies and that we observed a plateau in ILD JNDs for an interaural frequency mismatch starting at 6 mm, we predict that ILD JNDs will not increase beyond this point for either the PT or noise stimuli. Therefore, the increase in ILD JNDs of 1.5 dB is consistent across the two studies. The plateau in the ILD JNDs suggests ILD processing does not necessitate a substantial overlap of interaural areas of excitation, unlike ITD processing. In other words, the stimuli transition from a region of binaural processing of the ILD to a region of two monaural level comparisons.

It is possible to understand some of the effects in the discrimination JNDs of experiment 3 (Fig. 7) from the lateralization curves of experiment 2 (Fig. 6). When lateralization curves were flat (9-mm mismatch, 1.5-mm BW, ITDs), subjects had the largest ITD JNDs and many were immeasurable. Lateralization curves always showed a fairly large change in lateral position with ILD and all of the ILD JNDs were measurable. Also, ITD and ILD JNDs were smaller for the larger BWs, which is consistent with the lateralization curves having a larger range and steeper slope across the midline.

The results of experiment 2 suggested that auditory images were not perceptually centered when interaural frequency mismatch was introduced. Therefore, we tested the effect of centering our reference stimuli in experiment 3. An improvement with centering was expected because of previous studies using interaurally frequency matched stimuli (Yost, 1974; Yost and Dye, 1988). Centering did not significantly improve the JNDs. It is unclear if the lack of improvement with centering occurred because of our procedure, the stimuli, or some other reason.

Quality and shortcomings of the CI simulation

One novel aspect of this study was in the stimulus design to create a better CI simulation, which allowed us to better investigate the effects of interaural frequency mismatch. This was done by keeping the spatial BW constant in mm rather than the BW constant in Hz, as occurs in electrical stimulation and unlike CI simulations that use SAM or transposed tones. Furthermore, using pulses with a sine tone carrier produced relatively compact auditory images depending on interaural frequency mismatch unlike simulations that use decorrelated narrowband noises. However, because there are time-frequency limitations that arise from creating acoustic pulses, it should be acknowledged that these acoustic stimuli are not perfect electrical simulations. The biggest problem is that the pulse shape changed with the carrier frequency (Fig. 1). Because the BW in Hz increased with increasing interaural frequency mismatch, the attack and decay of each pulse became sharper with increasing interaural frequency mismatch. It has been show that the sharper the attack of a modulated tone (Bernstein and Trahiotis, 2010; Klein-Hennig et al., 2011) or pulse train (Laback et al., 2011) improves ITD discrimination JNDs and alters ITD and ILD lateralization (Bernstein and Trahiotis, 2012). However, given that the attack of our stimuli even for the 4-kHz carriers were relatively sharp (less than 1 ms rise-fall time) compared to the sharpest attack of the stimuli from Bernstein and Trahiotis (2012), we think changing temporal shape of the stimuli had a small effect for the stimuli in our study.

Another aspect of using bilateral CIs that could not be accounted for in this study is that the neural plasticity, which is often seen in CI subjects, may compensate for interaural frequency mismatch on some levels. All of the experiments in this study allowed our subjects very little time to adapt to interaural frequency mismatch and should be considered acute measurements. It may be that repeated testing with interaural frequency mismatched stimuli would improve binaural performance.

In an attempt to roughly determine the quality of this simulation and the importance of performing these CI simulations, we compared our results in NH listeners to CI subjects. Subjective fusion was previously studied in a bilateral CI subject (van Hoesel et al., 1993). They showed that more multiple auditory image responses occurred for increasing interaural frequency mismatch, consistent to that found in the simulations in experiment 1 (see Figs. 45). Kan et al. (2011) performed the same fusion task as performed in experiment 1 in nine post-lingually deafened bilateral CI users. They measured a majority of single-image responses, 84%, most comparable to the 83% measured for the 3-mm PTs in our NH subjects. Kan et al. also observed a systematic shift in the lateral position toward the ear stimulating the more basal electrode.

van Hoesel et al. (1993) performed a lateralization experiment that showed lateralization was affected by interaural frequency mismatch imposed on loudness-balanced electrode pairs. The effect was seemingly random, although a majority of the responses were on the right side, which the authors postulated was due to more experience with the right CI (six years) vs the left CI (half a year). Kan et al. (2011) performed the same lateralization task as performed in experiment 2 in CI subjects. They found that lateralization from ITDs was more affected by mismatch than lateralization from ILDs and there was a systematic shift in the lateral position toward the ear stimulating the more basal electrode. Likewise, our data in NH subjects showed that lateralization was affected by interaural frequency mismatch in a systematic way, such that the lateral position of an auditory image moved towards the ear with the higher carrier frequency. Because of the many factors to consider in bilateral CIs (neural degeneration, placement of electrode arrays, loudness growth, etc.), it would be unlikely that a bilateral CI subject would demonstrate a systematic effect on lateralization as strong as the effect demonstrated in our simulations. Therefore, the lateralization results are in general agreement between CI and NH subjects, but the data in NH subjects showed trends likely more difficult to observe in the highly variable data from the CI subjects.

We can also compare the results of the discrimination experiment between NH and CI subjects. van Hoesel and Clark (1997) measured ITD JNDs in two bilateral CI subjects and showed that large interaural frequency mismatches, between four and eight electrodes (three to six mm), were necessary before ITD JNDs increased. Poon et al. (2009) showed ITD JNDs changed by less than a factor of 2 over a range of electrodes as small as 0.8 mm and as large as 5.7 mm. For one subject, the ITD JND was about 1000 μs for an interaural frequency mismatch of 13 mm, although most of the other CI subjects in that study did not show such tolerance to interaural frequency mismatch. These values roughly correspond to the values that we measured in our study. Figure 7 shows that three to six mm of interaural frequency mismatch increased ITD and ILD JNDs by approximately a factor of 2. Kan et al. (2011) performed both ITD and ILD discrimination experiments for non-centered and centered reference positions. They found a similar increase in ITD JNDs as found in Poon et al. (2009), and ITD JNDs increased relatively more than ILD JNDs.

In conclusion, the CI simulations used in this study were admittedly not perfect because of the time-frequency relationship of sound. However, they do show a better correspondence between the NH and CI interaural frequency mismatch data than previous reports using signals other than acoustic pulse trains. We suggest that future binaural studies that compare CI subject performance to NH subject performance using CI simulations consider the role of spread of excitation and a relatively constant spatial BW in mm as has been done in some other studies (Goupell et al., 2009; Goupell et al., 2010).

SUMMARY AND CONCLUSIONS

We performed three binaural experiments (fusion, lateralization, and discrimination) to investigate the effect of interaural frequency mismatch in a CI simulation using acoustic pulse trains. We found the following.

• (1)An increase in interaural frequency mismatch caused an increase in the number of multiple auditory image responses in the binaural image fusion and lateralization tasks.
• (2)A decrease in BW caused an increase in the number of multiple auditory image responses in the binaural image fusion and lateralization tasks.
• (3)An increase in interaural frequency mismatch caused a systematic shift of the perceived intracranial location towards the ear with the higher carrier frequency in the fusion and lateralization tasks.
• (4)An increase in interaural frequency mismatch caused a reduced range of lateralization, particularly for ITD lateralization. Furthermore, an increase in interaural frequency mismatch produced an increasing distortion of the lateralization curves compared to the interaural frequency matched lateralization curves.
• (5)An increase in interaural frequency mismatch caused an increase in both ITD and ILD JNDs in the discrimination task. However, for large mismatches (6 mm or greater), ITD JNDs kept increasing and became immeasurable for many subjects while ILD JNDs stopped increasing.
• (6)A decrease in BW caused an increase in ITD and ILD JNDs in the discrimination task.
• (7)Attempting to center the reference location for conditions with interaural frequency mismatch (found in the binaural image fusion and lateralization tasks), did not significantly improve ITD or ILD JNDs in the discrimination task.
• (8)There was a relatively good correspondence between the data for the NH subjects listening to acoustic CI simulations and previous CI data.