Abstract
Many hearing aids introduce compressive gain to accommodate the reduced dynamic range that often accompanies hearing loss. However, natural sounds produce complicated temporal dynamics in hearing aid compression, as gain is driven by whichever source dominates at a given moment. Moreover, independent compression at the two ears can introduce fluctuations in interaural level differences (ILDs) important for spatial perception. While independent compression can interfere with spatial perception of sound, it does not always interfere with localization accuracy or speech identification. Here, normal-hearing listeners reported a target message played simultaneously with two spatially separated masker messages. We measured the amount of spatial separation required between the target and maskers for subjects to perform at threshold in this task. Fast, syllabic compression that was independent at the two ears increased the required spatial separation, but linking the compressors to provide identical gain to both ears (preserving ILDs) restored much of the deficit caused by fast, independent compression. Effects were less clear for slower compression. Percent-correct performance was lower with independent compression, but only for small spatial separations. These results may help explain differences in previous reports of the effect of compression on spatial perception of sound.
INTRODUCTION
Dynamic range compression is routinely used in hearing aids to address the limited dynamic range available to hearing-impaired listeners (Moore, 2007). Such compression generally improves audibility and speech intelligibility (Moore, 1996; Jenstad et al., 1999). However, when applied independently to both ears, dynamic range compression can alter interaural level differences (ILDs), which provide important information about acoustic source location (Byrne and Noble, 1998). It is not clear, however, how such alterations in ILDs influence spatial auditory perception. Compression has little effect on the ability of either normal-hearing or hearing-impaired listeners to accurately localize sounds presented in isolation (Keidser et al., 2006; Musa-Shufani and Walger, 2006). Yet compression can degrade the ability to discriminate small differences in ILD (Musa-Shufani and Walger, 2006), and can affect normal-hearing listeners' perception of other spatial attributes, such as source diffuseness and perceived movement (Wiggins and Seeber, 2011, 2012). Recent work suggests that independent compression impairs the ability to use spatial cues to selectively attend to a target talker in the presence of other, simultaneous talkers (Kalluri and Edwards, 2007). Motivated by this finding, the current study sets out to further explore whether independent compression interferes with the ability to attend to target speech based on its location in the presence of competing speech even though it may not adversely affect other aspects of spatial perception. Such a finding can help to resolve the apparent inconsistencies in previous reports of effects, or lack thereof, of compression on different aspects of spatial hearing.
While intuitively sound localization is related to the ability to attend to sounds based on their location, accurate localization is neither necessary nor sufficient for predicting the importance of spatial cues in understanding a signal in a mixture of sounds (Noble et al., 1997; Gallun et al., 2008; Schwartz et al., 2012). How dynamic range compression affects this ability cannot be easily predicted by how it affects localization. Furthermore, many previous studies examining the effect of compression on localization used isolated stimuli. In this case, the stimulus onset is unaffected by compression for some time (depending on the compression time constants), and the “clean” spatial cues at onset may support accurate localization. The compressed ILDs during the ongoing portion of an isolated stimulus also follow a predictable pattern that listeners may be able to learn how to localize (e.g., Bauer, 1966; Shinn-Cunningham et al., 1998). Such factors may help explain why some previous reports find little or no effect of dynamic range compression on localization accuracy for sources in isolation (Keidser et al., 2006; Musa-Shufani and Walger, 2006).
Spatial acoustic cues such as ILD can be particularly helpful in allowing listeners to attend to and understand a desired sound source when multiple competing sources are present (e.g., Shinn-Cunningham, 2005, 2008; Shinn-Cunningham and Best, 2008). The term “spatial selective auditory attention” refers to cases in which listeners specifically use spatial cues to focus on a desired sound source and mediate competition from distracting sources from other locations (e.g., Ruggles and Shinn-Cunningham, 2011). Spatial separation between competing sound streams can also make it easier to understand a desired sound source by changing the signal-to-noise ratio (SNR) of the signals reaching the ears due to acoustic head shadow (Zurek, 1993); however, such “energetic” factors are often modest compared to effects on spatial selective attention (e.g., Kidd et al., 2005b).
In order to predict how dynamic range compression influences spatial selective auditory attention, it is important to consider the ways in which it alters binaural cues. In general this will depend both on stimulus factors and on compression parameters. A simple dynamic range compression scheme applies linear gain for low-level sounds, and provides progressively less amplification of sounds whose level exceeds a set threshold. Overall, compression that operates independently at the two ears will tend to reduce ILDs, applying a greater gain at the ear receiving the less intense signal. Since many natural stimuli, including speech, fluctuate in level, compression that is applied independently at the two ears will also introduce fluctuations to the ILD of an isolated sound source even if it is stationary in space. The resulting ILD fluctuations are likely to increase source image diffuseness and to cause listeners to perceive moving and split images, even if the source produced constant spatial cues prior to compression (Wiggins and Seeber, 2011, 2012). When multiple sound sources are present in an acoustic scene, the ILD of a target sound source can be altered due to the compressors' response to an unrelated source. In this case, even a target with zero ILD prior to compression can contain fluctuating ILDs; moreover, the ILD fluctuations can occur unpredictably in time and in unpredictable directions. Thus the problems reported by Wiggins and Seeber may be exacerbated in situations where multiple, dynamic stimuli are present, such as speech mixtures.
Dynamic range compression in hearing aids is typically set to operate on timescales anywhere from a few milliseconds to several seconds. If compression is fast (less than 10 ms) then only stimuli that are more or less simultaneous will affect each other's ILDs. Moderate compression speeds on the order of tens of microseconds could increase interactions between sources because the difference in gain applied to the left and right ears due to a preceding stimulus can affect a target stimulus' ILD, particularly at its onset. If compression is very slow (seconds or more), however, then the response of the compressors will be roughly constant for any given source configuration, resulting in stable spatial cues.
Given these observations, we hypothesized that bilaterally independent dynamic range compression operating on fast-to-moderate timescales would increase the minimum azimuthal separation between competing speech sources required for listeners to effectively attend to a target source. More specifically, when two stimuli are sufficiently close in location, so that ILD fluctuations cause the ILD distributions associated with the two stimuli to overlap, the ability to direct spatial selective auditory attention should suffer and performance should decrease. If, however, the sound sources are sufficiently separated in azimuth such that ILD fluctuations do not cause any such overlap, then compression may not have any effect on spatial selective auditory attention (i.e., the compression-altered ILDs still identify the sources uniquely, with or without these fluctuations). In normal-hearing listeners, the benefit of spatial separation on spatial selective auditory attention increases with azimuthal separation up to about 30°, where it reaches a maximum (Marrone et al., 2008a). Therefore, as the spatial separation of sources increases beyond 30°, we might expect to see decreasing effects of compression.
To test whether compression influences spatial selective auditory attention, we estimated “spatial thresholds,” defined as the amount of spatial separation required to achieve a threshold level of performance in a selective attention task, for normal-hearing subjects. Target and maskers were comprised of digits spoken by the same talker. Because of this design, cues such as pitch and semantic context could not be used to focus selective attention, making spatial cues critical for performing the task. We simulated various spatial configurations using head-related transfer functions (HRTFs), preserving realistic spatial cues, including interaural time differences in the resulting stimuli. We compared spatial threshold estimates when amplification was linear (uncompressed), compressive and independent at the two ears, and compressive but linked at the two ears (i.e., left and right ears get an identical gain at each time instant in each frequency channel). The overall stimulus level was set to be similar across conditions. As discussed above, the time constants used by the compressors will influence the compressors' effect on ILDs in the mixture; therefore, Experiment 1 measured spatial thresholds for different combinations of attack and release time constants. Because reverberant energy tends to reduce ILD cues (Shinn-Cunningham et al., 2005), room acoustics are likely to interact with effects of compression on spatial selective auditory attention. Therefore, in Experiment 2, we measured spatial thresholds for different levels of reverberant energy.
METHODS
Stimuli
All source stimuli were digits (0 to 9) recorded in our laboratory by a male talker in a sound-isolated booth with perforated metal walls, ceiling, and door, and a carpeted floor. The digits were recorded individually, so there was no co-articulation, with a sample rate of 16 kHz. Ten instances of each digit were recorded; when selecting any digit, one of these ten was selected at random.
For each trial, three sequences of four digits were created: one target sequence and two masker sequences. The digits for each sequence were selected at random with the restriction that no digit was presented at the same temporal position in any of the three sequences (for example, if the first digit of the target was 1, then neither of the maskers could also have first digits of 1). We randomly staggered the onsets of each of the digits in the target and two masker sequences. Specifically, for each temporal position (1 to 4) in the sequences, one of the digits from the three sequences was selected randomly to start first; one of the remaining two digits was randomly selected to start 150 ms after the onset of the first digit, and the final remaining digit started 300 ms after the first digit. As a result of this temporal randomization, the digits within each sequence were not isochronous; the inter-digit interval between two digits in each sequence could be between 300 and 900 ms.
The choice of randomly staggering the onsets of target and maskers was motivated by two ideas. First, synchrony of competing sounds reduces the benefit of spatial separation of the sounds (Best et al., 2011); therefore, staggering the onsets was likely to maximize effects in cases where spatial cues were useful. Second, in natural settings, listeners typically hear a target amidst maskers whose amplitude fluctuations are independent of those in the target, and this independence affects the way in which the maskers will alter that target's ILD. As noted below, we tested performance when maskers were placed symmetrically on either side of a central target. If both maskers were played synchronously without staggering their onsets, the overall levels at the ears would be unnaturally similar at all moments. This in turn could lead us to underestimate any effects of independent compression on the influence of spatial cues on performance.
Spatialization
Because the target and maskers were selected from the same recordings all using the same talker, the target could not be distinguished from the maskers using voice or pitch cues; only spatial cues enabled the listener to select the target stream from the ongoing source mixture. The target sequence was always simulated from straight ahead of the listener, digits from one masker sequence were simulated from locations left of the midline, and digits from the other masker sequence were simulated from locations right of the midline. To help listeners focus attention on the correct sequence, 1 s before the start of the sequences listeners were cued by a presentation of the target sequence's first digit played in isolation, simulated from straight ahead. In other words, each trial consisted of a cue digit presented from straight ahead, followed by a 1-s pause, followed by a presentation of three nearly simultaneous streams (left masker, center target, and right masker). Because the first target digit (after the 1-s gap) was the same as the cue digit, responses to the first digit were not included in analyses of performance (post hoc analysis confirmed that subjects were at ceiling in reporting the first, cued target digit).
To simulate realistic spatial positions with normally occurring spatial cues, sources were convolved with spatial filters. Experiment 1 used head-related impulse responses that were recorded in an anechoic chamber, sampling every 5° on the azimuthal plane (Gardner and Martin, 1994). Experiment 2 used binaural room-impulse responses (BRIRs) recorded in our laboratory from the ears of the first author, following the procedures described in Shinn-Cunningham et al. (2005). These recordings were made in a 9 × 5 × 3.5 m room with a carpeted floor and acoustic tile ceiling; the room had a reverberation time of T60 = 650 ms. We recorded BRIRs every 5° from −30° to +30°, as well as at ±40°, 50°, 60°, 70°, and 90°. Three different levels of reverberant energy were tested in Experiment 2. The “Reverberant” condition used the measured BRIRs. These BRIRs were modified to create “Intermediate” and “Anechoic” conditions by locating the first reflection of each recorded impulse response manually (separately for left and right recordings). The BRIR was then temporally windowed to isolate the direct sound impulse response (up to the onset of the first reflection) and reverberant energy (from the first reflection onwards). For the Intermediate condition, the reverberant component of each BRIR was attenuated by 6 dB, and then added back to the direct sound. For the Anechoic condition, only the direct sound portion of the BRIR was used. Subjective listening confirmed that these intermediate and pseudo-anechoic BRIRs produced spatialized sources without noticeable artifacts. As noted above, the target sequence was always simulated from 0° azimuth. The masker positions varied as described in the adaptive procedure below; however, the two masker digits presented at a given time were symmetrically positioned around midline (e.g., if one masker was at +30°, the other masker was at −30°). This symmetric masking setup was adopted to limit the influence of differences in the long-term SNR between the mixtures reaching the two ears due to head shadow (Marrone et al., 2008a). Nonetheless, short-term SNR will still fluctuate at the two ears even when maskers are symmetrically placed (especially due to the onset staggering we employed); this in turn can affect the ability to hear the target. Moreover, as discussed above, these fluctuations likely interact with the dynamic amplification used in a given condition and thereby may affect how spatial separation influences performance.
Compression
After the binaural speech mixtures were generated, they were put through a simulation of hearing-aid compression. Compression operated independently on 16 frequency bands, equally spaced on the ERB scale from 100 Hz to 8 kHz (Glasberg and Moore, 1990). The compression threshold within each band was set to the level received in that band from speech that was presented at an overall level of 50 dB sound pressure level (SPL) (estimated using a 5-s token of speech-shaped noise). Linear gain was applied below this threshold. For all conditions employing non-linear compression, a compression ratio of 3:1 was always used above this threshold. This compression ratio is a relatively extreme value compared to typical hearing-aid fittings, and represents a “worst-case” scenario in order to reveal any potential effects of compression. The linear gain below the compression threshold was set so that the 0 dB point (i.e., the level within a band at which 0 gain was applied) was the in-band level of 70 dB SPL speech. The level of each individual digit was set to 70 dB SPL before filtering and compression; therefore, the overall stimulus level was roughly equivalent regardless of the compression condition.
In both Experiments 1 and 2, we used three compression conditions: linear processing, independent compression, and linked compression. For linear processing, the same multiband compressor algorithm was used as in the other conditions, but with the compression ratio set to 1:1 (ensuring that any effects we observed were not due to the multiband analysis/resynthesis, but due to the compression). For linked compression, in any given 8-ms time window, the gain applied to both the left and right ear signals in a particular frequency band equaled the minimum of the gains that would have been applied to the two signals when the compression was independent. The linked compression condition therefore had a slightly lower binaural level than the independent compression condition; whenever a non-zero ILD was present in a compression band, the ear with the less intense signal received less gain in the linked compression condition compared to in the independent compression condition. In Experiment 1, the “Fast” condition used attack and release times of 11 and 82 ms, respectively (ANSI, 2003), and the “Slow” condition used attack and release times of 48 and 730 ms, respectively. Experiment 2 used only the fast attack and release times. In all cases, the compression scheme estimated power within each band using 8-ms time windows, then smoothed this power estimate to produce the appropriate attack and release time constants before determining the amount of gain to apply.
Adaptive procedure
We designed an adaptive procedure to estimate subjects' spatial threshold, defined as the separation needed between target and maskers to obtain threshold-level performance. Specifically, the lateral position of the symmetrically placed maskers was adaptively varied until the percentage of target digits correctly reported reached threshold. In Experiment 1, the adaptive procedure tracked 67% correct using a weighted up-down procedure (Kaernbach, 1991): the masker position was decreased by 5° after each correct response and increased by 10° after each incorrect response. In Experiment 2, the 50%-correct threshold was found using a 1-up 1-down procedure (Levitt, 1971). Note that in Experiment 2, the BRIRs were not spaced evenly throughout the azimuthal plane. Therefore, the adaptive track increased or decreased the lateral positions of the maskers by one azimuthal sample (5° for sources near midline; 10° for more lateral locations). In both experiments, an adaptive run continued until 12 reversals were recorded; spatial threshold for that run was then estimated as the median of the last 8 reversals.
One concern with this adaptive procedure is that the distribution of source positions being heard can alter spatial sensitivity over relatively short time periods of time, essentially optimizing spatial resolution over the expected stimulus range (Shinn-Cunningham et al., 1998; Dahmen et al., 2010). As an adaptive run converges on some nominal value of a spatial threshold, the range of presented spatial locations narrows to a limited range around the adaptive threshold. This may allow the listener to achieve better spatial resolution than what we might expect in a typical crowded environment, where sounds come from unpredictable directions (precluding the kind of short-term adaptation that would yield better resolution). We therefore interspersed “probe” presentations (those in which the locations of the maskers were varied to adapt to threshold, as described above) with “fixed” presentations within each trial. Specifically, as described above, each trial consisted of a sequence of four target digits presented with symmetric maskers. For one of these four digits, each pair of symmetric masker digits came from one of three fixed spatial separations: ±15°, ±30°, and ±90°. The remaining digit was the probe digit, whose masker spatial angle was determined by the adaptive procedure. Only the response to the probe digit determined whether to increment or decrement the symmetric masker azimuths of the probe digit in the next trial. The order of the fixed and probe digits were randomized on each trial as follows: (1) One of the two middle digits was randomly designated as the probe digit (reducing the effect of recency and primacy on the subject's probability of obtaining a correct response to the probe digit; e.g., Jahnke, 1965; Ruggles and Shinn-Cunningham, 2011); (2) the first pair of masker digits were always given azimuths of ±30°; and (3) the remaining two pairs of masker digits were randomly assigned fixed azimuths so that one pair was at ±15° and the other at ±90°. Recall that the first target digit is used to cue the subject to the target's location; therefore, listeners were expected to be near perfect at identifying the first target digit. This procedure produced useful observations for maskers at the fixed azimuths of ±15° and ±90° at the cost of having no useful observations at the ±30° separation used for the first pair of masker digits. This procedure therefore not only estimates spatial threshold from the probe digits, but also yields fixed-increment estimates of performance for spatial separations of 15° and 90°.
Subjects first ran at least four adaptive runs as training. This training was conducted in two experimental blocks, each comprised of one adaptive track using linear processing and one adaptive track using independent compression, ordered randomly. Subjects were allowed to perform additional training blocks until they were comfortable with the task. Subjects then ran a block of 12 adaptive runs (four for each compression condition). To reduce any effects of learning over the course of the experiment as a confound in our analysis, compression conditions (independent, linear, and linked) in these 12 runs were randomly ordered subject to the following conditions: (1) runs were always paired so that subjects completed two runs of the same kind in a row, and (2) subjects completed one pair of each of the three compression conditions before encountering a second pair of any condition. Spatial threshold was averaged over the four runs of any given compression condition.
Performance for 15° and 90° maskers was computed from the percent-correct responses to fixed-azimuth digits that were in the middle of the sequence and transformed into rationalized arcsine units (RAU; Sherbecoe and Studebaker, 2004). RAU scores are similar to percent correct scores for values in the range of 20% to 80%. For more extreme values, RAU values have a greater range than the corresponding percent-correct scores, but have more uniform variance than percent-correct scores.
Task
Subjects were instructed to type in the four digits spoken by the target talker coming from center, using the midline cue digit (which was identical to the first target digit) to help them focus attention on the target. Subjects were told to guess when they were unsure of any given target digit in a 4-digit sequence so that each other response digit was in the correct position in the sequence. Feedback was provided for every trial; once a listener pressed enter, the correct digits turned green and the incorrect digits were replaced by a display of the correct digits in red. This display would hold for 1.5 s, then the digits would clear and the next trial would start. Subjects were not informed that any aspect of the stimulus was being controlled adaptively, based on performance; similarly, there was no indication of which digits were from the fixed angular separations and which were part of the embedded adaptive run.
Subjects
In total, 39 subjects participated in the experiments described. All subjects, ranging in age from 18 to 22, had clinically normal hearing (15 dB hearing level or better) as verified by pure-tone audiometry for frequencies between 250 Hz and 8 kHz. Subjects gave written consent (overseen by the Boston University Charles River Campus IRB), and were paid an hourly wage in compensation for their efforts.
Subjects were permitted to participate in more than one group, but many subjects were not able to commit to more than a few experiment sessions. We therefore analyze each group separately, making only limited inferences across groups. Subjects were excluded from a particular group analysis if they failed to achieve sufficiently high performance when target and maskers were separated by 90°. Specifically, we computed the percentage of correctly identified target digits when the maskers were fixed at ±90°, averaged across all compression conditions. In most conditions, only those subjects who achieved above 70% correct on these ±90° trials were included; the only exception was the Reverberant group in Experiment 2 (as described below). In all groups except the Reverberant group, recruitment continued until at least ten subjects met the inclusion criterion. In Experiment 1, one subject was excluded from each of the Fast and Slow subject groups. In Experiment 2, four subjects were excluded from the Anechoic group, and no subjects were excluded from the Intermediate group. Seventeen subjects performed the task in the Reverberant group; of these 17, only 7 met the 70% criterion. Therefore, for this group we relaxed our criterion to include subjects who scored at least 60% correct on the average of the fixed ±90° trials (13 subjects). Table Table I. summarizes how many subjects performed each condition.
Table I.
Summary of the groups tested.
| Spatial filters | Condition | Attack / release time constant | Subjects tested | Subjects included | |
|---|---|---|---|---|---|
| Exp. 1 | Gardner and Martin, 1994 | Fast | 11/82 ms | 11 | 10 |
| Slow | 48/730 ms | 11 | 10 | ||
| Exp. 2 | Recorded in classroom | Reverberant | 11/82 ms | 17 | 13 |
| Intermediate (reverb -6 dB) | 11/82 ms | 10 | 10 | ||
| Anechoic (direct sound) | 11/82 ms | 14 | 10 |
RESULTS
Spatial thresholds
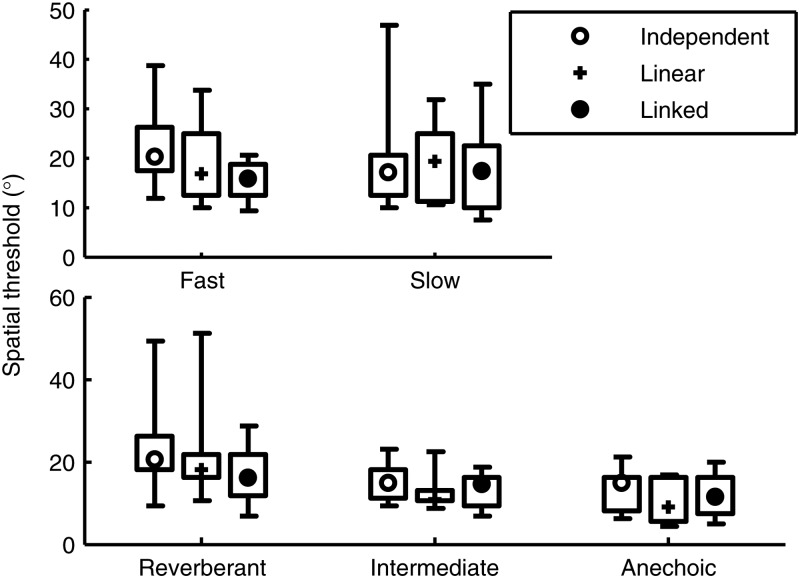
In all groups, spatial thresholds were typically below 30°, consistent with previous reports using a similar symmetrical masking paradigm (Marrone et al., 2008a). In Experiment 1 (Fig. 1, top), in which the threshold for 67% correct performance was estimated, thresholds were typically between 10° and 30°. Note that the linear processing condition was identical for both Fast and Slow groups, as no dynamic range compression was applied. Consistent with this, these groups showed similar spatial thresholds for this condition, suggesting that this metric was similar across the two different subject groups tested. In Experiment 2 (Fig. 1, bottom), the 50% correct performance level was estimated. In the Reverberant group, the 50% thresholds were largest (around 20°), consistent with the idea that utility of spatial cues is reduced in reverberant environments (Nabelek and Pickett, 1974; Marrone et al., 2008b; Ruggles and Shinn-Cunningham, 2011), although we also had to relax our inclusion criterion to 60% correct for this group, which makes it especially difficult to directly compare groups. Spatial thresholds for the Intermediate and Anechoic groups tended to fall between 10° and 20°, with no subjects having spatial thresholds greater than 25°. These values suggest that ceiling effects may limit the observable differences in spatial thresholds across compression conditions in Experiment 2.
Figure 1.
Spatial thresholds in Experiment 1 (top) and Experiment 2 (bottom), for independent (open circles), linear (plusses), and linked (filled circles) compression. Symbols mark the medians of each data set, boxes indicate the inter-quartile range, and whiskers indicate the full range of results. N = 10 for each condition except Reverberant, in which N = 13.
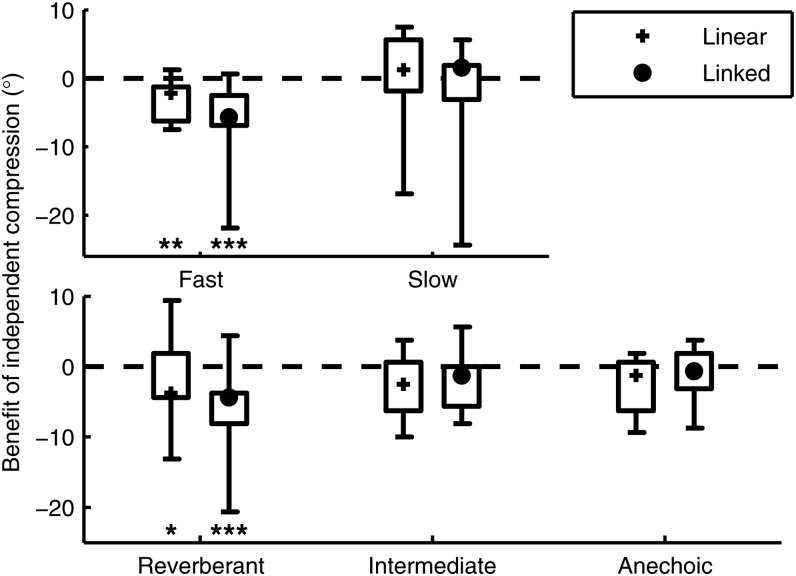
Figure 2 plots within-subject differences in spatial thresholds relative to the spatial threshold in the independent condition (which we hypothesized would be largest, due to ILD fluctuations and image diffuseness). For all groups using fast compression (Fast condition in Experiment 1 and all three conditions in Experiment 2), subjects tended to perform worse with independent compression than for either linear processing or linked compression. This produced negative spatial threshold differences in Fig. 2, consistent with our hypothesis. These differences were small, generally under 10°. Because little is known about the distribution of spatial thresholds across subjects, we used a directional Wilcoxon sign-rank test, a non-parametric test of significance, for these within-subject differences. In the Fast group (Experiment 1, top panel of Fig. 2) and the Reverberant group (Experiment 2, bottom panel of Fig. 2), the differences in spatial threshold relative to independent compression were significant for both linked compression (p < 0.005 for both groups) and linear compression (p < 0.01 for Fast, p < 0.05 for Reverberant). The Intermediate and Anechoic groups tested in Experiment 2 showed the same trends, but the differences in spatial threshold for linear processing and linked compression relative to independent compression were not statistically significant (p > 0.05 for all comparisons). As mentioned above, smaller differences in these two groups may have resulted from ceiling effects, making it difficult to detect a significant effect of compression. We therefore performed a post hoc analysis, pooling together the Intermediate and Anechoic groups to increase sample size. This post hoc test supports the notion that independent compression caused a real, albeit small, decrease in performance (p < 0.05 for both linear processing and linked compression). For the Slow group of Experiment 1, there was not even a trend for the spatial threshold to be larger in the independent compression condition compared to the linear or linked conditions, suggesting that slower compression speeds may alleviate the detrimental effect of fast compression on selective attention performance.
Figure 2.
Within-subject differences of spatial thresholds for linear (plusses) and linked compression (filled circles), both relative to independent compression. Symbols mark the medians of each data set, boxes indicate the inter-quartile range, and whiskers indicate the full range of results. Negative values indicate smaller thresholds (better performance) compared to independent compression. Statistical significance is assessed by a directional Wilcoxon signed-rank test, and indicated by a * for p < 0.05, ** for p < 0.01, and *** for p < 0.005.
We also analyzed whether spatial threshold changed over the time course of the experiment. For each condition, we computed the difference in spatial threshold averaged over the first two runs and over the final two runs. We found no differences between results in the first and final pairs of runs for any individual group or compression condition; we also found no differences when pooling across groups, compression conditions, or both groups and compression conditions (Wilcoxon sign-rank test, p > 0.05 for all comparisons). These results suggest that performance was stable over the course of our experiment. We therefore combined all four runs of any given condition to compute mean spatial threshold.
Fixed-azimuth performance
While the focus of our data collection was to estimate spatial thresholds, our methods also allowed us to perform post hoc analysis on subjects' performance for digits with masker azimuths fixed at 15° and 90°. Performance for fixed digits was computed (in RAU) separately for digits that occurred in the middle of the four-digit target sequence and digits that occurred at the end of the sequence. No consistent within-subject differences were found in performance between middle and end digits (t test; p > 0.05). All remaining analyses were therefore performed by combining results for the fixed-azimuth digits regardless of where in the sequence they occurred. The exact number of trials included in this computation for a given condition varied due to the adaptive procedure employed; across all conditions and groups, individual subjects completed between 78 and 130 trials for any given compression condition, with a majority of subjects performing between 90 and 110 trials per condition.
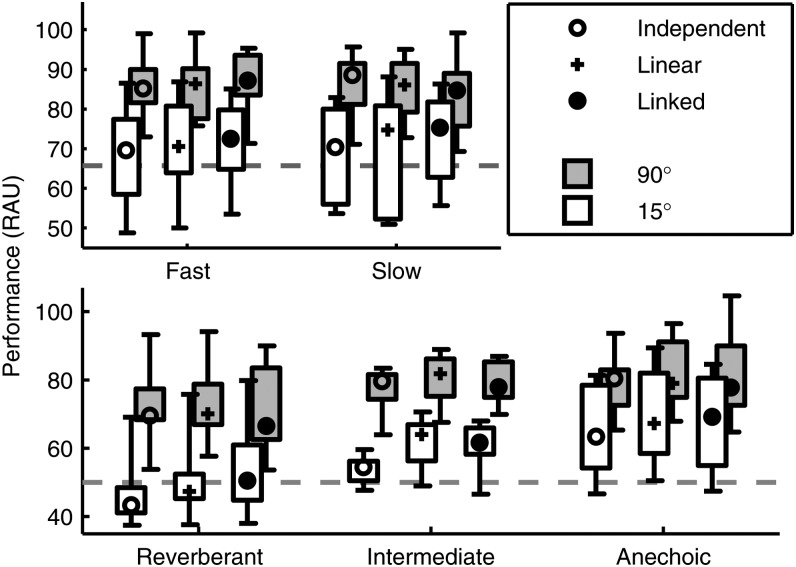
Figure 3 plots the RAU scores for fixed-azimuth maskers. The dashed line shows the threshold performance level estimated by the adaptive procedure (corresponding to 67% correct in Experiment 1 and 50% correct in Experiment 2). Averaged across groups, performance was 17.2 ± 4.2 RAU better for 90° maskers than for 15° maskers (mean ± standard deviation; however, in some groups a few subjects were excluded from all analyses based on poor performance for 90° maskers). Note that for all subject groups in both experiments, except the Reverberant group, RAU scores tended to be above this dashed line, even for 15° maskers; therefore, spatial threshold estimates made by fitting these data would tend to produce values less than 15°. Spatial thresholds estimated by the adaptive procedure, on the other hand, often fell near or above 15°, indicating that these two methods produce slightly different estimates of performance. This difference is not surprising with near-ceiling performance, as the adaptively varied azimuth was bounded by ceiling (0°), producing a biased estimate of spatial thresholds. Yet, even despite this bias, which should limit observable differences in the spatial thresholds across conditions, both spatial thresholds and fixed-azimuth performance measures produce similar effects.
Figure 3.
RAU scores for fixed-azimuth digits with maskers at 15° (white boxes) and 90° (gray boxes) for linear, independent compression, and linked compression (plusses, open circles, and filled circles, respectively). Symbols mark the medians of each data set, boxes indicate the inter-quartile range, and whiskers indicate the full range of results. Gray-dashed lines represent the spatial threshold performance point estimated by the adaptive procedure for the corresponding groups (∼65.5 and 50 RAU for the TIME groups and the REVERB groups, respectively).
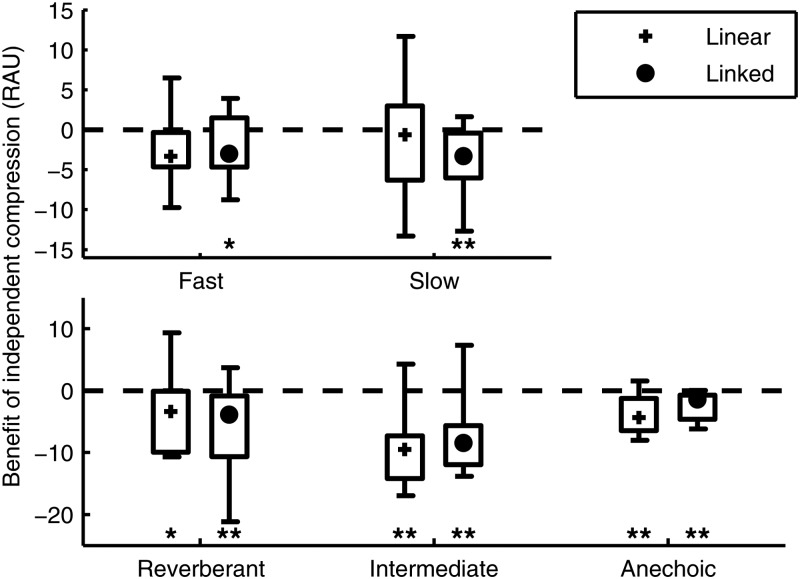
Figure 4 plots within-subject differences in RAU scores for independent compression relative to linear and linked compression for the 15° separation (90° results are not plotted for visual clarity since none of these differences were significant). The effect of compression was assessed separately for 15° and 90° maskers using one-sided t-tests on the differences between linear and linked compression relative to independent compression, all in a within-subject design. These differences revealed a distinctive pattern. There were no significant differences between compression conditions for 90° maskers for any group in either Experiment 1 or Experiment 2. However, for 15° maskers, all groups in Experiment 2 had better performance for linear processing than for independent compression (directional t-test: p < 0.05 for Reverberant, p < 0.01 for Intermediate and Anechoic). Moreover, all groups in both Experiment 1 and Experiment 2 had better performance for linked compression than for independent compression (directional t-test: p < 0.05 for Fast group in Experiment 1, p < 0.01 for all other groups). The size of this effect varied across subjects, with a mean effect size across all groups of 4.0 and 4.7 RAU for linear processing and linked compression, respectively, vs independent compression. In Experiment 2, the mean difference was larger for the Intermediate condition than for the other two conditions. While our experiment design does not support direct across-group comparisons, the tendency for the Intermediate condition to reveal the largest effects of independent compression may reflect the fact that subjects' spatial thresholds were more consistently close to 15° in this condition (see Fig. 1), resulting in relatively more sensitive measures of performance compared to conditions where subjects had thresholds greater than 15° (e.g., Reverberant) or smaller than 15° (e.g., Anechoic).
Figure 4.
Within-subject differences of RAU scores for linear (plusses) and linked compression (filled circles) relative to independent compression for 15° maskers. Symbols mark the medians of each data set, boxes indicate the inter-quartile range, and whiskers indicate the full range of results. Positive values indicate better performance compared to independent compression. Statistical significance was assessed by pairwise t-tests, and is marked with a * for p < 0.05 and ** for p < 0.01. Differences for 90° maskers were not significant for any group and are omitted for visual clarity.
The timing of target and masker digits within each of the four temporal positions of the digit sequences was randomly staggered by 0, 150, or 300 ms. While this was not the focus of our study, post hoc analysis revealed an effect of this temporal staggering on performance, with target identification tending to be better when the target was given a 150 or 300 ms delay compared to when it was given no delay. However, this effect did not interact with any of the effects of compression, which was the focus of our study. We are currently investigating this effect further.
Error type analysis
We analyzed the types of errors made by subjects on each individual digit when maskers were fixed at 15°. Specifically, we categorized errors into “switch” errors, in which the reported digit was present in the reported temporal position, but came from one of the two masker sequences, and “drop” errors, in which the reported digit was not present in the reported temporal position in any of the three sequences. For this analysis, we included all tested subjects regardless of their average performance for 90° maskers. Due to the random temporal staggering we imposed on the digits, it is possible that subjects may have mistaken masker digits for target digits not in exactly the same temporal position (for example, the third target digit might be separated by ±300 ms both from the third digit in a masker sequence and also the second digit in a masker sequence). Therefore, some small percentage of errors that truly result from improper selection across temporal positions within a digit sequence may be incorrectly counted as drop errors in this analysis. Nevertheless, if errors resulted entirely from random guessing, then switch errors should make up roughly 22% of all errors (2 masker digits out of 9 possible non-target digits). However, even with the potential for undercounting switch errors, they made up 79% ± 11% of all errors (mean ± standard deviation across all subjects). Moreover, each individual subject made significantly more switch errors than would be expected by chance (binomial test, p ≪ 0.0001). This result indicates that most errors were made not due to lack of intelligibility of the digits, but instead due to a failure to select the correct digit among the three digit sequences (see also Kidd et al., 2005a; Ihlefeld and Shinn-Cunningham, 2008; Ruggles and Shinn-Cunningham, 2011).
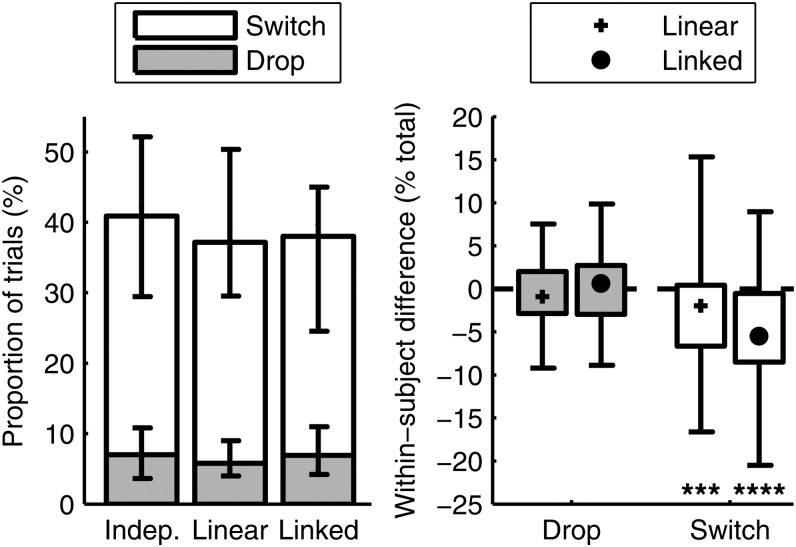
In all groups, the overall error rate for 15° maskers with independent compression was greater than for either linear processing or linked compression by an average of 3.2% and 4.7% of trials, respectively (mean error rates were 42.1%, 38.9%, and 37.3% of trials for the three conditions, respectively). Even though most errors were switch errors, these differences between conditions might depend on the pattern of drop errors, rather than switch errors. To explore this, we compared the percentage of switch and drop errors for linear and linked compression to the percentage for independent compression on an individual subject basis. Figure 5 plots both the overall error rates for switch and drop errors (left panel), and within-subject differences in the switch and drop error rates for linear processing or linked compression compared to independent compression (right panel). Drop errors constituted less than 10% of the responses in all conditions, while switch errors occurred on almost 1/3 of all responses (see left panel of Fig. 5). On an individual subject basis, drop errors rates were statistically the same when comparing independent compression to linear and to linked compression (average differences of 0.6% and −0.2%, respectively, p > 0.05 for both using a one-tailed t-test on RAU-transformed values; shaded boxes in the right panel of Fig. 5). Switch error rates, however, were significantly higher for independent compression than for either linear processing or linked compression (an average increase of 2.5% and 5.0% of trials; one-tailed t-test on RAU transformed values, p < 0.001 and p << 0.0001, respectively; white boxes in the right panel of Fig. 5). These results suggest that independent compression in our experiment impaired performance by interfering with selection of the proper source, not by degrading overall signal intelligibility.
Figure 5.
Left: Error rates for switch errors, in which subjects reported a masker digit, and drop errors, in which subjects reported a digit not in either target or masker sequences. Bars indicate median error rate across all subjects (N = 63) in both experiments; error bars represent inter-quartile range. Right: Within-subject differences in error rates for switch and drop errors for linear and linked compression relative to independent compression. Negative values indicate lower drop or switch errors relative to independent compression. Symbols indicate the median across all subjects, boxes show the interquartile range, and whiskers show the full range. Statistical significance is assessed by Wilcoxon sign-rank tests, and is marked by *** for p < 0.001 and **** for p < 0.0001.
DISCUSSION
Fast, independent compression elevates spatial thresholds in normal-hearing listeners
In all groups using fast compression, average spatial thresholds were larger (a greater spatial separation was needed for listeners to perform at threshold) for independent compression compared to linear or linked compression (Fig. 2). Differences were modest on average (around 5°), with large inter-subject differences. It is yet unclear what practical effect on communication and listening effort such differences may imply for real-world settings, particularly using more realistic and complex hearing aid compression schemes; nevertheless, these results support the idea that independent compression interferes with spatial selective auditory attention and increases the difficulty of attending to a target sound source among competing sources. Such listening situations are considerably more effortful for hearing-impaired than for normal-hearing listeners (Gatehouse and Noble, 2004; Edwards, 2007). If effects like those demonstrated here are also seen in hearing-impaired listeners (see Sec. 4C), they could have an important impact on the ability of hearing-aid users to communicate in everyday settings.
Effects of slow compression in our data are less clear than those for fast compression. Some previous studies support the idea that slow compression has a smaller effect on spatial perception than faster compression. For instance, ILD sensitivity in quiet is more adversely affected by compression using faster time constants compared to slower time constants (Musa-Shufani and Walger, 2006). Slow compression also yields better performance than fast compression in hearing-impaired individuals asked to report target sentences presented with spatially separated speech maskers (Moore et al., 2010). Slower compression will generally result in smaller ILD fluctuations, as the gain changes in either ear are relatively less affected by instantaneous fluctuations in signal power and relatively more by longer-term average power at the two ears. Slower fluctuations in ILD can also be more easily tracked by the binaural system compared to fast fluctuations, which increase image diffuseness (Grantham and Wightman, 1978; Culling and Colburn, 2000). Slow compression may also provide longer clean ILDs at stimulus onsets that dominate spatial perception (Freyman et al., 1997; Stecker and Hafter, 2002); these onsets are also further enhanced by dynamic range compression (Verschuure et al., 1996), which may increase onset dominance.
Spatial and non-spatial factors can contribute to effects
In addition to the elevation of spatial thresholds, our results support the idea that spatial attention plays a role in our paradigm: we found that performance was significantly worse with fast, independent compression than with linear processing or linked compression only when target and maskers were separated by a small angular separation (15°). Independent compression did not affect performance for large azimuthal separations (90°). We suggest that increased image width and diffuseness caused by independent compression (Wiggins and Seeber, 2012) only affect spatial selective attention if competing sources are sufficiently close to each other in azimuth such that these effects cause confusion about whether a particular sound is from the target or a masker. A more thorough analysis of the acoustic effects of compression on the spatial cues available to normal-hearing and hearing-impaired listeners can lend further insight into this idea, and is one focus of our future research.
Differences across the compression conditions were driven by switch errors, in which subjects selected one of the masker digits, further supporting the idea that compression interfered primarily with source selection rather than with speech intelligibility. Similar results can occur even in diotic mixtures (increased “reversals”; Stone et al., 2009), indicating that overall cognitive load, and not necessarily spatial factors, may also contribute to our results. In considering this possibility, it is important to note that the previous study that found increased reversals for diotic mixtures used a cognitively demanding task in which subjects divided attention between two simultaneous streams (see also Gallun et al., 2007; Best et al., 2010) and responded only after performing an unrelated, visual distractor task (further increasing cognitive load). In addition, in that study listeners could report the content of the two streams in any order for them to be counted as correct. It is plausible then that the reversals reported in this earlier diotic study might not reflect a failure of incorrect selection, but instead may represent a memory failure in which, for example, listeners could recall the words spoken but were unable to accurately bind the identified speech tokens to the correct talker identity (see also Treisman and Gelade, 1980; Woods et al., 1998). In contrast, our results show a clearer failure of selection using a task that requires subjects to attend to only a single source (comprised of only four digits, which should not stress working memory) and without any secondary task. As correct selection could only be done in our task using spatial cues, and as switch errors were reduced when compressors were linked across the two ears, our data are consistent with the main effect of independent compression in the current study coming about from failures of spatial selection, rather than due to non-spatial effects.
Nevertheless, non-spatial factors, including reduced spectral and temporal modulation and across-signal modulation correlation (Stone and Moore, 2003, 2007; Stone et al., 2009), may have also played a role in our results. For example, it may be that only when maskers were located at 15°, but not at 90°, was our task sufficiently challenging to show effects on performance due to fast, independent compression. In addition, we linked the left and right compressors to preserve ILDs; however, improved performance in this condition relative to independent compression may also be due to a lower “effective compression ratio” (Stone and Moore, 1992) rather than due to preservation of ILDs. Future work could be done to clarify this difference by using a higher target compression ratio in the linked compression condition so that the effective compression ratios are equal.
Compression may affect ILD utility differently in hearing-impaired listeners
Our results demonstrate that fast independent compression with a high compression ratio can elevate spatial thresholds in normal-hearing listeners. However, the same manipulations may influence hearing-impaired listeners differently. The acoustic features that allow normal-hearing listeners to segregate the target from the maskers and selectively listen to the target may not be fully available to hearing-impaired listeners (e.g., see discussion in Shinn-Cunningham and Best, 2008). Hearing-impaired listeners may have reduced sensitivity to binaural cues or use different listening strategies, so that the practical consequences of compression on the influence of spatial perception are limited. For example, if binaural processing is compromised, further corruption of ILDs by compression may have no noticeable effect on selective auditory attention.
Another issue is that healthy ears naturally compress acoustic inputs through the nonlinear amplification of the cochlea. In contrast, hearing impairment is often accompanied by a loss of compressive cochlear amplification (Moore, 2007). Hearing-aid compression may approximately restore the kind of compressive amplification that occurs naturally in a healthy ear. Given this, the reduction of ILDs caused by compression may in fact restore “normal” neural representations of ILDs in many individuals with hearing loss, leading us to overestimate the effects of compression by testing normal-hearing listeners. However, even if the restoration of normal ILDs improved sound localization accuracy, it would not necessarily improve the ability to use spatial cues to direct attention (Noble et al., 1997; Gallun et al., 2008; Schwartz et al., 2012). We argue that in order to correctly select a target talker using spatial cues (or any other cues), listeners only need to be able to distinguish the target from the maskers using one or more perceptual features, such as location. Even if hearing-aid compression approximately restores the neural representation to ILDs to be more like that experienced by normal-hearing listeners, it may still impair spatial selective attention. Specifically, the compression will reduce ILDs. Imagine competing sources, one from just left of center and one just right of center. If the ILDs are just barely resolvable without compression, they are likely to be unresolvable with compression. More generally, compression is likely to make it more difficult to use ILDs to distinguish the target from the maskers in any acoustic mixture where competing sources are close together in space.
Additionally, ILD fluctuations, especially those imposed on an attended source by other, unattended sources, may also affect spatial selective auditory attention in hearing-impaired listeners, even if the compression restores neural ILDs to something more like normal. Previous data suggest that ILD fluctuations due to the dynamic nature of compression, more than the overall ILD reduction, are primarily responsible for perceptually relevant effects in normal-hearing listeners (Wiggins and Seeber, 2011, 2012). It is reasonable to suspect then that the dynamics of hearing aid compression may have deleterious effects on the ability of hearing aid wearers to use spatial cues to attend to a desired sound source. Further research with hearing-impaired listeners, using a more representative range of compression settings, can help clarify the practical consequences of the effects being explored here.
Symmetric spatial configuration may have reduced observed differences
In our experiment, we chose to place maskers symmetrically about midline. In retrospect, this choice may have led us to underestimate the possible size of effects. We found that performance was impaired when the maskers were close (15°) to the target, but not when they were far (90°). For close maskers, the magnitude of ILDs in the acoustic mixture is small relative to those present when maskers are far; consequently, the effect of the maskers on the target ILDs is relatively small. If performance is impaired due to ILD fluctuations imposed on the target by distracting sources, then we would expect to see a relatively larger effect by, for example, placing one masker close to the target and the other masker at a more lateral location. Such an experiment would also help clarify the contributions of spatial and non-spatial effects of compression.
CONCLUSIONS
Fast, independent binaural compression impairs the ability of normal-hearing listeners to select a desired target from a mixture containing spatially separated maskers. Linking left- and right-ear compressors so that the gain applied to the two ears is the same at each time instant preserves normally occurring spatial cues, and restores the ability of normal-hearing listeners to successfully hear out a target stream based on its location. For large spatial separations, performance is relatively good, and not affected by any of the compression schemes tested, consistent with the idea that even when spatial images are made more diffuse, sufficient spatial separation allows for the successful selection of the target. These results highlight the importance of considering a variety of spatial configurations when assessing binaural listening performance rather than using only a single, relatively large separation. Effects of slower compression on performance are less clear. Further investigation should be conducted to reveal if similar detrimental effects on spatial selective attention occur in hearing-impaired listeners, and, if so, whether such effects may exacerbate the problem of increased listening effort in noisy situations experienced by many such listeners.
ACKNOWLEDGMENTS
Many thanks to the researchers at Starkey Hearing Research, Berkeley, CA, including Sridhar Kalluri, Olaf Strelcyk, Jing Xia, Brent Edwards, Nazanin Nooraei, and Joyce Rodriguez for helping to create the original hypotheses that drove this work and for creating a better understanding of the practical context and implications of this research. Thanks also to Tim Streeter and Scott Bressler for setting up and running the HRTF measurements, and to Justin Fleming for work contributing to the analysis of temporal offsets on performance. This work was supported by Grant No. NIDCD ROI DC009477.
References
- ANSI (2003). Specification of Hearing Aid Characteristics (ANSI S3.22-2003) (American National Standard Institute, New York: ). [Google Scholar]
- Bauer, R. W. (1966). “ Noise localization after unilateral attenuation,” J. Acoust. Soc. Am. 40, 441–444. 10.1121/1.1910093 [DOI] [Google Scholar]
- Best, V., Gallun, F. J., Mason, C. R., Kidd, G., and Shinn-Cunningham, B. G. (2010). “ The impact of noise and hearing loss on the processing of simultaneous sentences,” Ear Hear. 31, 213–220. 10.1097/AUD.0b013e3181c34ba6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best, V., Mason, C. R., and Kidd, G. (2011). “ Spatial release from masking in normally hearing and hearing-impaired listeners as a function of the temporal overlap of competing talkers,” J. Acoust. Soc. Am. 129, 1616–1625. 10.1121/1.3533733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrne, D., and Noble, W. (1998). “ Optimizing sound localization with hearing aids,” Trends Amplif. 3, 51–73. 10.1177/108471389800300202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Culling, J., and Colburn, H. (2000). “ Binaural sluggishness in the perception of tone sequences and speech in noise,” J. Acoust. Soc. Am. 107, 517–527. 10.1121/1.428320 [DOI] [PubMed] [Google Scholar]
- Dahmen, J. C., Keating, P., Nodal, F. R., Schulz, A. L., and King, A. J. (2010). “ Adaptation to stimulus statistics in the perception and neural representation of auditory space,” Neuron 66, 937–948. 10.1016/j.neuron.2010.05.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards, B. (2007). “ The future of hearing aid technology,” Trends Amplif. 11, 31–46. 10.1177/1084713806298004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freyman, R. L., Zurek, P. M., Balakrishnan, U., and Chiang, Y. C. (1997). “ Onset dominance in lateralization,” J. Acoust. Soc. Am. 101, 1649–1659. 10.1121/1.418149 [DOI] [PubMed] [Google Scholar]
- Gallun, F. J., Durlach, N. I., Colburn, H. S., Shinn-Cunningham, B. G., Best, V., Mason, C. R., and Kidd, G. (2008). “ The extent to which a position-based explanation accounts for binaural release from informational masking,” J. Acoust. Soc. Am. 124, 439–449. 10.1121/1.2924127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallun, F. J., Mason, C. R., and Kidd, G. (2007). “ Task-dependent costs in processing two simultaneous auditory stimuli,” Percept. Psychophys. 69, 757–771. 10.3758/BF03193777 [DOI] [PubMed] [Google Scholar]
- Gardner, B., and Martin, K. (1994). “HRTF measurements of a kemar dummy-head microphone.” Retrieved May 16, 2012, from http://sound.media.mit.edu/resources/KEMAR.html.
- Gatehouse, S., and Noble, W. (2004). “ The speech, spatial and qualities of hearing scale (SSQ),” Int. J. Audiol. 43, 85–99. 10.1080/14992020400050014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasberg, B. R., and Moore, B. C. (1990). “ Derivation of auditory filter shapes from notched-noise data,” Hear. Res. 47, 103–138. 10.1016/0378-5955(90)90170-T [DOI] [PubMed] [Google Scholar]
- Grantham, D. W., and Wightman, F. L. (1978). “ Detectability of varying interaural temporal differences,” J. Acoust. Soc. Am. 63, 511–523. 10.1121/1.381751 [DOI] [PubMed] [Google Scholar]
- Ihlefeld, A., and Shinn-Cunningham, B. G. (2008). “ Spatial release from energetic and informational masking in a selective speech identification task,” J. Acoust. Soc. Am. 123, 4369–4379. 10.1121/1.2904826 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahnke, J. C. (1965). “ Primacy and recency effects in serial-position curves of immediate recall,” J. Exp. Psychol. 70, 130–132. 10.1037/h0022013 [DOI] [PubMed] [Google Scholar]
- Jenstad, L. M., Seewald, R. C., Cornelisse, L. E., and Shantz, J. (1999). “ Comparison of linear gain and wide dynamic range compression hearing aid circuits: Aided speech perception measures,” Ear Hear. 20, 117–126. 10.1097/00003446-199904000-00003 [DOI] [PubMed] [Google Scholar]
- Kaernbach, C. (1991). “ Simple adaptive testing with the weighted up-down method,” Percept. Psychophys. 49, 227–229. 10.3758/BF03214307 [DOI] [PubMed] [Google Scholar]
- Kalluri, S., and Edwards, B. (2007). “ Impact of hearing impairment and hearing aids on benefits due to binaural hearing,” in 19th International Congress on Acoustics (Madrid, Spain: ). [Google Scholar]
- Keidser, G., Rohrseitz, K., Dillon, H., Hannacher, V., Carter, L., Rass, U., and Convery, E. (2006). “ The effect of multi-channel wide dynamic range compression, noise reduction, and the directional microphone on horizontal localization performance in hearing aid wearers,” Int. J. Audiol. 45, 563–579. 10.1080/14992020600920804 [DOI] [PubMed] [Google Scholar]
- Kidd, G., Arbogast, T. L., Mason, C. R., and Gallun, F. J. (2005a). “ The advantage of knowing where to listen,” J. Acoust. Soc. Am. 118, 3804–3815. 10.1121/1.2109187 [DOI] [PubMed] [Google Scholar]
- Kidd, G., Mason, C. R., and Gallun, F. J. (2005b). “ Combining energetic and informational masking for speech identification,” J. Acoust. Soc. Am. 118, 982–992. 10.1121/1.1953167 [DOI] [PubMed] [Google Scholar]
- Levitt, H. (1971). “ Transformed up-down methods in psychoacoustics,” J. Acoust. Soc. Am. 49, 467–477. 10.1121/1.1912375 [DOI] [PubMed] [Google Scholar]
- Marrone, N., Mason, C. R., and Kidd, G. (2008a). “ Tuning in the spatial dimension: Evidence from a masked speech identification task,” J. Acoust. Soc. Am. 124, 1146–1158. 10.1121/1.2945710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrone, N., Mason, C. R., and Kidd, G. (2008b). “ The effects of hearing loss and age on the benefit of spatial separation between multiple talkers in reverberant rooms,” J. Acoust. Soc. Am. 124, 3064–3075. 10.1121/1.2980441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore, B. C. (1996). “ Perceptual consequences of cochlear hearing loss and their implications for the design of hearing aids,” Ear Hear. 17, 133–161. 10.1097/00003446-199604000-00007 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J. (2007). Cochlear Hearing Loss: Physiological, Psychological and Technical Issues (Wiley, Chichester, UK: ), pp. 1–344. [Google Scholar]
- Moore, B. C. J., Füllgrabe, C., and Stone, M. A. (2010). “ Effect of spatial separation, extended bandwidth, and compression speed on intelligibility in a competing-speech task,” J. Acoust. Soc. Am. 128, 360–371. 10.1121/1.3436533 [DOI] [PubMed] [Google Scholar]
- Musa-Shufani, S., and Walger, M. (2006). “ Influence of dynamic compression on directional hearing in the horizontal plane,” Ear Hear. 27, 279–285. 10.1097/01.aud.0000215972.68797.5e [DOI] [PubMed] [Google Scholar]
- Nabelek, A. K., and Pickett, J. M. (1974). “ Monaural and binaural speech perception through hearing aids under noise and reverberation with normal and hearing-impaired listeners,” J. Speech Hear. Res. 17, 724–739. [DOI] [PubMed] [Google Scholar]
- Noble, W., Byrne, D., and Ter-Horst, K. (1997). “ Auditory localization, detection of spatial separateness, and speech hearing in noise by hearing impaired listeners,” J. Acoust. Soc. Am. 102, 2343–2352. 10.1121/1.419618 [DOI] [PubMed] [Google Scholar]
- Ruggles, D., and Shinn-Cunningham, B. (2011). “ Spatial selective auditory attention in the presence of reverberant energy: Individual differences in normal-hearing listeners,” J. Assoc. Res. Otolaryngol. 12, 395–405. 10.1007/s10162-010-0254-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz, A., McDermott, J. H., and Shinn-Cunningham, B. (2012). “ Spatial cues alone produce inaccurate sound segregation: The effect of interaural time differences,” J. Acoust. Soc. Am. 132, 357–368. 10.1121/1.4718637 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherbecoe, R. L., and Studebaker, G. A. (2004). “ Supplementary formulas and tables for calculating and interconverting speech recognition scores in transformed arcsine units,” Int. J. Audiol. 43, 442–448. 10.1080/14992020400050056 [DOI] [PubMed] [Google Scholar]
- Shinn-Cunningham, B. G. (2005). “ Influences of spatial cues on grouping and understanding sound,” in Proceedings of the Forum Acusticum (Budapest,Hungary: ). [Google Scholar]
- Shinn-Cunningham, B. G. (2008). “ Object-based auditory and visual attention,” Trends Cogn. Sci. 12, 182–186. 10.1016/j.tics.2008.02.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinn-Cunningham, B. G., and Best, V. (2008). “ Selective attention in normal and impaired hearing,” Trends Amplif. 12, 283–299. 10.1177/1084713808325306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinn-Cunningham, B. G., Durlach, N. I., and Held, R. M. (1998). “ Adapting to supernormal auditory localization cues. I. Bias and resolution,” J. Acoust. Soc. Am. 103, 3656–3666. 10.1121/1.423088 [DOI] [PubMed] [Google Scholar]
- Shinn-Cunningham, B. G., Kopco, N., and Martin, T. J. (2005). “ Localizing nearby sound sources in a classroom: Binaural room impulse responses,” J. Acoust. Soc. Am. 117, 3100–3115. 10.1121/1.1872572 [DOI] [PubMed] [Google Scholar]
- Stecker, G. C., and Hafter, E. R. (2002). “ Temporal weighting in sound localization,” J. Acoust. Soc. Am. 112, 1046–1057. 10.1121/1.1497366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone, M. A., and Moore, B. C. (1992). “ Syllabic compression: effective compression ratios for signals modulated at different rates,” Br. J. Audiol. 26, 351–361. 10.3109/03005369209076659 [DOI] [PubMed] [Google Scholar]
- Stone, M. A., and Moore, B. C. J. (2003). “ Effect of the speed of a single-channel dynamic range compressor on intelligibility in a competing speech task,” J. Acoust. Soc. Am. 114, 1023–1034. 10.1121/1.1592160 [DOI] [PubMed] [Google Scholar]
- Stone, M. A., and Moore, B. C. J. (2007). “ Quantifying the effects of fast-acting compression on the envelope of speech,” J. Acoust. Soc. Am. 121, 1654–1664. 10.1121/1.2434754 [DOI] [PubMed] [Google Scholar]
- Stone, M. A., Moore, B. C. J., Fuellgrabe, C., and Hinton, A. C. (2009). “ Multichannel fast-acting dynamic range compression hinders performance by young, normal-hearing listeners in a two-talker separation task,” J. Audio Eng. Soc. 57, 532–546. [Google Scholar]
- Treisman, A., and Gelade, G. (1980). “ A feature-integration theory of attention,” Cogn. Psychol. 12, 97–136. 10.1016/0010-0285(80)90005-5 [DOI] [PubMed] [Google Scholar]
- Verschuure, J., Maas, A. J., Stikvoort, E., De Jong, R. M., Goedegebure, A., and Dreschler, W. A. (1996). “ Compression and its effect on the speech signal,” Ear Hear. 17, 162–175. 10.1097/00003446-199604000-00008 [DOI] [PubMed] [Google Scholar]
- Wiggins, I. M., and Seeber, B. U. (2011). “ Dynamic-range compression affects the lateral position of sounds,” J. Acoust. Soc. Am. 130, 3939–3953. 10.1121/1.3652887 [DOI] [PubMed] [Google Scholar]
- Wiggins, I. M., and Seeber, B. U. (2012). “ Effects of dynamic-range compression on the spatial attributes of sounds in normal-hearing listeners,” Ear Hear. 33, 399–410. 10.1097/AUD.0b013e31823d78fd [DOI] [PubMed] [Google Scholar]
- Woods, D. L., Alain, C., and Ogawa, K. H. (1998). “ Conjoining auditory and visual features during high-rate serial presentation: processing and conjoining two features can be faster than processing one,” Percept. Psychophys. 60, 239–249. 10.3758/BF03206033 [DOI] [PubMed] [Google Scholar]
- Zurek, P. (1993). “ Binaural advantages and directional effects in speech intelligibility,” in Acoustical Factors Affecting Hearing Aid Performance, edited by Studebaker G. and Hochberg I. (Allyn and Bacon, Boston, MA: ), pp. 255–276. [Google Scholar]