Electrostatic frequency shifts in amide I vibrational spectra: Direct parameterization against experiment

Abstract

The interpretation of protein amide I infrared spectra has been greatly assisted by the observation that the vibrational frequency of a peptide unit reports on its local electrostatic environment. However, the interpretation of spectra remains largely qualitative due to a lack of direct quantitative connections between computational models and experimental data. Here, we present an empirical parameterization of an electrostatic amide I frequency map derived from the infrared absorption spectra of 28 dipeptides. The observed frequency shifts are analyzed in terms of the local electrostatic potential, field, and field gradient, evaluated at sites near the amide bond in molecular dynamics simulations. We find that the frequency shifts observed in experiment correlate very well with the electric field in the direction of the C=O bond evaluated at the position of the amide oxygen atom. A linear best-fit mapping between observed frequencies and electric field yield sample standard deviations of 2.8 and 3.7 cm⁻¹ for the CHARMM27 and OPLS-AA force fields, respectively, and maximum deviations (within our data set) of 9 cm⁻¹. These results are discussed in the broader context of amide I vibrational models and the effort to produce quantitative agreement between simulated and experimental absorption spectra.

INTRODUCTION

The backbone carbonyl stretching vibrations of proteins, usually referred to as amide I, have been extensively useful in probing protein structure and dynamics.^{1, 2, 3} Delocalized amide I states provide sensitivity to secondary structure, while local peptide conformations can be probed by studying individual sites along the protein backbone, usually via isotope labels.^{4, 5, 6, 7} Although the rich information content of amide I spectra has been appreciated for many years, the complexity and congestion of the absorption spectra and the difficulty of accurately predicting the spectral features of individual protein structures have in many ways limited the utility of amide I spectroscopy in answering detailed structural questions. More recently, the advent of two-dimensional infrared (2DIR) spectroscopy has begun to assist in overcoming amide I spectral congestion,^{8, 9, 10} while on the theoretical front, spectroscopic “maps” linking protein structure to specific spectral features have greatly improved our ability to interpret experimental data.^{11, 12, 13, 14, 15, 16, 17, 18, 19}

Spectroscopic maps translate protein structural and electrostatic information from classical force field simulations into vibrational frequencies and couplings between peptide groups which allow prediction of infrared spectra. To describe multidimensional IR spectra, Hamm et al.⁹ extended the normal mode descriptions of Miyazawa²⁰ and Krimm²¹ to a weakly anharmonic exciton model, in which individual amide bonds are assigned isolated carbonyl stretch frequencies (site energies) and pairwise coupling constants to produce a site-basis Hamiltonian of the form⁹

$$\begin{array}{ccc}\hfill H& =& \sum _{n=1}^N{\omega }_n|n⟩⟨n|+\sum _{m,n=1}^N{J}_{mn}|m⟩⟨n|\hfill \\ & & +\sum _{m\ge n=1}^N\left({\omega }_m+{\omega }_n-\Delta {\delta }_{mn}\right)|mn⟩⟨mn|\hfill \\ & & +\sum _{m\ge n=1}^N\sum _{\begin{array}{c}\\ j\ge k=1\\ \left(m,n\right)\ne \left(j,k\right)\end{array}}^N{J}_{mn,jk}|mn⟩⟨jk|.\hfill \end{array}$$ (1)

The indices m, n, i, and j denote individual amide site excitations, |n⟩ is a one-quantum state consisting of a single excitation on site n (with associated energy ω_n), |mn⟩ is a two-quantum state consisting of excitations on sites m and n, Δ is the anharmonicity associated with double excitation of an individual site, δ_mn is the Kronecker delta, and the values J_ab indicate coupling constants between the site-basis states (J_mn is between one-quantum states and J_mn,jk between two-quantum states). Spectral predictions for an individual protein structure are produced by assigning values to the one-quantum site energies ω_n and coupling constants J_mn in this Hamiltonian; for nonlinear spectra, two-quantum energies, and couplings are usually assigned based on the assumption of weak diagonal anharmonicity, determined by the parameter Δ ≈ 16 cm⁻¹.⁹

Although simple in form, the accurate structure-based parameterization of this Hamiltonian is non-trivial and has been the subject of numerous computational studies.^{11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 23, 24, 25, 26} Site-to-site coupling constants are generally extracted by a combination of electrostatic models (e.g., dipole-dipole^{22, 27} or transition charge coupling^{11, 13, 15, 28}) and DFT-parameterized dihedral maps for nearest-neighbor interactions.^{11, 13, 18, 22, 26} Site energy maps are based on the observation that electrostatic interactions (particularly hydrogen bonding) between a solvated molecule and its environment are the primary predictors of local vibrational frequencies.²⁹ Early models for amide I frequencies employed simple geometric criteria such as hydrogen bond count and length;^{9, 30, 31, 32, 33} although these models have proven intuitively useful and reasonably accurate for simple calculations,³⁴ they are generally regarded as insufficient for detailed spectral simulations.³⁵ Most current vibrational frequency models are based on a linear mapping of frequency against various combinations of electrostatic variables evaluated at different positions within the peptide group

$$\begin{array}{ccc}\hfill {\omega }_n& =& {\omega }_o+\sum _{i=1}^{N_{sites}}[c_i^{\left(pot\right)}\Phi \left({\vec{x}}_i\right)+\sum _{\alpha =1}^3{c}_{i,\alpha }^{\left(field\right)}{E}_{\alpha }\left({\vec{x}}_i\right)\hfill \\ & & +\sum _{\alpha =1}^3\sum _{\beta =\alpha }^3{c}_{i,\alpha \beta }^{\left(grad\right)}{G}_{\alpha \beta }\left({\vec{x}}_i\right)].\hfill \end{array}$$ (2)

Here, ω_n is the frequency of the nth amide oscillator, $\Phi \left({\vec{x}}_i\right)$, $E_{\alpha }\left({\vec{x}}_i\right)$, and $G_{\alpha \beta }\left({\vec{x}}_i\right)$ are the electrostatic potential, field, and field gradient components evaluated in a molecular dynamics (MD) simulation at the location ${\vec{x}}_i$ of mapping site i. An additional frequency shift parameterized by dihedral (ϕ, ψ) angles can be included to account for nearest-neighbor interactions assumed to extend beyond simple electrostatics.^{11, 18, 26} In parameterizing the expansion coefficients c_i in Eq. 2, generally either the field^{12, 19, 24, 26} or the potential^{13, 14, 17, 18, 25} is chosen to have non-zero coefficients, but not both. The theoretical arguments behind each choice have been discussed in detail by Cho.³⁶ Briefly, field-based models have the intuitive appeal of carrying a form similar to the familiar Stark shift expression $\Delta \omega =-\Delta \vec{\mu }·\vec{E}$ describing the change in a system transition frequency due to an applied electric field. Moreover, such models have proven to be extremely useful for describing the vibrational spectra of the OH stretch of water.^{19, 37, 38} Note, however, that the standard Stark problem differs importantly from these field-parameterized solvation models in that Eq. 2 is intended to describe a quite complex, local, and non-uniform solvation environment rather than a uniform external field; as a result, Eq. 2 typically implies a parameterization against electrostatic variables evaluated at multiple points around the amide bond rather than against a single field variable $\vec{E}$. Based in part on this observation, Cho³⁶ has suggested that the electrostatic potential evaluated at multiple sites may be a more suitable choice for multi-atom groups such as the amide bond. Clear experimental evidence in support of either model has been difficult to obtain, however, and a surprising degree of variability has grown up surrounding the choice of both electrostatic components and map sites for parameterization, ranging from the two-site/field model of Skinner and co-workers¹² to the seven-site/potential model of Watson and Hirst¹⁸ or the four-site/four-component (field/gradient) model of Jansen and Knoester.²⁴

Unfortunately, amide I computational maps still have limited accuracy and are usually specialized to specific systems or force fields. Although useful for qualitative interpretation, comparison with experimental data is generally limited (at best) to peak shapes and must be assisted by the application of arbitrary frequency shifts to simulated spectra.^{11, 12, 26, 39, 40, 41, 42} The development of accurate spectral maps faces several formidable challenges. At the outset, spectral calculations are limited by the practical requirement to make simplifying assumptions that neglect certain physical features. For instance, Eq. 1 neglects coupling to vibrational modes outside the amide I manifold and strong anharmonic effects. The consequences of these assumptions are difficult to evaluate against experimental data due to equally significant uncertainties in the large range of input parameters, which include the site energies and coupling constants between sites. Entangled with these issues are questions regarding the reliability of the electrostatics and conformational sampling in MD simulations. As a result of this complexity, spectral parameter assignments are typically based on density functional theory (DFT) calculations for small model systems (most frequently N-methylacetamide-d₁, NMA) or on the vibrational frequency shifts associated with different solvation environments.^{12, 16, 17, 18, 24, 26, 43} Although these approaches provide an excellent starting point for amide I parameterization, they remain to some extent unsatisfactory since they rely heavily on the accuracy of the quantum chemistry calculations or molecular force fields employed and since they are based on model compounds with significantly different physical properties from the peptides and proteins they are designed to model. For example, while NMA undoubtedly serves as a useful qualitative model for peptide vibrations, significant differences in both molecular structure (capping methyl groups in place of α-carbons and side chain groups) and physical properties (e.g., a melting point near room temperature) make quantitative comparison with larger peptide systems somewhat questionable. Finally, even after a spectral map has been constructed, validation and testing against experimental data is likewise complicated by the lack of a reliable set of simple, cheap, and well-understood calibration standards. In particular, the large number of coupled residues in most stable peptide/protein structures makes it difficult to independently evaluate specific frequency or coupling assignments. These obstacles can be overcome in part by ¹³C=¹⁸O isotope labeling in which the vibrational frequency of a specific site is shifted far out of resonance with its coupling partners,^{44, 45} but the difficulty and expense of preparing isotope labeled peptides is prohibitive for large-scale testing. More subtly, isotope labeling also faces the uncertainty that vibrational mode composition must, to some extent, be affected by the non-uniform alteration of atomic masses in an isotope labeled bond.

Dipeptides with no capping groups—two amino acids linked by a single amide bond—provide a unique opportunity for experimentally evaluating the influence of local electrostatics on peptide vibrational frequencies. By adjusting the pH (or pD) of the solution, it is possible to directly control the local electrostatic environment of the amide bond via protonation and de-protonation of the C- and N-termini of the fragment. The simplicity of the system eliminates both the need to consider coupling between adjacent amide sites and, to some extent, the complexities of protein structure variation in solution given the relatively small number of degrees of freedom. Most importantly, the simplicity of the sample makes it feasible to collect data from a large number of different dipeptides, adding significant statistical weight to the analysis. Motivated by these considerations, we present here a detailed study of pD-dependent frequency shifts of 28 dipeptide fragments in D₂O solution. By comparing the experimental frequencies with calculated electrostatic components taken from MD simulations of the individual fragments, we are able to evaluate directly the contribution of various electrostatic variables to the dipeptide amide I vibrational frequency. The data set and electrostatic model described should provide a concrete starting point for the development of a more complete, experimentally based model for amide I spectroscopy.

METHODS

Dipeptide samples

Lyophilized dipeptide samples were purchased from Sigma Aldrich and used without further purification. Unless otherwise noted, all dipeptides consist of two L-amino acids linked by a single amide bond in the uncapped NH₂–X–X–COOH form. Note that the AA dipeptide discussed here differs from the capped “alanine dipeptide” frequently encountered in IR literature.^{39, 46, 47} The samples studied here consist of 23 “standard” dipeptides (AA, ML, VM, VY, MS, FV, YA, VS, AY, FA, YF, VT, EE, HG, AG, LG, WG, GH, GE, GG, GF, GS, and GL), three proline-containing dipeptides (FP, LP, and PL), and two stereochemically mixed dipeptides (D-Leu-L-Tyr and L-Leu-D-Leu).

All experiments were performed on samples dissolved in deuterated water (D₂O) to avoid spectral overlap with the H₂O bend vibration near 1650 cm⁻¹, which leads to deuterated peptide groups in all amino acids but proline. (Strictly speaking we report amide I^′ spectra, though we use the terms amide I and amide I^′ interchangeably here). Samples were dissolved in D₂O at 0.05 M concentration, and solution pD was adjusted using 1 M DCl and 1M NaOD solutions obtained by dilution with D₂O from concentrated DCl (∼11 M) and 40% w/v NaOD (∼14.1 M in D₂O) stock solutions purchased from Cambridge Isotope Laboratories. The solution pH^* values reported below correspond to the pH value of D₂O dipeptide solution measured with a standard glass electrode pH meter, with no correction applied for the difference between pH and pD calibration (roughly 0.4 pH units).⁴⁸ For FTIR measurements, dipeptide samples were mixed with a variable number of equivalents of acid or base to control the protonation state of the COO⁻ and NH₃⁺ terminal groups; detailed conditions for each dipeptide sample are described in the supplementary material.⁷³

FTIR absorption spectra

Absorption spectra were collected on a Nicolet 380 FTIR spectrometer at 2 cm⁻¹ resolution. For each sample acid/base condition, background spectra were collected for the same volume of DCl and NaOD added to 20 μL D₂O. Peak frequencies were extracted automatically via processing in MATLAB (R2011a, The MathWorks, Inc.); see supplementary material for further details.⁷³ Under basic conditions, the amide I absorption peaks of the LP and FP dipeptides overlap strongly with the C-terminal carboxylic acid peak near 1590 cm⁻¹, giving rise to a single peak with a full width at half maximum of ∼35 cm⁻¹. Since in this case the two underlying curves could not be reliably distinguished from each other, the LP and FP amide I frequencies reported here under “base” conditions are in fact the peak frequencies of the combined amide I/COO⁻ peak. Note that in all cases, our analysis neglects any couplings between the amide carbonyl group and the COO-/COOH terminus, based on the observation that their respective transitions are split by frequencies much larger than the expected vibrational couplings. Carbonyl couplings are expected to be <10 cm⁻¹ in magnitude, while the energy splitting is at least ∼30 cm⁻¹ (1630–1680 cm⁻¹ for amide I vs. ∼1590 cm⁻¹ for COO⁻ and ∼1725 cm⁻¹ for COOH) in all cases except LP and FP.

MD simulations

For each dipeptide studied experimentally, 5 ns MD simulations were carried out for each dipeptide protonation state, i.e., NH₃⁺/COOH (“acid”), NH₃⁺/COO⁻ (“neutral”), and NH₂/COO⁻ (“base”), along with additional simulations (“intermediate”) for protonated/deprotonated Glu and His side chains. All simulations were carried out using the GROMACS 4.5 simulation package using fully solvated dipeptide structures (SPC/E water) and either the CHARMM27 or OPLS-AA force fields.^{49, 50, 51, 52, 53} Dipeptide starting structures were generated automatically in a β-sheet conformation using the PyMOL software package;⁵⁴ for D-amino acids, the stereochemistry was switched directly in PyMOL followed by a coarse geometry optimization in the Avogadro structure editing and visualization package.⁵⁵ Starting PDB structures were then converted to GROMACS input files with the appropriate protonation states for each titrateable group before adding 2 nm of explicit SPC/E water surrounding the dipeptide in each direction (i.e., cubic box dimensions were larger than 4 nm, containing approximately 3800 molecules); for the longer (20 ns) and more finely sampled (10 fs) trajectories used for line shape analysis of the VT dipeptide, only 1 nm of water was added in each direction (cubic box dimensions ∼2.95 nm) to limit trajectory storage size. Neutral and basic His residues were arbitrarily assigned a His-ɛ protonation state (i.e., the proton was placed on the ɛ nitrogen). The solvated structures were then geometry optimized and equilibrated via consecutive 100 ps NVT and NPT ensemble trajectories with constrained peptide coordinates (T = 300 K, modified Berendsen thermostat; P = 1 bar using Parrinello-Rahman coupling for the NPT run).^{56, 57, 58} Production trajectories were then continued for 5 ns in the NVT ensemble (T = 300 K, Nosé-Hoover thermostat).^{59, 60} All trajectories were carried out with 2 fs time steps with all bond lengths fixed using the LINCS algorithm.⁶¹ Long-range electrostatics were treated using the reaction field method with a cutoff of 1.4 nm.

During production trajectories, coordinates were saved every 100 fs, for a total of 50 000 frames over the 5 ns trajectory. For CHARMM27 line shape calculations for the VT dipeptide, simulations were carried out for 20 ns with coordinates sampled every 10 fs. Each trajectory was post-processed by evaluating the electrostatic potential (Coulomb's law), field (first derivatives of the potential), and gradient of the field (mixed second derivatives of the potential, six unique components) at 7 sites around the amide bond: the positions of the C, O, N, and H atoms, and the mid-points of the CO, CN, and NH bonds. All electrostatic calculations were performed using in-house (C programming language) code calling GROMACS 4.5 libraries for trajectory parsing. The contributions from all atoms in the box were summed over explicitly (using the analytical expressions from Coulomb's law and its derivatives), excluding only the amide bond N, H, C, and O atoms and the two adjacent C_α carbons. Following the convention of Jansen and Knoester,²⁴ electrostatics are reported here in units of Hartrees per elementary charge (E_h/e) for the electrostatic potential, E_h/a_oe for electrostatic field, and $E_h/a_o^{2}e$ for the gradient of the field. We choose these natural units so that (aside from converting the MD coordinates to units of Bohr radii) no numerical prefactor is necessary to convert units in the electrostatic calculations.

RESULTS

Amide I pH dependence

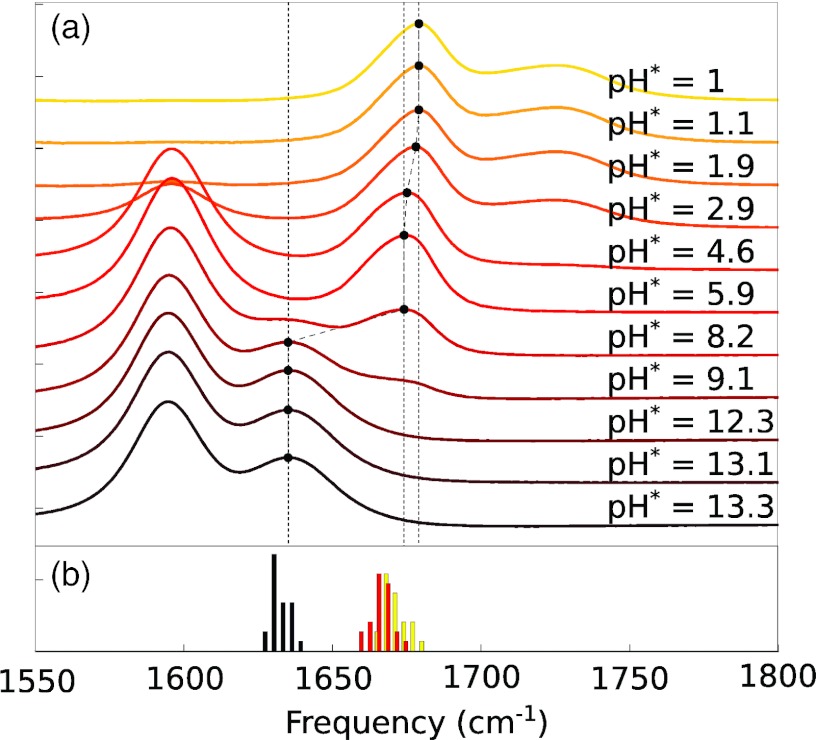
Our first consideration in evaluating the influence of local electrostatics on dipeptide vibrational spectra is to determine to what extent the spectroscopic properties of these systems are determined by the charges within the dipeptide itself—primarily the protonation and de-protonation of the N- and C-termini—and to what extent by the pH of the surrounding solution. To address this issue, Figure 1a shows the linear absorption spectrum for the GG dipeptide in aqueous (D₂O) solution as a function of pH^*. The primary feature of interest for us is the amide I band at 1635–1679 cm⁻¹. The protonation state of the C-terminus is indicated by the carboxylic acid bands at ∼1725 cm⁻¹ (low pH, COOH) and ∼1595 cm⁻¹ (high pH, COO⁻). Importantly, the amide I^′ band is clearly seen to be a “stepwise” function of pH, taking on only the values 1635 cm⁻¹ (basic conditions: both C- and N-termini deprotonated), 1675 cm⁻¹ (neutral pH: protonated N-terminus, deprotonated C-terminus), and 1679 cm⁻¹ (acidic conditions: both C- and N-termini protonated). In other words, for reasonable pH values, the amide I^′ absorption frequency appears to be determined solely by the protonation state of the terminal NH₂/NH₃⁺ and COO⁻/COOH groups, essentially independent of the proton concentration in the surrounding solution.

Figure 1.

(a) Experimental FTIR absorption spectra for the GG dipeptide as a function of pH. Dashed vertical lines mark the amide I peak maxima. See text for details. (b) Frequency histograms (4 cm⁻¹ bins) for 23 standard dipeptides under acidic (yellow), neutral (red), and basic (black) conditions.

Similar trends are observed for the remaining dipeptides in our study: starting from a transition frequency of ∼1630 cm⁻¹ under basic conditions, a blueshift of typically ∼36 cm⁻¹ is observed on protonation of the N-terminus, followed by an additional ∼5 cm⁻¹ blueshift on protonation of the C-terminus. These trends are summarized in Figure 1b which plots a histogram of absorption peak frequencies in 4 cm⁻¹ intervals under basic, neutral, and acidic conditions for 23 standard dipeptides (see Sec. 2). Peak frequencies and FTIR spectra for all dipeptides are provided in the supplementary material.⁷³

Correlation with MD electrostatics

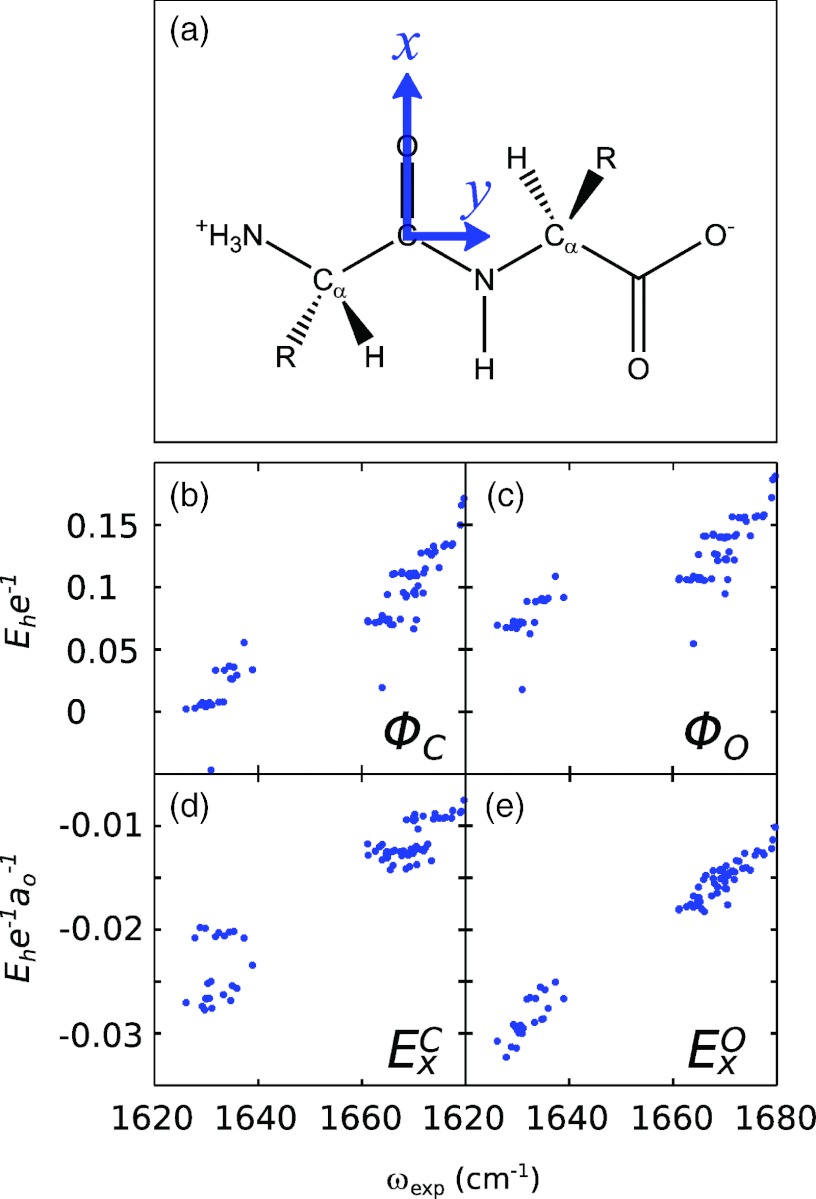
To evaluate the physical origins of these frequency shifts, we performed 5 ns fully solvated (SPC/E water) MD simulations of each of the 23 dipeptides listed above in various protonation states (acid, base, and neutral) using the CHARMM27 force field. The resulting trajectories were analyzed by evaluating the electrostatic potential, field, and gradient of the field at 7 sites around the amide bond: the positions of the C, O, N, and H atoms, and the mid-points of the CO, CN, and NH bonds. The coordinate system has been defined here such that the x axis points from C to O along the carbonyl bond (Frame A). In correlating these values with experimental peak frequencies, it should be emphasized that potential maps (such as those originally introduced by Cho^{43, 62}) necessarily rely on the value of the potential evaluated at multiple sites since linear correlation of any single potential variable with frequency is not expected. While literature field maps (such as those in use by Skinner and co-workers^{12, 19}) also employ multiple field variables, physically one might expect some level of direct correlation with a single electric field component, as in the vibrational Stark effect. As typical results, Figures 2b, 2c, 2d, 2e show the resulting scatter plots between the experimental amide I^′ peak frequencies and the averaged values of the electrostatic potential (Φ) and field x-component (E_x) evaluated at the C and O atomic positions. The most interesting observation here is that a surprisingly strong correlation exists between the experimental peak frequencies and the calculated field component $E_x^{\mathrm{O}}$, i.e., the x-component of the electric field evaluated at the position of the O atom (Fig. 2e). While the $E_x^{\mathrm{C}}$ component (evaluated at the C atom; Fig. 2d) displays a similar (though much noisier) correlation, as expected, very little direct correlation (across the entire data set) is observed between the experimental frequency shift and the potential variables evaluated at either site.

Figure 2.

(a) Structure of a generic dipeptide; our coordinate system is defined so that the x axis points along the amide C=O bond and the y axis is in the plane of the amide unit. (b)–(e) Scatter plots of experimental peak frequencies for 23 standard dipeptides with individual electrostatic variables evaluated from 5 ns CHARMM27 MD simulations (see labels in figure).

Interestingly, the $E_x^{\mathrm{O}}$ parameter is not the only observable showing a linear relation with experimental peak frequencies. To explore other variables in more detail, we carried out linear least-squares fits between the experimental peak frequencies and all 70 electrostatic site/variable combinations (ten variables evaluated at each of seven sites) and sorted them by the value of the resulting Pearson correlation coefficient between the experimental and best-fit linear predicted values. The results for the six best fitting variables are plotted in Figure 3. As expected, the $E_x^{\mathrm{O}}$ combination shows the best performance (c = 0.988) with the best-fit equation

$$\omega =2707.8·E_x^{\mathrm{O}}+1710.3,$$ (3)

where ω and the offset 1710.3 are in units of cm⁻¹ and the coefficient 2707.8 is in units of cm⁻¹a_oe/E_h. This correlation is followed closely by the gradient component G_zz evaluated at the O atom ($G_{zz}^{\mathrm{O}}$) and the field x-component evaluated at the CO bond midpoint ($E_x^{\mathrm{CO}}$). The implications of these observed correlations for the physical mechanism behind amide I solvation-induced frequency shifts will be discussed in more detail in Sec. 4. However, from our earlier discussion of electrostatic frequency maps, it should already be clear that a linear correlation of frequency with local electric field is not entirely surprising, having become generally accepted, for example, for the OH stretch vibration of water^{19, 37, 38} and bearing close analogy to the linear frequency shift observed for various systems in vibrational Stark experiments.^{63, 64} Although we cannot a priori exclude that the correlation observed between frequency shift and the gradient components $G_{zz}^{\mathrm{O}}$ and $G_{zz}^{\mathrm{C}}$ is physical in origin, it seems likely that the correlation here is rather due to a coincidental linear relation between the gradient components and the more physically relevant field variable. For this reason, we focus primarily on field and multi-site potential components in the discussion which follows.

Figure 3.

Correlation scatter plots for experimental amide I peak frequencies (horizontal axis) and predicted frequencies (vertical axis) from linear least-squares best fit equations to various electrostatic parameters as labeled. The c values reported for each frame are Pearson correlation coefficients.

Amino acid composition

The dipeptide data presented above include a variety of amino acids, representing charged, polar, and hydrophobic side chains; the self-consistency of the data set seems to indicate that the electric field is the primary determinant of the vibrational frequency, largely independent of side chain composition. In this section, we test this assumption against two important variations on the “standard” dipeptide structure: the presence of the cyclic proline side chain or of mixed L/D or D/L stereochemistry within a single dipeptide.

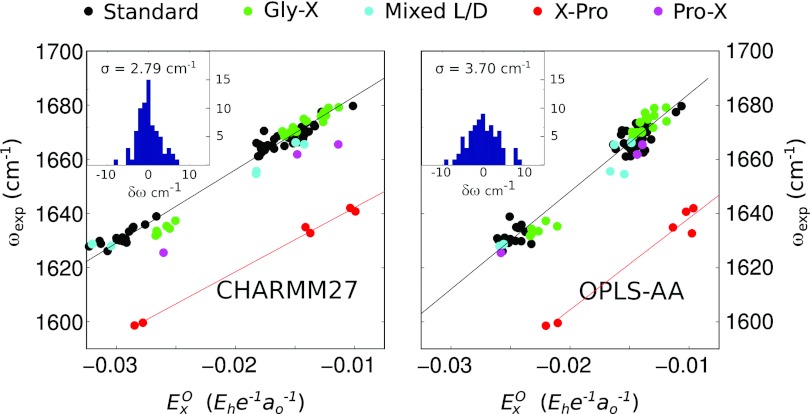
It is well known that the presence of a Pro side chain in the residue after an amide bond (i.e., in X-Pro amide I bonds) induces a (∼30 cm⁻¹) redshift of the amide I frequency.²⁶ This is primarily a result of the higher reduced mass of the oscillating unit caused by the replacement of the usual NH moiety with the cyclic N–C bond of the Pro side chain. To explore this effect in our dipeptide data, we added three Pro-containing dipeptides to our data set: Pro-Leu, Leu-Pro, and Phe-Pro. The results are presented in Figure 4a in which dipeptide frequency is plotted against $E_x^{\mathrm{O}}$ electric field with data points partially categorized by amino acid composition; PL data points are plotted in magenta and LP and FP points in red. The most apparent feature of the new data is the expected ∼35 cm⁻¹ shift between the X-Pro dipeptides (LP and FP) in which a proline residue follows the amide bond; aside from this net redshift, however, the X-Pro dipeptides show a similar linear dependence of the net frequency shift on the $E_x^{\mathrm{O}}$ electric field with a best fit line

$$\omega =2371.4·E_x^{\mathrm{O}}+1666.0$$ (4)

(units are as in Eq. 3) nearly parallel with the best fit line for the “standard” dipeptides described above. In fact, if the experimental XP vibrational frequencies are shifted by +35 cm⁻¹ the linear fit for the standard dipeptides describes the XP data quite well, suggesting that in practice a simple frequency shift may be sufficient to bring XP amide bonds into agreement with standard frequency maps. Note, however, that a more complicated correction will be required for any electrostatic map which parameterizes the N or H atoms (e.g., Ref. 26) since the proline side chain either replaces or bonds directly to these sites.

Figure 4.

Scatter plots of experimental amide I peak frequencies with MD electrostatics for CHARMM27 (left panel) and OPLS-AA (right panel) force fields. Amino acid composition is labeled by color (see legend). The inset for each panel plots an error histogram (deviation between experimental and best-fit simulation frequencies) for the 23 standard dipeptides in each data set.

In sorting dipeptides according to amino acid composition, two other interesting features become apparent. First, our only example of a Pro-X type dipeptide (Pro-Leu) shows a small but definite (∼10 cm⁻¹) redshift with respect to the best fit line of our “standard” dipeptides under all protonation states. Second, in the fully deprotonated state, peptides of the form Gly-X fall into a group redshifted by approximately 5 cm⁻¹ compared to other dipeptides (note the small cluster of green points near (−0.026, 1633) in the figure). While these shifts could represent a true frequency shift resulting from altered steric interactions or amide bond properties in these dipeptides, one should also bear in mind that Pro and Gly are the only two amino acids in the CHARMM27 force field which have independent parameterizations for the N-terminus. From a purely technical point of view, then, it may not be surprising that differences in the details of charge parameterization may lead to changes in predicted frequency.

The effect of mixed side chain stereochemistry on amide I frequencies is less clear than for proline-containing amide bonds, although one could imagine that changes in steric strains within the dipeptide unit could induce additional amide I frequency shifts, independent of electrostatics. To check for such effects in our data set we added two dipeptides with mixed stereochemistry, L-Leu-D-Leu and D-Leu-L-Tyr, plotted as cyan data points in Figure 4. Both dipeptides appear to show nearly identical frequency dependence as our earlier set of “standard” amino acids, suggesting that at least for these examples steric considerations are not important in determining the frequency shift of the isolated amide bond.

Force field dependence

Finally, to explore the influence of force field parameterization on our results, we repeated our analysis using MD simulations from the OPLS-AA force field (simulations were otherwise identical to the CHARMM27 simulations already described). The results are presented in Figure 4b. Two differences are apparent in comparing the data sets for the two force fields. First, the correlation between electric field and observed peak frequencies is somewhat weaker for the OPLS-AA force field than for CHARMM27; while a linear relationship between observed frequency and the $E_x^{\mathrm{O}}$ field is still apparent, the OPLS-AA data points are more widely scattered around their best fit line ($\omega =3608.3·E_x^{\mathrm{O}}+1720.3$) compared with the CHARMM27 data set. Second, except for the X-Pro dipeptides (best-fit line: $\omega =3387.8·E_x^{\mathrm{O}}+1672.2$) which show a ∼40 cm⁻¹ redshift from the best fit line, no clear effect can be seen in the OPLS-AA data set from factors such as side chain composition (Gly-X or Pro-X) or stereochemistry. It is interesting to note that the slope and zero-field values for the OPLS-AA best fit line are significantly larger than for the CHARMM27 line, highlighting the need for customization of electrostatic frequency maps to the force field used.

DISCUSSION

The results presented above indicate clearly that the vibrational Stark effect—a linear frequency shift proportional to the projection of the solvent electric field along the C=O bond axis—is the primary determinant of amide I vibrational frequencies in solution, at least for simple dipeptide oscillators. What is perhaps surprising about this observation is that such a simple mechanism should be apparent despite the complexity of the aqueous solvent environment and the presumable influence of other forces (e.g., short range steric and van der Waal's forces and higher order electrostatics). To be practically useful, however, several important points must be considered.

Accuracy of spectral simulations

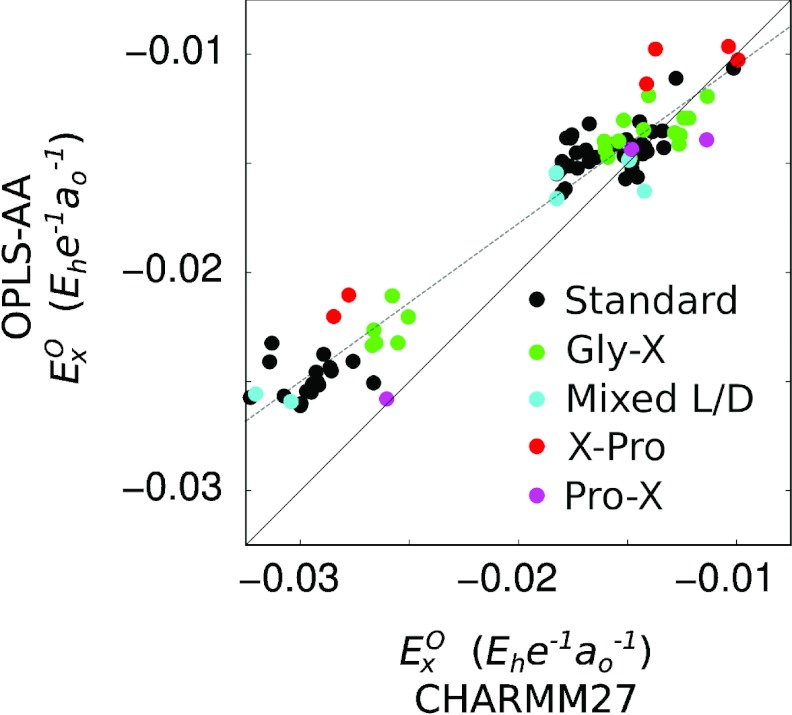
Our first point is to consider the accuracy with which the electric field alone can be used as an indicator of vibrational frequency in spectral simulations. The answer is in part illustrated by the error histograms inset in Figure 4, plotting the deviation between predicted and observed frequencies for the 23 standard dipeptides not containing proline or mixed stereochemistry. The sample standard deviations corresponding to the two histograms are 2.8 cm⁻¹ and 3.7 cm⁻¹ for the CHARMM27 and OPLS-AA force fields, respectively, indicating that for most of the dipeptides studied, the electric field is an effective indicator of vibrational frequency within the range of a few wavenumbers. However, for both force fields, outliers do exist, deviating from their predicted frequency values by as much as ±9 cm⁻¹. At present, it is difficult to definitively assign a reason for the discrepancies. One possibility is, of course, that in some cases the electric field is simply insufficient as an indicator of vibrational frequency. On the other hand, a perhaps equally plausible explanation is that the MD trajectories employed here do not represent an adequate sampling of dipeptide and solvent conformations and/or that the atomic charges employed are not entirely self-consistent for spectroscopic purposes. This suggestion finds some support from a comparison of the electrostatic variables calculated according to the two force fields: if the two force fields themselves are adequately sampled and physically consistent (for spectroscopic purposes), the predicted electric field values should at least be strongly correlated, if not identical. Figure 5 presents a scatter plot of the trajectory-averaged $E_x^{\mathrm{O}}$ values calculated from trajectories for each force field; as in Figure 4, the data points are partially categorized by dipeptide amino acid composition. Significant differences are clear; not only are the two sets of values linearly offset from each other, but the data points are strongly scattered around the best-fit line (E_OPLS = 0.7246·E_CHARMM − 0.033 for the standard dipeptides). While we cannot at present distinguish whether the discrepancy between the two force fields originates in charge parameterization or in trajectory sampling, it is at least clear that the two force fields predict significantly different values for the spectroscopically relevant $E_x^{\mathrm{O}}$ variable. In this light, the scatter observed in Figure 4 in predicted vibrational frequencies should perhaps not be surprising.

Figure 5.

Scatter plot comparing the average electric field values $E_x^{\mathrm{O}}$ for CHARMM27 and OPLS-AA trajectories. Data points are colored according to amino acid composition (see legend). The dashed line is the least-squares best fit line for the standard dipeptide data (black points): E_OPLS = 0.7246 · E_CHARMM − 0.033. The correlation coefficient is 0.975.

It should be emphasized here that our 5 ns trajectories are not intended to represent an exhaustive sampling of the conformational space even of these relatively simple dipeptide systems. Our intention is rather that the large size of our data set can accommodate some degree of noise while leaving trends across the data set intact. In future work, it would be of great interest to see whether more ambitious MD simulations could improve agreement between simulation and experiment. It is worth noting that in our limited sampling here significant differences are observed between dipeptide conformations under the two force fields, with the CHARMM27 simulation generally sampling a somewhat larger distribution of dihedral ψ angles (see supplementary material for (ϕ, ψ) plots).⁷³ These differences serve to highlight that even more extensive simulations will ultimately be limited by the accuracy of the chosen force field in determining equilibrium conformational distributions. Indeed, metadynamics simulations of the free energy surface of the capped alanine dipeptide as a function of dihedral angles reveal significant deviations between common force fields (including CHARMM27 and OPLS/AA),⁶⁵ although direct comparison with our un-capped dipeptides should be made cautiously. Likewise, the discrepancy between electric field values for the two force fields suggests that the force field charges should not be regarded as reliable spectroscopic variables but rather as empirical parameters which must be explicitly considered when developing a frequency map.

In evaluating simulation performance, it is important to consider not only the average frequency of an absorption peak, but also its line shape, calculated as¹⁹

$$A\left(\omega \right)\propto Re{\int }_{-\infty }^{\infty }d\tau e^{-i\left(\omega -{\omega }_o\right)\tau }{e}^{-\frac{\left|\tau \right|}{2T_1}}F\left(\tau \right),$$ (5)

where ω_o is the average vibrational frequency across the trajectory, T₁ ≈ 1.2 ps is the experimentally determined vibrational lifetime for amide I in water,⁹ and F(τ) the dephasing function

$$F\left(\tau \right)=⟨\exp \left[i{\int }_0^{\tau }dt\delta \omega \left(t\right)\right]⟩,$$ (6)

where δω(t) = ω(t) − ω_o and the angular brackets ⟨⋯⟩ indicate a time-average over the MD trajectory. To this end, Figure 6 compares experimental absorption spectra with simulated frequency histograms (dashed lines) and absorption spectra (solid lines) for the VT dipeptide under neutral and basic conditions from 20 ns MD simulations with frequencies sampled every 10 fs. Note that while no additional shifts were applied to the simulated spectra, this sample was chosen intentionally as an example of reasonable agreement between simulated and experimental peak frequencies to allow for clear comparison of line shapes; Figure 4 provides a better indication of overall frequency prediction error. While the static frequency histogram, which ignores motional narrowing, is much too broad, the simulated absorption line shapes are in good agreement with the experimental data (the clipped peak near 1600 cm⁻¹ in the experimental spectrum is due to the C-terminus carboxylate stretch, not included in the simulation), with the exception that the simulation fails to capture a slight asymmetry on the red edge of the experimental spectrum under neutral conditions. This asymmetry is in fact present in many of the experimental spectra analyzed here (see supplementary material),⁷³ particularly for those dipeptides with bulky side chains. Intriguingly, for all but the mixed stereochemistry dipeptides, the asymmetry is toward the same side, with a shoulder or broad tail extending to the red of the main absorption peak; for the mixed stereochemistry dipeptides (L-Leu-D-Leu and D-Leu-L-Tyr) however, the asymmetry is reversed, with a tail extending to the high-frequency side of the dominant peak. As this asymmetry is not reproduced in our simulations, we cannot at present determine its origin with confidence, although it most likely indicates either multiple hydrogen bonding configurations for the dipeptide amide group or separate dihedral angle bins which are not well sampled by our MD simulations.

Figure 6.

A comparison of experimental absorption spectra (blue circles) with simulated frequency histograms (dashed lines) and absorption spectra (solid lines) for the VT dipeptide under neutral and basic conditions. Note that the clipped peak near 1600 cm⁻¹ is due to the C-terminal carboxylate absorption peak which is not included in our simulations.

Electrostatic mapping variables

As discussed in the Introduction, amide I frequency maps parameterized by different groups have made use of a variety of different mapping sites and variables.^{12, 13, 14, 16, 17, 18, 19, 24, 26, 43} Although our present results indicate that the electric field at the O atom provides an accurate (and physically meaningful) mapping parameter for amide I frequencies, they do not preclude the possibility that the inclusion of additional mapping variables might improve the overall fit to experimental data. To investigate this possibility, we performed least-squares fits to the experimental data for all possible combinations of 1, 2, 3, or 4 of the 70 electrostatic variables considered here (7 sites and 10 components). For four-variable combinations, standard deviations as low as ∼2 cm⁻¹ could be obtained (requiring the presence of at least one gradient component), an improvement of ∼0.8 cm⁻¹ over the physically meaningful $E_x^{\mathrm{O}}$ variable. In our view, this rather slight improvement is not significant enough to warrant inclusion of multiple parameterization sites or variables in electrostatic models. In this regard, it should be kept in mind that, while additional variables may compensate for subtle electrostatic effects not well predicted by the electric field, they also pose several possible dangers to a robust electrostatic map. First, for any finite data set (our standard set consists of 73 points), increasing the number of free parameters always increases the risk that the final fit will compensate for noise in the data set (e.g., poor MD sampling or improperly assigned peak frequencies), rather than reflecting the correct physical behavior of the system. Second, in the context of electrostatic maps in particular, whereas parameterization of the $E_x^{\mathrm{O}}$ variable alone ensures a smooth (and physically meaningful) decay of the predicted frequency shift as a charged group moves away from the C=O bond, multiple parameterization sites can give rise to physically unreasonable oscillations in the predicted frequency shift due to interference between positive and negative contributions from different sites.

It is important to note that the difference between the electrostatic potentials evaluated at the C and O sites acts as an excellent proxy for the $E_x^{\mathrm{O}}$ electric field—which is, after all, just the derivative of the potential along the C=O bond axis. Indeed, an unconstrained least squares fit using the Φ_C and Φ_O variables results in the best fit equation

$$\omega =1700+1095·{\Phi }_{\mathrm{C}}-1072·{\Phi }_{\mathrm{o}}$$ (7)

(units of cm⁻¹a_oe/E_h on the potential coefficients) representing a frequency shift essentially proportional to the difference of the two potential values, i.e., to the electric field. Similar results are obtained for a four-parameter fit consisting of the potential evaluated at each atomic position (see Table 1). Note that for a linear fit against electrostatic potential variables, we expect physically that the sum of all potential coefficients should be zero since application of a spatially uniform potential is not expected to change the vibrational frequencies.⁶² In fact, as seen in Eq. 7, this condition appears quite naturally (albeit approximately) even in an unconstrained fit to our data, both for 2- and 4-site potential models. Both potential parameterizations produce best-fit standard deviations comparable to or better than the $E_x^{\mathrm{O}}$ parameter alone. These observations indicate that, while the electric field may indeed be the physically relevant variable, site energy maps based on the potential may serve as well for practical purposes, provided that they are properly parameterized. On the other hand, the commonly used parameters of the electric field on only the C and N sites,¹² would appear based on this data alone to be a poor choice for mapping variables, giving a best-fit standard deviation of 4.9 cm⁻¹ (nearly twice that obtained for the O site alone). At this point, the inclusion of gradient terms, as found in some literature maps,^{24, 26} appears to us to be unnecessary. Best-fit parameters and standard deviations for several common variable combinations are presented in Table 1 for comparison to literature results (note that in these fits the coefficients within each potential map have been constrained to sum to zero). In interpreting these results, it should be remembered that our electrostatic values include contributions from all atoms except for the amide bond atoms C, O, N, and H (or C_δ for Pro) and their immediately bonded α-carbon neighbors. Literature electrostatic maps, generally exclude all backbone atoms from neighboring peptide units, often accounting for their induced frequency shifts via dihedral angle maps.²³ Exclusion of nearest-neighbor electrostatics is clearly not an option for analyzing our data since the charges of the neighboring termini are the primary determinants of our frequency shifts; nonetheless this difference in definitions should be kept in mind when comparing different electrostatic maps.

Table 1.

Best-fit data for various combinations of electrostatic variables evaluated for the CHARMM27 force field against experimental frequencies for our 23 standard dipeptides. The first data column presents the sample standard deviation (σ) of the error between best-fit prediction and experimental values. The second column reports the predicted zero-field (i.e., vacuum) frequency, and the third column the linear coefficients for the respective variables (see, e.g., Eqs. 4 and (8)). The units on the potential are E_h/e and on the field E_h/a_oe, as above. Note that for the potential fits, the coefficients are constrained to sum to zero.

	σ (cm−1)	ωo (cm−1)	Electrostatic coefficients
$E_x^{\mathrm{O}}$	2.79	1710.3	$+2707.8·E_x^{\mathrm{O}}$
$E_x^{\mathrm{C}}/E_x^{\mathrm{N}}$	4.92	1677.9	$+2557.8·E_x^{\mathrm{C}}$
			$-1099.5·E_x^N$
ΦC/ΦO	2.95	1702.6	+1136.5·ΦC
			−1136.5·ΦO
4-site Φ	2.77	1724.9	+1123.5·ΦC
			−1383.4·ΦO
			−11.819·ΦN
			+271.66·ΦH

Along the same lines, we should also note that it remains to be seen whether the frequency relations provided in Table 1 can be applied directly to protein systems. Although we expect the trends observed here to be quite general, it would not be surprising if the zero-field values and slope coefficients of the $E_x^{\mathrm{O}}$ best-fit equation require modification before application to larger systems. Differences in parameterization could arise from fundamental physical sources (e.g., variations in the zero-field frequency due to longer backbone chains on either terminus) or, perhaps more likely, from inconsistencies in force field charge parameterizations compared with spectroscopic observables. This last issue is particularly important to guard against since our calculations are calibrated largely against the protonation state of peptide end groups, while mid-chain amide bonds in larger proteins will have frequencies largely determined by the electrostatics of other mid-chain oscillators, solvating waters, and side chain groups. However, given that our model consists of only two free parameters (slope and zero-field value), adjustments against experimental data for larger protein systems should be straightforward.

Outlook for amide I spectroscopic models

As described in the Introduction, accurate modeling of amide I spectra requires (in addition to accurate MD sampling) well developed models for both site energies and inter-site coupling constants. Our work here is intended to remove as much as possible the issues of site-to-site coupling and MD sampling from our data set, allowing us to focus directly on the variation of amide I vibrational frequency with local electrostatics. However, several important issues remain to be dealt with before these results can be extended to real protein systems. Most importantly, the rather thorny problems of site-to-site coupling and transition dipole moment orientation must be evaluated carefully with close reference to experimental data. The experimental testing of dipole moment orientation and magnitude parameters (which in some cases have been taken to vary with solvent electrostatics^{17, 24, 26}), in particular appear to have been largely ignored in recent years, despite the substantial effect that these parameters can have on spectral features.

The spectral models developed over many years and by various groups have done much already to increase our understanding of amide I vibrations and their associated spectra. Nevertheless, to move the field forward, the comparison of these models with experimental data must, in our view, become significantly more rigorous, particularly as applications to experimental data interpretation become increasingly demanding. In the past, direct comparison between simulated and experimental spectra has been generally limited to analysis of peak widths^{41, 66} (rather than frequencies) or is accompanied by arbitrary peak shifts of up to 30 cm⁻¹ in order to improve agreement between simulation and experiment.^{11, 26, 39, 40} A particular difficulty appears to be the assignment of ¹³C=¹⁸O isotope label frequency shift, since nearly any frequency shift between −75 cm⁻¹ (Ref. ⁵) and −59.6 cm⁻¹ (Ref. ⁴⁵) has been either assigned^{44, 45, 67} or assumed^{12, 41, 42} in various applications in the literature. In the absence of a well-defined shift, the absolute frequencies of isotope labeled units do not appear to us to be a meaningful metric for map performance, although relative frequency shifts between different isotope labels within the same peptide can, of course, provide a qualitative comparison.

Several different strategies may be pursued to allow for quantitative analysis of simulation performance. First, a systematic study of isotope label frequency shifts for various peptides (with localized amide I transitions) would serve greatly to reduce uncertainty in evaluating experimental site frequencies. Given a reliable ¹³C=¹⁸O label frequency shift, preparation of a large number of isotope labeled standards—proteins or peptides with stable and well-understood secondary structures—would enable the direct evaluation of site energy models, particularly the contribution of non-electrostatic effects (e.g., dihedral shift maps). Pairs of isotope labeled oscillators would likewise allow for the development of experimentally based coupling models. For this purpose, label pairs should be intentionally chosen both to have stable structures (e.g., larger peptides than in some previous studies^{68, 69}) and to have significant coupling constants since experimental validation of a coupling constant less than a few wavenumbers in the presence of tens of wavenumbers of disorder is not practically feasible (see, e.g., Ref. 42).

This label-based approach to map validation has the significant advantage of allowing for direct evaluation of individual parameters for specific sites. On the other hand, it relies heavily both on the expensive and technically challenging synthesis of a large number of stable peptides and on the assumption that isotope labeled oscillators differ from unlabeled sites only in a single frequency shift. Alternatively, one could envision the evaluation of model performance against a very large number of unlabeled protein or peptide standards (e.g., the rationally selected proteins set⁷⁰ recently analyzed by Karjalainen et al.³⁴). In principle, if agreement between simulation and experiment is reasonably good to begin with, comparison of simulations with a large enough database of experimental spectra should allow for the refinement of a limited number of model parameters. This approach would avoid the complications discussed above in the context of isotope labeling, but at the cost of specificity: all parameters (transition dipole, site energies, coupling constants, etc.) would have to be considered simultaneously, seriously complicating the refinement of any spectroscopic model against experiment. A more tractable, but nonetheless important, issue is that for comparison of simulated spectra to real protein data, it becomes very important to account for the absorption of various amino acid side chains (particularly Gln and Asn as considered in Ref. 12, although Tyr, Glu, Asp, and Arg also have partially overlapping transitions).⁷¹ Finally, since this approach relies intrinsically on the spectra of large, coupled, many-oscillator systems, calculation of accurate line shapes becomes substantially more difficult than for individual isotope labeled oscillators, requiring computationally expensive approaches such as numerical integration.^{39, 72}

In light of these considerations, perhaps the best approach forward in amide I model development involves a combination of selective isotope labeling and a large database of bulk protein spectra. If even the single issue of site energy shifts could be reliably addressed using isotope labeled data, the refinement of other parameters (transition dipoles and coupling constants) against bulk spectra would be substantially simplified. Ultimately, a satisfactory amide I spectral model must be able to reliably reproduce both isotope labeled data and bulk spectra for larger proteins, and only by comparison to data of both types can both the accuracy of model parameters and even the viability of the standard model Hamiltonian be concretely tested. In short, although much work remains to be done, addressing these fundamental issues should open the door to a fascinating variety of deeper questions, such as the mixing of amide I modes with other protein backbone vibrations (particularly amide II^′) and even solvent and side chain motion.

CONCLUSION

In conclusion, by studying the pH-dependence of the amide I bands of 28 dipeptide fragments, we have demonstrated that amide I frequency shifts can be accurately modeled by considering only the projection of the electric field along the C=O bond axis evaluated at the O atom position (denoted $E_x^{\mathrm{O}}$). The validity of this treatment is benchmarked by comparison to simulated peak frequencies and absorption spectra. We find that from our sample size of 73 data points, the $E_x^{\mathrm{O}}$ map using the CHARMM27 force field for MD simulations gives a standard deviation of only 2.8 cm⁻¹ away from the experimental values (though for some samples deviations as large as 9 cm⁻¹ occur) and predicts absorption line shapes which agree well with experiment. Results for the OPLS-AA force field are similar, but with somewhat larger error (standard deviation of 3.7 cm⁻¹ from experiment). We also find that, while parameterization of the electrostatic potential at multiple sites can act as a suitable proxy for the electric field, inclusion of multiple field/gradient components or multiple sites appears to be unnecessary for good agreement with experiment. Best-fit electrostatic maps for several choices of mapping variable are provided for application in amide I modeling studies.