Inner-ear sound pressures near the base of the cochlea in chinchilla: Further investigation

Abstract

The middle-ear pressure gain G_MEP, the ratio of sound pressure in the cochlear vestibule P_V to sound pressure at the tympanic membrane P_TM, is a descriptor of middle-ear sound transfer and the cochlear input for a given stimulus in the ear canal. G_MEP and the cochlear partition differential pressure near the cochlear base ΔP_CP, which determines the stimulus for cochlear partition motion and has been linked to hearing ability, were computed from simultaneous measurements of P_V, P_TM, and the sound pressure in scala tympani near the round window P_ST in chinchilla. G_MEP magnitude was approximately 30 dB between 0.1 and 10 kHz and decreased sharply above 20 kHz, which is not consistent with an ideal transformer or a lossless transmission line. The G_MEP phase was consistent with a roughly 50-μs delay between P_V and P_TM. G_MEP was little affected by the inner-ear modifications necessary to measure P_ST. G_MEP is a good predictor of ΔP_CP at low and moderate frequencies where P_V ⪢ P_ST but overestimates ΔP_CP above a few kilohertz where P_V ≈ P_ST. The ratio of P_ST to P_V provides insight into the distribution of sound pressure within the cochlear scalae.

INTRODUCTION

This paper is a continuation of our examination of sound power transmission through the external and middle ear (ME) to the cochlear partition (CP) (Ravicz and Rosowski, 2012b). In this paper we examine the ME pressure gain, defined as the transformation of ear canal (EC) sound pressure to sound pressure inside the oval window (OW), and the sound pressure difference across the CP near the base of the cochlea in chinchilla.

The middle-ear pressure gain G_MEP, the ratio of sound pressure inside the OW P_V to EC sound pressure at the tympanic membrane (TM) P_TM, is one descriptor of ME function (e.g., Shera and Zweig, 1992). G_MEP is a complex function of frequency f, with a magnitude |G_MEP| and a phase angle ∠G_MEP, as are most sound pressures and transfer ratios described in this paper.1 An advantage of using G_MEP over other ME descriptors is that sound pressures are scalar quantities rather than vectors and so are insensitive to the direction of measurement (in contrast to stapes velocity; e.g., Heiland et al., 1999; de La Rochefoucauld et al., 2008).

The differential sound pressure across the base of the CP ΔP_CP is believed to be the driving force for basilar membrane motion, and several studies support this assumption (e.g., Dancer and Franke 1980; Lynch et al., 1982; Voss et al., 1996). Previous studies have estimated the drive to the basilar membrane from more peripheral measurements, e.g., stapes velocity or sound pressure near the OW. Recently we published preliminary results of a new investigation into the differential sound pressure across the CP near the base of the cochlea ΔP_CP in chinchillas computed from measurements of P_V and in scala tympani (ST) near the round window (RW) P_ST in the same animals (normalized by sound pressure near the TM; Ravicz et al., 2010). This paper continues that study with new data, refinements in technique, and a more complete discussion of the results.

This study also provides normative data for more definitive investigations of the hypothesized connection between ΔP_CP and hearing. The “window-pressure difference” or “difference-mode” hypothesis of cochlear stimulation (e.g., von Békésy, 1947; Peake et al., 1992; Voss et al., 1996) suggests that the cochlear response (as measured by cochlear potentials) should be proportional to ΔP_CP. Normative results will aid in the understanding of the effect of different normal cochlear “third windows” (e.g., the cochlear and vestibular aqueduct) as well as various inner-ear pathologies on ΔP_CP and hearing; e.g., inner-ear dehiscences (e.g., Songer and Rosowski, 2006), enlarged vestibular aqueduct, or RW atresia and fixation (see Merchant and Rosowski, 2008 for a review). These results will also help in the development of an animal model to evaluate the utility of direct RW stimulation (Lupo et al., 2012).

Prior to 1998, nearly all studies of intracochlear sound pressure in animals used hydrophones connected to the cochlear scalae via probe tubes (Lynch et al., 1982, in cat; Dancer and Franke, 1980, in guinea pig; Décory et al., 1990, in cat, guinea pig, and chinchilla). In this study we use miniature fiber-optic pressure sensors developed by Olson (1998) with dimensions that allow placement of the entire transducer within the scalae.2 These miniature sensors, which can be used in air or water, allow measurements close to the OW and RW and have been used to measure scalae sound pressures in live gerbils (e.g., Olson, 1998, 2001; Dong and Olson, 2006), live chinchillas (Slama et al., 2010; Ravicz et al., 2010), and human temporal bones (Nakajima et al., 2009).

In this paper we present G_MEP and ΔP_CP computed from measurements of P_V, P_ST, and sound pressure in the EC P_near-TM in seven individual chinchillas. [ME input admittance (Ravicz and Rosowski, 2012b) and stapes velocity (Ravicz et al., 2011) were also measured in these same animals.] We also examine the effect of simple preparation-related ME and cochlear manipulations on P_V, P_ST, and ΔP_CP. The G_MEP and ΔP_CP data presented here are part of the measurement set required for computation of power delivery to the cochlea and the CP by the ME.

METHODS

Preparation

These experiments were performed in accordance with guidelines published by the U.S. Public Health Service and were approved by the Massachusetts Eye & Ear Infirmary Institutional Animal Care and Use Committee. Seven chinchilla ears were used in this study and in the companion paper (Ravicz and Rosowski, 2012b). Animals remained alive throughout the experiment. The preparation and anesthesia3 have been described in detail earlier (Ravicz and Rosowski, 2012b). The bony EC was greatly shortened in order to expose the TM to view, and a short brass tube (5 mm in diameter and 9 mm in length) was glued to the skull around the bony EC to allow the sound source (see Sec. 2B) to be coupled repeatably to the ear. A stainless steel sleeve (0.8 mm inner diameter and 1.9 cm in length) was glued under the brass coupler to position the tip of a probe tube microphone to measure sound pressure P_near-TM within 1 to 1.5 mm of the umbo in the center of the TM. Thin sheets of bone posterior to the RW were removed to provide access to the bone covering the vestibule just posterior to the OW and to the surface of the cochlear capsule inferior and posterior to the RW.

A small hole was drilled through the vestibular wall posterior to the footplate with a fine pick, and a pressure sensor was introduced through the hole to measure sound pressure within the vestibule P_V. The desired hole size was between 150 and 200 μm diameter, slightly larger than the sensor tip (145 μm diameter), but the resulting holes ranged from 170 to 340 μm diameter. The sensor was inserted to a depth of 150 to 500 μm into the vestibule. After P_V measurements, a similar small hole was made in the cochlear capsule approximately 1 mm inferior to the RW (near the apical extent of the “hook” region) with a 0.006 in. (150 μm) pivot drill to allow a second pressure sensor to be introduced into scala tympani for P_ST measurements. The hole provided a reasonably tight seal around the sensor tip, and the tip was placed approximately at the level of the inner cochlear wall. The location of the ST hole corresponded to a characteristic frequency (CF) of 12 to 18 kHz (Eldridge et al., 1981; Müller et al., 2010). Before the end of the experiment, the ossicular chain was interrupted by breaking the narrow shaft between the long process of the incus and the lenticular process.

Stimuli, responses, and equipment

Synthesized chirp and sinusoidal voltage stimuli were produced by a computer-controlled signal generator (33120 A, Hewlett-Packard, Palo Alto, CA). Stimulus levels were controlled by a programmable attenuator (PA-5, Tucker-Davis, Alachua, FL) and a reconstruction filter with programmable gain (3901, Krohn-Hite, Lake Mary, FL). A power amplifier (1001 A, Crest Audio, Meridian, MS) was used to drive (a) a low-impedance earphone (40-1377, Radio Shack, Fort Worth, TX) to generate sound in the EC or (b) a shaker for pressure sensor calibration. Three sound stimuli were used: A broadband chirp with uniform component magnitude from 49 Hz to 49 kHz, or one of two tone sequences: 98 Hz to 49 kHz at 6 pts/octave or, for better frequency resolution at high frequencies, 14 to 49 kHz at 12 pts/octave.4

Three responses were measured: (1) Sound pressure in air near the TM (P_near-TM); and sound pressure in the perilymph (2) in the vestibule (P_V) and (3) in scala tympani (P_ST). P_near-TM was measured with a small microphone (FG23652, Knowles, Itasca, IL) attached to a thin probe tube. Scalae sound pressures were measured with fiber-optic pressure sensors (Olson, 1998) inserted into the scalae as described above. Responses were amplified if necessary (air sound pressure: Grass P5; scalae sound pressure: Custom differential amplifiers), digitized at 400 kHz by a data acquisition board (PCI6122 or PXI6122, National Instruments, Austin, TX), and saved on a computer. Up to four response channels could be saved at a time.

Calibrations

Ear canal microphone

The P_near-TM microphone, including the probe tube, was calibrated against 1/4 in. and 1/8 in. reference microphones as described previously (Ravicz et al., 2010; Ravicz and Rosowski, 2012b). Repeated calibrations showed variations of generally less than 2 dB in magnitude and 0.01 cycle in phase.

Pressure sensors

Although a basic description of the calibration of the miniature pressure sensors has been presented previously (e.g., Olson, 1998; Ravicz et al., 2010), several aspects of our experiments required us to expand the technique. We required greater precision in sensitivity, especially at high frequencies, and we needed to account for the temperature sensitivity of some sensors, as the temperature during calibration was lower than during use in live ears (body temperature). The expanded calibration technique is described below.

The pressure sensor calibration S_P(f) includes two components: (1) The frequency response of the sensor S_f(f), defined as the ratio of sensor output voltage v_sens(f) to sound pressure P(f) across frequency, normalized to 1 at a selected frequency f₀; and (2) the sensitivity S₀, defined as |v_sens/P| at f₀ (Ravicz et al., 2010):

$$\text{Sensor}\hspace{0.17em}\text{calibration}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{S}}_{\mathbf{P}}\left(f\right)=S_0·{\mathbf{S}}_{\mathbf{f}}\left(f\right),$$ (1a)

where

$$\text{frequency response}\hspace{0.17em}{\mathbf{S}}_{\mathbf{f}}\left(f\right)=\frac{{\mathbf{v}}_{\mathbf{s}\mathbf{e}\mathbf{n}\mathbf{s}}(f)/\mathbf{P}(f)}{{\mathbf{v}}_{\mathbf{\text{sens}}}(f_0)/\mathbf{P}(f_0)}\hspace{1em}\text{and}\hspace{0.17em}\text{sensitivity}\hspace{0.17em}{S}_0={\left|\frac{{\mathbf{v}}_{\mathbf{\text{sens}}}}{\mathbf{P}}\right|}_{f_0}.$$ (1b)

For these sensors, the frequency response is nearly constant: The magnitude and phase of S_f(f) decrease smoothly and only slightly (by 2 to 10 dB and no more than 0.1 cycle) between 100 Hz and 50 kHz (see also Olson, 1998), and this frequency dependence is relatively constant during the active life of the sensor. In contrast, the sensitivity S₀ can be quite variable, and this variability affects all frequencies equally (Olson, 1998; Ravicz et al., 2010). Additionally, in some sensors, the sensitivity S₀ varied with temperature, and limitations of our calibration setups (see below) precluded using a single measurement as a calibration across the entire frequency range. We therefore used a calibration constructed from several different types of measurements.

We used two stimulus methods: Air calibration, using a microphone; and water calibration, using a shaker, a small vial, and an accelerometer.

Air calibration provided a good estimate of the sensor frequency response above several kilohertz. For air calibration, the tip of the pressure sensor was positioned inside a closed calibration cavity to within 1 mm of a 1/8 in. reference microphone (see Ravicz et al., 2007), and sensor and microphone outputs were measured in response to a tone sequence. This method had limited utility at lower frequencies (because a sound-tight seal could not be made without damaging the sensor; hence, we were not able to generate sufficiently high sound pressure to overcome the sensor noise floor) but was free of potential sources of error that affected water calibrations (see below) at frequencies above a few kilohertz.

Water calibration gave a more reliable estimate of the sensitivity in vivo, was well suited for measuring temperature effects, and was quicker and easier to perform during experiments but was subject to errors at low and high frequencies. For water calibrations, the sensor tip was submerged 1 mm deep into a small vial attached to a shaker head and accelerometer (4290, Brüel & Kjær, Denmark; see Nedzelnitsky, 1980). Acceleration of the vial in response to a tone stimulus generated a time-varying sound pressure in the vial [Schloss and Strasberg, 1962, Eq. 6] expressed in the frequency domain

$$\mathbf{P}\left(f\right)={\rho }_{\mathrm{w}}\hspace{0.17em}h\hspace{0.17em}\hspace{0.17em}\ddot{\mathbf{X}}\left(f\right)\hspace{0.17em}\frac{\sin (\omega h/c)}{\cos (\omega h/c)\cos (\omega l/c)},$$ (2a)

where ρ_w is the density of water, $\ddot{\mathbf{X}}$(f) is the acceleration of the vial, h is the immersion depth of the sensor in the vial, l is the total depth of the water in the vial, c is the speed of sound in water, and ω = 2πf. The fraction describes “wave effects,” the relationship between the sound wavelength (in water) and the vial dimensions. In our setup, the wave effect fraction is negligible below about 20 kHz, and Eq. 2a reduces to

$$\mathbf{P}\left(f\right)\approx {\rho }_{\mathrm{w}}\hspace{0.17em}h\hspace{0.17em}\ddot{\mathbf{X}}\left(f\right) .$$ (2b)

The effect of temperature on probe sensitivity S₀ was assessed by heating the water and vial to chinchilla body temperature (37 °C) and measuring sensitivity repeatedly while the water cooled.5 Temperature sensitivity was determined by averaging the response at each temperature over several low- and mid-frequency ranges where the signal-to-noise ratio was best.6 During experiments, the vial and water were maintained at the highest temperature practical (usually 30 °C to 35 °C) to minimize the temperature difference between the calibration and body temperatures, and the sensors were calibrated before being inserted into the cochlear scala and immediately after being withdrawn.

Errors and uncertainty in water calibrations at low and high frequencies arose from several sources. Resonances in the sensor support excited by shaker and background vibrations contaminated calibrations at several low frequencies, especially near 300 to 400 and 900 to 1000 Hz. Limitations in shaker output at high frequencies caused a low signal-to-noise ratio, and bubbles in the vial and a shaker resonance near 50 kHz caused high-frequency calibration errors. Heating the vial increased bubble production, even when degassed distilled water was used. The effects of the vial dimensions [described by the fraction in Eq. 2a] are 1 dB at 20 kHz and about 6 dB at 50 kHz.

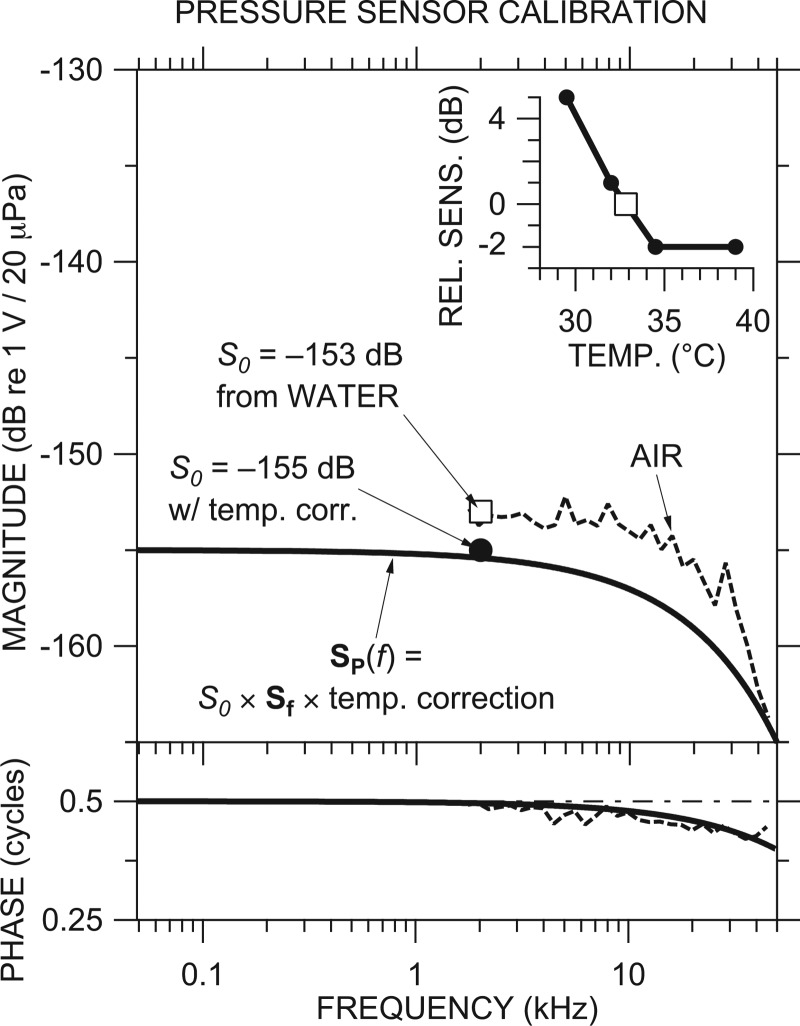
We therefore constructed a calibration for each sensor from measurements described above and a simple model based on observations of many sensors (ours7 and Elizabeth Olson's, e.g., Olson, 1998) —see Fig. 1 for an example. For each set of scalae pressure measurements, we set the absolute sensitivity S₀ (open square in Fig. 1) equal to the mean of water calibration measurements at frequencies near f₀ = 2 kHz. In our example, S₀ = −153 dB re 1 V/20 μPa. The water calibration was made immediately after withdrawing the sensor from the inner ear (IE), in the belief (borne out by experience8) that the sensor was less likely to be damaged during withdrawal rather than upon insertion. S₀ was adjusted for the difference in temperature between the vial (33 °C in this example) and 37 °C, if necessary (−2 dB in our example; see Fig. 1 inset). Because all sensors showed a similar frequency response (similar to that shown in Fig. 2 of Olson, 1998), we modeled the frequency dependence of the sensitivity of each probe S_f as essentially flat, with a linear magnitude and phase roll-off with frequency determined by the air calibration (dashed curve in Fig. 1). The solid black line in Fig. 1 illustrates our best estimate of this sensor's frequency-dependent calibration S_P at body temperature, computed using Eq. (1) from S_f and the temperature-corrected S₀.

Figure 1.

Example of a pressure sensor calibration. The final calibration S_P(f) (thick black line) was constructed from the sensitivity S₀ of −153 dB (open square) from a water calibration in a vial evaluated at 2 kHz, high-frequency response S_f and phase accumulation modeled from air calibration (dashed line), and a correction for the temperature difference (inset) between calibration (at 33 °C; open square) and use (2 dB at 37 °C) (filled circle). Top: Magnitude; bottom: Phase.

Noise floor, artifact, and frequency limits

Our measurements were limited at high frequencies by noise. Noise floor (microphones or pressure sensor) was determined practically by a measurement of the sensor output when no stimulus was present. In general, noise floors were computed from the measured spectra of the responses to tonal stimuli as the average of responses at nearby non-stimulus frequencies.9 The high-frequency limit for P_TM was generally around 44 kHz, and for P_V and P_ST, generally above 40 kHz. Data at frequencies where the responses were within 10 dB of the noise have been omitted.

An artifact, defined as spurious sensor response at a stimulus frequency, was determined for microphones by measuring microphone output with the probe tube plugged and was negligible. Because the artifact could not be measured directly for pressure sensors, we determined an upper bound on the artifact as the sensor output when the sensor was in the IE and the ossicular chain was interrupted [see Fig. 2B], a situation in which intracochlear sound pressures were expected to be reduced.

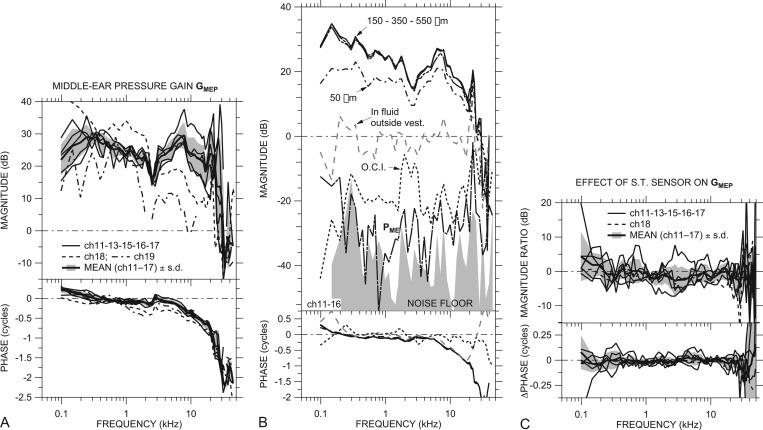
Figure 2.

(A) ME pressure gain G_MEP in dB in all ears with a sensor in the cochlear vestibule and intact scala tympani: ch18 (dashed line), ch19 (dotted-dashed line), and others (thin solid lines). Also shown is the mean G_MEP (thick solid line) ±1 s.d. (shaded area) of all ears except ch18 and ch19 (see the text). (B) P_V in an example ear (ch11) at different insertion depths (solid and dotted-dashed lines) and sound pressure in fluid outside the vestibule (dashed gray line); also, P_V with the ossicular chain interrupted (O.C.I.; dotted line), ME sound pressure (in air) P_ME (long-dashed-dotted line), and sensor noise floor for the O.C.I. measurement (shaded area) in another example ear (ch16). No phase data are shown for P_ME or the noise floor. All data are normalized by P_near-TM. (C) Effect of opening ST and inserting a sensor on G_MEP: Ratio of ${\mathbf{G}}_{\mathbf{\text{MEP}}}^{\mathbf{T}}$ with ST sensor in six ears to G_MEP with ST intact. Mean effect (thick solid line) ±1 s.d. (shading) of all ears except ch18 and ch19. All panels: Top: Magnitude; bottom: Phase.

Course of experiment

Scalae and EC sound pressures were measured after making a hole into the cochlear vestibule and inserting a pressure sensor into it; after making a hole into scala tympani; after inserting a second sensor into the ST hole; and after interrupting the ossicular chain. In these conditions, ME input admittance (Ravicz and Rosowski, 2012b) and stapes velocity (Ravicz et al., 2011) were also measured. The pressure sensors were calibrated before and after each of these measurements as described above. In most experiments, one or both pressure sensors failed at some point during the experiment and were replaced. Data shown below incorporate data from one or more sensors per ear and show no dependence on the sensor.

RESULTS

All quantities described in this section were measured with the ME widely opened and are normalized by sound pressure in the EC near the TM P_near-TM.

Vestibule sound pressure P_V and ME pressure gain G_MEP

ST intact (sensor in vestibule)

ME pressure gain G_MEP with a sensor in the cochlear vestibule was computed from measurements of P_V and P_near-TM in seven ears by

$${\mathbf{G}}_{\mathbf{\text{MEP}}}={\mathbf{P}}_{\mathbf{V}}/{\mathbf{P}}_{\mathbf{\text{near}}-\mathbf{\text{TM}}},$$ (3)

and is shown in Fig. 2A. The curve for each ear is the logarithmic mean of 2 to 7 measurements; the standard deviation (s.d.) of these measurements was 1 to 2 dB. Several measurements with similar normalized results were taken in each ear at lower stimulus levels. Two ears (ch11, ch13) showed hints of a level dependence in G_MEP at low frequencies but no sign of response nonlinearity was seen in other ears. As described above, data at frequencies where P_V or P_near-TM may be contaminated by noise or artifact are omitted.

The magnitude of G_MEP was between 20 and 35 dB in nearly all ears (thin lines) between 150 Hz and 10 kHz, and |G_MEP| was somewhat lower at frequencies below a local maximum between 150 and 350 Hz. ∠G_MEP was near +0.25 cycles at the lowest frequencies in almost all ears and decreased to near 0 by 300 to 500 Hz. In all ears G_MEP showed a small magnitude dip and phase ripple around 2.5 kHz, presumably due to a resonance between the compliance of the air in the ME and the bulla hole (Rosowski et al., 2006). At higher frequencies |G_MEP| increased again in almost all ears to a broad peak between 7 and 10 kHz, and ∠G_MEP steadily decreased. G_MEP magnitude and phase angle decreased gradually at frequencies above the broad peak, up to about 20 kHz. ∠G_MEP between 3 and 22 kHz is well fit by a delay of about 50 μs.

We observed another sharp peak in |G_MEP| between 21 and 28 kHz, and ∠G_MEP showed a 1/2-cycle decrease at the frequency of the |G_MEP| peak. Above the peak frequency, |G_MEP| decreased sharply to a value less than 0 dB. ∠G_MEP showed a 1/2-cycle increase between 32 and 35 kHz, then continued to decrease with frequency in some ears and was nearly constant in others. This |G_MEP| peak and 1/2-cycle ∠G_MEP step are discussed more in Sec. 3D below.

P_V magnitude varied little with sensor insertion depth (up to 550 μm or so), as long as the sensor was inserted at least 150 to 200 μm into the vestibule, as shown for an example ear in Fig. 2B. |P_V| decreased with shallower insertions.

G_MEP was similar among most ears except ch18 and ch19 (dashed and dotted-dashed lines, respectively). In these ears, |G_MEP| was lower by 10 to 15 dB above 2.5 kHz relative to measurements at 1 kHz, and |G_MEP| was lower in ear ch19 than in other ears across nearly the entire frequency range. Similarly, ∠G_MEP showed a greater phase lag in ears ch18 and ch19 than in the other ears at most frequencies. This lower |G_MEP|, especially at high frequencies, would be expected if the ossicles were fractured or the ossicular joints were loosened. Stapes velocity was also lower in these ears (Ravicz et al., 2011), consistent with ME damage,10 and ME input admittance varied less upon interrupting the ossicular chain in these ears (Ravicz and Rosowski, 2012b).

Also shown in Fig. 2A is the mean (in the dB or logarithmic domain) of G_MEP in ears ch11, ch13, ch15, ch16, and ch17 (thick line) ±1 s.d. (shading). Data from ears ch18 and ch19 are omitted from the mean in this and all subsequent figures because of the suspected damage described above. The mean G_MEP captures the features of G_MEP in the five individual ears.

We checked the validity of P_V measurements by also measuring sound pressure with the sensor withdrawn from the vestibule but still in the fluid that accumulated in the OW niche, or in air in the open ME, also shown in Fig. 2B. In this situation, the sensor measured the sum of (a) IE sound pressures radiated from the vestibule hole and RW and (b) ME sound pressure P_ME produced by the motion of the TM. The measured sound pressure magnitude in these situations was 20 to 60 dB lower than |P_V| when the sensor was in the vestibule (P_ME was virtually indistinguishable from the sensor noise floor), which suggests that our P_V measurements were influenced very little by sound pressures outside the cochlea.

As mentioned in Sec. 2D above, |P_V| decreased substantially (20 to 50 dB) when the ossicular chain was interrupted [“OCI” in Fig. 2B]. In this case, the measured P_V is probably due mostly to sound conducted through the skull (“bone conduction”). The substantial reduction in phase accumulation supports this conclusion. As P_V in this case was the lowest vestibule pressure we could measure, it provides an upper bound to P_V stimulus artifact.

With a sensor in ST also

Sound pressure ${\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}}$ was also measured in the vestibule in six of the seven ears (except ch19) with pressure sensors in both the vestibule and ST. Figure 2C shows the ratio of ${\mathbf{G}}_{\mathbf{\text{MEP}}}^{\mathbf{T}}$ = ${\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}}$/P_TM to G_MEP in each ear and the mean change of five ears (thick black line; shading indicates ±1 s.d.). Because the ST sensor had no effect on P_TM, changes in G_MEP are directly attributable to changes in P_V. In any ear, there were only small changes in P_V that were associated with the placement of the ST sensor, and the mean change showed virtually no effect. Placing the ST sensor caused a small (<2 dB) but statistically significant11 reduction in |G_MEP| near 1.5 kHz but no other changes were significant. We use ${\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}}$ measured simultaneously with P_ST in discussions of differential sound pressure below.

Normalized scala tympani sound pressure P_STn

Individuals and mean

Scala tympani sound pressure P_ST was measured in six of the seven ears (no P_ST measurements were made in ear ch19), and P_STn (P_ST normalized by P_near-TM) is shown in Fig. 3A. Each curve is the logarithmic mean of two to five measurements, and several measurements with similar results were taken at lower stimulus levels. The normalized pressures showed no signs of stimulus level dependence. As above, data at frequencies where P_ST or P_near-TM may be contaminated by noise or artifact are omitted.

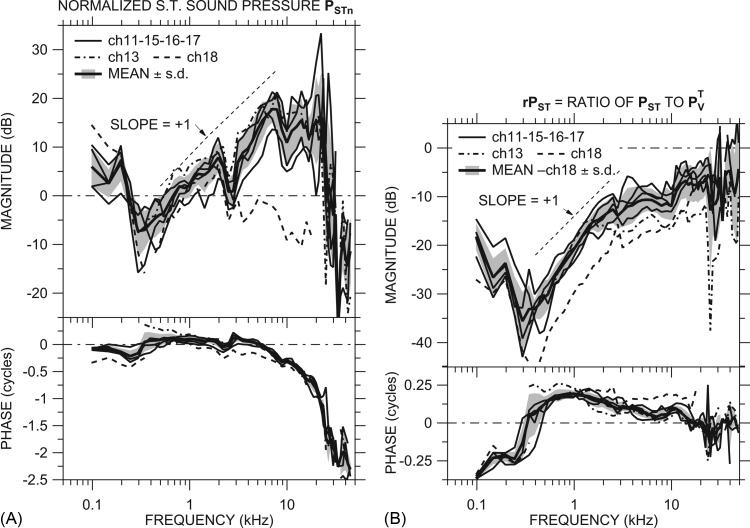
Figure 3.

(A) Scala tympani sound pressure P_STn (normalized by P_near-TM) in dB in all ears: ch13 (dotted-dashed line), ch18 (dashed line), and others (thin solid lines). Also shown is the mean P_STn of all ears except ch18 (thick solid line) ±1 s.d. (shaded area). (B) Ratio of P_ST to ${\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}}$ = rP_ST in all ears measured. Line codes as in (A). Also shown is the mean rP_ST of all ears except ch18 (thick solid line) ±1 s.d. (shaded area). Both panels: Top: Magnitude; bottom: Phase; slope of +1 shown by dotted line.

The magnitude of P_STn was similar in 5 of the 6 ears: In these 5 ears, |P_STn| was between 0 and +10 dB at the lowest frequencies measured, decreased below 0 dB between 150 and 900 Hz, and increased gradually with frequency (magnitude slope ≈ + 1: Dotted line) to 10 to 20 dB by about 5 kHz. All data points shown, even those near 400 Hz, are above noise and artifact (defined as for G_MEP above). ∠P_STn was generally near 0 between 500 Hz and 5 kHz and between −0.25 and 0 cycles at lower frequencies, although the variation among ears was higher at the lower frequencies. The magnitude dip and phase ripple in P_STn in all ears near 2.5 kHz is believed to be due to the bulla-hole resonance (see Sec. 3A). |P_STn| was approximately constant between 5 and 20 kHz, and ∠P_STn accumulated steadily as frequency increased above about 5 kHz. The ∠P_STn slope with frequency between 3 and 22 kHz suggests a P_STn delay of about 50 μs, which is comparable to the G_MEP delay.

P_STn showed a sharp magnitude peak and 0.5-cycle phase change between 21 and 28 kHz as described for G_MEP above. |P_STn| decreased sharply at higher frequencies to <0 dB, and ∠P_STn decreased with frequency, similar to ∠G_MEP (Fig. 2) at high frequencies. In ear ch18, |P_STn| was higher than in other ears at the lowest frequencies and lower (≤0 dB) than in others at all other frequencies, and ∠P_STn showed more phase lag than the other ears at almost all frequencies.

In ear ch13, ∠P_STn was higher than in other ears below 800 Hz (P_STn was contaminated by an artifact below 350 Hz) but P_STn was similar to other ears at higher frequencies. In this ear there was a crack in the cochlear capsule caused by drilling the ST hole. This low-frequency behavior is similar to that seen previously in another ear with an otic capsule crack (Ravicz et al., 2010).

We checked the validity of P_ST measurements by also measuring sensor output in some ears with the sensor withdrawn from ST: In the fluid that accumulated in the OW niche, or in air in the open ME (as described for P_V in Sec. 3A1). Sensor output in these circumstances was much lower than |P_ST|, which suggests that our P_ST measurements were influenced very little by sound pressures outside the cochlea.

Also shown is the logarithmic mean of P_STn in ears ch11, ch13, ch15, ch16, and ch17 (thick line) ±1 s.d. (shading). Because the differences in P_STn between ear ch13 and the other ears occur only in ∠P_STn and only at low frequencies, we include it in the mean. The mean clearly captures the features of P_STn in individual ears.

Ratio of P_ST to P_V measured simultaneously

The ratio of simultaneous measurements of P_ST and ${\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}}$ provides a useful view of the relationship between P_ST and ${\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}}$. This ratio, defined as

$$\mathbf{r}{\mathbf{P}}_{\mathbf{\text{ST}}}={\mathbf{P}}_{\mathbf{\text{ST}}}/{\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}},$$ (4)

is shown in six ears in Fig. 3B. rP_ST was similar among the 6 ears, except that rP_ST was about 10 dB lower in ear ch18 below 15 kHz than in the other ears. The mean rP_ST (thick line) ±1 s.d. (shading) was representative of rP_ST in the individual ears, and the ratio of mean P_ST to mean P_V was representative of the mean rP_ST.

The rP_ST ratio showed different behavior in different frequency ranges. Below about 350 Hz |rP_ST| decreased as frequency increased, and ∠rP_ST was −0.25 cycles or less. There was a minimum in |rP_ST| of −30 dB or lower near 350 Hz, and ∠rP_ST crossed 0 at that same frequency, which suggests that there is a resonance within the cochlea near 350 Hz (discussed further in Sec. 4D below).

Above the |rP_ST| minimum, |rP_ST| increased with frequency, with a slope of +1 (dotted line), to a plateau between ˗8 and ˗17 dB between about 3 and 10 kHz. ∠rP_ST was about +0.2 cycles in this frequency range (∠P_ST led ∠P_V) and gradually decreased, consistent with P_V and P_ST being controlled by different components (e.g., P_V by resistance and P_ST by mass). The slightly negative slope of ∠rP_ST with frequency is consistent with a small delay in P_ST relative to P_V (∼5 μs) but is also consistent with a transition to the control of P_V and P_ST by similar acousto-mechanical components (e.g., both by mass).

In all ears, |rP_ST| abruptly increased to a higher plateau (˗2 to ˗14 dB) above 10 kHz, and ∠rP_ST decreased to about 0 above 12 kHz. rP_ST remained constant at these values to the highest frequencies measured (45 kHz).

Differential pressure across the CP ΔP_CP

The driving force for input to the cochlear traveling wave is the differential sound pressure across the CP. We compute the normalized differential sound pressure ΔP_CP near the cochlear base from simultaneous measurements of ${\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}}$_,P_ST, and P_near-TM by

$$\Delta {\mathbf{P}}_{\mathbf{\text{CP}}}=\frac{{\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}}-{\mathbf{P}}_{\mathbf{\text{ST}}}}{{\mathbf{P}}_{\mathbf{\text{near}}-\mathbf{\text{TM}}}}={\mathbf{G}}_{\mathbf{\text{MEP}}}^{\mathbf{T}}\left(1\hspace{0.17em}–\mathbf{r}{\mathbf{P}}_{\mathbf{\text{ST}}}\right).$$ (5)

ΔP_CP computed in each of the six ears by Eq. 4 [Fig. 4A] was generally quite similar to G_MEP measured in those ears without the ST hole (Fig. 2) or with the ST sensor (${\mathbf{G}}_{\mathbf{\text{MEP}}}^{\mathbf{T}}$). The mean ΔP_CP is representative of ΔP_CP in most individual ears, although the s.d. of the mean (shading) is larger than the s.d. of P_STn or G_MEP. The change in ∠ΔP_CP with frequency is consistent with a delay of about 50 μs.

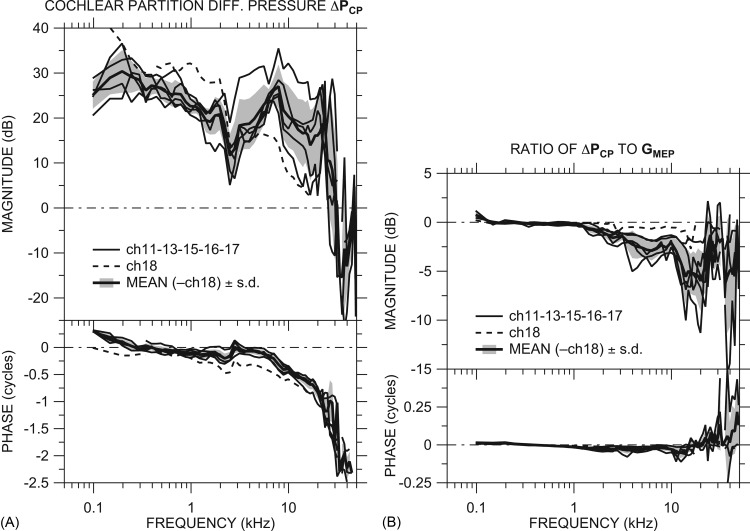
Figure 4.

(A) Differential sound pressure across the CP at the base ΔP_CP in dB in all ears: ch18 (dashed line) and others (thin solid lines). Also shown is the mean ΔP_CP (thick solid line) of all ears except ch18 ± 1 s.d. (shaded area). (B) Ratio of ΔP_CP to G_MEP in all ears: ch18 (dashed line), others (thin solid lines), and mean (omitting ch18) ±1 s.d. (thick solid line and shaded area). All panels: Top: Magnitude; bottom: Phase.

The ratio of ΔP_CP to ${\mathbf{G}}_{\mathbf{\text{MEP}}}^{\mathbf{T}}$ measured simultaneously [Fig. 4B] emphasizes the similarity between ΔP_CP and ${\mathbf{G}}_{\mathbf{\text{MEP}}}^{\mathbf{T}}$ at low frequencies and highlights the differences at high frequencies. Below 3 kHz ΔP_CP ≈ ${\mathbf{G}}_{\mathbf{\text{MEP}}}^{\mathbf{T}}$ because |P_ST| ≪ |${\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}}$| [|rP_ST| ≪ 1; see Fig. 3B]. At higher frequencies |ΔP_CP| < |${\mathbf{G}}_{\mathbf{\text{MEP}}}^{\mathbf{T}}$| by 5 to 10 dB because the magnitude and phase of P_ST and ${\mathbf{P}}_{\mathbf{V}}^{\mathbf{T}}$ are similar [|rP_ST| is about ˗10 dB and ∠rP_ST ≈ 0; see Fig. 3B]. ${\mathbf{G}}_{\mathbf{\text{MEP}}}^{\mathbf{T}}$ [and G_MEP, because ${\mathbf{G}}_{\mathbf{\text{MEP}}}^{\mathbf{T}}$ ≈ G_MEP; see Fig. 2C] is a good predictor of ΔP_CP at low frequencies but overestimates |ΔP_CP| at frequencies above a few kilohertz.

High-frequency correction to P_TM, G_MEP, and ΔP_CP

A question of recent interest concerns the presence or absence of some high-frequency limit on ME function. In this section we use an EC model developed earlier (Ravicz and Rosowski, 2012b, Fig. 4) to investigate limitations in our measurements of sound pressure near the TM on G_MEP and ΔP_CP at higher frequencies.

P_TM correction from the EC model

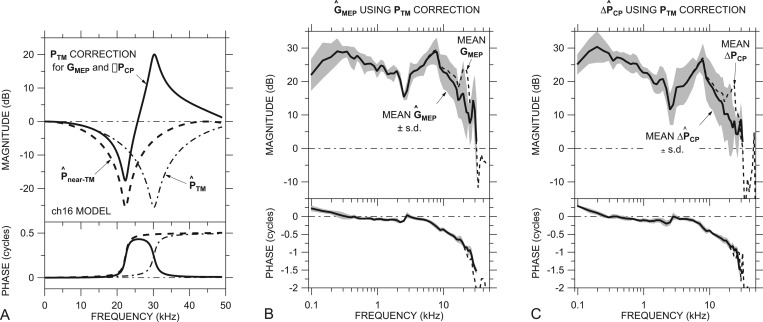
In a previous paper we presented a simple uniform-tube acoustical model of the chinchilla EC that successfully predicted the ratio of sound pressures measured at two points in the EC, at the P_near-TM measurement location near the TM and near the entrance to the sound coupler (see Ravicz and Rosowski, 2012b, Fig. 1). This model suggests that sound pressure at the near-TM location P_near-TM (1 to 1.5 mm from the TM) can differ substantially from the sound pressure at the TM P_TM at frequencies above 16 kHz. Figure 5A shows the model prediction of ${\widehat{\mathbf{P}}}_{\mathbf{\text{near}}-\mathbf{\text{TM}}}$ (dashed line) from Ravicz and Rosowski (2012b, Fig. 3) as well as the predicted sound pressure approximately at the TM location ${\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ (dotted-dashed line), 1 mm closer to the model EC termination in an example ear (ch16).12 [In Fig. 5A, both ${\widehat{\mathbf{P}}}_{\mathbf{\text{near}}-\mathbf{\text{TM}}}$ and ${\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ are normalized by the sound pressure at the termination of the model EC.] A comparison of these curves suggests that |P_near-TM| underestimates sound pressure 1 mm closer to the TM by more than 15 dB around 22 kHz and overestimates it by more than 15 dB around 30 kHz.

Figure 5.

(A) Correction factor c${\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ (solid line) to estimate sound pressure at the TM P_TM from measured P_near-TM in an example ear (ch16), computed as the inverse of the ratio of ${\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ (dotted-dashed line) to ${\widehat{\mathbf{P}}}_{\mathbf{\text{near}}-\mathbf{\text{TM}}}$ (dashed line; both normalized by sound pressure at the EC termination) in an ear-canal model. (B) Predicted mean ${\widehat{\mathbf{G}}}_{\mathbf{\text{MEP}}}$ ±1 s.d. (thick line and shading) and (C) predicted mean $\Delta {\widehat{\mathbf{P}}}_{\mathbf{\text{CP}}}$ ± 1 s.d. (thick line and shading) computed from P_V, P_ST, and P_near-TM using a c${\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ correction for each ear as in (A). The uncorrected G_MEP (Fig. 2) and ΔP_CP (Fig. 4) are shown by dashed lines. All panels: Top: Magnitude; bottom: Phase.

Figure 5A also shows a correction factor $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ for this ear, computed as $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ = (${\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$/${\widehat{\mathbf{P}}}_{\mathbf{\text{near}}-\mathbf{\text{TM}}}$)^˗1 (thick solid line), that could be applied to P_near-TM to compute a more accurate estimate of P_TM in ear ch16. Using the model, we developed a $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ correction for each ear from appropriate EC parameters (see Ravicz and Rosowski, 2012b, Table I) and computed improved estimates of G_MEP and ΔP_CP for each ear by

$${\widehat{\mathbf{G}}}_{\mathbf{\text{MEP}}} ={\mathbf{G}}_{\mathbf{\text{MEP}}}·\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$$ (6a)

and

$$\Delta {\widehat{\mathbf{P}}}_{\mathbf{\text{CP}}} =\Delta {\mathbf{P}}_{\mathbf{\text{CP}}}·\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}.$$ (6b)

The frequency of the peak in |$\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$| (27 to 42 kHz, depending on the ear) depends on the distance from the near-TM measurement location to the TM. We have made the conservative assumption that this distance was 1 mm; if the distance were actually closer to 1.5 mm, the peak in |$\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$| for ear ch16 (our example) would be closer to 36 kHz, and estimates of ${\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ near 30 kHz would be in error. Because of errors due to this uncertainty in the distance between the probe tube tip and the TM, we omit data above the frequency where the variation in $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ due to the distance uncertainty exceeds the s.d. of the mean G_MEP (roughly a factor of 2): 24 to 34 kHz, depending on the ear.

G_MEP and ΔP_CP with P_TM correction

The predicted mean ${\widehat{\mathbf{G}}}_{\mathbf{\text{MEP}}}$ and $\Delta {\widehat{\mathbf{P}}}_{\mathbf{\text{CP}}}$ ±1 s.d. are shown in Figs. 5B, 5C, respectively (solid line and shaded area in each panel). Also shown are the mean uncorrected G_MEP and ΔP_CP (dashed lines) from Figs. 2A, 4A, respectively. The effects of the $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ correction are to remove the peak in |G_MEP| and |ΔP_CP| between 21 and 28 kHz and to increase ∠G_MEP and ∠ΔP_CP between about 25 kHz and the highest frequency (31 kHz). Note that the rP_ST data of Fig. 3B are unaffected by uncertainties in EC sound pressure, as rP_ST is a ratio of scalae pressures and does not include EC sound pressure, so no $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ correction is necessary.

These predictions of ${\widehat{\mathbf{G}}}_{\mathbf{\text{MEP}}}$ and $\Delta {\widehat{\mathbf{P}}}_{\mathbf{\text{CP}}}$ represent our best estimates of G_MEP and ΔP_CP at high frequencies. Application of the $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$ correction removed a peak in G_MEP and ΔP_CP and reduced the frequency where the magnitude begins to roll off with frequency. We will use the notation G_MEP and ΔP_CP for ${\widehat{\mathbf{G}}}_{\mathbf{\text{MEP}}}$ and $\Delta {\widehat{\mathbf{P}}}_{\mathbf{\text{CP}}}$ in the following sections.

DISCUSSION

We have presented the results of measurements of sound pressure in the EC, vestibule, and ST in individual chinchillas and computed the CP differential pressure ΔP_CP. In this section we (a) examine the assumption that these sound pressures are primarily compressional or “fast-wave” pressures little influenced by basilar membrane motion (e.g., Olson, 1998; Dong and Olson, 2008). We (b) examine the effects of experimental conditions on our measurements and computed values and (c) compare our results to those from previous studies. We (d) discuss the implications of our rP_ST results and rP_ST computed from other studies on cochlear mechanics and (e) examine the advantages and limitations of the chinchilla model for further studies of the effects of cochlear pathologies and manipulations on hearing.

Validity of compressional-wave assumption

The intracochlear sound pressures we measured are the sum of a compressional cochlear pressure wave that propagates virtually instantaneously throughout the cochlea and a traveling pressure wave associated with motion of the CP (Dong and Olson, 2008).13 We assumed in Sec. 3 that our measured P_V and P_ST were due primarily to the compressional wave. P_V was measured in the vestibule just posterior to the OW. Our P_V and the SV pressure measured in gerbil at locations on the cochlear side of the OW showed no signs of the frequency-dependent nonlinearities or rapid phase accumulation associated with traveling-wave effects (Olson, 1998; Dong and Olson, 2008), so we believe that our measured P_V is dominated by the compressional wave and that the contribution of the traveling wave is negligible.

The likelihood that our P_ST measurements include contributions from the cochlear traveling wave varies in different frequency ranges, as the distance that the traveling wave penetrates ST at a given location varies with the ratio of stimulus frequency to the CF at that location (Olson, 2001; Yoon et al., 2006). As discussed above, signs of traveling wave contributions include ∠P_ST accumulation, |P_ST| level dependence, and |P_ST| notches in the half-octave below CF (Cooper and Rhode, 1996; Olson, 1998, 2001).

At frequencies well below CF at our P_ST measurement location, P_ST represents the compressional wave, as P_ST was measured relatively far from the CP, and the traveling wave should be detectable only very close to the CP (Olson, 2001; Yoon et al., 2006). In this “long-wavelength” regime, the relationship between P_V and P_ST can be described by lumped model elements (Ravicz et al., 2010). Figure 3B shows that the phase angle difference between P_ST and P_V (∠rP_ST) was always within ±0.25 cycles (except below at the lowest frequencies) and that ∠rP_ST tended not to accumulate with frequency, consistent with a lumped-element model.

Near CF (∼12 kHz), traveling wave effects extend further into ST from the CP (Olson, 2001; Yoon et al., 2006).14 We saw little evidence of level dependence in P_ST but the abrupt increase in |P_ST| and decrease in ∠P_ST near 12 kHz might be due to a contribution from the traveling wave. These are discussed more in Sec. 4D below.

At frequencies above CF, the traveling wave is absent, and our P_ST represents the compressional wave (perhaps including a contribution from a fast evanescent wave invoked to explain observations of non-zero basilar membrane motion above CF; de La Rochefoucauld and Olson, 2007). |rP_ST| was about ˗6 dB in all ears, similar to its value near CF (see above), and P_V and P_ST were in phase (∠rP_ST ≈ 0), although the variability of both |rP_ST| and ∠rP_ST was higher, perhaps due to noise. The result that |rP_ST| was constant and ∠rP_ST ≈ 0 at these highest frequencies is consistent with P_V and P_ST determined by the compressional wave.

It should be noted that the condition that the compressional wave propagates virtually instantaneously throughout the cochlea does not imply that the sound pressure is uniform throughout the cochlea. Because the RW impedance is much lower than the cochlear input impedance at moderate and high frequencies (compare Nedzelnitsky, 1980 and Lynch et al., 1982 in cat; Slama et al., 2010 and Ravicz et al., 2010 in chinchilla), the RW acts as a zero-pressure boundary condition, and intracochlear pressure must vary continuously from P_V at the OW to approximately zero at the RW. The observation that |P_ST| ≪ |P_V| below about 2 kHz supports this view. This pressure gradient has been predicted to vary along the CP in a non-uniform and frequency-dependent fashion, as it is affected by the local CP impedance (e.g., Peterson and Bogert, 1950; Lighthill, 1981) as well as the acoustic impedances of the enclosed scalae (Puria and Allen, 1991) and the helicotrema (Dallos, 1970; Lynch et al., 1982). We will discuss the implications of variations in rP_ST in Sec. 4D below.

Effect of experimental conditions on measured quantities

For these experiments it was necessary to make two large holes in the auditory bulla for access to the stapes, OW and RW, and stapedius muscles (see Sec. 2A). The measurement of P_V required that a hole be made into the cochlear vestibule, and the measurement of P_ST required that an additional hole be made into ST.

Estimated effect of opening the ME

Measuring the effect of opening the ME on P_V was difficult, as we needed to open the ME to introduce the P_V sensor into the IE. It has been shown (e.g., Zwislocki, 1962; Ravicz et al., 1992; Huang et al., 1997) that the impedance related to the compression and rarefaction of the air in the ME cavities (air spaces) can be considered to act “in series” with the impedance of the TM, ossicles, and cochlea; consequently, variations in ME cavity impedance, for instance, by opening holes in the bulla, have no effect on the cochlear input impedance (the ratio of P_V to stapes velocity). This independence of the cochlear input impedance means that the effect of opening the ME on P_V is the same as the effect on stapes velocity.

Ruggero et al. (1990) used umbo velocity measurements and previous studies of cochlear microphonic to infer that the effect of opening the ME on stapes velocity was the same as the effect on umbo velocity, which they showed was significant only at low frequencies (less than a factor of 2 above 300 Hz; Ruggero et al., 1990, Figs. 56). It has been shown that the resonant frequency between the compliance of the air within the ME cavities and the mass of the air in the bulla holes varies with hole size (Rosowski et al., 2006). Above the resonant frequency, the effects of opening the hole are insignificant. Although we have no information on the size of the bulla hole or hole-cavity resonant frequency in the Ruggero et al. (1990) experiments, we assume that the resonant frequency for effects on stapes velocity and ME admittance is the same for a given hole size. The bulla hole size used in this and previous studies caused an increase in ME input admittance magnitude and a ˗0.25 cycle phase shift below 1 kHz (Ravicz and Rosowski, 2012b; Rosowski et al., 2006), and we assume that the effect on stapes velocity and therefore P_V was similar.

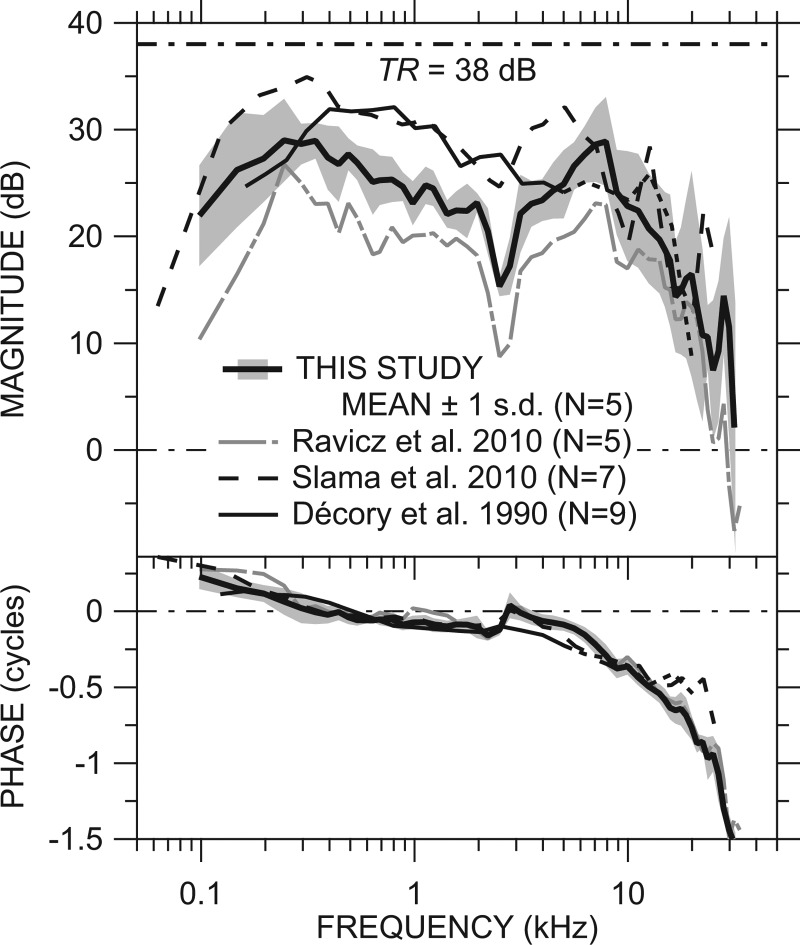
Figure 6.

Comparison of our mean G_MEP with ST intact [from Fig. 5B; thick line] ±1 s.d. (shading) to previous measurements of ME gain in chinchilla by Ravicz et al. (2010, Fig. 6; sensor in ST; gray long-dashed-dotted line), Slama et al. (2010, Fig. 8; dashed line), and Décory et al. (1990, Fig. 4; thin black line solid or dotted above 5 kHz, see text) and the anatomical “transformer ratio” TR = 38 dB (dotted-dashed line). The ME was opened widely for all measurements. Top: Magnitude; bottom: Phase.

Because P_V is the principal driving force for P_ST (Nedzelnitsky, 1980), the effect of opening the ME on P_ST is expected to be similar to the effect on P_V. P_ST might also be affected by sound pressure outside the RW (Peake et al., 1992) but our measurements of ME sound pressure outside the OW [Fig. 2B] and RW are at least 40 dB lower than P_V, and measurements of ME sound pressure with an intact or open ME (personal communication from D. C. Chhan, 2012) demonstrate that the effects of ME sound pressures outside the OW and RW are negligible.

We did observe a magnitude notch and phase ripple in G_MEP and P_STn near 2.5 kHz, the frequency of a resonance observed in the ME input admittance (Ravicz and Rosowski, 2012b) between the acoustic mass of the bulla hole and the acoustic compliance of the air in the ME.

Effect of vestibule hole and sensor on P_V

Because our technique for measuring P_V required making a hole into the vestibule, we were unable to determine the effect of the IE hole and vestibule sensor on P_V, and the narrow OW niche precluded sealing the hole around the sensor.15 Previous measurements in cat (Lynch et al., 1982) indicate that the hole will decrease the cochlear input impedance and therefore P_V at low frequencies. The theoretical impedance of the hole increases with frequency (e.g., Beranek, 1986; Slama et al., 2010), so its effect on the cochlear input impedance and therefore P_V should decrease as frequency increases. Since the impedance of the hole depends inversely on a high power of its radius (or, in this case, on the distance between the edge of the hole and the sensor; e.g., Backus, 1975; Beranek, 1986), larger holes were expected to have larger effects. For this reason, we tried to make the hole as close to the sensor size as possible but the resulting hole was generally two times the diameter of the sensor or more.

Several observations suggest that the effect of the vestibule hole is most significant at low frequencies and less important at higher frequencies: (a) Withdrawing the sensor from the vestibule (leaving the hole open) caused a 5 to 9 dB reduction in |P_STn| below 1 kHz but very little change at higher frequencies. (b) Slama et al. [2010, Fig. 3C] were able to increase low-frequency G_MEP slightly in one ear by sealing around the sensor but saw no effect above a few hundred hertz. (c) Ravicz et al. (2010) observed that in ears where the bone near the OW cracked (equivalent to a large vestibule hole), G_MEP was substantially lower at frequencies below 1 kHz than in other ears where the bone was not cracked but very similar at higher frequencies. (d) Opening the IE and inserting the vestibule sensor caused an increase in stapes velocity that was largest (a factor of 3 ≈ 10 dB) below 500 Hz (Ravicz et al., 2011). The size of the effect of the hole on low-frequency G_MEP is not known, but a mathematical analysis suggests that the hole reduces |G_MEP| by 15 dB at 100 Hz and has a negligible effect above 250 Hz (Ravicz and Rosowski, 2012a).

The pressure sensor itself could affect IE pressure measurements if its impedance were comparable to or lower than the cochlear input impedance (e.g., Olson, 1998). The impedance of the sensor's enclosed air volume (<1 nl), a conservative estimate of sensor impedance, is at least a factor of 10 larger than the cochlear input impedance (e.g., Slama et al., 2010) at frequencies below 30 kHz; therefore, the effect of the sensor on the measured IE pressures is negligible.

We did not find a strong correlation between the size of the vestibule hole and aspects of low-frequency |G_MEP|. There was a weak correlation between the hole area and the frequency of the low-frequency |G_MEP| peak but we saw no correlation between the hole area and G_MEP magnitude.

During the experiment, fluid frequently collected in the OW niche, which could conceivably have added an additional mass load on the ossicular chain and reduced P_V (and therefore P_ST) at high frequencies. The effect of OW fluid contributes to the variability of G_MEP (and therefore P_STn) in individual ears but should not affect rP_ST. The RW remained above the fluid level and dry, so P_ST should not have been affected directly by OW fluid.

Effect of ST hole and sensor on P_V and P_ST

Opening ST and inserting another sensor to measure P_ST had only a small effect on P_V, as shown in Fig. 2C above. This result is reasonable: (a) The hole for the ST sensor was generally a closer fit to the sensor and longer than the vestibule hole (the bone of the otic capsule was thicker than the vestibular wall), which would make its impedance very high and make the hole appear acoustically closed at the frequencies measured; and (b) most effects of the hole are probably masked by the effect of the low-impedance RW (see Lynch et al., 1982, in cat).

It was not possible to measure the effect of the ST sensor on P_ST for the reason described above for P_V. The observation that |P_ST| > |P_near-TM| at very low frequencies [|P_STn| > 0 dB below 250 Hz; Fig. 3A], where the effect of the ST hole should be maximal (by the reasoning in Sec. 4B2 above), suggests that the effect of the ST hole on P_ST was small.

Comparison of measured quantities to previous studies

ME pressure gain

The mean G_MEP in 5 ears [including high-frequency correction, from Fig. 5B; solid black line] ±1 s.d. (shading) is compared to previous measurements of ME gain in chinchilla in Fig. 6. In all studies the ME was opened widely. The mean |G_MEP| in this study was about 5 dB higher than that from Ravicz et al. (2010), although the frequency dependence was remarkably similar, which supports the idea that the previous Ravicz et al. (2010) data included an uncertainty in the overall sensor sensitivity S₀ due to uncompensated temperature effects16 (Ravicz et al., 2010; see also Sec. 2C2 above).

The mean |G_MEP| in this study is generally about 5 dB lower than the means presented by Slama et al. (2010, Fig. 2 and Fig. 8; dotted-dashed line) and Décory et al. (1990; gray line) below 5 kHz and more similar to the Décory data above 3 kHz and to the Slama data above 6 kHz. Part of the difference between our G_MEP and the ME gain of Décory et al. (1990) may have to do with the measurement location: In the Décory et al. (1990) study, sound pressure was measured in scala vestibuli (SV) at a location about 5.5 mm from the OW, which is near the best place for a 5-kHz signal. Décory et al. (1990) suggest that their measured SV sound pressure at higher frequencies (shown as a dotted line) might not be a good representation of SV sound pressure at the stapes.

Figure 8.

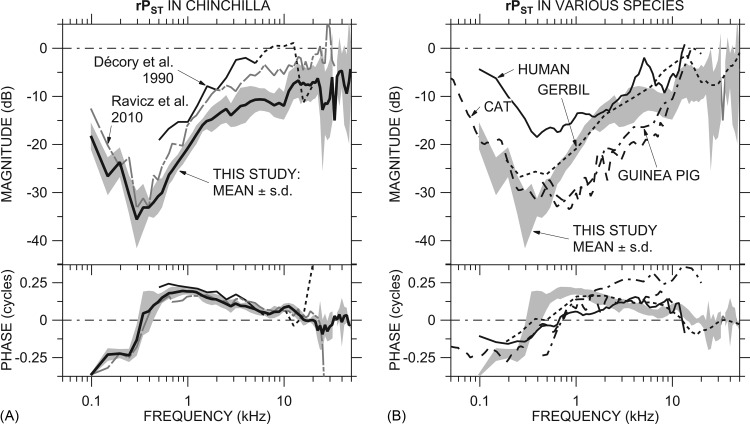
Comparison of our mean rP_ST to data from previous studies. (A) Comparison of the mean rP_ST ± 1 s.d. [Fig. 3B; thick line and shading] to rP_ST in Ravicz et al. (2010, Fig. 4; gray dotted-dashed line) and rP_ST computed from SV and ST sound pressures (not necessarily in the same ears) from Décory et al. (1990, Figs. 4 and 5; thin black line solid or dashed >5 kHz, see Sec. 4C1). (B) Comparison of rP_ST ± 1 s.d. (shading) to that computed from SV and ST sound pressures (not necessarily in the same ears) in cat (Nedzelnitsky, 1980; dashed line), human temporal bones (Nakajima et al., 2009; solid line), guinea pig (Décory et al., 1990; dotted-dashed line), and gerbil (Olson, 2001; dotted line). The ME was opened widely for all measurements. Both panels: Top: Magnitude; bottom: Phase.

Our mean |G_MEP| rolled off less sharply at low frequencies than ME gain in other studies, and the roll-off began at a lower frequency than in most other studies. Accordingly, our ∠G_MEP was closer to zero and crossed zero at a lower frequency than in the other studies. The Ravicz et al. (2010) roll-off was at a similar frequency (∼250 Hz) but was much sharper. To the extent that the low-frequency roll-off seems to be related to the size of the vestibule hole and existence of cracks or other damage to the petrous bone (Slama et al., 2010; Ravicz et al., 2010), this result suggests that the IEs in this study were in a more intact state for the G_MEP measurements than those in the previous studies.

Our mean |G_MEP| was comparable to the other studies at high frequencies (above 8 kHz) but our ∠G_MEP accumulated much faster than that of Décory et al. (1990) and Slama et al. (2010) above 12 kHz. Our mean |G_MEP| was higher than that in the Ravicz et al. (2010) study above 20 kHz, which might also be a result of better experimental technique.

Figure 6 also includes the “anatomical transformer ratio” (TR) (Wever and Lawrence, 1954; Rosowski, 1994). The TR is the product of (1) the ratio of the areas of the pars tensa of the TM and the stapes footplate (“area ratio;” 56 and 2 mm², respectively) and (2) the ratio of the lengths of the malleus manubrium and incus long process (“lever ratio” = 2.84; all values from Vrettakos et al., 1988); i.e.,

$$\text{TR}=\frac{\hspace{0.17em}\text{TM}\hspace{0.17em}\text{area}}{\text{Footplate}\hspace{0.17em}\text{area}}\times \frac{\text{malleus}\hspace{0.17em}\text{length}}{\text{incus}\hspace{0.17em}\text{length}}=\hspace{0.17em}\text{area}\hspace{0.17em}\text{ratio}\hspace{0.17em}\times \hspace{0.17em}\text{lever}\hspace{0.17em}\text{ratio} \approx \hspace{0.17em}79\hspace{0.17em}=\hspace{0.17em}38\hspace{0.17em}\text{dB}\hspace{0.17em}.$$ (7)

The mean |G_MEP| measured in this study is about 8 to 10 dB below the anatomical TR over much of the frequency range and is even further below TR near 2.5 kHz and above 10 kHz. The observation that TR overestimates |G_MEP| is consistent with observations in other species (Rosowski, 1994; Puria et al., 1997) and supports the idea that the mechanical properties of the middle and IE act to limit the ear's transformer action (Wever and Lawrence, 1954; Ravicz et al., 2010).

ST sound pressure and CP differential pressure

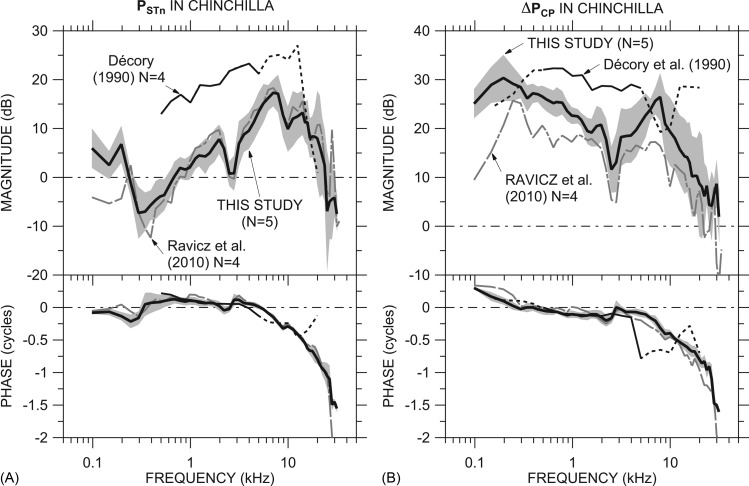
Our mean P_STn (of five ears from Fig. 3), adjusted by the high-frequency correction as described for G_MEP and ΔP_CP in Sec. 3D above, is compared to that from two previous studies in Fig. 7A. Our mean P_STn is very similar to that of Ravicz et al. (2010) above 250 Hz and has a slightly higher magnitude at low and high frequencies than that measured in the previous study. The magnitude of the normalized P_ST from Décory et al. (1990) is substantially higher than our |P_STn| below 12 kHz. The phase was similar to our ∠P_STn below 12 kHz. As for P_V above, the Décory et al. (1990) data were measured at a more apical location than ours, approximately 5.5 mm from the RW; hence, we show the Décory et al. (1990) data with a dotted line above 5 kHz (see Sec. 4B2 above).

Figure 7.

Comparison of our mean P_STn and ΔP_CP to data from previous studies. (A) Comparison of our mean P_STn ± 1 s.d. [computed from Fig. 3A; thick line and shading] to previous measurements by Ravicz et al. (2010, Fig. 3; gray dotted-dashed line) and Décory et al. (1990, Fig. 5; thin black line solid or dotted >5 kHz, see Fig. 6). (B) Comparison of our mean ΔP_CP ± 1 s.d. [Fig. 5C; thick line and shading] to previous measurements by Ravicz et al. (2010, Fig. 8; gray dotted-dashed line) and to that computed from measurements of vestibular and ST sound pressure (not necessarily in the same ears) by Décory et al. [1990; thin black line solid or dotted <500 Hz (see text) and >5 kHz (see Fig. 6)]. The ME was opened widely for all measurements. Both panels: Top: Magnitude; bottom: Phase.

Our mean ΔP_CP [computed from five ears, from Fig. 5C] is compared to ΔP_CP presented in Ravicz et al. (2010) and that computed from Décory et al. (1990, Figs. 45) in Fig. 7B. [The Décory et al. (1990) data above 5 kHz are shown by a dotted line as explained above.] The differences between our ΔP_CP and ΔP_CP in the previous Ravicz et al. (2010) study are comparable to those between G_MEP in the two studies (Fig. 6). Below about 3 kHz, where |P_ST| ⪡ |P_V|, |ΔP_CP| computed from the Décory et al. (1990) study17 was 8 to 10 dB higher than ours (consistent with their G_MEP; Fig. 6). (We extrapolate the computation to lower frequencies by assuming that ΔP_CP ≈ P_V; dotted line.) At higher frequencies, ΔP_CP from the Décory et al. (1990) study was much different than ours: For example, the Décory |ΔP_CP| decreases above 4 kHz to a dip near 8 kHz where our data increase to a |ΔP_CP| peak, and the Décory ∠ΔP_CP data vary in a fashion opposite to ours above 4 kHz. Our ΔP_CP was computed in each individual ear while that for Décory et al. (1990) was computed from means in different ears (although there may have been some overlap), but this probably does not explain all of the difference.

A comparison of Fig. 7B with Fig. 8 from Ravicz et al. (2010) shows other similarities among our ΔP_CP and that computed for other species from other studies. As in cat, guinea pig, and gerbil, |ΔP_CP| in chinchilla has a broad low-frequency peak and a plateau that extends to 5 kHz or beyond.

In the results we present here, the magnitude of ΔP_CP decreases nearly to 0 dB near 28 kHz. This 0-dB-gain frequency is higher than that in previous ΔP_CP measurements (20 kHz; Ravicz et al., 2010) and is approximately equal to the high-frequency limit of chinchilla hearing (29 kHz; Rosowski, 1992). The rapid decrease of |ΔP_CP| with frequency in this frequency range is similar to the rapid decrease in auditory sensitivity shown by the steep positive high-frequency slope to the chinchilla audiogram (e.g., Miller, 1970).

Ratio of ST and vestibular sound pressures

Figure 8A compares our mean rP_ST (from individual ears) ± s.d. to rP_ST from the previous study (Ravicz et al., 2010) and that computed from the mean P_ST and P_V presented by Décory et al. (1990). The 2010 rP_ST has a similar frequency response to rP_ST from this study between 100 Hz and 25 kHz but |rP_ST| was higher in the 2010 study because |G_MEP| was lower. The minimum in |rP_ST| near 300 Hz and ∠rP_ST < ˗0.25 cycles below 200 Hz are common to both studies.

Over the frequency range where the Décory et al. (1990) measurements overlap ours (0.5 to 20 kHz), ∠rP_ST was quite similar. The |rP_ST| computed from the Décory data is 10 to 15 dB higher than ours and exceeds 0 dB (|P_STn| > |G_MEP|) between 6 and 12 kHz. [The Décory et al. (1990) data above 5 kHz are shown by a dotted line as explained in Sec. 4C1 above.] This difference in rP_ST between this study and Décory et al. (1990) will be discussed further in Sec. 4D.

The rP_ST we observed has many similar features to that computed from P_ST and P_V in other species [Fig. 8B]. rP_ST in the other species shows the low-frequency |rP_ST| minimum and ∠rP_ST transition, although the ∠rP_ST slope with frequency in the transition is less steep in most other species, implying that the resonant structures (see Sec. 3B2 above) are more highly damped in other species. |rP_ST| was generally higher in human than in chinchilla and generally lower in cat and guinea pig than in chinchilla below about 8 kHz. ∠rP_ST was higher at frequencies above 1 kHz in guinea pig than in the other species, and |rP_ST| in guinea pig also exceeded 0 dB at a high-frequency point, similar to other observations in this species (Dancer and Franke, 1980; Dancer et al., 1997). rP_ST in gerbil was generally similar to rP_ST in chinchilla across the entire frequency ranges of measurements.

Implications of rP_ST and scalae pressures for cochlear mechanics

High-frequency limit on ΔP_CP

The ratio rP_ST contains a significant amount of information about cochlear mechanics. P_ST is the “back pressure” that reduces ΔP_CP for a given P_V: The more similar |P_STn| is to |G_MEP| (the closer |rP_ST| is to 0 dB), the greater the difference between G_MEP and ΔP_CP [see Eq. 5 and Sec. 3B above]. The high compliance of the RW serves to reduce P_ST at low frequencies so that most of P_V goes into moving the CP, although P_ST at the lowest frequencies may be due to the finite RW compliance (Nedzelnitsky, 1980). At higher frequencies, P_ST is affected by the mass of the ST perilymph between our measurement site and the RW. The high RW compliance makes P_ST just inside the RW effectively zero (e.g., Nedzelnitsky, 1980) but models of the region between the RW and the CP indicate that the mass of the ST fluid between the RW and the measurement location can explain the nonzero P_ST (Olson, 2001; Ravicz et al., 2010). The value of rP_ST [˗10 dB or higher; Fig. 3B] and the corresponding reduction in |ΔP_CP| relative to |G_MEP| above 4 kHz [Fig. 4B] indicate that the mass of ST perilymph is a limitation on high-frequency ΔP_CP and hence cochlear sensitivity.

Possible evidence of traveling-wave effects

We argued in Sec. 4A above that P_ST and P_V are due primarily to the compressional cochlear wave at most frequencies. Near 12 kHz, the presumed CF of the P_ST measurement location, rP_ST was different than at lower and higher frequencies: |rP_ST| increased abruptly to about ˗6 dB in all ears [see Fig. 3B], and ∠rP_ST reversed its downward trend with frequency and showed a broad peak at about +0.1 cycles. It is noteworthy that a similar magnitude jump is seen in rP_ST computed from the Décory et al. (1990) mean P_ST and P_V data [Fig. 8A] but shifted to lower frequencies: ∼ 5 kHz, the CF of their measurement location. As this rP_ST behavior seems to be linked to CF, it could show the influence of the traveling wave.

Usefulness of this preparation for studying IE function and pathology

The ability to measure sound pressures inside the cochlear scalae provides opportunities to study changes in cochlear mechanics and hearing due to pathological or unconventional methods of stimulating the cochlea, especially in preparations such as temporal bones that provide no neural response. For example: The effects of a semicircular canal dehiscence can be quantified at the level of the mechanical drive to the CP; reverse cochlear stimulation can be studied on the benchtop; and the mechanisms of stimulation of the CP by different modes of bone conduction can be compared.

The limitation on this preparation is sealing of the holes into the cochlea for the pressure sensors at low frequencies. Mathematical techniques may provide a description of the effects of the cochlear holes sufficient for a correction (Ravicz and Rosowski, 2012a), or different approaches to the cochlear vestibule (for example, through a posterior cranial fossa; Chhan et al., 2012) may overcome this problem.

SUMMARY AND CONCLUSIONS

• (1)We have measured vestibular and ST sound pressures P_V and P_ST with more care for calibration (Fig. 1) and measurement details than in previous studies. We have used these data and measurements of sound pressure near the TM to compute ME pressure gain G_MEP (Fig. 2), normalized ST sound pressure P_STn (Fig. 3), and the CP differential pressure at the cochlear base ΔP_CP (Fig. 4) together in individual animals. We have used a previously-developed EC model to compute a better estimate of G_MEP and ΔP_CP (Fig. 5) at frequencies above 15 kHz.
• (2)Because |P_V| ≫ |P_ST| at low frequencies and P_V ≈ P_ST at high frequencies, G_MEP is a good estimate of ΔP_CP at low frequencies but overestimates ΔP_CP by a factor of 1.5 to 2 above 2 to 3 kHz (Fig. 4).
• (3)G_MEP and ΔP_CP presented here show many similarities to those presented in previous studies in chinchilla and extend those data to higher frequencies. Like other G_MEP measurements in chinchilla and other species, the magnitude of our G_MEP is smaller than the predicted anatomical TR (e.g. Rosowski, 1994; Puria et al., 1997), with a magnitude within the range of the other studies in chinchilla (Fig. 6). P_STn presented here is very similar to a preliminary study (Ravicz et al., 2010) but our P_STn and ΔP_CP differ substantially from results of a previous study (Décory et al., 1990) in which P_ST was measured at a more apical location (Fig. 7).
• (4)The ratio of P_ST to P_V provides insight into cochlear mechanics. Low-frequency rP_ST reveals the behavior of the RW. Near the CF of the P_ST measurement location rP_ST provides insight into how rP_ST and the differential pressure across the CP vary along the cochlea (Fig. 8).
• (5)The magnitudes of both G_MEP and ΔP_CP are shown to decrease sharply to ∼0 dB as stimulus frequency increases above 20 kHz, a frequency near the high-frequency limit of audibility in chinchilla. Such behavior is consistent with a high-frequency limit to the processes that conduct sound to the IE and CP. The measured high-frequency roll-off depends on the estimate of stimulus sound pressure at the TM in the high-frequency range.
• (6)Our preparation and technique is useful for several avenues of IE research at moderate and high frequencies and, with small modifications, could be more useful for low-frequency investigations as well.

NOMENCLATURE

c

Speed of sound in water

CF

Characteristic frequency

CP

Cochlear partition

$\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{\text{TM}}}$

P_TM correction factor from an EC model

EC

Ear canal

f

Frequency (Hz)

f₀

Frequency at which pressure sensor sensitivity S₀ is evaluated

G_MEP

Middle-ear pressure gain

h

Immersion depth of sensor in calibration vial

IE

Inner ear

l

Depth of water in calibration vial

ME

Middle ear

OW

Oval window

P

Sound pressure

P_ME

Sound pressure in the ME air space

P_near-TM

Sound pressure measured near the TM

P_ST

Sound pressure in scala tympani near the RW

P_STn

Sound pressure P_ST normalized by P_TM

P_TM

Sound pressure at the TM

P_V

Sound pressure in the cochlear vestibule

ΔP_CP

Sound pressure differential across the cochlear partition

rP_ST

Ratio of P_ST to P_V with a sensor in ST

RW

Round window

s.d.

Standard deviation of the mean

S_f

Pressure sensor frequency response

S_p

Pressure sensor calibration as a function of f

S₀

Pressure sensor sensitivity at a given frequency f₀

ST

Scala tympani

TM

Tympanic membrane

TR

Anatomical transformer ratio

v_sens

Pressure sensor output voltage

$\ddot{\mathbf{X}}$

Acceleration

ρ_w

Density of water

ω

Frequency (in radians/s) = 2πf

Real variables, e.g., S₀, are shown in italics, and complex variables, e.g., P_TM, are shown in bold type. All complex variables are functions of frequency. Superscript ^T refers to sound pressure measured with a sensor in scala Tympani. The circumflex (^) denotes quantities estimated from an EC model (Ravicz and Rosowski, 2012b).