Commissioning dose computation models for spot scanning proton beams in water for a commercially available treatment planning system

Abstract

Purpose: To present our method and experience in commissioning dose models in water for spot scanning proton therapy in a commercial treatment planning system (TPS).

Methods: The input data required by the TPS included in-air transverse profiles and integral depth doses (IDDs). All input data were obtained from Monte Carlo (MC) simulations that had been validated by measurements. MC-generated IDDs were converted to units of Gy mm²/MU using the measured IDDs at a depth of 2 cm employing the largest commercially available parallel-plate ionization chamber. The sensitive area of the chamber was insufficient to fully encompass the entire lateral dose deposited at depth by a pencil beam (spot). To correct for the detector size, correction factors as a function of proton energy were defined and determined using MC. The fluence of individual spots was initially modeled as a single Gaussian (SG) function and later as a double Gaussian (DG) function. The DG fluence model was introduced to account for the spot fluence due to contributions of large angle scattering from the devices within the scanning nozzle, especially from the spot profile monitor. To validate the DG fluence model, we compared calculations and measurements, including doses at the center of spread out Bragg peaks (SOBPs) as a function of nominal field size, range, and SOBP width, lateral dose profiles, and depth doses for different widths of SOBP. Dose models were validated extensively with patient treatment field-specific measurements.

Results: We demonstrated that the DG fluence model is necessary for predicting the field size dependence of dose distributions. With this model, the calculated doses at the center of SOBPs as a function of nominal field size, range, and SOBP width, lateral dose profiles and depth doses for rectangular target volumes agreed well with respective measured values. With the DG fluence model for our scanning proton beam line, we successfully treated more than 500 patients from March 2010 through June 2012 with acceptable agreement between TPS calculated and measured dose distributions. However, the current dose model still has limitations in predicting field size dependence of doses at some intermediate depths of proton beams with high energies.

Conclusions: We have commissioned a DG fluence model for clinical use. It is demonstrated that the DG fluence model is significantly more accurate than the SG fluence model. However, some deficiencies in modeling the low-dose envelope in the current dose algorithm still exist. Further improvements to the current dose algorithm are needed. The method presented here should be useful for commissioning pencil beam dose algorithms in new versions of TPS in the future.

INTRODUCTION

There has been increased interest in proton therapy in recent years, primarily due to its ability to spare healthy tissues beyond the range of the proton beam. Several approaches to deliver proton therapy are available, including double scattering, uniform scanning, and spot scanning.^{1, 2} In spot scanning delivery, a proton pencil beam (spot) is magnetically scanned in lateral directions, creating a large field without requiring scattering elements into the beam path.^{3, 4} Monoenergetic pencil beams with different energies from an accelerator can be stacked to create the desired dose distribution along the beam direction. Neither an aperture nor a compensator is necessary for spot scanning proton therapy (SSPT) delivery.⁴

At The University of Texas MD Anderson Cancer Center, the delivery system for SSPT has been commissioned⁵ and used for treating patients since May 2008. The first group of patients treated were prostate patients.⁶ The scanning nozzle delivers the discrete spot scanning “spot-by-spot” and energy “layer-by-layer.”^{5, 7} The energy, spot position, and number of monitor units (MUs) of each spot are determined by a treatment planning system (TPS). That is, absolute doses must be calculated by the TPS for spot scanning delivery. The TPS used in this work employs the same fluence-dose calculation method used for double scattering, uniform scanning, and spot scanning beam. The difference between different delivery methods is accounted by different in-air fluence modeling.^{8, 9, 10} Previous dose algorithms for SSPT normally used a single Gaussian (SG) function to describe the shape of an in-air lateral profile of an individual pencil beam.^{4, 11} However, our recent works have demonstrated that a SG function could not describe in-air lateral profiles well for an individual pencil beam from our scanning nozzle.^{12, 13, 14, 15} The TPS vendor, therefore, implemented a double Gaussian (DG) fluence model to account for the spot fluence due to contributions of large angle scattering from the devices within the scanning nozzle. In this work, we present our method and experience of commissioning a pencil beam algorithm with DG fluence model. All optional devices in the scanning nozzle,⁷ including scatter device, energy filter, energy absorber, and treatment aperture, are not considered.

MATERIALS AND METHODS

Discrete spot scanning beam delivery system

The details of our delivery system have been described in Refs. ⁵ and ⁷. Only a brief description is provided here. There are 94 energies between 72.5 and 221.8 MeV, corresponding to proton ranges of 4.0–30.6 g/cm² in water, available from our synchrotron in the proton therapy facility (PROBEAT Proton Beam Therapy System, Hitachi America, Ltd., Tarrytown, NY) at MD Anderson Cancer Center. The maximum field size is 30 × 30 cm at isocenter. A schematic of the scanning nozzle is shown in Fig. 1. Briefly, after entering the nozzle, a pencil beam goes through the profile monitor first. Then the X and Y scanning magnets direct the beam to the desired lateral position. The main dose monitor determines how long the spot will remain in the position, and the spot position monitor checks the position of the spot. For the scanning nozzle, a MU is defined on the basis of a fixed amount of charge collected in the main dose monitor ionization chamber, corresponding to a physical dose to water of 1 cGy, which was determined using the International Atomic Energy Agency (IAEA) TRS 398 protocol¹⁶ under a specific reference condition.⁵ The minimum and maximum MU values for delivering each spot are 0.005 and 0.04, respectively.^{5, 7, 17} The resolution is 0.0001 MU, which is 1/50 of the minimum MU.⁵ Absorbed doses at the Bragg peak irradiated by a single spot with 0.04 MU varies from 1.6 to 4.4 cGy, depending on the energy of the pencil beam. The proton beam with the energy of approximate 160 MeV has the maximum Bragg peak absorbed dose.⁵

Figure 1.

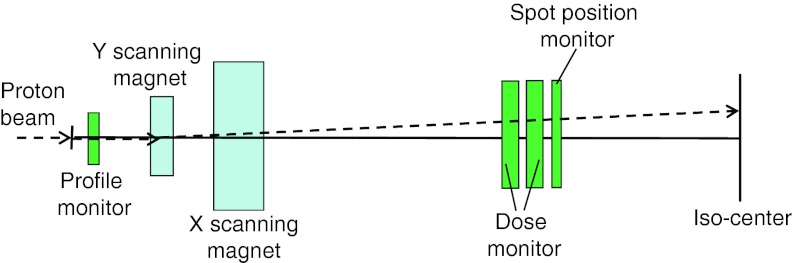
Schematic of the scanning nozzle illustrating its major components.

Treatment planning system

The TPS used in this work was Eclipse version 8.120 and 8.917 (Varian Medical Systems, Palo Alto, CA) with a proton module for double scattering and spot scanning delivery. A pencil beam algorithm is used by the TPS,^{8, 9, 10, 18, 19} which is briefly described in Sec. 2B1. The input data required for the spot scanning beam are integral depth doses (IDDs) and in-air lateral profiles (see Sec. 2B3). The SG fluence model was only used by Eclipse version 8.120.⁶ The DG fluence model has been available since version 8.908.

Pencil beam algorithm

The dose is calculated using a pencil beam algorithm, individual proton beamlets, $D_{E_k}^{\mathrm{Beamlet}}(x,y,d\left(z\right),)$, convolved with the fluence, ${\Phi }_{E_k}(x,y,z)$, at the position of the beamlet for the kth energy layer, E_k. A beamlet is the 3D dose distribution of an infinitesimal pencil beam of protons in a water phantom.⁹ Let the beam central axis be the z-axis, the isocenter plane be defined at z = 0 cm, the positive z toward the proton source, and x and y axes be the transverse coordinates. The general 3D dose distribution can be written as follows:^{8, 9, 10, 18, 19}

$$\begin{array}{ccc}\hfill D(x,y,z)& =& \sum _{E_k}\sum _{\mathrm{Beamlet}j}{\Phi }_{E_k}(x_j,y_j,z)D_{E_k}^{\mathrm{Beamlet}}\hfill \\ & & \times (x-x_j,y-y_j,d\left(z\right)),\hfill \end{array}$$ (1)

where d(z) is the water equivalent depth of position z along the beamlet direction. Particles contributing to the proton beam absorbed dose include primary protons and secondary particles. Primary protons include protons that only undergo elastic interactions with electrons and elastic proton-nucleus scatterings in the medium. Secondary particles are generated through nonelastic nuclear interactions and include secondary protons and other fragments (deuterons, tritons, alphas, neutrons, etc.).¹⁴ The beamlet dose distribution is assumed to have radial symmetry and can be written as^{10, 18, 19}

$$\begin{array}{ccc}\hfill D_{E_k}^{\mathrm{Beamlet}}\left(r,d\left(z\right)\right)& =& \frac{1}{{\rho }_{{\mathrm{H}}_2\mathrm{O}}}[S_{\mathrm{pp}}\left(d\left(z\right)\right)K_{\mathrm{lat},\mathrm{pp}}(r,d\left(z\right))\hfill \\ & & +S_{\mathrm{sp}}\left(d\left(z\right)\right)K_{\mathrm{lat},\mathrm{sp}}(r,d\left(z\right))],\hfill \end{array}$$ (2)

where r is the radial coordinate in the transverse plane, $r=\sqrt{x^2+y^2}$, ${\rho }_{{\mathrm{H}}_2\mathrm{O}}$ is the density of water and S(d) is the weighted stopping power at the position of the z-axis with a water equivalent depth of d; subscript pp stands for primary protons, and sp represents secondary particles; K_lat,pp describes the lateral dose distribution of the primary protons for the beamlet. This lateral distribution is mainly caused by multiple Coulomb scattering of protons off nuclei, including protons of hydrogen, which can be described by the well-known Molière theory.²⁰ The Molière theory is approximated by the sum of two Gaussian functions representing the scattering angles probability; the second Gaussian describes the tail of the scattering distribution due to large angle scattering, which accounts for only 4% of the contributions.^{10, 19}K_lat,sp describes the lateral dose distribution of the secondary particles for the beamlet and is represented by the third Gaussian function in Eq. 2.¹⁹

The secondary particles deposit energy outside the primary proton beam; therefore, the low-dose envelope from these secondary products, also known as a nuclear “halo” dose, is expected to have a broad lateral distribution.^{4, 14, 15} It should be noted that the parameters in Eq. 2 are not adjustable for the purpose of commissioning the TPS. Pencil beam algorithms similar to Eq. 2 have been reported,^{4, 11} although normally only two Gaussians are used, one for multiple Coulomb scattering and the other for nuclear interactions, accounting for the “halo” dose.

Single and double Gaussian fluence models

The fluence (protons/mm²) for the kth energy layer is calculated as the sum of fluence over all spots in this layer, ${\Phi }_{E_k}(x,y,z)={\sum }_m{\varphi }_{E_k}(x,y;x_m,y_m,z)$, where ${\varphi }_{E_k}(x,y;x_m,y_m,z)$ is the fluence at position (x, y, z) contributed by the spot centered at (x_m, y_m) and could be described by Eq. 3 for the double Gaussian fluence model,

$$\begin{array}{ccc}& & {\varphi }_{E_k}(x,y;x_m,y_m,z)\hfill \\ & & ={\varphi }_{E_k}^m\left(z\right)\left[\begin{array}{c}\frac{w_1\left(E_k\right)}{2\pi {\sigma }_1^2(E_k,z)}\exp \left(-\frac{{(x-x_m)}^2+{(y-y_m)}^2}{2{\sigma }_1^2(E_k,z)}\right)+\hfill \\ \frac{w_2\left(E_k\right)}{2\pi {\sigma }_2^2(E_k,z)}\exp \left(-\frac{{(x-x_m)}^2+{(y-y_m)}^2}{2{\sigma }_2^2(E_k,z)}\right)\hfill \end{array}\right],\hfill \end{array}$$ (3)

where ${\varphi }_{E_k}^m\left(z\right)$ is the maximum fluence of the spot centered at (x_m, y_m), w₁(E_k) and w₂(E_k) are the weights of the first and second Gaussian function and satisfies w₁(E_k) + w₂(E_k) = 1, and ${\sigma }_i(E_k,z)=\sqrt{\left(\frac{A_i\left(E_k\right)}{2}+B_i\left(E_k\right)z+\frac{C_i\left(E_k\right)}{2}{z}^2\right)}$ is the spot size for the first (i = 1) or second (i = 2) Gaussians, A_i(E_k), B_i(E_k), and C_i(E_k) are phase space parameters as a function of energy. It is common to use a SG to describe the spot fluence, i.e., w₂(E_k) = 0. Recently, we have demonstrated that the SG fluence model is not accurate enough because of the contributions of large angle scattering from the devices within the Hitachi scanning nozzle.^{14, 15} In general, σ_i in the x and y directions are different due to the elliptical shape of the initial beam. For the first Gaussian, the values of σ₁ in the x and y directions change with the gantry angle due to changes in the magnetic fields of steering and focusing magnets with the treatment gantry rotation.²¹ However, the Eclipse TPS has not modeled this change with the gantry angle. The difference of σ₁ in the x and y directions was small,⁵ the average values in the x and y directions was used as σ₁. For the second Gaussian caused by large angle scattering in the materials inside the scanning nozzle, we assumed that σ₂ is independent of the x and y directions.

When the DG fluence model was first introduced (Eclipse version 8.908), w₂ was assumed to be constant for all proton energies and σ₂ was a linear function of z. In the current version of DG fluence model (Eclipse version 8.917), w₂ can vary with proton energy and σ₂ is described by phase space parameters, as defined in Eq. 3. In this work, the DG fluence model refers to the current model in Eclipse version 8.917, unless otherwise specified. The SG fluence model in Eclipse version 8.120 was used only for creating plans for targets in disease sites where tumor sizes and depths were similar to those in prostate cancer.⁶ After the release of the version 8.908 of Eclipse in March 2010, the SG fluence model was removed from clinical use.

Required input data

The TPS system requires in-air profiles at three to five positions from the isocenter (e.g., Z = 0, ±10, ±20 cm, i.e., at the isocenter plane, 10 and 20 cm above and below the isocenter plane) for every 10–20 MeV in both the x and y directions for each beam energy. If range shifting devices are used, the profile data sets for different thicknesses of the devices are required. In this work, range shifting devices are not considered.

The required depth doses are IDDs for single pencil beam for each of the available proton energies. The IDD is defined as the integral of dose for a single spot over a very large plane normal to the beam direction (the total dose deposited at a depth), which is the well-known Bragg curve.²² The IDDs should be measured with a parallel plate ionization chamber large enough to ostensibly capture the entire beam and be expressed in units of Gy/MU multiplied by the active area of the ionization chamber in mm², i.e., Gy mm²/MU. This leads to values of IDDs in Gy/MU as if all of the doses were applied to a water column of 1 mm². The input data must be as accurate as possible because they define the parameters that the dose algorithm uses for calculation of absorbed dose distribution in the patient's computed tomography (CT) volume. Such measurements are very time-consuming and require an extensive amount of beam time and well-trained personnel. Moreover, the area of the largest commercially available ionization chamber is insufficient to capture the entire beam,^{5, 13} as discussed in Sec. 2C. Considering these limitations in performing accurate measurements, we used Monte Carlo (MC) simulations to generate the input data. A limited number of measurements of in-air profiles and IDDs were performed to validate a MC model of the scanning nozzle. The agreements between MC generated data and measurements using a large area ionization chamber were within 3% in the proximal region of the pristine Bragg curves. The MC generated ranges agreed with measurements within 0.13 cm. Details of the MC model's validation of the scanning nozzle have been published in Ref. 13.

Conversion of MC-generated IDDs

We used a Bragg peak chamber (BPC) (model 34070, PTW-Freiburg, Freiburg, Germany) to perform the absolute dose measurements at an effective depth of 2 cm to convert MC-generated IDDs in units of MeV cm⁻³ per history to units of Gy mm²/MU. The BPC has an effective radius of 4.08 cm and the water equivalent thickness (WET) of the front window was 0.4 cm. The product of the cobalt-60 calibration factor in absorbed dose to water and the beam quality factor of the BPC was previously determined, N_D,Wk_q = (3.181 ± 0.023) × 10⁶ Gy/C.⁵ In the MC simulations, the tallies used to score dose had the same dimensions of the sensitive volume of the ionization chamber. The choice of 2 cm depth for these measurements was to ensure that measurements were made in a low-dose gradient region of the pristine Bragg curves for all energies. The measured IDD for a pencil beam with energy E, at an effective depth of measurement of 2.0 cm can be simply obtained by

$$\begin{array}{ccc}\hfill {\mathrm{IDD}}_{\mathrm{meas}}(E,d=2\mathrm{cm};r_1)& =& M(E,d=2\mathrm{cm})\hfill \\ & & \times N_{D,W}{k}_q\times \pi r_1^2,\hfill \end{array}$$ (4)

where M(E, d = 2 cm) is the corrected ionization chamber reading in Coulomb per MU, N_D,Wk_q is the calibration factor multiplied by the beam quality factor, and πr₁² is the sensitive area of the BPC with r₁ = 4.08 cm. IDD_meas determined by Eq. 4 is expressed in units of Gy mm²/MU. If the BPC is large enough to capture the entire beam, we could simply scale the MC-generated IDDs by measured IDDs in Eq. 4.

To determine whether the BPC is large enough, IDDs for virtual ionization chambers (VICs) with radii of 4.08, 8.00, and 20.0 cm were generated using the MC simulations. The area of the BPC was found to be not sufficient large, even at the depth of 2 cm, to capture the entire pencil beam, especially for pencil beams with lower energies.^{5, 13} For high-energy proton pencil beams, secondary protons produced at large angles in the water phantom are the main contributors to the large size of the beam. At low energies, the large size of the pencil beam is specific to our scanning nozzle. Correction factors (CFs) to account for the size limitation of BPC were derived on the basis of the ratios of MC-generated IDDs at a depth of 2 cm for the VIC with a large radius, r₂,

$$\mathrm{CF}(E,d=2\mathrm{cm})=\frac{{\mathrm{IDD}}_{\mathrm{MC}}(E,d=2\mathrm{cm};r_2)}{{\mathrm{IDD}}_{\mathrm{MC}}(E,d=2\mathrm{cm};r_1)},$$ (5)

where r₁ = 4.08 cm is the radius of BPC. We used r₂ = 20.0 cm to ensure the VIC is sufficiently large to include the total integral dose to calculate the correction factor. It was estimated that the MC generated CFs had accuracy of about 1% since some of the uncertainties in MC IDD (within 3%) canceled out each other in Eq. 5. The corrected IDDs in Gy mm²/MU as a function of depth can then be calculated,

$$\begin{array}{ccc}\hfill \mathrm{IDD}(E,d;r_2)& =& \frac{{\mathrm{IDD}}_{\mathrm{MC}}(E,d;r_2)}{{\mathrm{IDD}}_{\mathrm{MC}}(E,d=2\mathrm{cm};r_2)}\hfill \\ & & \times {\mathrm{IDD}}_{\mathrm{meas}}(E,d=2\mathrm{cm};r_1)\hfill \\ & & \times \mathrm{CF}(E,d=2\mathrm{cm}),\hfill \end{array}$$ (6)

where IDD_meas(E,d = 2 cm; r₁) is the measured value given by Eq. 4. We have not further simplified Eq. 6 to make clearer the meaning of the equation: the ratio of IDD_MC normalizes the MC-generated IDD to the depth of 2 cm; the IDD_meas × CF term converts normalized MC-generated IDD in units of Gy mm²/MU. This approach, based on absolute dose per MU, is equivalent to the approach based on absolute dose per particle used at other institutions.^{4, 23}

Commissioning double Gaussian model in Eclipse TPS

DG parameters tuning procedure

The parameters describing the DG fluence model include w₂(E_k) and σ₂(E_k,z). The z dependence of σ₂(E_k,z) is described by three phase space parameters A₂(E_k), B₂(E_k), and C₂(E_k). All the parameters were initially determined in the TPS by fitting the input data to the DG fluence model. We call the DG fluence model with Eclipse fitted parameters (EFP), DG-EFP. It was noted that the weights w₂ for the second Gaussian from the TPS fitting procedure were nearly a constant over the entire range of proton energies (average ± standard deviation = 0.119 ± 0.002). It was found, however, that the contribution of the second Gaussian was still not large enough to predict the field size factors (FSFs) (see next paragraph for FSF definition) with the DG-EFP fluence model. To overcome this difficulty, we systematically measured FSFs of square fields of 20 monoenergetic proton beams at different depths (typically two depths, one was at 2 cm, and the other was a few millimeters proximal to the pristine Bragg peak; for high-energy proton beams, we also measured a few intermediate depths). With the phase space parameters for the first Gaussian determined from the Eclipse fitting procedure, an empirical method was then used to determine the parameters for the second Gaussian: (1) for the lowest, intermediate, and highest proton beam energies, we first increased the values of w₂(E_k) to improve the agreements between measured and calculated FSFs [this resulted in w₂(E_k) linearly varying from 0.155 at 72.5 MeV to 0.190 at 221.8 MeV]; (2) for the same three energies, the phase space parameters for the second Gaussian were then adjusted to obtain better agreements between measured and calculated FSFs simultaneously for both depths of measurements; (3) for the remaining 17 energies for which the measured FSFs were available, w₂(E_k) was linearly interpolated and step (2) was repeated; and (4) w₂(E_k) and the phase parameters for the second Gaussian for the remaining 74 proton energies were linearly interpolated from those determined from the 20 energies.

The square fields with nominal field sizes ranging from 2 × 2 cm to 20 × 20 cm were created by superposition of a number of spots laterally spaced at 0.5 cm between the centers of adjacent pencil beams at the isocenter plane.¹⁵ The FSF was defined as the ratio of dose at the center of a square field to that of the 10 × 10 cm field. Comparison of measured and calculated FSFs allows us to estimate the second Gaussian parameters. The selection of 10 × 10 cm field size as the normalization point was arbitrary, but serves as an intermediate field size for which the center of the field can be reliably measured.¹⁵ Our approach of using FSFs of square fields is similar to using concentric square frames to determine the characteristic width of the nuclear beam halo described by Pedroni et al.⁴

Verification measurements for TPS commissioning

Eclipse input data verification (selected IDDs and in-air lateral profiles) were measured for monoenergetic pencil beams for several different energies.¹³ IDDs were measured point-by-point with the BPC.⁵ In-air lateral profiles were measured with a “Pinpoint chamber” (model 31014, PTW-Freiburg), and another chamber with similar sensitive volume as the reference chamber. The data acquisition system included a large water phantom (MP3 Phantom Tank, model 981010, PTW-Freiburg) and dual-channel electrometer (TANDEM, PTW-Freiburg). The in-air lateral profiles were measured by scanning the Pinpoint chamber with a dwell time of 4 s and step sizes of 0.1–1 cm. The details of the measurements has recently been reported.¹⁵

FSFs of square fields of monoenergetic proton beams in water were measured by an “Advanced Markus” ionization chamber (model 34045, PTW-Freiburg) in a small rectangular water phantom. Volumetric dose distributions were generated by stacking multiple layers of square fields of pencil beams. Verification measurements in the volumetric dose distributions included point doses in the center of SOBP and field, depth doses along the central axis, lateral dose profiles along the center of the SOBP, and two-dimensional (2D) dose distributions in selected plans perpendicular to the beam incident direction for selected SOBPs. All point doses at the center of the fields, including depth doses, were measured as a function of nominal field size (ranging from 2 × 2 to 20 × 20 cm), the width of the SOBP (from 2 to 20 cm), and the range of the highest proton energies (from 6 to 30.6 cm) in the same way as the FSF measurements. For all fields created by superposition of pencil beams measured with an ionization chamber, the chamber was positioned at each selected location when the entire field was delivered. After completing each position, the chamber was remotely moved to the next location by a computer. A Pinpoint ionization chamber was also used to verify the results of the Advanced Markus chamber measurements for the small fields. Lateral dose profiles were measured with a Pinpoint ionization chamber and radiochromic film (Gafchromic EBT Film, International Specialty Products, Wayne, NJ) in a water phantom. Isodose distributions were measured with radiochromic films and a 2D ionization chamber array detector (MatriXX, IBA Dosimetry, Schwarzenbruck, Germany). Radiochromic films were used for relative measurements in the planes perpendicular to the incident beam, therefore, their LET dependences are not considered.

Correction table for the absolute doses

The Eclipse TPS provided a depth dose normalization table (DDNT) to allow the user, if necessary, to scale the calculated absolute doses in order to obtain better agreement with measured absolute doses. This is a 2D table, which is a function of the proton range and of the width of the SOBP. If the model is perfect, it would be unnecessary to use the DDNT. In the current clinical implementation, the DDNT entries are a slowly varying function of proton range (energy) but not of SOBP width. We expanded the use of this table to have doses for treatment planning expressed as biological doses of a constant RBE. We expressed the input IDDs in physical dose (Gy), not in biological dose [Gy (RBE)]. If no scaling is required, the values of the DDNT table would be equal to 1/RBE = 1/1.1 ≅ 0.9091, not RBE = 1.1. This is purely due to how the DDNT is defined within the TPS. Thus, while the input commissioning data are in physical dose Gy, the treatment plan dose distributions are in biological dose Gy (RBE). We compared all measured absolute doses, in the center of fields and SOBPs, with the calculated doses to obtain scaling factors. The decision to use physical dose for IDDs and to use DDNT to convert them to biological doses for treatment planning was arbitrary but believed to be more convenient. Alternatively, one could certainly convert IDDs into biological doses before inputting them into the TPS.

Measurements for patient-specific quality assurance

Before treating the first patient, we replanned using scanning beam several patients previously treated with passive scattering proton beams to evaluate the entire planning, dose validation, and delivery process. The details of patient-specific measurements for prostate cancer patients receiving single field uniform dose (SFUD) have recently been reported.⁶ Patient-specific measurements included point dose for each plan, depth dose for each field, and 2D measurements in the planes perpendicular to the beam incident direction for each field at multiple depths. Comparison of calculated (by the DG and SG fluence models) and measured dose distributions for two patient plans obtained with a SFUD technique will be presented in Sec. 3E4, as examples.

RESULTS

TPS input data generated by MC

The MC-generated IDDs used as a part of input data for the TPS system are plotted in Fig. 2a. The 94 IDDs for discrete energies ranging from 72.5 to 221.8 MeV were converted to absolute doses in units of Gy mm²/MU, as discussed in Sec. 2C. The values of MC-generated IDDs at the depth of 2 cm and at the Bragg peaks as functions of proton energies are graphed in Fig. 2b. At the depth of 2 cm, the IDDs increased as the proton energy decreased. This is due to the fact that a constant depth (e.g., 2 cm) becomes closer to the rising edge of the Bragg peak of the lower energy proton beams as seen in Fig. 2a. We also noticed that the values of IDDs at the Bragg peak increased with decreasing the proton energy except at the low energy end where a maximum existed at the proton energy of 88.8 MeV. This could result from two competing effects between increasing lateral scattering (causing a lower Bragg peak) and decreasing depth penetrating (resulting in a higher Bragg peak) as the proton energy decreased. The small variability in the MC data of Fig. 2b for higher energies is due to statistical uncertainties in the MC simulations. Displayed in Fig. 2c is the MC-generated FWHM of the Bragg peaks in the depth direction, which shows an increase as the proton energy increases due to range straggling. The choice of 94 energies in the design of our scanning nozzle was based on a criterion of creating a uniform depth dose (i.e., without ripple) with superposition of pristine Bragg peaks for distal ranges from 4 up to 30.6 cm.^{5, 7} The smaller range separations were designed for the low energy beams because the widths of Bragg peak become smaller [see Fig. 2a]. The MC-generated in-air lateral profiles used as a part of input data for the TPS system are plotted in Figs. 3a, 3b. The in-air lateral profiles clearly reflected the variation of spot size with proton energy due to multiple Coulomb scattering in the nozzle's components as well as the beam optics. σ₁ and σ₂ for the first and second Gaussian at the isocenter plane (z = 0) are plotted in Fig. 3c as a function of proton energy. The MC data shown in Figs. 23 were validated by measurements.¹³

Figure 2.

(a) IDDs for all 94 energies in units of Gy mm²/MU generated using MC simulations; (b) IDDs values at a depth of 2 cm (MC and measurement) and at the Bragg peak (MC) as a function of proton energy; the inset is MC-generated CFs at a depth of 2 cm; and (c) FWHM of Bragg peaks (MC) in the depth direction as a function of proton energy.

Figure 3.

MC simulation-generated lateral in-air dose profiles at different positions (z = 0, ±10, ±20 cm, z = 0 is defined at the isocenter). (a) For all energies; (b) for the pencil beam with energy of 221.8 MeV; and (c) σ₁ and σ₂ in the plane of isocenter (z = 0) versus energy.

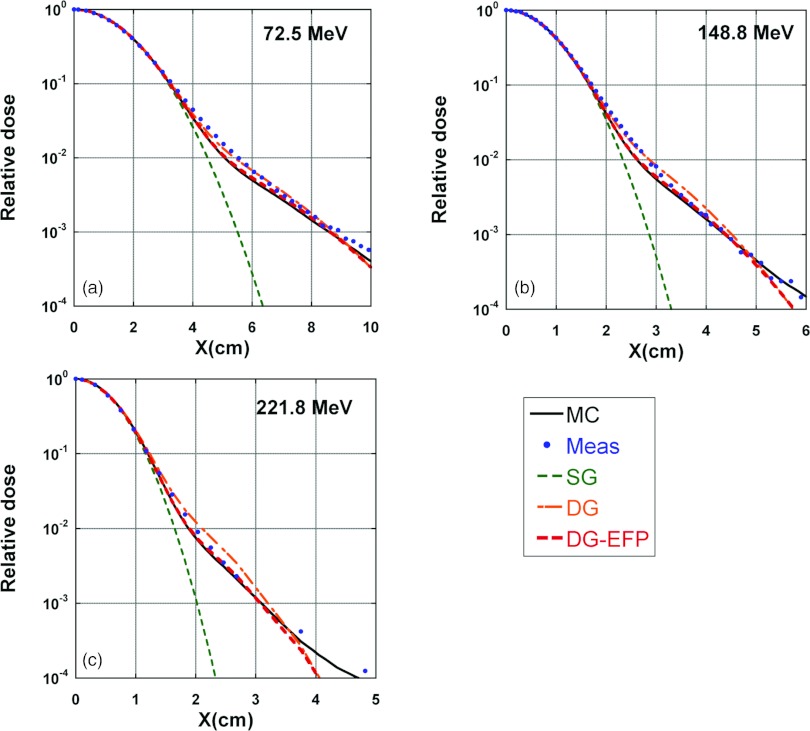
Examples of comparison between MC-generated and measured in-air lateral profiles are shown in Fig. 4. Also included in Fig. 4 are in-air lateral profiles calculated by the SG, DG-EFP, and DG fluence models. The MC data agree with the measured results well, but not perfect. The SG fluence model clearly underestimated the low-dose tail. The DG-EFP fluence model fitted to the MC data quite well. The DG fluence model results matched reasonably well with measured data.

Figure 4.

In-air lateral profiles for pencil beams with three different energies. Solid lines: MC; dots: measured data; dashed lines: calculated by SG fluence model; dashed-dotted lines: calculated by DG fluence model with empirical parameters; and dashed lines: calculated by DG-EFP. (a) 72.5, (b) 148.8, and (c) 221.8 MeV.

Corrections for IDDs

The measured and corrected IDDs at a depth of 2 cm are displayed in Fig. 2b. The CFs [inset in Fig. 2b] were small (about 1%) for high-energy beams and increase up to 14% for the lowest proton energy.⁵ The CFs would be different if the measurements were done at different depths. For the proton beam with energy of 221.8 MeV, for example, the BPC could underestimate the IDD as much as 7.8% at a depth of about 18 cm.¹³

FSFs for tuning the DG fluence model

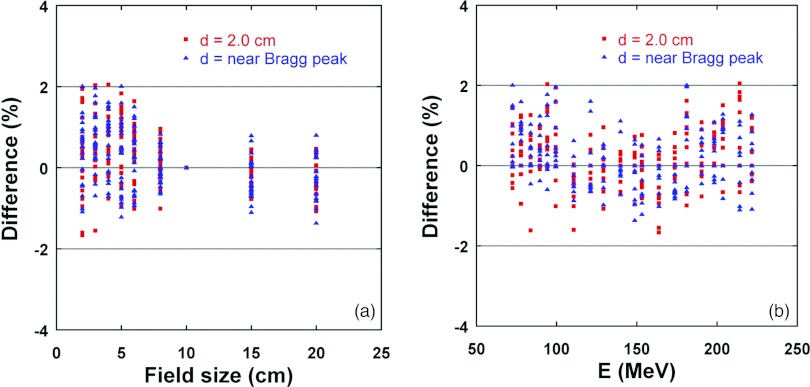
Figure 5 shows comparison between the calculated, by the SG, DG-EFP, and DG fluence models in TPS, respectively, and measured FSFs of square fields with field sizes of 2 × 2 to 20 × 20 cm. We have also included the percentage differences between calculated and measured FSFs in Fig. 5. Two depths are included in Figs. 5a, 5b, 5c, 5d; one is at a depth of 2 cm and the other is at a deeper depth near the Bragg peak. The calculated FSFs deviated from the measured values by 8.5% to 13%, 3.4% to 7.2%, and 1.0% to 1.9% for the SG, DG-EFP, and DG fluence models, respectively. For the highest energy of 221.8 MeV, a comparison for an intermediate depth of 23.2 cm is also shown in Fig. 5f, where the nuclear “halo” effect is expected to be larger (the largest percentage differences in FSFs were 16.9%, 10.7%, and 3.5% for the SG, DG-EFP, and DG fluence models, respectively). The results of FSF in Fig. 5 clearly demonstrated the necessity of the DG fluence model with empirical parameters in the current version of TPS.

Figure 5.

Comparisons between calculated (SG, DG-EFP, and DG fluence models) and measured FSFs of square fields. Positive values in percentage differences represent calculated FSFs larger than measured ones. For FSFs, dotted-dashed lines: SG; dashed lines: DG-EFP; solid lines: DG; and squares: measured. For percent differences, dotted-dashed lines with circles: SG; dashed lines with triangles: DG-EFP; and solid lines with diamonds: DG. (a) and (b) for energy of 72.5 MeV (4.0 cm range) at depths of 2.0 and 3.7 cm; (c) and (d) for energy of 148.8 MeV (15.2 cm range) at depths of 2.0 and 15.0 cm; (e)–(g) for energy of 221.8 MeV (30.6 cm range) at depths of 2.0, 30.0, and 23.2 cm, respectively.

Figure 6 summarizes the percentage differences between calculated and measured FSFs for all 20 monoenergetic fields at a depth of 2 cm and at larger depths near the Bragg peak as a function of field size and proton energy, respectively. The spread of the differences became somewhat larger for smaller field sizes, as shown in Fig. 6a, which was due to the selection of normalization field size of 10 × 10 cm. If the small field was used for normalization, the larger differences would be observed for larger field sizes. No clear energy dependence was observed, as displayed in Fig. 6b. The differences (mean ± standard deviation) were 0.2% ± 0.7% (range: −1.7% to 2.1%).

Figure 6.

Percentage differences between the calculated (by DG fluence model) and measured FSFs for 20 monoenergetic fields at two depths as a function of field size (a) and proton energy (b). Positive values in percentage differences represent calculated FSFs larger than measured ones.

Values of depth dose normalization table

Depending on the range (energy) of the proton beam, the DDNT table values ranged from 0.9288 to 0.9445 for the DG fluence model, which were 2.2%–3.9% larger than the ideal value (see Table 1). This indicates the DG fluence model (including the parameters for the second Gaussian) and the commissioning process, including MC simulation and measurements, are not perfect. But the largest difference is still less than 4%. The deviations from the ideal value in the DDNT could be attributed to the limitations of current dose models, MC and measurements uncertainties in determining the IDDs, in-air lateral profiles, and verification dose measurements. The fact that we used the average values in the x and y directions for σ₁ in Eq. 3 might also contribute to this discrepancy. Pedroni et al.⁴ also used an energy-specific correction factor, ranging from 0.978 to 1.008, i.e., a 3% spread, to fine-tune the agreement between measurements and calculations for the absolute doses.

Table 1.

Values of DDNT at selected energies/ranges for the DG fluence model. The ideal value of DDNT = 1/1.1 = 0.9091. The percentage difference is the difference in percent between DDNT values used by the DG fluence models and the ideal value.

Energy/range
E (MeV)	Range (cm)	DDNT	Percentage difference
72.5 ≤ E < 90	4.0 ≤ E < 6.0	0.9339	2.7
111	9.0	0.9445	3.9
153 ≤ E ≤ 221.8	16.0 ≤ E ≤ 30.6	0.9288	2.2

Dose verification

Absolute doses in the center of the SOBP

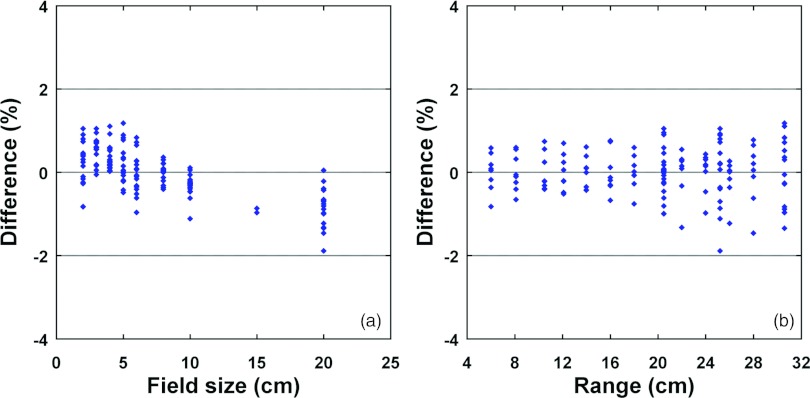
Figure 7 shows percentage differences between doses calculated by the SG and DG fluence models and measured at the center of the field and at the depths of the center of SOBP (4 cm wide) as a function of field size for three different proton ranges, 10.5, 20.0, and 30.6 cm, corresponding to maximum energies of 121.2, 173.7, and 221.8 MeV, respectively. The maximum differences were 13.8%, 6.8%, and 1.3% for the SG, DG-EFP, and DG fluence models, respectively. Figure 8 summarizes the percentage differences between the doses calculated by the DG fluence model and those measured at the center of the field and the SOBP as a function of field size and range, with SOBP widths ranging from 2 to 24 cm. The differences (mean ± standard deviation) are 0.0% ± 0.6% (range: −1.9% to 1.2%) for the data included in Fig. 8.

Figure 7.

Percent differences between calculated (by both SG and DG fluence models) and measured doses at the center of the field and SOBP (4 cm) as a function of field size for three different proton ranges, 10.5, 20.0, and 30.6 cm. Positive values represent calculated doses larger than measured ones. (a) SG fluence model; (b) DG-EFP; and (c) DG fluence model with empirical parameters.

Figure 8.

Percentage differences between doses calculated by the DG fluence model and those measured at the center of the field and the SOBP as a function of field size (a) and range (b). The SOBP widths range from 2 to 24 cm. Positive values in percentage differences represent calculated doses larger than measured ones.

Absolute depth doses along the central axis

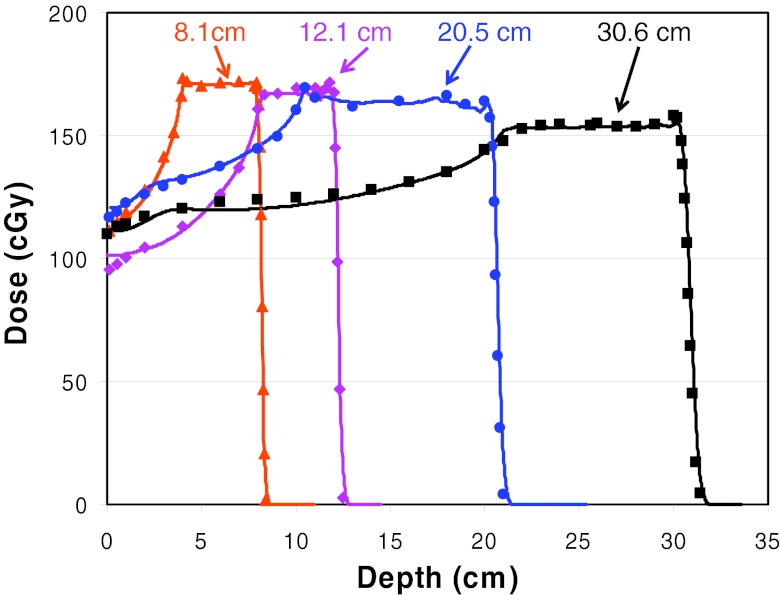
The measured and calculated depth doses, along the central axis of proton fields with a nominal field size of 10 × 10 cm are compared in Fig. 9. The SOBP width was 4 cm for fields with ranges 8.1 and 12.1 cm, and was 10 cm for fields with ranges 20.5 and 30.6 cm. The corresponding maximum energies were 105.2, 131.0, 176.2, and 221.8 MeV, respectively. Figure 9 demonstrates that the depth doses calculated by the DG fluence model are in excellent agreement with measured data.

Figure 9.

Comparison of the depth doses calculated using the DG fluence model and measurements along the central axis of proton fields with the nominal field size of 10 × 10 cm for four different proton ranges with SOBP width of 10 or 4 cm.

In-water lateral dose profiles

Figure 10 compares doses calculated by both SG and DG fluence models with measured inplane lateral dose profiles at the center of a 4 cm wide SOBP for proton ranges of 8.1 and 12.1 cm (measured with EBT film) and a 10 cm wide SOBP for proton ranges of 20.5 and 30.6 cm (measured with a Pinpoint ionization chamber). The results from DG fluence model clearly demonstrated a better agreement with the measurements than the SG fluence model, especially in the areas of the shoulder and outside the field. Both SG and DG fluence models predicted the 50%–50% field size within 1 mm of the measured ones. Table 2 lists other dosimetric parameters for the lateral profiles presented in Fig. 10. The 20%–80% penumbras predicted by the DG model agreed with the measurements within 0.1 cm and were 0.15–0.2 cm larger than the SG model. The half-widths of the shoulder at the 95% level calculated by the DG fluence model agreed with measurements within 0.1 cm and were 0.25–0.39 cm smaller than the SG fluence model. The half-widths of the low-dose region outside the field at the 5% level predicted by the DG fluence model were consistent with measurements within 0.2 cm and were 0.4–0.8 cm larger than the fluence SG model. These results are consistent with the fact that the SG fluence model underestimates the dose a few centimeters away from the center of the pencil beam (Fig. 4).

Figure 10.

Comparison of the DG, SG fluence models calculated and measured inplane lateral dose profiles at the center of the SOBP for four different proton ranges and SOBP widths of 10 or 4 cm. Dots: measured data; solid lines: calculated by the DG fluence model; dashed lines: calculated by the SG fluence model. (a) Range = 30.6 cm, SOBP = 10 cm; (b) range = 20.5 cm, SOBP = 10 cm; (c) range = 12.1 cm, SOBP = 4 cm; and (d) range = 8.1 cm, SOBP = 4 cm.

Table 2.

Comparison of dosimetric parameters of lateral dose profiles in water presented in Fig. 10.

					Half-width of shoulder			Half-width of low-dose
		Penumbra 20%–80% (cm)			at 95% (cm)			outside field at 5% (cm)
Range (cm)	SOBP (cm)	Meas	DG	SG	Meas	DG	SG	Meas	DG	SG
30.6	10	1.61	1.60	1.40	3.87	3.93	4.32	7.48	7.45	7.07
20.5	10	1.59	1.58	1.38	3.71	3.79	4.17	7.29	7.22	6.79
12.1	4	1.69	1.77	1.62	3.76	3.64	3.89	7.23	7.33	6.83
8.1	4	2.06	2.09	1.93	3.29	3.25	3.51	7.36	7.57	6.74

Examples of clinical verification

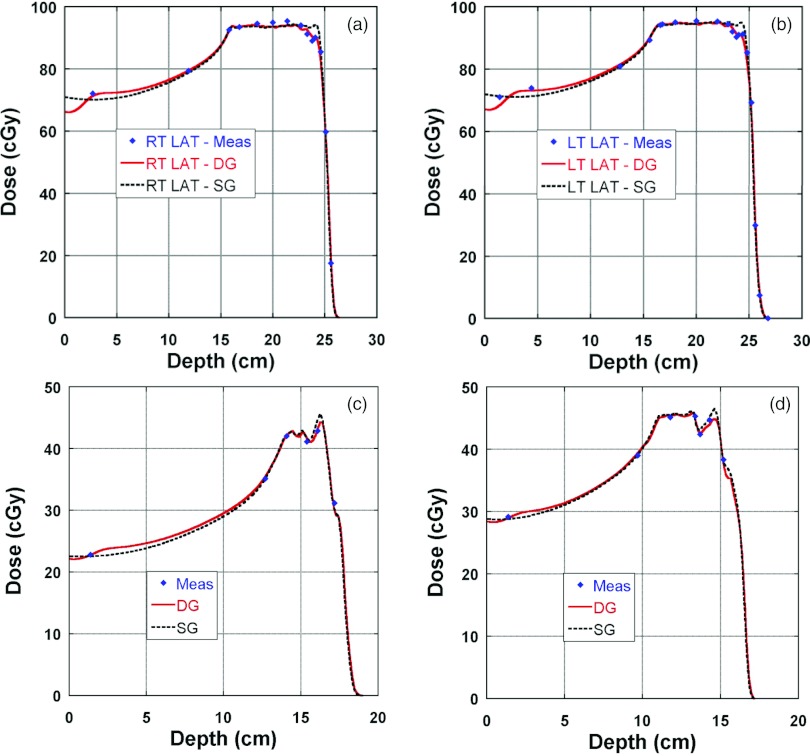
Figure 11 presents clinical examples of TPS calculated and measured depth doses along the central axis; Figs. 11a, 11b are for a patient with prostate cancer treated with right and left lateral fields. The depth doses of the original plan, which was optimized and calculated with the SG fluence model, were recalculated with use of the DG fluence model. Much better agreement (within 2%) was observed at the distal end for the DG fluence model. In this case, the SG fluence model also had reasonable agreement with measurements except at the distal end. It should be pointed out that there is a buildup in the depth doses calculated with the DG fluence model. The calculated buildup was induced by Landau tails,¹⁰ which were introduced to the TPS at the same time as the DG fluence model but are not strictly related. Figures 11c, 11d are for two of the four fields for a pediatric patient with chordoma in the base of the skull. We observed a good agreement (within 2% or 2 mm) between the calculated by the DG fluence model and the measured depth doses, which was satisfactory for clinical use. Also included in Figs. 11c, 11d are depth doses calculated by the SG fluence model. Agreement between depth doses calculated by the SG fluence model and measured seemed also acceptable for clinical use (within 3%).

Figure 11.

Clinical examples of comparison of depth doses between measured and calculated by the DG and SG fluence models. Diamonds: measured; solid lines: calculated by the DG fluence model; and dashed lines: calculated by the SG fluence model. (a) and (b) are for a patient with prostate cancer treated with right and left lateral fields. The depth doses were recalculated with the DG fluence model for the original plan which was optimized and calculated with the SG fluence model as the dose model; (c) and (d) are for two of four fields for a pediatric patient with chordoma in the base of skull. The patient plan was optimized and calculated with the DG fluence model and the SG depth doses were recalculated with SG fluence model for the purpose of comparison.

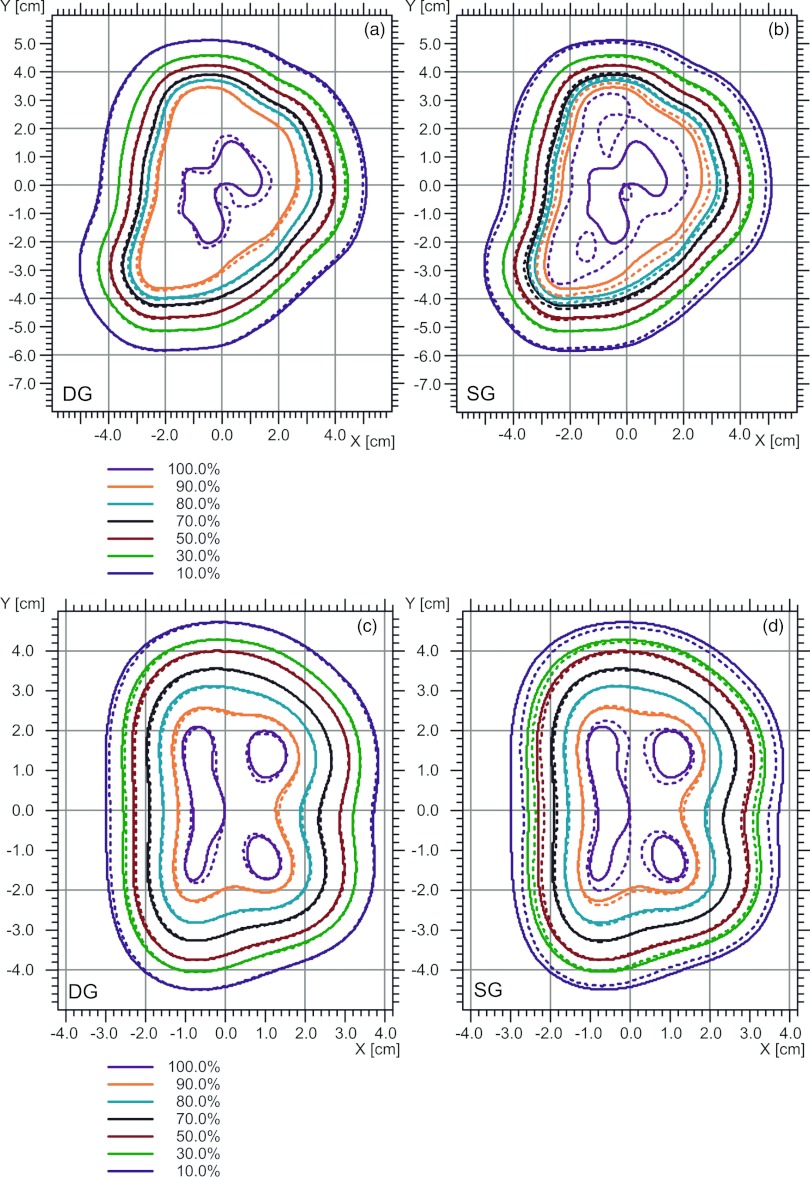
Figure 12 shows TPS calculated and measured (with the MatriXX) isodose distributions: Figs. 12a, 12b compare the calculated distributions by the DG and SG fluence models, respectively, and measured isodose distributions for a right lateral prostate field at a depth of 18.4 cm in a plastic water phantom. The DG fluence model provided much better agreement with measurement than the SG fluence model did. For the DG fluence model, 100% of the points passed the 2%-dose/2-mm distance criteria of the γ-index;²⁴ for the SG fluence model, only 80% of points passed the 2%-dose/2-mm distance criteria. Figures 12c, 12d show the dose distributions calculated by the DG and SG fluence models, respectively, and the measured dose distributions for one of the vertex fields at a depth of 11.9 cm, for the same chordoma patient shown in Fig. 11. For the DG model, 100% of the points passed the 2%-dose/2-mm distance criteria of the γ-index, while only 78% points passed the 2%-dose/2-mm distance criteria of the γ-index.

Figure 12.

Clinical examples of comparison of isodose distributions between measured and calculated by the DG [(a) and (c)] and SG [(b) and (d)] fluence models, respectively. Solid lines: measured isodose lines; and dashed lines: calculated isodose lines. (a) and (b) are for a right lateral prostate field at the depth of 18.4 cm; (c) and (d) are for one of the vertex field [the same field as in Fig. 11d] at a depth of 11.9 cm.

DISCUSSION

We have presented our method and experience in commissioning dose models in TPS for spot scanning proton beams. This experience helped us better understand the limitations of the dose models. The major challenge was modeling the low-dose envelope surrounding the incident pencil beams. The low-dose envelope is caused by two major effects: (1) primary particles scattered in beam line components and in water and (2) secondary particles produced in water, especially for high-energy beams.^{14, 15} We demonstrated that modeling the lower-dose envelope improved the overall dose calculation accuracy of the dose beam models in the TPS.

To account for the scattering in the beam line components, a second Gaussian is added to the fluence model, resulting in the DG fluence model. In this work, we have demonstrated that the DG fluence model is significantly better than the SG fluence model (Figs. 57101112). For example, the depth dose curves for a prostate patient treatment plan, shown in Figs. 11a, 11b were originally optimized and calculated with the SG fluence model. The dip of 5% at the distal end in the measurements was not reproduced by the SG model. This was presumably caused by the narrowing of the effective field size near the distal ends to conform to the rounded shape of the prostate. The SG model underestimates the dose a few centimeters away from the center of each spot (see Fig. 4), therefore, it cannot predict the field size dependence [Fig. 7a]. When the SG models was configured for field sizes such as those required near the center of prostate, it overestimated the doses for the much smaller fields. The DG fluence model, on the other hand, could predict the field size dependence and therefore reasonably predicted the dip near the end of depth dose curve. Comparison of depth dose can show limitations of the SG fluence model only if the effective field size of the beam changes significantly along the depth [see Figs. 11c, 11d]. On the other hand, comparison of isodose distribution in the planes perpendicular to the incident beam is more effective at revealing the limitations of the SG fluence model. For example, in Fig. 12, the isodose lines calculated by the SG and DG fluence models show a pattern consistent with the results of lateral profiles displayed in Fig. 10; that is, the SG fluence model overestimates the dose in the shoulder region and underestimates the dose outside the field.

The results in Figs. 457b, 7c demonstrate the challenges in configuring the DG fluence model. First, in Fig. 4, the DG-EFP fluence model calculated lateral in-air profiles agree with MC simulated data well; and the MC data match with the measured data also well. However, DG-EFP fluence did poorly in predicting field size dependence [Figs. 57b]. One could argue that MC simulated in-air lateral profiles might not be accurate enough compared to measured data [i.e., MC data are somewhat lower than measured ones, see Figs. 4a, 4b, at distances near 5 and 2.5 cm, respectively, away from the center of the spot]. But further improvement of MC data might be limited by statistical noises and measurement uncertainties. On the other hand, the DG fluence model calculated in-air lateral profiles agree with measured data well, except in some regions, such as at the distances near 3.5 and 2.5 cm [see Figs. 4b, 4c], where the DG data are higher than measured. All these differences are small and within experimental uncertainties.¹⁵ But the data in Figs. 57c suggest that DG fluence model has significantly improved the field size dependence. The data in Figs. 457 demonstrate that direct comparison of in-air lateral profiles, which may not be accurately known, would be difficult to properly tune the DG parameters. Therefore, we used FSFs of square fields of monoenergetic fields to determine the empirical DG parameters. Pedroni et al.⁴ used concentric frames to carry out similar tasks.

The empirical parameters determined for the second Gaussian should be considered as the current “best-estimated” parameters for the DG fluence model. The physical meanings of these parameters might not be straight forward. The second Gaussian in the fluence model was intended for describing the low-dose envelope due to the scattering from the beam line components in the nozzle. One would expect larger scattering angles for protons with lower energies. However, the empirical values of w₂(E_k) increase linearly from 0.155 to 0.190 with increasing proton beam energy. One of possible explanations might be that the TPS inadequately modeled inphantom interactions, including multiple-Coulomb scattering and secondary particles originated from nuclear interactions, and the second Gaussian of the DG fluence model used nonphysically larger weights to compensate the deficiency of the model for proton beams with high energies.

Nuclear interactions are more important for the high-energy proton beams in water. The secondary particles produced in water for the high-energy beams are challenging to model. The low-dose envelope due to nuclear interactions changes with depth for a given proton energy, building up and reaching the maximum at an intermediate depth, and then receding.^{11, 14, 15} The TPS must accurately model this variation. The observed larger differences at some intermediate depths for high proton energies (e.g., 23.2 cm for 221.8 MeV, as shown in Fig. 5) suggests that the current dose model in the TPS may need to be further improved. Within the framework of current pencil beam dose algorithm, a simple and straight forward approach might be to fix (not using empirical tuning) the parameters of the second Gaussian in the DG fluence model after the TPS fitting process. Then, better agreement between calculated and measured FSFs of all depths can be achieved by adjusting some of the parameters for the dose distribution of secondary particles found in Eq. 2. For further improvements, the TPS vendor could implement functions other than Gaussian to describe the lateral dose distribution of the secondary particles. In fact, we have recently demonstrated that a modified Cauchy–Lorentz distribution function is a better choice for modeling the low-dose envelopes in the water phantom.²⁵

Between March 2010 and June 2012, we treated more than 500 patients with scanning proton beams using the DG fluence model, including approximately more than 150 patients with central nerve system, head and neck, and other cancers. We used SFUD, single field integrated boost, and IMPT for these treatments. From patient treatment field-specific quality assurance measurements, we have found that the TPS calculated and measured absolute doses normally agree within 3% or 2 mm [an example shown in Figs. 11c, 11d]. For relative 2D dose distributions in the planes perpendicular to the incident beam direction, usually more than 90% of the pixels passed the 2% dose/2 mm distance agreement criteria of the γ-index [an example shown in Figs. 12a, 12c].

CONCLUSIONS

In this work, we have presented our method and experience in commissioning dose models for SSPT. Input data required by the TPS were generated by measurement-validated MC. A method for correcting the effect of finite detector size for IDDs was derived from MC-generated data. One of the most challenging and highly laborious tasks was to determine the empirical parameters for the second Gaussian function in the DG fluence model. We have demonstrated that the DG fluence model is significantly better than the SG fluence model. However, our results suggest that there are still limitations in modeling the low-dose envelope, especially for in-phantom interactions of high-energy proton beams. Dose algorithms for proton beam therapy will continue to improve as more and more institutions start to offer proton therapy to cancer patients worldwide. Medical physicists face the challenging task of commissioning and recommissioning the new and improved dose models as they become available. The authors hope that the method and experience presented here would be useful for commissioning the dose models.