Arabidopsis thaliana root elongation growth is sensitive to lunisolar tidal acceleration and may also be weakly correlated with geomagnetic variations

Abstract

Background

Correlative evidence suggests a relationship between the lunisolar tidal acceleration and the elongation rate of arabidopsis roots grown under free-running conditions of constant low light.

Methods

Seedlings of Arabidopsis thaliana were grown in a controlled-climate chamber maintained at a constant temperature and subjected to continuous low-level illumination from fluorescent tubes, conditions that approximate to a ‘free-running’ state in which most of the abiotic factors that entrain root growth rates are excluded. Elongation of evenly spaced, vertical primary roots was recorded continuously over periods of up to 14 d using high temporal- and spatial-resolution video imaging and were analysed in conjunction with geophysical variables.

Key Results and Conclusions

The results confirm the lunisolar tidal/root elongation relationship. Also presented are relationships between the hourly elongation rates and the contemporaneous variations in geomagnetic activity, as evaluated from the disturbance storm time and ap indices. On the basis of time series of root elongation rates that extend over ≥4 d and recorded at different seasons of the year, a provisional conclusion is that root elongation responds to variation in the lunisolar force and also appears to adjust in accordance with variations in the geomagnetic field. Thus, both lunisolar tidal acceleration and the geomagnetic field should be considered as modulators of root growth rate, alongside other, stronger and more well-known abiotic environmental regulators, and perhaps unexplored factors such as air ions. Major changes in atmospheric pressure are not considered to be a factor contributing to oscillations of root elongation rate.

INTRODUCTION

Living organisms on Earth are continually exposed to diurnal variations in the lunisolar tidal force due to the orbital motions of the Earth and Moon around the Sun. In an earlier paper (Fisahn et al., 2012), it was shown that time series of the hourly elongation rates recorded from primary roots of Arabidopsis thaliana growing under free-running conditions in which environmental parameters are held constant, displayed oscillations, over periods of many days, which were significantly correlated with simultaneous variations of the lunisolar tide (δg). The two sets of oscillations appeared to be in synchrony. Results are now presented from further observations of the elongation rates of arabidopsis roots, made at high temporal–spatial resolution, which confirm this coupling between elongation rate and the lunisolar tide. Also presented are results indicating some form of correlative relationship between root elongation rates and contemporaneous variations in the Earth's geomagnetic field (GMF). These geomagnetic variations are of two types. One is determined by processes intrinsic to the magnetosphere (Olsen, 1982); these are termed ‘quiet’ GMF variations. They are characteristic of the magnetic latitude, every one of which has its own unique seasonal and daily pattern of variation. The second type of GMF variation is associated with magnetic storms (Gonzalez et al., 1994, 1999). These are detectable around the Earth's globe as significantly increased variations of GMF originating from interaction between the magnetosphere and the stream of charged particles which comprises the solar wind. Both types of GMF variations are thought to affect the behaviour of animals and humans (e.g. Friedman et al., 1963; Babayev and Allahverdiyeva, 2007; Khabarova and Dimitrova, 2009; Mulligan et al., 2010). Magnetic storms, in particular, are supposed to affect human cardiovascular activity (Papailiou et al., 2011), neuropsychological states (Persinger and Richards, 1995; Mulligan and Persinger, 2012), and may perhaps also interfere with epigenetic controls of human cerebral development (Kay, 2004), all of which could involve disturbance to the natural bioelectrical fields of the respective biological system. There is also evidence suggesting that variations in GMF affect living plant processes (Brown and Chow, 1973) – processes in which natural bioelectrical fields again play a role. Such fields operate in and around root apices (Toko et al., 1989; Ezaki et al., 1990; Masi et al., 2009) and affect the development of root systems (Miller and Gow, 1989). They also play a role in root growth orientation (Collings et al., 1992) and in the interaction of roots with soil micro-organisms (van West et al., 2002). Results of early investigations of biological processes purportedly affected by variations in the GMF, much of which was performed in Russia and eastern Europe, were reviewed by Dubrov (1978), who gave to this discipline the name ‘geomagnetobiology’.

Indices of geomagnetic variation (Rostocker, 1972) selected for evaluation in the present study were the disturbance storm time (Dst) index and the ap index. The Polar Cap (PC – Thule) index was also evaluated, although this index reflects only the sensitivity of the magnetosphere to changes in solar wind parameters (Frank-Kamenetsky and Troshichev, 2012). There is, however, a correlation between values of the PC and Dst indices (Troshichev et al., 2011). Together, the three mentioned indices help substantiate an overall picture of the possible interaction between geophysical and biological variables. In earlier work, variations in the PC index were shown to correlate, in a statistically significant manner, with a simultaneous variation in stem diameter of two species of tree, one a softwood, the other a hardwood (Barlow et al., 2010a, b; M. Mikulecký Sr, P. Barlow and J. Střeštík, unpub. res.).

There are a number of older reports about the responses of plants to magnetic, geomagnetic and atmospheric ion and atmospheric pressure effects, and their possible link with lunar phase (Brown et al., 1955; Pittman, 1963, 1965; Maw, 1967; Abrami, 1972). After some years of neglect, this type of work has been pursued more actively in the light of some of these factors' possible contribution and application not only to plant growth and productivity (Hajnorouzi et al., 2011; Radhakrishnan et al., 2012) but also in relation to their effects upon ecosystem viability (Khabarova et al., 2010). Furthermore, both the spatial and the temporal aspects of geomagnetic variations have been offered in explanation of some of the more subtle aspects of plant development, such as the handedness of leaf formation upon stems of palm trees (Davis and Davis, 1987; Minorsky and Bronstein, 2006). The present study continues this investigation of the possible natural sensitivity of arabidopsis roots to these less frequently considered geophysical environmental factors of lunisolar gravity and geomagnetism (Fisahn et al., 2012). However, it should be appreciated that whatever patterns of plant growth and development are linked with geophysical variations, these supplement natural variations inherent to organ growth and development which, under certain circumstances, can be discerned as ‘primary’, automorphogenetic processes (see Hoson et al., 2001; Paul et al., 2012).

MATERIALS AND METHODS

Roots and root elongation

Seedlings of Arabidopsis thaliana (L.) Heynh. (var. Col-0) were grown in a controlled-climate chamber maintained at a constant temperature (21 ± 0·5 °C) and subjected to continuous low-level illumination (photon flux density 90 µmol m⁻² s⁻¹) from fluorescent tubes (for technical details, see Yazdanbakhsh and Fisahn, 2012). These conditions approximate to a ‘free-running’ state in which most of the abiotic factors that entrain root growth rates are excluded.

Elongation of evenly spaced, vertical primary roots was recorded continuously over periods of up to 14 d using high temporal- and spatial-resolution video imaging (1 frame per 30 min at a resolution of 6·0 µm × 5·8 µm per pixel) adequate to define the tips and edges of the growing roots (Yazdanbakhsh and Fisahn, 2009, 2010, 2012). The positions of the tips of each root were recorded and stored as XML.data library files. Root elongation rates were estimated, in μm h⁻¹, every half-hour throughout the observation period and average rates prepared for each experimental group. In two instances, time series of individual roots were analysed separately. The local time at Potsdam, Germany, as CET or CEST = UTC + 1 h or UTC + 2 h, depending on the time of year, provided the timescale. All data time series revealed that the elongation rates of all the individual roots within each experimental group exhibited oscillations, which were in near-synchrony with each other. Table 1 summarizes the various observation periods and their corresponding time series.

Table 1.

Summary of experiments performed to estimate root elongation rates in relation to lunisolar tide and geomagnetic variations

Expt no.	Time series no.	No. of roots	Date of root elongation rate measurements	Duration (d)	Lunar phase	Lunar tidal pattern	Marine tidal pattern	Figure no.
1	1	6	19–22 January 2008	3	FQ on 16 January 2008; NM on 12 January 2008	Unimodal → bimodal	Bimodal	S4
2	2	23	27 May 2008– 2 June 2008	6·5	LQ on 28 May 2008; NM on 4 June 2008	Bimodal	Bimodal	1; S1
2A	3	1 (root no. 2224)	27 May 2008–3 June 2008	7	NM on 4 June 2008	Bimodal	Bimodal	2; S2
2B	4	1 (root no. 222)	27 May 2008–2 June 2008	6·5	LQ on 28 May 2008; NM on 4 June 2008	Unimodal → bimodal	Bimodal	Not shown
3	5	10	13 April 2012–20 April 2012	8	LQ on 13 April 2012; NM on 21 April 2012	Bimodal	Bimodal	3; S3

Figures mentioned are either in main text or in the Supplementary Data at www.aob.oxfordjournals.org.

Geophysical variables

Lunisolar tidal acceleration

Variations in the progression of the gravimetric tide (± δg) at the experimental site of Potsdam (54°24′N, 12°58'E; 50 m a.s.l.) were estimated at 15-min intervals using the program ‘Etide’. The units of the gravimetric (lunisolar) tide δg are expressed in μGals. Lunisolar tides were checked against marine tides at a nearby site in Hamburg (St Pauli) using data from the website: http://tbone.biol.sc.edu/tide/sites_othernorth.html

Lunar phases

The lunar phases (New Moon, Full Moon and First and Last Quarters) during a synodic lunar month of approx. 29 d have a bearing on the temporal pattern of δg. The dates of these phases during the various root observation periods were determined at http://www.moonconnection.com/moon_phases_calendar.phtml.

Atmospheric pressure

Values of atmospheric pressure at Potsdam, in units of mb (1 mb = 10² Pa), were obtained from Deutscher Wetterdienst Regionales Klimabüro, Potsdam. These evaluations were similar to those recorded at Kiel, Germany, which are available on-line at http://www.nmdb.eu/nest/search.php.

Geomagnetic variation

Averaged hourly values of the Polar Cap (PC – Thule) index, and values of the other geomagnetic indices, Dst (hourly), ap and Kp (3-hourly averaged), were obtained from the OMNI website (http://omniweb.gsfc.nasa.gov/form/dx1.html) for the dates relevant to the investigation.

All index values, including the values of δg estimated by the Etide program, were recorded with reference to Universal Time, UTC, and stored in Excel files. The timescales were then adjusted to conform to the local time at Potsdam.

Attributes of the geomagnetic indices

Because the geomagnetic indices considered in the present work may be unfamiliar to many biologists, a short summary of their attributes is presented here, before proceeding to the Results section, where the time series of data associated with each of the indices are analysed in relation to both root elongation rate and δg. Physical properties evaluated by some of these geomagnetic indices have been reviewed by Rostocker (1972).

The disturbance storm time (Dst) index is evaluated at four low-level magnetometer stations located near the equator (http://wdc.kugi.kyoto-u.ac.jp/dstdir/dst2/onDstindex.html). The index is derived from hourly measurements of variations, in units of nanoTesla (nT), of the horizontal component of the GMF. It is used for the world-wide monitoring of magnetic storms. These storms are characterized by negative values of Dst; strong storms are typically associated with Dst index values of –100 nT or more, and weak storms with Dst values of < –30 nT (Gonzalez et al., 1994, 1999). Possible coupling between the Dst and PC index values has been discussed by Troshichev et al. (2011).

The a (and K) indices characterize the maximum fluctuations of the horizontal components of the GMF relative to a quiet base line. They also reflect the interaction between the solar wind and the magnetosphere and, hence, this effect is expressed in the degree of displacement of the northern Aurora: the higher the index value, the greater the displacement (http://www.swpc.noaa.gov/Aurora/ and http://www.swpc.noaa.gov/info/kp-aurora.html).

The Kp index (Bartels, 1957), a planetary average, is a standardized index derived from 13 observation sites between 44° and 60° northern/southern geomagnetic latitudes. The index is evaluated on a quasi-logarithmic scale, ranging from 0 to 9. Geomagnetic storms are indicated by values of Kp ≥ 5, whereas lesser values are characteristic of quiet-time geomagnetic variations. Because the scale of Kp is quasi-logarithmic (i.e. non-linear), it is more convenient to use the related ap index, which has a linear scale with units of nT (see http://www-app3.gfz-potsdam.de/kp_index/apdescription.html). Because values of this latter index, as it pertains to the locality of Potsdam, were not available, the planetary a index (ap) was used in the present paper.

The Polar Cap (PC) index, first proposed by Troshichev et al. (1988), evaluates geomagnetic activity over the polar caps of the Earth with respect to the parameters of the solar wind. Data for the estimation of the PC index are gathered at sites close to the North and South Poles, at Thule (now Qaanaaq), Greenland, and at Vostok, Antartica, respectively. Values from the North Pole site are recorded at 15-min intervals, and averaged hourly values are used in the present paper. There are no units attached to the PC index, though a natural equivalent unit would be mV m⁻¹ (UK Solar System Data Centre).

Statistical analysis

The roots used in the present case showed increasing elongation rates throughout each of the observation periods (see Fisahn et al., 2012). These trends conformed to a logistic function. The rates were then de-trended, or normalized, so that they varied above or below an average value which was set at zero, thereby revealing an oscillatory deviation of rates, ± δR. Normalized time series of δR, as well as normalized time series of the contemporaneous geophysical data, were used in auto- and cross-correlations, and in local tracking correlations.

Periodic components of the various biological and geophysical time series were obtained by a fast Fourier transform (FFT), taking into consideration the restrictions on interpretation of FFT results reviewed by Bergland (1969). Auto- and cross-correlation were used to search for significant time delays between oscillations in pair-wise combinations of the various time series. Periods of the gravimetric tide [intervals between successive maxima or minima (extrema) of δg] were read directly from the Etide output.

Statistical programs for the FFT and the auto- and cross-correlation procedures were obtained from OriginLab at http://www.originlab.com or from Wessa Free Statistics Software at http://www.Wessa.net. Local tracking correlation and local Pearson correlation procedures were performed according to methods described by Papadimitriou et al. (2006).

RESULTS

Correlations between variations of both root elongation rates, δR, and geophysical parameters – lunisolar tidal acceleration (δg) and geomagnetic index variations – were examined for three types of relationships: (1) between δR and contemporaneous δg values; (2) between δR and variations in the values of the Dst, ap and PC geomagnetic indices; and (3) between δg and the geomagnetic variations. Because δg is regarded as independent of the other parameters, the third assay may help distinguish those effects of geomagnetic variation acting upon δR in conjunction with δg, from those effects which arise independently of δg. The present analysis focuses primarily upon the correlations which pertain to the relatively long, circadian periods of oscillation within the time series that characterize the lunisolar tidal rhythms and the root elongation rates, and perhaps the geomagnetic indices, also. A secondary focus concerns shorter, ultradian oscillations, or unanticipated variations, which might exist within the δR time series, and which possibly relate to abrupt variations of the geomagnetic indices.

Alignment of Arabidopsis thaliana root elongation rates with lunisolar tidal profiles

Results from expts 1–3 (see Table 1 and Figs 1–3) concern oscillations of root elongation rates, δR, in relation to those oscillations characteristic of the ever-changing lunisolar tidal force, δg. Oscillations of δR, recorded in expts 2A and 3 (Table 1), and depicted in Figs 2 and 3, have not been published previously. The elongation rates determined for roots in expts 1 and 2 have already been considered in relation to δg (Fisahn et al., 2012), and so will not be discussed from this perspective. However, because these data for δR will be examined for their relationship with the contemporaneous geomagnetic variations, all the data of expts 2, 2A and 3 are illustrated in Figs 1–3. The results from the corresponding statistical analyses, including those from expt 1, are illustrated in Supplementary Data Figs S1–S4. The associated correlative details are presented in Table 2.

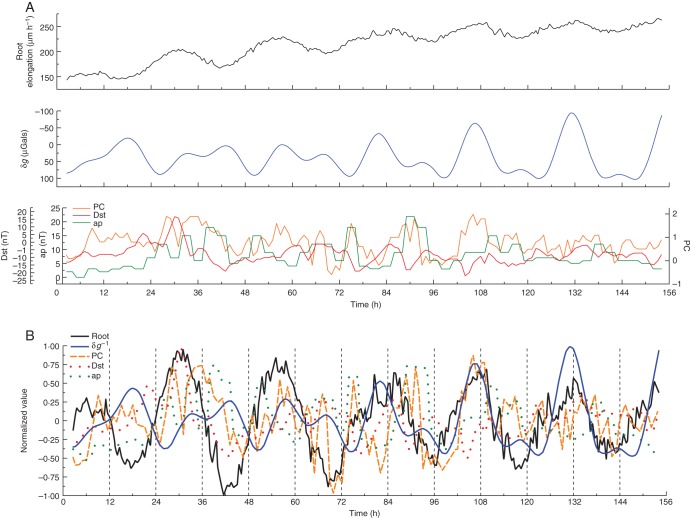
Fig. 1.

Relationships between root elongation rates, lunisolar gravimetric and geomagnetic parameters during early summer of 2008. Time series commenced 27 May 2008 and concluded 2 June 2008. Last Quarter Moon occurred on 28 May 2008. (A) Time series of the mean rates of root elongation (μm h⁻¹) estimated at half-hourly intervals for a set of 23 roots in free-running conditions (top panel), lunisolar tidal acceleration, δg (middle panel) and geomagnetic indices, PC, Dst and ap (lower panel). (B) Same time series as shown in (A), but after removal of the trends displayed by the data points. The normalized curve represents the root elongation rate variation δR. For clarity, the graph of the lunisolar tidal acceleration δg has been inverted relative to this same graph shown in (A), as denoted in the key by δg⁻¹.

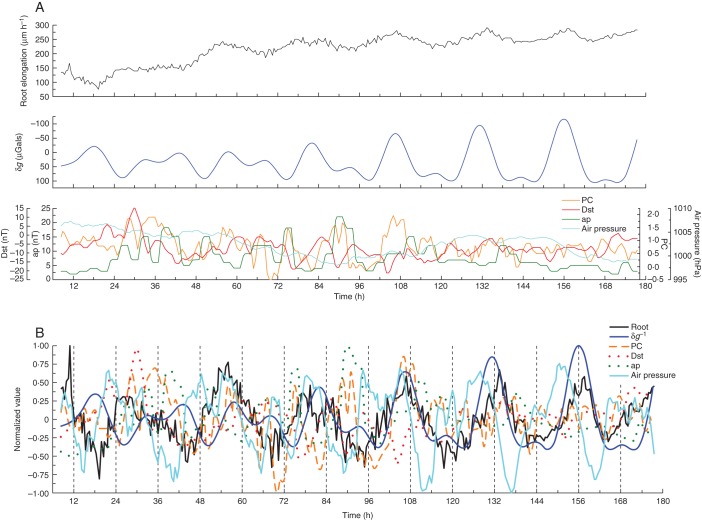
Fig. 2.

Similar to Fig. 1, except that the data for root elongation rate are for one root only (no. 2224) and were extracted from the averaged dataset, illustrated in the upper panel of Fig. 1A. Time series commenced 27 May 2008 and concluded 3 June 2008. The lower panel in (A) includes the actual air pressure (blue line). Shown in (B) is the normalized air-pressure variation.

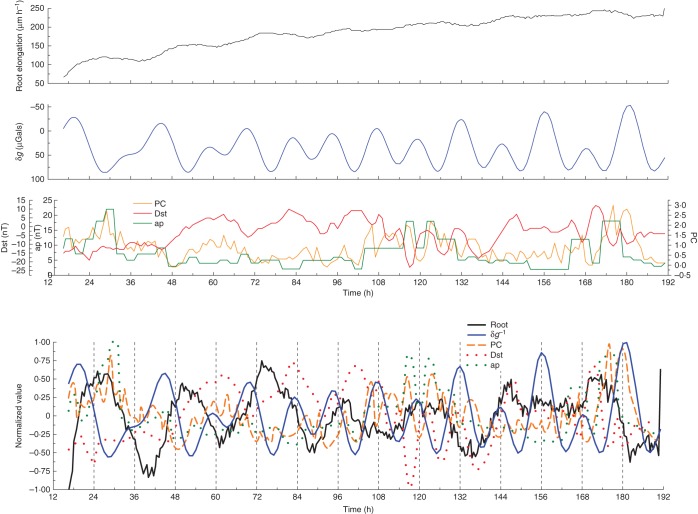
Fig. 3.

Similar to Fig. 1. Time series commenced 13 April 2012 and concluded 22 April 2012. Last Quarter Moon occurred on 13 April 2012 and New Moon on 21 April 2012.

Table 2.

Summary of the local Pearson correlations

(A) δR
	δR vs. δg		δR vs. ap		δR vs. Dst		δR vs. PC
Figure	6 h	12 h	6 h	12 h	6 h	12 h	6 h	12 h
S1A, B	41·2	43·4	17·2	11·1	23·0	21·1	23·4	17·2
S2A, B	26·4	43·0	4·0	7·0	14·1	17·5	17·4	15·0
S3A, B	38·6	32·5	6·6	2·9	33·7	28·7	26·3	16·4
S4A, B	86·3	79·6	49·7	32·9	55·8	35·0	61·5	58·6

(B) δg
	δg vs. ap		δg vs. Dst		δg vs. PC
Figure	6 h	12 h	6 h	12 h	6 h	12 h
S1C	24·7	22·6	41·2	14·7	48·8	37·6
S2C	23·6	19·7	37·7	12·1	47·7	37·9
S3C	17·7	9·3	46·9	30·0	51·8	38·4
S4C	59·2	40·0	55·1	40·4	61·5	61·1

Tabulated are the percentages throughout the various time series when the local Pearson correlations (using sliding windows of 6 h and 12 h) attained values >0·725. The values given are with reference to data in the respective Supplementary Data Figs S1–S4. (A) Local correlations between time series of root elongation rate δR and time series of either the gravimetric tide δg, or the geomagnetic indices ap, Dst and PC (Thule). (B) Local correlations between time series of δg and time series of the geomagnetic indices ap, Dst and PC (Thule).

Experiment 2A relates to observations on one single root (root no. 2224; Fig. 2A, B, and Fig. S2A–D), which was included within the group of roots considered in expt 2 (Table 1). This root was selected at random from the 23 roots whose average elongation rate was determined during May–June 2008 (see Fig. 1A, B). The reason for presenting results from one single root is that both the elongation profile of each root and its possible relationship to geophysical factors are unique. Details of δR are revealed which may be obscured in averaged data (cf. top panels in both Fig. 1A and Fig. 2A), especially when the rates, collectively, conform to a logistic pattern of growth.

Throughout the observation of this single root (root no. 2224), an oscillation in elongation rate was evident (Fig. 2A), with pronounced extrema evident when the rates were normalized (Fig. 2B). On the 5th day, the rate attained a stable value of 220–280 µm h⁻¹, this range of values being accounted for by the oscillation of rates. On each day, the maximum elongation rate coincided with a ‘low’ gravimetric tide (a trough with negative μGal values), whereas minimum elongation rate coincided with a ‘high’ tide (a peak with positive μGal values) (Fig. 2B). On the 3rd day of the time series (at 72–96 h in Fig. 2B, on 30 May 2008), a double peak of rates indicated a disturbance of elongation that commenced 2 d earlier (on 28 May 2008), at Last Quarter Moon. At this time, the gravimetric tide was acquiring a bimodal pattern after 2 d of unimodality (on 25–26 May 2008).

Alteration to the pattern of δR during the period when the gravimetric tide was changing from a unimodal to a bimodal pattern was found in another single root (no. 222, expt 2B – data not shown), though this alteration was perhaps not so clearly expressed as it was in the normalized averaged data of δR from the set of 23 roots of which the two single roots (nos 222 and 2224) were part (see Fig. 1B; 72–96 h, on 29–30 May 2008). The bimodal gravimetric tide became firmly established as the day of New Moon approached, on 5 June 2008, and during this time δR for these roots (Fig. 1B) appeared to adjust to the changing tidal pattern by lengthening the period of elongation rate oscillation (the interval between successive maxima of δR) from 25 h, on 30–31 May 2008, to 30 h on 31 May to 1 June 2008. On the following days (1–3 June 2008), the period diminished to 22 h and 24 h; thereafter, the peak root elongation rates were ‘in tune’ with the major low tides of δg. These characteristics were seen also in the rates from the two individual roots (cf. Figs 1B and 2B).

The ‘re-tuning’ of the variable elongation rate δR with respect to the lunar tidal pattern δg was also evident in results from expt 3, where records of root elongation commenced at the time of Last Quarter Moon, on 13 April 2012 (at 12–24 h on this date, as shown in Fig. 3A, B). On days immediately following the unimodal gravimetric tide (which occurred on 11–13 April 2012), maxima of δR coincided with high gravimetric tides. The rates became disturbed on the days (17–19 April 2012) when the bimodal tidal pattern developed (at 96–168 h in Fig. 3A, B). At these times, maxima of δR occurred at the time of one of the two daily high tides of δg indicative of tidal bimodality. Thus, in each case (expts 2 and 3), disturbance appeared in the pattern of root elongation rates at around the time of Last Quarter Moon. Then, after being broken at the time of tidal unimodality, 2 d before Last Quarter Moon, the coincidence between maximal root elongation rates and high gravimetric tide was re-established. However, it is not yet possible to generalize about how the change from unimodal to bimodal tides affects δR because, on the two dates studied (May 2008 and April 2012), there were differences in the detail of how the pattern of δg changed before, during and after the dates of Quarter Moon.

Alignment of Arabidopsis thaliana root elongation rates with geomagnetic variations

Putative interactions between variations in the terrestrial magnetic field, monitored by the geomagnetic indices, and the growth performance of arabidopsis roots were investigated by aligning the time series of δR with those of the contemporaneous values of the Dst, ap and PC (Thule) indices. Visual inspection indicated that, at various points throughout the geomagnetic time series, there were coincidences between their respective extrema (see upper and lower panels in Figs 1A, 2A and 3A). Local Pearson correlation offered statistical insights into the putative interrelationships between δR and the geomagnetic variations, as well as the relationships between the last-mentioned variations and δg (see Supplementary Data Figs S1A, B, S2A, B, S3A, B and S4A, B). Bar charts denoting the degrees of local correlation (panels at the right side of Figs S1A–S4A) support a general relationship between δR and the Dst, ap and PC indices. Summarized in Table 2A are the percentages of time within the time series when local Pearson correlations exceeded 0·725. Whereas the most frequent local correlations in all time series were between δR and δg, the next most frequent set of correlations was with the geomagnetic index, ap (Table 2A). The frequency data also indicated a relationship between ap and δg (Table 2B).

Detailed inspection of the graphs (Figs 1A–3A) indicated that ap might affect root elongation directly, and in a way independent of δg. One caveat is that, because the values of ap are averaged at intervals of 3 h, the temporal resolution of this index is low, although, in the present case, smoothing and interpolation of hourly values into the 3-hourly averages allowed a correspondence to be made with the hourly values of δR. Similar percentage values (Table 2A) emerged from correlations between δR and the geomagnetic indices, Dst and PC. The point at issue is whether the ‘unexpected’ deviations in δR (‘unexpected’ in the sense that the time courses of the elongation rates are not exactly in accordance with ‘expected’ smooth sinusoidal progressions), an example of which is indicated in Fig. 4, can be associated with evident alterations in geomagnetic index values (‘evident’ in the sense that they exceed a threshold value of 20 nT, which from other evidence is known to be associated with a biological response).

Fig. 4.

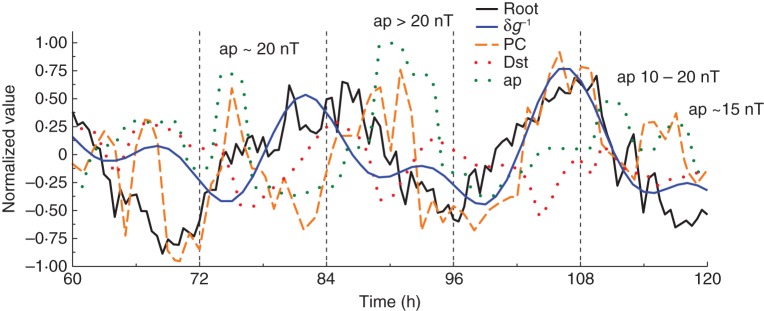
A portion of the normalized graph of Fig. 1B. Root elongation rate variation δR (black line) displayed disturbances simultaneous with temporarily elevated values of the ap and PC indices (green and orange lines, respectively). Also shown is the corresponding portion of the δg profile (blue line).

An attempt was made to characterize these portions of the root elongation rate time series more closely. A damped sine wave was fitted to the normalized values of δR and the residual variations above and below (δRr⁺ and δRr^–, respectively) the fitted line were plotted together with the corresponding normalized time series of the geomagnetic indices (Figs 5–7). Portions of the graph in which δRr⁺ occurred (i.e. where elongation rate was accelerated) sometimes, but not always, coincided with elevated positive index values of ap and PC, and negative values of Dst. For example, in Fig. 5, in which the normalized mean root elongation rate time series for 27 May to 2 June 2008 was used, elevated ap and PC index values corresponded to positions of δRr⁺ at 24–36 h, 48–60 h and 84–106 h; they also corresponded to a position where δRr^– began to ascend from a minimum at 72 h. To analyse further this suggestive feature, the values of δRr⁺ and δRr^– within the time series were plotted against the corresponding index values of Dst, PC and ap. Although there were trends suggesting that increased deviations of root elongation (δRr⁺) were associated with greater PC and ap index values, whereas decreased values (δRr^–) were associated with lesser index values – for the Dst index, it was the negative values which were associated with the positive δRr⁺ values, and vice versa – the large number of data points due to the long time series used meant that there was a great deal of scatter resulting in low correlation coefficients. Nevertheless, certain outlying clusters of points suggested that some of the geomagnetic index values were associated with extrema of δRr⁺ or δRr^–.

Fig. 5.

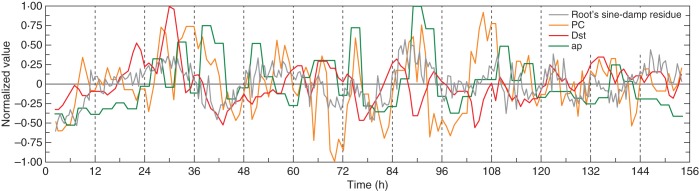
Residuals of the normalized root elongation rate δR, which were shown in Fig. 1B, after fitting a damped sine wave. Residuals δRr⁺ and δRr^– correspond to values above and below the fitted line, respectively. Also plotted are the normalized geomagnetic indices

Fig. 6.

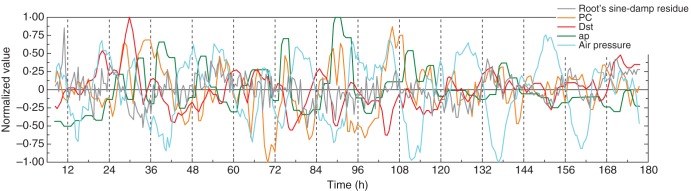
As Fig. 5, except that the data for the residuals were taken from Fig. 2B. The figure also includes the normalized data for atmospheric pressure.

Fig. 7.

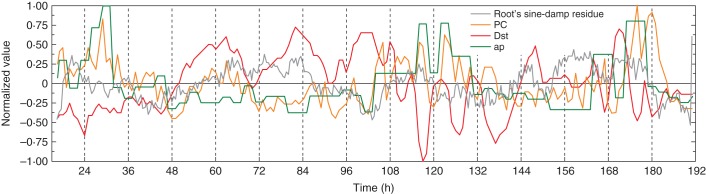
As Fig. 5, except that the data for the residuals were taken from Fig. 3B.

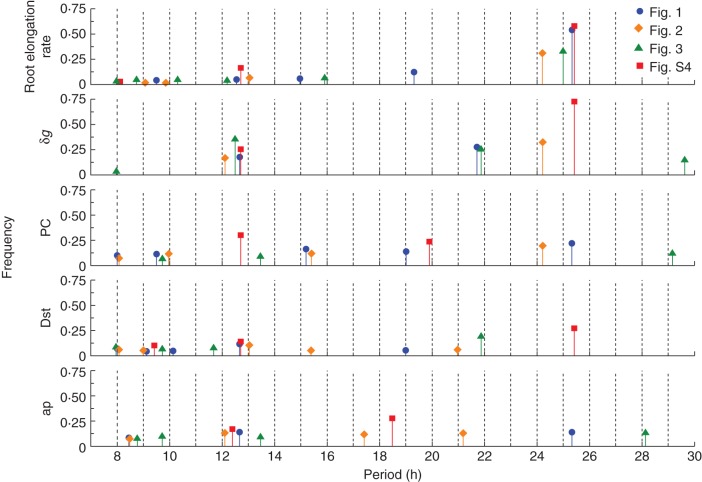
Support for the sensitivity of root elongation rates to geomagnetic variations was also derived from a spectral analysis (FFT) of root elongation rates δR and the geomagnetic index values. The results, summarized in Fig. 8, indicated that there were similar periodicities within the time series of the geomagnetic indices, as well as within those of δg and δR. The most evident periods were approx. 12·5 h and 25 h, values which, although close to the periods of the lunisolar tide, are also close to the period of the solar day; moreover, although they are rather far from the period between sunrise and sunset (approx. 16·75 h and 14·25 h, in the case of expts 2 and 3, respectively), indicating that these two limiting solar conditions are not particularly influential. In one case, periods of 15 h and 19 h were present in both the root elongation data and in the time series of the PC index. Coincidences such as these may indicate relationships between geomagnetic index variations and δR that were independent of δg, particularly since no such periods were found in FFT analyses of the δg time series. Minor periods of 8–12 h emerged in the FFT analysis of the geomagnetic time series as well as in the root elongation data (Fig. 8). Some of these small variations in elongation rate may coincide with the above-mentioned abrupt increases in the geomagnetic indices (see Figs 4–7). However, only with time series more extensive and with a higher density of data than those presently available could the frequency and significance of such correspondences be substantiated.

Fig. 8.

Summary bar chart of periodicities (h) and their relative frequencies, derived by FFT analysis, for root elongation rate and the four geophysical parameter values. Results are from each of expts 1–3 (Table 1) and have been depicted in Figs 1–3 and in Supplementary Data Fig. S4.

Alignments between the time series of all three geomagnetic indices and δR during different seasons of the year were also examined. Relationships during winter (January) 2008 (see Fig. S4) were estimated from FFT analysis and point to mutual correlations. With respect to the Dst and ap indices (but not the PC index), a repeat period of about 12 h was evident in the January 2008 data, presented in Fig. S4; a similar period was found for δR. These periods were also found within data obtained in early summer (May) 2008 (Fig. 8, and Figs 1 and 2). Geomagnetic and δR time series for April 2012 revealed periodicities of 25 h (Fig. 8), particularly for the Dst index. Also, a period of approx. 9–10 h appeared in both δR and the geomagnetic index values (Fig. 8). Thus, seasonality does not seem to affect the relationships between the biological and the geomagnetic variables.

Alignment of Arabidopsis thaliana root elongation rates with atmospheric pressure variations

According to Ortega (2010), atmospheric pressure could theoretically affect cellular turgor pressure (Ortega, 2010) and, hence, influence the rate of cell elongation. Therefore, this relationship was briefly explored because oscillation of atmospheric pressure might contribute to the small-scale variations of growth which underlie the oscillations of root elongation. Although periodicity of atmospheric pressure was noted during the course of the experiments (see Fig. 2A), the major pressure oscillations had periods different from those observed for the elongation rates, and the maxima and minima of δR did not coincide with the analogous extrema of atmospheric pressure. On one occasion, however, normalization of the pressure data did reveal a regular oscillation embedded within the total time series, and which appeared to relate to the residual of δR (e.g. Fig. 6). A feature such as this should be noted when any further work of this nature is undertaken.

DISCUSSION

Apparent relationships between diurnal variations of biological parameters – arabidopsis root elongation rate, in the present case – and geophysical parameters, such as the lunisolar tidal variation and geomagnetic indices, are necessarily correlative; and even when accompanied by statistical significance, the validity of such dependence would benefit from experimental support. At present, this type of support is difficult to achieve. Nevertheless, genetic analysis of rhythmic diurnal- and lunar-modulated developmental controls (Kaiser et al., 2011), as well as knock-out genetic techniques (Takekata et al., 2012) have been able to dissect the relationships between rhythmic biological responses and their putative timekeepers, or Zeitgebers. Furthermore, experimental work is beginning also to replicate – and hence complement – the purely correlative evidence that has accrued from biological observations with respect to geomagnetic variations (Michon and Persinger, 1997; Mulligan and Persinger, 2012).

Although the correlation between root elongation rate and the lunisolar tidal acceleration δg has been discussed elsewhere (Barlow and Fisahn, 2012; Fisahn et al., 2012), the inclusion here of geomagnetic indices adds an additional dimension to the putative relationship between variation of root elongation rate δR and extrinsic factors (cf. Brown, 1962, 1969). This might be especially interesting if geomagnetic variation were strongly influenced by the lunisolar tide; in short periods of a few days, this seems not to be the case, however. Equally interesting would be the alternative possibility: that there could be geomagnetic effects on δR independent of δg.

Each of the four time series of root elongation rate, illustrated in Figs 1–3, and also Fig. S4A, show an oscillation of δR in synchrony with that of the lunisolar tide δg. This synchronization has been validated by cross-correlation and local tracking correlation (Fisahn et al., 2012). It seems, therefore, to indicate an integrated ‘cosmic–biological’ response (Barlow, 2012). The oscillations of δR were revealed under free-running conditions of continual low light, a condition which, in many experiments with animals, has revealed behavioural rhythms co-ordinated with the lunar tide (Brown et al., 1956; Naylor, 1958; Brown, 1965; Zeng and Naylor, 1996; and see also Barlow, 2012). It should be added that variations in the capacity of the roots to lubricate the path along which they grow, as noted by Iijima et al. (2003), appeared not to apply here to the arabidopsis roots: no visible changes were observed at the root tips which could have indicated rhythms of mucilage secretion from the cap.

Furthermore, in regimes of alternating light and dark, fast-growing shoots of Hibiscus cannabinus also showed oscillations in elongation rate which were in synchrony with the lunisolar tide; and here the times of maximum and minimum growth bore no relationship to the times of light or dark (Yamamoto, 2012). One implication for both root and shoot structure of an oscillating elongation rate, especially if both cell growth and cell production have achieved steady state, is the expectation of an oscillation of final, mature cell length, resulting in alternating zones of long and short cells along the length of the respective organs. An alternative possibility is that meristem cell-production rates may oscillate, perhaps in accordance with a diurnal timing of stem-cell divisions (Aguilar-Arnal and Sassone-Corsi, 2011).

So far, the only theory which links not only lunisolar gravitational acceleration with plant growth but also suggests a means by which the weak lunar force might be registered by plants, is that proposed by Dorda (2010) and elaborated by Barlow and Fisahn (2012) and Fisahn et al. (2012). In this model, growth is modulated by a lunisolar gravity-regulated movement of coherent water aggregates into and out of deformable cells.

With respect to GMF variation, it is possible that this factor is a weak modulator of root growth rate, perhaps in conjunction with the lunar tide. In the present study, however, the recorded geomagnetic variations were due to the variability inherent to ‘quiet-day’ GMFs. In this regard, data from longer time series, perhaps in conjunction with the exploratory tool of principal component analysis, might begin to pinpoint more accurately the influence on root growth of geomagnetic variation, even on ‘quiet’ days. From the point of view of discovering strong responses in the biological material in relation to geomagnetic variation, magnetic storm conditions would need to apply, when ap values >50 nT and Dst values <–50 nT are attained during the course of the observations. Such events were not present; but probably they would have helped emphasize the putative geomagnetic interaction with root elongation, as they did during the observations of Neamţu and Morariu (2005) on seedling root growth, when ap values >20 nT were associated with stimulatory responses in their test material.

Nevertheless, as considered by Brown (1969), it may be that, when certain relationships exist between the geomagnetic variation and the lunisolar tidal force, there could be periods when either enhanced or diminished growth takes place. Also possible is that geomagnetic variations modulate growth irrespective of δg; inspection of the respective portions of normalized time series (Figs 4–8) suggests this may be so. Intrinsic geomagnetic variation, therefore, although unpredictable in its occurrence, may serve as a weak modulator of root growth, supplementing the stronger guidance system provided by δg (Fisahn et al., 2012). However, once consideration is given to short-term, ultradian oscillations of root elongation, one is then inevitably drawn to consider all the other ultradian oscillations, such as apply to neutron fluxes, which exist within the external environment and which may or may not contribute to some of the ‘noise’ evident in the plots of the δR time series.

An unsolved question is whether the contribution of each factor – lunisolar and geomagnetic – to growth modulation can be separated or distinguished. Local Pearson correlations for geomagnetic parameters versus root elongation rate indicate that there are many occasions when the correlations are significant (Pearson correlation values >0·725) (Table 2A). Results from FFT analysis (Fig. 8) point in the same direction. Moreover, there are positions along the δR time series where unexpected deviations from a smooth rate of change of elongation rate coincide with abrupt alterations in the geomagnetic indices (Figs 5–7). The local Pearson correlations suggest that the geophysical conditions which underlie the ap index may be influential to root growth. Interestingly, in a recent model (Khabarova et al., 2010) of biomass production within both deciduous and evergreen coniferous forests of northern Eurasia in response to incoming photosynthetically active radiation (PAR) plus geomagnetic variations over a 25-year period, the correlation between the cumulative PAR and biomass was significantly less when the cumulative annual Kp index values were omitted from the estimated radiation energy input. In such studies, variations in acidity (pH) of the soil in response to variations in the Kp index have to be taken into account (Mullenax et al., 2001); Dubrov (1978) draws attention to relatively large variations in the rate of secretion of ‘physiologically active substances’ by roots into the soil and correspondingly large contemporaneous variations in the GMF. Therefore, in the wider environment, GMF variations, besides their possible direct effects on whole plant growth, may also affect growth indirectly, via alterations to soil chemistry and their consequent effects on root growth and function.

The complexity of interactions between geophysical parameters and experimental biological material has been described by Brown et al. (1957), Brown (1962, 1969), Levengood (1965) and Truchan and Boyer (1972). Although conventional growth chambers reduce much of the variation inherent to the immediate environment of the experimental plants, other variables within the wider environment, such as the lunisolar tidal force, atmospheric pressure and atmospheric ions, cannot be entirely removed or compensated for. However, growing conditions have been developed whereby external geomagnetic influences are counteracted (Neamţu and Morariu, 2005; Mo et al., 2011; Xu et al., 2012), so enabling the biological material to respond to intrinsic or storm-induced geomagnetic variations. Moreover, experiments are envisaged for the International Space Station (Spacelab) where the mutually interacting effects of gravity and geomagnetism can be uncoupled (Yamashita et al., 2004), thus enabling the effects of each to be studied separately. In future, it should be possible to make comparative studies of the oscillation of root growth rates, such as we have observed, using facilities where GMF variations are simultaneously either compensated for or allowed free expression.

Experimental work on plant responses to magnetic fields has often involved short-term application of fields with strengths in the range of milliTesla (mT), whereas the intrinsic variation of GMFs at the Earth's surface (where the field strength is about 20–50 × 10³ nT) is, on magnetically ‘quiet’ days, in the range of a few nanoTesla (nT). Increases to the field of up to 100 nT occur only during ‘strong’ magnetic storms. The latter conditions occurred during the experiments on seed germination performed by Neamţu and Morariu (2005). However, in both cases – where experimental magnets have provided fields in the order of mT, and magnetic storms have generated geomagnetic variations in the range of tens of nT – the outcomes were similar: in neither case did the effects on seed germination rate exceed 10 % (magnets – see Phirke et al., 1996; Flórez et al., 2007, Radhakrishnan and Kumari, 2012; Vashisth and Nagarajan, 2012; Reddy et al., 2012: magnetic storms – see Neamţu and Morariu, 2005). This suggests that the threshold dose to achieve the maximum 10 % response with germination rate is quite low – perhaps about 20–50 nT, according to data of Neamţu and Morariu (2005). Thus, small variations of the intrinsic GMF may be able to achieve minute variations in growth rate, such as we observed in the present work with arabidopsis roots. Interestingly, in observations of the responses of rat and human subjects to applied magnetic variation, 20 nT was also the threshold for a measurable effect (Persinger and Richards, 1995; Michon and Persinger, 1997; Mulligan and Persinger, 2012). However, an increase in magnetic field strength of 70 nT was found to inhibit the response (Mulligan and Persinger, 2012), a finding which is in line with one result in the series of germination tests performed by Neamţu and Morariu (2005) where geomagnetic variation of 100 nT was inhibitory.

The mechanisms which have been proposed to mediate the responses of biological material to magnetic fields are various and largely untested (Binhi, 2001; Belyavskaya, 2004; Binhi and Rubin, 2007). However, the biomolecule, cryptochrome, has become a focus of attention, not only with respect to plant responses in magnetic and GMFs (Galland and Pazur, 2005) but also on account of its function in the pathway to the circadian clock of Arabidopsis thaliana (Tóth et al., 2001). Moreover, experimental and theoretical work of Ahmad et al. (2007) and Solov'yov et al. (2007) has demonstrated this molecule's sensitivity to blue light and the possibility that this sensitivity is affected by weak magnetic fields. Cryptochrome has been therefore tentatively proposed as one possible mediator of the effects of magnetic fields upon plant growth; and it is also this molecule which is proposed to mediate the navigational ability of birds with respect to the Earth's magnetic field (Solov'yov et al., 2007; Ritz et al., 2009).

The observation of Neamţu and Morariu (2005) that seed germination was sensitive to conditions of magnetic storms has already been mentioned. These authors also observed that the growth of rye roots was sensitive to storm conditions, being either diminished or stimulated (Neamţu and Morariu, 2005). It is possible that, during magnetic storms, there are also changes in the ionic charge (electrostatics) of the ambient atmosphere; and it is this change, rather than variation in the GMF per se, which enhances seed germination rate. The possibility of magnetic-induced electrostatic, air-ion effects has been proposed by Levengood (1965) and Krueger and Reed (1976) in relation to cellular and developmental responses. However, Maw (1967) in his examination of cress (Lepidium sativum) seedling development in relation to artificially generated atmospheric ions, claimed that, whereas seed germination rate was unaffected by such ions, these air-ions were instrumental in affecting the rate of seedling growth.

Interestingly, Maw (1967) also found that, over a 20-month period, maximum seedling growth in response to negative air-ions occurred close to the time of First Quarter Moon whereas minimal ion-stimulated growth occurred between Last Quarter and New Moon. Atmospheric electricity has been reported to increase and then decrease on the days, respectively, just before and after Full Moon (Mehra, 1989), and often there are corresponding rises and falls in the Kp index during this period (Stolov and Cameron, 1964; Bell and Defouw, 1964, 1966). The timing and degree of the variation in Kp are also modulated by the celestial latitude (declination) of the Moon in accordance with the season of the year (Stolov, 1965; Matsushita and Maeda, 1965), features which might have a bearing on the finding of seasonal effects on growth in response to air-ions (Maw, 1967). Therefore, it seems that with the equipment now available to define growth rates with great precision, it would be worthwhile to devise experiments to uncover the effects of atmospheric ions on plant growth – and root elongation rate should here be a sensitive marker of such effects – and their possible links with the lunisolar tide, and GMF variation.

CONCLUDING REMARKS

The data presented provide support for effects upon root elongation of both the lunar tide and variations in the magnetic field of the Earth. These effects have implications for the performance and productivity of higher plants in general. For instance, annual variation of the GMF, as evaluated by the ap and Kp indices, could be a factor accounting for temporal variations of plant biomass production. Variations of these geomagnetic indices may also impinge upon the growth of arabidopsis roots under free-running conditions. Although co-ordination, or co-operation, between the lunisolar tide and geomagnetic variation may sometimes be apparent, this does not necessarily indicate a close coupling between these parameters in the regulation of growth. Nevertheless, it suggests that biological material may perceive GMF variations, in addition to guidance received from the lunisolar tide, thereby maintaining a rhythmic pattern of growth, including that of root elongation. One important feature could be that this relationship helps adjust the rhythm of growth at times when the lunisolar tide passes from unimodality to bimodality and vice versa.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of Figures S1–S4, which detail the Pearson correlations relating to Figs 1–3 in the main text.