Probing microscopic material properties inside simulated membranes through spatially resolved three-dimensional local pressure fields and surface tensions

Abstract

Cellular lipid membranes are spatially inhomogeneous soft materials. Materials properties such as pressure and surface tension thus show important microscopic-scale variation that is critical to many biological functions. We present a means to calculate pressure and surface tension in a 3D-resolved manner within molecular-dynamics simulations and show how such measurements can yield important insight. We also present the first corrections to local virial and pressure fields to account for the constraints typically used in lipid simulations that otherwise cause problems in highly oriented systems such as bilayers. Based on simulations of an asymmetric bacterial ion channel in a POPC bilayer, we demonstrate how 3D-resolved pressure can probe for both short-range and long-range effects from the protein on the membrane environment. We also show how surface tension is a sensitive metric for inter-leaflet equilibrium and can be used to detect even subtle imbalances between bilayer leaflets in a membrane-protein simulation. Since surface tension is known to modulate the function of many proteins, this effect is an important consideration for predictions of ion channel function. We outline a strategy by which our local pressure measurements, which we make available within a version of the GROMACS simulation package, may be used to design optimally equilibrated membrane-protein simulations.

1. Introduction

Pressure and surface tension are important macroscopic observables of soft materials such as lipid membranes. These properties can be used to explain processes like phase separation, micelle formation, and the structure and assembly of biological membranes. Although pressure and surface tension are ensemble averages, they are not spatially uniform, and local variations often play a critical role in membrane structure. Protein insertion or membrane deformation causes inhomogeneous and often asymmetric perturbation in local pressure, and the surface tension can also undergo substantial local fluctuation; the magnitude of these fluctuations may be important for lipid–protein interactions and membrane shape changes. For instance, antimicrobial peptides are thought to induce lateral pressure anomalies as part of their activity (Liu and DeGrado, 2001; Schibli et al., 2002; Tieleman et al., 2003; Zhao et al., 2002), and mechanosensitive channels are responsive to pressure changes (Gullingsrud and Schulten, 2004; Moe and Blount, 2005; Perozo et al., 2002; Weiss et al., 2003). These quantities are extremely difficult to measure with high spatial resolution via experiment, although macroscopic measurements of their average are feasible.

Due to the magnitude of the fluctuations involved, substantial sampling is required to achieve converged predictions of surface tension via simulation. Until recently, this sampling requirement and the computational power available dictated heavy spatial averaging for computational predictions of local pressure (Lindahl and Edholm, 2000b). Recent advances in computational capacity and parallel simulation technology have enabled much more extensive simulation sampling of membranes on a routine basis.

The ability to measure pressure in a 3D-resolved manner presents several advantages. It enables the evaluation of spatially inhomogeneous phenomena such as the behavior of bilayer lipids around proteins. It also enables the measurement of local fluctuations in a simulated system and the relation of surface tension fluctuations to changes in bilayer structural properties. In more complex lipid mixtures, it enables the measurement of surface tension in regions of composition fluctuation, a quantity believed important to the formation of lipid microdomains or cholesterol–lipid complexes (Baumgart et al., 2003; Honerkamp-Smith et al., 2008; Rietveld and Simons, 1998).

However, local pressure itself is not trivial to calculate: even the first calculations on ordered systems (Lindahl and Edholm, 2000b) showed that the z-component was not constant, which it should be at equilibrium. Part of this is due to finite molecular size being a natural limit to the resolution, but there have also been methodological issues where bond length (and potentially other) constraints in particular appear to introduce artifacts in non-isotropic systems such as membranes.

Here, we present a means to calculate 3D-resolved local pressure fields and surface tension in simulations that is a substantial advance over the traditional 1D profiles previously used by us and others. We also present a new correction to correctly account for constraints in local virials and thus spatially resolved pressure fields. We have integrated this measurement capability into a publicly available special version of the GROMACS molecular simulation software. In this work we employ atomistic representations of lipids and proteins in these simulations to maximize quantitative reproducibility of experimental phenomena, particularly those relating to lipid tail order and protein conformational dynamics. Calculations using an early version of our code without the constraints corrections were previously reported for coarse-grained lipid systems (Ollila et al., 2009). The present implementation has explicitly been designed to support virtually any force field based on pairwise interactions, including atomistic representations, tabulated forms and coarse-grained representations – and it will provide accurate results for systems with constrained bond lengths We calculate the full 3D spatially resolved pressure tensors over arbitrary-size subcells of the triclinic box used to represent the system in GROMACS, enabling local pressure computation in non-rectangular geometries such as hexagonal boxes, truncated octahedra, or rhombic dodecahedra. Local differential pressure along any surface can easily be calculated as the difference between the tangential and normal components of the local pressure, for instance along a vesicle surface or local membrane patch. The surface tension is simply the integral of this quantity across a leaflet or bilayer.

We report the use of this technical advance to measure local pressure and surface tension fluctuations within simulations of large fluid bilayers and the local perturbation of bilayer properties by transmembrane proteins. In particular, resolving local pressure beyond simple profiles provides a means to assess long-range effects from membrane perturbations and to guide inter-leaflet membrane equilibration; we present the use of local differential pressure measurements as an efficient and accurate way to direct the construction of membrane-protein simulations with the optimal number of lipids in each leaflet.

2. Theory

Pressure is formally an ensemble property of a system corresponding to the surface integral of the external force. This is not directly accessible in a molecular simulation but can be calculated by using the virial theorem (Hansen and McDonald, 1976):

$$2\mathbf{K}=\mathrm{\Xi }$$ (1)

where K is the full average kinetic energy tensor, and Ξ is the virial

$$\mathrm{\Xi }=-\sum _{i=1}^N{\mathbf{r}}_i\otimes {\mathbf{F}}_i$$ (2)

where F_i is the force on particle i located at position r_i. This total virial has an internal component from intra-system forces (available in the simulation) and an external contribution caused by the normal pressure p_N on the cell surface S,

$${\mathrm{\Xi }}_{int}=-\sum _{i=1}^N{\mathbf{r}}_i\otimes {\mathbf{F}}_i^{int}$$ (3)

$${\mathrm{\Xi }}_{\text{ext}}={\int }_S{p}_N\mathbf{r}\otimes d\mathbf{S}$$ (4)

From this it is possible to solve for the pressure tensor and get an expression that can be evaluated in a simulation

$$\mathbf{p}=2\frac{\mathbf{K}-{\mathrm{\Xi }}_{int}}{V}$$ (5)

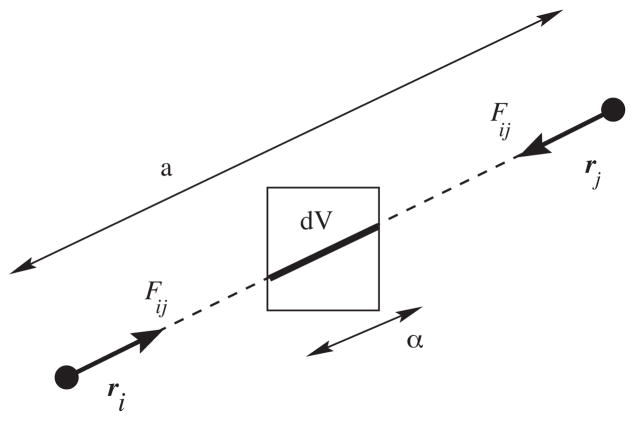
where V is the volume of the system. While formally still an ensemble property, this expression can be extended to microscopic subsystems. The kinetic energy tensor reduces to a sum over the particles present in such a subvolume. In the case of central pair-additive potentials for particle interactions, the internal virial can be written on the Irving–Kirkwood contour form (Irving and Kirkwood, 1950):

$${\mathrm{\Xi }}_{int}=-\sum _{i<j}{\mathbf{r}}_{ij}\otimes (-{\mathbf{F}}_{ij}){\int }_0^1\delta [\mathbf{R}-\lambda {\mathbf{r}}_j-(1-\lambda ){\mathbf{r}}_i]d\lambda$$ (6)

This amounts to tracing a linear path between each pair of interacting particles, dividing the virial uniformly along the path, and obtaining the total virial as a path integral. This definition of the virial can obviously be made local by limiting the integral to the part of the path that falls in a particular volume (Fig. 1). Unfortunately this approach does not readily extend to lattice summation methods where an interaction cannot be attributed to a specific path between pairs of particles. Sonne et al. (2005) have shown that the alternative Harasima contour makes it possible to calculate the local component from classical Ewald summation, subject to certain assumptions. Due to the high O(N²) computational complexity this is not a realistic alternative for large simulations, but their tests on smaller reference systems confirmed that the Irving–Kirkwood result for medium to long cut-offs are very close to the Harasima/Ewald result.

Fig. 1.

The configurational part of the local pressure is evaluated as the projection of the pairwise virial on subvolumes (3D grid cells). If the force between particles i and j is F_ij, the interaction contribution to the local virial in this cell will be Ξ_ij = −(α/a)r_ij ⊗ F_ij.

2.1. Local virial calculation with bond constraints

The presence of bond constraints can lead to difficulties when calculating the local virial as defined above. Usually, the forces in a system with constraints are determined by first calculating the unconstrained forces as if no constraints were present in the system. During the application of the constraints, a correction to the force is then derived. The result for the force on atom i is simply the sum of the unconstrained force and constraint force correction

$${\mathbf{F}}_i={\mathbf{F}}_i^{\text{unc}}+{\mathbf{F}}_i^{\text{constr}}$$ (7)

The virial contribution from the potential including constraint effects is also easily determined, since forces are additive

$$\mathrm{\Xi }=-\sum _{i<j}{\mathbf{r}}_{ij}\otimes {\mathbf{F}}_{ij}^{\text{unc}}-\sum _c{\mathbf{d}}_c\otimes {\mathbf{F}}_c$$ (8)

Here, d_c denotes the distance over which constraint c is being applied, and F_c is the corresponding force correction. However, in contrast to the normal force, it is not correct to simply distribute the constraint contribution in Eq. (8) along the vector d_c when spatially assigning virial contributions to the 3D field. Forces between the two particles in a constraint will be canceled out from the virial, but any difference in force between two atoms in a constraint due to forces from other atoms in the system will lead to artificial virial contributions along the constraint vector. A simple example would be a monopole–dipole interaction where the dipole consists of two oppositely charged particles connected by a constraint. At large distances, the opposing forces acting on the two particles would largely be canceled by the large constraint force acting on each of them. In Eq. (8), this would lead to a large virial contribution along the short constraint vector inside the dipole, together with a large virial contribution along the monopole–dipole vector. For long distances the virial contribution along the monopole–dipole vector is independent of distance, whereas it really should be inversely proportional to the distance. These artifacts mainly show up for long-range Coulomb interactions since the virial contribution might not decay with distance for arbitrary net charge Coulomb interactions. In practice biomolecular systems are approximately locally neutral due to their isotropy and homogeneity, and Coulomb forces between molecules and their virial contributions do decay – but this holds at large distances! Systems with inhomogeneous charge distributions such as solvated bilayers will exhibit large virial effects over length scales of several nanometers.

The solution to these artifacts is to take the constraints explicitly into account when determining the local virial contributions. Since the main effects come from Coulomb monopole–dipole and dipole–dipole forces, a first-order approximation that only considers the constraints in strong dipoles should suffice for most purposes. If groups of atoms or particles are rigid, the forces between their centers-of-mass can be used in the virial calculation. This exact solution is particularly useful with rigid water models or constraints on bonds connecting hydrogens to heavier atoms. When constraints are applied on all bonds in a molecule, the exact calculation becomes complicated and an approximation is preferred. This can be done using groups with approximately zero (or unit) net charge, similar to the charge group concept that long has been used in force fields to avoid cut-off artifacts. If such groups are not completely rigid internally, a small error is introduced, but since this is a short-range effect it will have little effect on the total virial. The effect from constraints between atoms in different charge groups can be approximated by distributing the forces equally over the atoms in the groups, applying the constraints, and finally distributing the force correction over the constraint vector. This too will only lead to small local errors. The required approximations can make this methodology difficult to apply on-the-fly in a parallel molecular dynamics simulation, but since local pressure calculations are very slow in the first place and there are long correlations, pressure analysis is anyway typically done on ensembles of conformations from trajectories. Running the above calculations in a serial manner on a previously determined trajectory is much more straightforward.

3. Implementation

An obvious and straightforward implementation of one-dimensional local pressure is to simply sum over x–y slices in a simulation box (Goetz and Lipowsky, 1998; Lindahl and Edholm, 2000b). The situation in 3D is a bit more complicated; the virial cannot be equally divided between all cells crossed by the path, but must be weighted by the fraction of the interaction path in Eq. (6) that falls within that cell. While that can be calculated exactly, it is unnecessarily expensive for normal simulations. Instead, for every pairwise interaction in the system we first define a connecting linear path, on which we place N_point (100–1000) evenly distributed points. Each of these points will fall in a given volume cell and will contribute a factor 1/N_point of the local virial for the interaction to that cell.

The large number of cell updates unfortunately makes the calculation of 3D pressure fields significantly slower than one-dimensional profiles. However, since pressure de-correlates slowly, it is typically more efficient to perform a two-pass calculation as follows. The first pass is to run a normal simulation and save velocities and coordinates at suitable intervals (we use 100 ps for atomistic systems). A second pass evaluates local pressure on the saved frames only, resulting in a ~500,000-fold speedup compared to local pressure evaluation every time step.

We have implemented this definition of 3D pressure fields in a special version of GROMACS 4, since it requires full evaluation of the virial inside the innermost kernels. This procedure is computationally quite expensive and thus best used for rerunning trajectories as described above. The pressure field grid can have arbitrary triclinic shapes, and the full anisotropic local pressure tensor is computed for each grid cell. This also makes it possible to calculate local surface tensions along arbitrary surfaces.

4. Simulation methods

Simulations were run using GROMACS 4 (Hess et al., 2008); full simulation parameters are given in Table S1. Berger force field parameters were used for the lipids (Berger et al., 1997), AMBER03 parameters for the proteins (Duan et al., 2003), and TIP3P parameters for the water (Jorgensen et al., 1983). Temperature and pressure were controlled via Berendsen weak coupling; a temperature of 300 K was used for the former with 0.1 ps coupling time, and the latter employed semi-isotropic pressure coupling with a time constant of 1.0 ps.

Simulation trajectories were computed using Particle Mesh Ewald electrostatics (Darden et al., 1993) with a direct-space cutoff of 1.0 nm and a grid spacing of 0.12 nm. The non-local component of PME cannot be readily utilized for local pressure computation, so rerun virials were computed using reaction-field electrostatics on the coordinates generated via the PME trajectories. This may cause a slight bias in the local pressure calculation, but we believe this is the best compromise between the better accuracy of long-range electrostatics and the challenge of calculating local pressure for reciprocal-space interactions. The spatially varying component of pressure part is well described by the short-range forces, and while the long-range forces contribute to the net pressure on the system they are unlikely to cause local and rapidly changing components. A cutoff of 1.4 nm and a dielectric constant of 20 were used for the reaction-field calculations. Bond lengths were constrained with LINCS (Hess, 2008), and a time step of 2 fs was employed.

The membrane protein was inserted in the membrane using the GROMACS genbox program to delete all lipid and water molecules that that overlap Van der Waals radii with protein atoms. Due to the shape of the protein, this typically results in an asymmetric distribution of lipids between upper and lower monolayers. Insertion using the g membed utility (Wolf et al., 2010) yielded a similar asymmetric distribution (with the numbers of lipids deleted varying depending on the initial scaling). Because bilayers are relatively sensitive to pressure changes and typical simulations have only several hundred lipids per leaflet, a small imbalance may have large effects on protein conformation and dynamics.

The protein was position restrained for 10 ns of equilibration, and during the first 5 ns the water was also restrained in the z-dimension to avoid solvent entering the space between protein and lipids. Subsequently, 0, 10, or 20 lipids were removed from each layer to construct five test systems to assess surface tension equilibration between monolayers. Each system was re-equilibrated again for 10 ns prior to a 100-ns production run.

5. Results

Spatially resolved local pressure calculations allow analysis of both pressure fluctuations and spatial inhomogenieties in membrane structure. Here, we present simulation data on three systems that illustrate these applications: a pure POPC bilayer, a bilayer containing the core domain of the Gloeobacter violaceus pentameric ligand-gated ion channel (GLIC), and a series of GLIC-bilayer simulations where the number of lipids in each leaflet were systematically varied to assess pressure equilibration.

5.1. Pure POPC bilayer

We first analyzed local pressure in a pure POPC bilayer. Measurements in this context are important in assessing the materials properties of the bilayer and the equilibrium fluctuations of a planar membrane. Previous work using 2D-averaged surface tension calculations has examined a 256-lipid DPPC bilayer simulated for 5 ns (Lindahl and Edholm, 2000b). We now examine a substantially larger 1024-lipid POPC bilayer simulated for 100 ns; this increased sampling lets us address spatial variation and fluctuation of local differential pressure in a robust manner. A study by Ollila et al. (2009) used a preliminary version of our software to examine coarse-grained lipids; in this work we have used atomistic-resolution lipids, aiming to maximize quantitative reproducibility of experimental observables. NMR ²H order parameters calculated from our simulation well reproduce experimental values (Seelig, 1977) at the same temperature (Fig. S1; r = 0.98, average difference = 0.04) and also experimental areas per lipid head group (70 ± 1 A²/lipid compared to 68.3 ± 1.5 (Kucerka et al., 2005); the slightly higher area per head group in the simulation is reflected in the slightly lower SCD value).

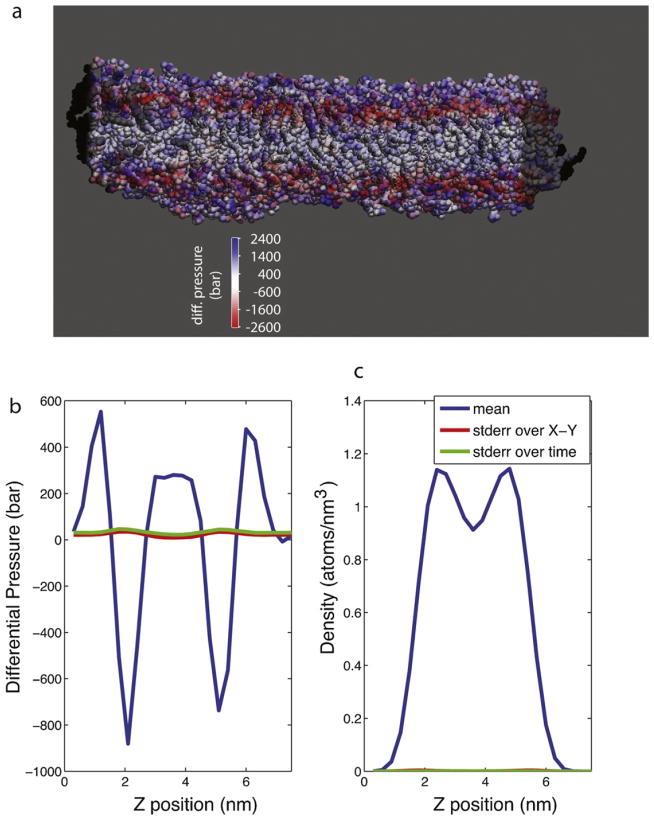
Time-averaged differential pressure values for the 100 ns simulation are rendered in Fig. 2; the bilayer undergoes substantial pressure fluctuations both within each x–y slice and over time. These fluctuations are largest in the head-group region, while the hydrophobic core remains more stable. Local differential pressure averaged across the x–y plane over the entire simulation (Fig. 2b) shows a similar profile to that previously calculated for DPPC (Lindahl and Edholm, 2000b) with a peak and then a dip in the head group region and a slight elevation in the hydrophobic core region; the fine-scale difference in the hydrophobic core likely reflects differences in the tail group structure between POPC and DPPC.

Fig. 2.

Surface tension in a pure POPC bilayer. Rendered in (a) is a snapshot of the lipid bilayer colored by local differential pressure to show the substantial spatial variation. Water molecules are not shown. The differential pressure is plotted in (b) as a function of z-coordinate in the bilayer, and lipid density is plotted in (c) as a function of z-coordinate. Blue lines denote the average over each x–y slice and over the full 100-ns simulation. The standard error within each x–y slice, averaged over time, is plotted in red, and the standard error over time, averaged over each x–y slice, is plotted in green. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

Simulated planar bilayers are known to undergo undulations, or local fluctuations in position along the bilayer normal (Lindahl and Edholm, 2000a; Marrink and Mark, 2001); we observe such motions in our simulation (Fig. 2c), which we assess as both static and dynamic variation in the local membrane curvature energy (Safran, 1994). It is unknown whether these local curvature deformations induce imbalances in local pressure or if the local density and pressure remain in equilibrium despite surface displacements. In our simulations, we do not detect any correlation between local differential pressure at a given point on the bilayer surface and displacement in the z-direction: |r| < 0.1 between γ(x,y,z) and ρ(x, y, z) − ρ_avg(x, y, z), where γ is differential pressure and ρ is lipid density. We also do not detect a correlation (|r| < 0.1) between local differential pressure γ(x, y) and local curvature energy E_und(x, y) = 0.5k_c|∇²f(x, y)|² + 0.5γ|∇f(x, y)|² for a function f(x,y) denoting the membrane surface, the bending modulus k_c, and an external surface tension γ, which is 0 in our case (Lindahl and Edholm, 2000a; Safran, 1994). This lack of a linear correlation does not preclude a more complex nonlinear relationship, however.

5.2. A POPC bilayer containing the GLIC transmembrane domain

Proteins can have bidirectional interactions with the physical properties of their membrane environment. The function of many membrane proteins is affected by changes to their surrounding bilayer (McIntosh and Simon, 2006), while others are known to modulate bilayer properties such as curvature or local ordering (Hu et al., 2008; Martens et al., 2007; Zimmerberg and Kozlov, 2006). Such effects, though experimentally observable, are difficult to probe at spatial high resolution using currently available experimental techniques. Computational measurements of local pressure and surface tension provide another means to assess protein effects on bilayer order and bilayer materials properties. Here we report analyses of a POPC bilayer containing the transmembrane region of the GLIC ion channel, a prokaryotic pentameric protein that has been studied as a prototype for the nicotinic acetylcholine receptor family (Bocquet et al., 2009; Hilf and Dutzler, 2009). Several studies have shown that lipid composition and the membrane environment can affect ion flux through nicotinic acetylcholine receptors and other channels (McIntosh and Simon, 2006; Sunshine and McNamee, 1994). One key question in constructing simulations of such large proteins is how much membrane is necessary – if the simulation represents a “dilute” case where copies of the channel do not interact, the materials properties of the bilayer should return to bulk before encountering the next periodic image. 3D measurements of surface tension provide one means to analyze such behavior.

Our differential pressure and surface tension calculations on GLIC in a pure POPC bilayer show distinct local effects on pressure in the immediate neighborhood of the transmembrane helices (Fig. 3). The automatically generated conformation of the membrane around the GLIC protein contained 91 lipids in the upper monolayer and 109 in the lower due to the asymmetric shape of the protein. The GLIC channel was equilibrated for 10 ns and simulated for a 100-ns production run. Over the course of the simulation, the maximum cRMS from the starting crystal structure was 2.8 Å. Local perturbations in differential pressure are particularly evident in the hydrophobic core region (Fig. 3a); in the head group region, perturbations of a similar magnitude would not be distinguishable from the baseline fluctuation (Fig. 3b). The magnitude and mean root variance of the differential pressure are plotted in Fig. 3c and d using cylindrical coordinates, showing an increase in variance close to the protein within the hydrophobic core region (Fig. 3c). Interestingly, we do not detect longer-range effects on differential pressure. This may be due to the relative fluidity of the POPC bilayer at 300 K, well above the experimental T_m of 271 K (Silvius, 1982). Such long-range ordering may be more readily manifest in phospholipid–sterol mixtures, but in this case the ~200 total lipids appear to be more than enough to reach bulk bilayer conditions away from the protein.

Fig. 3.

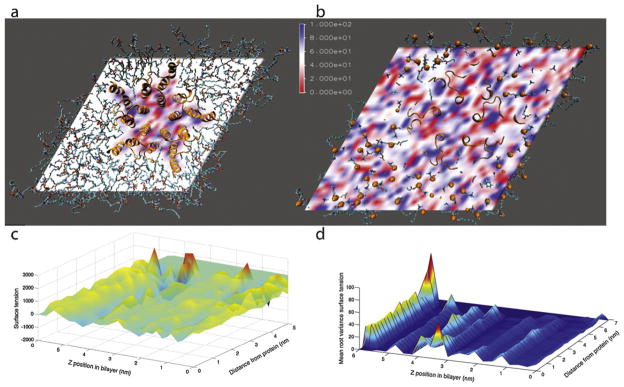
Differential pressure in a POPC bilayer containing the GLIC ion channel transmembrane region. Spatially-resolved differential pressure is rendered for a midplane slice through the bilayer (a) and a slice through the phosphate layer (b). Phospholipids are rendered in stick form, while the protein is shown in ribbon form. In (b), phosphorus atoms are shown as orange spheres. The differential pressure is plotted in (c) as a function of z-position in the bilayer and radial distance from the nearest protein atom. The mean root variance of pressure is shown in (d). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

5.3. Varying lipid density in a protein-containing bilayer

Spatially resolved differential pressure calculations can also serve to assess and guide pressure equilibration in a membrane protein simulation. Pressure-coupling schemes can equilibrate the lateral expansion and contraction of a planar bilayer relatively rapidly, but equilibration between the two leaflets is limited by the slow flip-flop rates of phospholipids. At equilibrium, the bulk lipid phases of the two leaflets should have equal surface tension, but if the number of lipids in each layer is not correct relative to the protein size there will be a systematic curvature force. Such forces can substantially alter the dynamics of the membrane protein (Bigay et al., 2005; Weiss et al., 2003). As we show here, this equality condition can guide the explicit addition or deletion of phospholipids from the upper or lower leaflet of a membrane protein simulation to yield an equilibrated system.

The thermodynamic basis for this is as follows:

$$\gamma ={\left(\frac{\partial G}{\partial A}\right)}_{N,T,P}$$ (9)

where G is Gibbs free energy and A is the area of the surface interface. Since a bilayer has two surfaces, at constant temperature and pressure we have:

$$dG={\gamma }_1{dA}_1-{\gamma }_2{dA}_2+\mu dN$$ (10)

where γ₁, γ₂, A₁, and A₂ denote the surface tensions and areas of the two leaflets and μ is the chemical potential for transfer between leaflets. At inter-leaflet equilibrium, dG and dN are 0. One solution to these equations is to have a net curvature of the bilayer. For a flat bilayer, however, A₁ = A₂, so γ₁ = γ₂.

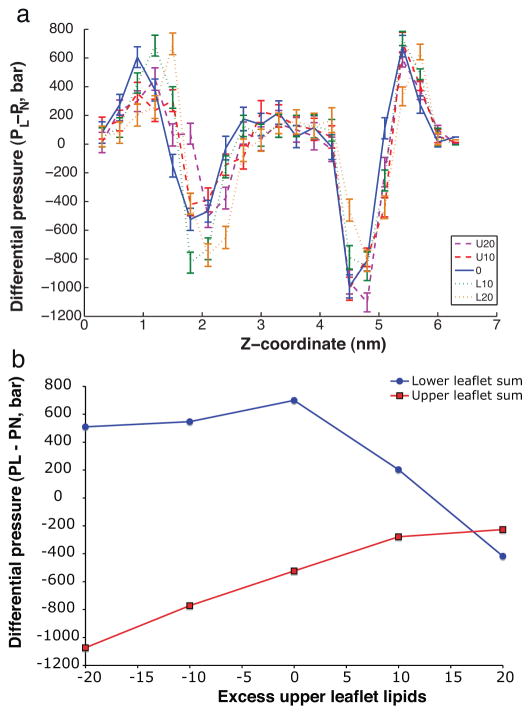
We demonstrate this procedure for testing inter-leaflet pressure equilibrium with simulations of the GLIC ion channel. In addition to the “reference” case described above, we ran four additional simulations in which 10 or 20 lipids were removed from either the upper or the lower leaflet. Each system was equilibrated for 5 ns and then run for 100 ns under NPT conditions with the lateral and normal pressures coupled separately. As pressure de-correlates on a nanosecond timescale within our simulations, this run length gives a large number of uncorrelated samples. The differential pressure P_L – P_N was measured for all simulation lipids more than 10 Å from the nearest protein atom; pressure profiles binned by z coordinate are plotted in Fig. 4a. The surface tension in each leaflet was then calculated by integrating the differential pressure for all bulk-phase lipids above or below the bilayer midplane (calculated using phosphate densities). As shown in Fig. 4b, the leaflets attain equal surface tension with between 10 and 20 lipids removed from the lower leaflet – a relative excess of upper-leaflet lipids compared to the initial simulation system prepared via standard methods.

Fig. 4.

Surface tension profiles for membrane-protein simulations with different numbers of lipids. Plotted in (a) are differential pressures for five simulations: the original GLIC-bilayer system in blue, the systems with 20 and10 lipids removed from the upper leaflet (U20, U10) in purple and red respectively, and the systems with 20 and 10 lipids removed from the lower leaflet (L20, L10) in orange and green respectively. The surface tension for each leaflet is plotted in (b) as a function of number excess upper-leaflet lipids relative to standard solvation methods. In order to consider bulk membrane properties, lipids within 9A of the protein were excluded from this analysis. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

This approach allows systematic selection of optimal lipid densities in each leaflet and is trivially extensible to allow a binary search in lipid density space. Each of the five 100-ns simulations described here required approximately 4 days of run-time on 128 cores of a 2.33 GHz Clovertown cluster with a DDR Infiniband interconnect. Given the computational capabilities of contemporary clusters, this type of sampling is not an onerous requirement for systems where the observables of interest may be sensitive to lipid materials properties. Our simple search protocol could also be extended to include a Monte Carlo algorithm for lipid insertion or deletion using inter-leaflet surface tension mismatch to determine the move acceptance probability.

6. Conclusions

We have presented a means to calculate local pressure fields in a 3D-resolved manner that solves the long outstanding issue with constraints in molecular systems, and demonstrated its utility in evaluating inhomogeneous properties of biomolecular systems beyond simple profiles. Local pressure measurements in molecular dynamics simulations are particularly helpful in assessing spatially-varying phenomena such as membrane fluctuations and perturbations by membrane proteins. As we have shown, pressure calculations can also serve as a quantitative guide to inter-leaflet equilibrium, as pressure is a sensitive and physiologically relevant indicator of leaflet mismatch. This is particularly important because leaflet mismatch equilibrates much more slowly than the length of a typical simulation, can be non-obvious to visual inspection, and yet can affect protein function.

Software availability

The 3D local pressure field version of the software used in this work is available at ftp://ftp.gromacs.org/ as well as the website http://www.gromacs.org/. There is also a local pressure branch available in the public GROMACS Git version control system.

Appendix A. Supplementary data

Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.chemphyslip.2013.01.001.