Abstract
We develop a proof-of-principle model for auto-regulation of water volume in the lung airway surface layer (ASL) by coupling biochemical kinetics, transient ASL volume, and homeostatic mechanical stresses. The model is based on the hypothesis that ASL volume is sensed through soluble mediators and phasic stresses generated by beating cilia and air drag forces. Model parameters are fit based on available data on human bronchial epithelial cell cultures. Simulations then demonstrate that homeostatic volume regulation is a natural consequence of the processes described. The model maintains ASL volume within a physiological range that modulates with phasic stress frequency and amplitude. Next, we show that the model successfully reproduces the responses of cell cultures to significant isotonic and hypotonic challenges, and to hypertonic saline, an effective therapy for mucus hydration in cystic fibrosis patients. These results compel an advanced airway hydration model with therapeutic value that will necessitate detailed kinetics of multiple molecular pathways, feedback to ASL viscoelasticity properties, and stress signaling from the ASL to the cilia and epithelial cells.
Keywords: Volume regulation, mechanochemical mathematical model, respiratory epithelia, cilia, mucus, viscoelasticity
Introduction
Mucus traps inhaled foreign particles and pathogens entering the lung, which are subsequently cleared by mucus transport [9]. Proper hydration of the mucus layer is a fundamental prerequisite of efficient transport, thus a detailed kinetic understanding of fluid volume regulation in the respiratory epithelium is highly relevant to therapeutic strategies for treating lung diseases that are associated with dehydrated mucus, such as cystic fibrosis (CF) and chronic obstructive pulmonary disease (COPD) associated with dehydrated mucus [5, 30].
Recent experimental evidence has shown that soluble mediators and extracellular nucleotides play a critical, and perhaps primary, role in airway surface liquid volume regulation by modulating ion channel activity. Soluble mediators govern ASL volume by actively controlling ion channels and thus changing the overall salt content in the ASL. Epithelial tissue is highly permeable to water, which results in equivalent osmotic pressures at steady-state in the ASL and the basolateral layer. The epithelial Na+ channel (ENaC) must be proteolytically cleaved by endogenous channel-activating proteases (CAPs) in order to activate and conduct Na+ [36, 2, 8]. It has been inferred that these CAPs are tethered to the apical membrane of respiratory epithelia [35, 25]. It has also been proposed that ENaC activity is negatively regulated by water-soluble ENaC-inhibitors (ENaCinh) e.g., SPLUNC1, that are released into the ASL by the epithelium [35, 13]. Thus, while membrane-attached CAPs remain constant at the surface of the epithelia, the concentration of ENaCinh is increased whenever ASL volume drops, leading to lower rates of Na+ absorption via ENaC. This cascade hyperpolarizes the apical membrane, creating a driving force for Cl− secretion. If CFTR is active, this causes a transient increase in ASL osmolarity and liquid secretion, and thereby ASL volume increases to keep the ASL osmolarity consistent with that of basal and epithelial compartments. A similar argument explains how excess liquid can be absorbed from the ASL. In this case, the concentration of ENaCinh decreases, leading to activation of ENaC by CAPs and a drop in the mass of ions in the ASL. Thus, the concentration or dilution of soluble reporter molecules provides a stable mechanism for ASL volume regulation [35, 13].
Extracellular nucleotides (e.g. adenosine triphosphate (ATP), uridine triphosphate (UTP), and adenosine (ADO)) have also been shown to influence ASL volume by regulating ion channels. Furthermore, recent experiments show that concentrations of these nucleotides are strongly dependent on external mechanical stresses felt by epithelial cells [3, 31, 32], and thus there is compelling evidence that stress-mediated nucleotide release in the ASL plays a role in regulating ASL hydration. For example, it has been shown that cyclic oscillations in air pressure at the frequency of tidal breathing (14 cycles per minute) cause an increase in liquid secretion and ASL volume in cultured airway epithelium, which is carried out by stress-mediated increases in extracellular ATP and ADO [3]. In clinical practice, percussive therapies, heavy breathing, and cough therapies are currently employed to stimulate mucus clearance in cystic fibrosis patients [28]. The modulational role of phasic stress in the model presented in this paper is hypothesized and constructed on the basis of several experimental studies [3, 31, 32] which explore ion-nucleotide kinetics in diverse phasic stress conditions. Extracellular nucleotides (ATP and its metabolite ADO) act as signaling molecules that activate G-protein coupled receptors (purinoceptors), thus regulating ion fluxes through ion channels and controlling the mass of ions on the ASL. This, in turn, regulates the ASL height due to water permeability and osmotic pressure, and we therefore deem it crucial to include the effect of stress on volume regulation.
There has been a great deal of effort to mathematically model epithelial ion transport [15, 26, 37, 10, 40, 12]. These model developments have helped gain insights on the kinetics, multiple signaling pathways, and detailed processes happening within the lung. Hartmann and Verkman [15] developed an electrokinetic model to capture the kinetics of electrical parameters, ion fluxes, and intracellular ion activity; Novotny and Jakobsson [26] developed the first computational model describing ion and water flux, using Michaelis-Menten kinetics to describe ion transport. More recently, these models have begun to incorporate more sophisticated details: Warren et al [37] developed a model which describes fluid secretion after the rise of intracellular calcium; Falkenberg and Jakobsson [10] describe ASL pH regulation.
While these models have accomplished a great deal in helping us understand the processes and kinetics of volume and ion regulation, they have not yet delved into functional dependencies of ATP release rates arising from stress, nor have they fully incorporated the role of CAP inhibitors. Much of the literature indicates that stress events will have a significant impact on ion kinetics. For example, in [40], the authors change the constitutive release rate of ATP in order to simulate ATP release triggered by stress and find a significant increase in steady-state ASL ATP concentration, which is in agreement with experiments. In [38], the authors examine the effects of Ca+ kinetics and how they vary with initially increased ATP concentrations; they acknowledge that mechanical stress is the cause of this increase in initial ATP, however do not mathematically model its origin. To our knowledge, the present paper provides the first predictive model that closes the stress-nucleotide-ion-volume feedback loop.
In order to demonstrate this relationship, we have deliberately chosen to construct a simplified proof-of-principle model that establishes the consequences of coupling of these novel regulatory mechanisms. We elect not to incorporate full biochemical kinetics of all ion and nucletotide species, nor specificity of the various signaling pathways that could be stress-activated. The feedback loop between stress, volume, and ion-nucleotide kinetics is the core element of our model, which already constitutes a non-trivial dynamical system, and further details available within our own research group will be addressed only after proof-of-principle is established. The payoff of modeling the biochemical kinetics and mechanics of lung physiology is two-fold: a further understanding of mechanochemical coupling in lung physiology, and to provide platform to test existing and proposed therapies in silico.
The Model
This section starts with a qualitative overview of the model, which is then followed by a detailed description of the model equations, and then a discussion of the parameter values. Many of the model features are inspired by recent experimental observations. We expose the important observations in the present paper and provide a short review in the supplemental material.
An Overview of the Model
In the lung, release of nucleotides (ATP, ADP, AMP) into the ASL is strongly stimulated by changes in the stresses transmitted to the apical membrane [3, 31, 32]. In the ASL, a series of enzymes metabolize these nucleotides into adenosine and inosine (INO), which are then taken up by epithelial cells. The conversion of ATP to inosine involves a series of enzymes that carry out the following chemical reactions: ATP → ADP → AMP → ADO → INO. Both ATP and ADO are signaling molecules that bind to and activate G-protein coupled receptors (P2Y2 and A2B, respectively). A complete description of extracellular nucleotide kinetics can be found in [40, 12]. The balance equation for nucleotide dynamics includes sources due to secretion and sinks due to metabolism and reabsorption [40, 12]. We describe ATP influx as a function of mechanical stresses experienced by the airway epithelial cells which is developed in detail below.
Nucleotide concentrations will, in turn, affect ion channels which will affect ion fluxes between the ASL and epithelial cells. Sodium is absorbed from the ASL by ENaC and, subsequently, actively pumped out from the cytoplasm to the basolateral compartment by Na+-K+ pumps, with K+ being recycled across the basolateral membrane. Increased levels of ATP and ADO in the ASL cause an increase in ASL ion mass by closing sodium channels and opening chloride channels. This in turn causes water secretion from the basolateral compartment towards the ASL.
In addition to the effect of nucleotides on the ion channels, we also infer from [35] that there is a chemical species in the ASL which inhibits ENaC and that has a constant concentration in the time scale of a few hours. We will refer to this species as ENaCinh. The idea is the same as in the Introduction: when ENaCinh is diluted, ENaC is more active and ion absorption is higher; when ASL height is lowered, ENaC is inhibited and the rate of ion absorption decreases. This means that Na+ absorption is a function of the concentration of ENaCinh; fixing the molar number of ENaCinh to be constant, absorption becomes a function of the ASL height.
Finally we turn to ASL hydration which will be affected by the above processes. The total ASL concentration of ions (mainly Cl−, Na+ and K+) is near 300 mOsm at basal levels in both CF and normal airways [18]. The ASL concentrations of nucleotides range from 1 to 200 nM at steady-state [27]. Because there is a large difference between the ionic concentrations and the nucleotide concentrations, the main contributors to ASL osmolarity are the ion concentrations. Ion fluxes are driven by electrochemical gradients across the cell membranes. ATP and ADO regulate these fluxes by controlling the permeability of ion channels located in the apical membrane. Water will move to balance osmotic gradients between the mucosal and serosal compartments. The basolateral (serosal) compartment represents a large reservoir, where ion concentrations can and will be considered constant (Fig. 1).
Figure 1.
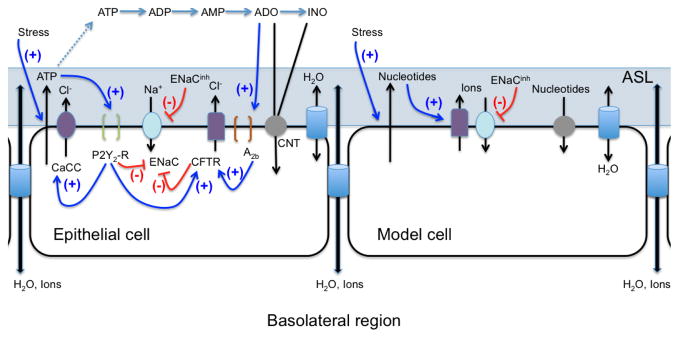
Diagram of the respiratory epithelium summarizing the complex signaling pathways that regulate ASL volume (LEFT) compared to the proof-of-principle model cell (RIGHT). Abbreviations: CaCC = calcium-activated chloride channel, ENaC = epithelial sodium channel, CFTR = cystic fibrosis transmembrane conductance regulator, CNT = concentrative nucleoside transporter, P2Y2-R = receptor sensitive to extracellular ATP, A2B = receptor sensitive to extracellular adenosine (ADO); see text for more information.
Instead of resolving all of the detail found both in the above presentation and in the referenced works, our proof-of-principle model extracts the fundamental elements of a general biochemical network model [40, 12] by reduction to three variables: one generic nucleotide/nucleoside, one generic ion, and ASL height. The nucleotide (which we will simply denote as ATP) summarizes the roles of ATP, UTP and ADO in promoting fluid secretion through the receptors P2Y2 and A2B [3, 29]. Similarly, the generic ion accounts for all ions and molecules that contribute to ASL osmolarity, such as sodium, chloride and potassium. ASL height HASL is likewise proportional to volume as many of the experiments are carried out on flat cell cultures, allowing us to approximate volume as VASL = HASLSASL where SASL is the surface area of the ASL. Coupled with a dynamic ASL height, and the key new feature of mechanochemical coupling, we derive below a simplified form of the biochemical network model previously described in [40, 12]. We add, however, a stress-mediated nucleotide flux, with a phasic (time-periodic) stress condition, along with an ENaCinh term in the ion re-absorption term. This gives a three-dimensional dynamical system for the generic nucleotide and ion species coupled to ASL height. We illustrate the simplification in Fig. 1 and present the functional dependence of the secretion and degradation terms as
| (1) |
| (2) |
| (3) |
Here, τ⃗ represents all components (from cilia and breath) of stress felt by the epithelial cells, (units of mols/s.m2) is the nucleotide release rate which explicitly depends on the rate of change of stresses as inferred from [3], while the rate of ATP degradation (units of mols/s.m2) is described by a Michaelis-Menten kinetics [40, 12]. N represents the number of moles per unit surface area. Letting denote the height of the ASL made up of the liquid and mucus regions (as opposed to contributions from cilia) the concentration of a species X can be derived as . We further note that the total height of the ASL is given by , where in the absence of cilia and , which is the estimated contribution of the volume of cilia, calculated by taking the density of cilia to be 5 cilia per μm2 [6], the length of cilia to be 7μm [23], and radius of cilia to be 150nm [1]. Nion has units of mols/m2; (units of mols/s.m2) are the rates of ion secretion and absorption into and out of the ASL; VH2O (units of m3/mol) is the molar volume of water, and (units of m/s) is the transepithelial water permeability of airway epithelia. OsmASL is the ASL osmolarity and is equivalent to ; Osmbasal is the osmolarity of the Krebs Bicarbonate Ringer (KBR) solution commonly used in the basolateral region in cell culture experiments [39], and acts as a baseline toward which the ASL osmolarity tends. Equations 1 through 3 form a three-dimensional dynamical system for (NATP,Nion,HASL). The system becomes explicit once the functional forms of the flux functions for absorption and secretion are specified, as described in the following sections.
The Flux Functions
Nucleotide Fluxes
In order to fit the functional dependence on ATP release to stress, we note that it has been experimentally observed that the ATP steady-state concentration in the ASL changes when an oscillatory stress is applied to cell cultures of human airway epithelia [3, 32]. We note also that the ASL ATP concentration is not affected by different constant air pressures. Thus, we posit that the nucleotide secretion rate ( ) depends on the rate of change of stress, and does so monotonically. Although there are many functional choices that satisfy this simple monotonic criterion, we choose to construct a sum of traditional quadratic Hill functions, which yields
| (4) |
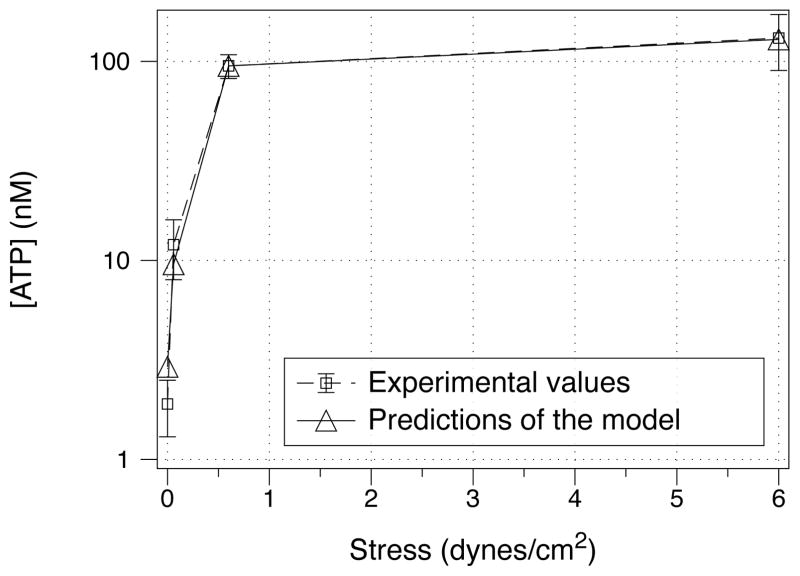
where is the maximum influx response to the different types of stress (stress experienced via shear stress experienced via tidal breathing vs. stress experienced via cilia), is the stress level that elicits half of the maximum response for each type of stress, τ⃗ is the vector of stress types, and τi is the ith component of this vector. represents a non-stimulated, constant influx of nucleotide into the ASL. The notation ∂t represents a time derivative. We further note that the choice of quadratic Hill functions (as opposed to linear or of arbitrary nth power) was taken to account for the sharp change in the ATP concentrations vs. imposed stress (fig. 5); we expect the response to be stronger than linear, however no fitting was done to find the optimal value of the Hill exponent.
Figure 5.
Nucleotide concentration in the model compared to experimental measurements of ATP concentration as a function of applied stress. The experimental data is taken from [32].
We note that, experimentally, the ATP release rates have extremely different sensitivity to different sources of stress. The magnitude of stress from the cilia is roughly four orders of magnitude greater than stress from breathing [16], however epithelial cells are much more sensitive to breathing-induced stress than cilia-induced shear stress. More specifically, whereas ciliated and non-ciliated cell cultures have similar ATP concentrations and ASL volume, the low shear stresses from experiments mimicking tidal breathing lead to significant spikes in ATP concentration. We assume the contributions to ATP flux from different sources of shear stress sum linearly, a common assumption in rheology. Taking this simple relationship, the model accounts for the contrasts in sensitivity associated with each source of stress.
The phasic stress due to ciliary motion is taken from the biophysical model described in [21, 24], which describes stress distributions throughout a viscoelastic layer with a phasic strain or stress driving condition. Indeed, these studies were carried out precisely to understand stress conditions in the ASL due to forcing by coordinated cilia or tidal breathing, and in particular how induced stresses vary with ASL height. Several sources (strain versus stress) of phasic stress on the viscoelastic layer as well as boundary conditions on the opposing layer boundary (stationary or stress free) were analyzed in [21, 24].
For our purposes, we use the closed-form, analytical formulas which follow from a model called the upper convected Maxwell(UCM) model for the ASL. This model generalizes linear viscoelastic models with the ability to resolve the storage modulus and loss modulus of the ASL at the frequency of the driving condition. The idea is that mucus can be modeled via the UCM and that cilia beat at a regular frequency despite changes to the underlying viscoelastic properties. We assume that a layer of fluid moves with the tips of the cilia. In this setting, the lower the ASL height is the greater amount of work the cilia need to do to keep beating because the fluid at the epithelial surface holds a no-slip assumption. Although this model only acts to approximate the stress experienced by the cell tips, it does provide the most accurate model currently available. More detailed models must take into account individual cilium and how they interact with the surrounding fluid. With these assumptions in place, this model incorporates the local ASL height and the dynamic storage and loss moduli at the driving frequency ω of coordinated cilia into an explicit formula for the rate of change of shear stress:
| (5) |
where
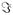 () denotes the imaginary part of a complex number, η′ and η″ are the elastic and viscous moduli of the ASL at frequency ω, respectively, A is the strain driving amplitude, ρ is the density of the ASL liquid, and z is a complex constant determined by the ASL properties and driving frequency ω, namely
() denotes the imaginary part of a complex number, η′ and η″ are the elastic and viscous moduli of the ASL at frequency ω, respectively, A is the strain driving amplitude, ρ is the density of the ASL liquid, and z is a complex constant determined by the ASL properties and driving frequency ω, namely
| (6) |
Equation 5 is derived in [21, 24].
For this paper we use a ciliary beat frequency of 10Hz (ω) [19], and take the viscoelastic moduli to be η′ = 25 dyne s/cm2 and η″ = 5 dyne s/cm2 [17].
The ASL viscoelastic moduli η′ and η″ are presumed constant over the timescales of our simulations, since very little is known about how these moduli vary in vivo. The dynamics of ASL properties can easily be incorporated, including the release of mucins which continuously replenish the ASL and maintain viscoelasticity in some range, once these dynamical processes are better understood. Finally, the choice for A, the strain driving amplitude, is approximated to be proportional to the length of a cilium as an estimate of the result of coordinated cilia. We note that this constant of proportionality can be absorbed in the and parameters, thus it is approximated as the actual length of a cilium. The parameter choices for the stress dynamics are given in Table 1.
Table 1.
Parameter values
| Parameter | Value | Units | References | ||
|---|---|---|---|---|---|
| JATP parameters | |||||
|
|
24.3 × 105 |
|
[12] | ||
|
|
140 |
|
free | ||
|
|
408.16 |
|
free | ||
|
|
5100 |
|
free | ||
|
|
35.28 |
|
free | ||
|
|
3.9511 × 1010 |
|
[12] | ||
|
|
61.5 |
|
[20] | ||
| Stress parameters | |||||
| η′ at 10Hz | 25 |
|
[17] | ||
| η″ at 10Hz | 5 |
|
[17] | ||
| A | 7 × 10−4 | cm | [23] | ||
| ω | 10 | s−1 | [19] | ||
| ρ | 1.015 |
|
[14] | ||
| Jion parameters | |||||
|
|
10−3 |
|
free | ||
|
|
3 × 10−3 |
|
free | ||
|
|
100 | mM | [32] | ||
| Kl | 10 | μM | [35] | ||
| NENaCinh | 13.85 | μM | derived | ||
| HASL parameters | |||||
| VH2Of | 18.1 × 10−6 |
|
[22] | ||
|
|
200 |
|
[22] | ||
| Osmbasal | 300 | mOsm | [39] | ||
We note further that we only employ the formula for shear stress and suppress normal stress in these simulations. Because the ASL is viscoelastic, normal stresses naturally arise in shear. The formula for normal stress is exposed in [21] and can easily be added when the model is expanded to include more biochemical detail. We also acknowledge that stress in this idealized model is imperfectly communicated to the epithelial cells, which would correspond to an underestimate of the true value for .
External stresses on the ASL surface (i.e. stresses not contributed by the cilia), have been experimentally measured in two scenarios. The first was carried out in [32], where the cultures were radially accelerated, then held at constant speed, and then decelerated; the process happens at a rate of 14 cycles per minute to mimic breathing. In this study the cell cultures undergo centripetal forcing as well as air drag via the air drag on the epithelium. The authors claim that air drag is the primary source of stress and approximate the resulting shear through a series of simplifying assumptions (see supplemental material of [32]). In a second set of experiments [3], the pressure of the surrounding air was changed phasically, 20 cycles per minute, and the authors reported similar results in the response of steady state ATP concentrations. We will denote stress from these experiments as τbreath to denote the stresses from tidal breathing acting on the cell.
For the model, we suppose that we have a stationary epithelial layer and that the mucus-air interface is driven at a particular stress τH. Given these boundary conditions we can read the analytic solution from [24]. Assuming that the cell will read stress at the epithelial layer, we take the shear stress at the base of the layer as
| (7) |
with z as above. Because the magnitude of the height is small compared to z, we approximate cosh(zHASL(t)) ≈ 1. As in [32], we take the frequency of forcing to occur at 14 cycles per minute. We have idealized the stress input to occur with a single frequency mode. For more complex signal inputs, however, we can take a Fourier decomposition and sum along different wave modes to find the true time rate of change of shear stress; this is beyond the scope of this work.
For the nucleotide degradation flux ( ), we use Michaelis-Menten kinetics and write the function in terms of nucleotide concentration ( ) as
| (8) |
The maximum velocity was obtained by summing over all enzymes that metabolize ATP, while the average Michaelis-constant was calculated so that the steady-state ATP concentration provided by Eq. (1) matches the experimental value (≈ 1 nM; see Table 1). As described in [12], condensing the effects of all enzymes into a single Michaelis-Menten term is an accurate approximation of extracellular nucleotide metabolism for low nucleotide concentrations (< 200nM).
Ion Fluxes
We use a generic Hill function to mediate the ion flux which is meant to account for an average effect over all ions, but suppose that we can model the half response value at a the same level as the P2Y2-R response. This idea leads to the following equation for ion secretion:
| (9) |
where is again the nucleotide concentration in the ASL as above, and is the nucleotide dose that elicits half the maximum response of ion secretion via the P2Y2 – R receptor pathway. is left as a free parameter to fit the experimental data with the simulation.
Ions are constantly leaving the ASL either across the cell (Na+) or through the paracellular pathway (Cl−, K+, Na+). Since ENaC-mediated Na+ transport is regulated, but ion transport through the paracellular pathway is passive (down the electrochemical gradient), we assume that ion removal from the ASL is regulated primarily through ENaC regulation, which relies on ENaCinh. Thus, ion removal from the ASL is modeled as:
| (10) |
where Kl is the inhibition constant; is the ASL osmolarity; is a free parameter used to fit the experimental data; and is the concentration of soluble inhibitors that reduce the ENaC-mediated Na+ absorption. We consider NENaCinh to be a constant that we determine by first finding or setting the other parameters, setting variables equal to their experimental steady-state values, and then solving for NENaCinh by setting Ṅion = 0. The denominator is taken to the fourth power to simulate a sharper signal cutoff; we found similar behavior when squaring it.
It is worthy of comment as to why we allow ATP flux to be stress-dependent, yet do not include stress-induced ion channel activity. In [32] the authors show that ASL height is strongly dependent on the presence of ATP and ADO in the ASL and degradation/inhibition of these two signaling molecules causes ASL height to collapse. Extending this experiment, the authors found that in the absence of ATP/ADO, the epithelia can no longer respond to applied phasic shear stress from air drag. Furthermore, they detected a Ca2+ spike and a concomitant increase in Cl− secretion every time shear stress was either turned on or off. This signaling event was abolished by the addition of apyrase, which degrades ATP to AMP [32]. Thus, while we cannot exclude the possibility that mechano-sensitive ion channels or other mechanisms are being activated by shear stress, we can conclude that ATP release is paramount for shear stress-induced regulation of ASL height. For this reason we hypothesize that stresses on the cell do not directly influence the channel permeabilities.
Therefore, the closed system of equations reads
| (11) |
| (12) |
| (13) |
Parameter Values
All parameter values are given in Table 1, while the steady-state experimental values of ASL ATP concentration, ASL osmolarity, and ASL height are given in Table 2. If no reference is given the parameter is labeled as free or derived as a function of other parameters (as in the case of NENaCinh, as previously described). The free parameters were fitted as follows. First, we considered non-stressed, non-ciliated cells and fitted so that the steady-state variables and time scales after isotonic and hypotonic challenges were reproduced. Next, we fixed the parameters found for non-stressed cells and used and to fit the experimental data for stressed cells. Parameters for the stress from cilia ( ) were found by fitting the experimental data in Fig. 2. Parameters for the stress from tidal breathing ( ) were fit by ignoring cilia and fitting the data in Fig. 5. With the fitted parameter values, we went back and added cilia and verified that the model predictions remained within experimental ranges.
Table 2.
Preciliated (i.e. non-ciliated) experimental steady-state values of ASL ATP concentration ([ATP]), ASL osmolarity (OsmASL), and ASL height (HASL).
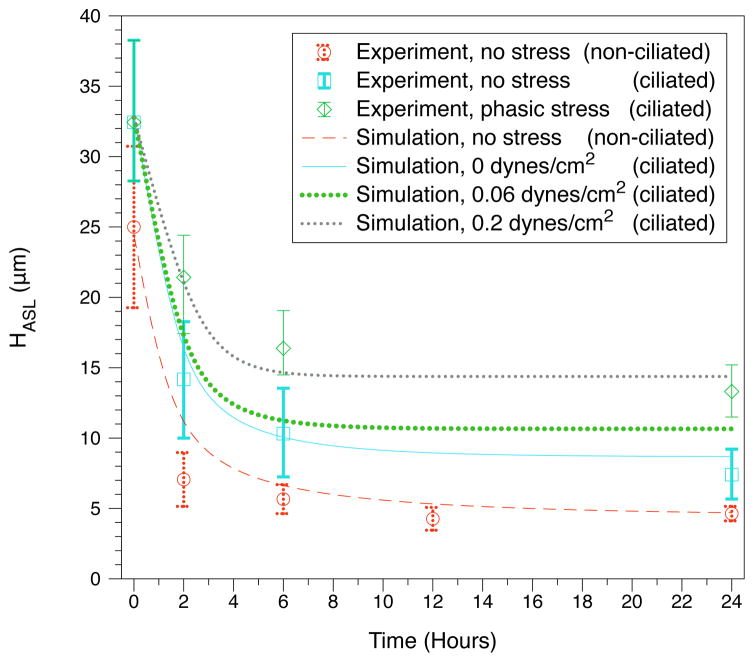
Figure 2.
Response to isotonic challenge. Experimental data [35, 32] are compared to model simulations for non-ciliated vs. ciliated cells for various levels of applied stress.
Numerical Methods
The model is solved using a Runge-Kutta-Fehlberg algorithm in the GNU scientific library ordinary differential equation (ODE) routines [11]. The code is scripted and results are visualized using DataTank by Visual Data Tools, Inc. The equations are non-dimensionalized in the numerical code in order to ensure minimal numerical truncation error and then rescaled in post-processing.
Results
Comparing the model with experiment
Non-ciliated, non-stressed cells
We now reveal how well the chosen parameter values mimic the biological behavior of non-ciliated, non-stressed cells. In the model, this means that ion secretion is limited to the non-stimulated term, namely . In this case, the model must be able to reproduce the following experimental behaviors and data:
- The system should reach a steady-state in the limit t → ∞. At steady-state, the ASL nucleotide concentration ([ATP]) must be in the experimental range (1–10nM for ATP) [27]. The total ASL ion osmolarity ([ion]) must be 300 mOsm, which is the osmolarity of the KBR buffer used in the experiments (see Table 1).
- Following addition of isotonic liquid, so that the ASL height increases four-fold, the system returns to steady state in 6–18 hours [4, 31, 32].
- After ASL dilution by adding pure water, ASL height recovers quickly to steady state. We note that physically, this is a consequence of the epithelium being water permeable. However if the parameters are chosen so that ion recovery occurs at a faster time scale than volume changes, then volume recovery can be slow for both the isotonic and hypotonic challenges.
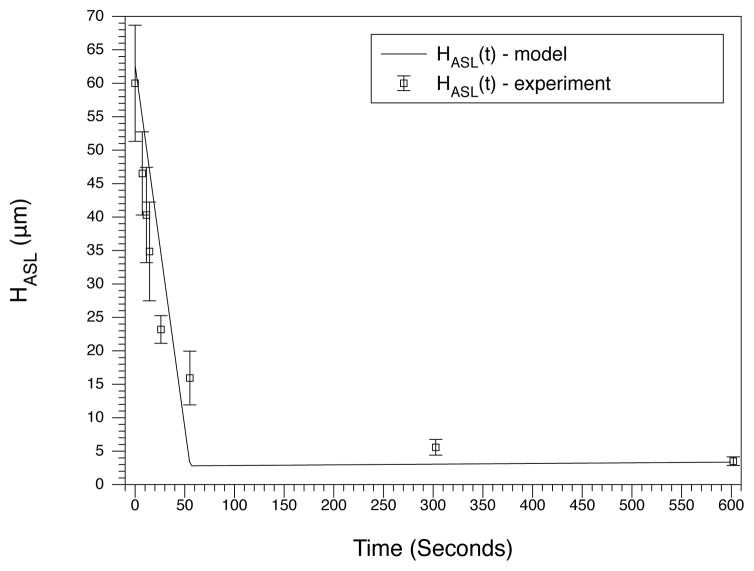
The model reproduces these desired behaviors. For long time periods, the experimental steady-state values are reached (see Table 3) thus satisfying the first requirement. Following addition of isotonic liquid (requirement 2), the model returns to its steady-state within 6–12 hours, which is a timescale that is similar to the experimental results [32, 4] (see Fig. 2). Finally, after ASL dilution, the recovery to steady-state is much faster than after addition of isotonic liquid. We present and compare the model with an experimental result found in [33]. In this work, the ciliated ASL was stripped of nearly all water and ions and pure water was then added to the system. We show that the model reproduces this behavior which verifies the third requirement (see Fig. 3). In both the experiment and the model, the ASL height dips below the length of out-stretched cilia (7μm), and we note that the volume contribution of the cilia is present in both. This means there is a very small amount of liquid present in the culture which is physically and mathematically interpreted as there being a very low mass of ions in the ASL.
Table 3.
Model predictions for the quasi steady state values of ASL ATP concentration ([ATP]), ASL osmolarity (OsmASL), and ASL height (HASL) in cells with and without cilia. The heights for ciliated cells have a volume correction (height due to the cilia plus height due to the liquid); the height without cilia only includes the liquid height.
| Experiment | [ATP] nM | OsmASL mOsm | HASL μm |
|---|---|---|---|
| No Cilia | 1.00 | 300.0 | 4.5 |
| Ciliated Cells with the following shear stresses from tidal breathing: | |||
| 0 breath stress | 2.92 | 300.0 | 8.69 |
| .06 | 9.57 | 300.0 | 10.65 |
| .6 | 94.91 | 300.0 | 17.04 |
| 6 | 129.01 | 300.0 | 18.51 |
Figure 3.
Response to hypotonic challenge. Ions are stripped from the ASL and water is added which causes a large drop in the osmotic pressure. The volume decays over the course of 1 minute. Experimental data is taken from [33] in which ciliated cell cultures which have been washed of salt to give a height of 3μm (with collapsed cilia). In the experiment, pure water is added to the ASL and the ASL height quickly collapses back down to a height of 3μm.
Ciliated cells
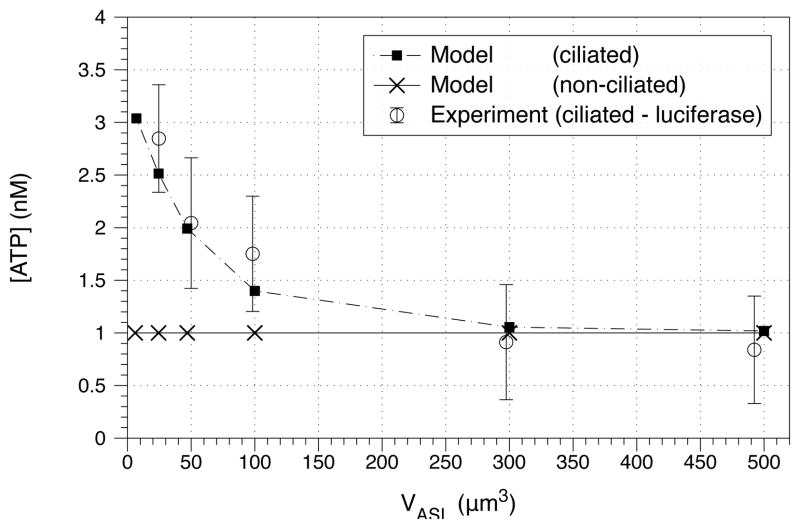
Experiments by Okada and colleagues [27] suggest that the steady-state ASL ATP concentration is weakly dependent on ASL height. When various volumes of isotonic fluid were added to the cell cultures, the steady-state [ATP] decreased when ASL height increased (Fig. 4). Model simulations predict that the steady-state nucleotide concentration ([ATP]) is independent of ASL height in non-ciliated cells, but that it decreases with ASL height in ciliated cells (Fig. 4).
Figure 4.
Model simulations compared to experimental measurements of ATP steady-state concentration, with height held constant. The experimental data was taken from ciliated cell cultures using soluble luciferase [27]. The model predicts that non-ciliated cells will have steady-state nucleotide concentrations independent of ASL height (crosses ×). In contrast, the model predicts that ciliated cells will have steady-state nucleotide concentrations that decrease with ASL height (solid boxes ■). Only the ciliated model agrees with experimental data ranges.
The effect of cilia on the response to isotonic challenge is shown in Fig. 2. The model matches experimental ranges found by Okada [27], and predicts that cilia play a minor role in this experiment, by influencing ATP release rates.
External stresses
Finally, we consider the effects of external stresses applied to ciliated cell cultures. Increasing stress in the model increases the steady-state ASL volume as observed experimentally (Fig. 2 and Table 3). The model is in close agreement with experimental timescales and numerical ranges. The model correctly shows that ASL height increases with stress, and predicts that once a certain level of stress is reached, ASL height will not appreciably increase [4] (Table 3). We further demonstrate that there exists a level of stress (0.2 dynes per cm2) which fits the experimental range [32]. This contrasts to the experimental estimate by Tarran et. al. [32] that epithelial cells were subjected to stress levels of .06 dynes/cm2 at the same frequency. We note that this discrepancy may come from the simplified choice of our breath stress function, but that it may also come from the way stress was measured in the experimental set up. In the experiment, cell cultures were rotated giving regions of zero stress and high stress; the average was approximated as the reported values. This complexity may cause the reported stress to not directly correspond to the value of the true stress that would lead to the observed response. Despite this, the trend in the model is consistent with the experiment.
Finally we consider the change in the nucleotide steady-state concentration with increasing stress (Fig. 5). The model accurately captures nucleotide increase as a function of applied stress, and lies within experimental uncertainty (see Table 3 and Fig. 5).
Blind Model Predictions
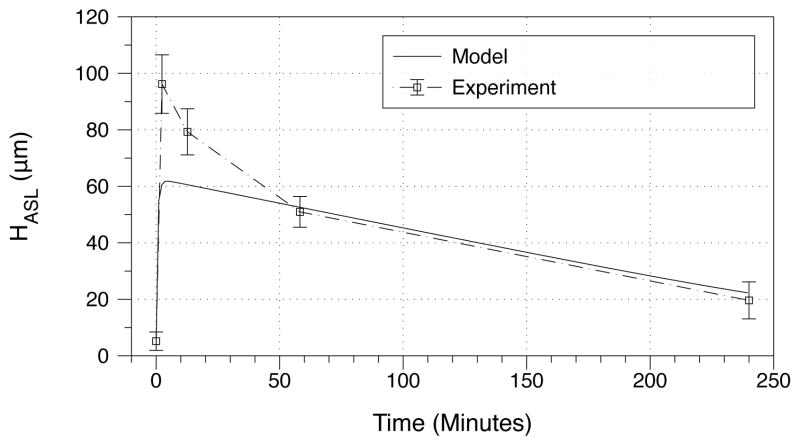
To test the predictive power of the model, we now test model predictions against experimental data that was not used to fit the model parameters. We first consider the addition of salt to ASL as a proposed therapy for mucus hydration. In the experiment described both in [7] and the supplemental material of the present paper, 0.8mg of sodium was added to epithelia from patients with cystic fibrosis. We mimic this experiment by starting from steady state and increasing the ASL salt concentration 16–fold (Fig. 6). In both the experiment and the model, there is an immediate and sharp increase in ASL height. The model predicts that ASL height increases to 70μm, while in the experiment ASL height goes to 96 μm. The experiment has a fast reponse period in which the culture height drops to 51μm over the first hour, after which the rate of ASL height decline begins to slow. The model is only able to pick up the long term drop rate, and we note that the average rate of change between the model and the experiment are nearly identical from hours 1–4. This discrepancy, however, is not surprising, since the ASL ionic composition has been course grained over a single ion and the model has been fit to mimic long time scale behaviors. This test suggests that there is more than one control for ion absorption; modeling the potential sources and coupling them to the present dynamics is worthy of future study.
Figure 6.
Response to hypertonic challenge. Addition of salt to the ASL leads to dramatic increases in ASL height. Here we compare the model to an experimental test [7] carried out by adding 0.8mg of sodium to epithelial cells of patients with cystic fibrosis. The numerical test was done by increasing the ion concentration 8 fold from quasi-equilibrium.
We next perform sensitivity analyses (Fig. 7 and Fig. 8). In Fig. 7, we consider constant phasic shear stress levels from tidal breathing, and the effect of taking away ENaCinh. We find that as stress increases, the ASL volume becomes more sensitive to diminishing ENaCinh, suggesting that an ASL hydrated primarily by stress is vulnerable to an insult which neutralizes ENaCinh. We also show the effect of modulating stress over cultures in which the mass of ENaCinh is held constant at different fractions of its original level (Fig. 8). We find that for diminished ENaCinh, stress plays a less important role in volume regulation. This suggests that in the above mentioned insult that neutralizes ENaCinh, increasing stress will not be an effective therapy for recovering healthy hydration.
Figure 7.
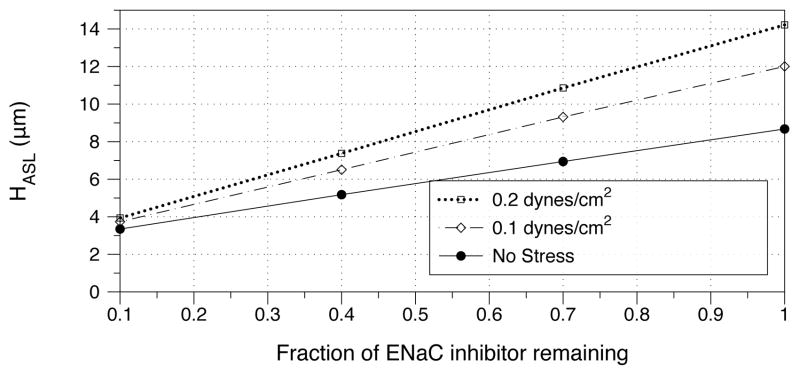
Model prediction of steady-state ASL height as a function of ENaCinh concentration. Under a given amplitude of phasic shear stresses, we examine the effect of taking away ENaCinh on ciliated cells, where a value of 1 on the x-axis corresponds to the predicted value of ENaCinh from Table 1.
Figure 8.
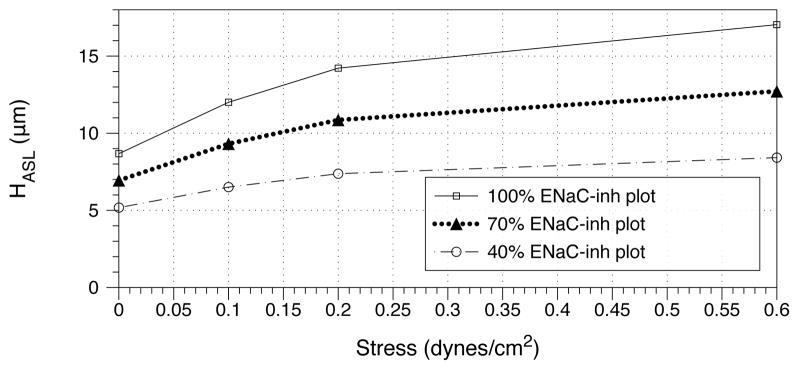
Model prediction of steady-state ASL height as a function of stress. Holding the mass of ENaCinh constant on ciliated cells, we modulate the tidal breathing shear stress from 0 to 0.6 dynes/cm2. The constant values of ENaCinh correspond to the predicted level from Table 1 (100%), half this value (50%), and a fifth of this value (20%).
We now speculate how the next generation of our model has the potential for use in CF treatment. Patients with CF are asked to breathe heavily into tubes as a therapeutic treatment [28], however there is no predictive guide for how hard they need to breathe. Our model opens the door for these breathing apparatuses to be coupled to anemometers which can be used to predict the stress epithelial cells are experiencing. The model can then be used to predict if the patient is breathing hard enough for the ASL volume to respond in a favorable way. This can especially be useful in sick patients who are laboring to breathe and such instruments could foreseeably be used to predict whether or not one should proceed with this type of therapy or explore other options.
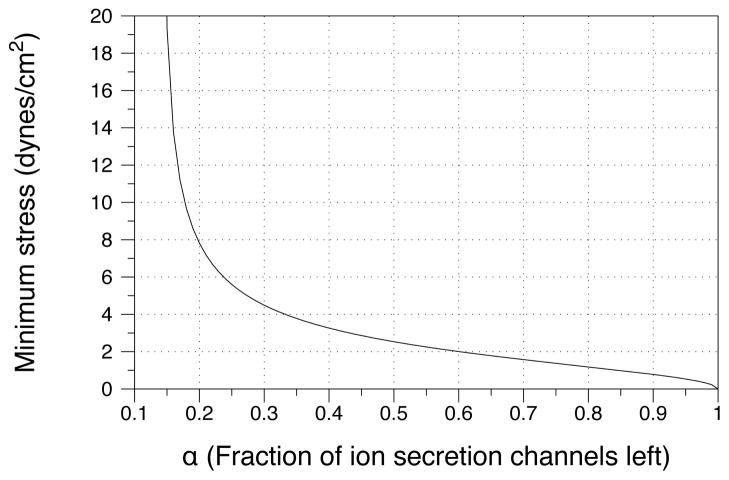
To demonstrate such a clinical application, we hold ASL volume constant and effectively knock down ion influx channels by multiplying by a channel percentage factor α. For example, suppose 50% of channels are available for ion influx - we then set where α = 0.5. Since the volume is always greater in the ciliated case, we can analytically solve for a stress that guarantees we will achieve a particular volume in the non-ciliated case. We visualize the results of this prediction in Figure 9, which shows a sufficient amount of shear stress from breathing needed to keep the liquid ASL volume above normal values for both the ciliated and non-ciliated cases. It is not hard to imagine a fully detailed model in which specific channels can be more accurately accounted for to calculate the requisite amount of stress needed to maintain a particular volume. We could also use such a model to determine the optimal repetition frequency of the therapy so that the volume does not fall below a particular threshold.
Figure 9.
We ask for a sufficient amount of stress needed to keep the liquid volume above 4.5μm in both the ciliated and non-ciliated cases. As the fraction of secretion channels drops by a fraction of α, more tidal breathing shear stress is needed to pump nucleotides into the system and increase ion secretion. The results are found by analytically solving for the required constant rate of change of shear stress stress when there is no cilia. Because of it’s analytic form, no data points are shown.
A testable hypothesis
Due to the form of its construction, this model is the first to allow for the possibility that the steady-state nucleotide concentration increases when ASL volume decreases in ciliated cell cultures (Fig. 4). Furthermore, it predicts that this effect will not be seen in non-ciliated cultures (Fig. 4). This additional term and behavior in the model is consistent with the experimental data for ciliated cells by Okada and collaborators [27]. Non-ciliated cells have not, to our knowledge, been tested for this effect. If non-ciliated cells, absent of external stress, do not show an increase of ATP levels when ASL height decreases, then we can conclude that the cilia (and possibly the stress from cilia) are a necessary component to capture this effect. Thus, we propose a novel experiment which tests one of the basic elements of the model.
Discussion
We judiciously reduced the biochemical network of at least nine degrees of freedom [12, 10, 15] to a three dimensional non-autonomous dynamical system to demonstrate the effects of ENaC-inhibitor, ion-nucleotide kinetics and mechanical stresses on ASL volume regulation. Where previous models mimic stress by changing a constant influx parameter [40] or by changing an initial condition [38], our model incorporates stress as an integral element which we have used for a functional exploration of stress as a modulator of ASL volume.
We have also included a new term for ENaCinh. Experimental data demonstrates that ENaC, which is activated by extracellular serine proteases and inactivated by a secreted protein inhibitor (SPLUNC1), appears to set the tone for ASL volume regulation [13] while extracellular nucleotides modify this response [34]. Using the fact that non-ciliated cells are able to regulate volume in the absence of stress, we have first demonstrated that the model is able to regulate volume in this setting, and then we have demonstrated how volume is modified by stress. The model also predicts that if ENaCinh is removed by an outside source, phasic stress therapies may no longer be an effective treatment for aiding in ASL hydration.
Since we employ a coarse-grained approach, we have condensed ATP and ADO into a single nucleotide. We note that ATP typically acts on a fast time scale and ADO on a slow time scale. This averaging of two timescales is consistent with the effect we see in the test with hypertonic salt increase (figure 6). The model-data comparison suggests that there are multiple absorptive pathways that have to be delineated in order to match the full transient behaviors. Furthermore, hypertonic saline induces rapid cell shrinkage [34] which may cause drastic changes in the cellular parameters that are outside the ranges that we have modeled.
Despite the shortcomings associated with coarse-graining over ion-nucleotide species and their detailed kinetic cascades, our proof-of-principle model matches qualitatively in all cases and quantitatively in some cases with the available data. This demonstrates the plausibility of our hypothesis of ENaCinh and phasic stress as important effectors on ASL volume. The primary result of this model is to establish proof of principle for the stress-nucleotide-ion-volume feedback loop in lung airways and cell cultures. We have stated at the outset that we deliberately suppressed full details that are available for the full ion and nucleotide species and their kinetic cascades, and for the multiple signaling pathways and channels. These generalizations of our model are now rationalized with the results presented here.
The role of mucus viscoelasticity in the overall story of ASL volume regulation remains a fascinating and open question. For example, it is widely held that mucus viscoelasticity is tuned for enhanced clearance by phasic strain from coordinated cilia and by phasic air drag from tidal breathing; however this notion of enhanced mucus transport has yet to be established. Our model is the first, to our knowledge, to demonstrate how mucus viscoelasticity plays a key role in ASL hydration. In planned extensions of the model, the dynamics of ASL viscoelasticity through ASL hydration, stress-induced mucin release and mucin concentration dynamics, will be considered.
As mentioned above, there is still a great deal that is unknown about the biochemical signaling pathways in respiratory epithelia. The most important outstanding issue that we do not address is how the cell regulates ENaCinh, which we have assumed constant. However, we have identified ENaCinh as central to ASL volume regulation and challenge future experiments to investigate its regulation.
The goal of this and future generations of models is to evaluate hypotheses for the mechanisms of ASL volume regulation. As this model becomes more quantitative and reflects more resolved ion, nucleotide and inhibitor species, we plan to use the model to test and evaluate percussive, breathing and cough therapies which are already effective in the treatment of disorders such as cystic fibrosis [28]. We present a coarse grained approximation to one such test above, however many more lay open to be tested and explored.
Supplementary Material
HIGHLIGHTS.
We develop a model for auto-regulation of surface airway liquid in the lung.
Sources of stress (from cilia and breath) and channel inhibitors are included.
Functional relations are proposed and tested; we compared our results to experiments.
Acknowledgments
This research effort was supported in part by the National Science Foundation grants DMS-0943851, 0908423, 1100281, DMR-1122483, and the National Institutes of Health Grants R01 HL077546-0105, 5-RC1-ES018686-01-02, and HL108927. The research of Garcia was supported by the Brazilian science agency CNPq. We thank David Hill for fruitful discussions, and all participants in the Virtual Lung Project whose interactions have strongly influenced this work.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Blake J. On the movement of mucus in the lung. J Biomech. 1975;8:179–190. doi: 10.1016/0021-9290(75)90023-8. [DOI] [PubMed] [Google Scholar]
- 2.Bridges RJ, Newton BB, Pilewski JM, Devor DC, Poll CT, Hall RL. Na+ transport in normal and CF human bronchial epithelial cells is inhibited by BAY 39-9437. Am J Physiol. 2001;281:L16–L23. doi: 10.1152/ajplung.2001.281.1.L16. [DOI] [PubMed] [Google Scholar]
- 3.Button B, Boucher RC. Roles of mechanical stress in regulating airway surface hydration and mucus clearance rates. Resp Physiol & Neurobio. 2008;163:189–201. doi: 10.1016/j.resp.2008.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Button B, Picher M, Boucher RC. Differential effects of cyclic and constant stress on ATP release and mucociliary transport by human airway epithelia. J Physiol. 2007:577–592. doi: 10.1113/jphysiol.2006.126086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Com G, Clancy JP. Adenosine receptors, cystic fibrosis, and airway hydration. Handb Exp Pharmacol. 2009;193:363–381. doi: 10.1007/978-3-540-89615-9_12. [DOI] [PubMed] [Google Scholar]
- 6.Dirksen ER. Ciliary basal body morphogenesis: the early events. Symp Soc Exp Biol. 1982;35:439–463. [PubMed] [Google Scholar]
- 7.Donaldson SH, Bennett WD, Zeman KL, Knowles MR, Tarran R, Boucher RC. Mucus clearance and lung function in cystic fibrosis with hypertonic saline. N Engl J Med. 2006;354:241–250. doi: 10.1056/NEJMoa043891. [DOI] [PubMed] [Google Scholar]
- 8.Donaldson SH, Hirsh A, Li DC, Holloway G, Chao J, Boucher RC, Gabriel S. Regulation of the epithelial sodium channel by serine proteases in human airways. Am J Physiol. 2002;277:8338–8345. doi: 10.1074/jbc.M105044200. [DOI] [PubMed] [Google Scholar]
- 9.Fahy JV, Dickey BF. Airway mucus function and dysfunction. N Engl J Med. 2010;363:2233–2247. doi: 10.1056/NEJMra0910061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Falkenberg CA, Jakobsson E. A biophysical model for integration of electrical, osmotic, and pH regulations in the human bronchial epithelium. Biophysical Journal. 2010;98:1476–1485. doi: 10.1016/j.bpj.2009.11.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Galassi M. GNU Scientific Library Reference Manual. 3. [Google Scholar]
- 12.Garcia GJ, Picher M, Zuo P, Okada SF, Lazarowski ER, Button B, Boucher RC, Elston TC. Purinergic regulation of respiratory diseases. chapter 3 Springer Publishing; Computational model for the regulation of extracelular ATP and adenosine in airway epithelia. in press. [Google Scholar]
- 13.Garcia-Caballero A, Rasmussen JE, Gaillard E, Watson MJ, Olsen JC, Donaldson SH, Stutts MJ, Tarran R. SPLUNC1 regulates airway surface liquid volume by protecting ENaC from proteolytic cleavage. PNAS. 2009;106:11412–11417. doi: 10.1073/pnas.0903609106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hannides AK, Dunn SM, Aller RC. Diffusion of organic and inorganic solutes through macrofaunal mucus secretions and tube linings in marine sediments. J of Marine Research. 2005;63:957–981. [Google Scholar]
- 15.Hartmann T, Verkman AS. Model of ion transport regulation in chloride-secreting airway epithelial cells: Integrated description of electrical, chemical, and fluorescence measurements. Biophysical J. 2009;58:391–401. doi: 10.1016/S0006-3495(90)82385-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hill DB, Swaminathan V, Estes A, Cribb J, O’Brien T, Davis CW, Superfine R. Force generation and dynamics of individual cilia under external loading. Biophysical J. 2010;98:57–66. doi: 10.1016/j.bpj.2009.09.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hill DB, Vasquez P, Mellnik J, Mckinley S, Vose A, Mu F, Boucher R, Forest MG. Microbead rheology reveals pathological concentration-dependent transitions in human bronchial epithelial mucus. 2012. submitted. [Google Scholar]
- 18.Knowles MR, Robinson JM, Wood RE, Pue CA, Mentz WM, Wager GC, Gatzy JT, Boucher RC. Ion composition of airway surface liquid of patients with cystic fibrosis as compared with normal and disease-control subjects. J Clin Invest. 1997;100:2588–95. doi: 10.1172/JCI119802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lansley AB, Sanderson MJ. Regulation of airway ciliary activity by Ca2+: Simultaneous measurement of beat frequency and intracellular Ca2+ Biophys J. 1999;77:629–38. doi: 10.1016/S0006-3495(99)76919-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lazarowski ER, Tarran R, Grubb BR, van Heusden CA, Okada S, Boucher RC. Nucleotide release provides a mechanism for airway surface liquid homeostasis. J Bio Chem. 2004;279:36855–64. doi: 10.1074/jbc.M405367200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lindley B, Howell EL, Smith BD, Rubinstein GJ, Forest MG, Mitran SM, Hill DB, Superfine R. Stress communication and filtering of viscoelastic layers in oscillatory shear. J Non-Newtonian Fluid Mech. 2009;156:112–20. [Google Scholar]
- 22.Matsui HC, Davis CW, Tarran R, Boucher RC. Osmotic water permeabilities of cultured, well-differentiated normal and cystic fibrosis airway epithelia. J Clin Invest. 2000;105:1419–1427. doi: 10.1172/JCI4546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Matsui HC, Grubb BR, Tarran R, Randell SH, Gatzy JT, Davis CW, Boucher RC. Evidence for periciliary liquid layer depletion, not abnormal ion composition, in the pathogenesis of cystic fibrosis airways disease. Cell. 1998;95:1005–1015. doi: 10.1016/s0092-8674(00)81724-9. [DOI] [PubMed] [Google Scholar]
- 24.Mitran SM, Forest MG, Yao L, Lindley B, Hill DB. Extensions of the Ferry shear wave model for active linear and nonlinear microrheology. J Non-Newtonian Fluid Mech. 2008;154:120–35. doi: 10.1016/j.jnnfm.2008.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Myerburg MM, Butterworth MB, McKenna EE, Peters KW, Frizzell RA, Kleyman TR, Pilewski JM. Airway surface liquid volume regulates enac by altering the serine protease-protease inhibitor balance a mechanism for sodium hyperabsorption in Cystic Fibrosis. J Bio Chem. 2006;281:27942–27949. doi: 10.1074/jbc.M606449200. [DOI] [PubMed] [Google Scholar]
- 26.Novotony JA, Jakobsson E. Computational studies of ion-water flux coupling in the airway epithelium. Am J Physiol Cell Physiol. 1996;270:C1751–C1763. doi: 10.1152/ajpcell.1996.270.6.C1751. [DOI] [PubMed] [Google Scholar]
- 27.Okada SF, Nicholas RA, Kreda SM, Lazarowski ER, Boucher RC. Physiological regulation of ATP release at the apical surface of human airway epithelia. J Bio Chem. 2006;281:22992–3002. doi: 10.1074/jbc.M603019200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Orenstein DM. Cystic Fibrosis; A Guide for Patient and Family. 3. Lippincott Williams and Wilkins; 2003. [Google Scholar]
- 29.Rollins BM, Burn M, Coakley RD, Chambers LA, Hirsh AJ, Clunes MT, Lethern MI, Donaldson SH, Tarran R. A2b adenosine receptors regulate the mucus clearance component of the lung’s innate defense system. Am J Respir Cell Mol Biol. 2008;39:190–7. doi: 10.1165/rcmb.2007-0450OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schmid A, Clunes LA, Salathe M, Verdugo P, Dietl P, Davis CW, Tarran R. Nucleotide-mediated airway clearance. Subcell Biochem. 2011;55:95–138. doi: 10.1007/978-94-007-1217-1_5. [DOI] [PubMed] [Google Scholar]
- 31.Tarran R, Button B, Boucher RC. Regulation of normal and cystic fibrosis airway surface liquid volume by phasic shear stress. Annu Rev Physiol. 2006a;68:543–61. doi: 10.1146/annurev.physiol.68.072304.112754. [DOI] [PubMed] [Google Scholar]
- 32.Tarran R, Button B, Picher M, Paradiso AM, Ribeiro CM, Lazarowski ER, Zhang L, Collins PL, Pickles RJ, Fredberg JJ, Boucher RC. Normal and cystic fibrosis airway surface liquid homeostasis. J Bio Chem. 2005;280:35751–9. doi: 10.1074/jbc.M505832200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tarran R, Grubb BR, Gatzy JT, Davis CW, Boucher RC. The relative roles of passive surface forces and active ion transport in the modulation of airway surface liquid volume and composition. J Gen Physiol. 2001a;118:223–36. doi: 10.1085/jgp.118.2.223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tarran R, Grubb BR, Parsons D, Picher M, Hirsh AJ, Davis CW, Boucher RC. The CF salt controversy: In vivo observations and therapeutic approaches. Mol Cell. 2001b;8:149–58. doi: 10.1016/s1097-2765(01)00286-6. [DOI] [PubMed] [Google Scholar]
- 35.Tarran R, Trout L, Donaldson SH, Boucher RC. Soluble mediators, not cilia, determine airway surface liquid volume in normal and cystic fibrosis superficial airway epithelia. J Gen Physiol. 2006b;127:591–604. doi: 10.1085/jgp.200509468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Vallet V, Chraibi A, Geaggeler HP, Horisberger JD, Rossier BC. An epithelial serine protease activates the amiloride-sensitive sodium channel. Nature. 1997;389:607–610. doi: 10.1038/39329. [DOI] [PubMed] [Google Scholar]
- 37.Warren NJ, Tawhai MH, Crampin EJ. A mathematical model of calcium-induced fluid secretion in airway epithelium. J Theor Bio. 2009;256:837–849. doi: 10.1016/j.jtbi.2009.04.026. [DOI] [PubMed] [Google Scholar]
- 38.Warren NJ, Tawhai MH, Crampin EJ. Mathematical modelling of calcium wave propagation in mammalian airway epithelium: evidence for regenerative atp release. Exp Physiol. 2010;95:232–249. doi: 10.1113/expphysiol.2009.049585. [DOI] [PubMed] [Google Scholar]
- 39.Willumsen NJ, Davis CW, Boucher RC. Intracellular Cl− activity and celular Cl− pathways in cultured human airway epithelium. Am J Physiol. 1989;256:C1033–44. doi: 10.1152/ajpcell.1989.256.5.C1033. [DOI] [PubMed] [Google Scholar]
- 40.Zuo P, Picher M, Okada SF, Lazarowski ER, Button B, Boucher RC, Elston TC. Mathematical model of nucleotide regulation on airway epithelia. J Bio Chem. 2008;283:26805–19. doi: 10.1074/jbc.M801516200. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.