Abstract
The purpose of the study was to determine the contributions of endpoint variance and trajectory variability to the endpoint accuracy of goal-directed isometric contractions when the target force and contraction speed were varied. Thirteen young adults (25 ± 6 years) performed blocks of 15 trials at each of 2 contraction speeds and 4 target forces. Subjects were instructed to match the peak of a parabolic force trajectory to a target force by controlling the abduction force exerted by the index finger. The time to peak force was either 150 ms (fast) or 1 s (slow). The target forces were 20, 40, 60, and 80% of the maximal force that could be achieved in 150 ms during an MVC. The same absolute forces were required for both contraction speeds. Endpoint accuracy and variability in force and time along with intramuscular EMG activity of the agonist (first dorsal interosseus) and antagonist (second palmar interosseus) muscles were quantified for each block of trials. The principal dependent variables were endpoint error (shortest distance between the coordinates of the target and the peak force), endpoint variance (sum of the variance in peak force and time to peak force), trial-to-trial variability (SD of peak force and time to peak force), SD of the force trajectory (SD of the detrended force from force onset to peak force), normalized peak EMG amplitude, and the SD of normalized peak EMG amplitude. Stepwise multiple linear regression models were used to determine the EMG activity parameters that could explain the differences observed in endpoint error and endpoint variance. Endpoint error increased with target force for the fast contractions, but not for the slow contractions. In contrast, endpoint variance was greatest at the lowest force and was not associated with endpoint error at either contraction speed. Furthermore, force trajectory SD was not associated with endpoint error or endpoint variance for either contraction speed. Only the trial-to-trial variability of the timing predicted endpoint accuracy for fast and slow contractions. These findings indicate that endpoint error in tasks that require force and timing accuracy is minimized by controlling timing variability but not force variability, and that endpoint error is not related to the amplitude of the activation signal.
Keywords: Hand, First dorsal interosseus, Force control, Neural noise
Introduction
Despite efforts to the contrary, the actions produced during a voluntary muscle contraction always vary within a trial (trajectory variability) and from trial-to-trial (endpoint variability; Christou et al. 2002a, b; Enoka et al. 2003). The variable output of the neuromuscular system is often regarded as noise superimposed on a descending motor command (Harris and Wolpert 1998; Slifkin and Newell 1999), but the actual sources of this variability have not been determined (Stein et al. 2005).
The minimum variance theory (Harris and Wolpert 1998; Hamilton and Wolpert 2002; Jones et al. 2002; Hamilton et al. 2004) suggests that noise in the central nervous system (CNS) distorts the motor command to spinal neurons and consequently impairs the accuracy of voluntary movements. One consequence of the superimposed noise is to cause the endpoint location of a trajectory to vary across repeat performances of a task. Because noise increases linearly and proportionally with the magnitude of the motor command (Schmidt et al. 1979), higher centers are presumed to minimize the variability in endpoint location by optimizing the motor command (van Beers et al. 2004) and by activating muscles that limit the amount of variability in the trajectory (Hamilton et al. 2004).
Based on computer simulations, Harris and Wolpert (1998) reported that an optimization model could successfully predict the trajectories of arm and eye movements, the relations described by Fitts’ law (Fitts 1954), and the two-thirds power law (Lacquaniti et al. 1983). Subsequently, the model was extended to isometric contractions involving several muscle groups (Jones et al. 2002; Hamilton et al. 2004), and three sets of results are consistent with the theoretical concepts associated with the minimum variance theory. First, endpoint variability (Schmidt et al. 1979; Sherwood and Schmidt 1980; Newell and Carlton 1985; Carlton and Newell 1993; Christou and Carlton 2001) and trajectory fluctuations increase with the amplitude of the activation signal (Jones et al. 2002; Todorov 2004). Second, faster movements, which require a greater activation signal, exhibit greater variability and are less accurate than slower movements (Woodworth 1899; Fitts 1954; Christou et al. 2003). Third, accurate isometric contractions (Christou et al. 2007) and movements (Christou et al. 2003) are often associated with smoother trajectories.
However, several features of the minimum variance theory are not consistent with some experimental findings. For example, many studies indicate that the relation between the variability in force (noise) and the level of force (magnitude of the descending command) is neither linear nor proportional (Fullerton and Cattell 1892; Jenkins 1947; Newell and Carlton 1985; Slifkin and Newell 1999, 2000; Christou and Carlton 2001, 2002; Christou et al. 2002a, b; Taylor et al. 2003; Yao 2004). Second, an increase in the level of agonist–antagonist muscle coactivation, which requires an augmentation of the descending command, can improve rather than impair movement accuracy (Osu et al. 2004). Third, the accuracy of slow movements in the absence of visual feedback is likely influenced by proprioceptive and especially cutaneous feedback (Johansson and Birznieks 2004; Johansson and Westling 1987) in addition to features of the command signal (Todorov 2004).
Previous studies have examined the influence of force trajectory variability and endpoint variability on endpoint accuracy during goal-directed isometric contractions either to a single target force (25% maximum) and contraction speed (150 ms time target) (Christou et al. 2007; Poston et al. 2008a, b) or to a target that did not require accuracy in both force and time (Christou et al. 2003; Hamilton et al. 2004). Although these studies collectively provided partial support for several of the predictions of the minimum variance theory, none addressed the question of whether measures of accuracy and variability scaled with the size of the activation signal. The purpose of the current study was to determine the contribution of endpoint variance and trajectory variability to the endpoint accuracy of isometric contractions when target force and contraction speed were varied. The findings from this study provide a more thorough understanding of the interaction between motor-output variability and endpoint accuracy of the healthy nervous system and allow for comparisons with individuals who exhibit greater motor-output variability (e.g., older adults or persons with Parkinson’s disease). A preliminary account of these results has been published in abstract form (Poston et al. 2005).
Methods
Thirteen young adults (25 ± 6 years; 7 men) volunteered to participate in the study. All subjects were right-handed according to the Edinburgh Handedness Inventory (Old-field 1971), had no known neurological disorders, and none reported use of medications known to influence neurological function. Subjects provided written, informed consent before participating in the experiment, and the Human Subjects Committee at the University of Colorado in Boulder approved all experimental procedures.
Experimental arrangement
Subjects were seated and faced a computer monitor located at eye level. All subjects affirmed that they could clearly see the visual display provided by the monitor. The left (non-dominant) arm was abducted by 45° with the elbow joint flexed to 90°. The forearm was placed in a prone position and allowed to rest comfortably on an experimental table. Nylon straps were placed over the upper forearm and wrist to minimize arm movement. The third to fifth digits and the thumb of the left hand were restrained to set an angle of ~90° between the index finger and the thumb. Only the left index finger was free to move and push against the force transducer. The left index finger was placed in a modified orthosis to maintain extension of the middle and distal interphalangeal joints.
Force measurement
The metacarpophalangeal joint of the index finger was set at 5° of abduction for all trials. The abduction force was measured with a force transducer (Sensotec, 060-0571-04, Model 41, Columbus, OH) that was aligned perpendicular to the proximal interphalangeal joint. To minimize the involvement of other muscles and maximize the force in the abduction direction, subjects pushed against the rigid surface of the force transducer via a low-friction contact point that comprised half a ball bearing (Valero-Cuevas 2000; Christou et al. 2007). This arrangement ensured that the index finger maintained the required posture and that the force exerted by the index finger was directed primarily in the abduction direction. The first dorsal interosseus (FDI) and second palmar interosseus (SPI) muscles exert most of the abduction and adduction forces, respectively, when the index finger is in this position (Chao et al. 1989; Li et al. 2003; Zijdewind and Kernell 1994).
EMG measurement
The EMG activity of these two muscles was measured with intramuscular bipolar electrodes that were inserted percutaneously into each muscle. Each electrode comprised two stainless steel wires (50-μm diameter) that were insulated with Formvar (California Fine Wire, Grover Beach, CA). The electrodes were inserted into the belly of each muscle using a 30-gauge hypodermic needle. After the insertion of the electrodes, the needle was removed and the wires remained in the muscle belly for the duration of the experiment. Reference electrodes were placed on the styloid process of the ulna for the FDI and on the dorsal surface of the fifth metacarpophalangeal joint for the SPI. The EMG signals were amplified (×1,000–5,000) and band-pass filtered (100–5,000 Hz; Coulbourn Instruments, Allentown, PA). The EMG of both muscles was sampled at 10 k samples/s with a data-acquisition interface power 1401 [Cambridge Electronic Design (CED), Cambridge, UK] and stored on a personal computer.
Experimental procedures
Experiments were performed on the FDI muscle of the left hand. Subjects reported to the laboratory on two occasions and performed the following three tasks: (1) maximal voluntary contractions (MVCs) with the SPI muscle; (2) MVCs with the FDI muscle; (3) a series of endpoint accuracy trials involving isometric contractions of the FDI muscle to four force targets at two speeds (8 blocks of 15 trials). The target forces for the accuracy trials were based on the peak force achieved during the MVCs.
Each subject participated in a familiarization session and an experimental session that each lasted 2 h. The two sessions were performed on consecutive days. In the familiarization session, subjects received a written description of the project and signed the consent forms that were approved by the Human Subjects Committee at the University of Colorado in Boulder. The subjects were given an extensive demonstration of the experimental procedures by one of the investigators before performing MVCs and practicing 120 aiming trials (15 trials × 8 blocks), which is sufficient practice to reach a plateau in performance (Christou et al. 2007; Poston et al. 2008a, b). Similar procedures were used during the experimental session.
MVC task
Subjects were instructed to produce the maximal force in the shortest time possible and to hold this maximum for 2 s. Three to five trials were recorded for each muscle and subjects rested for 60 s between trials. The force exerted by each subject at 150 ms was taken as the maximal force and used as the reference for the target forces during the endpoint accuracy trials (Christou et al. 2007). Similarly, the EMG amplitudes for the FDI and SPI were normalized to the maximum of the rectified and filtered EMG during the 2-s hold phase of the MVC task.
Endpoint accuracy task
Accuracy was assessed for goal-directed, isometric contractions with the FDI muscle. A template was displayed on the computer monitor in front of the subject indicating the target force and target time. Subjects were instructed to match the endpoint of the abduction force exerted by the index finger (peak force) to the endpoint of the line (target = 0.1 cm2) as accurately as possible by producing a force–time parabola (Fig. 1). The quantification of endpoint accuracy has been described previously (Christou et al. 2007; Poston et al. 2008a, b). The endpoint of the line had the target coordinates of 150 ms or 1,000 ms and a target force of 20, 40, 60, or 80% of MVC force. The x axis on the screen was adjusted so that the error in time presented on the monitor was the same relative value for both the slow and fast contractions; the length of the x axis was three times the target time to peak force. These relative adjustments of the x axis lead to the appearance of different sized errors in absolute time, but this was preferable to providing an absolute adjustment of the x axis that would have made it difficult to identify the time error during the fast contractions. In contrast, the relative adjustment made it easier for subjects to interpret the feedback after each trial.
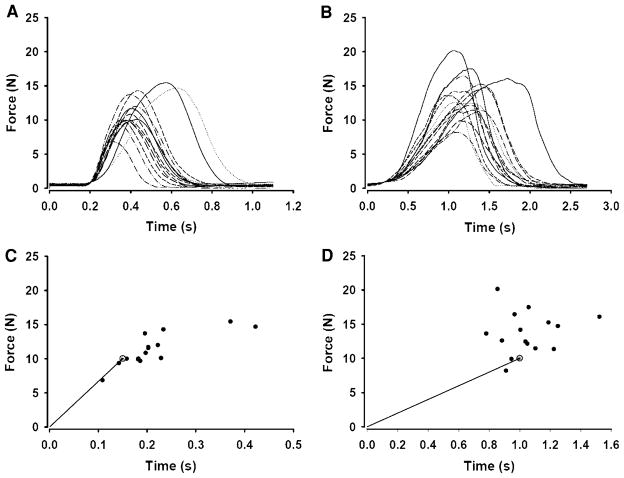
Fig. 1.
Representative endpoint accuracy trials for fast and slow contractions. a The force–time profiles for a block of 15 trials during fast isometric contractions to a target force that was set at 80% of MVC force. b The force–time profiles for a block of 15 trials for the same subject during slow isometric contractions to a target force that was 80% of MVC force. c, d Corresponding endpoints (peak force and time to peak force) relative to the target (gray circle) for the fast and slow trials shown in a and b, respectively
Prior to each trial, subjects were required to exert a light force against the force transducer (~1.5% of MVC force) for 3–5 s. The baseline force was necessary to avoid a collision of the ball bearing with the force transducer, which caused a large artifact in the force signal. Once the baseline force was established, subjects performed the endpoint accuracy task at their convenience (no reaction time component) upon hearing the cue “GO” from one of the investigators. After the abduction force reached a threshold of 3% of MVC, the force trace was hidden from the subject for the duration of the trial. The start of the trial was taken as the time when the force exceeded the threshold. Subjects were provided with visual feedback (a red line on the target template) of their performance 500 ms after each trial and the feedback was displayed for 2 s. Endpoint error was indicated as the distance between the peak of the force exerted by the index finger and the end of the target line, and subjects were instructed to minimize this distance.
Each subject performed 8 blocks of 15 trials at each of 2 contraction speeds and 4 forces (120 total trials). Four blocks were performed with a target speed of 150 ms (fast contractions) and 4 blocks were performed with a target speed of 1 s (slow contractions). The target forces were 20, 40, 60, and 80% of the maximal force that each subject achieved at 150 ms during the MVC trials, which meant that the same absolute target forces were used for both contraction speeds. The performance order for movement speed was counterbalanced, whereas the order for force was randomized across subjects.
Prior to each block of trials, subjects were told the target force required for that block as a percentage of their maximum (20, 40, 60, or 80%) to minimize the learning effect often observed in the first few trials of each block. Three minutes of rest were given between each block of trials. Removal of the first 1–3 trials did not influence the overall results of the ANOVAs, which indicated that any possible learning effect did not differentially influence any of the eight conditions. Outliers (≥±3SD from the mean) were removed for each block regardless of the trial number (see below).
Data analysis
All data collected during the experiments were acquired using custom-written script in the Spike2 programming language (Cambridge Electronic Design, Cambridge, UK) and analyzed offline using custom-written programs in Matlab (Mathworks Inc., Natick, Massachusetts, USA). The force signals were digitized at 1 k samples/s and smoothed using a fourth-order Butterworth digital filter with an optimal cut-off frequency of 6 Hz.
Endpoint error
The endpoint error was calculated as the shortest distance between the coordinates of the target and the peak force for each trial. Errors were measured between the endpoint of the trial (peak force) and the target in force (N; force error), time (s; time error), and endpoint error (cm) dimensions. Endpoint error was determined by transforming the x (time) and y (force) coordinates of each trial into distance (cm) (Christou et al. 2007; Poston et al. 2008a, b). The distance to the target was directly related to the size of the visual feedback presented to the subject on the monitor. In addition to these absolute measures, the relative force, time, and endpoint errors were determined as a percentage of the required target forces and times.
Motor-output variability
The variability in performance across trials was quantified with four measures: endpoint variance, force trajectory variability, peak force variability, and timing variability. The distribution of endpoint locations across trials was quantified as the endpoint variance and was determined as the sum of the variance in peak force (N) and time to peak force (s) (van Beers et al. 2004) after these values had been transformed to distance (cm) for each block of 15 trials (Christou et al. 2007; Poston et al. 2008a). Endpoint variance provided a measure of the variability of the force–time endpoints relative to the average performance of the subject. The variability within each trial was expressed as the force trajectory variability and was determined as the SD of the detrended force from force onset to peak force for each trial using the detrend function in Matlab, which removes the linear trend from the data (Fig. 2). In addition, trial-to-trial variability for force was quantified as the standard deviation (SD) of the peak force and trial-to-trial variability in timing was quantified as the SD of the time to peak force.
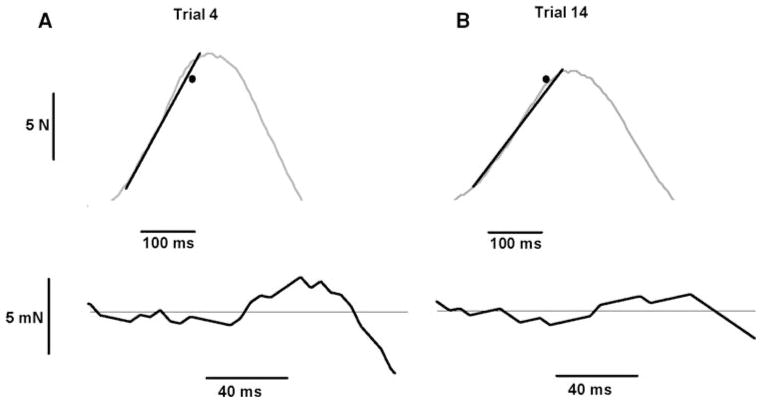
Fig. 2.
Representative endpoint accuracy trials for a single subject and the associated force trajectory SDs and force–time target (black dot) for the trials. a The force–time profile (top panel) for a trial during a fast isometric contraction to a target of 80% of MVC force and the corresponding force trajectory SD (bottom panel) for the same trial. b The force–time profile (top panel) for a trial during a fast isometric contraction to a target of 80% of MVC force and the corresponding force trajectory SD (bottom panel) for the same trial. The force trajectory SD was calculated as the SD of the detrended force signal from force onset to peak force (distance between dashed lines) and was 2.60 mN for the trial shown in a and 1.44 mN for the trial shown in b
Agonist and antagonist EMG activity
The interference EMG for the FDI and SPI muscles was rectified and smoothed using a fourth-order Butterworth digital filter with a cut-off frequency of 6 Hz (Christou et al. 2007; Poston et al. 2008a, b). This filter was used to identify the amplitudes, onsets, and offsets of the EMG bursts for the agonist and antagonist muscles. The EMG activity was characterized by calculating the normalized peak EMG amplitude relative to the maximal MVC value to obtain a gross estimate of the size of the activation signal for the single agonist and antagonist muscles. Furthermore, multiple regression models (see “Statistical analysis”) were used to determine the EMG parameters that contributed to differences in endpoint error and variability between conditions based on the results of the significant interactions and main effects. The following EMG parameters were quantified for both muscles during each block of trials for inclusion in the multiple regression models: (1) onset (start) of EMG: >15% of the peak EMG; (2) offset (end) of EMG: <15% of the peak EMG; (3) normalized peak EMG amplitude; (4) EMG duration: the time between the onset and offset; (5) EMG-force delay: time between peak EMG amplitude for FDI and SPI and peak force; (6) SPI-to-FDI peak delay: time between peaks in FDI and SPI EMGs; (7) SPI-to-FDI onset delay: time between onsets in FDI and SPI EMGs; and (8) time to peak EMG. Finally, trial-to-trial variability of these parameters was quantified as the SD of each parameter for each block of trials and included in the multiple regression models.
Statistical analysis
The major dependent variables were: (1) endpoint error; (2) endpoint variance; (3) Force trajectory variability; (4) SD of peak force; (5) SD of time to peak force; (6) force error; (7) time error; (8) relative force, time, and endpoint errors; (9) Peak EMG amplitude of the FDI and SPI muscles. Two-factor ANOVAs (2 contraction speeds × 4 force levels) with repeated measures on both factors were used to compare the dependent variables. Paired contrasts (t tests with Bonferroni corrections) were used to locate differences among pairs of means when appropriate.
Bivariate linear regressions were used to examine the associations between selected measures of motor-output variability and accuracy. Stepwise multiple linear regression models were used to establish statistical models that could predict the differences in endpoint error or endpoint variance (criterion variables) from the FDI and SPI muscle activity (predictor variables). The goodness-of-fit of the model, which indicates how well the linear combination of the variables predicted the spatial and time endpoint error, was given by the squared multiple correlation (R2) and the adjusted squared multiple correlation (adjusted R2). The adjusted R2 is reported because the R2 can overestimate the percentage of the variance in the criterion variable that can be accounted for by the linear combination of the predictor variables, especially when the sample size is small and the number of predictors is large (Green and Salkind 2002). The relative importance of the predictors was estimated with the part correlations (part r), which provide the correlation between a predictor and the criterion after removing the effects of all other predictors in the regression equation from the predictor but not the criterion (Green and Salkind 2002). A positive part correlation indicates that the predictor and the criterion are directly related, whereas a negative sign denotes an inverse relation.
A significance level was set at P < 0.05 for all statistical tests, except when modified by Bonferroni corrections. Trials in which the dependent measures were greater than ±3 standard deviations from the mean were excluded from the analysis; less than 2% of all trials were excluded. Data are indicated as mean ± standard deviations in the tables and mean ± standard errors in the figures.
Results
This study compared endpoint error and four measures of motor-output variability during isometric contractions performed with a hand muscle at 2 target speeds to 4 target forces. Subjects were instructed to match the peak of a parabolic force trajectory to the targets as accurately as possible. The means and standard deviations for the dependent measures are reported in Table 1 and represent the group averages.
Table 1.
Mean (SD) of the error and variability measures during the goal-directed trials
| Fast (150 ms)
|
Slow (1 s)
|
|||||||
|---|---|---|---|---|---|---|---|---|
| 20% | 40% | 60% | 80% | 20% | 40% | 60% | 80% | |
| Endpoint error (cm) | 3.87 (1.64) | 3.60 (1.44) | 4.83 (2.21) | 6.97 (3.98) | 3.97 (1.68) | 3.49 (1.31) | 3.58 (1.09) | 3.46 (0.95) |
| Endpoint variance (cm2) | 47.7 (29.9) | 21.2 (7.3) | 29.4 (25.7) | 25.7 (23.8) | 40.9 (27.5) | 22.9 (17.4) | 17.4 (10.5) | 11.3 (10.1) |
| SD force trajectory (N) | 0.12 (0.06) | 0.22 (0.13) | 0.31 (0.18) | 0.49 (0.29) | 0.14 (0.06) | 0.31 (0.18) | 0.43 (0.25) | 0.66 (0.52) |
| SD peak force (N) | 0.87 (0.40) | 1.33 (0.61) | 1.93 (0.99) | 0.99 (1.00) | 0.92 (0.43) | 1.37 (0.95) | 2.21 (1.76) | 1.89 (0.82) |
| SD time to peak force (s) | 0.036 (0.019) | 0.034 (0.015) | 0.046 (0.021) | 0.053 (0.03) | 0.219 (0.067) | 0.226 (0.085) | 0.225 (0.079) | 0.207 (0.076) |
| Force error (N) | 0.89 (0.44) | 1.22 (0.06) | 1.95 (1.11) | 2.21 (0.86) | 0.87 (0.41) | 1.29 (0.86) | 2.02 (1.71) | 2.25 (1.28) |
| Time error (s) | 0.034 (0.16) | 0.033 (0.014) | 0.045 (0.023) | −0.066 (0.041) | 0.233 (0.114) | 0.209 (0.081) | 0.214 (0.067) | 0.201 (0.076) |
Endpoint error and variability
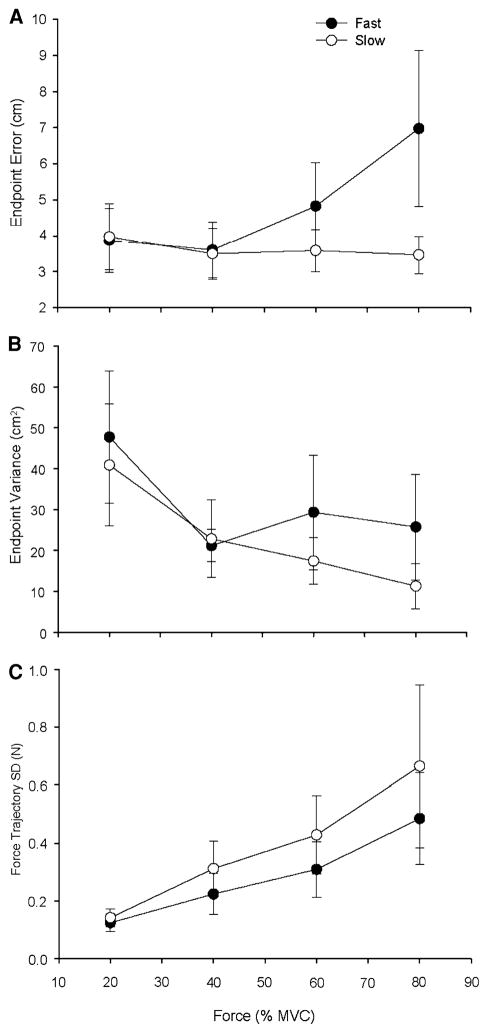
Endpoint error (Fig. 3) varied with target force (P = 0.024) and contraction speed (P = 0.001) and there was a significant interaction between contraction speed and force (P = 0.003). The interaction indicated that endpoint error was greater for fast contractions compared with slow contractions, but only for the 60 and 80% target forces, and it increased with target force during the fast contractions but not the slow contractions. Endpoint variance (Fig. 3b) decreased similarly for both contraction speeds with an increase in target force (P < 0.001).
Fig. 3.
Endpoint error, endpoint variance, and force trajectory SD for the fast and slow contractions as a function of target force. Each data point corresponds to the mean ± SE for 1 block of 15 trials at each target force for fast (filled circles) and slow (open circles) contractions. a Endpoint error increased with target force for the fast contractions, but not the slow contractions. A significant contraction speed × force interaction (P = 0.001) indicated that endpoint error was greater for fast contractions compared with slow contractions at the 60 and 80% target forces. b Endpoint variance was greater at the 20% target force compared with all the other target forces and did not differ across the two contraction speeds. c Force trajectory SD increased with target force for both contraction speeds and was greater for the slow contractions compared with the fast contractions (P < 0.001)
Force trajectory variability
The force trajectory SD (Fig. 3c) increased with target force for both contraction speeds (P < 0.001), but a main effect for speed (P = 0.012) indicated greater force trajectory SD during the slow contractions compared with the fast contractions. There was no significant interaction between contraction speed and force.
Force and timing errors and variability
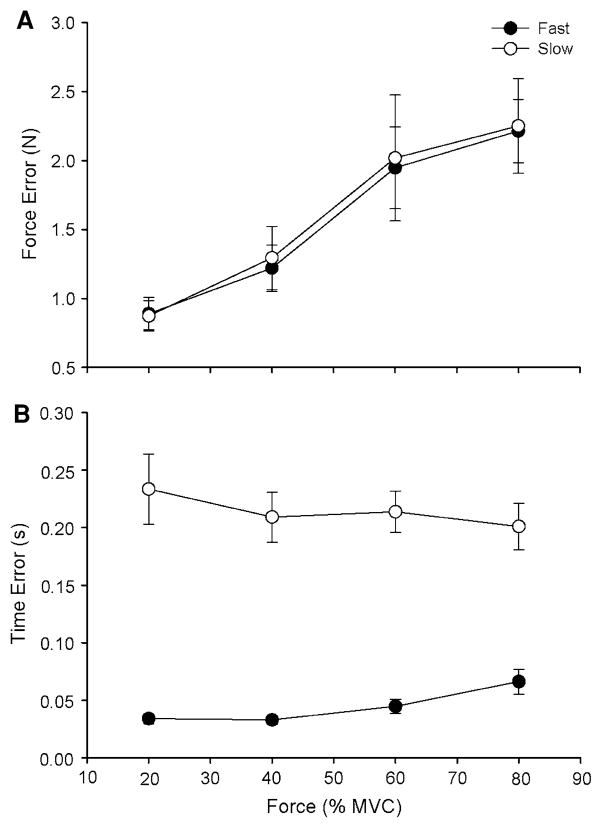
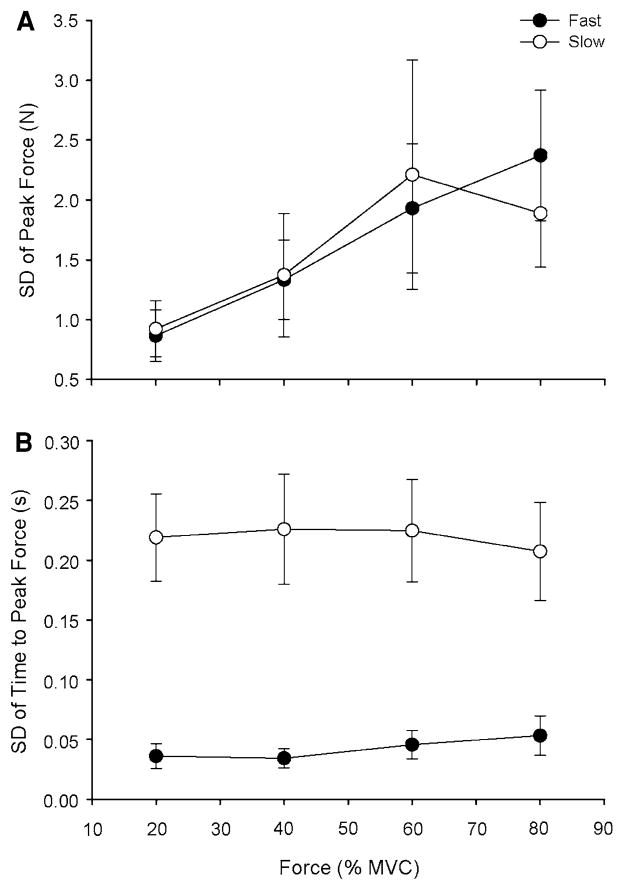
Both the force error (Fig. 4a) and the SD of peak force (Fig. 5a) increased with target force for both contraction speeds (P < 0.001). There were no significant interactions between contraction speed and target force for either the force error or the SD of peak force. Both the time error (Fig. 4b) and the SD of the time to peak force (Fig. 5b) were greater for the slow contractions than for the fast contractions (P < 0.001) and did not change with target force at each contraction speed.
Fig. 4.
Force and time error for the fast and slow contractions as a function of target force. Each data point corresponds to the mean ± SE for 1 block of 15 trials at each target force for fast (filled circles) and slow (open circles) contractions. a The force error increased with target force for the fast and slow contractions (P < 0.001). b The time error was greater for the slow contractions compared with the fast contractions (P < 0.001)
Fig. 5.
The SDs of peak force and time to peak force for the fast and slow contractions as a function of target force. Each data point corresponds to the mean ± SE for 1 block of 15 trials at each target force for fast (filled circles) and slow (open circles) contractions. a The SD of peak force increased similarly with target force for the fast and slow contractions (P < 0.001). b The SD of time to peak force was greater for the slow contractions than for the fast contractions at all target forces (P < 0.001)
Relative errors
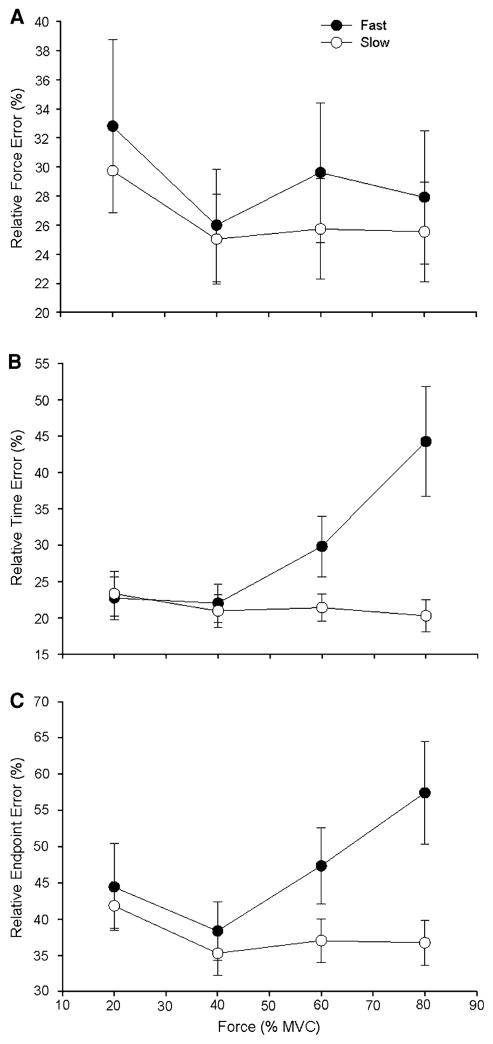
The relative force, time, and endpoint errors were determined as a percentage of the required target forces and times. The relative force error was similar for the two contraction speeds, did not vary with target force, and there was no significant interaction between contraction speed and target force (Fig. 6a). The relative time error increased with force for the fast contractions but not the slow contractions, which resulted in the fast contractions having significantly greater relative time error compared with the slow contractions (speed × force interaction P = 0.001; Fig. 6b). The relative endpoint error was significantly greater for the fast contractions than for the slow contractions (P = 0.001; Fig. 6c). Although the speed × force interaction was not significant (P = 0.1), the relative endpoint error was greater for the fast contractions at the higher force levels.
Fig. 6.
Relative force error, relative time error, and relative endpoint error for the fast and slow contractions as a function of target force. Each data point corresponds to the mean ± SE for 1 block of 15 trials at each target force for fast (filled circles) and slow (open circles) contractions. a The relative force error was similar for the two contraction speeds and four target forces, and there was no significant interaction between contraction speed and target force. b The relative time error increased with target force for the fast contractions, but not the slow contractions. Furthermore, the fast contractions exhibited significantly greater relative time error compared with the slow speed contractions, especially at higher force levels (speed × force interaction P = 0.001). C. The relative endpoint error was significantly greater for the fast contraction than for the slow contractions (P = 0.001). However, the speed × force interaction was not significant (P = 0.1) despite the greater relative endpoint error for the fast contractions at the higher force levels
Agonist and antagonist EMG amplitude
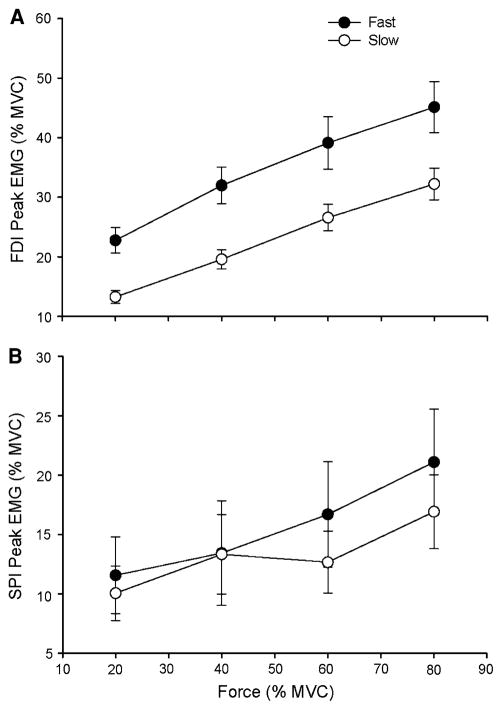
The EMG amplitude for FDI (Fig. 7a) increased with target force for both contraction speeds (18.0 ± 8.84, 25.8 ± 11.1, 32.8 ± 14.3, and 38.4 ± 14.5% of MVC for the 20, 40, 60, and 80% target forces, respectively; P < 0.001), but a main effect for speed (P = 0.001) indicated greater EMG amplitude during the fast speed contractions (34.7 ± 9.63% of MVC) compared with the slow contraction speeds (22.9 ± 8.25% of MVC). There was no significant interaction between contraction speed and force. Although the main effect for EMG amplitude of SPI failed statistical significance due to the high variability in SPI activation by the subjects, there was a trend (P = 0.07) for an increase in EMG amplitude of the SPI as a function of target force (10.8 ± 10.3, 13.4 ± 14.4, 14.7 ± 13.5, and 19.0 ± 14.2% of MVC for the 20, 40, 60, and 80% target forces, respectively; Fig. 7b). The main effect for contraction speed (15.7 ± 4.17% of MVC = fast contractions vs. 13.3 ± 2.83% of MVC = slow contractions; P = 0.283) and the speed × force interaction were not significant.
Fig. 7.
The peak EMG amplitudes of the agonist (FDI) and antagonist (SPI) muscles for the fast and slow contractions as a function of target force. Each data point corresponds to the mean ± SE for 1 block of 15 trials at each target force for fast (filled circles) and slow (open circles) contractions. a The FDI peak EMG increased linearly with target force for the fast and slow contractions (P < 0.001) and was greater for the fast contractions compared with the slow contractions (P < 0.001). b There was no significant change in SPI peak EMG (P = 0.283) as a function of target force for the fast and slow contractions. There was no main effect for SPI peak EMG across contraction speed (P = 0.07)
Associations between motor-output variability and error
Bivariate linear regression analyses were used to determine the associations between the measures of error and variability. First, the association between endpoint variance and endpoint error for both the fast and slow contractions at each target force was examined. Endpoint variance was not significantly correlated (r ranged from −0.36 to 0.29) with endpoint error for any of the force levels at each contraction speed, except for 80% target force at the fast speed (r = 0.671). Second, a regression analysis examined the influence of force trajectory SD on endpoint error, force error, and time error (Table 2). Force trajectory SD was not significantly correlated with either endpoint error or time error, but it was correlated with the force error (Table 2; r ranged from 0.52 to 0.74). Third, regression analyses evaluated the associations between the SD of peak force (Table 3) and the SD of the time to peak force (Table 4) with the three measures of error. The SD of peak force was systematically correlated (r ranged from 0.67 to 0.97) with the force error, but not the endpoint error or the time error (Table 3). The SD of time to peak force was always associated with the endpoint error (r ranged from 0.49 to 0.84) and the time error (r ranged from 0.63 to 0.87), and was positively associated with the force error for the fast contractions at the 60 and 80% target forces and was negatively associated for the slow contractions at the 20 and 80% target forces (Table 4). In general, these results indicate that force trajectory SD was associated with measures of force accuracy and variability but not with measures that included a timing accuracy or variability component.
Table 2.
Correlations between force trajectory SD (N) and the measures of error and variability during the goal-directed trials
| Fast (150 ms)
|
Slow (1 s)
|
|||||||
|---|---|---|---|---|---|---|---|---|
| 20% | 40% | 60% | 80% | 20% | 40% | 60% | 80% | |
| Endpoint error (cm) | 0.30 | 0.15 | 0.37 | 0.45 | 0.03 | −0.31 | 0.11 | −0.06 |
| Time error (ms) | 0.38 | 0.20 | 0.42 | 0.47 | 0.05 | −0.38 | 0.06 | 0.04 |
| Force error (N) | 0.67 | 0.70 | 0.53 | 0.74 | 0.52 | 0.72 | 0.62 | 0.30 |
| Endpoint variance (cm2) | −0.36 | 0.11 | 0.20 | 0.67 | 0.00 | 0.29 | 0.00 | 0.29 |
Bold indicates P < 0.01
Table 3.
Correlations between peak force SD (N) and the three measures of error during the goal-directed trials
| Fast (150 ms)
|
Slow (1 s)
|
|||||||
|---|---|---|---|---|---|---|---|---|
| 20% | 40% | 60% | 80% | 20% | 40% | 60% | 80% | |
| Endpoint error (cm) | 0.42 | 0.47 | 0.37 | 0.34 | −0.21 | −0.28 | 0.36 | −0.15 |
| Time error (ms) | 0.47 | 0.48 | 0.38 | 0.36 | −0.07 | −0.36 | 0.16 | −0.11 |
| Force error (N) | 0.67 | 0.80 | 0.86 | 0.69 | 0.93 | 0.81 | 0.97 | 0.86 |
Bold indicates P < 0.01
Table 4.
Correlations between time to peak force SD (N) and the three measures of error during the goal-directed trials
| Fast (150 ms)
|
Slow (1 s)
|
|||||||
|---|---|---|---|---|---|---|---|---|
| 20% | 40% | 60% | 80% | 20% | 40% | 60% | 80% | |
| Endpoint error (cm) | 0.72 | 0.67 | 0.84 | 0.70 | 0.49 | 0.82 | 0.59 | 0.73 |
| Time error (ms) | 0.85 | 0.72 | 0.87 | 0.71 | 0.49 | 0.83 | 0.63 | 0.76 |
| Force error (N) | 0.31 | 0.16 | 0.72 | 0.73 | −0.54 | −0.10 | −0.22 | −0.50 |
Bold indicates P < 0.01
Prediction of change in endpoint error
Stepwise multiple linear regression models were used to identify those features of the EMG activity for the two muscles that could explain the differences observed in endpoint error. The main differences in endpoint error included the following: (1) greater endpoint error for fast compared with slow goal-directed contractions to the 60 and 80% MVC target forces; (2) greater endpoint error for 80% relative to 20% for fast contractions; (3) an average (both fast and slow contractions) decline in endpoint variance from 20 to 80% MVC.
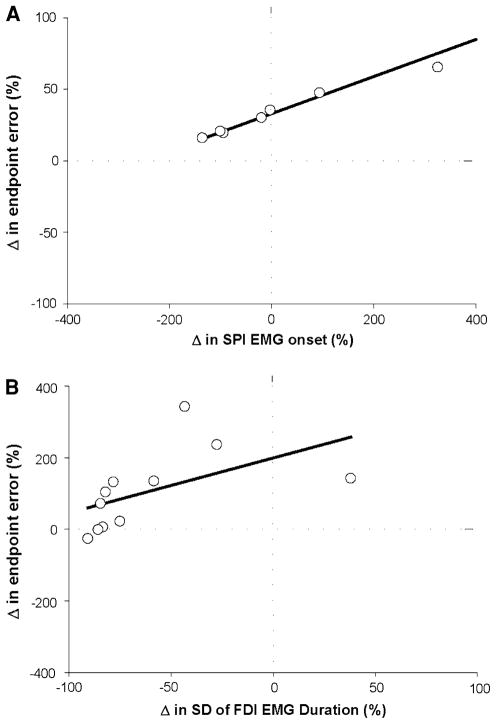
The greater endpoint error for the fast goal-directed contractions was quantified as the percent change from the slow contractions [(fast error − slow error)/slow error × 100]. The change (increase) in endpoint error for the fast contraction to the 60% MVC target force was predicted (R2 = 0.75; adjusted R2 = 0.71; P < 0.001; Fig. 8a) by the difference in SPI EMG onset for the slow and fast contractions (part r = 0.87). However, the change (increase) in endpoint error for the fast contraction to the 80% MVC target force was predicted (R2 = 0.73; adjusted R2 = 0. 69; P < 0.001; Fig. 8b) by the difference in FDI EMG duration for the fast and slow contractions (part r = 0.85).
Fig. 8.
Prediction of the change (increase) in endpoint error for fast contractions relative to slow contractions at 60% and 80% of MVC. Each open circle in the two panels represents that data from one subject. a Stepwise, multiple linear regression analysis indicated that the change (increase) in endpoint error at 60% MVC was strongly predicted (R2 = 0.75; adjusted R2 = 0.71; P < 0.001) by the difference in SPI EMG onset for the slow and fast contractions (part r = 0.87). b Stepwise, multiple linear regression analysis indicated that the change (increase) in endpoint error at 80% MVC was strongly predicted (R2 = 0.73; adjusted R2 = 0.69; P < 0.001) by the difference in FDI EMG duration (part r = 0.85) for the slow and fast contractions
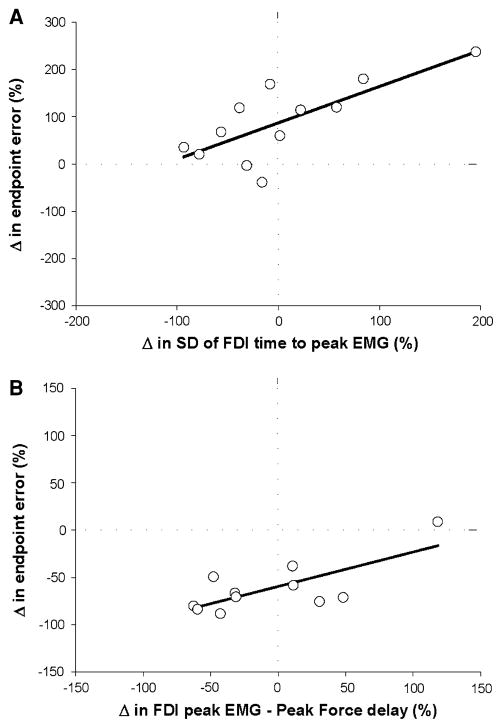
The greater endpoint error for the 80% target relative to 20% target for the fast contractions was quantified as the percent change from the 20% values [(80% error − 20% error)/20% error × 100]. It was predicted (R2 = 0.65; adjusted R2 = 0.6; P < 0.001; Fig. 9a) by the change in the SD of the FDI time to peak EMG (part r = 0.85). The average decrease in endpoint variance from 20 to 80% MVC target force was quantified as the percent change from the 20% value [(80% error − 20% error)/20% error × 100] and was predicted (R2 = 0. 54; adjusted R2 = 0.49; P = 0.003; Fig. 9b) by the change in the SD of the FDI peak EMG (part r = 0.78) and the change in the variability of the time delay of the FDI peak EMG relative to the peak force (part r = 0.73).
Fig. 9.
Prediction of the change of endpoint error and endpoint variance for 80% relative to 20% MVC of the fast contractions. Each open circle in the two panels represents that data from one subject. a Stepwise, multiple linear regression analysis indicated that the change (increase) in endpoint error from 20 to 80% MVC target force was predicted (R2 = 0.65; adjusted R2 = 0.6; P < 0.001) by the difference in the SD of the time to peak EMG for FDI (part r = 0.85). b Stepwise, multiple linear regression analysis indicated that the change (decrease) in endpoint variance from 20 to 80% MVC target force was predicted (R2 = 0. 54; adjusted R2 = 0.49; P = 0.003) by the difference in the SD of the FDI peak EMG (part r = 0.78) and the change in the variability of the time delay between the FDI peak EMG relative to the peak force (part r = 0.73)
Discussion
The study examined the influence of motor-output variability on the endpoint accuracy of goal-directed isometric contractions for which the intensity of the muscle contraction was varied by using different target forces and contraction speeds. The findings indicate that endpoint error increased with target force for the fast contractions, but not for the slow contractions. The variability in timing was the best predictor of endpoint error, whereas endpoint variance, peak force SD, and force trajectory SD were not associated with endpoint error.
Although these results are consistent with the broad predictions of the minimum variance theory that the nervous system minimizes noise to achieve endpoint accuracy (Harris and Wolpert 1998), the following findings differed from specific predictions of the theory: (1) despite an increase in endpoint error with the amplitude of muscle activation (target force) for fast contractions, as predicted by the minimum variance theory, there was no increase with target force for slow contractions. (2) Trial-to-trial variability in force and trajectory variability (force SD) were associated with force error and trial-to-trial variability in timing was associated with time error. However, other purported predictors of accuracy, such as endpoint variance and trajectory variability, were not associated with endpoint error.
Endpoint error and the intensity of the neural control signal
One major prediction of the minimum variance theory is that neuromuscular noise increases linearly with the absolute value of the neural control signal (Harris and Wolpert 1998). As noted by Stein et al. (2005), however, an explicit definition of the neural control signal was never provided by Harris and Wolpert (1998). The neural control signal cannot correspond to the mean discharge rate for either single or groups of cortical neurons because the standard deviation of discharge rate does not increase linearly with the mean discharge rate (Stein et al. 2005). Therefore, the intensity of the neural control signal is probably best represented by the net force or torque exerted by a muscle or muscle group (Stein et al. 2005).
In the present study, the intensity of the activation signal was varied by using target forces 20, 40, 60, and 80% of maximum at two contraction speeds (150 ms and 1 s). Accordingly, the EMG amplitude of the agonist (FDI) muscle increased linearly with the target force for both contraction speeds (Fig. 7a). Similarly, the amplitude of the antagonist (SPI) muscle also seemed to increase linearly with the target force (Fig. 7b); however, this increase was highly variable across subjects and just failed statistical significance. The EMG activity was greater for fast contractions and endpoint error increased non-linearly with target force for fast contractions, whereas endpoint error remained constant across forces for slow contractions (Fig. 3a). The findings from the slow isometric contractions, therefore, contradict the prediction of the minimum variance theory that endpoint error should increase with the absolute value of the neural control signal. In addition to the absolute measures of force error, time error, and endpoint error, the relative errors (% of target forces and time) were also calculated (Fig. 6). The overall results were similar for the absolute and relative measures of error and the relative error did not increase as a function of force for the slow contractions. Taken together, the results for the absolute and relative error measures are consistent with the suggestion of Todorov (2004) that the minimum variance theory may not be able to predict the accuracy of slow goal-directed contractions.
The lower endpoint error during slow contractions was likely due to differences in the type and efficacy of feedback-mediated corrections to the force trajectory and its peak that are possible in slow contractions. In contrast, the variability in peak force during rapid isometric contractions of 150 ms or less is likely constrained by the monitoring of efferent commands through propriospinal neurons (Gordon and Ghez 1987). However, the monitoring of efferent commands could only explain 1–14% of the variance of peak force in the study by Gordon and Ghez (1987). It seems, therefore, that only small corrections to the force trajectory could be made during the 150-ms contractions as there was not enough time to process sensory feedback (no visual feedback) (Cordo et al. 1994). In contrast, the slow contractions (1,000 ms) surely involved peripheral feedback from proprioceptive sources and especially cutaneous receptors located in the skin to provide information on the magnitude, direction, and rate of force exerted by the finger (Johansson and Birznieks 2004; Johansson and Westling 1987). Accordingly, a slower onset of the antagonist muscle predicted the greater error observed for fast relative to slow contractions at 60% MVC (Fig. 8a), whereas increased variability in the agonist muscle duration predicted the greater error observed for fast relative to slow contractions at 80% MVC (Fig. 8b). These results likely indicate that sensory feedback from proprioceptive and cutaneous receptors during the slow contractions modified the timing of the agonist and antagonist muscle activity to lower the endpoint error. Regardless of the exact mechanisms underlying the lower endpoint error for the fast contractions, the results strongly suggest that the minimum variance theory has a limited ability to predict the accuracy of slow contractions (Todorov 2004).
Previous studies on goal-directed isometric contractions to a target force focused exclusively on the variability of the peak force as a function of target force (Schmidt et al. 1979; Christou and Carlton 2001; Christou and Carlton 2002). As a result, these studies did not quantify the endpoint error (distance in force–time coordinates) between the peak force and the target force and, therefore, do not directly link endpoint variability to endpoint error. These distinctions are important because endpoint variability and endpoint error are not related when a subject produces a consistent performance that is relatively far from the target (Muller and Sternad 2004; Christou et al. 2007).
Endpoint error and motor-output variability
Neuromuscular noise is typically quantified from various measures of motor-output variability, including endpoint variance (Poston et al. 2008a, b; van Beers et al. 2004), trajectory variability (Christou et al. 2003, Hogan 1984; Darling and Cooke 1987), and endpoint variability (Christou et al. 2007; Muller and Sternad 2004). According to the minimum variance theory, motor-output variability should increase with the amplitude of the neural control signals and impair the ability of an individual to perform accurate actions. In contrast to this expectation, endpoint variance decreased with target force for the fast and the slow contractions and was greater for the 20% target force compared with all other forces (Fig. 3b). In addition, there were no significant differences in endpoint variance across contraction speeds. The finding of different relations for endpoint error and endpoint variance with target force further indicates that reductions in endpoint variance do not always lead to decreases in endpoint error (Muller and Sternad 2004; Christou et al. 2007). Furthermore, there were no strong or systematic associations between endpoint error and endpoint variance for either of the two contraction speeds (Table 2).
Although force trajectory variability (force SD) increased linearly with target force for both contraction speeds, it was greater for the slow contractions and they had lower endpoint error than the fast contractions. Thus, force trajectory variability did not predict endpoint error. Nonetheless, force trajectory variability was a good predictor of force error, which is one of the two contributors to endpoint error (Table 2). These observations, therefore, support the prediction by Hamilton et al. (2004) that smooth trajectories should lead to improved accuracy during goal-directed contractions. Nonetheless, smooth trajectories contributed only to force accuracy and not to timing accuracy or overall accuracy of the contraction.
Studies of goal-directed arm movements have indicated that trajectory smoothness is an important control variable modulated by the nervous system under different task conditions (Morasso 1981; Hogan 1984; Darling and Cooke 1987; Darling et al. 1989; Uno et al. 1989; Shadmehr and Mussa-Ivaldi 1994; Gribble et al. 2003). In contrast, the current study and other experiments that involve goal-directed isometric contractions with hand muscles (Poston et al. 2008a, b; Christou et al. 2007) demonstrate that force trajectory SD influences only the force and not the timing endpoint accuracy. Therefore, it appears that the role of trajectory variability differs for goal-directed movements and isometric contractions. It is unclear, however, if these differences are a result of the type of contraction (shortening, isometric), the effector used to perform the task (arm, finger), the task requirements (force accuracy vs. force–time accuracy), or a combination of these factors. For example, the dissimilarities could be due to mechanical factors such as the influence of joint interaction torques during arm movements (Zhang et al. 2006) or due to differences in the activation of hand muscles compared with limb muscles (Lemon 1993; Devanne et al. 2002). Irrespective of the exact mechanisms underlying these differences in trajectory control, the current findings suggest that force trajectory variability is a good predictor of force error but not endpoint error during goal-directed isometric contractions with a hand muscle.
In contrast, trial-to-trial variability in timing was significantly associated with endpoint error for both fast and slow contractions. This is a novel finding and demonstrates that timing variability may be an important control variable for the nervous system to accomplish accurate contractions when there are both force and time constraints. Therefore, the current results support the broad predictions of the minimum variance theory and findings from previous studies that the nervous system attempts to limit the noise of the control variable to improve endpoint accuracy (Harris and Wolpert 1998; Faisal et al. 2008). Nonetheless, the findings suggest that the control variable likely varies across tasks (timing instead of force) and may not necessarily be related to the intensity of the contraction.
One limitation of the current study is that it mainly tested the prediction of the minimum variance theory that neuromotor noise increases with the size of the control signal under isometric conditions. Goal-directed isometric contractions were studied because proponents of the minimum variance theory expanded the original theory from observations on goal-directed arm and eye movements to constant isometric contractions (Jones et al. 2002; Hamilton et al. 2004). The current data, however, provide no insight on the associations between endpoint accuracy and variability and the size of the control signal during arm and eye movements. Nonetheless, Osu et al. (2004) demonstrated that an increase in the size of the control signal through coactivation can improve rather than impair movement accuracy. However, Osu et al. (2004) used a single-joint arm movement task in which the movement trajectory was fixed by an apparatus that constrained the trajectory of the limb. As the minimum variance theory predicts that trajectory variability is related to endpoint accuracy and variability, it is difficult to determine if the task used by Osu et al. (2004) was an appropriate test of the theory.
Taken together, several studies have supported some of the predictions of the minimum variance theory (Christou et al. 2003, 2007; Harris and Wolpert 1998; Hamilton and Wolpert 2002; Jones et al. 2002; Hamilton et al. 2004), whereas others either have not or have found mixed results (Christou et al. 2007; Osu et al. 2004; Poston et al. 2008a, b; Tanaka et al. 2006; Todorov 2004). The issue should be examined with experimental data on arm and eye movements and not just computer simulations (Harris and Wolpert 1998; Tanaka et al. 2006).
In summary, endpoint error increased with the amplitude of the activation signal (target force) for fast but not slow contractions, which questions the validity of applying the minimum variance theory to slow contractions (Todorov 2004). When the task requires force and timing accuracy, however, the strategy appears to emphasize the control of timing variability to minimize endpoint error. These findings partially support the predictions of the minimum variance theory (Harris and Wolpert 1998) during goal-directed isometric contractions with a hand muscle.
Acknowledgments
This work was supported by National Institute on Aging (NIA) awards AG024662 and AG031769 (EAC) and AG09000 (RME). B. Poston was supported by NIA Predoctoral Training Fellowship T32 AG00279-05 (PI Robert Schwartz).
Contributor Information
Brach Poston, Email: brach.poston@nih.gov, brach.poston@asu.edu, Department of Kinesiology, Arizona State University, Tempe, AZ, USA. Human Motor Control Section, Medical Neurology Branch, NINDS, National Institutes of Health, Building 10, Room 7D37, 10 Center Drive MSC 1428, Bethesda, MD 20892-1428, USA.
Evangelos A. Christou, Department of Health and Kinesiology, Texas A&M University, College Station, TX, USA
Joel A. Enoka, Department of Integrative Physiology, University of Colorado, Boulder, CO, USA
Roger M. Enoka, Department of Integrative Physiology, University of Colorado, Boulder, CO, USA
References
- Carlton LG, Newell KM. Force variability and characteristics of force production. In: Newell KM, Corcos D, editors. Variability and motor control. Human Kinetics; Champaign, Illinois: 1993. [Google Scholar]
- Chao EYS, An KN, Cooney WP, III, Linscheid RL. Biomechanics of the Hand, A Basic Research Study. World Scientific Publishing; Teaneack, NJ: 1989. [Google Scholar]
- Christou EA, Carlton LG. Old adults exhibit greater motor output variability than young adults only during rapid discrete isometric contractions. J Gerontol A Biol Sci Med Sci. 2001;56:B524–B532. doi: 10.1093/gerona/56.12.b524. [DOI] [PubMed] [Google Scholar]
- Christou EA, Carlton LG. Motor output is more variable during eccentric compared with concentric contractions. Med Sci Sports Exerc. 2002;34:1773–1778. doi: 10.1097/00005768-200211000-00013. [DOI] [PubMed] [Google Scholar]
- Christou EA, Grossman M, Carlton LG. Modeling variability of force during isometric contractions of the quadriceps femoris. J Mot Behav. 2002a;34:67–81. doi: 10.1080/00222890209601932. [DOI] [PubMed] [Google Scholar]
- Christou EA, Tracy BL, Enoka RM. Progress in motor control, volume II: structure–function relations in voluntary movements. Human Kinetics; Champaign: 2002b. The steadiness of lengthening contractions; pp. 195–207. [Google Scholar]
- Christou EA, Shinohara M, Enoka RM. Fluctuations in acceleration during voluntary contractions lead to greater impairment of movement accuracy in old adults. J Appl Physiol. 2003;95:373–384. doi: 10.1152/japplphysiol.00060.2003. [DOI] [PubMed] [Google Scholar]
- Christou EA, Poston B, Enoka JA, Enoka RM. Different neural adjustments improve endpoint accuracy with practice in young and old adults. J Neurophysiol. 2007;97:3340–3350. doi: 10.1152/jn.01138.2006. [DOI] [PubMed] [Google Scholar]
- Cordo P, Carlton L, Bevan L, Carlton M, Kerr GK. Proprioceptive coordination of movement sequences: role of velocity and position information. J Neurophysiol. 1994;71:1848–1861. doi: 10.1152/jn.1994.71.5.1848. [DOI] [PubMed] [Google Scholar]
- Darling WG, Cooke JD. Changes in the variability of movement trajectories with practice. J Mot Behav. 1987;19:291–309. doi: 10.1080/00222895.1987.10735414. [DOI] [PubMed] [Google Scholar]
- Darling WG, Cooke JD, Brown SH. Control of simple arm movements in elderly humans. Neurobiol Aging. 1989;10:149–157. doi: 10.1016/0197-4580(89)90024-9. [DOI] [PubMed] [Google Scholar]
- Devanne H, Cohen LG, Kouchtir-Devanne N, Capaday C. Integrated motor cortical control of task-related muscles during pointing in humans. J Neurophysiol. 2002;87:3006–3017. doi: 10.1152/jn.2002.87.6.3006. [DOI] [PubMed] [Google Scholar]
- Enoka RM, Christou EA, Hunter SK, Kornatz KW, Semmler JG, Taylor AM, Tracy BL. Mechanisms that contribute to differences in motor performance between young and old adults. J Electromyogr Kinesiol. 2003;13:1–12. doi: 10.1016/s1050-6411(02)00084-6. [DOI] [PubMed] [Google Scholar]
- Faisal AA, Selen LPJ, Wolpert DM. Noise in the nervous system. Nat Rev Neurosci. 2008;9:292–303. doi: 10.1038/nrn2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitts PM. The information capacity of the human motor system in controlling the amplitude of movement. J Exp Psychol. 1954;47:381–391. [PubMed] [Google Scholar]
- Fullerton GS, Cattell JM. On the perception of small differences. University of Pennsylvania Press; Philadelphia: 1892. [Google Scholar]
- Gordon J, Ghez C. Trajectory control in targeted force impulses III. Compensatory adjustments for initial errors. Exp Brain Res. 1987;67:253–269. doi: 10.1007/BF00248547. [DOI] [PubMed] [Google Scholar]
- Green SB, Salkind NJ. Using SPSS for the Windows and Macintosh: Analyzing and Understanding Data. Prentice Hall; Upper Saddle River, NJ: 2002. [Google Scholar]
- Gribble PL, Mullin LI, Cothros N, Mattar A. Role of cocontraction in arm movement accuracy. J Neurophysiol. 2003;89:2396–2405. doi: 10.1152/jn.01020.2002. [DOI] [PubMed] [Google Scholar]
- Hamilton AF, Wolpert DM. Controlling the statistics of action: obstacle avoidance. J Neurophysiol. 2002;87:2434–2440. doi: 10.1152/jn.2002.87.5.2434. [DOI] [PubMed] [Google Scholar]
- Hamilton AF, Jones KE, Wolpert DM. The scaling of motor noise with muscle strength and motor unit number in humans. Exp Brain Res. 2004;157:417–430. doi: 10.1007/s00221-004-1856-7. [DOI] [PubMed] [Google Scholar]
- Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394:780–784. doi: 10.1038/29528. [DOI] [PubMed] [Google Scholar]
- Hogan N. An organizing principle for a class of voluntary movements. J Neurosci. 1984;4:2745–2754. doi: 10.1523/JNEUROSCI.04-11-02745.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins WO. The discrimination and reproduction of motor adjustments with various types of aircraft controls. Am J Psychiatr. 1947;60:397–406. [PubMed] [Google Scholar]
- Johansson RS, Birznieks I. First spikes in ensembles of human tactile afferents encode complex spatial fingertip events. Nat Neurosci. 2004;7:170–177. doi: 10.1038/nn1177. [DOI] [PubMed] [Google Scholar]
- Johansson RS, Westling G. Signals in tactile afferents from the fingers eliciting adaptive motor responses during precision grip. Exp Brain Res. 1987;66:141–154. doi: 10.1007/BF00236210. [DOI] [PubMed] [Google Scholar]
- Jones KE, Hamilton AF, Wolpert DM. Sources of signal-dependent noise during isometric force production. J Neurophysiol. 2002;88:1533–1544. doi: 10.1152/jn.2002.88.3.1533. [DOI] [PubMed] [Google Scholar]
- Lacquaniti F, Terzuolo C, Viviani P. The law relating the kinematic and figural aspects of drawing movements. Acta Psychol (Amst) 1983;54:115–130. doi: 10.1016/0001-6918(83)90027-6. [DOI] [PubMed] [Google Scholar]
- Lemon RN. The G. L. Brown Prize Lecture. Cortical control of the primate hand. Exp Physiol. 1993;78:263–301. doi: 10.1113/expphysiol.1993.sp003686. [DOI] [PubMed] [Google Scholar]
- Li ZM, Pfaeffle HJ, Sotereanos DG, Goitz RJ, Woo SL. Multi-directional strength and force envelope of the index finger. Clin Biomech (Bristol, Avon) 2003;18:908–915. doi: 10.1016/s0268-0033(03)00178-5. [DOI] [PubMed] [Google Scholar]
- Morasso P. Spatial control of arm movements. Exp Brain Res. 1981;42:223–227. doi: 10.1007/BF00236911. [DOI] [PubMed] [Google Scholar]
- Muller H, Sternad D. Decomposition of variability in the execution of goal-oriented tasks: three components of skill improvement. J Exp Psychol Hum Percept Perform. 2004;30:212–233. doi: 10.1037/0096-1523.30.1.212. [DOI] [PubMed] [Google Scholar]
- Newell KM, Carlton LG. On the relationship between peak force and peak force variability in isometric tasks. J Mot Behav. 1985;17:230–241. doi: 10.1080/00222895.1985.10735346. [DOI] [PubMed] [Google Scholar]
- Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia. 1971;9:97–113. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- Osu R, Kamimura N, Iwasaki H, Nakano E, Harris CM, Wada Y, Kawato M. Optimal impedance control for task achievement in the presence of signal-dependent noise. J Neurophysiol. 2004;92:1199–1215. doi: 10.1152/jn.00519.2003. [DOI] [PubMed] [Google Scholar]
- Poston B, Enoka JA, Christou EA, Enoka RM. The minimum variance theory fails to predict endpoint accuracy during slow goal-directed, isometric contractions. Soc Neurosci Abstr. 2005;990:21. [Google Scholar]
- Poston B, Enoka JA, Enoka RM. Endpoint accuracy for two hand muscles of different sizes in young and old adults during rapid-goal directed isometric contractions. Exp Brain Res. 2008a;187:373–385. doi: 10.1007/s00221-008-1309-9. [DOI] [PubMed] [Google Scholar]
- Poston B, Enoka JA, Enoka RM. Practice and endpoint accuracy with the left and right hands of old adults: The right-hemisphere aging model. Muscle Nerve. 2008b;37:376–386. doi: 10.1002/mus.20954. [DOI] [PubMed] [Google Scholar]
- Schmidt RA, Zelaznik H, Hawkins B, Frank JS, Quinn JT., Jr Motor-output variability: a theory for the accuracy of rapid motor acts. Psychol Rev. 1979;47:415–451. [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci. 1994;14:3208–3224. doi: 10.1523/JNEUROSCI.14-05-03208.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherwood DE, Schmidt RA. The relationship between force and force variability in minimal and near-maximal static and dynamic contractions. J Mot Behav. 1980;12:75–89. doi: 10.1080/00222895.1980.10735208. [DOI] [PubMed] [Google Scholar]
- Slifkin AB, Newell KM. Noise, information transmission, and force variability. J Exp Psychol Hum Percept Perform. 1999;25:837–851. doi: 10.1037//0096-1523.25.3.837. [DOI] [PubMed] [Google Scholar]
- Slifkin AB, Newell KM. Variability and noise in continuous force production. J Mot Behav. 2000;32:141–150. doi: 10.1080/00222890009601366. [DOI] [PubMed] [Google Scholar]
- Stein RB, Gossen ER, Jones KE. Neuronal variability: noise or part of the signal? Nat Rev Neurosci. 2005;6:389–397. doi: 10.1038/nrn1668. [DOI] [PubMed] [Google Scholar]
- Tanaka H, Krakauer JW, Qian N. An optimization principle for determining movement duration. J Neurophysiol. 2006;95:3875–3886. doi: 10.1152/jn.00751.2005. [DOI] [PubMed] [Google Scholar]
- Taylor AM, Christou EA, Enoka RM. Multiple features of motor-unit activity influence force fluctuations during isometric contractions. J Neurophysiol. 2003;90:1350–1361. doi: 10.1152/jn.00056.2003. [DOI] [PubMed] [Google Scholar]
- Todorov E. Optimality principles in sensorimotor control. Nat Neurosci. 2004;7:907–915. doi: 10.1038/nn1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uno Y, Kawato M, Suzuki R. Formation and control of optimal trajectory in human multijoint arm movement. Minimum torque-change model. Biol Cybern. 1989;61:89–101. doi: 10.1007/BF00204593. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ. Predictive modulation of muscle coordination pattern magnitude scales fingertip force magnitude over the voluntary range. J Neurophysiol. 2000;83:1469–1479. doi: 10.1152/jn.2000.83.3.1469. [DOI] [PubMed] [Google Scholar]
- van Beers RJ, Haggard P, Wolpert DM. The role of execution noise in movement variability. J Neurophysiol. 2004;91:1050–1063. doi: 10.1152/jn.00652.2003. [DOI] [PubMed] [Google Scholar]
- Woodworth R. The accuracy of voluntary movement. Physiol Rev Monogr. 1899;3:1–114. [Google Scholar]
- Yao WX. Roles of motor-unit recruitment in producing force variability of simulated muscle contractions. Mot Control. 2004;8:64–75. doi: 10.1123/mcj.8.1.64. [DOI] [PubMed] [Google Scholar]
- Zhang W, Sainburg RL, Zatsiorsky VM, Latash ML. Hand dominance and multi-finger synergies. Neurosci Lett. 2006;409:200–204. doi: 10.1016/j.neulet.2006.09.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zijdewind I, Kernell D. Index finger position and force of the human first dorsal interosseus and its ulnar nerve antagonist. J Appl Physiol. 1994;77:987–997. doi: 10.1152/jappl.1994.77.2.987. [DOI] [PubMed] [Google Scholar]