Limits of social mobilization

Abstract

The Internet and social media have enabled the mobilization of large crowds to achieve time-critical feats, ranging from mapping crises in real time, to organizing mass rallies, to conducting search-and-rescue operations over large geographies. Despite significant success, selection bias may lead to inflated expectations of the efficacy of social mobilization for these tasks. What are the limits of social mobilization, and how reliable is it in operating at these limits? We build on recent results on the spatiotemporal structure of social and information networks to elucidate the constraints they pose on social mobilization. We use the DARPA Network Challenge as our working scenario, in which social media were used to locate 10 balloons across the United States. We conduct high-resolution simulations for referral-based crowdsourcing and obtain a statistical characterization of the population recruited, geography covered, and time to completion. Our results demonstrate that the outcome is plausible without the presence of mass media but lies at the limit of what time-critical social mobilization can achieve. Success relies critically on highly connected individuals willing to mobilize people in distant locations, overcoming the local trapping of diffusion in highly dense areas. However, even under these highly favorable conditions, the risk of unsuccessful search remains significant. These findings have implications for the design of better incentive schemes for social mobilization. They also call for caution in estimating the reliability of this capability.

The Internet and online social media are now credited with the unprecedented ability to coordinate the mobilization of large masses of people to achieve incredible feats that require coverage of large geographical and informational landscapes in very limited time. Social media have been used to mobilize volunteers to map natural disasters in real time (1) and to conduct large-scale search-and-rescue missions (2). Online social networks also have been an important tool in the coordination of mass political rallies (3, 4).

Endeavors such as the Defense Advanced Research Projects Agency (DARPA) Network Challenge (5) aimed to test the power of the Internet and social media in time-critical social mobilization to its absolute limits. The Network Challenge required competing teams to locate and submit the coordinates of 10 tethered weather balloons dispersed at random locations all over the continental United States. The winning team, based at Massachusetts Institute of Technology (MIT), won the challenge by locating all balloons in less than 9 h. The MIT team used an incentive scheme to kick start an information and recruitment cascade that resulted in 4,400 sign-ups to the team’s Web site within 48 h. Analysis of the diffusion revealed that the recursive incentive scheme may have played an important role in maximizing the speed and branching of the diffusion to limits above what normally are observed in viral propagation schemes (6–8).

More recently, the State Department’s Tag Challenge required competing teams to locate and photograph five target “thieves” (actors) in five different cities in the United States and Europe, based only on a mug shot released at 8:00 AM local time (9). The targets were visible for only 12 h and followed normal itineraries around the cities of Stockholm, London, Bratislava, New York, and Washington DC. Our winning team located three of the five suspects using social media, without any of the team members being based in any of the target cities (10), demonstrating yet another example of time-critical social mobilization in tasks that require coverage of large geographies.

Despite these numerous successes, we still have limited understanding of the limits of technology-mediated mobilization. If we are to rely on social media to react to time-critical emergencies, it is important to understand the conditions under which they can be successful and the risks of failure associated with them. A particular case, of highly practical importance, is to understand the extent to which we can expect to cover a certain geographical area in a given amount of time. For this, we must understand the complete statistical characterization of the population recruited, geographical area covered, and completion time it takes for social mobilization to succeed in a particular task, as well as to quantify the likelihood of failure.

This lack of understanding is especially prone to selection bias over few successful social mobilization strategies and may lead to inflated expectations of the reliability and efficacy of these techniques (11, 12). However, it is beyond experimental capabilities to perform randomized experimentation with large crowdsourcing challenges [with notable exceptions emerging recently (13, 14)].

Modeling efforts in the wake of the H1N1 and other global pandemics also have provided a valuable insight into time-sensitive human dynamics on a large scale, via spatial simulation (15) or network-based diffusion (16, 17). In common with these efforts, we model the interaction and connection of large numbers of agents; however, we consider the propagation of a message that may be transmitted without direct physical proximity and generally shorter “incubation” times, leading to faster spreading. Thus, the mechanism of “infection” (recruitment) is independent of human mobility patterns (18–20), which, in our case, contribute only to the area searched.

In this work, we build on recent results on social network structure, information diffusion, and urban economics to elucidate the constraints they pose on social mobilization. In particular, we conduct high-resolution simulations of the DARPA Network Challenge. We obtain statistical characterizations of the population recruited, geography covered, and time to locate the 10 balloons, together with their dependencies on the instrumental variables.

Our results demonstrate, surprisingly, that the DARPA Network Challenge outcome is plausible and thus not simply a fluke that can be explained only by the role of mass media. Therefore, the challenge lies at the limit of what time-critical social mobilization can achieve. Mobilization requires highly connected, highly active individuals to be motivated to propagate the message to many friends and to mobilize people in distant locations, overcoming the local trapping of diffusion in highly dense areas. Moreover, even under highly favorable conditions, the risk of mobilization failure remains significant. These findings have implications for the design of better incentive schemes for social mobilization. They also call for caution in estimating the reliability of this capability.

Simulation Model

In seeking to understand social mobilization, we must consider the many different dynamics that underpin such a process, particularly the branching dynamics of recruitment, the temporal dynamics of message propagation, the geographical spread of social networks, and the scales and aspects of human mobility. A full accountability of each process will render the simulation and its understanding impossible, and thus we concentrate on the main ingredients that explain the observed behavior in each of the processes.

Recruitment

Examination of the dynamics of the branching recruitment process in empirical data from the challenge (6) suggests several key features. After a large initial round of recruitment from the seed node, the reproductive number is well below the tipping point (SI Appendix). Thus, many subtrees first are created spreading from the root node, then steadily die out. To describe the typical branching recruitment process, we fit to the observed branching data assuming an atypical burst of recruitment when the search commences. We find a power law distribution with a mean 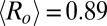. (See Materials and Methods for details of fit.)

Response Time

The importance of the heterogeneity in response times in viral recruitment processes has been demonstrated (21). In a study of a viral e-mail campaign, the time taken to forward a message was found to be log-normally distributed, as opposed to the commonly used Gaussian assumption, with a mean of 1.5 d with an SD of 5.5 d. This large heterogeneity has a deep impact on the propagation of information: cascade dynamics may be halted by the few individuals with very long response times, and thus recruitment events may continue up to the order of years after the seed node starts the cascade. The waiting-time distribution in a time-critical campaign such as the DARPA Network Challenge might differ fundamentally because it necessarily must end by a fixed deadline regardless of whether the campaign is successful. However, we use the distribution of ref. 21 as a reasonable approximation. We do not apply a cutoff at large times, although the tail of the distribution may be effectively truncated because a search may terminate if all balloons are found before recruits with waiting times drawn from the tail of the distribution can act. The role of burstiness in diffusion in temporal networks was investigated systematically in ref. 22 by characterizing tie strength due to both topological and temporal characteristics. Paradoxically, burstiness was found to promote efficient diffusion at small scales but to hinder it on large scales.

Geography of Ties

Several studies have been made of geographical scaling laws for friendship (23–25). Liben-Nowell et al. (26) analyzed a blogging network and the relationship between friendship and distance. They concluded that friendship correlates more strongly with a person’s rank, a measure of the number of closer people, than simply with the distance between people:

where 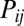is the probability of friendship between agents in two distinct grid cells i and j, 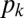is the population in cell k, and 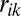is the distance from cell i to cell k. The quantity on the right-hand side is the rank of an agent in i with respect to agent in j; it is a measure of the number of people located between i and j. Thus, the spatial distribution of a person’s friends is now strongly dependent on the local population density, with the effect that two people separated by a given large distance are more likely to be friends in a rural region than in a dense, urban environment. It also was noted that friends could be classified into two distinct types. One group comprises rank-based friends chosen because of geographical proximity (e.g., a shared workplace) in accordance with rank scaling. The authors also observed a “background” probability that an agent might be friends with any other randomly chosen agent from across the country; in this case, friendships are independent of geography. Further, these two types of friends were found to exist in a ratio of 2.5 distance-independent friendships to 5.5 rank-based friendships among the user average of 8 friends. In our simulation, we apply this model of friendship to high-resolution population density data derived from census data (27, 57) (Materials and Methods).

Passive Recruitment

In addition to the branching, temporal, and friendship mechanisms described above, we investigated the role of two other mechanisms: passive recruitment and mobility. We describe these in turn below. The data collected during the DARPA Network Challenge recorded each person who officially registered with the MIT team, allowing them to recruit others and to report findings. However, this is only a subset of all the people who became aware of the search; the record of sign-ups gives a measure of the number of new recruits each individual successfully invites, but not the larger hidden network of individuals who search but do not sign up or recruit others. We refer to this process as passive recruitment, quantified by the number of passive recruits per individual 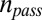. There was a considerable number of single nodes reporting findings directly, separate from any recruitment tree (5 of the 10 balloons were reported in this way). The reported traffic to the MIT team’s Web site of more than 100,000 individuals given only 4,400 sign-ups is further evidence of an unreported, hidden network. This suggests that in addition to the observable chain of individuals who actively recruit others after being recruited themselves, there is a supplementary process whereby individuals become aware of the search and the associated incentives and will report any balloons in their vicinity, yet are not sufficiently motivated to recruit others. This may be the result of low affinity with the potential parent node from which they became aware of the search (28–30). The effect of mass media and possibly word of mouth would manifest itself similarly. By definition, the participation of these individuals is difficult to measure unless they report a balloon, but given the large number of submissions attributed to single nodes that were not part of a recruitment chain, we expect that a sizable number of passive recruits also were participating in the search. This process gives rise to an interesting multiplicative factor, separate from the exponential growth of recruits due to branching.

Although the number of passive recruits a person can mobilize is intrinsically hard to quantify, a good measure of this number is the number of friends of a user of a typical social networking service, such as Facebook. The average degree of the entire global network is around 200, with a large range, but it is observed to be up to 400 among the most active users (31). It is these users who have been observed to drive such viral recruitment processes (21). As discussed in SI Appendix, we study this parameter for a wide range of passive recruits: however, because we aim to test the behavior of successful social mobilizations, we set it to the upper limit of 400 friends. Note also that maintaining a large social network requires a high level of activity (31). Thus, by selecting this level of passive recruitment, we ensure that those users also are the most “temporally active” population.

Mobility

Census data provide a record of where individuals live, but limiting an individual’s effective search area to his or her home ignores that individual’s ability to search his or her vicinity because of his or her mobility. Because of the high resolution of the simulations (1 km²), it is fair to expect that recruits will find a balloon instantaneously in their own cell. However, agents likely will be mobile during the course of a search, allowing them to locate balloons in nearby cells. We quantify this with a radius of gyration (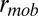). The realistic modeling of individual mobility patterns on short timescales (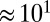h) is nontrivial. These patterns have a proven seasonal nature due to commuting patterns, circadian rhythms (32), and friendship (33), but an exact individual agent-scale model would require a complex probabilistic treatment to account for differences in mobility between rural and urban areas (34), putting it beyond the scope of this model. Therefore, we define a fixed mobility radius allowing agents to locate balloons within a neighborhood of size 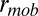. The radius of gyration has been investigated extensively using mobile phone data, although typically these studies have focused on the statistical properties of mobility over the course of weeks and months. However, a recent study found that on timescales appropriate for time-critical social mobilization (i.e., up to 12 h), radii of gyration reached 1–2 km (35), with a large range. Because a large spread in radii around the mean is expected on this timescale, we also investigate radii in the range of 0–5 km in our simulations. This parameter also assimilates other mechanisms, such as recruited agents becoming aware of a balloon via face-to-face, word-of-mouth communication.

In light of recent results finding variability in mobility radius with respect to rank (34) and population density (36), we investigated a variable mobility radius in inverse proportion to local population density (SI Appendix). Although the number of passive recruits is unknown, it likely would follow a distribution because the number of active recruits in the branching recruitment process demonstrated a large range. Therefore, we also investigated the effect of a distribution of passive recruits. Our findings are insensitive to the introduction of both a variable mobility radius and a distribution of passive recruits (SI Appendix).

Results

DARPA Balloon Challenge Feasibility.

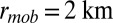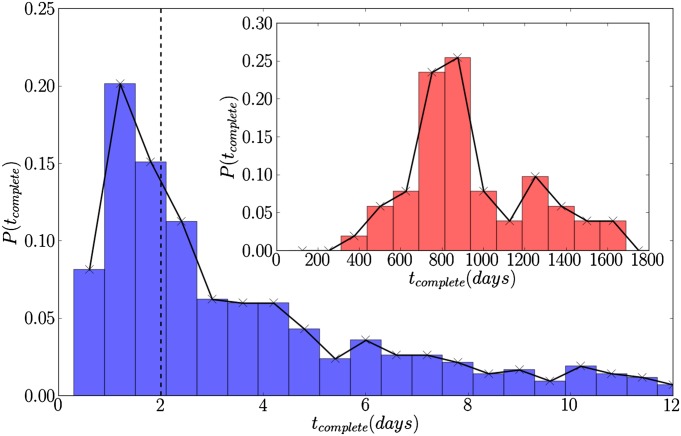
We conducted 500 searches for the 10 DARPA Network Challenge balloon locations using parameters of and 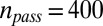. We found a success rate of 89%. A large variation was seen in completion times (Fig. 1, main plot); however, the median completion time among successful searches was 2.3 d, demonstrating a remarkable agreement with the observed time of 48 h between the beginning of recruitment and completion (6). The combined effect of the heavy tailed distribution for branching factor and large heterogeneity in response time gives rise to a large spread in the time for the pure branching process to terminate (21). Successful searches terminate upon completion, which naturally leads to a completion time distribution that is truncated with respect to the underlying distribution of termination times of the pure branching process. It is against this “natural” range of termination times of the branching (Fig. 1, Inset) that the truncated distribution of completion times for successful searches must be compared. The full range of parameters is investigated in SI Appendix. We find that minimum values for mobility radius and passive recruits of 2 km and 200, respectively, are required for a reasonable level of success.

Fig. 1.

Histogram of completion times for successful searches out of 500 instances with parameters 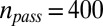and 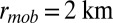(blue) and (Inset) for the remaining unsuccessful searches that fail to locate all 10 balloons (red). Dashed vertical line shows completion time of DARPA Network Challenge after MIT team recruitment commenced. The search continues until all agents have acted; because of the heavy tailed waiting time distribution, this may take as long as several years. However, because most recruits act on much shorter timescales, the searches that succeed in locating all the balloons drastically truncate this distribution.

General Balloon Locations.

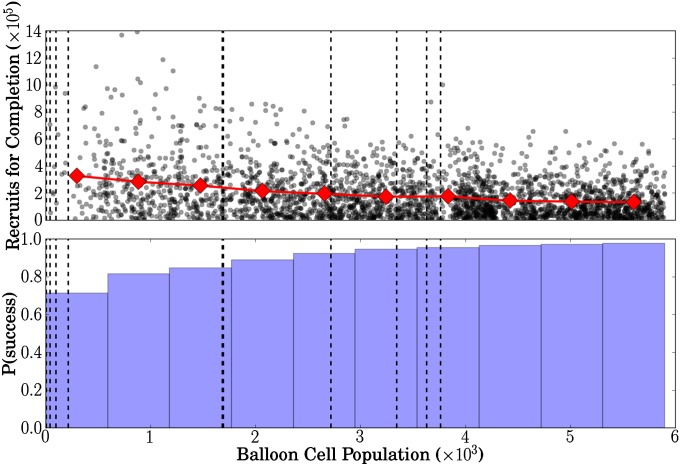
We investigated the hypothesis that the specific balloon locations chosen in the DARPA balloon challenge contributed positively to the speed with which the balloons were found. We randomly chose cells, uniformly sampling a large range of the population. Further, we simulated the search for a single balloon in each simulation to clearly isolate the effect of the balloon’s location on the number of recruits needed to locate it. Fig. 2 plots the number of recruits needed to locate a balloon as a function of the population density of the balloon cell. Although the plot contains some noise, there is a clear trend showing that balloons in sparsely populated areas both require significantly more people to find and are less likely to be found at all, compared with those in well-populated areas. This is the result of a combination of effects; a cell containing fewer potential recruits has a greater likelihood of being searched later. However, this is exacerbated by the fact that the population is far from homogeneously distributed, demonstrating strong spatial autocorrelation (SI Appendix). Rather, a sparsely populated cell likely is surrounded by other sparsely populated cells; thus, there are considerably fewer opportunities for recruitment into that cell from its neighbors. Conversely, well-populated cells in urban areas experience the opposite effect. We have highlighted the extent to which a balloon becomes more easily found as it is moved to a location with higher density. In this context, it may be seen that a few of the chosen balloon locations were in challenging locations but that overall success was expected.

Fig. 2.

Scatter plot of the number of recruits at completion in a search for a single randomly placed balloon as a function of the population in the cell in which the balloon is placed for 5,000 randomly selected balloon locations. Black dots represent only successful searches (Upper). The histogram represents the probability of successfully finding the balloon. Dashed black vertical lines indicate the populations of the locations used in the DARPA Balloon Challenge. The red line represents the mean number of recruits for each histogram bin (Lower).

Searchability, Blendability, and Findability.

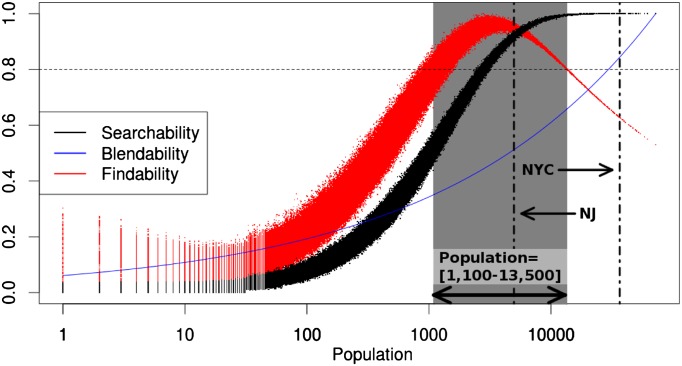
To draw more general conclusions about the probability of searching a location, we move away from the specific balloon locations. We now can measure the ease with which each cell may be searched over the course of many different search realizations. With this in mind, we map the searchability (s) of each cell i as

where 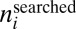is the number of instances in which someone is recruited in cell i out of N searches ( for the following results). We see (Fig. 3) that cells located in dense metropolitan areas are easily searchable because there are many more potential searchers to recruit in those cells, whereas the opposite is true for sparsely populated areas. Fig. 3 (black points) demonstrates this saturating trend above cell population 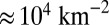. This is far from a linear mapping, as some places are highly searchable despite having only intermediate population. Adding more people to a cell located in a small town increases the searchability a great deal; however, the payoff for adding more people to a cell in a large city is negligible.

Fig. 3.

Scatter plot of searchability (black), population-scaled blendability function (blue), and their ratio, defined as findability (red), as a function of population for all 5,060,288 cells. The shaded region marks the range of population density for which cells have a findability greater than 0.8. The vertical dashed lines represent midtown Manhattan, NY, and Asbury Park, NJ. [The cells within 15 km of the starting cell at MIT have been removed because they are extraordinarily searchable due to their privileged position close to the source of the search (SI Appendix).]

Intuitively, we also might expect an added difficulty in locating a target in a region of high population density, such as Manhattan, despite its density-driven high searchability. We model this difficulty to locate a target at a given place successfully by the blendability 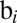of a cell i. There are (at least) two distinct sources for this difficulty. One is a characteristic of the city itself: the increased density leads to increased complexity of the physical urban environment (37–39), providing more possibilities for a target to be concealed (e.g., an adobe house in Santa Fe, NM vs. a skyscraper in Manhattan). The other contributor to the degree of blendability of a location comes from the individual perspective: sensory overload in busy places, leading to inattentional blindness (40–42), diminished feelings of individual responsibility to report sightings in large crowds (43, 44), and/or reduced cognitive processing ability due to stress (45). In all the above cases, we may infer safely that the larger the population of a cell 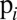, the larger its blendability 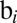. We assume that 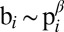, similar to how other urban indicators scale with population (46, 47), e.g., wages and crime with 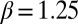. We also consider walking speed with 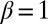in SI Appendix.

Thus, if we define the blendability per person, we obtain

and we rescale 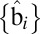to lie in the range .

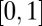The tension between the searchability and blendability of places is modeled by the findability per cell i:

Again we scale 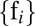to be in the range 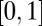and plot Eq. 4 as the red points in Fig. 3 for 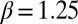(we repeat the analysis using 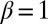in SI Appendix). We isolate a regime of high findability defined by a value greater than 0.8, which corresponds to the gray-shaded region, with a population density in the range of 1,100–13,500 km⁻². We emphasize that the exact findability threshold is not important, as the blendability is defined only up to a constant. Comparing midtown Manhattan (population density, 36,627 km⁻²) with nearby Asbury Park, NJ (population density, 4,975 km⁻²), we see (Fig. 3) that, counterintuitively, it may be easier to hide in the former than in the latter. The origin of this result is that if 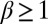, then for a large 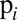, the rate at which searchability increases with population is insufficient to overcome the rate at which blendability increases with population; thus, the findability is maximized in places of intermediate density (which happens when is an increasing function of 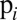; a detailed derivation of the condition for β to display this behavior may be found in SI Appendix).

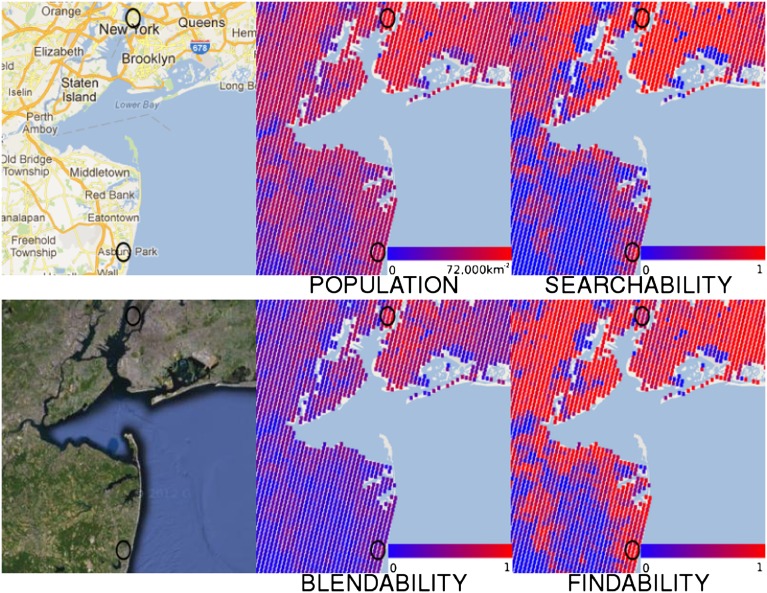
Finally, in Fig. 4 we visualize the variation of the searchability, blendability, and findability in the vicinity of Manhattan and Asbury Park (see SI Appendix for a full map of the continental United States). Manhattan has extremely high population density (strong red shading in upper circle), leading to high searchability. However, this again is counteracted by a very high blendability, resulting in a relatively lower findability than intuitively expected (medium shading in findability map). In contrast, the intermediate population density in Asbury Park leads to a fairly high searchability (medium shading in lower circle). However, because the blendability is very low (blue shading of blendability map), the findability is very high. In general, it can be seen that areas of intermediate population have high findabilities.

Fig. 4.

Maps of Manhattan and Asbury Park showing variation in population density, searchability, blendability, and findability, as well as underlying satellite and road maps. Black circles indicate locations of Manhattan, NY (Upper), and Asbury Park, NJ (Lower). Population density is on a logarithmic scale; all others are on a linear scale. Unpopulated cells are not shown.

Discussion

Our goal is to understand the practical limits of time-critical social mobilization, and to do so in light of contemporary wisdom about the factors that may affect it: the structure and geographical distribution of social ties, the branching and temporal dynamics of information diffusion via social media, and urban economics. Where possible, we used parameters measured from large-scale empirical results to create a realistic, high-resolution simulation of a mobilization scenario akin to the DARPA Network Challenge.

The popular reaction to the DARPA Network Challenge was that it would be impossible without mass media. Our main finding is that success actually is expected only with social media and under realistic parameters. Assuming an initial burst of motivated individuals, success takes place despite the branching factor being lower than the critical point.

That being said, we found two sobering and instructive qualifiers. First, despite the average completion time coinciding with the experience in the actual challenge, the long tail distribution of completion time suggests that the risk of failing to locate the targets within a short time frame also is significant. Second, the challenge lies at the limits of what social mobilization can achieve. Success relies on all parameters being at their practical limits: highly connected individuals must be motivated to propagate the message to many friends and to mobilize people in distant locations, overcoming the local trapping of diffusion in highly dense areas.

Our results have implications for the use of social mobilization to achieve time-critical tasks, such as mapping crises in real time or conducting search-and-rescue operations over large geographies. Novel mobilization mechanisms need to focus on incentivizing the elements of the network that are most conducive to successful mobilization: highly connected people with distant friends, and rapid reaction time. These characteristics may be exploited in a new measure of influence. One may envisage variants of the winning team’s recursive incentive strategy that provide network centrality, distance, and/or time-sensitive rewards to recruit such influentials.

We studied the tension between the benefits and difficulties of searching for physical objects in highly populated areas by defining measures of searchability, blendability, and findability. On one hand, hiding in a sparsely populated town makes it less likely for someone from that town to be recruited to find the target. However, as soon as someone gets recruited, identification becomes trivial. On the other hand, in a city with high density, one might be able to “blend into the crowd.” Our results show that, short of hiding “in the middle of nowhere,” one’s best bet is to hide “in plain sight.” The role of human mobility in the context of blendability is not completely clear and certainly warrants further investigation using a more detailed treatment. Models of geographical ties and mobility should explicitly account for variations in density, particularly the deviation from pure rank scaling (48) demonstrating the increased likelihood of city-based users to have longer-range ties.

It is worthwhile to put our work in the context of search in social networks. Milgram’s landmark “small-world” experiment showed that, in principle, people are findable using six hops on the global social network (49), a result that has been reaffirmed in the Internet age (29). However, Milgram searchability relies on people’s ability to form a reliable estimate of distance to the target to exploit the large jumps afforded by small-world networks (50–52). For example, if the target is known to be a professor who lives in Kyoto, one might try to reach her through a friend who lives in Tokyo, Japan, as he or she is more likely to know someone who lives in Kyoto, who in turn may know someone in academia, and so on. However, if information about a target is scarce (e.g., searching for a person in an entire country based only on a mug shot), we cannot rely on distance estimates. In other words, the problem becomes that of “uninformed” (i.e., “blind”) search (53) and thus requires large-scale social mobilization. Endeavors such as the Tag Challenge (54), in which search may benefit from partial knowledge of target location, require elements of both uninformed and heuristic search, a topic that deserves further study in the context of social mobilization.

Our work is not without limitations. First, we focused on mobilization processes that are fully driven by social ties. In reality, however, mobilization often also benefits from the use of mass media [e.g., AMBER (America’s Missing: Broadcast Emergency Response) Alerts distributed via radio stations and cable television] and social media hubs (e.g., highly followed blogs or Twitter accounts). Surely, such media can accelerate social mobilization, as they complement the social diffusion process and seed it over large areas (55, 56). Second, our work is limited by our use of a simple model of human mobility. For a task like the Network Challenge, this is unlikely to be a problem. However, for scenarios that involve searching for mobile targets, as was the case in the Tag Challenge (54), more sophisticated models of human mobility should be incorporated (32).

Materials and Methods

Materials.

High-resolution population data were taken from publicly available sources (57) based on US census data (27). These data comprise 7,820,528 cells, each with an area of 1 km², of which 5,060,288 are populated (i.e., 2,760,240 are empty). Empirical data from ref. 6 were used to parameterize the branching factor power law distribution as follows. We exclude the first generation of recruitment directly from the MIT team, as this is anomalously high (164 child recruits) and, because of the team’s own unique personal association with the task, likely to be atypical. We also exclude 611 single nodes who signed up directly and did not recruit any child nodes; we assume these are examples of passive recruits who signed up independently. The distribution of the branching factor among a subset of the remaining nodes is described by a power law with mean 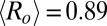(SI Appendix).

Methods.

A set of seed nodes located at MIT is chosen, the number of which matches those initially recruited by the MIT team. All these nodes are active, i.e., they continue to recruit themselves in contrast to passive recruits, which do not continue the recruitment tree. Each newly activated node looks around in its vicinity (within a distance radius of 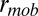) and reports any balloon it sees within that radius. Each newly activated node also chooses an outdegree (a constant number 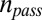of “passive” recruits and a power law-distributed number 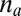of “active” recruits, where 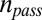is drawn from the distribution seen in the MIT Red Balloon team’s recruitment data). Each chosen friend, passive or active, is chosen to be rank-based with respect to geography, using 1-km² population density data across the United States, with probability 5.5/8 and uniform overpopulation with probability 2.5/8. Each active new recruit selects a delay, chosen from a log-normally distributed waiting time distribution with mean 1.5 d and SD 5.5 d (21), becomes activated, and completes its own recruitment after that time delay.