Population heterogeneity and causal inference

Abstract

Population heterogeneity is ubiquitous in social science. The very objective of social science research is not to discover abstract and universal laws but to understand population heterogeneity. Due to population heterogeneity, causal inference with observational data in social science is impossible without strong assumptions. Researchers have long been concerned with two potential sources of bias. The first is bias in unobserved pretreatment factors affecting the outcome even in the absence of treatment. The second is bias due to heterogeneity in treatment effects. In this article, I show how “composition bias” due to population heterogeneity evolves over time when treatment propensity is systematically associated with heterogeneous treatment effects. A form of selection bias, composition bias, arises dynamically at the aggregate level even when the classic assumption of ignorability holds true at the microlevel.

Two philosophical views have dominated the practice of science. In the classic view, firmly established by Plato and still well represented in physical science today, scientific discoveries consist of abstract knowledge about observed phenomena that essentially share the same properties. Plato (1) separated the “world of being” (or the world of forms) from the “world of becoming” (or the world of things). The world of being is where true knowledge resides. The world of becoming is what we actually observe in real life. An alternative view, first developed by Charles Darwin and now well represented in social science, holds that members of a population are inherently different from each other and should be studied as such. Ernst Mayr (2) called the first view “typological thinking” and the second view “population thinking.”

Typological thinking has had enormous influence on physical science and remains, arguably, the dominant view of what constitutes scientific truths. According to typological thinking, science should focus on the discovery of universally valid and unchanging laws. Toward this end, scientists should extract abstract but conceptually homogeneous relationships in the universe by eliminating the influences of extraneous, confounding factors, with the objective being to obtain knowledge that would be valid anywhere in the universe. A strong assumption that has worked well in natural science is homogeneity: Once we obtain knowledge about a type of phenomenon, we can generalize the knowledge to individual, concrete cases. Observed variation in the real world is treated as apparent, and thus insignificant. Aided by measurement theory, this view culminated in Adolphe Quételet's “social physics,” which naively essentialized population averages, in the form of the “average man,” as the main objective of social science (3, 4).

It was Charles Darwin who first challenged typological thinking in a fundamental way (2). In fact, the proposition that individual variability is real rather than apparent is essential to Darwin’s theory of evolution by natural selection (5). Deviations from the average in a population were no longer considered scientifically trivial, as in typological thinking, but were seen as the very basis of evolution. The importance of variation was later introduced to social science by Francis Galton. Galton departed from the typological tradition by concerning himself with “how the quality is distributed” (ref. 6, pp. 35–36). A historian of science characterizes Galton as someone to whom “Individual differences…were almost the only thing of interest” (ref. 7, p. 221).

Population thinking pioneered by Darwin and Galton led to the emergence of a new kind of science: population science. Instead of discovering universal laws, a population science is concerned with the understanding of what Jerzy Neyman defined as a population, “categories of entities satisfying certain definitions but varying in their individual properties” (ref. 8, p. 96). Note that in a population science, the scientist no longer assumes that all concrete units in a population are essentially the same, or homogeneous. Rather, it is explicitly recognized that units of analysis in a population are different from one another, or heterogeneous. In my view, most social science disciplines, including economics, demography, psychology, sociology, political science, and anthropology, are population sciences in that they cannot afford to discard individual-level variation as a mere nuisance or measurement error by assuming that all units of analysis are essentially the same. The recognition of inherent individual-level heterogeneity has important consequences for research practices. For example, because units of analysis in a population all differ from one another, scientific (or random) sampling is important to ensure representativeness of a well-defined population. In this article, I will draw from a large existing literature to illustrate some implications of this heterogeneity for causal inference (9–13).

1. Causal Inference Under Population Thinking

Suppose that a whole population, U, is being studied. Let Y denote an outcome variable of interest that is a real-valued function for each member of U, and let D denote a dichotomous treatment variable (with its realized value being d) with D = 1 if a member is treated and D = 0 if a member is not treated. For clarity, let subscript i represent the ith member in U. We further denote 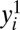as the ith member’s potential outcome if treated (i.e., when d_i = 1) and 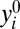as the ith member’s potential outcome if untreated (i.e., when d_i = 0). Due to the ever-present population heterogeneity, we should conceptualize a treatment effect as the difference in potential outcomes associated with different treatment states for the same member in U:

where δ_i represents the hypothetical treatment effect for the ith member. The fundamental problem of causal inference is that for a given unit i, we observe either 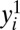(if d_i = 1) or 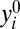(if d_i = 0) but not both (10). Holland (10) describes two possible solutions: the “scientific solution” and the “statistical solution.”

Based on typological thinking, the scientific solution capitalizes on homogeneity in assuming that all members in U are exactly the same: 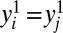and 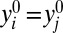, where j ≠ i are different members in U. This strong assumption would allow the researcher to identify individual-level treatment effects. Indeed, one would need as few as two cases in U (say, i and j with different treatment conditions) to reveal treatments effects for all members in the entire population, because the following would hold true:

for any j ≠ i, where we drop the subscript of δ because it does not vary. However, heterogeneity is the rule rather than the exception in social science. Thus, the scientific solution under the homogeneity assumption (Eq. 2) is of no practical value in social science.

In social science, the ubiquity of population heterogeneity dictates the statistical solution as a necessity. One limitation of the statistical approach is that we can compute quantities of interest about causal effects only at an aggregate level. However, when we estimate aggregate-level quantities of interest, we overlook within-group, individual-level heterogeneity. Here, I hasten to distinguish between inattention to within-group heterogeneity and the assumption of within-group homogeneity. I do not believe that we can ever assume within-group homogeneity in social science, but we may choose not to analyze (say, by averaging over) within-group, individual-level heterogeneity in a research setting for practical reasons.

We have now come full circle. We began with the realization that social science takes the view of population thinking, and thus should consider individual-level variability. However, the ubiquitous presence of individual-level variability makes it impossible to study individual-level causal effects. To draw a causal inference, it is necessary to pool information from different members in a population into aggregates. This constant tension between the ontological reality of heterogeneity on the one hand and the epistemological need for inattention to heterogeneity on the other hand is the hallmark of empirical social science. Hence, I propose the following fundamental paradox in social science: Whereas there is always variability at the individual level, causal inference always requires statistical analysis at an aggregate level overlooking individual-level variability.

A common quantity of interest is the average difference between a set of members in U who were randomly selected for treatment and another set of members who were randomly selected for control. Because this quantity is equivalent to the average effect of treatment over the entire population, it is called the average treatment effect (ATE):

where E(.) is the expectation operator over the whole population U.

Quantities of interest in the statistical approach can also be defined for other groups (or subpopulations), as long as they are well defined. For example, treatment effect of the treated (TT) refers to the average difference in Y between treatment and control among those individuals who are actually treated:

Analogously, treatment effect of the untreated (TUT) refers to the average difference by treatment status among those individuals who are not treated:

Estimation of these quantities is a nontrivial matter. Let us partition the total population U into the subpopulation of the treated 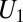(for which D = 1) and the subpopulation of the untreated 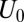(for which D = 0). Selection bias arises if:

and

Observed data allow the researcher to estimate 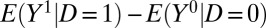, which, however, differs from ATE. Let p be the proportion treated (i.e., the proportion of cases in which D = 1) and q be the proportion untreated (i.e., the proportion of cases in which D = 0).

Using the iterative expectation rule, we can decompose ATE as follows:

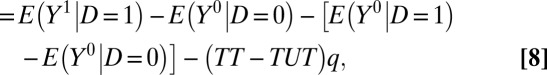where TT and TUT were previously defined in Eqs. 4 and 5. Thus, as has long been known (14), Eq. 8 reveals two potential sources of bias for using the naive estimator 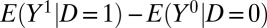for ATE.

The average difference between the treatment and control groups in outcomes if neither group receives the treatment is 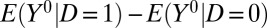. I call this the “pretreatment heterogeneity bias” or “type I selection bias.”

The difference in the ATE between the treatment and control groups 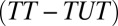, is weighted by the proportion untreated, q. The weight of q results from our choice to define pretreatment heterogeneity bias for the untreated state. I call this the “treatment-effect heterogeneity bias” or “type II selection bias.”

Type I selection bias occurs if subjects are systematically different in relevant but unobserved pretreatment attributes between the treatment and control groups. Type II selection bias occurs when treatment effect is correlated with treatment status. When 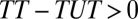, there is a sorting gain, so that the ATE for the treated is greater than the ATE for the untreated. Conversely, if 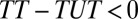, there is a sorting loss. The fixed effects method widely used in social science is designed to eliminate type I selection bias by differencing out unobserved, fixed attributes common between a treated and control matched pair. However, the method is powerless regarding type II selection bias because it requires the assumption that treatment effect is the same between a treated unit and its control unit, resulting in 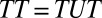. Type II selection bias does not exist if the research interest centers on the TT.

2. Random Assignment, Ignorability, and Propensity Score

Social scientists study causal effects through either experimental or observational data. An experiment eliminates both sources of selection bias by random assignments: A unit in U receives either the treatment or control condition by chance only. Let 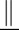denote independence. Random assignment ensures:

so that we can easily compute ATE, TT, and TUT as:

In social science research, experimental studies are rare and usually conducted at a local level. Generalizing experimental results at a local level to quantities of interest at the population level requires additional assumptions (15). Even when assignment into experimental conditions is random, subjects’ compliance with assignments may not be random. In other situations, often called “natural experiments,” it may be assumed that some factors that affect treatment conditions may be random and extraneous, although treatment conditions may not be independent with respect to potential outcomes. This approach is called “instrumental variable (IV) estimation.” For a variable to qualify as an IV, it must meet the exclusion restriction assumption: It affects the likelihood of treatment condition (D) but affects the substantive outcome variable (Y) only indirectly via the treatment status (D) (11, 15–18). One limitation of the approach is that if treatment effects are heterogeneous, IV only identifies the average effect of a narrowly defined subpopulation that is induced into treatment by the IV (17, 18).

Another common approach is to use observational data. The basic idea is to collect rich data measuring population heterogeneity, called covariates, that pertain to potential systematic differences between the treatment and control groups in either the baseline level or the treatment effect. Because only covariates that affect both the treatment assignment and the outcome can cause biases to the observed relationship between treatment and outcome, the researcher hopes that he/she can adequately control for all covariates that simultaneously affect the treatment assignment and the outcome. After controlling for the covariates, the researcher hopes that treatment status will be independent of potential outcomes. This conditional independence assumption is called “ignorability,” “unconfoundedness,” or “selection on observables.” Let X denote a vector of observed covariates. The ignorability assumption states:

Comparison of Eqs. 9 and 10 highlights the crucial role of covariates X. Note that the ignorability condition is always an unverifiable assumption. The plausibility of the ignorability assumption depends on how rich the covariates are, and thus is a substantive issue in actual research rather than a methodological question that can be debated in general. Typically, the researcher may tentatively consider the ignorability assumption and then assess its plausibility in a concrete setting through sensitivity or auxiliary analyses (19, 20).

Conditioning on X can be difficult in applied research if it is of high dimension. However, under the ignorability assumption, it is sufficient to condition on the propensity score as a function of X (21, 22):

where 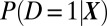denotes the propensity score of treatment given X. In practice, the propensity score is unknown and can be estimated from observed data. The propensity score serves to balance out the distribution of observed covariates X between the treatment group and the control group within a given level of the propensity score. Given this function, what matters is the relative magnitudes of propensity scores associated with different values of covariates X. For this reason, it is legitimate to use response-based samples in constructing propensity scores (23–25).

The result of Eq. 11 states that under ignorability, there is no bias after controlling for the propensity score. Given our earlier discussion stating that bias can manifest in two types, this is tantamount to two “no-bias” conditions: There is neither type I nor type II selection bias, conditional on p(X) (26). Thus, we have:

3. Composition Bias

In this article, I show that “composition bias,” a type of selection bias, arises through dynamic processes when treatment propensity is systematically associated with heterogeneous treatment effects. By composition bias, I mean situations in which the average effect of treatment of the units being newly recruited for treatment is not the same as TT, TUT, or ATE. Fundamentally, composition bias results from aggregation across units with unit-level heterogeneous treatment effects, even though the ignorability assumption is satisfied at the microunit level.

To understand composition bias, it is useful to conceptualize selection into treatment as a dynamic process, akin to survival analysis. A well-known property of a survival process is selective attrition so that the composition of the remaining population at risk for selection changes dynamically. We now introduce a time variable 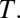Let us denote the treatment status as a function of time: 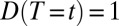if a unit is treated at time t and 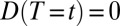if a unit is untreated at time t. For simplicity, we make the treatment condition an absorbing state, so that for 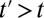, 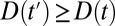. Substantively, this means that additional untreated units are recruited into treatment over time, but a unit stays in the condition of being treated once treated.

Situations like this in practical settings are abundant. I give three simple examples for illustration. First, in a strictly qualification-determined college admission system, an expansion of the admitted slots means that additional, less qualified applicants are now given admission, whereas those who had been admitted before stay admitted. Second, means-tested financial aid is typically given to persons with the lowest economic resources in a pool. If a policy expands the threshold for the means-tested financial aid, additional, relatively better-off persons would qualify. Finally, as a particular new technology (say, cell phones) penetrates a consumer market over time, the price for using the technology tends to drop as more consumers adopt it. If we assume that price is the only factor determining adoption, it is thus reasonable that with time, penetration increases incrementally, recruiting additional new consumers as the price drops. In all three examples, we can assume that treatment is an absorbing state, nondecreasing with time.

Let F(t) denote the proportion of treated units in U at time t. Given the absorbing state assumption, F(t) is nondecreasing in t. At any time t, the hazard of treatment probability is:

Of course, F(t) results from the accumulation of past hazards:

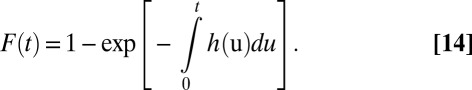Obviously, 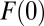= 0. For simplicity, I assume that all units would potentially be treated so that 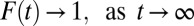. This assumption is typically made in the causal inference literature, so that we are only concerned with units that all have a nonzero probability of treatment. When 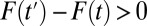, I define a new quantity of interest, “increment treatment effect” (ITE) as the ATE for the subgroup that is recruited into treatment between times 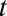and ():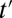

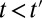where the expectation is over these incremental units with treatment status changed from not being treated at time t to being treated at time 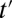. Like TT and TUT, ITE is the average effect of a group. However, whereas TT and TUT are defined by a unit’s observed status of treatment at any given time, ITE is defined by a change in treatment status.

ITE is different from two related quantities of interest, the local average treatment effect (LATE) (17, 18) and the marginal treatment effect (MTE) (27–29). At first glance, ITE, as defined in Eq. 15, appears very similar to LATE:

where 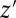and z are two values of IV Z. The focus of ITE is on the subgroup that changes treatment status when treatment proportion is changed, regardless of source. When the change is induced by an IV, ITE reduces to LATE. For example, if the selection of additional units into treatment during the expansion of the treatment pool from t to 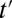is unrelated to potential outcomes 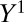and 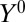, as when they are time-invariant, T can be considered as a valid IV, albeit an unusual IV. In this case, we can estimate ITE:

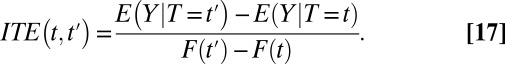MTE is more structural, pertaining to the treatment effect of a relatively homogeneous subgroup with an assumed latent factor of treatment being fixed at a particular point, the point at which a unit’s treatment status does not favor either treatment or control. In contrast, ITE is the ATE of heterogeneous units defined by a change in treatment regimes over time. Like TT and TUT, ITE is defined for a specific subpopulation with heterogeneous units for which treatment status is observed to have changed between regimes over time.

Let 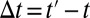. When T changes from t to 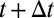, there is a corresponding change in the proportion of being treated: 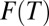changes from 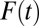to 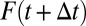. Now, further define 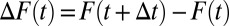. As 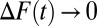, we can define the limit form of ITE(t) as:

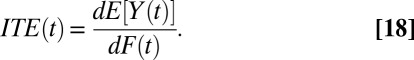We further demonstrate the relationships of ITE to TT and TUT. Note that in our setup, TT and TUT are functions of T. The following simple expressions link ITE to TT, TUT, and ATE:

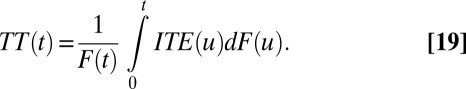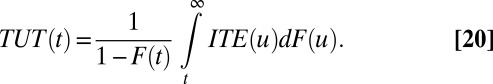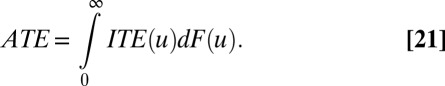From these formulas, we may formally define composition bias as the situation in which:

Of course, there would be no composition bias if the researcher could appropriately condition analysis on either the propensity score p(X) or its underlying full covariates X. However, composition bias emerges if the researcher observes neither p(X) nor X but conditions the analysis instead on time T.

As remarked earlier, if T only affects the proportion of the treated pool but not the outcome Y directly, T can be considered as an IV. The remainder of this article is devoted to the discussion of this particular situation, in which the proportion being treated affects the actual propensities of all units being treated, even though the intrinsic relative propensities of treatment for individual units remain unchanged.

ITE is sensitive to the proportion being treated at both t and 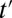. This occurs because selection into treatment is a dynamic process (akin to survival analysis), so that net “composition” changes with 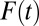, the proportion of the subpopulation being treated (30). When 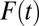is small, an increment from 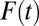to 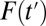is likely to recruit units with high propensities of treatment; ITE is then an average of treatment effects weighted heavily by high-propensity units. When 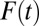is high, high-propensity units are already in the treatment group; an increment from 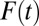to 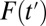is likely to recruit units with relatively lower propensities of treatment because the representation of high-propensity units in the untreated subpopulation decreases with T. Consequently, ITE is weighted toward low-propensity units as 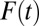increases. Because ITE, TT, and TUT all depend on the compositional changes in the treated and untreated subpopulations, I call the bias resulting from this dynamic process the composition bias.

4. Toy Example for Illustration

I now illustrate how the composition bias comes out in a dynamic process with a simple toy example. I conducted a simulation with a closed population of 1,000 units that are divided into 10 evenly sized (n = 100) strata (denoted by j, j = 1…10). All 100 units in each stratum have the same intrinsic propensity potential (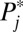) and the same treatment effect 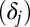. In other words, I allow for heterogeneity in both intrinsic propensity of treatment and treatment effect across the 10 strata, but, for simplicity, I assume homogeneity across the 100 units within each stratum. Let 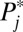, in the second column, vary linearly from 0.05 to 0.95. In the third column, we assign a series of arbitrary numbers to baseline counterfactual outcome under control 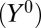. We let 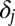increase linearly from 50 to 950, as shown in the fourth column, resulting in a correlation of 1 between the two parameters across the 10 strata. In this artificial example, ATE = 500. The detailed setup for the toy example is given in Table 1.

Table 1.

Setup of a toy example: A hypothetical population (n = 1,000) with 10 strata

Strata (j)	Propensity potential (Pj*)	Baseline outcome (Y0)	Treatment effect (δj)	No. of units (nj)
1	0.05	100	50	100
2	0.15	100	150	100
3	0.25	200	250	100
4	0.35	200	350	100
5	0.45	300	450	100
6	0.55	300	550	100
7	0.65	400	650	100
8	0.75	400	750	100
9	0.85	400	850	100
10	0.95	400	950	100

The total population is set to be 1,000, with ATE = 500.

For convenience of illustration, I also make increments discrete, developing in 10 steps: [F(0) = 0.0, F(1) = 0.1], [F(1) = 0.1, F(2) = 0.2], [F(2) = 0.2, F(3) = 0.3], [F(3) = 0.3, F(4) = 0.4], [F(4) = 0.4, F(5) = 0.5], [F(5) = 0.5, F(6) = 0.6], [F(6) = 0.6, F(7) = 0.7], [F(7) = 0.7, F(8) = 0.8], [F(8) = 0.8, F(9) = 0.9], and [F(9) = 0.9, F(10) = 1.0]. For the first round of increment [F(0) = 0.0, F(1) = 0.1], 100 units are moved from the untreated subpopulation (U₀) to the treated subpopulation (U₁). However, the distribution of these 100 units across the 10 strata is not even. For simplicity, I use expected, rounded numbers rather than realized numbers when utilizing the known stratum-specific intrinsic 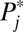. For example, 19 units in stratum 10 are recruited for treatment because 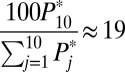at round 1. This strategy is tantamount to ignoring the influence of the sample size, which is arbitrarily set at 1,000. The first round of increments from F(0) = 0.0 to F(1) = 0.1 results in 100 new units being treated. The detailed results for the first round of increments are given in the first panel of Table 2.

Table 2.

Dynamic recruitment of treated units at the first two rounds [first round: F(0) = 0.0 to F(1) = 0.1, second round: F(1) = 0.1 to F(2) = 0.2]

Strata (j)	ΔU1,j	U1,j	U0,j	ΔU1,j	U1,j	U0,j
1	1	1	99	1	2	98
2	3	3	97	3	6	94
3	5	5	95	5	10	90
4	7	7	93	8	15	85
5	9	9	91	9	18	82
6	11	11	89	11	22	78
7	13	13	87	13	26	74
8	15	15	85	15	30	70
9	17	17	83	16	33	67
10	19	19	81	18	37	63
Total	100	100	900	100	200	800
Effect measures	ITE	TT	TUT	ITE	TT	TUT
	665	665	482	652	659	460

U_1,j and U_0,j, respectively, denote the treated and untreated groups in the jth stratum. For each round of increments, ΔU_1,j denotes the newly recruited units from the jth stratum that change the treatment status from D = 0 to D = 1 (i.e., increments to U_1,j).

In Table 2, U_1,j and U_0,j, respectively, denote the treated and untreated groups in the jth stratum. ΔU_1,j denotes the newly recruited units from the jth stratum that changed the treatment status from 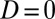to 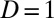, or increments to U_1,j. Because this is the first round of increments from F(0) = 0.0 to F(1) = 0.1, ΔU_1,j (the increment to the treated), given in column 2, is identical to U_1,j itself (column 3). The untreated subpopulation, U_0,j, is simply the complement of U_1,j, given in column 4. It is apparent that the 100 newly treated cases (the second column, labeled ΔU_1,j) are not evenly distributed across the 10 strata, although we started with equal-sized strata in the population. Because the 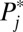in a higher numbered stratum is greater than that in a lower numbered stratum, the number of units recruited into treatment in a higher numbered stratum is also higher than that in a lower numbered stratum. In fact, for the first round of increments, the ratio in the number being treated between two strata is exactly the same as the ratio in 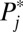. For example, the ratio in treated cases between stratum 10 and stratum 1 is 19, reflecting their ratio in 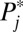: 0.95:0.05. In addition, ΔU_1,j, U_1,j, and U_0,j are unequally distributed across strata. The uneven distributions constitute different weights in the calculation of respective treatment effects, given in the last row. For this round, ITE = TT at 665, which is much higher than TUT at 482. None of them is equal to ATE at 500.

We now conduct the second round of increments, from F(1) = 0.1 to F(2) = 0.2. We use the same recruiting mechanism and keep the intrinsic properties of all units intact. A key difference between the second round and the first round of increments is a compositional change in the exposure population from which increments are drawn. For the first round, the exposure population is the original population with an equal distribution across strata, shown in the last column in Table 1 (labeled 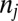). For the second round, the exposure population is now changed to the untreated subpopulation in the first round, shown in the fourth column in Table 2 (labeled U_0,j). Due to this difference in exposure composition, the resulting increments in the second round, shown in the fifth column (labeled ΔU_1,j), have a different across-strata distribution than their counterparts in the first round (second column, also labeled ΔU_1,j). Comparing strata 10 and 1 again, for example, we see the ratio in ΔU_1,j between stratum 10 and stratum 1 reduced to 18, from 19 in the first round.

The reason for a decline in the representation of high-numbered strata in ΔU_1,j in the second round compared with the first round is simple: Because high-numbered strata have higher intrinsic 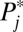, they are overrepresented in ΔU_1,j in the first round, and thus in U_1,j . As a result, higher numbered strata are now underrepresented in U_0,j, which serves as the exposure population for the next round of increments. Given the fixed 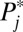, a lower representation in the exposure population results in a lower representation in the newly recruited units (i.e., ΔU_1,j in the second round).

Now, let us pretend that we do not know the mechanisms underlying the simulation, and thus treat the data as observational. From the observed data, we can compute both the average outcome value and the proportion treated at rounds 1 and 2. Under the assumption that T can serve as an IV, we can then apply the estimator of Eq. 17 to obtain ITE between the rounds:

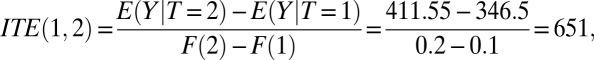a number that is only slightly different due to sampling from the simulation result (ITE = 652) given in Table 2, because the simulation does not allow the treatment of fractional units. Thus, we obtain the same result from the ITE estimator for the observed data.

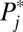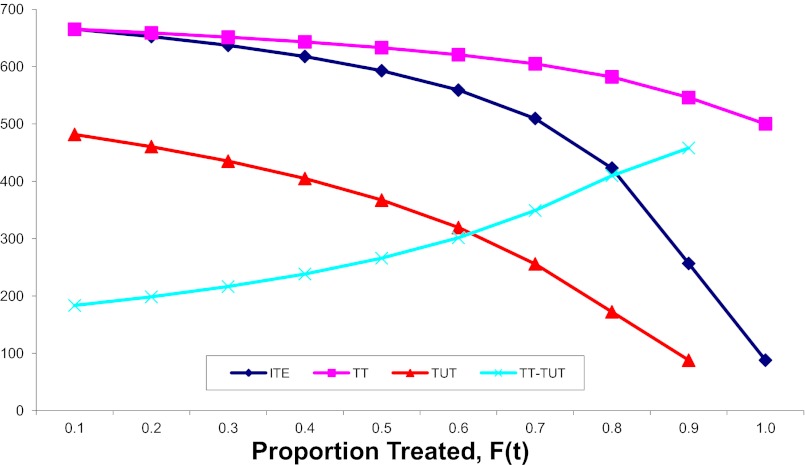
This dynamic process can continue and further compound the compositional process. In general, units with higher intrinsic s are likely to be recruited into treatment when F(t) is low, whereas units with lower intrinsic 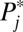s are likely to be recruited into treatment only when F(t) is high. When intrinsic propensities and treatment effects are positively correlated, as is the case in this toy example, a positive selection bias arises due to sorting, so that TT > TUT. In Fig. 1, I present the full results when I carried out the toy example to its end, all the way to 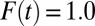. I present four quantities of interest as functions of the proportion treated, .

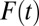Fig. 1.

Treatment effects by increment rounds.

ITE begins at a high level at 665 in the first round. It coincides with TT in round 1 and then diverges from TT by moving downward at a faster speed than that of TT. In the eighth round [F(7) = 0.7 to F(8) = 0.8], ITE(8) is 423, substantially below ATE (which is 500). This shows that ITE is highly sensitive to changes in the composition of U_0,j. In contrast, TT is cumulative as the average of ITE in earlier rounds (Eq. 19), and it declines more slowly. Note that 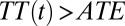for all 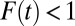due to my setup for a positive selection. However, the gap between TT and ATE diminishes gradually over 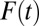, especially after the eighth round [ 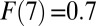to 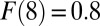]. Similarly, TUT is also cumulative but in reverse, from 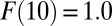backward. By normalization, TUT(10) is undefined. I define ITE(t) in discrete time intervals, so that 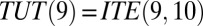. Note that 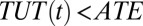for all 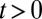. Furthermore, as in the case of TT, TUT also trends downward with .

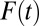One way to evaluate the type II selection bias is to measure composition bias, the difference between TT and TUT. Hence, in Fig. 1, I present 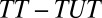as a function of the treatment proportion 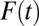. A counterintuitive finding from this exercise is that the amount of bias as measured by the sorting gain actually increases, rather than decreases, as the proportion treated increases. This is due to the fact that the downward trend of TUT is steeper than that of TT. This pattern results from the shape of ITE, because the decline of ITE is slower when 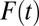is small but accelerates when 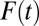is close to 1. The increasing trend in the amount of type II selection bias depicted in Fig. 1 is surprising because one might think that as treatment extends to a larger and larger portion of a population, treated units should become less and less selective (which we show is true); thus, selection bias should decline (which is not true). Of course, my conclusion is based on using TUT instead of ATE as the reference for measuring the amount of composition bias. As 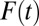increases, units being treated become less positively selective but units not being treated become more negatively selective. Although the two trends are in the same direction, the decline in selectivity among the treated is slower than the change in selectivity among the untreated. In other words, by the time almost every unit in a population is treated, only those with extremely low intrinsic propensities of treatment remain in the untreated subpopulation (i.e., severe selectivity).

5. Discussion and Conclusion

Due to the ubiquity of heterogeneity in social phenomena, it is impossible to draw causal inferences at the individual level. All efforts to draw causal inferences in social science must take place at the group level. However, comparison of groups requires classification of intrinsically heterogeneous individuals into seemingly homogeneous groups. This is a fundamental dilemma facing all researchers in social science.

It is a truism that any group-level comparison can be further decomposed into comparisons of subgroups. For causal inference, it is now well established that a useful dimension for decomposition is the propensity score, which summarizes information in a multidimensional space from multiple covariates into a single variable. Therefore, one potential source of heterogeneity that should receive particular attention in causal inference is the interaction between the treatment effect and the propensity score (31). Such interactions can be detected without any new requirement, because this can be done under the assumption of ignorability. When such interactions are found, however, the interpretation of the results may differ. If the researcher believes that ignorability is true, the estimated heterogeneous treatment effects may be generalized. However, the researcher may alternatively interpret the heterogeneous pattern in the estimated effects as an indication that the process of assigning treatment may be selective, driven by unobserved factors (32).

All quantities of interest at the group level, such as TT and TUT, are essentially weighted averages of treatment effects across subgroups. Therefore, composition is important in causal inference. Understanding the potential role of composition is important for policy evaluations of intervention programs when we wish to generalize results from particular study settings to target populations because composition may differ between study settings and target populations. In this article, I have shown the presence of composition bias, a form of selection bias. This composition bias is generated by a dynamic process when the treatment proportion changes. Interestingly, this form of selection bias can be generated at the aggregate level even when the ignorability assumption holds true at the microlevel. All that is required is a combination of three things: (i) substantial intrinsic heterogeneity in treatment propensity, (ii) substantial intrinsic heterogeneity in treatment effects, and (iii) nontrivial correlation between heterogeneity in treatment propensity and heterogeneity in treatment effects. Under these simple conditions, a classic scenario for selection bias may arise: Units more responsive to treatment are more likely to receive treatment early than units less responsive (26).

A composition bias is essentially driven by the fact that units with a higher intrinsic propensity of treatment are likely to be overrepresented when the treatment proportion is small. As the treatment proportion expands, the degree of overrepresentation of units with high intrinsic propensities among the newly recruited into treatment declines. A general lesson is that researchers should always be mindful of the population or subpopulation of interest when deriving and interpreting average causal estimates from potentially heterogeneous subgroups.

A substantive example would be the administration of a medical treatment or social intervention on a graduated schedule. Assume that participation is need-based, with the poorest persons being most eligible and thus chosen first, and, further, that the poorest persons would also stand to benefit most from treatment. Under these conditions, individuals selected at later stages (i.e., becoming eligible only after the eligibility cut-point is moved up) would exhibit lower ATEs simply by virtue of coming from a less responsive subpopulation.

For the same reason, it is always dangerous to extend research results from a particular study, be it observed or experiment, beyond the setting in which the study was conducted. Population heterogeneity means not only that treated units may be incomparable to untreated units in the study, an issue of internal validity, but that external validity can be difficult to establish. Because the researcher generalizes results from a particular study to the general population, we cannot know whether the subjects in the study are comparable to those in the population. The potential systematic differences between the subjects in the study and the general population may dramatically alter the ATE due to compositional biases.