Microscopic structure of water at elevated pressures and temperatures

Abstract

We report on the microscopic structure of water at sub- and supercritical conditions studied using X-ray Raman spectroscopy, ab initio molecular dynamics simulations, and density functional theory. Systematic changes in the X-ray Raman spectra with increasing pressure and temperature are observed. Throughout the studied thermodynamic range, the experimental spectra can be interpreted with a structural model obtained from the molecular dynamics simulations. A spatial statistical analysis using Ripley’s K-function shows that this model is homogeneous on the nanometer length scale. According to the simulations, distortions of the hydrogen-bond network increase dramatically when temperature and pressure increase to the supercritical regime. In particular, the average number of hydrogen bonds per molecule decreases to ≈0.6 at 600 °C and p = 134 MPa.

Water is one of the most fascinating and controversially discussed substances in condensed matter research (1). Several experimental investigations have been carried out to decipher the local structure of water at various thermodynamic conditions. However, there is still no consensus on how to describe the microscopic structure of this elusive liquid (2–4). The most prominent methods of study are the determination of site-site correlation functions using neutron or X-ray diffraction (5–8), the analysis of density fluctuations by small angle X-ray and neutron scattering (9–11), and the investigation of the oxygen’s local environment by spectroscopic methods (2, 3, 10, 12, 13) providing controversial interpretations of the local atomic structure of water. This has resulted in an intense discussion of whether the microscopic structure of ambient water can be described as a liquid with homogeneous density (e.g., refs. 4, 11, 14) or as an inhomogeneous mixture of two types of structural states with a hydrogen-bond (H-bond) distorted structure surrounding less dense, tetrahedrally-like coordinated patches (e.g., refs. 7, 10, 12). In this article, we present significant information obtained by an in situ study of changes of the water structure at high pressure and temperature conditions up to the supercritical state.

Due to experimental difficulties, water under supercritical conditions has only rarely been the subject of detailed in situ spectroscopic investigations to date (12, 15). The pressure (p) and temperature (T) regime of supercritical water, however, is especially interesting for geoscientists because water plays a key role in heat and mass transfer as well as element fractionation processes in the Earth’s lithosphere, such as volcanism and ore deposit formation (16, 17). Geochemical processes and reactions, such as the formation of petroleum (18) and even contributions to the origin of life (19), have been linked to the high-temperature and high-pressure properties of water. The polar character of the H₂O molecule and the tendency to dissociate makes it a more powerful solvent than other volatiles. This is also taken advantage of in chemical processing, where supercritical water is used as a reaction medium for chemical and material synthesis, waste destruction, plastics recycling, and biomass processing (20). These solvent properties of H₂O depend not only on density and dissociation but on structural parameters, which are poorly understood, particularly at the supercritical conditions prevalent in the Earth’s upper mantle and crust.

A large degree of disorder with an essentially broken H-bond network in supercritical water was reported by Postorino et al. (9) using neutron scattering data. Although this conclusion was softened later, newly derived site-site pair correlation functions (PCRs) from the old data still suggest a highly distorted arrangement of water molecules with a largely reduced degree of H-bonding compared with water at ambient conditions (5, 21). Optical Raman spectra of water indicate that a significant fraction of network water is still present even at high temperatures, pressures, and solute concentrations (22–24). Likewise, NMR studies of water up to 600 °C and 400 bar suggest a significant amount of H-bonding up to the highest temperatures and pressures studied (25). Sit et al. (15) used Compton scattering to measure the bonding and coordination in water up to supercritical conditions and found a large increase in the number of water monomers on transition to the supercritical regime, but they also report a remaining number of higher coordinations, such as dimers and trimers. Based on X-ray Raman spectroscopy (XRS) measurements, Wernet et al. (12) proposed that supercritical water consists of small H-bonded patches surrounded by less dense non–H-bonded regions in line with local density inhomogeneities revealed by small angle neutron scattering (26) but reported a relatively small proportion of non–H-bonded H₂O species. However, Clark et al. (27) and Sedlmeier et al. (28) have shown that the interpretation of small angle scattering data is not straightforward. They found no strong spatial correlation between structure and density fluctuations even in ambient water and affirmed these claims by reproducing all features of measured small angle scattering spectra using the tip4p/2005 and extended simple point charge models, respectively. On the other hand, analyses of tip4p/2005 water models using tetrahedral order parameters imply tendencies toward clustering of low- and high-tetrahedrality regions (29, 30). Heterogeneity has also been reported, for example, in terms of nucleation of small molecular clusters (31) or tetrahedrally coordinated patches connected by less ordered nets, building up a gel-like network that persists in pressurized high-temperature water up to T = 473 K and ρ = 0.88 g/cm³ (32). However, the occurrence of these structural species might be transient (4). More distorted H-bonded networks were found when using new van der Waals functionals (33).

In the current work, we use XRS as a probe of the local water structure over a large temperature and pressure range. The experimental results are compared with spectra calculated from ab initio molecular dynamics (MD) simulations. These spectra give a good description of the changes of the experimental spectra with temperature and pressure in the sub- and supercritical regimes. On this resemblance of the experimental data and the simulation results, more detailed information on the microscopic local structure of water is extracted from the underlying MD simulations.

In the ab initio MD structures, the water molecules at ambient conditions have, on average, a near-tetrahedral coordination with a considerable number of water molecules having five nearest oxygen neighbors. With increasing temperature and pressure along the liquid-vapor equilibrium, the extended H-bonded network is strongly distorted and broken. However, H-bonded species are found even for the highest temperatures and pressures investigated. From a detailed analysis of the MD model, we find that the spectra are most sensitive to the direct local environment (i.e., the number of formed H-bonds and nearest oxygen neighbors) but even reflect the influence of the intermediate range order. Based on a spatial statistical analysis, we find the MD simulations to predict structures that are homogeneous on the length scale of the simulation boxes. The experimental spectra are in good agreement with those derived from the simulations using density-functional theory (DFT).

Results and Discussion

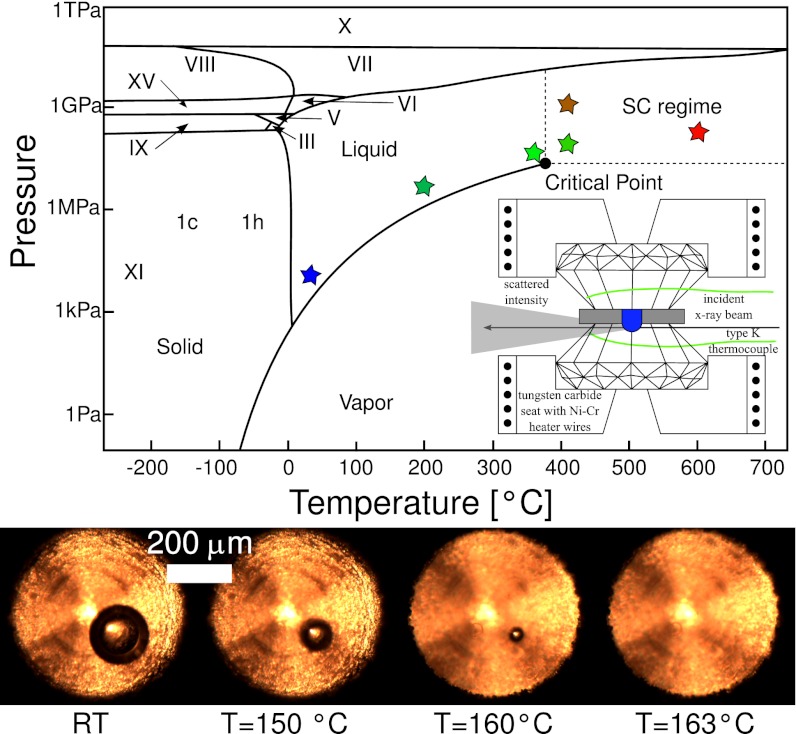
XRS spectra of the oxygen K-edge were measured along the vapor pressure curve and in the supercritical regime for conditions as indicated in the H₂O phase diagram in Fig. 1. High pressures and high temperatures were reached using a hydrothermal diamond anvil cell (HDAC; Fig. 1, Inset). Temperature calibration was achieved using type-K thermocouples, and the pressure/density was obtained by measuring the liquid-vapor homogenization temperature using visual observation of a vapor bubble in the sample volume as shown in Fig. 1 (Lower) (details are provided in Materials and Methods).

Fig. 1.

Phase diagram of water shows the numerous ice phases at high pressures and low temperatures and the region of interest for this study (i.e., high temperatures and high pressures). Oxygen XRS K-edge spectra were recorded at the pressure and temperature values indicated by colored stars. (Inset) Schematic drawing of the HDAC. (Lower) Photographs of the water sample in the HDAC at different temperatures and pressures are shown to demonstrate the visual control of the sample, exemplified by a measurement of the homogenization temperature of a vapor bubble and liquid, which is used to determine the density and pressure.

The measured XRS oxygen K-edge spectra are shown in Fig. 2. Spectra taken along the vapor pressure curve are presented in Fig. 2A. The spectrum of water at ambient conditions agrees well with other oxygen K-edge spectra reported earlier (e.g., ref. 34), showing a pronounced pre-edge shoulder at 535 eV of energy loss (feature A in Fig. 2), a dominating main-edge at 538 eV (feature B in Fig. 2), and a post-edge (feature C in Fig. 2) with significant spectral weight up to energy losses of 546 eV. With increasing pressure and temperature, spectral weight is transferred from the post-edge region into the pre- and main-edge regimes. Moreover, a shift of the energy loss position of both the pre-edge and main-edge toward the position of the O-H anti-bonding 4a₁ and 2b₁ orbitals of a free water molecule at 534 and 536 eV, respectively, can be observed. The interpretation of K-edge X-ray absorption (XAS) or XRS spectra of water is neither unambiguous nor straightforward (3, 35–37). As temperature and pressure increase along the vapor pressure curve, a gradual transition from a water-like spectrum to a more gas-phase–like spectrum can be observed. However, a clear difference between the gas-phase spectrum and the experimental data at supercritical conditions remains.

Fig. 2.

(A) Spectra of the oxygen K-edge of water at different temperatures and pressures along the liquid-gas coexistence curve. The pre-, main-, and post-edge are indicated by A, B, and C, respectively. (B) Calculated spectra for similar temperatures and densities as in A, as well as a water monomer spectrum. The densities are indicated in the figure, and the color code corresponds to the color of the respective spectrum. (C) Effect of pressure on the spectra measured at T = 400 °C in comparison to the ambient-water spectrum. (D) Calculated spectra for temperatures and densities corresponding to the experiments presented in C. (E) Comparison of the integrated post-edge intensities between 537 and 544 eV of energy loss obtained from experiment (exp.) and theory (theo.). Here, “high” refers to measurements at a similar density but higher temperature than indicated in A. (F) Energy loss position of the pre-edges for the different densities determined from theory and experiment. arb., arbitrary.

Fig. 2C shows the influence of pressure, and thus density, on the K-edge spectrum of water at T = 400 °C. A clear drop of intensity in the pre-edge regime is visible for the spectrum measured at 371 MPa (0.86 g/cm³) compared with the spectrum measured at 48 MPa (0.54 g/cm³). The spectrum at ambient temperature and pressure is also shown as a reference. The structural origin of spectral changes similar to the ones observed here has been discussed extensively in the literature. For instance, the role of distorted or broken H-bonds and the influence of the non–H-bonded molecules in liquid water and ice polymorphs were recently addressed (36). In those cases, broken or highly distorted H-bonds were shown to increase spectral weight in the pre-edge and non–H-bonded molecules approaching the first coordination shell were shown to increase intensity in the main-edge region. Pylkkänen et al. (38) also pointed out that the non–H-bonded neighboring molecular fraction has a significant influence on the shape of the spectra in high-pressure ice phases. Furthermore, the H-bond network order has been shown to influence the spectra in liquid water and ice phases (39, 40). These observations clarify the difficulty of assigning changes of certain features in the oxygen K-edge spectra to particular structural changes related to, for example, H-bond breaking, density changes, or single structural motifs.

To gain deeper insight into the interpretation of the experimental spectra, we performed DFT calculations from ab initio MD simulation snapshots. We calculated spectra from geometries directly extracted from MD snapshots with no restraints on the molecular configurations, such as including or excluding structures subject to specific H-bond statistics (details are provided in Materials and Methods). Calculated spectra for temperature and pressure values similar to the experimental parameters are shown in Fig. 2 B and D. All calculated spectra were shifted on the energy loss scale so that the main edge feature B of the experimental and calculated spectra coincide. Although the pre- and post-edge features of the calculations are underestimated for the highest density spectra (0.99 and 0.86 g/cm³), the overall agreement between the experimental data and the calculated spectra is good. This is valid especially if we consider the systematic evolution of both experimental and theoretical spectra as a function of temperature and pressure. For ambient water, the deviations between experiment and theory are similar to what has been reported earlier (42).

For a quantitative comparison of the experimental and calculated spectra, the integral over the post-edge and the energy loss position of the pre-edge were determined and are presented in Fig. 2 E and F, respectively. Compared with the values derived from the experimental data, the integrated post-edge intensities of the simulated spectra show the same dependence on the water density with only a slight constant offset, which is due to a systematic underestimation of the post-edge intensity by the theory. This is caused by the theoretical approach used to calculate the spectra. As suggested by Chen et al. (36), the energy-independent exchange potential in DFT calculations is too strong close to the ionization threshold, and thus results in a post-edge feature that is too narrow. Almost quantitative agreement between experimental XAS and XRS spectra of ambient water and ice was recently achieved by the use of path integral ab initio MD simulations in conjunction with a Bethe–Salpeter equation (BSE)-based approach for the spectrum calculation (43). Most notably, the BSE benefits from accounting for the electron-hole interaction, which ensures a better representation of the pre-edge feature in the calculated spectra (36, 43). The computational cost of such methods, however, forbids this approach in the current case. Using a real-space multiple scattering approach to calculate the oxygen K-edge in different ice phases results in a post-edge feature that closely resembles the experimental findings but fails to reproduce the pre- and near-edge (44). In our results, good quantitative agreement is achieved when comparing the energy loss position of the pre-edge for all p, T conditions (Fig. 2F). It should be noted that both our theoretical and experimental spectra at T = 400 °C and p = 48 MPa, corresponding to ρ = 0.54 g/cm³, differ from those reported by Wernet et al. (12) for similar conditions. However, the overall systematic agreement between the theoretical and experimental spectra, considering both the overall spectral features and their dependence on thermodynamic conditions, gives confidence to the quality of our data. The theoretical results describe both the overall experimental spectra and their systematic spectral changes with varying thermodynamic conditions to a very high degree, especially in the unprecedented supercritical regime. This gives confidence that the underlying structural model can now be used to extract detailed information on the local atomic structure of water.

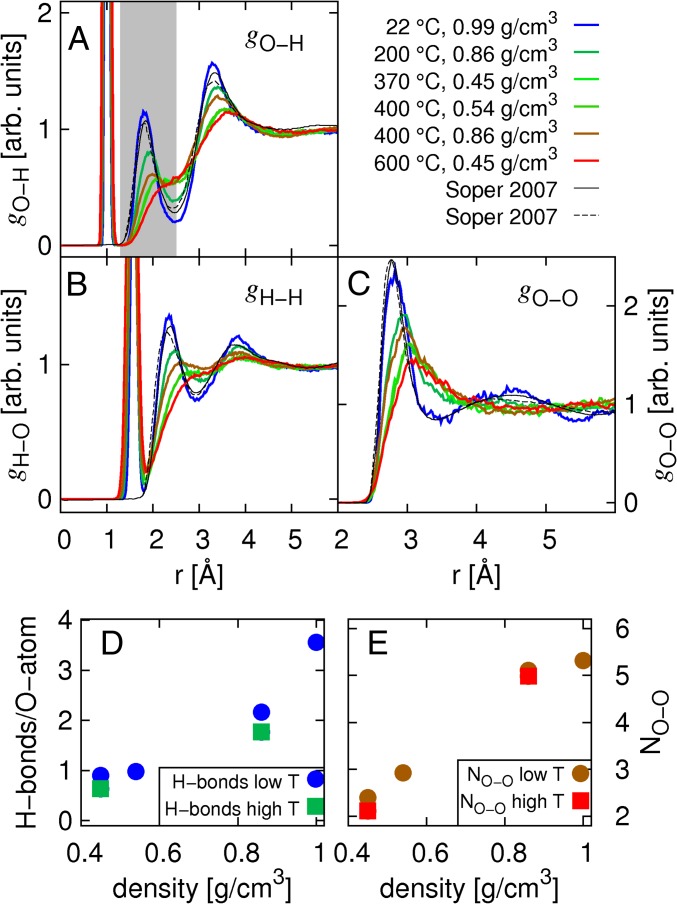
The O-H, H-H, and O-O PCFs extracted from the MD trajectories are shown in Fig. 3 A–C, respectively. For each set of PCFs, the room temperature (RT) PCF is compared directly with PCFs taken from Soper (45) and shows good agreement with these. The PCFs extracted from simulations at higher temperature and pressure also follow the trends reported by Soper (5) and Ikeda et al. (46), but they cannot be compared directly with the presented results because the exact temperature and pressure conditions differ. With increasing p and T, the second peak in the O-O PCF loses intensity and disappears at supercritical conditions. The first intermolecular peaks in the O-H and H-H correlation function also weaken with increasing p and T. Similar behavior was recently observed in MD simulations of water along different isochores using the Matsuoka-Clementi-Yoshimine with nonadditives model (47). These results were interpreted as a transition of a tetrahedral structure at ambient temperature to a more disordered medium-density fluid at elevated temperatures. Nevertheless, simple H-bonding between two water molecules was found to persist even beyond the critical point.

Fig. 3.

(Upper, A–C) O-H, H-H, and O-O PCFs, respectively, as derived from the MD trajectories and in comparison to the two experimental results from a study by Soper (45). (Lower, D and E) Number of H-bonds per molecule and number of nearest neighbors as a function of density extracted from the MD simulation snapshots. (Lower) Term “high T” refers to values determined for equal density but higher temperature conditions, as indicated in the other part of the figure (Upper). arb., arbitrary.

As a measure of the local structure in water, the average number of H-bonds per molecule (n_HB) and nearest neighboring oxygen atoms (n_OO) were calculated from the MD snapshots. Thus, n_HB was determined using geometric criteria of Marti et al. (48), and n_OO is simply the number of oxygens within a sphere with a radius of 3.6 Å from the central oxygen atom. The results are depicted in Fig. 3 D and E. Both n_HB and n_OO increase with density and differ only slightly for equal density but different temperature [i.e., 0.45 g/cm³ (370 °C and 600 °C) and 0.86 g/cm³ (200 °C and 400 °C)]. For a density of 0.86 g/cm³, n_HB is found to be above the percolation threshold of (31) for both studied temperatures, which suggests a strongly distorted H-bonded, tetrahedral, percolating network. This is reflected in the experimental spectra by similar pre- and main-edge structures in both measurements at this density. An average number of nearest neighbors n_OO ≈ 5, as well as the increase in n_OO with increasing density, is in good accordance with findings from X-ray diffraction (49, 50) and other MD simulation data (36, 47). The average number of H-bonds as a function of density is also in line with previously reported experimental and theoretical values (48).

A more detailed analysis of the local arrangements around the scattering oxygen atoms is achieved by a classification of the MD geometries used for the XRS spectra calculations for sub- and supercritical conditions with respect to n_HB and n_OO. The resulting histograms for each p and T are shown in Fig. 4. For ambient water, the distributions of n_HB and n_OO are clearly peaked at four H-bonds per water molecule and five nearest oxygen neighbors (denoted H4O5). At all other state points, both distributions are much broader, indicating more distorted local arrangements. Although the average number of H-bonded molecules decreases quickly with increasing temperature, H-bonded species can be found even at the highest temperature probed, where simple H-bonding between two water molecules (one H-bond) dominates. The fact that at elevated temperatures, the average number of nearest neighbors exceeds the average number of H-bonds per molecule can be interpreted as a sign of a more gas-like behavior at these temperatures and densities in line with the X-ray and neutron data and MD simulations.

Fig. 4.

(Lower Left) Distribution of the number of H-bonds of the central water molecule in the clusters extracted from the different MD snapshots for all pressure and temperature conditions estimated by geometric criteria (details are provided in main text). (Lower Center) Same except for the number of oxygen neighbors within 3.6 Å from the central oxygen atom. (Lower Right) Averages over XRS spectra calculated for snapshots resembling the most frequently occurring subset of configurations from the histograms (Lower Left) as well as representative stick and ball plots of these motifs. arb., arbitrary. (Upper) Comparison of calculated XRS spectra of similar local motifs for different p, T conditions (details are provided in main text).

A spatial statistical analysis using Ripley’s K-function of the different structural motifs supports the assumption of a more homogeneous structure because no heterogeneities beyond the first coordination shell (r 5 Å) could be identified. Using the local structure index (LSI) (7, 51) to identify high (I > 0.03) and low (I < 0.03) structured local coordinations results in an amount of high-LSI molecules of ∼50% at ambient conditions and a rapid decrease of this number with increasing p, T. However, a spatial statistical analysis of these subpopulations also shows no spatial correlations beyond r 5 Å even for the high-LSI molecules (SI Text), which indicates that molecules with different local environments are present at all simulated temperatures and pressures but are not spatially correlated beyond their characteristic distances (i.e., the second coordination shell). This is in line with the findings of English et al. (4).

The calculated XRS spectra resulting from averaging over clusters resembling the most frequently occurring structural configuration (with respect to n_HB and n_OO) at each p, T condition are shown in the third column of Fig. 4. The positions of the pre-edge and main-edge, the intensity of the pre-edge feature, and the overall shape of the spectrum change systematically for different distributions of H-bonds and number of nearest oxygen neighbors (Fig. 4, columns 1 and 2). It is noticeable that smaller numbers of H-bonds and nearest oxygen neighbors result in distinct pre- and main-edge features (H1O1 and H1O3), whereas distributions with higher n_HB and n_OO result in smaller pre-edges and more spectral weight in the post-edge region (H2O5 and H4O5). In this respect, the spectral changes observed for constant temperature and different density (Fig. 2C) are caused by a different microscopic topology (i.e., a change from mainly one H-bond and three nearest oxygen neighbors to predominantly two H-bonds and five oxygens in the first coordination shell).

The sensitivity of the XRS spectra on the local structure is illustrated in Fig. 4 (Upper) by a comparison of similar local configurations for different thermodynamic conditions. In Fig. 4 (Upper Left), spectra from local environments having four H-bonds and five oxygen neighbors at ambient conditions (1.00 g/cm³), 200 °C (0.86 g/cm³), and 400 °C (0.86 g/cm³) are compared and show significant spectral weight in the post-edge region and only minor intensity in the pre-edge region. In Fig. 4 (Upper Right), spectra from local environments having one H-bond and three nearest oxygen neighbors at 370 °C (0.45 g/cm³), 400 °C (0.54 g/cm³), and 600 °C (0.45 g/cm³) are shown. Here, independent of the state point, pronounced pre- and main-edges are visible. Obviously, XRS spectra related to distinct structural motifs conserve their spectral shape for similar densities at different temperatures. The remaining differences systematically depend on temperature, which stresses the effect of increasing disorder even in the first coordination shell with increasing temperature, along with the influence of non–H-bonded molecules in the immediate and intermediate local environments.

Conclusion

The microscopic structure of water under high pressure and high temperature conditions, as prevailing, for example, in the deep Earth, was investigated using XRS as well as ab initio MD simulations. The XRS spectra show a continuous evolution from a water-like spectrum at RT and atmospheric pressure to a more gas-like spectrum at the highest temperatures and pressures investigated. Comparison with spectra calculated from ab initio MD snapshots demonstrates that the spectral features and systematic changes in the spectral shape over the entire pressure and temperature regime probed can be understood in terms of a homogeneous microscopic structure.

Based on the close resemblance of the calculated spectra and the measured data, as well as the accordance of PCFs extracted from the MD runs and published data, more detailed information on the local structural environment of the scattering oxygen atoms, such as the number of H-bonds and nearest oxygen neighbors, was extracted from our MD model. At ambient conditions, species with four H-bonds and five oxygen neighbors within a distance of 3.6 Å dominate. With temperature and pressure increasing along the vapor pressure curve, the number of H-bonds per molecule decreases to 0.6 at T = 600 °C and p = 134 MPa. Typical local structural environments, with specific spectral fingerprints, could be identified to describe water at different pressure/temperature conditions. However, no clustering of these motifs could be found by a spatial statistical analysis of the MD simulation boxes. Hence, the present study implies a homogeneous spatial distribution of these motifs. By comparing simulated spectra from specific local environments at different temperatures and pressures, the sensitivity to and systematic dependence of the shape of the oxygen K-edge spectrum on the direct local environment of the oxygen atoms in water over a wide range of temperatures and pressures is stressed. The presented experimental spectra provide a benchmark for further theoretical investigations using other means to simulate the atomic structure and other approaches to calculate XRS spectra from the models, such as BSE-based methods.

Materials and Methods

A resistively heated HDAC (52, 53) with a rhenium gasket was used to produce high-pressure, high-temperature conditions. The X-rays penetrated the sample, Milli-Q (Millipore) water, contained in a recess hole with a diameter of 500 μm and a depth of 120 μm in the culet of the lower diamond right below the rhenium gasket. Thus, the pathway of the X-ray through the diamond was optimized, together with an increase of probed sample volume. The temperature was measured by a type-K thermocouple on each of the two diamonds (Fig. 2, Inset). The HDAC was loaded before measuring at each state point, and pressures were calculated from the liquid-vapor homogenization temperature, which was determined by visual observation of a vapor bubble contained in the sample volume, before and after each experiment. The equation of state according to the method of Wagner and Pruss (54) was used. XRS (55) was used to measure the oxygen K-edge spectra in situ at high-pressure and high-temperature conditions. The XRS experiment was conducted at the inelastic X-ray scattering beamline ID16 of the European Synchrotron Radiation Facility in Grenoble, France. A detailed description of the instrument can be found elsewhere (56). Using the 1-m Rowland geometry spectrometer, XRS spectra were collected by scanning the incident energy at a fixed analyzer energy of 9.69 keV, such that the energy loss was scanned across the oxygen K-edge at 535 eV. Scattering from nine bent (R = 1 m) Si(660) crystals was focused onto a photon-counting pixel detector. Using the imaging properties of the analyzer crystals in combination with the 2D detector (57), scattering from the sample could conveniently be discriminated against parasitic scattering from the HDAC. Using a Si(220) channel-cut monochromator in succession to a Si(111) high-heat-load double-crystal monochromator, an overall energy resolution of 0.7 eV was obtained. The incoming X-ray beam was focused to ∼50 × 130 μm² (vertical × horizontal) on the sample. For the RT spectrum, count rates for one analyzer were ca. 40 counts per second at the maximum of the oxygen K-edge on top of a background of ∼90 counts per second. At the lowest density of 0.45 g/cm³ and 600 °C, we could measure 20 counts per second at the maximum of the oxygen K-edge on top of a background of 120 counts per second per analyzer crystal. For the final spectra, the signals from all nine analyzer crystals and multiple individual scans were checked for consistency and summed up taking the statistical weight into account, such that an average momentum transfer of q = (1.6 ± 0.2) atomic units (a.u.) was achieved. A linear background was subtracted from the summed data. Typical counting times were 4–5 h per state point. Final XRS spectra were normalized to the integral intensity between 531 eV and 555 eV. Details of the data processing and analysis can be found in a study by Sternemann et al. (58). Because we could observe the sample during the experiment through a microscope, we can exclude any sample damage due to the X-ray exposure. The structure of liquid and supercritical water was modeled by ab initio MD simulations using the Car–Parrinello method (59) as implemented in the CPMD code (60). The simulation cells contained 64 H₂O molecules, and simulations were performed at a constant volume and temperature (i.e., in the NVT ensemble). Densities were adjusted to those of the experiments. Temperature was controlled by a Nosé–Hoover thermostat (61, 62). For the electronic structure calculations, plane-wave basis sets, the Becke–Lee–Yang–Parr exchange correlation functional (63, 64), and Goedecker-type pseudopotentials (65) were used. The Kohn–Sham orbitals were expanded up to an energy of 70 Ry. For the Car–Parrinello dynamics, a fictitious electron mass of 600 a.u. was used. The equations of motion were integrated with a time step of 0.12 fs. The initial water structure was modified from a previous simulation study of supercritical aqueous solutions (66). After equilibration at each state point, production runs of 5–10 ps were performed. From the recorded trajectories, partial radial distribution functions were computed. CPMD has been shown to give a representative measure of the local atomic environment in supercritical water despite the limited simulation box size (67). With the limited MD simulation box size used, large-scale fluctuations are not taken into account. However, in our experiment, there was no indication from the liquid-vapor homogenization behavior that any of our spectra were significantly affected by density fluctuations and no critical phenomenon, such as critical opalescence, was observed. The XRS spectra of the individual MD snapshots were calculated with ERKALE (68) in the transition-potential approximation (69) within DFT, using the revised Perdew–Burke–Ernzerhof functional (70–72). The IGLO-III basis set (73) was used for the excited oxygen site, whereas Dunning's augmented correlation consistent polarized valence double zeta basis set (74) was used for all other atoms. The localization of the core hole was enforced by freezing the other oxygen core orbitals in the system (68). Broyden mixing (75) of the Kohn–Sham–Fock matrix was used in solving the self consistent field (SCF) equations. To improve the description of the virtual orbitals, a large set of diffuse functions was added on the excited site after SCF convergence was attained. For each p, T condition, spectra of 128 spherical clusters of ∼90 atoms each were calculated and averaged over. For the XRS spectra of the most frequently occurring motifs, calculated spectra of 120 clusters, extracted from the MD trajectories, were averaged over. The calculations were converged with respect to the basis set.