Circular Symmetric Laplacian Mixture Model in Wavelet Diffusion for Dental Image Denoising

Abstract

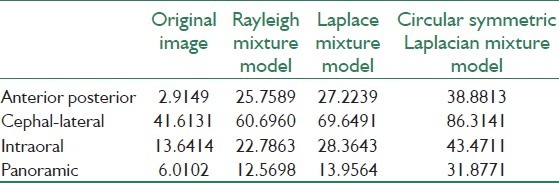
In this paper, we try to find a particular combination of wavelet shrinkage and nonlinear diffusion for noise removal in dental images. We selected the wavelet diffusion and modified its automatic threshold selection by proposing new models for speckle-related modulus. The Laplacian mixture model, Rayleigh mixture model, and circular symmetric Laplacian mixture models were evaluated and, as it could be expected, the latter provided a better model because of its compatibility with heavy tailed structure of the wavelet coefficients besides their interscale dependence. The numerical evaluation of contrast-to-noise ratio (CNR) along with simple observation of the results showed reasonably acceptable improvement of CNR from 2.9149 to 38.8813 in anterior--posterior images, from 41.6131 to 86.3141 in cephal–lateral images, from 13.6414 to 43.4711 in intraoral pictures, and from 6.0102 to 31.8771 in panoramic datasets. Furthermore, technical ability of the proposed filtering method in retaining the possible cavities on dental images was evaluated in two datasets with natural and artificially applied cavities.

INTRODUCTION

The radiological examinations in dentistry can be classified into intraoral (with film or the sensor placed in the mouth) and extraoral imaging techniques. Extraoral imaging includes (1) panoramic X-ray showing a curved section of the whole-maxillo-facial block (more or less mandible shape), and (2) cephalometric X-ray showing a projection, as parallel as possible, of the whole skull. The cephalometric X-ray may be achieved from the lateral side or from the anterior–posterior view.

There is no doubt that having an exact and noiseless view of such images can offer an invaluable help to the dentist in better diagnosis and treatment. Most of prevalent techniques of dental imaging are going to be acquired, processed, and even evaluated in digital form; however, the low contrast and the noise pollution are inevitable problems. The proposed method tries in reduction of noise level in different kinds of the mentioned dental image types and provides a better visualization for the dentist and a good contrast to the noise ratio by numerical computation. Furthermore, the method is of benefit to real-time image processing due to its fast response.

Several papers reported current methods in dental noise reduction, first of which proposed by Goebel[1] in 2005 and was based on removal of a multiplying background using polynomial scaling and the A-Trous multiresolution transform. In 2006, Frosio[2] proposed a mixture model made up of two Gaussian distributions and one inverted lognormal distribution to analyze the image histogram. A similar approach was also proposed by Sayadi[3] for enhancing digital cephalic radiography using mixture models and local gamma correction. In 2008, Frosio introduced a filter based on the classical switching scheme in which the pulses were first detected and then corrected through a median filter.[4,5] One year later, Lucchese[6] reported a principled method for setting the regularization parameter in total variation filtering, which was based on the analysis of the distribution of the gray levels on the noisy image. Along with this research, Frosio[7] proposed a statistical based impulsive noise removal. The application of anisotropic nonlinear tensor-based diffusion[8] in dental images was also reported in 2009 and 2010 by Kroon[9,10] for cone-beam CT images. Ju[11] also proposed the application of Ridgelet transform for denoising of the root canal image in dental films. In 2010, Serafini[12] used a gradient projection method for image denoising and deblurring on dental radiographies. More recently, in 2011, Bonettini[13,14] reported the application of the extra gradient method for total variation-based image restoration from Poisson data and interior point methods for edge-preserving removal of Poisson noise in dental radiographies.

In spite of the sophistication of the recently proposed methods, most algorithms have not yet attained a desirable level of applicability. All show an outstanding performance when the image model corresponds to the algorithm assumptions but fail in general and create artifacts or remove image fine structures. Among a great deal of denoising and deblurring methods introduced for digital images[15–17] the mentioned list seems too short for a wide variety of dental images, the quality of which is of fundamental importance in diagnosis and treatment of diseases pertaining to dentistry. Dental image denoising problem seems to be better solved if a powerful signal/noise-separating tool (e.g., wavelet analysis) is incorporated in the noise-reducing diffusion process. In simple words, multiresolution and sparsity properties of wavelet transform on the top of edge preservation ability of nonlinear diffusion can make a significant help to the noise reduction process.[18]

Having this in mind, we proposed the application of wavelet diffusion in dental image denoising. Three different approaches to selecting the constant value of the nonlinear diffusion are proposed: the manual selection of λ, semi-automatic calculation of λ, and the automatic method. In the final approach, a classification of image to homogenous and nonhomogenous areas is required subject to modeling the distribution of wavelet modulus. Two novel plans in this application are proposed: Laplace-mixture model and circular symmetric Laplacian model.

The rest of this paper is organized as follows: In the “Material” section the material is illustrated and the proposed method is further elaborated in the “Wavelet Diffusion,” “The Manual and Semiautomatic Method,” and “The Automatic Method” sections. Quantitative results on natural noisy dental images are reported in the “Experimental Results” section. The method is discussed and conclusions are drawn in the “Discussion and Conclusion” section.

MATERIALS AND METHODS

Material

For evaluation of our algorithm, we used 104 images of cephal-lateral, 38 images of anterior--posterior, 27 images of intraoral radiology, and 12 panoramic images. The intraoral and panoramic datasets were recorded in Dental Department of Isfahan University of Medical Sciences and the rest of the dataset is obtained in Dental Department of Shahid Beheshti University. The dental apparatus for cephal-lateral, anterior-posterior, and panoramic imaging was a Planmeca ProMax X-ray unit, and for intraoral images, a Planmeca intra X-ray unit was utilized along with two sizes of Planmeca ProSensor sets in 33.6×23.4 mm and 39.7×25.1 mm with a resolution of 17 lines per millimeter.

Wavelet Diffusion

To clear up our method, we should consider that the nonlinear diffusion[8] technique relies on the gradient operator to distinguish signal from noise. Such a method often cannot achieve a precise separation of signal and noise. During last decades, discrete wavelet transform has also been introduced as a powerful denoising method;[19] however, wavelet shrinkage suffers from ringing artifact. To eliminate this artifact several methods such as cycle spinning[20] were suggested which usually increase the computational complexity.

Dental image denoising problem is better solved if a powerful signal/noise-separating tool (e.g., wavelet analysis) is incorporated in the noise-reducing diffusion process. In simple words, multiresolution and sparsity properties of wavelet transform on the top of edge preservation ability of nonlinear diffusion can make a significant help to the noise reduction process.[18] Furthermore, the time complexity of this proposed method is considerably lower than conventional nonlinear diffusion. This combination was employed by Yue[21] for speckle suppression in ultrasound images and it was proved that a single step of nonlinear diffusion can be considered equivalent to a single shrinkage iteration of coefficients of Mallat-Zhong dyadic wavelet transform (MZ-DWT).[22]

Two years later in 2008, Rajpoot[23] extended the diffusion wavelet idea by investigating the ability of conventionally used orthogonal and biorthogonal filters like Haar, Daubechies, and Coiflet (undecimated form) to be replaced by quadratic Mallat-Zhong filters. The steps of wavelet diffusion can therefore be classified in next steps:[23]

• Wavelet decomposition into low frequency subband (A_j) and high frequency subbands (Wⁱ_j)

• Regularization of high frequency coefficients (Wⁱ_j) by multiplication with a function p

• Wavelet reconstruction from low frequency subband (A_j) and regularized high frequency subbands

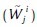
A two level structure of wavelet diffusion is shown in Figure 1[23].

Figure 1.

A two-level structure of wavelet diffusion[23]

Regularization is the second step of the algorithm and the regularization function should be defined as P_j(|η_j(x,y)|) = 1–g(|η_j(x,y)|) where g(|η_j(x,y)|) can be of the form

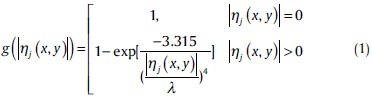
And |η_j(x,y)| is an edge estimate for each pixel which can be approximated by the modulus of high.frequency wavelet subbands at each scale j by

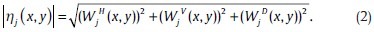
In implementation of algorithms based on nonlinear diffusion (Perona-Malik diffusion, Anisotropic Diffusion, or new wavelet-based approaches), the selection of proper value for the constant λ (in eq. 1) has a profound effect on performance of the denoising algorithm. We, therefore, proposed three different approaches in selection of this value. The first approach is manual selection of λ and finding an acceptable result with trial and error. The second method (semiautomatic) tries in calculating of λ based on the information obtained from a homogenous area in the image, the location of which should be determined by the user. And, finally, in the third approach, the homogenous area is found automatically using a likelihood classification and cross-scale edge consistence. The classification of the image to homogenous and nonhomogenous areas is subject to modeling the distribution of wavelet modulus which is proposed to be a Laplace-mixture model or a circular symmetric laplacian model.

The Manual and Semiautomatic Method

Using a manual manner, we tried the mentioned method utilizing Haar wavelet with different values of λ (in eq. 1) and for different levels of shrinkage, the outcomes of which are presented in the results.

Furthermore, we examined semiautomatic and automatic methods for deciding on the value of the best λ for each image. In the semiautomatic method, according to,[21] the user choused a homogenous area of the image (X_homo), which could be simply located for dental images with a wide consistent region. Then, the wavelet transform was applied on X_homo and |η_j^homo(x, y)| was calculated as the modulus of high-frequency wavelet subbands, in a similar manner to |η_j(x, y)|. Then a new scale was defined:

Now, the best fitting λ could be estimated for each level by

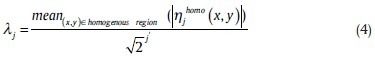
The Automatic Method

Rayleigh mixture model

In the automatic method for λ value, Yue[21] used a likelihood classification and cross-scale edge consistence to find the homogenous areas of an image, automatically. They tried to find a threshold for classification of image to edge-related class and the noise-related category. So, a Rayleigh model was proposed for the speckle-related modulus, since they assumed that both of speckle-related and edge-related wavelet coefficients are Gaussian distributed:

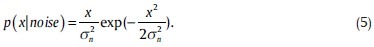
Similarly, p(x|edge) has the same form with σ²_e.

Therefore the distribution of the wavelet modulus could be estimated by a Rayleigh-mixture model:

p(x)=ω_np(x|noise)+(1–ω_n)p(x|edge)      (6)

parameters of which can be estimated by the well-known expectation-maximization (EM) method that is an iterative numerical algorithm. The requested threshold for each scale can then be estimated by

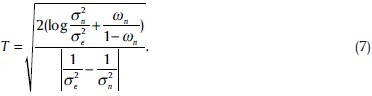
A coarse-to-fine classification method[24] can be used to determine the homogenous region U_j :

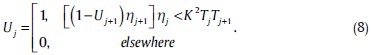
K may be changed and the higher amount of K make more coefficients close to edges contributed in calculation of the threshold.

The Laplace-mixture Model

In this paper, we also proposed another aspect in modeling the speckle-related and edge-related modulus. In 2006, Rabbani[25] suggested to design a maximum a posterior (MAP) estimator which relies on Laplace mixture distributions to better model the heavy-tailed property of wavelet coefficients. We use a similar idea to model the speckle-related modulus. Therefore, the wavelet modulus will be in the form of two Laplace pdfs:

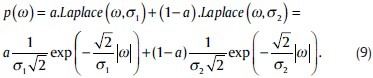
For this mixture model, we use the EM algorithm to estimate its parameters. This iterative algorithm has two steps. S(k,m) denotes variable S at point k for iteration m and we start the algorithm with m = 0 (first iteration), assuming the observed data ω (k), the E-step calculates the responsibility factors:

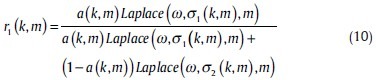
r₂(k,m) = 1–r₁(k,m)

The M-step updates the parameters a(k,m), σ₁(k,m) and σ₂(k,m). a(k,m) is computed by

where M is the number of coefficients and the parameters σ₁(k,m) and σ₂(k,m) are computed by

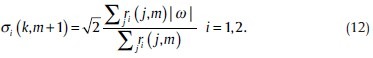
The Circular Symmetric Laplacian Model

The most important novelty of this paper is based on modeling the speckle-related modulus with a circular symmetric Laplacian[26,27] model. It is well known that one of the most important properties of the wavelet transforms is the persistence, i.e., the large/small values of wavelet coefficients tend to propagate across scales. This property means that the bivariate pdfs, such as circular symmetric Laplacian pdf,[26] which exploit the dependence between coefficients, better model the statistical properties of wavelet coefficients in comparison with univariate pdfs.[26] In this paper, we use a mixture of two circular symmetric Laplacian pdfs to describe the above property. Then we define a parent-child schematics of the wavelet domain as illustrated in Figure 2.

Figure 2.

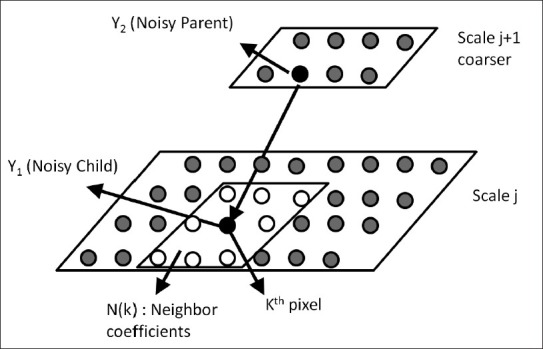
Illustration of neighborhood[26]

Consequently, ω in (9) should now be described by :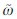

where ω₁(k) and ω₂(k) are the values in parent and child scales. The following circular symmetric Laplacian pdf with local variance is proposed in order to describe that ω₁(k) and ω₂(k) are uncorrelated while are dependent[26]:

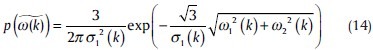
The bivarate mixture model then can be written as

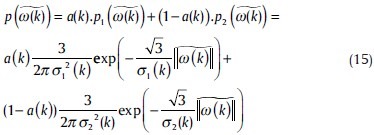
In the EM algorithm, the formulas will change to

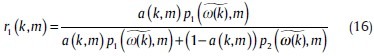
r₂(k,m) = 1–r₁(k,m)

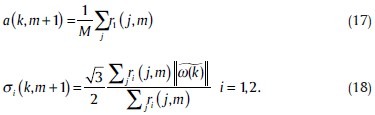
EXPERIMENTAL RESULTS

In this section, we demonstrate the performance of the proposed algorithms on different dental images. According to a great deal of similar papers, the denoising performance may be evaluated in different ways[16] like the method noise, the mean square error, PSNR, contrast-to-noise ratio (CNR), and the visual quality of the restored images. We chose CNR and the visual quality for this performance because this application is designed for natural noisy images (i.e., the noisy images are not constructed manually); therefore, methods like PSNR and mean-square error are not acceptable since we have no golden noise-free image to which we may compare the denoised results of the proposed algorithm.

In order to have a meaningful comparison between mentioned algorithms, we use contrast-to-noise ratio (CNR)[28] defined as

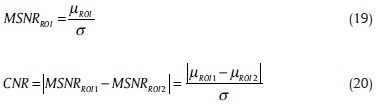
where μ_ROI is the mean signal value computed for a small region of interest (ROI). The desired ROI can be a homogeneous area of tissue with high signal intensity. The noise standard deviation (std) σ is computed from a large region outside the object, which represents the background noise. The CNR represents the contrast between two ROIs. Figure 3 shows the images from which we selected ROI samples. The white circles show the noise ROIs and the black ones indicate the ROI representing a homogeneous area of tissue. Table 1 shows the CNR values for different dental images using discussed methods.

Figure 3.

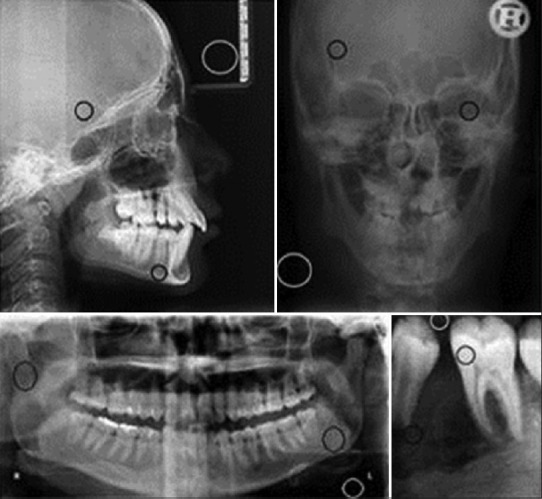
The selected ROI samples

Table 1.

The CNR values of various automatic methods

In Figure 4, the results of the manual method described in the “The Manual and Semiautomatic Method” section are shown. Figures 5–8 are also demonstrating the performance of the automatic algorithm using the Rayleigh mixture model, Laplace mixture, and circular symmetric Laplacian.

Figure 4.

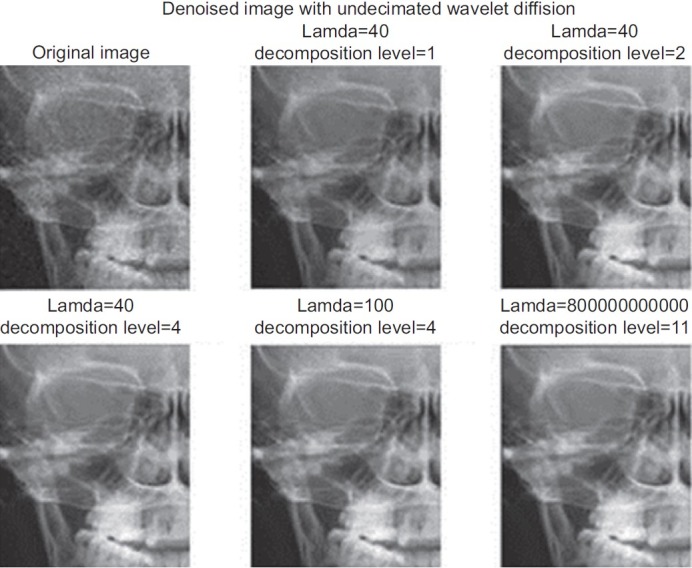
The results of choosing different values of λ for different levels in the manual method

Figure 5.

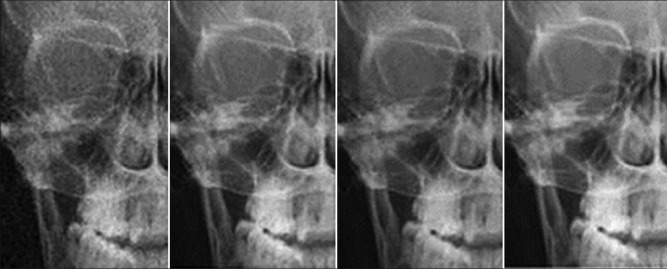
The comparison of different automatic methods in anterior-posterior images. Left image is the original one, the performance of the automatic algorithm with the Rayleigh mixture model (middle left), Laplace mixture (middle right), and circular symmetric Laplacian (most right)

Figure 8.

The comparison of different automatic methods in panoramic images. The left image is the original one, the performance of the automatic algorithm with the Rayleigh mixture model (middle left), Laplace mixture (middle right), and circular symmetric Laplacian (most right)

Figure 6.

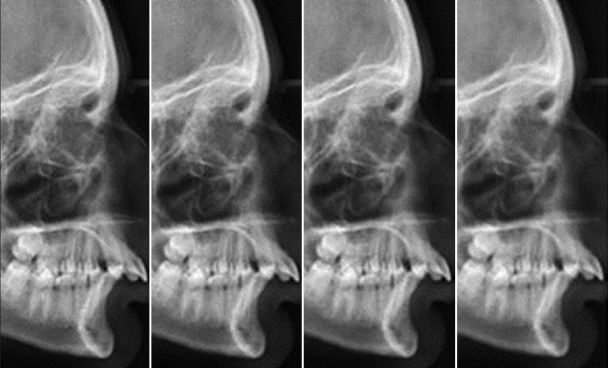
The comparison of different automatic methods in Cephal-lateral images. The left image is the original one, the performance of the automatic algorithm with the Rayleigh mixture model (middle left), Laplace mixture (middle right), and circular symmetric Laplacian (most right)

Figure 7.

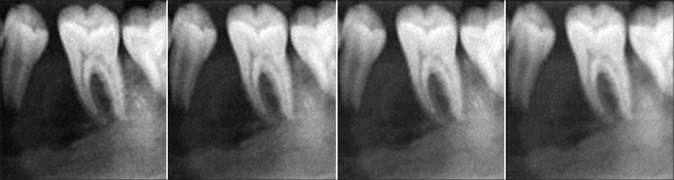
The comparison of different automatic methods in intraoral images. The left image is the original one, the performance of the automatic algorithm with the Rayleigh mixture model (middle left), Laplace mixture (middle right), and circular symmetric Laplacian (most right)

The other important aspect considered in dental image denoising is the ability of the filtering method in retaining the possible cavities on dental images. For this purpose, we collected new series of intraoral images with natural cavities on them and examined the cavity preserving ability of the method. Furthermore, we made radiographic images from a healthy extracted dent and then applied an artificial cavity to determine the mentioned ability. Figure 9 and 10 demonstrate the results of the circular symmetric Laplacian mixture model method for cavity preserving. As it can be seen in Figure 9, the left column demonstrates two extracted dents with natural intrinsic cavities and the right column shows the filtered images with the proposed method, preserving the local cavities. Similarly, it is obvious in Figure 10 that the manually applied cavity (Fig. 10, left) is filtered with the new method and the result (Fig. 10, right) has a good preservation on this cavity. The main advantage of this aspect is the reality that in clinical applications it is an important feature not to miss the cavities due to denoising and unfortunately this problem is prevalent in most of common denoising techniques which are usually found in software sold along with dental imaging equipment.

Figure 9.

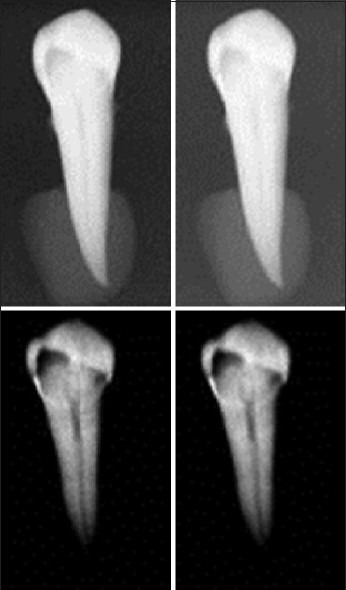
Cavity preserving in natural cavities (left column: original images, right column: filtered images)

Figure 10.

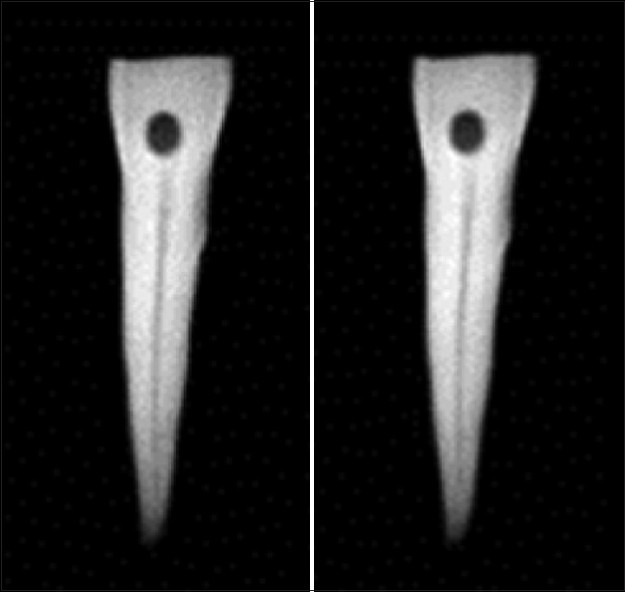
Cavity preserving in artificial cavities (left: original image, right: filtered image)

DISCUSSION AND CONCLUSION

In this paper, a particular combination of wavelet shrinkage and nonlinear diffusion for dental image denoising was proposed. For this purpose, wavelet diffusion was used and its threshold is selected automatically using the Laplacian mixture model and circular symmetric Laplacian mixture models for speckle-related modulus. The circular symmetric Laplacian mixture model could make a better model of data because of its compatibility with heavy tailed structure of wavelet coefficients besides their interscale dependence and produced better CNR in comparison with other models. The method also has an acceptable speed even when implemented in MATLAB™ without using mex files – Math Works, Inc., Natick, MA, USA.[29] This sounds quite promising for real-time application of this method in dental offices.

BIOGRAPHIES

Raheleh Kafieh received the BS degree from Sahand University of Technology, Iran, in 2005 and the MS degree from the Isfahan University of Medical Sciences, Iran, in 2008, both in biomedical engineering. She is currently working toward the PhD degree in the Department of Biomedical Engineering at Isfahan University of Medical Sciences. Her research interests are in biomedical image processing, computer vision, graph algorithms, and sparse transforms. She is a student member of the IEEE and the IEEE Signal Processing Society.

E-mail: r_kafieh@resident.mui.ac.ir

Hossein Rabbani is an Associate Professor at Isfahan University of Medical Sciences, in Biomedical Engineering Department also Medical Image & Signal Processing Research Center. Involved research topics include medical image/volume processing, noise reduction and estimation problem, image enhancement, blind deconvolution, video restoration, probability models of sparse domain's coefficients especially complex wavelet coefficients. He is a member of IEEE, Signal Processing Society, Engineering in Medicine and Biology Society, and Circuits and Systems Society.

E-mail: h_rabbani@med.mui.ac.ir

Mehrdad Foroohandeh is a dental student since 2007 at dental Department, Isfahan University of Medical Sciences. His research interests are in dental image process and oral cancer.

E-mail: mehrdad_foroohande@yahoo.com