Abstract
Many network analyses of fMRI data begin by defining a set of regions, extracting the mean signal from each region and then analyzing the correlations between regions. One essential question that has not been addressed in the literature is how to best define the network neighborhoods over which a signal is combined for network analyses. Here we present a novel unsupervised method for the identification of tightly interconnected voxels, or modules, from fMRI data. This approach, weighted voxel coactivation network analysis (WVCNA) is based on a method that was originally developed to find modules of genes in gene networks. This approach differs from many of the standard network approaches in fMRI in that connections between voxels are described by a continuous measure, whereas typically voxels are considered to be either connected or not connected depending on whether the correlation between the two voxels survives a hard threshold value. Additionally, instead of simply using pairwise correlations to describe the connection between two voxels, WVCNA relies on a measure of topological overlap, which not only compares how correlated two voxels are, but also the degree to which the pair of voxels is highly correlated with the same other voxels. We demonstrate the use of WVCNA to parcellate the brain into a set of modules that are reliably detected across data within the same subject and across subjects. In addition we compare WVCNA to ICA and show that the WVCNA modules have some of the same structure as the ICA components, but tend to be more spatially focused. We also demonstrate the use of some of the WVCNA network metrics for assessing a voxel’s membership to a module and also how that voxel relates to other modules. Last, we illustrate how WVCNA modules can be used in a network analysis to find connections between regions of the brain and show that it produces reasonable results.
Keywords: Functional Magnetic Resonance Imaging, Functional Connectivity, Graph Theory, Small World Networks
1 Introduction
It has long been recognized that understanding brain function requires a characterization of both functional localization and functional integration or connectivity (Friston, 1994). Although functional integration has historically been studied in the context of task-driven functional connectivity, recent work has focused heavily on the pattern of intrinsic functional connectivity present in resting-state fMRI data (Biswal et al., 1995; Greicius et al., 2003; Fox et al., 2005; Beckmann et al., 2005; DeLuca et al., 2006; Jafri et al., 2008; Damoiseaux et al., 2006; Dosenbach et al., 2007; Liu et al., 2008; Salvador et al., 2005; Achard and Bullmore, 2007; Cohen et al., 2008). In particular, there is growing evidence that functional networks in the brain exhibit “small world” properties, with a high degree of clustering and a short average path length between any two voxels (Bassett and Bullmore, 2006; Bullmore and Sporns, 2009).
Network analyses of fMRI data generally proceed by defining a set of regions, extracting the mean signal from each region, and then analyzing the correlations between regions. One essential question that has not been addressed in the literature is how to best define the network neighborhoods over which signal is combined for network anlayses. Most studies have used regions defined either on the basis of functional imaging activation or on the basis of anatomy. Here we present a novel unsupervised method for the identification of tightly interconnected voxels (or modules) from fMRI data. This method, weighted voxel coactivation network analysis (WVCNA), is based on an approach developed for the detection of gene co-expression networks (Zhang and Horvath, 2005). It employs the graph-theoretic concept of topological overlap (TO) (Ravasz et al., 2002), in which the relation between two voxels is determined not by their correlation with one another, but by the degree to which they are both highly correlated with the same other voxels. Further, rather than using thresholded correlation measures, it uses a weighted correlation measure that removes the need to choose an arbitrary correlation threshold. Finally, the weighting coefficient is chosen to maximize the scale-free nature of the network, thus resulting in a network with a biologically plausible connectivity distribution. Scale free networks are a class of small world networks characterized as having many nodes with few connections to other nodes and fewer highly connected nodes. By clustering the resulting topological overlap values, it is possible to detect a set of functionally coherent network modules, which can then be used for further analyses of network characteristics. Like independent components analysis (ICA), WVCNA can be considered a data reduction technique, but unlike ICA it does not impose independence (or orthogonality) on the resulting components. While the independence assumption has statistical advantages, it is biologically implausible in the context of fMRI data. It is quite possible that a module (corresponding to one brain region) is correlated with another (corresponding to another brain region). What also sets WVCNA apart from ICA is that it includes a whole host of measures for assessing the network structure, such as the connectivity of a voxel to other voxels overall and within a module. In addition, a module membership measure can be computed that reflects how strongly a voxel belongs to a particular module and can be used to identify voxels that are highly associated with a particular module versus those that are equally related to multiple modules. These measures will be useful in characterizing individual networks as well as comparing network structures between populations.
We first present an overview of the WVCNA method, and then demonstrate its application to a resting state fMRI data set. We show that it reliably detects network modules across independent resting state fMRI acquisitions within subjects, and that the resulting modules are anatomically plausible. We then compare it to independent components analysis (ICA) on the same dataset, showing that WVCNA detects much of the same structure as ICA, but that it provides a more spatially localized and separable decomposition of the brain into functionally coherent regions. We also illustrate some applications of WVCNA metrics for assessing network structure. Last, we show how WVCNA modules can be used in a network analysis to find connections between brain regions.
2 Methods
2.1 Data
The BOLD fMRI data were originally collected by Fox et al. (2007), and were obtained from the fBIRN Data Repository (http://fbirnbdr.nbirn.net:8080/BDR/). The data consisted of 4 fixation runs from each of 16 subjects using a 3T Siemens Allegra MR scanner (4 × 4 × 4 mm voxels, TE 25 ms, TR 2.16 s), as described in Fox et al. (2007). Subjects were instructed to look at a crosshairs, remain still and not fall asleep during the scans. Structural data included a high resolution (1 × 1 × 1.25 mm) sagittal, T1-weighted MP-RAGE (TR=2.1s, TE=3.93ms, flip angle=7°) and a T2 weighted fast spin echo scan.
2.2 Preprocessing
The first four TRs of each run were discarded to allow for scanner stabilization, for a total of 190 TRs per run. FMRI data preprocessing was carried out using the fMRI Expert Analysis Tool (FEAT) Version 5.98, part of the fMRIB Software Library (FSL, http://www.fmrib.ox.ac.uk/fsl/). The MCFLIRT tool was used to motion-correct each functional run of data and simultaneously created 6 transformation parameter time courses that were later modeled as nuisance (Jenkinson et al., 2002). The brain extraction tool (BET) of FSL was used for skull stripping and other preprocessing included multiplicative mean intensity normalization of the volume at each time point and highpass temporal filtering (Gaussian-weighted least-squares straight line fitting with σ = 30s). The six motion parameters as well as their first derivatives were regressed out of the data on a voxelwise basis using FSL’s FILM. The residuals from this analysis were registered to standard space using FSL’s FLIRT (Jenkinson and Smith, 2001; Jenkinson et al., 2002) using a 3 degree of freedom (dof) transformation from the functional to a T2-weighted image, a 6 dof registration between the T2 and T1-MPRAGE and a 12 dof transformation between the T1-MPRAGE and the MNI152 standard 2mm template. Data were then upsampled to 6mm voxels and grey matter voxels were isolated using grey matter regions of the Harvard Oxford Probabilistic Atlas thresholded at 25 percent and then upsampled from 2mm to 6mm.
2.3 Weighted voxel coactivation analysis
The methods used in the data analysis are based on the weighted gene co-expression network analysis approach of Zhang and Horvath (2005). Unlike other network approaches, where connections between voxels are either considered to be present or absent, the weighted network approach allows the connection between two voxels to be a continuous measure ranging between 0 and 1. In the present study, the measure of connectivity is topological overlap (TO), which differs from pairwise correlations in that it not only considers the adjacency between two voxels, but also the overlap of the two groups of voxels connected to the two original voxels (Zhang and Horvath, 2005; Ravasz et al., 2002; Yip and Horvath, 2007). Because it pools over a much larger set of correlations, it is less susceptible to noise than correlation between two single voxels. Another feature of TO is that the adjacency measure on which it is based is derived such that that the resulting network is a scale-free network, which is a class of small world networks. This is a desirable property as functional brain networks have been shown to have small world network characteristics (Bassett and Bullmore, 2006; Bullmore and Sporns, 2009).
For the within-run analyses, WVCNA was carried out on each run independently and for the subject analysis across runs, the within-run time series were normalized and concatenated. We will first describe how the adjacency measure is derived and then how this is used in the calculation of topological overlap. Last, we discuss how the modules are formed through the use of hierarchical trees.
Adjacency measure and the scale free topology criterion
The first step in the analysis is to calculate the Pearson correlation between all pairs of voxels, rij. Since we want to distinguish between positive and negative correlations, we use a signed similarity measure defined as and then the soft power adjacency function is defined as for i ≠ j and 0 when i = j (Zhang and Horvath, 2005). There are two types of weighted correlation networks. Signed networks lead to modules of positively correlated voxels while unsigned correlation networks lead to modules of highly positively or highly negatively correlated voxels (Mason et al., 2009). In genetic applications both signed and unsigned correlation networks have been successfully used and it is plausible that both types of networks will be useful in voxel network applications as well. Future empirical studies are needed to provide evidence of the utility of both types of networks.
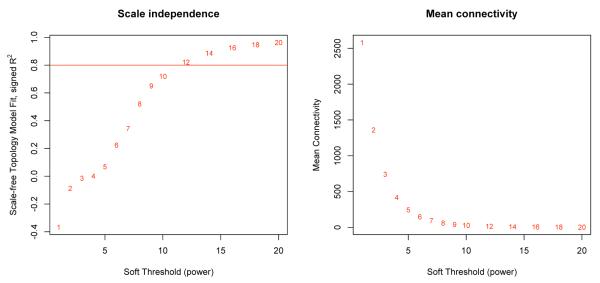
We use the scale free fit index, R2 = Scale Free Fit Index = cor(log(p(k)), log(k))2, to inform the parameter choice (the power) of the adjacency matrix. Many (but certainly not all) real networks have been found to exhibit approximate scale-free topology (Barabasi and Albert, 1999; Albert et al., 2000; Barabasi and Oltvai, 2004). The scale free fit index, R2, of a transformed network is a function of the power parameter β. In some network applications, prior knowledge suggests that the network should satisfy scale-free topology at least approximately. In this case, one can ignore power values that do not lead to approximately scale-free networks. Toward this end, one can use a signed version of the scale-free topology fitting index. Since it is biologically implausible that a network contains more hub genes than non-hub genes, we multiply R2 with -1 if the slope of the regression line between log(p(k)) and log(k) is positive. These considerations led Zhang and Horvath (2005) to propose the following scale-free topology criterion: Only consider those parameter values that lead to a network satisfying scale-free topology at least approximately, e.g. signed R2 > 0.80. In correlation network applications, we often find the relationship between R2 and the power parameter is characterized by a saturation curve type of relationship (see Figure 1).
Figure 1.
Illustration of the scale free index and mean connectivity for a range of soft threshold values for a representative subject. The power was chosen such that the signed R2 was greater than 0.8 for all data sets.
In many correlation network applications, we have used the first parameter value where saturation is reached as long as it is above 0.8. But is worth repeating that there does not have to be a monotonic relationship between the adjacency parameter and the scale free fit. Sometimes the scale free fitting index, R2, decreases for large values of the power parameter. Further, when dealing with a correlation network constructed on the basis of two heterogeneous and distinct groups, the scale free topology criterion may not work well. In this case, we recommend to choose a default values for the parameters, e.g. β = 6 for an unsigned correlation network and β = 12 for a signed correlation network.
It should be noted that it is possible to use other degree distribution criteria to choose the parameter, β. For example, it has been shown that the exponentially truncated power law distribution is a better fit to the degree distribution than the power law for resting state fMRI data (Achard et al., 2006) and for yeast co-expression networks (Zhang and Horvath, 2005). Due to the flexibility of the exponentially truncated power law distribution, all values of β tend to be associated with very good fits of the model. Because of this, the exponentially truncated power law distribution is not useful in tuning the parameter β in these brain networks or in gene networks (Zhang and Horvath, 2005).
Topological Overlap
As mentioned previously, the topological overlap measure compares the similarity of two voxels, as well as the groups of voxels connected to each voxel. The equation is given by
| (1) |
where aij is the adjacency measure, ki is the connectivity of voxel i, and lij = ∑u aiuauj measures the overlap between the two voxel neighborhoods. The numerator of wij is the strength of the overlap and will be largest when the two voxels are highly related and have common voxels that are also highly related to them. The denominator of wij is a normalization term.
Identifying modules
Modules are identified in a two step process. First, a dendrogram is created using average linkage hierarchical clustering with the TO dissimilarity measure, 1–wij. The clusters in the resulting dendrogram are then identified using the dynamic branch cutting algorithm of Langfelder et al. (2008). This approach finds clusters in a hierarchical tree based on the tree shape, as opposed to using a fixed height branch cutting technique where a cut height is chosen and continuous branches below the cut comprise the clusters. For all applications of the dynamic tree cutting algorithm to the first level dendrograms, a minimum module size of 20 voxels was specified. Once the first level modules are identified, the eigenvoxel time series (first principal component) for each module is calculated and used in a simple second level analysis. For the second level, correlations between the eigenvoxels are calculated and the correlation is subtracted from 1 and used to create the second level dendrogram using average linkage hierarchical clustering. The second level modules are found by again using the dynamic tree cutting algorithm with a minimum module size of 1. The dendrograms from the second level analysis are much simpler since the number of eigenvoxels (approximately 100) is much smaller than the original number of voxels (approximately 5000) and so this simpler method is appropriate.
WVCNA measures of connectivity
There are different connectivity measures that can be used to evaluate and study the modules that WVCNA creates. For example, to find the most highly connected voxels within a module, the measure of intramodule connectivity, for voxel i in module q is given by
| (2) |
where n(q) is the number of voxels in module q (Mason et al., 2009). If the network were unweighted, would be a count of how many voxels the ith voxel is connected to within module q. This measure can be thought of as the degree to which that voxel belongs to that module, where higher intramodular connectivity values correspond to more central voxels in the module.
A second connectivity measure is the module eigenvoxel based connectivity, , which is defined as
| (3) |
where xi is the original time series data for voxel i and E(q) is the eigenvoxel of module q. Since this value is a correlation, standard correlation hypothesis tests can be used to assess module membership.
2.4 Independent Component Analysis
Analysis was carried out using Probabilistic Independent Component Analysis (Beckmann and Smith, 2004) as implemented in Multivariate Exploratory Linear Decomposition into Independent Components (MELODIC) Version 3.09, part of FSL. Data were normalized and concatenated prior to analysis as well as converted to percent BOLD signal change. The data were whitened and projected into a 46-dimensional subspace using Principal Component Analysis.
The whitened observations were decomposed into sets of vectors which describe signal variation across the temporal domain (time-courses) and across the spatial domain (maps) by optimising for non-Gaussian spatial source distributions using a fixed-point iteration technique (Hyvarinen, 1999). Estimated component maps were divided by the standard deviation of the residual noise and thresholded by fitting a mixture model to the histogram of intensity values (Beckmann and Smith, 2004). The number of components was specified to match the number of modules that were found using the WVCNA approach so comparisons between the two approaches could be made.
2.5 Comparing Modules Across Runs
Since in each set of modules for each run of each subject the number of modules is not fixed and the module labels are not comparable across module sets, pairwise comparisons of sets of modules were carried out using a normalized version of the mutual information index (Kuncheva, 2004; Meunier et al., 2009). For two sets of modules A and B, where the number of modules in A and B are given by NA and NB, respectively and Nij is the number of voxels in the intesection of module i from set A and module j from set B, the normalized mutual information is given by,
| (4) |
Note that N is the total number of voxels and Ni. and N.j are the number of voxels in module i of set A and module j of set B, respectively. The mutual information index ranges between 0 and 1, where independent module sets would have a mutual information of 0 and identical sets would have a mutual information of 1.
2.6 Comparing Modules to ICA Components
In order to make a comparison between the WVCNA modules and ICA components, a similarity measure was needed to match each module to the most similar ICA component. Individual modules were compared to individual components using the Sorensen similarity measure, which is defined as the number of voxels in common to both the module and component divided by the average of the sizes of the module and component. This can also be expressed as
where M is a module, C is a component and the # operation counts how many voxels are in a set. This measure is preferred to Euclidean similarity since it takes into account the module sizes.
3 Results
3.1 WVCNA within subject
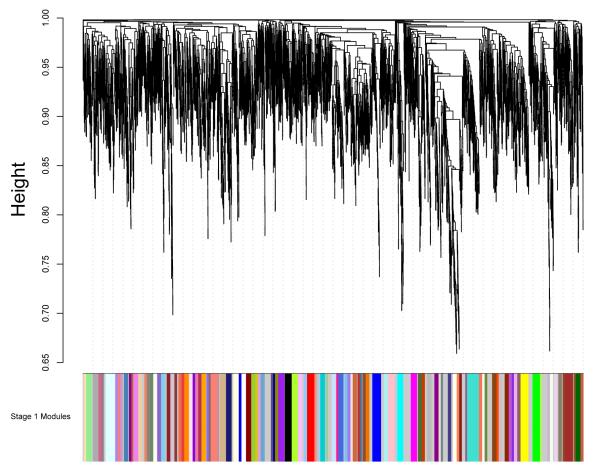
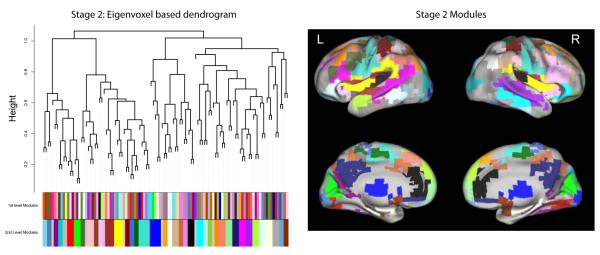
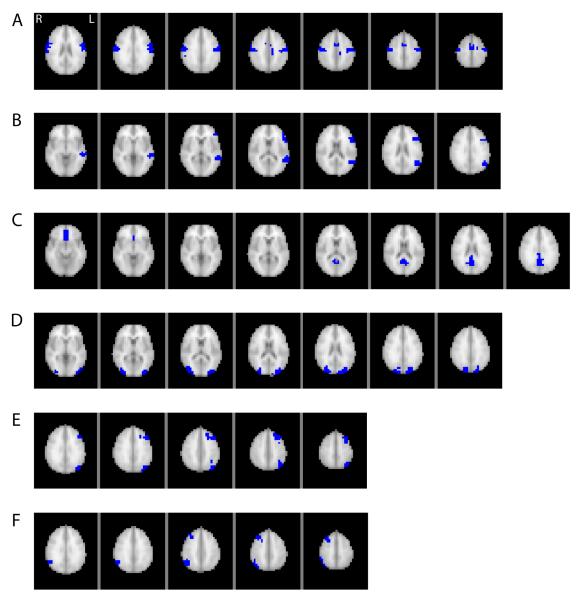
For each subject, the preprocessed data from the four runs were normalized and then concatenated for use in the WVCNA analysis. On average the adjacency power parameter, β, was set at 12.4 (sd=1.7), based on the criteria discussed in the Methods section. Figure 2 shows the dendrogram and modules resulting from using the dynamic tree cutting algorithm to cut the tree and the left panel of Figure 3 shows the second stage dendrogram and second stage modules found when setting the minimum number of modules to 1 in the dynamic tree cutting algorithm. The stage 1 dendrogram is based on all voxels of data (5054 voxels), whereas the stage 2 dendrogram illustrates the relationship between the eigenvoxels corresponding to each stage 1 module. Branches of the stage 2 dendrogram correspond to meta-modules, i.e. modules of module eigenvoxels (Langfelder and Horvath, 2007). On average over subjects, a total of 111.9 (sd=10.8) first level modules were found and after merging modules in the second stage analysis, an average of 42.9 (sd=5.6) modules were found per subject. The right panel of Figure 3 displays the second level modules on the brain, matching the colors indicating the second level modules in the left panel. Another view of 6 of the second stage modules is shown in Figure 4, illustrating modules corresponding to the motor system network, left frontal and middle temporal regions that are part of the language network, midline regions that are part of the default mode network, bilateral dorsal visual stream, and right and left dorsal fronto-parietal networks.
Figure 2.
First stage dendrogram and modules found using the dynamic tree cutting algorithm. The dendrogram is based on all grey matter voxels (5054) based on data from all four runs (concatenated) for a single subject. Minimum module size was set to 20 voxels in the dynamic tree cutting algorithm. Dedrograms for other subjects were qualitatively similar.
Figure 3.
Dendrogram from the second stage of the WVCNA analysis and second stage modules displayed on the brain for a single subject (all 4 runs concatenated). The dendrogram shown in the left panel illustrates the relationships between eigenvoxels based of the first level modules, revealing a higher order organization. The top row of colors correspond to the first stage modules and the bottom row correspond to the second stage modules found using dynamic tree cut. The right hand panel displays the second stage modules on the brain, where the colors corresponding to the second level modules in the image on the left match the colors of the modules on the brain.
Figure 4.
Illustration of 6 individual modules from Figure 3, showing the anatomical plausibility of the modules. The modules in panels A-F reflect the motor system network (A), left frontal and middle temporal regions that are part of the language network (B), midline regions that are part of the default mode network (C), bilateral dorsal visual stream (D) and the left and right dorsal fronto-parietal network (E and F).
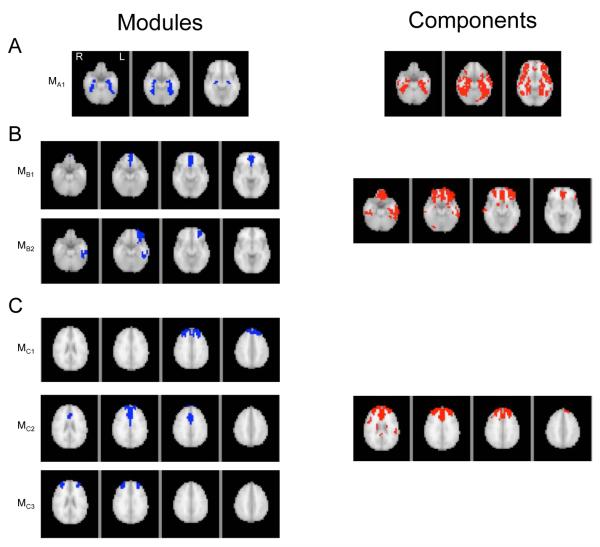
The comparison of WVCNA modules to ICA components is shown in Figure 5, where the left column displays modules in blue and are arranged in panels according to the ICA component in the right panel that they were closest to according to the Sorensen similarity measure. On average across subjects, 79% of the module/component groupings consisted of a single module grouped with a single component, 19.2% included 2 modules with 1 component and in a limited number of cases more modules (3-5) were grouped with a single component. Panels A, B and C of Figure 5 show examples of 1, 2, and 3 module matches, respectively, where 3-4 slices of the brain image are displayed to show the module location. The similarity distances between matched components and modules tended to be large (0.82 on average across all subjects), but this was due to the modules being much smaller than the components. On average the module size was 100.4 voxels, compared to the matched component, which had an average size of 342.1 voxels. The module/component intersection on average comprised 71.1% of the module and 23.1% of the matched component across all subjects, so modules tended to be mostly contained within a single component. In panel A the module location is very similar to the component, with the component slightly more dispersed. In panel B the component is bilateral, the modules separate the region into a medial component (MB1) as well as a unilateral component (MB2). Panel C shows a case where three modules matched with a single component, where the component is separated into two lateral modules (MC1 and MC3) and one medial module (MC2).
Figure 5.
Modules and the most highly related ICA components, found using the Sorensen distance measure. The left column displays individual modules, where each row displays 3-4 slices of brain to illustrate a single module. The right column displays the corresponding ICA components. Examples when 1, 2 and 3 modules matched with a single component are shown in panels A, B and C respectively. Only pertinent slices of the brain were displayed in each case.
We ran simple a simple fast greedy modularity-based (FGMB) algorithm (Clauset et al., 2004) based on a hard thresholded correlation matrix and found that generally very few modules resulted in these networks. Specifically, with a hard threshold of 0.5 on raw correlations an average of 5 FGMB modules were found across our 16 subjects. On average, each WVCNA module was 86% contained within a single FGMB module, indicating the WVCNA modules are a finer subdivision of the larger FGMB modules.
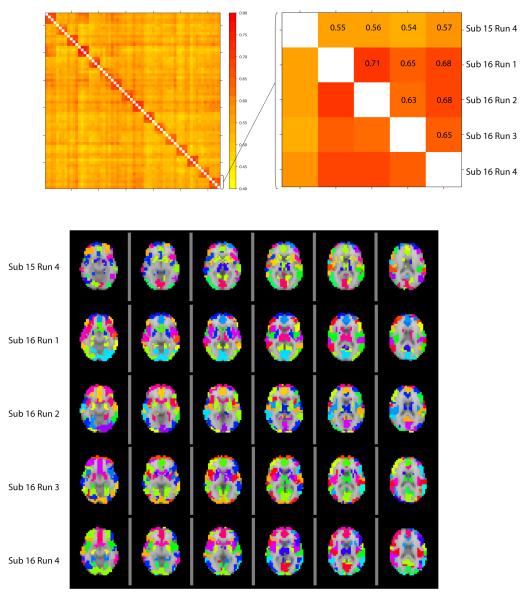
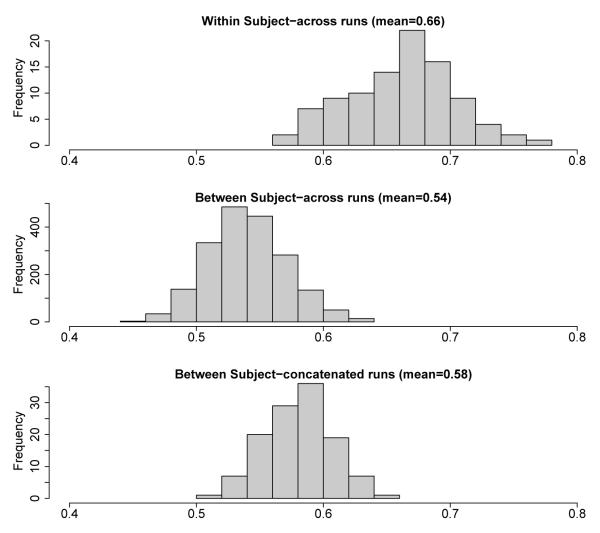
As described in the methods section, modules were compared between runs using the normalized mutual information measure. There were 16 subjects with 4 runs each, which yields the 64 × 64 similarity matrix shown in the top left panel of Figure 6. Larger values of the measure indicate higher levels of similarity and since each run has a similarity of 1 with itself, the diagonal elements are left blank. The entries are grouped by subject, so the bright red blocks along the diagonal illustrate that the module sets across runs within subject are more similar than between subject comparisons. The top right panel of Figure 6 shows a magnification of the lower right-hand corner of the similarity matrix, comparing the last 5 runs. Although the similarities are lower comparing the fourth run of subject 15 to the runs of subject 16, the images of the modules in the bottom of Figure 6 show that the module sets between subjects are still quite similar. Another view of this comparison is shown in the histograms in Figure 7. The top panel shows the distribution of the unique pairwise comparisons between runs within subject (within the blocks along the diagonal). The middle panel looks at the distribution of the normalized mutual information between runs between subjects (unique pairs only). The mean of this distribution is less than that of the runs within subject, indicating that the modules are more similar within subject than between. After concatenating runs and calculating the modules, comparisons were made between subjects (bottom panel) showing that after concatenation of runs the resulting modules are more similar than the individual runs were between subject. Using the same number of modules and module sizes as in the 16 subject specific module sets, random networks were found to have an average normalized mutual information of 0.07 over all pairwise comparisons. This is significantly different than the pairwise comparisons of the 16 subjects, which had a normalized mutual information of 0.58 (Kolmogorov-Smirnov test, D=1, P< 2 −16).
Figure 6.
The top left panel shows the normalized mutual information measures between modules for each specific run. The red blocks along the diagonal illustrate that the four runs within each subject create modules that are more similar to each other than modules from runs of other subjects and the blocks along the diagonal are left blank since a module set matches itself exactly. The top right panel is a magnification of the bottom corner of the first matrix and illustrates the normalized mutual information values. To gain intuition about the similarity measure, the bottom panel illustrates the module sets for these 5 runs. Note the colors in each image are arbitrary.
Figure 7.
Histograms showing the distribution of normalized mutual information measures between modules across runs within subjects (top) across runs between subjects (middle) and across subjects when using concatenated runs (bottom). The modules within subject are most similar to each other and the between subject similarities using concatenated runs are more similar than the separate runs (bottom vs. middle).
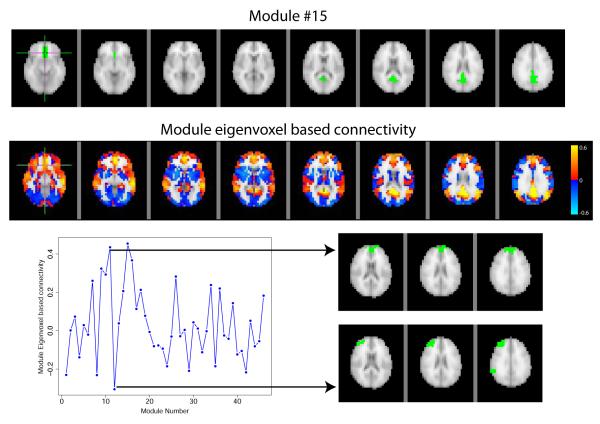
An illustration of the use of the eigenvoxel based connectivity is shown for a single subject (data over all four runs concatenated) in Figure 8. The top panel of the figure shows the location of module #15 and the middle panel shows the eigenvoxel based connectivity between all voxels and the eigenvoxel for module #15, where blue and red correspond to negative and positive correlations, respectively. The bottom panel focuses on the eigenvoxel based connectivity for a single voxel in module #15 (marked by the green hash in the top two panels) across all eigenvoxels for the 46 second stage meta-modules. Although this voxel is strongly connected to the module to which it is assigned (#15, corr=0.45), it is also strongly correlated with module #11 (corr=0.44) and negatively correlated with module #12 (corr=−0.31). Arrows point from the correlation in the bottom left to the module locations on the bottom right.
Figure 8.
Module membership for meta module #15. The top image shows the module of interest (#15) and the middle image shows the module eigenvoxel based connectivity for all voxels compared to module 15. In addition to looking at how voxels are related to a single module, the bottom panel also shows how a single voxel’s connectivity to other modules can be studied. Focusing on a voxel located within module #15 (indicated by crosshairs), this voxel is not only strongly correlated with the eigenvoxel from the module it belongs to (cor=0.45), but is also strongly correlated with the 11th module eigenvoxel (corr=0.44) and negatively correlated with the 12th module eigenvoxel (cor=−0.31). The bottom panel illustrates the module eigenvoxel based connectivity for this voxel and the arrows point to images of the 11th and 12th modules.
Recall that one of the goals of WVCNA is to parcellate the brain into functionally distinct regions in a data reduction step prior to running a network analysis. To illustrate that WVCNA modules are fit for this purpose we took the eigenvoxels from the 46 second level meta modules from a single subject and entered them in a standard network analysis. First pairwise correlations were calculated between the meta module eigenvoxels and then thresholded so that only connections with correlation magnitudes above 0.5 were considered connected. This binary adjacency matrix was then used in a greedy modularity-based approach for community detection (Clauset et al., 2004) and the resulting network is illustrated in Figure 9. The nodes represent second level meta-modules and are labeled according to their locations, where labels beginning with R/L indicate unilateral modules. The colors of the nodes correspond to the communities that were found using the community detection algorithm and show reasonable groupings of meta-modules according to spatial locations. Results from this network analysis thus support the usefullness of WVCNA as a data reduction step for identifying regions for use in a network analysis.
Figure 9.
An illustration of the use of the second level meta-modules. The WVCNA second level meta-module eigenvoxels were entered into a network analysis to see if eigenvoxels clustered in a meaningful way. In this case the eigenvoxels were correlated and using a hard threshold of 0.5 to create a hard threshold adjacency measure that was used in the greedy modularity-based method of community detection (Clauset et al., 2004), which identified the communities illustrated by the colors of the nodes. The labels on the nodes indicate where the meta-modules were located and illustrate that reasonable groups of modules are created in this analysis. If a label does not lead with a hemispheric label (R/L) the module was bilateral. Note that singletons have been removed from the graph.
4 Discussion
In this study we present a novel approach for clustering the brain into functionally related modules, based on resting state fMRI time series. This approach, the weighted voxel coactivation network analysis, is different from other approaches that find correlated clusters of voxels in many different ways. First, the modules that are identified are non-overlapping, leading to a parcellation of the brain into functionally distinct regions. Secondly, unlike ICA, this approach has been developed in the small world network framework, which has been shown to be an appropriate framework for fMRI networks. Additionally, WVCNA does not require that the modules are spatially or temporally independent, as it is assumed in ICA. Also, unlike alternative methods that use a hard threshold of pairwise correlations, this approach uses a weighted network approach using the topological overlap measure with soft thresholding. The topological overlap measure is somewhat similar to a measure used in a parcellation approach based on diffusion tensor imaging, where a set of seed voxels were correlated with all other voxels and then the seeds were split into two groups based on the correlation of the correlation profiles (Johansen-Berg et al., 2004). The modules are found using the dynamic tree cutting algorithm (Langfelder et al., 2008), which does not require a single cutoff for the hierarchical tree. Another benefit of WVCNA is that there are different network metrics that can be used to assess voxels as they are related to the modules that they are located in and other modules.
Our results illustrate that the modules found using WVCNA are similar to components found using ICA. On average, 79% of the module/component groupings consisted of a single module with a single component. Typically, in these cases, the module tended to be more spatially focused than the component. On average, in 19.2% of the matches, two modules were paired with the same ICA component and in a small number of other cases 3-5 modules were paired with the same component. As shown in the bottom two panels of Figure 5 when multiple modules are paired with a single component it is possible that the modules are separating out functionally distinct parts of the component. For example, in the bottom panel it is evident that whereas ICA collapses a large set of prefrontal regions into a single component, WVCNA separates these regions (e.g., anterior cingulate and dorsolateral prefrontal cortex, which are known to have distinct functions).
In order to verify that WVCNA consistently identifies modules, we examined the normalized mutual information measure for all pairs of module sets across all runs and all subjects. As Figure 6 shows, the similarity is much higher within subject and slightly lower across subjects. Additionally Figure 7 shows that similarity is highest between runs within the same subject and lowest between runs between subjects.
The similarity between subjects of the concatenated runs is higher that the between run between subject similarity, which is due to higher power in the concatenated runs data analysis. These comparisons using the normalized mutual information measure show that the consistency across modules follows a pattern expected based on previous knowledge about the sources of variability in fMRI data. Preliminary analyses have found that, despite the relatively lower agreement across subjects, it is possible to meaningfully align modules across subjects; these results will be expanded in a future publication.
Our results also illustrate the use of module eigengene based connectivity measures for assessing how central certain voxels are within a module and whether a voxel is solely related to a single module or if it is equally related to multiple modules. The metrics of WVCNA are another benefit over ICA.
Since one use of WVCNA would be to use it as a data reduction technique for identifying regions to use in a separate network analysis, we illustrate the use of second level metamodule eigenvoxels in a standard network analysis, where correlations were thresholded and used in a modularity algorithm for detecting communities (Clauset et al., 2004). Our network result, shown in Figure 9 illustrates that WVCNA can indeed be used to suit this purpose.
One of the innovations in the present study was the use of weighted networks rather than hard thresholding; the only previous examination of of weighted networks for fMRI analysis (Achard and Bullmore, 2007) found that weighted networks and hard thresholding produced similar networks, but there has been relatively little examination of this question. Previous work comparing hard-threshold and weighted network approaches to gene expression network analysis also found that similar networks were obtained using the two approaches. However, an important difference was found in the robustness of the approaches. The choice of the correlation threshold in a hard-threshold analysis is analogous to the choice of the adjacency parameter, β, in the present approach. Zhang and Horvath (2005) used the same small world criteria that were used to select β in the present analysis to select hard thresholds as well, specifically choosing a threshold for which the power law distribution was satisfied with high mean connectivity. Although this work also showed similar networks could be derived from both approaches, the major difference between the hard and soft thresholding techniques was in how robust measures, such as intramodular connectivity, were to misspecification of β and the hard threshold. They found that the measure of weighted intramodular connectivity for a gene, defined as g=wi = ∑j ωij, where ωij is the topological overlap between two genes, was robust to misspecification of the adjacency parameter β, whereas the hard threshold criteria only had a small window over which the intramodular connectivity measure performed well.
There have been applications of other graph theoretical methods for whole brain parcellation into functional regions based on resting state fMRI (van den Heuvel et al., 2008; Shen et al., 2010). van den Heuvel et al. (2008) also used a weighted network approach via the normalized cut algorithm (Shi and Malik, 2000) and compare to ICA results from other studies. In contrast, our work compared ICA results to the WVCNA results directly using analyses on the same data sets. Shen et al. (2010) compare the normalized cut algorithm, Gaussian mixture models and a modularity detection algorithm. In order to make direct comparisons between methods, simulated data with two distinct regions as well as a real data analysis parcellated into two regions were studied to rank these methods from best to worst, finding the normalized cut algorithm to work the best. Although this ranking of the methods is useful, it is limited in that the approach only looked at cases where a single region was divided into two functionally distinct sets. On the other hand, the WVCNA method proposed here divides the brain into multiple modules and by using the normalized mutual information measure we compared sets of parcellations with multiple regions. In addition, methods such as Gaussian mixture models, the normalized cut algorithm and modularity-based community algorithms favor larger modules (van den Heuvel et al., 2008; Newman, 2006; Fortunato, 2010; Meunier et al., 2009), whereas WVCNA is capable of finding both large and small modules. For example, our network analysis results using a fast greedy modularity-based (FGMB) algorithm using a hard thresholded correlation matrix resulted in large modules such that single FGMB modules tended to almost fully contain the smaller WVCNA modules (on average 86% was contained). For the normalized cut algorithm, an important consideration is that it requires the specification of the number of regions, which is an unknown quantity.
As a caveat of our network construction approach we should point out that it is not yet clear whether a functional connectivity matrix is best modelled using a scale free network. Whether functional connectivity in the human brain is scale-free or not remains an open question. Future research evaluating many functional connectivity matrices should provide empirical evidence that (approximate) scale free topology is a reasonable assumption. While scale-free networks have small-world properties of brain networks, it is entirely possible to create small-world networks that are not scale-free (see, e.g. the original Watts-Strogatz model). We are not aware of a neurobiological justification for scale free topology. The scale free topology criterion provides a heuristic for choosing the value of the power parameter. It has led to meaningful biological results in dozens of genetic applications but there are situations in which it is not meaningful (as described in the methods) A major advantage of weighted networks (visa vis unweighted networks) is that weighted networks are highly robust with regard to the parameter choice, i.e. very similar modules result for different choices of the power beta.
In conclusion, we have shown that it is possible to detect localized and functionally coherent brain regions from resting state fMRI data in an unsupervised manner, using methods originally designed to analyze gene expression data. The methods described here could potentially improve the modeling of large-scale brain networks by providing more biologically plausible specifications for the regions that enter into network analyses. Further work is necessary to establish the degree to which these methods can identify common modules between individuals.
Acknowledgments
This work was supported by NIH grants UL8UL1DE019580-04 and PL1MH083271 and the Office of Naval Research grant N00014-07-1-0116.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Achard S, Bullmore E. Efficiency and cost of economical brain functional networks. PLoS Comput. Biol. 2007;3:e17. doi: 10.1371/journal.pcbi.0030017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 2006 Jan;26:63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert R, Jeong H, Barabasi AL. Error and attack tolerance of complex networks. Nature. 2000;406:378–382. doi: 10.1038/35019019. [DOI] [PubMed] [Google Scholar]
- Barabasi AL, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- Barabasi AL, Oltvai ZN. Network biology: understanding the cell’s functional organization. Nat. Rev. Genet. 2004;5:101–113. doi: 10.1038/nrg1272. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Bullmore E. Small-world brain networks. Neuroscientist. 2006;12:512–523. doi: 10.1177/1073858406293182. [DOI] [PubMed] [Google Scholar]
- Beckmann CF, DeLuca M, Devlin JT, Smith SM. Investigations into resting-state connectivity using independent component analysis. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 2005;360:1001–1013. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, Smith SM. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Trans Med Imaging. 2004;23:137–152. doi: 10.1109/TMI.2003.822821. [DOI] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Clauset A, Newman ME, Moore C. Finding community structure in very large networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;70:066111. doi: 10.1103/PhysRevE.70.066111. [DOI] [PubMed] [Google Scholar]
- Cohen AL, Fair DA, Dosenbach NU, Miezin FM, Dierker D, Van Essen DC, Schlaggar BL, Petersen SE. Defining functional areas in individual human brains using resting functional connectivity MRI. Neuroimage. 2008;41:45–57. doi: 10.1016/j.neuroimage.2008.01.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damoiseaux JS, Rombouts SA, Barkhof F, Scheltens P, Stam CJ, Smith SM, Beckmann CF. Consistent resting-state networks across healthy subjects. Proc. Natl. Acad. Sci. U.S.A. 2006;103:13848–13853. doi: 10.1073/pnas.0601417103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLuca M, Beckmann CF, De Stefano N, Matthews PM, Smith SM. fMRI resting state networks define distinct modes of long-distance interactions in the human brain. Neuroimage. 2006;29:1359–1367. doi: 10.1016/j.neuroimage.2005.08.035. [DOI] [PubMed] [Google Scholar]
- Dosenbach NU, Fair DA, Miezin FM, Cohen AL, Wenger KK, Dosenbach RA, Fox MD, Snyder AZ, Vincent JL, Raichle ME, Schlaggar BL, Petersen SE. Distinct brain networks for adaptive and stable task control in humans. Proc. Natl. Acad. Sci. U.S.A. 2007;104:11073–11078. doi: 10.1073/pnas.0704320104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortunato S. Community detection in graphs. Physics Reports. 2010;486:75–174. [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci. U.S.A. 2005;102:9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Raichle ME. Intrinsic fluctuations within cortical systems account for intertrial variability in human behavior. Neuron. 2007;56:171–184. doi: 10.1016/j.neuron.2007.08.023. [DOI] [PubMed] [Google Scholar]
- Greicius MD, Krasnow B, Reiss AL, Menon V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc. Natl. Acad. Sci. U.S.A. 2003;100:253–258. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyvarinen A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans Neural Netw. 1999;10:626–634. doi: 10.1109/72.761722. [DOI] [PubMed] [Google Scholar]
- Jafri MJ, Pearlson GD, Stevens M, Calhoun VD. A method for functional network connectivity among spatially independent resting-state components in schizophrenia. Neuroimage. 2008;39:1666–1681. doi: 10.1016/j.neuroimage.2007.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5 doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Johansen-Berg H, Behrens TE, Robson MD, Drobnjak I, Rushworth MF, Brady JM, Smith SM, Higham DJ, Matthews PM. Changes in connectivity profiles define functionally distinct regions in human medial frontal cortex. Proc. Natl. Acad. Sci. U.S.A. 2004;101:13335–13340. doi: 10.1073/pnas.0403743101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuncheva L. Combining pattern classi ers: methods and algorithms. Wiley; 2004. [Google Scholar]
- Langfelder P, Horvath S. Eigengene networks for studying the relationships between co-expression modules. BMC Syst Biol. 2007;1:54. doi: 10.1186/1752-0509-1-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langfelder P, Zhang B, Horvath S. Defining clusters from a hierarchical cluster tree: the Dynamic Tree Cut package for R. Bioinformatics. 2008;24:719–720. doi: 10.1093/bioinformatics/btm563. [DOI] [PubMed] [Google Scholar]
- Liu Y, Liang M, Zhou Y, He Y, Hao Y, Song M, Yu C, Liu H, Liu Z, Jiang T. Disrupted small-world networks in schizophrenia. Brain. 2008;131:945–961. doi: 10.1093/brain/awn018. [DOI] [PubMed] [Google Scholar]
- Mason MJ, Fan G, Plath K, Zhou Q, Horvath S. Signed weighted gene co-expression network analysis of transcriptional regulation in murine embryonic stem cells. BMC Genomics. 2009;10:327. doi: 10.1186/1471-2164-10-327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meunier D, Lambiotte R, Fornito A, Ersche KD, Bullmore ET. Hierarchical modularity in human brain functional networks. Front Neuroinformatics. 2009;3:37. doi: 10.3389/neuro.11.037.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman ME. Modularity and community structure in networks. Proc. Natl. Acad. Sci. U.S.A. 2006;103:8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabsi AL. Hierarchical organization of modularity in metabolic networks. Science. 2002;297:1551–1555. doi: 10.1126/science.1073374. [DOI] [PubMed] [Google Scholar]
- Salvador R, Suckling J, Coleman MR, Pickard JD, Menon D, Bullmore E. Neurophysiological architecture of functional magnetic resonance images of human brain. Cereb. Cortex. 2005;15:1332–1342. doi: 10.1093/cercor/bhi016. [DOI] [PubMed] [Google Scholar]
- Shen X, Papademetris X, Constable RT. Graph-theory based parcellation of functional subunits in the brain from resting-state fMRI data. Neuroimage. 2010 doi: 10.1016/j.neuroimage.2009.12.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi J, Malik J. Normalized cuts and image segmentation. IEEE Transactions on pattern analysis and machine intelligence. 2000;22:17. [Google Scholar]
- van den Heuvel M, Mandl R, Hulshoff Pol H. Normalized cut group clustering of resting-state FMRI data. PLoS ONE. 2008;3:e2001. doi: 10.1371/journal.pone.0002001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yip AM, Horvath S. Gene network interconnectedness and the generalized topological overlap measure. BMC Bioinformatics. 2007;8:22. doi: 10.1186/1471-2105-8-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B, Horvath S. A general framework for weighted gene co-expression network analysis. Stat Appl Genet Mol Biol. 2005;4 doi: 10.2202/1544-6115.1128. Article17. [DOI] [PubMed] [Google Scholar]