Linking human brain local activity fluctuations to structural and functional network architectures

Abstract

Activity of cortical local neuronal populations fluctuates continuously, and a large proportion of these fluctuations are shared across populations of neurons. Here we seek organizational rules that link these two phenomena. Using neuronal activity, as identified by functional MRI (fMRI) and for a given voxel or brain region, we derive a single measure of full bandwidth brain-oxygenation-level-dependent (BOLD) fluctuations by calculating the slope, α, for the log-linear power spectrum. For the same voxel or region, we also measure the temporal coherence of its fluctuations to other voxels or regions, based on exceeding a given threshold, Θ, for zero lag correlation, establishing functional connectivity between pairs of neuronal populations. From resting state fMRI, we calculated whole-brain group-averaged maps for α and for functional connectivity. Both maps showed similar spatial organization, with a correlation coefficient of 0.75 between the two parameters across all brain voxels, as well as variability with hodology. A computational model replicated the main results, suggesting that synaptic low-pass filtering can account for these interrelationships. We also investigated the relationship between α and structural connectivity, as determined by diffusion tensor imaging-based tractography. We observe that the correlation between α and connectivity depends on attentional state; specifically, α correlated more highly to structural connectivity during rest than while attending to a task. Overall, these results provide global rules for the dynamics between frequency characteristics of local brain activity and the architecture of underlying brain networks.

Introduction

Relating structure and function is fundamental to understanding the mechanisms of information processing in the brain. Non-invasive functional brain imaging, specifically MRI/fMRI, has played a pivotal role in demonstrating structure-function rules due to its capability to localize activity and relate it to structural features across the whole brain, on the scale of millimeters. Recent studies examining brain activity during rest demonstrate large-scale functional organizational rules, thus revealing intrinsic dynamical properties of the brain (1). Likewise, functional connectivity (FC) of the brain during rest shows correspondences to structural connectivity (SC), although this relationship is intricate and not reciprocal -- i.e., SC is highly indicative of FC, but not vice versa (2–5). Still, rules with which structural and functional networks shape and constrain each other remain fundamental, unanswered questions in the field.

The power spectrum of brain activity signals is related to various network properties. This relationship has been captured across many studies using multiple methods such as fMRI (6, 7), EEG (8), cultured neuronal networks (9, 10), multi-unit activity (11), simultaneous single-unit recording and optical imaging (12), and computational models (13). These results have highlighted the central role of the spectral profile in understanding the structure-function interactions in the brain. However, most fMRI research has utilized only the low frequency component of the BOLD signal, assuming that frequencies above 0.1 Hz are contaminated with noise. On the other hand, BOLD frequencies above 0.1 Hz exhibit coherent patterns of activity (14) and show an anatomically constrained distribution of power as a function of BOLD frequency (15). Therefore, it remains largely unknown how the full bandwidth properties of the BOLD signal relate to brain network properties. Here we aim to show that the architecture of synchronous brain networks and white matter networks (structure) are tightly related to the fluctuations of local BOLD activity (function).

In the frequency domain, the full bandwidth power spectrum of fMRI BOLD signal (approximately 0–0.24 Hz) roughly follows a straight line when viewed in log power versus frequency: log (P) = -α(f). The value (α) offers a glimpse of the distribution of power across frequencies, and in a sense it provides some information about the heterogeneity of the informational content that is observed locally. The larger the absolute value of α, the higher the relative power at lower frequencies in the signal, whereas smaller values suggest that the fluctuations are more random, with less temporal redundancy, and are therefore more efficient in online information processing (16, 17). Here we examine the relationship between α and FC, i.e., the presence of temporal coherence of BOLD activity, as well as α and SC, i.e., the presence of anatomical connectivity based on diffusion tensor imaging probabilistic tractography, for fMRI activity during either resting state or during a visual-motor attention task. We assess this relationship at different spatial resolutions and as a function of its underlying regional synaptic wiring. First, we test the hypothesis that the distribution of power in local fluctuations, at a per voxel basis, is related to the number of functionally connected voxels across the whole brain. Second, we parcel the brain into 3 anatomical regions of differing hodology that correspond to synaptic wiring and functional complexity (including unimodal, heteromodal, and limbic-paralimbic regions (18)), and we examine differential relations between the power of local fluctuations and FC. Third, to our knowledge, the MRI structure-function studies have solely relied on resting scan conditions, perhaps due to the growing evidence that functional networks during rest and task are spatially (19, 20) and dynamically(21) similar. Previous work from our lab, however, counters this notion by demonstrating widespread shifts in BOLD frequency power between rest and task conditions (15). Here we demonstrate that BOLD power is differentially related to network architecture according to brain state, i.e., during rest versus attending to task. The significance of such an investigation lies in its potential to provide global rules for the dynamics between the spectral characteristics of local brain activity in relation to the architecture of underlying brain networks, as well as in relation to brain state.

Methods

Subjects

Thirty healthy participants (21 females, 40.2 ± 2.1 years old) were scanned for the high-spatial resolution voxel-wise mapping of α. A different set of 21 healthy subjects (18 females, 39.4 ± 2.4 years old) participated in a separate experiment that included a resting state scan, a task scan, and diffusion tensor imaging, for which analysis was performed at a lower spatial resolution at the level of brain regions that approximately equaled Brodmann areas (BAs). All subjects were right-handed and provided informed consent to procedures that were approved by the Northwestern University Institutional Review Board.

fMRI Acquisition

Whole-brain functional MR data was acquired with a 3T Siemens TIM Trio whole-body scanner with echo-planar imaging (EPI) capability. An 8-channel head coil optimized for prefrontal cortical activity was used. Multi-slice T2*-weighted echo-planar images were obtained with the following parameters: TR = 2.5 s, echo time TE = 30 ms, flip angle = 90°, slice thickness = 3 mm, in-plane resolution = 3.475×3.475 mm². The 36 slices covered the whole brain from the cerebellum to the vertex. Scans for the voxel-wise analysis were 300 volumes and lasted 12 minutes. Scans for the BA analysis lasted 10 minutes with 244 volumes.

For resting scans, participants were asked only to stay alert with their eyes open. Task scans required participants to rate the length of a bar fluctuating at ~0.01 to 0.05 Hz along an axis numbered 0 to 100. The bar was projected onto the screen in the scanner, and subjects continually rated its length as the bar moved by spacing their right thumb and forefinger, to which a voltage potentiometer recording device was attached with tape (22). For example, if the bar reached a height of 100, subjects had their thumb and forefinger tips as far apart as possible. If the bar dipped to 0, their fingertips were touching. Prior to scanning, subjects were trained on the task. All subjects performed the task such that their finger movements were highly correlated with the visual bar movement (r > 0.7 for all subjects).

Anatomical Scans

In addition to the functional scans, a T1-weighted anatomical MRI image was also acquired for each subject using the following parameters: TR = 2.1 s, TE = 4.38 ms, flip angle = 8°, FOV = 220 mm, slice thickness = 1 mm, in-plane resolution = 0.86 × 0.86 mm² and number of sagittal slices = 160.

DTI

Images were acquired using spin-echo EPI in one acquisition of 72 slices, covering the whole brain. DTI parameters were as follows: voxel size 2 × 2 × 2 mm; TR, 5000 ms; TE, 87 ms; flip angle = 90°; in-plane matrix resolution, 128 × 128; field of view, 256 × 256 mm; b0, 1000 s/mm². Diffusion was measured in 60 distinct, non-collinear directions, separated in time, into seven groups by no-diffusion weighted volumes. A total of eight no-diffusion weighted volumes were acquired for the purposes of registration and head motion correction. Preprocessing of DTI images was performed using FDT version 2.0 (FMRIB diffusion toolbox), part of FSL (FMRIB's Software Library, www.fmrib.ox.ac.uk/fsl), and included eddy current correction, head motion correction using affine registration to the reference volumes, and skull extraction.

BEDPOST (Bayesian Estimation of Diffusion Parameters Obtained using Sampling Techniques) was performed for each subject, which performs Markov-chain Monte Carlo sampling to establish distributions on the diffusion parameters at each voxel in the individual subject's space (23) . Probabilistic tractography was then performed for 6×6×6 mm centers of brain regions identified by the standard Automated Anatomical Labeling (AAL) map (24) and transformed into subject space. AAL regions are roughly equivalent to the classically defined BAs. We therefore refer to our brain regions as BAs. For each of the 21 subjects and from each BA, 5000 samples were drawn to build the a posteriori distribution of the whole brain connectivity distribution.

fMRI Data Preprocessing

Functional MRI data was preprocessed using FEAT (FMRI Expert Analysis Tool) Version 5.98, part of FSL. Preprocessing steps included: skull extraction, slice-timing correction, bulk head motion correction, spatial smoothing (Gaussian kernel of full-width-half-maximum 5mm), and a high-pass (150 sec) temporal filter, which removes artifacts associated with scanner drift at fluctuations less than 0.006 Hz. Peak to peak head motion was maintained at < 3 mm for all subjects. Independent component analysis was performed using MELODIC, and temporal and spatial components associated with motion, cerebrospinal fluid, and white matter were identified and their time courses were regressed out of the BOLD signal as covariates of no interest. Global mean BOLD signal and head motion were also regressed from the BOLD signal, voxel-wise.

Connectivity analysis (voxel-wise)

Subject connectivity maps were created in subject space by calculating pairwise BOLD time-series Pearson correlations for every gray matter voxel in the brain and counting the number of correlations greater than or equal to a predefined correlation threshold, Θ. This approach examines properties of local fluctuations in relation to the local, as well as long distance, architecture of the brain. Most voxel-wise results are reported at Θ = 0.3, as this threshold corresponds to a p-value <0.01 after correction for degrees of freedom using Bartlett theory. Therefore each voxel in a connectivity map corresponds to the number of voxels to which it has a time series correlation greater than 0.3. Results for Θ = 0.4 and 0.5 are reported in the supplementary materials. Mean group maps were generated by transforming subject maps to standard space, z-scoring, and averaging across subjects.

Connectivity analysis (Brodmann areas)

In a separate data set, we calculated FC and SC at a lower spatial resolution using grossly segregated brain regions, roughly equivalent to Brodmann areas (we refer to AAL regions as Brodmann areas, BAs). At this spatial resolution, we explored the relationship between BOLD fluctuations and the long-distance architecture of the brain. Functional images were registered to 2×2×2 mm voxel standard space using FLIRT (25). The mean time series from the 6×6×6 mm centers of each BA were extracted, and thus each time series consisted of the average BOLD signal from 27 standard space voxels. Subcortical BAs were excluded from the analysis, resulting in 82 BAs for each subject. A list of BAs with center coordinates is provided in table S1. Previous studies used slightly different classifications of BAs (table S2), particularly with unimodal BAs, but are overall consistent with the present study. Connection matrices were generated for each hemisphere separately, and all subsequent measures were averaged across hemispheres using custom Matlab routines (The Math Works, 2009). Pearson correlations were calculated pair-wise for all time series and transformed to Fisher’s z values, creating a 41×41 functional connection matrix for each subject.

Structural connection matrices were constructed based on probabilistic tractography. Similar to the functional connection matrices, structural connection matrices were generated using only the intrahemispheric connections, and all subsequent measures were averaged across hemispheres. The number of tractography counts from the 6×6×6 mm center of each BA to all other BAs was used to generate a 41×41 structural connection matrix for each subject. Because the tractography between 2 BAs is not reciprocal, matrices were symmetrized by averaging the number of counts between each pair of BAs. These matrices were then logarithmically transformed (to normalize the distribution of counts) and then normalized by dividing the number of counts at each element by the total number of counts to each BA from all other BAs.

Functional and structural connection matrices were multiplied by a matrix of normalized distances between pairs of nodes. Given the reduced degrees of freedom in the BA analysis, we were able to report FC and SC across a range of connection strength thresholds, as different network metrics can be threshold sensitive. We report these thresholds according to matrix ‘link densities’, which reflect the total proportion of connections in a matrix that exceed the given correlation threshold, Θ. Therefore, when the threshold for a connection is high, there will be fewer total connections in a matrix, which will thus correspond to a lower link density value. Accordingly, the connection matrices were thresholded and binarized such that the number of links in each connection matrix corresponded to all link densities, ranging from 0.4 to 0.2, as suggested by (26). All graph theory metrics were obtained in Matlab using scripts from the Brain Connectivity Toolbox (27). BAs were categorized as unimodal, heteromodal, or limbic-paralimbic, accordingly (18).

Determining fit of the BOLD power spectrum

Spectral analysis was carried out using custom Matlab routines. Frequency power of BOLD time courses were determined using Welch’s method and normalized by dividing by total power (total power/variance=1) (15). Least-squares fitting was then performed on the normalized power spectrum from 0.01 to 0.2 Hz in 500 random voxels in each subject, expressed on either linear, log-linear, or log-log axes:

• linear: P(f) = −α(f)

• log-linear: log(P(f)) = −α(f)

• log-log: P(f) = 1/f^α

where P is the power at frequency f. To test for goodness of fit, Kolmogorov-Smirnov distance (D) was calculated between the power spectrum and the least-squares regression (17). The average D was calculated across voxels and subjects, and the lowest value determined the scale of the power spectrum on which α was defined (figure S1).

Spectral power distribution in the brain

Values of α were obtained for every voxel in the brain. For the voxel-wise experiment, individual subject maps were transformed into standard space using FLIRT (25) and multiplied by a standard gray matter mask. Subject maps were then z-scored by subtracting the whole brain mean and dividing by the standard deviation. A group average α map was then generated by averaging maps voxel-wise across subjects. The α value was also calculated for each BA in the separate BA analysis. Negative α values were considered to indicate artifacts and were removed from the analyses. As a result, less than 1% of the data was removed.

Correlation between connectivity and α

For the voxel-wise analysis, Pearson correlations were calculated between group mean α and functional connectivity maps. To determine the significance of the correlation between α and FC maps, surrogate data was generated by spatially shuffling the group mean FC map with wavelet resampling (28) 5000 times. The Pearson correlation between the z-scored α map and z-scored resampled map was calculated with each iteration, generating a null distribution of α-FC correlations. Additionally, we tested the dependence of this relationship on the temporal pattern of BOLD activity by randomly shuffling the phase of BOLD time series in Fourier space. Connectivity maps were then generated from shuffled data (θ = 0.3), transformed to standard space, and averaged across subjects. Pearson correlations were then calculated between the group mean z-scored α and the group mean temporal surrogate z-scored connectivity maps.

For the BA experiment, Pearson correlations were calculated between α and connection metrics across all link density thresholds and transformed to Fisher’s z values. Therefore, all correlations reported refer to Fisher’s z. Significance was determined by comparing α correlation with experimental versus null connection matrices of equal link density and degree distribution. However, in to the case where we compare node degree of experimental networks to null networks, we generated null networks with a random degree distribution by thresholding symmetrical matrices with a random distribution of connection strengths.

Throughout the article, we refer to the correspondence between α and connectivity as either α-FC (α-functional connectivity) or α-SC (α-structural connectivity).

Linear discriminant analysis

To measure the accuracy of the characterizations of our 3 synaptic categories (unimodal, heteromodal, or limbic-paralimbic) based on α, FC, and their correlation, we employed linear discriminant analysis (LDA) using a k-nearest-neighbor classifier algorithm with a city-block distance metric. This analysis was performed using a leave-one-out algorithm such that classification for each subject (i.e., the sample set) was tested against our designated categorization of BAs (i.e., the training set). In other words LDA was performed for each subject, and the classification for each BA based on its α, FC, and their correlation was tested against the designated BA classification and the corresponding-BA group average of α, FC, and their correlation, of the remaining subjects. Confusion matrices were then generated for each subject, which demonstrate the accuracy by which synaptic wiring corresponds to α, FC, and their correlation.

To test whether the accuracy of classification was unique to our designated synaptic wiring categories, we repeated the same analyses with BAs designated into different groups based on either 1) their relative spatial distance from each other, or 2) random assignment. To categorize BAs based on their relative spatial distance, k-means clustering was used to identify 3 clusters in the BA distance matrix, defined by the pair-wise Euclidean distances between all BAs. As k-means clustering was implemented with random initial centroids, 5000 iterations were performed, and the resulting confusion matrices were averaged across all iterations for each subject. Null classification was performed in the same manner, except the categorization of BAs was randomly shuffled. Confusion matrices were generated for each subject using the same leave-one-out algorithm mentioned above. The reported values in all confusion matrices are expressed in percentages that indicate the fraction of BAs for each designated category that were classified as either unimodal, heteromodal, or limbic-paralimbic. For example, the top row of our confusion matrices indicate what percentage of unimodal BAs were classified as unimodal (column 1), heteromodal (column 2) or limbic-paralimbic (column 3). Comparisons across the categorization schemes were performed using repeated measures ANOVA. BAs with a negative correlation between α and FC were excluded from the analysis, as it was determined to be a fitting artifact (table S1).

Model for the correlation between connectivity and spectral content in fMRI

Basic model

It is possible to interpret the observation of a strong correlation between the degree of functional and anatomical connectivity and the exponent of the power-law behavior of the spectrum in qualitative terms: if we assume that the activity of a neural ensemble represents effectively a low-pass filter of its inputs, then the relative spectral content of its output will be highly colored towards lower frequencies as a function of their connectivity. More formally, consider the activity of a neural ensemble as

$$\vec{x}(t)=F(\vec{V})+\vec{g}(t)$$ (1)

where the components of x⃗ represent the activity of the ensembles, F is a low-pass linear filter such that in Fourier space F̃(ω_L) > F̃(ω_H) if ω_L < ω_H,the components of V⃗ are the total synaptic input:

$$V_n(t)=\mu {\mathrm{\Sigma }}_m{A}_{nm}{x}_m(t)$$ (2)

with A representing the connectivity matrix, the components of g⃗ the intrinsic driving activity, and μ the coupling parameter. Transforming the equation into Fourier space, we obtain

$$\vec{\tilde{x}}(\omega )=\mu A{\tilde{F}}^{*}(\omega )\vec{\tilde{x}}(\omega )+\vec{\tilde{g}}(\omega )$$ (3)

where * indicates complex conjugation, and the low-pass filter operation becomes a simple multiplication. Upon rearranging terms, Eq. 3 becomes

$$\vec{\tilde{x}}(\omega )={(I-\mu A{\tilde{F}}^{*}(\omega ))}^{-1}\vec{\tilde{g}}(\omega )$$ (4)

To derive a more intuitive understanding of this equation, we introduce a few simplifications: assuming a constant phase response for the filter (i.e. its effect is only to reduce the power of high frequencies, without phase distortions), a binary connectivity matrix (i.e. A ={0,1}), a homogenous intrinsic activity spectrum g̃_n(ω) = g̃(ω) ∀n (the internal drivers have all the same power profile) and expanding in the coupling parameter μ, we obtain

$$|{\tilde{x}}_n(\omega )|=|\tilde{g}(\omega )|+\mu D_n\tilde{F}(\omega )|\tilde{g}(\omega )|+0({\mu }^2)$$ (5)

Where D_n = Σ_j A_nj is the degree of node n. Eq. 5 immediately reflects the relationship between connectivity and spectral content in the model: for a low-pass filter, lower frequencies will contribute to the spectral distribution proportionally to the local connectivity, whereas for higher frequencies the spectrum will be proportional to that of the intrinsic activity, in accord to the observed relationship between connectivity and spectrum. It is worth to mention that the expansion in Eq. 5 is valid if |F̃(ω)| ‖A‖ <1, where ‖A‖ denotes the Frobenius norm. Assuming |F̃(ω)| ≤ 1 ∀ω, this imposes a constraint on the norm of A, however, the norm of a Barabasi-Albert network is significantly smaller than the largest degree (29), and therefore we expect the approximation to be generally applicable.

We present in figure S3A an instance of the model, showing the normalized spectral distribution |x̃(ω)| for a low-pass filter defined by |F̃(ω)|=(1+ω²)^−1/2 and an activity |g̃(ω)|~ω⁻¹. The blue trace represents a 'high degree' node μD_n = 1, while the red trace is a 'low degree' one, μD_n = 0.01. For the purpose of demonstrating the generality of our model, we implemented a simulation with more realistic assumptions for the dynamics and the connectivity. We computed 1,000 instantiations of a Barabasi-Albert scale-free network with 100 nodes, with a mean connectivity of low (high) degree nodes ~ 5 (25). On top of the basic architecture, we randomized the signs of the connections so that, p(A_nm = ±1)=0.5. We implemented a weakly non-linear low-pass dynamics for the units as follows:

$$\vec{x}(t)=-\mu \vec{x}(t)+\kappa \sigma (A\vec{x}(t)+\vec{g}(t))$$ (6)

The stochastic intrinsic activities are random mutually uncorrelated, 〈g_n (t) g_m (t)〉 = δ_nm, δ_nm = {1 if n = m, 0 if n ≠ m}, with power-law spectral distribution |g̃(ω)| ~ ω^−α, α > 0. Figure S3B shows the results of averaging the spectral distribution for the 10 nodes with highest degree (blue), and the 10 nodes with lowest degree (red). For the non-linear integration function we chose σ = tanh() for its limiting effect; the parameters of the simulation, however, tend to keep x⃗ within the linear regime. Finally, unstable connectivity configurations were discarded.

The hypothesis of low-pass filtering of neural inputs is consistent with well-established models of synaptic integration and synaptic plasticity (30). Note, however, that the low-pass effect of the electrophysiology-to-fMRI transformation has no bearing on our theory. We propose that the actual electrophysiological activity of a neuronal ensemble integrates differentially the low frequency components of its input, as represented in Eqs. 1–2. The fMRI signal, in this context, is just a low-pass version of x⃗, and as such cannot be affected by the connectivity. If we call this signal z⃗, then its spectral content would be simply $\vec{\tilde{z}}(\omega )=\tilde{H}(\omega )\vec{\tilde{x}}(\omega )$, with H representing the electro-haemodynamic coupling function.

Orstein-Uhlenbeck process

We can gain further insight into the relationship between connectivity and spectrum. Let us consider an Orstein-Uhlenbeck process, i.e. a stable multi-linear system driven by Gaussian noise. We will represent this process as

$$\vec{x}(t)=-(I-A)\vec{x}(t)+\vec{g}(t)$$ (7)

where g is Gaussian noise, and A_nm ≥ 0, ‖A‖ < 1 so that the positive feedback represented by A is balanced by self-inhibition, represented by I_nm = δ_nm, making the system stable. Such a system can be described by the relationship between the lagged covariance matrix C(τ) = 〈x⃗(t)x⃗^T (t+τ)〉_t and the full connectivity matrix  = −I+A

$$\widehat{A}C(0)+C(0){\widehat{A}}^T=-Q$$ (8)

$$C(t)=C(0)\text{exp}({\widehat{A}}^{T}t)(t>0)$$ (9)

$$C(t)=\text{exp}(-\widehat{A}t)C(0)(t<0)$$ (10)

where Q = 〈g⃗(t)g⃗^T〉_t is the covariance matrix of the input (31). If for simplicity we consider A = A^T (i.e. the connections are symmetric) and the noise proportional to the identity (Q=I, that is all the units have the same noise variance), it follows that the solution for the covariance at zero lag (Eq. 8) is $C(0)=\frac{{\widehat{A}}^{-1}}{2}$. Similarly, the solution for C(t) derives from Eqs. 9–10. Given that the covariance in real time is a convolution of the signal with itself, it is equivalent to the spectral power in Fourier space:

$$\vec{\tilde{x}}(\omega ){\vec{\tilde{x}}}^{†}(\omega )=\tilde{C}(\omega )={\int }_{-\infty }^{\infty }C(t)\text{exp}(-i\omega t)dt$$ (11)

where ^† indicates the conjugate transpose operation. Plugging in the solution for C(t), we obtain

$$\tilde{C}(\omega )={({(I-A)}^2+I{\omega }^2)}^{-1}$$ (12)

Expanding in A, we obtain

$$\tilde{C}(\omega )\approx I{(1+{\omega }^2)}^{-1}+2{(1+{\omega }^2)}^{-2}A+{(1+{\omega }^2)}^{-3}(3-{\omega }^2)A^2+0(A^3)$$ (13)

We assume that and A_nm = 0 and A_nm ≥ 0; given this, the second term in Eq. 13 drops out, and ${(A^2)}_{nn}={\mathrm{\Sigma }}_k{A}_{nk}^2$ is proportional to the 'degree' of the node. It follows then that the spectral power of node n is:

$$\tilde{C}{(\omega )}_{nn}~\frac{1}{1+{\omega }^2}+\frac{3+{\omega }^2}{{(1+{\omega }^2)}^3}{D}_n$$ (14)

showing that the relative spectral content of higher frequencies is diminished proportionally to the connectivity.

Results

Voxel-wise mapping of BOLD power to functional connectivity

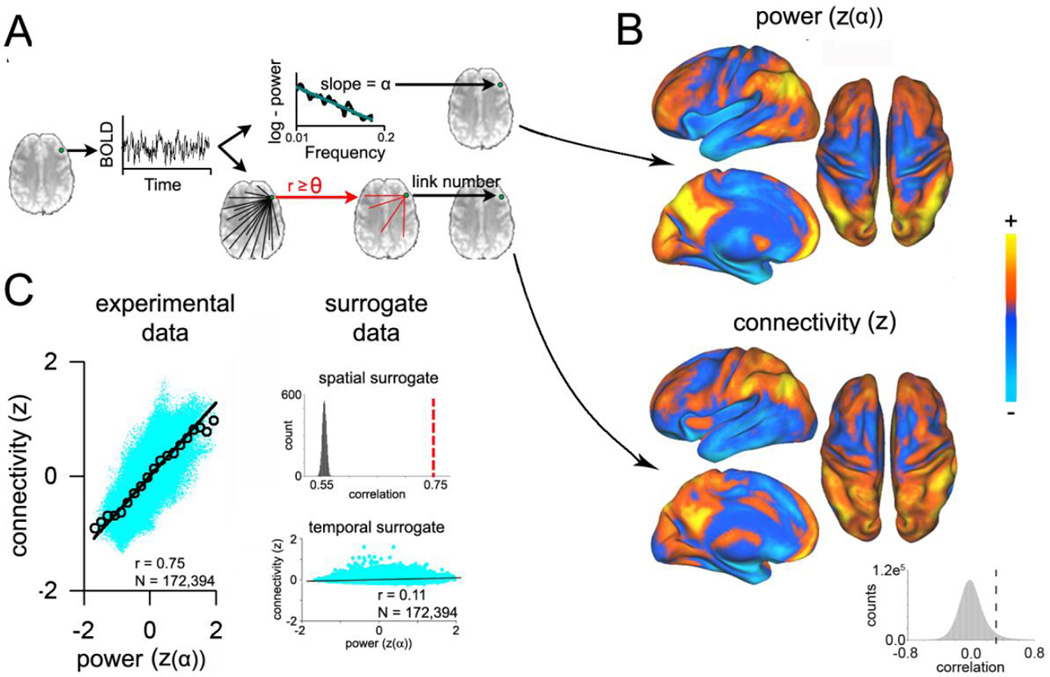
In a recent resting state fMRI study, we demonstrated that the full bandwidth BOLD power spectrum, when sub-divided into 4 bands, exhibits brain spatial specificity (15). Here we replicate this result by demonstrating the spatial variability of BOLD power when studied by the single parameter, α. Additionally, we demonstrate that this value is closely related to whole-brain FC. Resting state BOLD time series were transformed voxel-wise into frequency space, and the balance between the low and high frequency power was determined by α (figure 1A, top panel). The Kolmogorov-Smirnov distance (D) between the BOLD power spectrum and its least-squares fit was smallest on the log-linear scale (D = 0.16 ± 0.02), as opposed to the linear (D = 0.20 ± 0.02) and log-log (D = 0.23 ± 0.03) scales. Therefore, α was best described by the BOLD power spectrum as expressed on log-linear axes (figure S1). Connectivity was determined by calculating pairwise Pearson correlations between BOLD time-series for every voxel in the brain, and counting the number of correlations greater than or equal to a given threshold (Θ ≥ 0.3) (figure 1A, bottom panel). The mean and standard deviation of the pairwise Pearson correlations between 500 random voxels in each subject was 0.01 ± 0.16 (figure 1B, inset). Distribution of α revealed a frequency-specific spatial segregation of structures, with high α scores in the frontal, parietal, and occipital cortices, whereas lower scores were present in the temporal cortex, the limbic and the subcortical areas, thereby replicating earlier results (15). Spatial distribution of FC was generally similar to α (figure 1B), yet there were also obvious differences, such as in the thalamus, parts of the temporal lobe, and cingulate gyrus. The voxel-wise correlation between the connection density and α was highly significant (n=172,394 voxels, r = 0.75, p<<0.01, figure 1C), demonstrating that the frequency content of local BOLD frequency content is proportional to the number of functional connections that each voxel possesses. Such correlations may be due to a variety of sources, including BOLD signal artifacts, as well as MRI acquisition or data processing artifacts (32). We tested for spatial specificity of the α–FC relationship by scrambling the group mean FC map with wavelet resampling (28). Five-thousand correlations were calculated between α and the resampled FC maps, revealing a mean correlation (r = 0.56 ± 3.6×10⁻³, figure 1C, upper inset; note that if we use random spatial shuffling instead of wavelet resampling, then r = 0.0, which implyies that the residual correlation is due to intrinsic and preprocessing-imposed autocorrelations). We further tested the dependence of this relationship on the temporal pattern of BOLD activity by comparing it with a null model of FC by randomly shuffling the phase of BOLD time series in Fourier space. Relative to the original data, the null α-FC relationship was virtually flat (r = 0.11, figure 1C, lower inset). Surrogate group mean maps were spatially dissimilar from experimental data (figure S2). The correlation of α-FC also remained high at Θ = 0.4 and Θ = 0.5, and therefore the α-FC relationships are not specific to the choice of threshold (figure S3). These results demonstrate that the pattern of FC distributed throughout the brain is not random, as it depends on the spatial structure and the temporal properties of the BOLD signal.

Figure 1. Spatial distribution of BOLD power and degree of FC are highly correlated.

A) Methodology for voxel-wise analysis. To generate power distribution maps the resting state fMRI BOLD signal at each voxel was extracted and transformed to frequency space, using Welch’s method. The log-linear slope of the power spectrum was used to calculate α. Steeper slopes translate to higher α, or a greater distribution of power to the lower frequencies. Network degree, or connectivity, maps were generated by calculating the Pearson correlation at each voxel against all other voxels in the brain. The number of voxels exceeding threshold (r≥0.3) represent the number of functional links at each voxel. B) Group-averaged (N=21 subjects) distribution for α, and for connectivity (number of functional links). Individual α and connectivity maps were z-scored and averaged across subjects. Blue represents negative and yellow represents positive z-values. The spatial distributions of power and connectivity are generally similar. The inset histogram shows the distribution of pairwise correlations between 500 random voxels in each subject. The dotted line indicates the connection threshold at a Pearson correlation of 0.3. C) Voxel-wise spatial correlation (r = 0.75) of group average maps reveals high similarity between power and number of functional links (left). Spatially shuffling connectivity maps with wavelet re-sampling 5000 times reduces the average correlation to r = 0.56, which is significantly lower than the correlation with experimental data, referenced with the dotted line (upper inset). Similarly, after shuffling the phases of BOLD timeseries in Fourier space, and recalculating whole brain connectivity, correlation between α and connectivity was reduced to r = 0.11 (lower inset).

We built a computational model to capture the fundamental relationship between local activity fluctuations and functional connectivity, in which we treat voxel activity as a low-pass filter of synaptic inputs. The slope of the average power spectrum of the 10 nodes with the highest FC was steeper than that of the 10 nodes with the lowest FC, indicating a greater distribution of power in the lower frequencies for nodes with more functional connections (figure S4). Thus, we conclude that there is a general rule, at least for resting state fMRI, between BOLD power spectra and FC, and that for any given voxel, the greater dominance of low frequency power will correspond with a higher probability that the voxel has a large number of functional connections. Moreover, this relationship may be due to low-pass filtering by synaptic contacts.

BOLD power and functional connectivity vary according to regional synaptic wiring

It is suggested that the dynamics of the BOLD signal differentially represent neuronal network activity according to regional variations in the structural network architecture found throughout the brain (33). In agreement with this, we have previously shown that BOLD power is distinct in synaptically distinct brain regions (15). We therefore tested, at the whole brain level, that α and FC are differentially interrelated after dividing the brain according to regional synaptic wiring (figure 2A) (18). Unimodal voxels in the brain exhibited both the highest α and FC, whereas limbic-paralimbic voxels exhibited the lowest α and FC (figure S5A-C), indicating that the variation in synaptic wiring corresponds to varying BOLD dynamics. Some regions exhibited a negative α-FC relationship, and in general these were the result of a bad linear fit to the data, given that multiple clusters are visible within some of those regions (figure S5D). Overall, the unimodal areas exhibited the lowest α–FC correlation (r = 0.54, p<<0.01) whereas the heteromodal and limbic-paralimbic regions exhibit much higher correlations (r = 0.79 and r = 0.72, p<<0.01, respectively, figure S6).

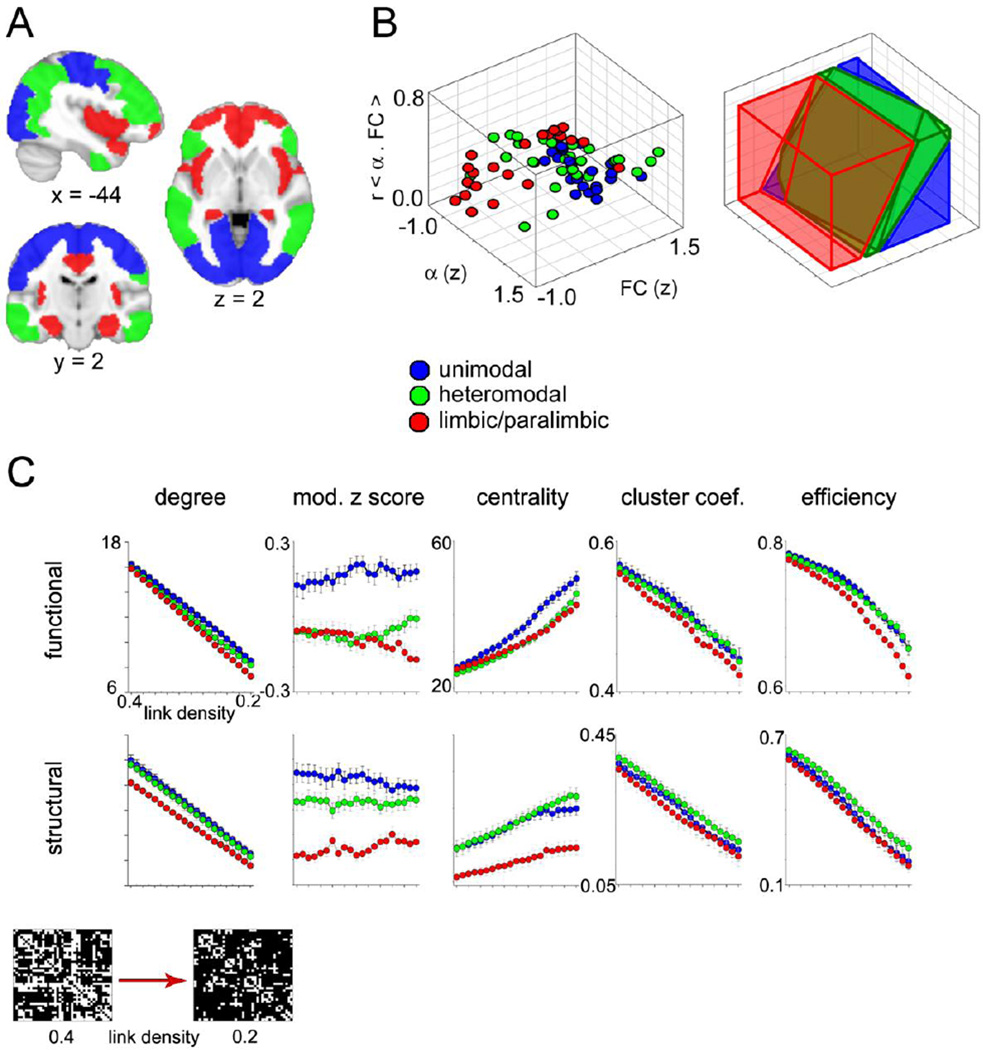
Figure 2. Frequency and network architecture properties vary with synaptic wiring.

A) Subdivisions of the brain based on synaptic hodology. B) Group mean Z scored connectivity and α, and their correlation is plotted for each BA (left). Linear discriminant analysis was then performed on this data to test for misclassification of BAs (table S3). Classification space is plotted demonstrating a general segregation of unimodal and limbic-paralimbic regions, with some overlap from heteromodal regions (right). C) Network metrics differed across synaptically-grouped BAs. Data points represent the mean of each synaptic group, averaged across all subjects (N=21). Error bars are standard error. All metrics were significantly different (p < 0.01), except cluster coefficient for task functional networks (table S4). Modular degree exhibited the greatest differences, while efficiency and clustering coefficient were the least different. Inset displays an example connection matrix at the highest and lowest link density thresholds for a single subject.

Linear discriminant analysis was performed to determine the distinctiveness of the spectral profile and connectivity amongst BAs based on different categorizations (figure 2B). Confusion matrices were generated for each subject to determine the accuracy of classifications for the groups of BAs based on their α, FC, and correlation values (table S1), as tested against our designated synaptic wiring categorization. In general, the correct classification was low, which was also reflected in the discrepancies of classifications across studies, especially with unimodal regions (table S2). Limbic-paralimbic BAs were most often correctly classified with a 65.5% accuracy rate, whereas 48.3% of heteromodal and 38.9% of unimodal BAs were correctly classified on average. The unimodal and limbic-paralimbic regions were largely distinct from each other, with only 10.3 – 18.9% misclassification between the two, whereas the heteromodal regions were misclassified at 21.9 – 42.1% (table S3).

To test the significance of this classification accuracy, we performed the same analysis designating BA groups based on 1) their relative spatial distance from each other, or 2) their random placement (as opposed to their synaptic wiring). We then compared the diagonals of the confusion matrices across the three categorization schemes using a repeated measures ANOVA. There was a significantly different rate of accuracy, depending on classification schemes, for both heteromodal (F(2,29) = 13.570, p < 0.001) and limbic-paralimbic (F(2,29) = 86.514, p < 0.001) categories. No significant differences were detected for the unimodal category. Post-hoc Holm-Sidak multiple comparisons testing indicated that the synaptic wiring and spatial distance categorizations were significantly different (p < 0.05) from the results of random shuffling, but not from each other. No significant differences were found amongst the unimodal BAs (table S3, figure S7). Thus, whereas the BOLD spectral properties and FC differentially reflect the regional synaptic wiring to a small extent, this segregation of BAs is inextricably linked to their spatial locations in the brain.

DTI structural and functional network architecture vary according to regional synaptic wiring

To demonstrate that distinct variations in synaptic wiring measured through tract tracing methods can translate to specific macroscopic network properties measured with MRI, we contrasted five graph theory network metrics across synaptic groups. Analysis was carried out at the lower resolution BA level, given that measuring voxel-wise white matter tractography is computationally expensive. Thus, the functional connections refer to the strength of correlation between the mean time series from each BA, whereas the structural connections refer to the number of DTI tractography counts that were extracted between BAs. The results we present here appear to be independent of spatial resolution, as the lower-resolution BA analysis parallels the higher-resolution voxel-wise analysis. Network metrics were calculated over a range of connection strength thresholds corresponding to connection matrix link densities between 0.4 and 0.2 (27) wherein lower link densities indicate stronger BA-to-BA connection thresholds must be met in order to be included in the network (figure 2C, inset). Network measurements included node degree (connectivity), modular degree, centrality, clustering coefficient, and efficiency for resting functional and structural data (figure 2C). A two-way ANOVA was used to determine differences in network metrics across synaptic groups and thresholds (statistical details are shown in table S4). Connectivity (node degree) was highest for the unimodal regions and lowest for the limbic-paralimbic regions, which parallels our results from the voxel-wise analysis (figure S3). Modular degree exhibited the greatest differences across synaptic groups, whereas efficiency and clustering coefficient exhibited the lowest. Likewise, modular degree was the only metric that was not significantly different across thresholds. Interaction effects between synaptic group and threshold were significant only for functional centrality and task-based functional efficiency (table S4). Therefore, we conclude that the variation in synaptic wiring across the brain is also reflected in the differential functional and structural network architecture.

The α-connectivity relationship shifts according to attentional state

We have previously shown that performing a visual rating task increases the high frequency power of BOLD throughout the cortex in areas unrelated to the task (15). Given that BOLD power reflects FC during rest, we tested how the α–connectivity relationship is influenced by attentional state using a simple visual-motor attention task in which subjects continuously rated the size of a moving bar with the spread of their fingers (22) as we recorded their brain activity. Analysis was carried out at the lower resolution BA level in order to include SC, which allowed us to determine how both functional and structural network architecture were related to α during different attentional states.

The α–FC and α–SC were calculated across all connection matrix link densities between 0.4 and 0.2. For corresponding matrix link densities, the mean α-FC connection strength across subjects ranged from r = −0.05 ± 0.25 to r = 0.34 ± 0.3 for resting state scans, and r = 0.13 ± 0.23 to r = 0.36 ± 0.23 for attention task scans. Mean α-SC connection strength was constant, ranging from 0.22 ± 0.19 to 0.23 ± 0.22 for the same link densities. Average correlations between connectivity and α across subjects were compared against random null-model networks. A two-way ANOVA was used to determine significant differences (p < 0.01) in α-FC and α-SC correlations between real and null data, and across multiple link density thresholds (detailed results shown in table S5). For both resting and attention task scans, α-FC and α-SC were significantly correlated. Interaction effects with threshold were significant for the functional networks, but not for the structural networks (figure 3A, table S5). This indicates, in general, that local measures of BOLD spectral profiles reflect both structural and functional network connectivity, and this rule is consistent across various thresholds of connection strengths.

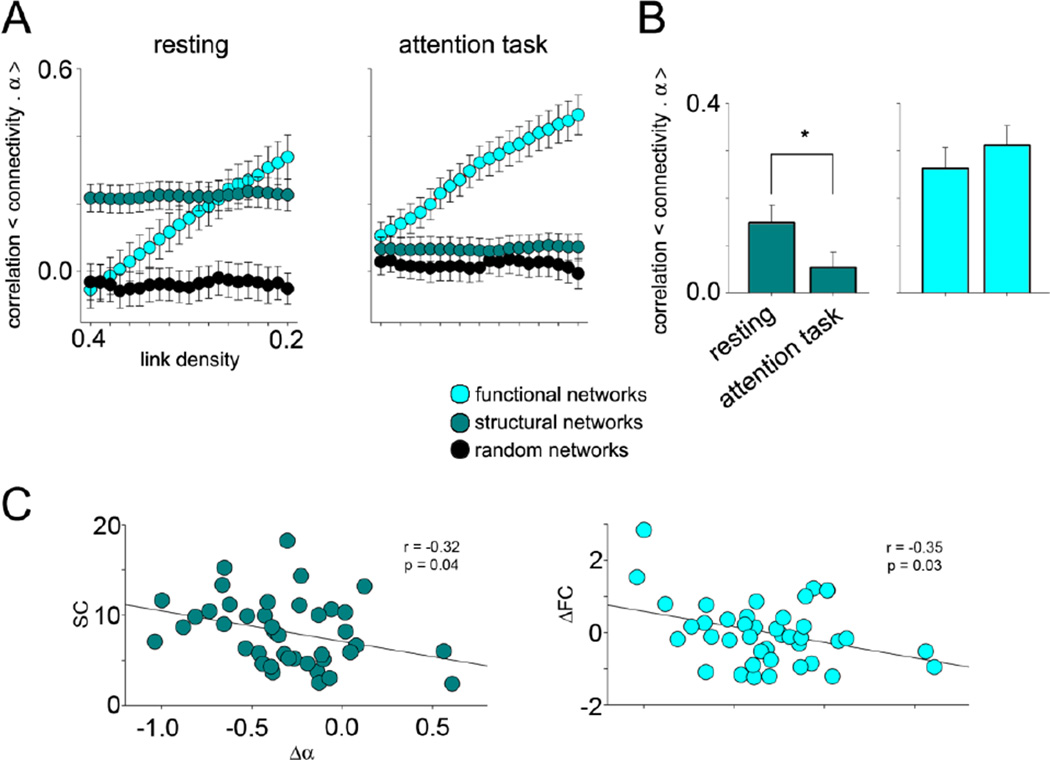
Figure 3. Local BOLD fluctuations reflect connectivity depending on brain state.

A) Structural and functional connectivity correlated differently with α according to scan condition. Each data point is the mean correlation for each synaptic group, averaged across subjects. Error bars indicate standard error. Two-way ANOVA revealed FC- α correlations were significantly greater than random networks for both scan conditions, but SC-α correlations were significant only during resting state. See table S5 for details. B) Differences between rest and task α-FC/SC correlations were averaged across link density thresholds for each subject. Bars represent the mean values across subjects, error bars represent standard error, and significance between task type is indicated with asterisks (p<0.001). In general, α-SC correlations were higher during rest while α-FC remained unchanged between scan conditions. C) The correlation between group mean change in α (Δα = task α – rest α) and SC, as well as between group mean Δα and ΔFC (task FC – rest FC) was calculated across BAs for all link densities (figure S8). Only the correlations at link density = 0.2 is shown here. SC and ΔFC were both negatively correlated to Δα, suggesting that BAs may be drawing energy from more local sources while attending to a task.

Upon visual inspection, it is clear that α-SC correlations are stronger than α-FC during resting state. On the other hand, the opposite appears to be true for task scans. To determine the differences in α-connectivity relationships between attention states, we averaged α-FC/SC correlation values across multiple link density thresholds for each subject and performed a paired t-test between scan conditions. The α-SC correlations were higher during resting state (p < 0.001). In constrast, the task α-FC correlations were not significantly different across conditions (p = 0.24, figure 3B). Collectively, we conclude from this result that the fluctuations in the BOLD signal during rest are more indicative of the architecture of structural networks. Interestingly, a change in α from rest to task (Δα) conditions was negatively correlated to a change in FC from rest to task (ΔFC). As functional connections across BAs can be considered to be distant connections, this finding would indicate a shift from distant to more local contributions of α within a BA, when attending to a task. Similarly, Δα was negatively correlated to SC. Therefore, the BAs with many structural connections exhibited smaller increases (or greater decreases) in α when attending to the task (figure 3C and figure S8). On the whole, therefore, the manner by which local BOLD frequency properties shift between brain states is likely dependent on regional embedding of the structural network, as well as on differences in the energy contribution from local and distant sources.

Similarity of functional and structural networks

Because the α-FC correlations tended to increase as link density decreased (i.e. the strength of connections comprising a network increased) and α-SC correlations did not (figure 3A), we measured the spatial similarity of structural and functional connection matrices to determine whether their organization converges to a similar architecture as the connection strength increases . In other words, we tested whether structural and functional networks became more similar as we whittled away the weaker network connections. The percentage overlap of connection matrices decreased with the link density threshold, indicating that the networks were actually less similar as their connection strength increased (figure S9A). Given that α is constant for any given region, the increase in the α-FC correlation across link density thresholds must then be due to a shift in the distribution of FC. Furthermore, as the α-SC correlation remained constant across thresholds, the distribution of SC necessarily remained relatively stable (demonstrated in figure S9B). Overall, these results imply that α encodes the number of connections to a network node without providing specific information about the locations of those connections. Additionally, although the properties of functional networks are likely to change as weaker connections are removed, the structural networks are less sensitive to this effect and therefore exhibit self-similar architecture.

Discussion

We show that the distribution of power along the BOLD frequency spectrum, α, differs across the brain, thereby reflecting characteristics of both SC and FC. The degree to which connectivity correlates with the slope of the power spectrum is related to regional synaptic wiring. In general, α more closely reflects SC during resting state than during attentional states related to a task. Collectively, these results support the notion that spectral profiles in the brain are not the exclusive products of local activity, but instead they are highly influenced by the architecture of the networks within which they are embedded. Moreover, the architectural influence on local activity fluctuations shows brain-state dependence.

Differential distribution of power

Given that the distribution of frequency-power for fMRI BOLD fluctuations, captured by α, appears to reflect the information processing capabilities of local neuronal populations (16, 17, 34, 35), its spatial variability and its relationship to network connectivity reveal underlying rules that guide the distribution and integration of information processing in the human brain. Voxel-wise, α was greatest in the primary sensory cortices and the neocortical regions overlapping with parts of the default mode network (3), whereas α was lowest in the limbic-paralimbic regions, as well as in portions of the temporal lobe and the subcortex. Similar results have been shown in studies examining the spatial distribution of frequency-power with both the power law exponent (36), as well as with frequency bands within the BOLD signal (15, 37–39). Greater α values, which signal greater shifts in power towards lower frequencies, suggest that each time point in the BOLD signal is more heavily influenced by past events (17). Therefore these results suggest that brain regions exhibiting lower α are more efficient at online information processing; in a sense, these regions are more easily influenced by incoming instantaneous signals. Thus, our results suggest that more functionally complex regions of the brain are more efficient at responding to rapid changes in information flow.

These findings contrast a recent studies suggesting that functional networks associated with basic sensory perception possess higher frequency BOLD (6) and electrocortigraphic power (40) fluctuations than those associated with more complex cognitive operations. We should emphasize that the higher-order brain regions they define mostly fall within our heteromodal classification, and we have shown these regions to have some frequency overlap with unimodal regions Nonetheless, the frequency-based fractionation of functional regions demonstrated in these studies illustrates the need for further investigations into the nature of spectral activity and hierarchical information processing within the brain.

Hodology

Recent work from our lab has demonstrated a general principle by which high frequency BOLD power coincided with brain regions regulating higher-order information processing (15) based on the idea that the entire cortical surface can be divided into five functional zones (primary sensory, upstream unimodal, downstream unimodal, heteromodal, paralimbic and limbic). Collectively, these regions display a continuous spectrum of cytoarchitectonic differentiation, from the most highly differentiated primary sensory-motor areas to the least differentiated limbic structures (18). In other words, the intricacy of synaptic wiring increases in proportion to the complexity of regional function. We note that the synaptic grouping of BAs based on this criterion implies only that a cortical region is wired mostly in a manner consistent with its hodological classification, and the spatial resolution of this classification results in some overlap across groups. This overlap is evident in our linear discriminant analysis, which demonstrates that the accuracy with which both spectral activity and connectivity corresponds to synaptic wiring is relatively low. Unimodal regions, in particular, show the greatest deviation from our hypothesis, as they were classified with the same accuracy as random classification.

This mixed classification is also evident when comparing studies that categorize BAs according to their functional roles (15, 41, 42) – i.e., the regions we defined as unimodal are classified under a different category across these studies. This may account for the contrasting results regarding which BAs are characterized by having the greatest connectivity – unimodal or heteromodal. For example, contrary to our results, (41) lists the largest functional hubs in the brain, noting that most are “association” (heteromodal) cortex. However, 10 of our 13 unimodal regions are included in this list, and 7 of those are categorized as “association” cortex. Further, in another study ranking the connectivity of BAs across the whole brain (43), 5 of top 10 regions with the highest degree are unimodal BAs in our study. Thus, it seems that the incongruity of results across studies is likely due to the inconsistency in how functional zones of the brain are defined, which may reflect anatomically meaningful or purely statistical boundaries.

Defining these boundaries continues to be a challenge. Our results show that when heteromodal and limbic-paralimbic BAs were classified according to synaptic wiring, it was no more accurate than when BAs were categorized based on their relative spatial distances. These findings indicate that 1) regions of similar spectral activity and connectivity are spatially proximal to each other, and 2) regional synaptic wiring is spatially continuous. Thus, while our hypothesis that the spectral profile of local neural activity is influenced by regional hodological features is supported, it is difficult to disentangle this relationship from the spatial coherence that is inherent in the architecture of the brain. Moreover, the overall poor classification accuracy of our linear discriminant analysis suggests there are other factors, in addition to synaptic wiring and spatial location, that influence local spectral activity and functional connectivity.

The BOLD power spectrum

The link between connectivity and intrinsic brain activity fluctuations has been extensively investigated. A number of studies have noted frequency-power differentiation among resting state functional brain networks (6, 39, 44–46). Similarly multiple findings, including the fractal scaling of functional connectivity across low frequency wavelet scales in MEG (47), the distinct 1/f power distribution across different brain regions (36), and the scale-free temporal recurrence of EEG microstates and fMRI intrinsic connectivity networks (48), suggest that the intricate relationship between brain activity fluctuations and functional networks is governed by laws that are characteristic of complex systems. Given that our power spectrum metric, α, is calculated on a log-normal scale, it is not scale-free. Yet, we do not take this as evidence that brain networks are random. Our own and extensive other data provide ample evidence that the network properties of the brain (based on multiple other measures) show robust power-law behavior (35, 49). Importantly, whether we fit the spectra with exponential or power relationships the results are >0.9 correlated with each other (data not shown); as a result these measures provide very similar information. On the other hand, often power law dependence is simply “assumed” rather than tested. Given that the power spectrum for BOLD is highly compressed, there is not enough dynamic range for a proper power law fit, and this limited spectrum as well as temporal whitening applied at preprocessing may be the reason why the long tail of the power spectra are not visible in BOLD spectra. Therefore, we maintain that the best fit remains the exponential function, yet we also assume that the slope of this fit is informative in terms of regional information processing.

Frequency power and connectivity

The direct proportionality between the frequency-power distribution and the number of connections, observed in both functional and structural brain networks, demonstrates a general rule of brain organization. The precision of the α-FC relationship was demonstrated by showing that it critically depends on spatial and temporal (e.g., phase) alignment. The overall significance of this finding is underlined by the idea that local brain activity is subject to network-wide influences. In fMRI, with our capability to localize brain activity to fractions of the global scale, this is a concept that can be easily overlooked. Much of the neuroimaging community remains focused on pinpointing brain function, with the assumption that BOLD activity at a single voxel is influenced primarily by the local activity contained therein. Contrary to this supposition we show, by taking advantage of the whole-brain recording capabilities of fMRI, that local BOLD activity is modulated by the concerted action of many distant brain regions. This conclusion is in agreement with recent works suggesting that functional networks emerge as a property of the connection-architecture of white matter tracts (2, 5, 33, 50, 51) and band-specific global-field synchronization (52, 53). Furthermore, our model that demonstrates α as product of synaptic low-pass filtering is consistent with previous work showing that BOLD amplitude is intricately related to synaptic input (54). As a result, brain regions with the highest α and largest FC/SC connections likely have more synaptic connections. We note that other factors not included in our model can influence the spectrum of neural dynamics, such as dendritic geometry, receptor type, and neurotransmitter-type. Thus, our model is primarily intended to describe a neural mechanism for the α-connectivity relationship that parallels the simple network characteristics that can be measured with fMRI. Correlating more intricate macroscopic network properties to local activity fluctuations might allow one to draw parallels to these other factors, such as dendritic geometry, yet our data shows no significant correlations with other network measures. However, it has recently been shown that local glucose metabolism and the fractality of the BOLD signal are highly correlated (17), and thus many physiological factors are likely to contribute to local dynamics. In fact, since the submission of this paper, regional cerebral blood flow has also been shown to be highly correlated to voxel-wise functional connectivity strength across the whole brain, indicating local metabolism is higher in brain regions that have overall stronger functional connections (55). Moreover, the same study demonstrated this metabolism-connectivity correlation was greater in brain regions associated with higher-order information processing, which directly parallels our results showing stronger α-FC correlations in more functionally-complex regions. Based on this finding, it makes sense to suggest that BOLD spectral activity might also be a marker of regional metabolic energy consumption. In any case, our results are an extension of the well-supported idea that local brain activity is influenced by network properties, and in particular by the number of connections to a region.

Frequency power and brain state

Most studies examining the correspondence between structure and function in the brain have been performed in the context of a task-free “resting state” environment. Therefore, it has remained unknown whether a task has any influence on this relationship. Recent studies show that the spatial and temporal properties of brain functional networks change only minimally between rest and task (3, 20, 21), thereby prompting the idea that resting scans may be sufficient to study brain function in various clinical populations without the need to design specific task paradigms (20). The significance of resting state fMRI studies cannot be overstated; however, here we show that the importance of task-based brain activity cannot be ignored. Specifically, a change in α from rest to task was accompanied by a shift in the structure-function relationship in two ways: first, α more closely reflected the architecture of structural networks during rest than while attending to the task. Second, greater decreases in α from rest to task were indicative of greater increases in functional connections and greater structural connectivity overall. As our analysis could be considered as measuring only distant connectivity from region to region, these results suggest a shift in the energy contribution from distant to local sources while performing a task, thus reflecting the modular properties of the brain (56–58). A high resolution analysis accounting for distance and modularity would provide a clearer picture of the α-connectivity relationship and its dependence on brain state. Such investigations would expand on the previous studies that have shown widespread shifts in power (15, 17, 59, 60) and fractality of brain activity (17, 61) in relation to state of attention. Similarly, functional network activity is modulated by alpha-band oscillatory power (52, 53), which is the EEG frequency range classically associated with alertness. Thus, it is not unfounded that attention plays an important role in influencing brain activity fluctuations and connectivity. Here we demonstrate for the first time, however, that attention modulates their interaction, suggesting that structure-function relationships are indeed dependent on brain state.

Whereas white matter networks have been reported to be stable on the order of weeks (62, 63), BOLD functional networks can change over a period of seconds (64). In the light of the findings that high α indicates a more stable signal (17), it makes sense that it is more reflective of a stable structural network. All subjects performed equally well on our simple task, but it remains to be seen whether different tasks or levels of difficulty might yield different results. For example, our task required subjects to continually rate the size of a bar that fluctuated in length well within the fMRI bandwidth (~0.05 Hz). It is unknown how α may have changed had we increased the difficulty of the task by increasing the rate of fluctuations, or whether the rate of the fluctuating bar has any effect on the distribution of α itself. Recent work that has shown functional connections in the brain change minimally between tasks with differential cognitive mechanisms, specifically in areas of the brain where low frequency power is greatest (65). This lack of variability suggests that modifications of the difficulty or temporal parameters of a task would have little effect on connectivity, and thus on the α distribution. Therefore, it may be the case that shifting brain state and attention from inward-reflection (resting state scans) to outward-reflection (task-based scans) may have the greatest effect on α. Regardless, our results prompt the need for further research into the emergent nature of functional connections, and question the notion that structure-function connectivity can be adequately explained with resting state scans.

Limitations

To our knowledge this is the first comprehensive fMRI study examining the influence of whole-brain connectivity on the spectral profile of the local BOLD signal. We use the term ‘whole-brain’ with some reservation as the low-resolution analyses were performed on each hemisphere separately and averaged; these steps were implemented to guard against potential contamination in tractography analyses that can arise from tracking crossing fibers in the corpus callosum (66). The properties of functional networks may also be different when viewed within versus across hemispheres, specifically in the case of heteromodal regions, as shown in a recent study (67). However, our high-resolution analysis was performed across both hemispheres, and is in general agreement with our low-resolution within-hemisphere analysis, suggesting that our results are applicable across both hemispheres. Both sets of analyses may also be influenced by preprocessing methods; specifically, the voxel-wise global regression of the BOLD signal may introduce negative correlations between brain regions (68). As our analysis examined only positive correlations, we do not suspect that exclusion of this preprocessing step would have changed our results.

Additionally, we did not address effective connectivity, which has been shown to influence the probability of functional connections in the monkey brain (2). Assessing the direction of information flow in fMRI data remains a challenge, although promising methodologies may soon allow for more accurate measurements (69). More studies are needed to determine what role directed signal transfer plays in the α-connectivity relationship.

Conclusion

In summary, we demonstrate that the local fluctuations of BOLD in the brain are modulated by network-specific properties of connectivity. We show, in agreement with previous studies (15, 36–38), that BOLD frequency power is spatially segregated throughout the brain, and this segregation coincides to some extent with regional network architecture and connectivity. Finally, contrary to recent suggestions that resting and task-based functional network properties are minimally different, we demonstrate that BOLD fluctuations differentially reflect structural connectivity during different states of attention.

Highlights.

• -Local brain fluctuations are correlated to network-specific architecture.
• -The slope of the BOLD power spectrum is dependent on regional wiring architecture.
• -BOLD reflects structural/functional networks differently between resting and task.