Natural History of Yersinia pestis Pneumonia in Aerosol-Challenged BALB/c Mice

Abstract

After a relatively short untreated interval, pneumonic plague has a mortality approaching 100%. We employed a murine model of aerosol challenge with Yersinia pestis to investigate the early course of pneumonic plague in the lung, blood, and spleen. We fit a mathematical model to all data simultaneously. The model fit to the data was acceptable. The number of organisms in the lung at baseline was estimated to be 135 (median) or 1,184 (mean) CFU/g. The doubling time was estimated as 1.5 to 1.7 h. Between 1 and 12 h postexposure, counts declined, but they then increased by 24 h, a finding hypothesized to be due to innate immunity. The model predicted that innate immunity declined with a half-time of 3 to 3.8 h. The threshold for bacteremia was 6.4 × 10⁴ to 1.52 × 10⁶ CFU/g. By 42 to 48 h, stationary phase was obtained. Lung bacterial burdens exceeded 10 log CFU/g. Obviating early defenses allows for rapid amplification of Y. pestis in bacteremia, making the rapid course with high mortality understandable.

INTRODUCTION

Plague is one of the oldest bioterror weapons known to humans. In 1346, the Mongols catapulted plague-infected corpses into the Crimean City of Caffa (1). Infection with Yersinia pestis, the causative organism of plague, results in three major syndromes (2). The most familiar syndrome is bubonic plague. In this syndrome, organisms arrive in lymph nodes and multiply there, generally after being introduced by the bite of infected fleas. In untreated cases of bubonic plague, mortality is approximately 50 to 70%. With treatment, mortality decreases to 15% or less.

In some cases, bubonic plague progresses to septicemic plague, which increases mortality and may result in pneumonic plague. In contrast to diseases caused by other agents of bioterror, such as Bacillus anthracis, pneumonic plague can result in person-to-person transmission once infection is established. Untreated pneumonic plague has a mortality approaching 100%. Intentional release scenarios predict great confusion in the therapeutic situation, as there would initially be no diagnosis due to a lack of familiarity in the medical community and an unknown drug susceptibility profile. It would certainly take a considerable number of hours to days until the exposed populations became symptomatic and individuals entered into the health care system. Pneumonic plague, unlike many other pneumonias, has a very foreshortened course, such that after approximately 2 to 3 days without appropriate treatment, mortality becomes very high, and the response to therapy after this time is poor (2).

We employed a whole-body murine aerosol challenge model to explore the rapid course of this disease and to better understand why pneumonic plague becomes poorly treatable after a relatively short interval following the onset of symptoms, with a consequently very high mortality. Because this murine infection model is used as a proof of principle for antibiotic therapies before advancement to nonhuman primate models, a better understanding of the treatment trigger and justification of that timing has been needed. The treatment point of 42 h postchallenge was based on previous studies of effective survival by initiating therapy at different times between 24 and 60 h postchallenge (3). While the 42-h treatment initiation time point has proven valid in other studies (4), the disease history and distribution of Y. pestis in the murine model before, around, and after this time point have not been defined fully.

MATERIALS AND METHODS

Mice.

Female BALB/c mice aged 7 to 9 weeks old (20 g) were obtained from the National Cancer Institute/Charles River Laboratories and used for all experiments. The mice had free access to food and water throughout the course of the study.

For all experimental procedures described here, we adhered to the guidelines promulgated in the Guide for the Care and Use of Laboratory Animals (5). Research was conducted in the biosafety level 3 (BSL3) laboratory of the University of Florida in Albany, NY, and was in compliance with the Animal Welfare Act and other federal statutes and regulations relating to animals and experiments involving animals. The facility is fully accredited by the American Association for the Accreditation of Laboratory Animal Care.

Preparation of Y. pestis challenge strain for aerosolization.

Y. pestis CO92 (obtained through the NIH Biodefense and Emerging Infections Research Resources Repository, NIAID, NIH) was originally isolated in 1992 from a person with a fatal case of pneumonic plague (6). The 50% lethal dose (LD₅₀) of this strain in mice is 6.8 × 10⁴ CFU inhaled when the strain is administered as an aerosol (whole body) (4). The inoculum for aerosol challenge was prepared as described elsewhere (3), and the suspension of Y. pestis was diluted to the appropriate aerosol challenge dose. Colonies were counted after serial dilution and plating on sheep blood agar plates (SBAPs). These plates were incubated for 2 days at 28°C.

Aerosol infection.

Inhaled doses of 20 LD₅₀ (1 LD₅₀ equals 6.8 × 10⁴ CFU) of Y. pestis were administered to mice by whole-body aerosol. Aerosol was generated using a 3-jet Collison nebulizer (7). All aerosol procedures were controlled and monitored using an automated bioaerosol exposure system (8) operating with a whole-body rodent exposure chamber. Integrated air samples were obtained from the chamber during each exposure, using an all-glass impinger. Aerosol bacteria were serially diluted and plated on SBAPs as described above. The inhaled dose (in CFU per mouse) of Y. pestis was estimated using Guyton's formula (9).

Assessment of animals.

The cohort size for statistical evaluation was 10 to 15 mice. At 1, 12, 24, 30, 36, 42, 45, 48, and 51 h postchallenge, groups of 15 (10 at 1 and 12 h) animals were anesthetized by injecting a mixture containing ketamine-acepromazine-xylazine (6, 0.30, and 0.66 mg/ml, respectively) in a 0.1-ml volume intramuscularly into the caudal thigh. Whole blood was collected by cardiac puncture and serially diluted in sterile saline. After bleeds, animals were sacrificed and their lungs and spleens removed, weighed, homogenized in 1 ml sterile saline, and serially diluted in sterile saline. Serial dilutions of blood, lung homogenates, and spleen homogenates were plated within 30 min after harvest onto SBAPs and incubated at 28°C for 2 days to determine bacterial loads.

Mathematical model of Yersinia pestis growth in the lung, blood, and spleen of the mouse.

The following series of inhomogeneous differential equations describes the growth of Y. pestis after inhalational challenge.

$$dX\left(1\right)/dt=\text{IC}\left(1\right)+K_{\text{growth}-\text{L}}\times X\left(1\right)\times \left\{1-\left[X\left(1\right)/\text{POPMAX}\right]\right\}\times K_{\text{tr}-\text{L}-\text{BL}}\times X\left(1\right)-K_{\text{INNATE}}X\left(1\right)\times {\text{e}}^{\left(-\text{NNATE}\_\text{DECL}\times t\right)}$$ (1)

$$\begin{array}{l}dX\left(2\right)/dt={\text{K}}_{\text{tr}-\text{L}-\text{BL}}\times X\left(1\right)-{\text{K}}_{\text{tr}-\text{BL}-\text{SPL}}\times X\left(2\right)\hfill \\ \text{IF}\left[\text{X}\left(1\right).\text{LE}.\text{THRESHOLD}\right]\text{THEN}\hfill \\ dx\left(2\right)/dt=0\hfill \\ \text{ELSE}\hfill \\ dx\left(2\right)/dt={\text{K}}_{\text{tr}-\text{L}-\text{BL}}\times X\left(1\right)\hfill \\ \text{END IF}\hfill \end{array}$$ (2)

$$dX\left(3\right)/dt={\text{K}}_{\text{tr}-\text{BL}-\text{SPL}}\times X\left(2\right)$$ (3)

In equation 1, the growth of the organism in the lung is described. IC(1) is the initial condition, i.e., the number of CFU/ml in the lung at time zero after challenge spray cessation. K_growth-L is the first-order growth rate constant for organisms in the lung. POPMAX is the maximal population density, and the term “{1 − [X(1)/POPMAX]}” is a logistic carrying function designed to prevent unconstrained bacterial growth and allowing for the organism population to achieve stationary phase. K_tr-L-BL is a first-order rate constant for transfer from the lung to blood. K_INNATE is a first-order kill rate constant generated by innate immunity. Since this was rapidly overwhelmed, as evidenced by the raw data obtained after hour 12, a term decrementing the size of the kill rate constant over time was introduced by multiplying K_INNATE by e^{(−INNATE_DECL × t)}. Equation 2 describes the time course of growth of organisms in blood. Again, by examining the raw data, it became clear that no organisms were detected by blood culture at hours 1 and 12 and were first detected in small numbers at hour 24. Consequently, we coded an “if/then/else” statement that allowed organisms from the lung to spill over into the blood only after a threshold value had been achieved. Equation 3 describes the time course of growth of organisms in the spleen. From the blood, organisms were filtered by the spleen, and K_tr-BL-SPL is the first-order rate constant for transfer of organisms from the blood compartment to the spleen.

All animal data from all three system outputs (lung, blood, and spleen) were simultaneously modeled with BigNPAG (nonparametric adaptive grid), a fully mathematically consistent nonparametric population modeling program described by Leary et al. (10). As the model was a destructive one and we never had more than one datum point per animal for each output, we did not use the “Adaptive γ” feature of BigNPAG. Weighting was performed as the inverse of the observation variance for each output for all the animals within a time cohort. Post-Bayesian estimates were obtained for each animal by employing the “Population of One” utility within the program.

Goodness of fit was examined by pre- and post-Bayesian observed-predicted plots and their regressions for each output. The mean weighted squared error served as the measure of bias, and the bias-adjusted mean weighted squared error served as the measure of precision.

RESULTS

CFU-time course curves for the lung (per g), blood (per ml), and spleen (per g) are presented in Fig. 1. As can be seen, there was a decline in the number of CFU/g in the lung between hour 1 and hour 12 (P < 0.001 by t test). This decrease resulted in the inclusion of an innate immunity term in our model. By hour 24 postexposure, there was again a significant change (increase) in the number of CFU/g of lung tissue, and at this point, we first saw organisms measured in the cultures from the blood and spleen. Note that there were more organisms measured in the spleen than in blood, most likely because of the filtering action of the spleen. Also, whereas the whole of the spleen was cultured, only a sample of limited volume was cultured for blood; at low density, there is a Poisson distribution of organisms in the blood, and the probability of a sample being positive is governed by the sample size. In the lung at the time of the first positive blood culture, there were circa 10⁵ CFU/g of tissue. The rise in counts in the lung between 12 and 24 h and the continuing increase in colony counts past hour 24 resulted in a model term wherein the innate immunity term is decremented in an exponential fashion. After hour 24, we saw exponential growth in all three compartments, until approximately hour 48 for the lung and hour 42 for blood and the spleen. The timing of achieving stationary-phase counts in all three compartments may have an impact on the clinical course of pneumonic plague in the untreated state.

Fig 1.

Counts of Yersinia pestis in the lung, blood, and spleen (CFU/g for lung and spleen and CFU/ml for blood) after an aerosol challenge to cohorts of mice (n = 15).

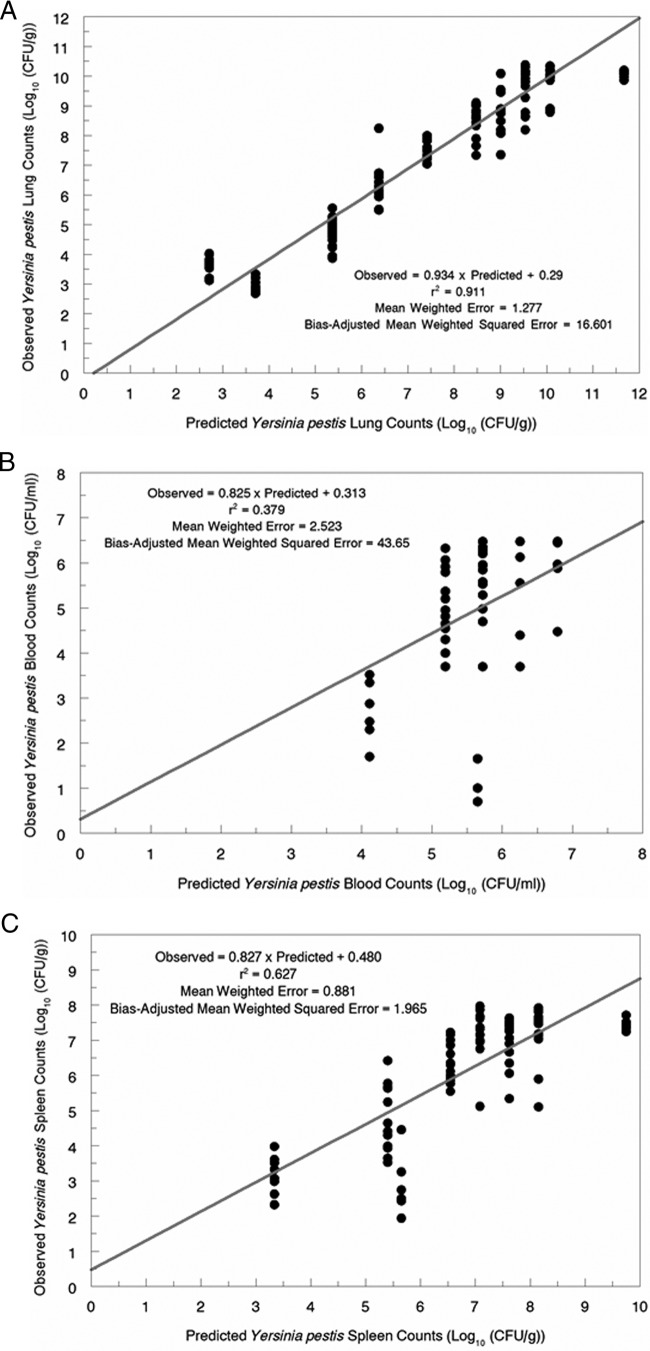
The fit of the model to the data prior to the Bayesian step was quite acceptable. The models are displayed in Fig. 2A to C. For panel A (lung), the r² value was 0.911 (P ≪ 0.001), the bias was 1.277, and the precision was 16.601, which are quite reasonable. For panel B (blood), these values were 0.379 (P ≪ 0.001), 2.523, and 43.65, respectively. The latter value is likely due to three outlier points in the pre-Bayesian estimation. For panel C (spleen), these values were 0.627, 0.881, and 1.965, respectively.

Fig 2.

(A) Observed-predicted plot prior to the Bayesian step of the model for lung counts of Yersinia pestis. (B) Observed-predicted plot prior to the Bayesian step of the model for blood counts of Yersinia pestis. (C) Observed-predicted plot prior to the Bayesian step of the model for spleen counts of Yersinia pestis.

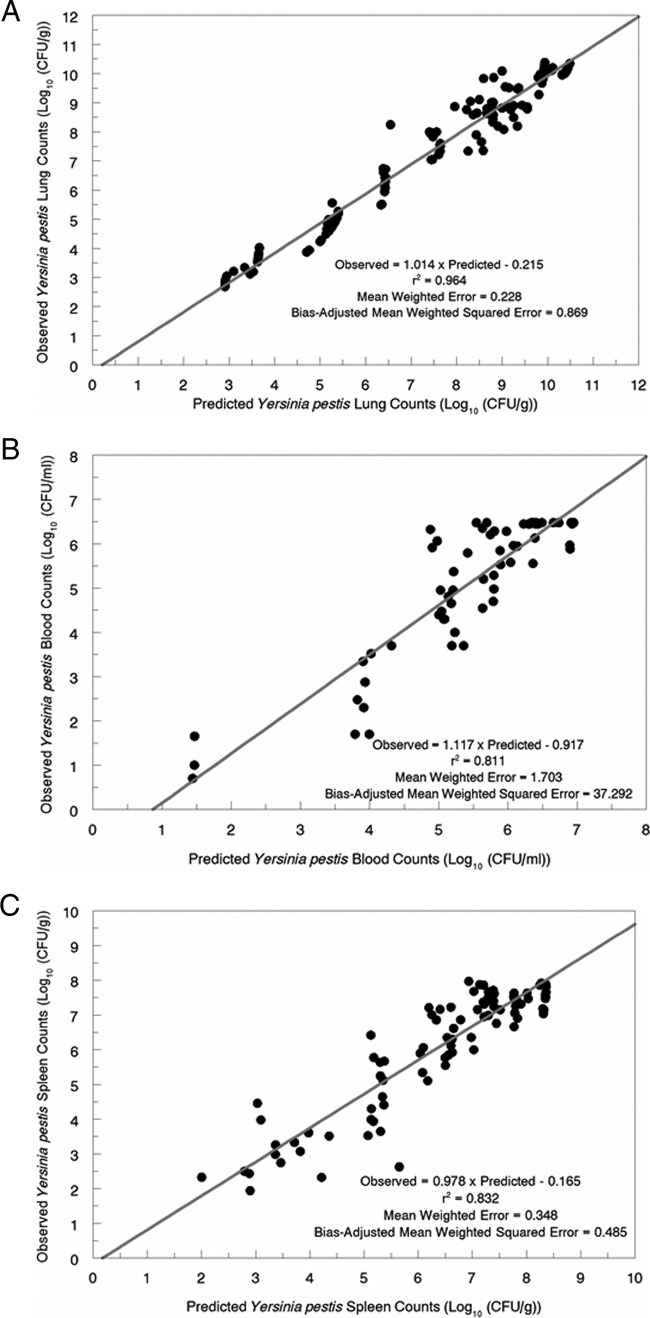
The observed-predicted regressions after the Bayesian step are shown in Fig. 3A to C. For the lung, the r² value was 0.964 (P ≪ 0.001), with a bias of 0.228 and a precision of 0.869. For blood, the values were 0.811, 1.703, and 37.292, respectively. For the spleen, the values were 0.832, 0.348, and 0.485, respectively. Consequently, the fit of the model to the data for all three outputs explained a substantial portion of the variance.

Fig 3.

(A) Observed-predicted plot after the Bayesian step of the model for lung counts of Yersinia pestis. (B) Observed-predicted plot after the Bayesian step of the model for blood counts of Yersinia pestis. (C) Observed-predicted plot after the Bayesian step of the model for spleen counts of Yersinia pestis.

In Table 1, the means, medians, and standard deviations of the population parameter estimates are displayed. K_growth-L in the lung was 0.409 h⁻¹ (mean) or 0.461 h⁻¹ (median), indicating a doubling time of Y. pestis in the lung of 1.5 to 1.7 h. This is quite consistent with the observed increase in lung colony counts seen between hours 24 and 48 (14 to 16 doubling times).

Table 1.

Model parameters

Parameter	Mean	Median	SD
Kgrowth-L (h−1)	0.409	0.461	0.0631
POPMAX (no. of colonies/g)	2.953 × 1014	3.337 × 1013	1.023 × 1015
Ktr-L-BL (h−1)	0.000213	0.0000879	0.000475
Initial condition in lungs (no. of colonies/g)	1,184	135	1,325
Threshold (no. of colonies/g)	1.52 × 106	6.40 × 104	3.20 × 106
Ktr-BL-SPL (h−1)	9.434	12.52	3.815
Kkill-innate (h−1)	3.374	4.934	1.951
Declinnate (h−1)	0.181	0.234	0.0607

The initial condition (number of lung organisms at the end of spray challenge) was between 135 and 1,184 CFU/g (median and mean, respectively). Because of the population nature of the estimation, it is likely that the mean values were somewhat influenced by outliers and that the median is the better measure of central tendency for the number of organisms in the lung at the end of aerosol challenge. Whole-body spray of the mouse produces a baseline lung load of 2 to 3 log organisms.

Again, as seen by examining Fig. 1, very low counts were first seen in the blood at hour 24. All earlier blood cultures were negative. Therefore, the threshold at which blood spillover occurs should be around the lung counts observed at this time. Indeed, the threshold parameter identified 6.4 × 10⁴ CFU/g (median) or 1.52 × 10⁶ CFU/g (mean) as the value. The value of K_tr-L-BL is quite small but is consistent with the rather large organism burden in the lung at the time of spillover into the blood. It should be noted that the increases in bacterial burdens in the three sites occurred in parallel, suggesting that the lung is the driver for all three (with organisms spilled over into the blood and then filtered from blood to the spleen).

The transfer rate constant for transfer from blood to the spleen is large when either the mean or median is examined and is testimony to the efficiency of the spleen's ability to filter the blood.

We hypothesize that the decrement of CFU/g between 1 and 12 h is attributable to innate immunity (the kill rate constant is substantial, at 3.37 to 4.93 h⁻¹) that is overwhelmed by 24 h. The decline in kill rate due to innate immunity has a half-time of about 3.0 to 3.8 h, indicating that between 12 h and 24 h, there is a decline of about 88.5% to 93.75%. Given the growth thereafter, this is a physiologically plausible result.

DISCUSSION

Pneumonic plague is a horrific disease. Unless treatment is started in short order after the onset of symptoms, mortality is 80 to 100% (2). In contradistinction to anthrax, plague pneumonia is highly transmissible from person to person (11). Consequently, early in the time sequence after an intentional release, there may be a number of patients in the first cohort who present in the later stages of the disease and, consequently, will have a low likelihood of survivorship, even with the most aggressive antimicrobial therapy. As it is likely to take a considerable length of time to confirm the identity of the causative pathogen as Yersinia pestis, and even longer to obtain a sensitivity profile for the index case, it is highly likely that secondary spread will occur.

Obviously, early aggressive chemotherapy is critical to patient survivorship. Perhaps as importantly, such early aggressive therapy may play a role in blocking person-to-person transmission. If this is true, it leaves us with the question of why the therapeutic window for plague pneumonia is so foreshortened and why there is such a propensity for person-to-person transmission. In order to obtain some insight into these questions, we employed a mouse model of whole-body aerosol challenge with Yersinia pestis CO92 and then employed a mathematical model to help understand the time course of the disease. As shown in Fig. 2 and 3, the fit of this model to the data is quite acceptable and allows insight into the pathophysiological process.

The raw colony counts in the lung, blood, and spleen shed considerable light on the issue and are displayed in Fig. 1. The 1-h time point after aerosol challenge shows an average CFU/g of lung tissue of 3.64 ± 0.3 log₁₀ CFU/g. Application of the mathematical model (Table 1) indicates that the initial condition in the lung after the cessation of aerosol challenge was 2.13 log₁₀ CFU/g (median estimate) to 3.07 log₁₀ CFU/g (mean estimate). This number increased quickly to the 1-h point but then, surprisingly, decreased to 2.92 ± 0.22 log₁₀ CFU/g at hour 12 (P < 0.01). At hour 24, the count increased to 5.07 ± 0.28 log₁₀ CFU/g. We hypothesized that the initial decrement was at least partially attributable to innate immunity. Since there was a rapid increase in counts, we also hypothesized that Yersinia pestis overcame innate immunity, perhaps attributable to Yersinia outer membrane proteins (Yops) (12, 14). The ability of the mice to suppress Y. pestis amplification was estimated to decline with a half-time of about 3 to 4 h.

At and after 24 h, organisms were first found spilling over into the blood and filtering into the spleen. The model demonstrates counts ranging from 4.81 to 6.18 log₁₀ CFU/g in the lung (threshold value) when we first see bacteremia. An exponential increase is seen thereafter, until stationary phase is obtained at around 48 h for all three compartments. Now the foreshortened course of pneumonic plague becomes understandable. Once the Yops allow innate immunity to be bypassed, the relatively small challenge in the lung can rapidly amplify, so that by 24 h sepsis is seen and, in the absence of intervention, colony counts at 48 h are 6 to 7 log₁₀ CFU/g in the blood, even with an intact spleen. The numbers in the lung are in excess of 10 log₁₀ CFU/g. These numbers are larger than would normally be seen in ventilator-associated bacterial pneumonia patients and occur rapidly. There seems to be a breakpoint of around 42 to 48 h in the course of untreated pneumonic plague where the ability of antibiotics alone to improve survivorship becomes limited (3, 4). It is clear that the ability of plague to circumvent innate immunity so quickly allows organisms to reach densities so great that sepsis becomes overwhelming. One may also speculate that because organisms appear near or at stationary phase in the window of 42 to 48 h, many of them may have a nonreplicative persister (NRP) phenotype and therefore be less sensitive to the lethal effects of antibiotics (13, 15). These results lend greater support to the 42-h postexposure time point for evaluating therapies in the murine model. Successful evaluation in the murine model under these conditions will allow easier decisions to move to nonhuman primate (NHP) studies, where body temperature, telemetry, and other triggers can be used to define when treatment should begin. As NHPs are an expensive and limited resource, in addition to the cost of good laboratory practice studies with telemetry, the importance of an accurate and robust defined treatment time in the murine model has been needed.

In the case of an intentional release, the key to an effective response will be early diagnosis, and the key to that is a high index of suspicion with regard to the causative pathogen on the part of “first responders” in the health care community. Early intervention with an appropriate antibiotic should provide nearly optimal therapy. Interestingly, as shown by Byrne et al. (3), β-lactam antibiotics often accelerate death (hypothesized to be due to endotoxin release), and therefore, initial treatment with β-lactam antibiotics alone is likely contraindicated in the case of pneumonic plague. The ability to initiate treatment when the burden of organisms in the lung is at or below the threshold should not only improve individual patient survivorship but also minimize the number of secondary cases. It is likely that increasing the number of patients who survive after the therapeutic window of opportunity has passed will be a function of the development of adjunctive therapeutics aimed at countering the sepsis syndrome. Treatment of pneumonic plague remains a great challenge, even with the availability of a modern therapeutic armamentarium.