Abstract
Bacterial cells utilize a living peptidoglycan network (PG) to separate the cell interior from the surroundings. The shape of the cell is controlled by PG synthesis and cytoskeletal proteins that form bundles and filaments underneath the cell wall. The PG layer also resists turgor pressure and protects the cell from osmotic shock. We argue that mechanical influences alter the chemical equilibrium of the reversible PG assembly and determine the cell shape and cell size. Using a mechanochemical approach, we show that the cell shape can be regarded as a steady state of a growing network under the influence of turgor pressure and mechanical stress. Using simple elastic models, we predict the size of common spherical and rodlike bacteria. The influence of cytoskeletal bundles such as crescentin and MreB are discussed within the context of our model.
The bacterial cell wall is a living structure that is responsible for maintaining the observed cell shape. The biochemical mechanisms of cell wall synthesis and growth have been extensively studied [1,2]. However, basic questions still remain: How do rodlike bacteria maintain a specific radius but grow in the axial direction? What controls the apparent size of bacterial cells? What are the roles of bacterial cytoskeletal proteins in determining the cell shape and size? To answer these questions, a number of ideas have been proposed. Koch, based on the work of Thompson [3], suggested that bacterial shapes are determined by the surface stress in the cell wall [4]. A different model [5] based on the growth mechanism of the plant cell argued that the growing bacterial cell wall is similar to plastic deformation, and bacteria grow only when a critical stress is reached. In these qualitative models, the relationship among growth, shape, and size of bacteria is not apparent, and the results are specific to certain cell types. In this paper, we develop a general mechanochemical model of the growing bacterial cell wall, which shows explicitly how growth and shape are coupled together to determine the growth velocity and the bacteria size.
The bacterial cell wall is a network of connected glycan strands and peptide chains. The glycan strands are made from a repeating subunit of N-acetylglucosamine (NAG) and N-acetylmuramic acid (NAM). Attached to the N-acetylmuramic acid is a peptide chain of a few amino acids. These peptide chains are cross-linked to peptide chains from other strands to form the meshlike peptidoglycan network (PG) layer (Fig. 1) [2]. NAG-NAM subunits are synthesized at the cytoplasmic side of the inner membrane and translocated to the periplasm. The exported subunits store chemical energy derived from their synthesis in the cytoplasm. This stored energy is released during the addition of new subunits to the existing network, forming new disaccharide and peptide bonds [6]. The PG layer is a constantly evolving network; new subunits are inserted in the existing cell wall, but the existing bonds are also broken by hydrolases and subunits are released from the existing network. The loss of PG subunits can be viewed as the inverse of cell wall growth. For Gram-positive bacteria such as Bacillus subtilis, the released material can be detected in the surrounding medium [7]. In Gram-negative bacteria such Escherichia coli, the released material is probably efficiently recycled [8].
FIG. 1.
(color online). The bacterial cell wall is a growing network of PG strands. PG subunits are inserted at random points along the cell by enzymes. The network is also under mechanical stress from turgor pressure and cytoskeletal influences. The cartoon shows the reversible assembly reaction where the cell wall area increases from A to A + dA. The net energy change of the reaction has a chemical component and a mechanical component [Eq. (1)]. The dotted line is the reaction energy without mechanical contributions, and the solid line includes the mechanical energy.
Although the PG synthesis and turnover processes are complex, at the simplest level, they can be viewed as a reversible assembly reaction. Enzymes catalyze the assembly, but the final PG synthesis steps do not require input of other energy such as ATP. Typically, the product is favored, and the chemical energy change is negative as more PG strands are added to the wall (Fig. 1). However, because the cell wall is under constant tension from turgor pressure, the reaction must be influenced by the mechanical stress in the network. To develop a theoretical description, let us examine the process where the cell wall area increases slightly, or A → A + dA (Fig. 1). The chemical energy released during this growth process is εdA, where ε is the released energy per unit area in the undeformed configuration. At the same time, the originally stress-free PG subunits are stretched and inserted into the existing PG network. Therefore, the mechanical energy of the PG subunits increases. The total change in energy is then
| (1) |
where dU is the change in the strain energy of the network. It should be noted that the insertion of new PG subunits may also change the stress state of the old network. dU depends on the shape and size of the cell wall. This indicates that there could be a size and shape of the cell where the increased strain energy exactly balances the decreased chemical energy and dG = 0. When this configuration is reached, assembly and disassembly reactions exactly balance and the cell wall stops growing.
To compute the mechanical energy, we can specify the undeformed midplane of the cell wall by a 3D surface: r̄(ξ1, ξ2), where a curvilinear coordinate system (ξ1, ξ2) is used. The tangential vectors of the surface are given by , from which a covariant basis (m̄1, m̄2, m̄3) and a contravariant basis (m̄1, m̄2, m̄3) can be constructed in the standard way [9]. In this paper, we use Greek letters to indicate index 1 or 2 and use English letters to indicate index 1, 2, or 3. The metric tensors are defined by ḡαβ = m̄α · m̄β and ḡαβ = m̄α · m̄β. The deformed shape of the cell wall can be described by another three-dimensional surface r(ξ1, ξ2), which is the surface after accounting for turgor pressure and other forces. In the same fashion, we introduce two sets of basis (m1, m2, m3) and (m1, m2, m3) and the metric tensor gαβ for the deformed surface.
Since the thickness of the cell wall, h, is much less than the overall dimensions of the cell, we can use the theory of thin shells to estimate the mechanical energy. The transverse shear stress resultants and the internal moments can be neglected. In this case, the stress resultants are symmetric and fully decoupled from the internal moments. The mechanical load on the wall is the turgor pressure P. Here we assume that the growth process is slow and the cell wall is always in mechanical equilibrium. The stress balance equations are
| (2) |
| (3) |
where Tαβ is the stress resultant tensor, are the Christoffel symbols of the second kind, and καβ is the curvature tensor [9]. The solutions of these equations allow us to compute the total cell wall energy
| (4) |
where the first term is the mechanical stretching and bending energies of the cell wall. The last term is the chemical energy. Here we define an elasticity tensor following Bower [9]: Dαβρμ = λḡαβḡρμ + μ(ḡαρḡβμ + ḡαμḡβρ), where and , with E and ν the Young’s modulus and Poisson ratio of the PG layer, respectively. The midplane Lagrange strain tensor is defined by .
The rate of wall growth should be proportional to the net flux of adding more materials to the cell wall. We postulate that this flux is proportional to the magnitude of the total energy change. For a small added area dA, the change in energy is dG. Therefore, we define the growth velocity as
| (5) |
where ḡ is the determinant of ḡαβ and M is a phenomenological constant that is determined by the kinetics of the growth mechanism. The driving force F for growth is the energy decrease in the cell wall per unit length of growth:
| (6) |
It is clear that growth stops when F = −δG/δr̄ = 0.
If the cell wall grows in a self-similar manner, i.e., the shape of the bacterial cell wall is determined by several parameters ai, then the change in the total energy is dG =Σi − Fidai. Fi is the driving force corresponding to the parameter ai:
| (7) |
The growth velocities can be described by
| (8) |
For growing spherical cells such as Cocci, the solutions of these equations are particularly simple. In this case, we have only one free parameter, the radius of the cell. If we assume small deformations, the total energy of the cell wall and the growth velocity are, respectively,
| (9) |
and
| (10) |
where R is the radius of the cell. The total energy has a minimum at which the increased strain energy is balanced by the released chemical energy as shown in Fig. 2(a). The radius corresponding to this minimum defines a steady state size Rs for the cell:
| (11) |
FIG. 2.
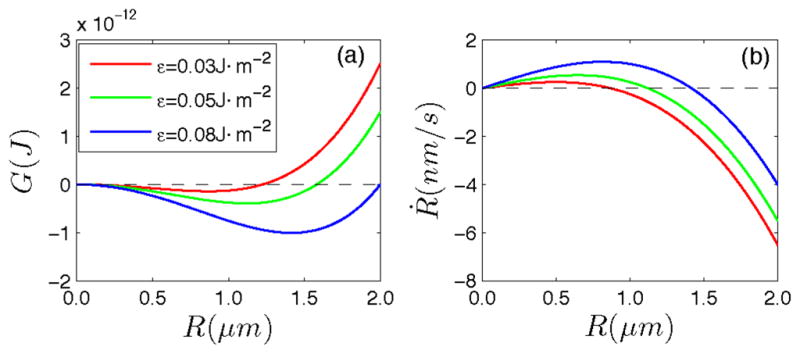
(color online). (a) The free energy of a spherical bacteria as a function of radius R. (b) The growth velocity of a spherical bacteria vs bacteria radius. The parameters are P = 0.2 MPa, E = 50 MPa, ν = 0.3, h = 7 nm, ε = 0.05 J m−2, and M = 0.01 m2 J−1 s−1.
This radius corresponds to the observed size of the cell and is also the stable fixed point of Eq. (10) as shown in Fig. 2(b). This implies that if any of the parameters are changed suddenly, a new steady state radius will develop. Equation (11) neglects cell wall bending energy since the bending energy is relatively small when compared to the stretching energy at this length scale. If we consider bending, Eqs. (9)–(11) would be modified slightly, but all conclusions are similar.
For rodlike cells such as E. coli the total energy is
| (12) |
where R is the bacterial radius and L is the length of the cylinder region. The cell poles are rigid and inert [10]. Therefore, we neglect the poles in this calculation. The growth equations are
| (13) |
| (14) |
The time evolutions of the radius and length of rodlike bacteria with varying initial radius are shown in Fig. 3. The phenomenological constant M is estimated to be 0.01 m2 J−1 s−1 since under optimal conditions E. coli doubles its length and divides every 20 minutes. Results show that there is always a steady radius
FIG. 3.

(color online). The time evolution of the radius and length of rodlike bacteria with varying initial radius. The inset of (b) is the growth velocity in the axial direction. The parameters are P = 0.2 MPa, E = 50 MPa, ν = 0.3, h = 7 nm, ε = 0.05 J m−2, and M = 0.01 m2 J−1 s−1. The cell lengths as functions of time in (b) are almost indistinguishable. (b) can be compared with experimental measurements in Ref. [20].
| (15) |
and bacteria grows at a constant speed in the longitudinal direction once this steady radius is reached. To explain exponential elongation [11] of bacteria, the left-hand side of Eqs. (13) and (14) is replaced by strain velocities Ṙ/R and L̇/L, respectively. The steady radius remains unchanged, but the length increases exponentially. Note that the phenomenological constant M should depend on the spatial and temporal distribution of penicillin-binding proteins. For example, during division, penicillin-binding proteins are concentrated near the midcell. Together, these results show that directionality of PG insertion is determined by the local strain energy, which is in turn determined by the local geometry. Therefore, growth, shape, and size of bacteria are coupled together through the strain energy.
The growth equations predict that the cell should elongate indefinitely if nutrients are optimal and division is inhibited. This is in accord with experimental observations [12]. Another interpretation is that division is simply a way to separate a continuously elongating cell. Furthermore, the growth velocity is correlated to the steady radius through ε as shown in Fig. 4(a). This may explain why the bacteria radius is larger under high growth rate conditions [13] because ε is directly proportional to the density of chemical bonds in the PG layer and the availability of enzymes. ε is one of the factors that will effectively control the radius and growth velocity of bacteria. Equations (13) and (14) also suggest that the longitudinal growth rate depends on the cell radius. If the cell radius is artificially controlled, for a critical radius , the elongation rate approaches zero.
FIG. 4.

(color online). (a) The growth velocity in axial direction for rodlike bacteria vs the steady radius Rs. Larger cells grow faster, although the (Rs, ε) → 0 limit is unphysical and should not be considered. The parameters are the same as Fig. 3. (b) MreB (red line) can be modeled as an additional mechanical influence on the cell wall. By solving Eq. (5), we observe that the shape of the cell can slowly morph from a sphere to a rod, in agreement with experimental observations.
Typical values of parameters for Gram-negative bacteria are P ≈ 0.2–0.3 MPa, E ≈ 20–70 MPa, and h ≈ 3–10 nm [10]. We assume ν = 0.3. The bond energy per unit area, ε, has not been measured specifically for bacteria. But for typical C-O covalent bonds in the glycan backbone, the bond energy is approximately 360 kJ/mol. Peptide bond energies are significantly lower. In each pore of area 25 nm2, there are roughly 2 C-O glycan bonds and 1 peptide bond per layer of PG network, giving ε ≈ 0.05 n J · m−2, where n is the number of PG layers. Usually, n = 1–3 for Gram-negative bacteria. For Gram-positive bacteria, the parameters are P ≈ 1.5 MPa, E ≈ 30 MPa, h = 20–40 nm, and n = 3–8 [10]. These parameters predict that Rs is roughly 0.5 μm for both Gram-negative and Gram-positive cells, in agreement with observations of most bacterial cells.
For crescent-shaped cells such as Caulobacter crecentus, the growth equations are similar to that of rodlike bacteria. In this case, the free parameters are the curvature radius of the center line R0 and the radius of cross section of the bacteria R. Under the assumption R0 ≫ R, the growth equations are identical to those of rodlike bacteria except that L in Eqs. (13) and (14) is replaced by R0. Similar to rod-shaped bacteria, the curvature radius R0 grows at a constant speed if there are no external or internal constraints. This is consistent with the experimental observations that the curvature is relaxed after curved E. coli is released from microchambers that constrained the growth of the cell [14,15].
An important question is how naturally curved bacteria, which are not influenced by external constraints, maintain their curvature. A possible answer is that these bacteria are restrained by intermediate filamentlike proteins inside the cell [16,17]. Experiments have shown that C. crescentus loses its helical shape and resembles a straight rod in the absence of crescentin [15]. Several other cytoskeletal filaments such as MreB and RodZ are also involved in changing the cell shape from spheroids to rods [16]. A potential mechanism for MreB is that it can exert forces on the lateral cell wall and oppose or enhance turgor pressure, depending on its spontaneous curvature. This force is likely small, ~5% of turgor pressure [18], and in the cylindrical geometry it does not affect the steady state radius of Eq. (15) significantly. But if the cell is not in the cylindrical geometry, the force MreB can influence the shape of the cell [Fig. 4(b)]. In a similar manner, the bacterial tubulin homologue FtsZ also influences cell shape by exerting a small contractile force at the midcell, generating a division septum [19]. These cases will be discussed more completely by examining force generation mechanisms of these cytoskeleton bundles and solving Eq. (5) for arbitrary shapes.
The main concept we introduced in this paper is that the competition between mechanical energy and chemical energy can determine the cell wall growth dynamics and lead to size limits of bacterial cells. Using a simple elastic model to describe the mechanical energy, we make predictions on the steady state geometry of regular bacteria. It is important to recognize that the total energy in the form of Eq. (1) is a simplified model. The molecular structure of the cell wall is complex, and a more accurate constitutive model should yield more quantitative results. It is also not clear whether the steady shape of the cell is entirely determined by energetics and not by kinetics of the growth mechanism. Nevertheless, mechanics and chemistry must be considered on an equal footing to understand the growth and morphology of living systems.
References
- 1.Holtje JV. Microbiol Mol Biol Rev. 1998;62:181. doi: 10.1128/mmbr.62.1.181-203.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Vollmer W, Bertsche U. Biochim Biophys Acta, Biomembr. 2008;1778:1714. doi: 10.1016/j.bbamem.2007.06.007. [DOI] [PubMed] [Google Scholar]
- 3.Thompson DAW. On Growth and Form. Cambridge University Press; Cambridge, England: 1917. [Google Scholar]
- 4.Koch AL. Bacterial Growth and Form. 2 Springer; New York: 2001. [Google Scholar]
- 5.Boudaoud A. Phys Rev Lett. 2003;91:018104. doi: 10.1103/PhysRevLett.91.018104. [DOI] [PubMed] [Google Scholar]
- 6.Koch AL. Appl Environ Microbiol. 2000;66:3657. doi: 10.1128/aem.66.9.3657-3663.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pooley HM. J Bacteriol. 1976;125:1127. doi: 10.1128/jb.125.3.1127-1138.1976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Park JT, Uehara T. Microbiol Mol Biol Rev. 2008;72:211. doi: 10.1128/MMBR.00027-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bower AF. Applied Mechanics of Solids. CRC Press; Boca Raton, FL: 2009. [Google Scholar]
- 10.Thwaites JJ, Mendelson NH. Adv Microb Physiol. 1991;32:173. doi: 10.1016/s0065-2911(08)60008-9. [DOI] [PubMed] [Google Scholar]
- 11.Nanninga N. Molecular Cytology of Escherichia coli. Academic; London: 1985. [Google Scholar]
- 12.Margolin W. Nat Rev Mol Cell Biol. 2005;6:862. doi: 10.1038/nrm1745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Young KD. Microbiol Mol Biol Rev. 2006;70:660. doi: 10.1128/MMBR.00001-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Takeuchi S, et al. Nano Lett. 2005;5:1819. doi: 10.1021/nl0507360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cabeen MT, et al. EMBO J. 2009;28:1208. doi: 10.1038/emboj.2009.61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cabeen MT, Jacobs-Wagner C. Nat Rev Microbiol. 2005;3:601. doi: 10.1038/nrmicro1205. [DOI] [PubMed] [Google Scholar]
- 17.Kim JS, Sun SX. Biophys J. 2009;96:L47. doi: 10.1016/j.bpj.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Allard JF, Rutenberg AD. Phys Rev E. 2007;76:031916. doi: 10.1103/PhysRevE.76.031916. [DOI] [PubMed] [Google Scholar]
- 19.Lan G, Wolgemuth C, Sun SX. Proc Natl Acad Sci USA. 2007;104:16 110. doi: 10.1073/pnas.0702925104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Reshes G, et al. Biophys J. 2008;94:251. doi: 10.1529/biophysj.107.104398. [DOI] [PMC free article] [PubMed] [Google Scholar]



