Abstract
Eukaryotic and prokaryotic cells use cytoskeletal proteins to regulate and modify cell shape. During cytokinesis or eukaryotic cell crawling, contractile forces are generated inside the cell to constrict the division site or to haul the rear of the cell forward, respectively. In many cases, these forces have been attributed to the activity of molecular motors, such as myosin II, which, by pulling on actin filaments, can produce contraction of the actin cytoskeleton. However, prokaryotic division is driven by the tubulin-like protein FtsZ and does not seem to require additional molecular motors to constrict the division site. Likewise, Dictyostelium discoideum and Saccharomyces cerevisiae can perform cytokinesis under motor-free conditions. In addition, many crawling cells can translocate when myosin is inhibited or absent. In this review, we point out another force-generation mechanism that can play a significant role in driving these processes in eukaryotes and prokaryotes. This mechanism is mediated by cross-linking and bundling proteins that form effective interactions between cytoskeletal filaments. Some recent studies in this area are reviewed and the physical underpinnings of this force-generation mechanism are explained.
Introduction
Cells and living organisms must maintain structural cohesion and generate forces in order to complete their life cycle. Cytoskeletal filaments, such as F-actin, microtubules, and intermediate filaments, are the primary components involved in these tasks. In the cell, cytoskeletal filaments serve a number of important roles: they are the primary structural scaffolds of the cell; they act as passive tracks for intracellular transport; and they are involved in essential cellular tasks such as division, signaling, and cell motility. All of these processes rely heavily on cytoskeletal growth, remodeling, and maintenance, and emerging insights are beginning to demystify cytoskeletal regulation [1–4]. For example, the growth of actin filaments is important in the generation of cell protrusions and cell motility: by virtue of momentum balance, these growing polymers can exert forces. And, indeed, the physical underpinnings of protrusive force generation, spanning from the molecular to the cellular level, are now reasonably well understood [3]. Computational modeling of these motions has captured many of the salient features observed in experiments, including the actions of the actin-nucleation factors Arp2/3 complex and formins [5]. Nevertheless, protrusive force generation is only part of the story. Equally important are contractile forces, which are needed to pull up the trailing edge during cell movement and to constrict the cell circumference during division. Traditionally, contractile forces are thought to originate from non-muscle myosin-II, an ATP-powered molecular motor that slides actin filaments relative to each other. However, emerging evidence suggests that bundling and cross-linking of cytoskeletal filaments may also be a general mechanism for generating these forces. In this review, we summarize a physical mechanism that may allow cells to produce contractile forces without molecular motors and discuss evidence that this mechanism plays a role in cell motility and cell division.
Using Cross-linking, Bundling, and Depolymerization to Contract
Force generation at the molecular level typically relies on harnessing energy in a strongly fluctuating thermal environment. While fluctuating random motions by themselves cannot do net work, chemical energy can be used to ratchet favorable fluctuations and accomplish useful tasks. Or, in physics-speak, force generation at the molecular level can be understood from the statistical thermodynamics concept of the free energy, which includes enthalpic and entropic contributions from molecular interactions such as chemical bond energies, solvent re-arrangement, and enzyme conformational change (Box 1). This is why ATP can be used as a fuel source for force generation: its terminal phosphate bond stores about 100 pN×nm of chemical free energy that is released during hydrolysis. Motor proteins utilize the phosphate bond free energy, and, in a manner similar to mechanical engines, channel it to perform mechanical work. Forces generated by growing actin filaments are also powered by the binding free energy of adding monomeric G-actin to the barbed end of F-actin. There are other ways that free energy changes can be leveraged. Classic examples are the entropic work performed by expanding gas in pistons, which still powers most mechanical engines, and the contraction of a heated polymer, which is also entropic in origin.
Box 1 A glossary of terms and equations describing the physics behind contraction induced by cross-linking
Binding energy
The energy required to break a chemical bond. For example, the actin cross-linking proteins fascin and α-actinin have binding energies of about 15kBT [1] and 2 kBT [2], respectively.
Elastic forces
In solid objects, the force between neighboring molecules is related to the distance between the molecules and the stiffness of the material. The stiffness of the material is usually stated in terms of the shear modulus and the Young’s modulus.
Enthalpy
The capacity to do non-mechanical work and/or release heat. In terms of chemical bonds, it defines the energy stored in the bonds.
Entropy
The number of accessible configurations (states) of a molecular system, which sharply varies with factors such as the internal energy and volume of the system. Therefore, the system will likely adopt energies and volumes with the highest number of accessible states, maximizing entropy.
Free energy
The available mechanical work that can be extracted from a system when entropic and enthalpic factors are taken into account. Bond energies are forms of free energy where molecular level interactions and fluctuations both contribute.
Stress
The force per area that acts on the surface of an arbitrary volume. The force per volume (f) is given by the divergence of the stress (σ): f = ∇ · σ. The stress can be derived by considering how the free energy changes with the density of the cytoskeletal filaments. When the free energy is written in terms of the fraction of filaments per volume, ϕ, the magnitude of the stress is approximately equal to
where ϕ0 is the preferred volume fraction, which depends on the binding energy and density of the cross-linking proteins, and Vm is the size of a single monomer of the cytoskeleton. From the definition of the force per volume, the total force generated inside a cell can be estimated as F = kBTϕ03L2/Vm, where L is a characteristic size of the cell. Assuming a volume fraction of 5%, a cell size of 10 µm, and a monomer volume of 10 nm3, this force is around 4 nN.
Viscous forces
In fluids, the viscous force between neighboring molecules is proportional to the velocity with which the molecules slide against each other. The strength of this interaction is given by the fluid viscosity η. In migrating cells, the viscosity of the actin cytoskeleton is around 50 pN×s/µm2 [4]. The magnitude of the viscous stress in a fluid is the viscosity times the velocity gradient. Balancing the viscous stress in the cytoskeleton, with the stress from the free energy, the maximal velocity can be estimated as Vmax = σL/η. Using the numbers above, the maximum velocities are a few microns per second. Drag between the substrate and the cytoskeleton can greatly reduce this maximum value.
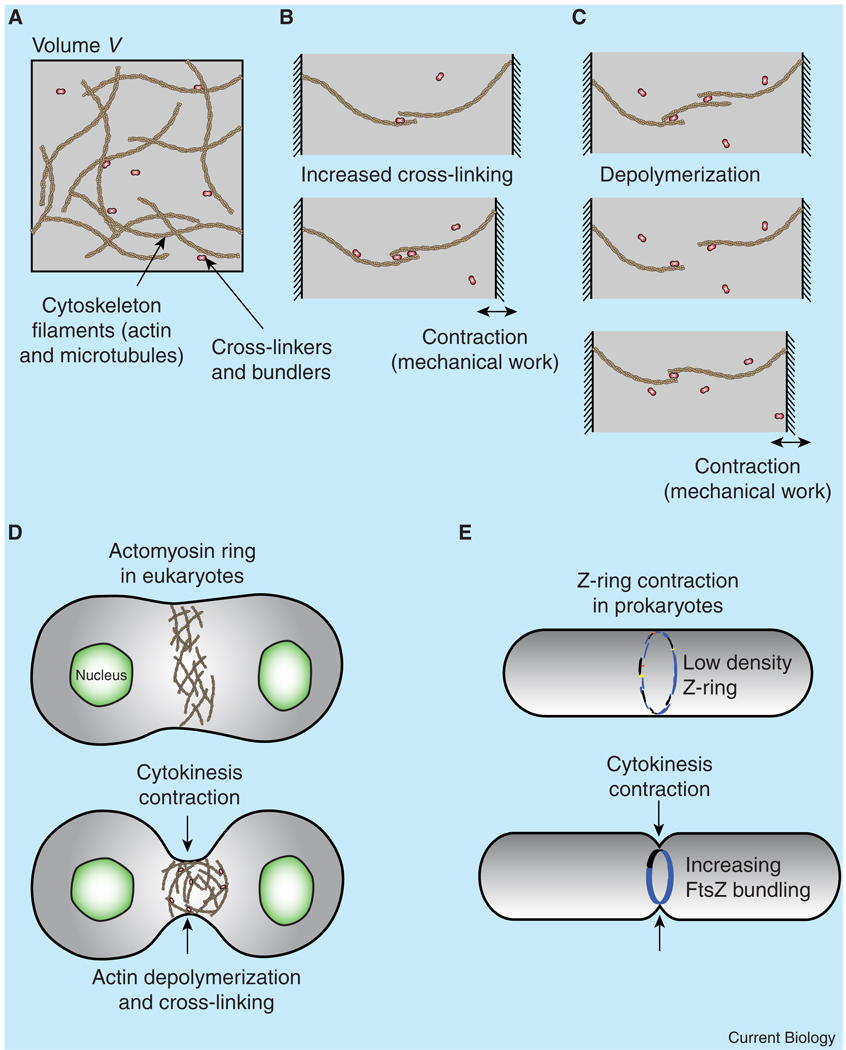
How might cells use similar mechanisms to generate contractile forces without molecular motors? Consider the case of a solution of non-interacting filaments. Random motions of the filaments (entropy) act to disperse the filaments evenly throughout the solution. If attractive interactions are then introduced between the filaments, such as by adding proteins that can cross-link the filaments, then there will be a tendency for the filaments to coalesce, i.e., the overall density of the network will tend to increase because it is favorable for the filaments to be closer to each other. If an external load is attached to some of the filaments, the density increase will generate mechanical work (Figure 1). And, if the total number of filaments is constant, then the density increase will also lower the volume of the network, leading to a contraction.
Figure 1. Mechanisms of contractile force production by cross-linking/bundling proteins and depolymerization.
(A) The cytoskeleton is composed of polymer filaments that can be cross-linked by cross-linking/bundling proteins in the cytosol. (B) Consider two moveable walls, each with a polymer grafted to it and with a solution of cross-linkers between them. When there is overlap between the two polymers, the cross-linking proteins can bind the filaments together, increasing the total binding energy of the system. Thermal fluctuations that increase the overlap between the filaments will be energetically favored, as they provide more opportunities for binding of the cross-linkers. Higher densities of cross-linking proteins produce larger, but slower, contractions. (C) Now consider a similar system with an intermediary filament bound to each of the grafted polymers. Disassembly of the central filament along with thermal fluctuations can allow the two remaining polymers to bind, which ratchets the system in a contracted state. These mechanisms may explain how cytokinesis can occur without motors. (D) In eukaryotic cells, a division ring made of F-actin, myosin II, and other cross-linking proteins is responsible for contracting the cell during division. The contraction can proceed without myosin motor activity, with some experiments suggesting that cross-linking and depolymerization of F-actin may play an important role. The mechanisms described in (C) could be responsible for contractile force generation. (E) In prokaryotic cells, division is carried out by the Z-ring, which is a disordered assembly of short FtsZ filaments. Again, lateral bundling interactions between FtsZ filaments can drive contraction.
These physical ideas can be quantified using simple models for the free energy, such as the original phenomenological theories of van der Waals, which are still the standard model for describing attractive gases, fluids, and polymers. In these models, the free energy of a system of particles is defined in terms of the density of the particles in the system. The entropic part of the free energy favors low particle (filament) density, which acts like a pressure that tries to expand the volume. The enthalpic part of the free energy includes attractive interactions between the particles (filaments), which favors high densities where the particles (filaments) can maximize their interactions with each other. These opposing factors compete and drive the system to a preferred density. If the density of the particles deviates from this preferred density, then there is a restoring force that tries to return the system to the preferred density. In other words, a network of filaments that is not at the ‘correct’ density will expand or shrink toward the preferred configuration, leading to force production. For soft filaments or polymers, additional free energy contributions arise from the configurations of the polymer. For example, in the absence of external constraints, polymers tend to adopt a compact globule shape. But these additional details do not change the basic picture outlined here.
For the eukaryotic cytoskeleton (i.e., F-actin and microtubules), direct attractive interactions between filaments are presumably weak. Indeed, microtubules themselves do not interact directly, even though tubulin protofilaments bundle together to form the microtubule. Cross-linking and bundling proteins, however, can produce effective interactions between actin filaments or microtubules, with the added benefit that these interactions can then be regulated. For F-actin, α-actinin and fascin are two common cross-linking and bundling proteins [6,7]. From the free energy standpoint, the configuration of two filaments cross-linked by one of these proteins is more favorable than the configuration where the filaments are not cross-linked. The free energy of cross-linking depends on the concentration of cross-linkers. Thus, by controlling the spatial and temporal concentrations of bundlers and cross-linkers, the cell has the ability to control the configuration of the cytoskeletal network and generate forces at appropriate times.
In addition to controlling bundling and cross-linking, cells can actively control the state of polymerization of the cytoskeleton. Perhaps counter-intuitively, depolymerization of cytoskeletal filaments in the presence of cross-linkers can generate contractile forces (Figure 1). Here, depolymerization reduces the filament density. The cytoskeletal network responds by reorganizing to return to the preferred density, i.e., it contracts. An important caveat of this mechanism is that the dissociated monomer must be able to escape the local region where it depolymerized, because the monomer will produce a pressure on the filaments that could act to swell the system.
Physical Requirements and Limitations
An important requirement for these mechanisms to work is that the cross-linking/bundling proteins must form transient connections between the filaments. If the cross-links are permanent, then the cytoskeleton will be unable to reorganize and would be unable to respond to changes in density. Therefore, the binding energy of a single cross-linking or bundling protein should not exceed a few kBT (where kB is Boltzmann’s constant and T is the absolute temperature). An interesting consequence of the transient binding of these proteins is that it naturally leads to viscoelastic behavior. On timescales shorter than the off-rate for the cross-linking proteins, the filament network will behave like an elastic solid, whereas on longer timescales, the network can flow and, therefore, behaves like a viscous fluid. And, indeed, the actin cytoskeleton shows viscoelastic behavior with a crossover time between these two regimes of a few seconds [4,8–11]. In fact, the dynamics of two cross-linked filaments sliding against each other can be described by a simple solvable model, which results in both elastic and viscous (friction) forces between the filaments, and, at the whole-cell level, these processes may allow cells to sense the mechanical properties of their environment [12].
The concepts presented in the last few paragraphs can be summed up in a convenient way. Attractive interactions between filaments pull the filaments together, where thermal fluctuations try to pull them apart. These two effects conspire to drive the filaments to a certain density. If the system is at a lower density, then there will be forces that act on the filaments that pull them together. If the binding energy between the filaments is large, then the force can be large. However, large binding energies mean that the cross-links that hold the system together are long-lived. Therefore, even though there are large forces, the system will contract slowly. At low binding energies, the turnover time of the cross-links is fast, but the forces are weak. The system still contracts slowly. In between these two regimes, however, it is possible to get moderate forces and moderate contraction velocities.
Estimating the Forces and Velocities Produced by Cross-linking, Bundling, and Depolymerization
But how much force can really be generated by cross-linking and/or depolymerization? The simplest case to consider is that of two parallel filaments with evenly spaced cross-linking sites arranged along the length. If the filaments do not completely overlap (as in Figure 1B), then an order of magnitude estimate of the force between the filaments is given by the binding energy of a single cross-link times the number of cross-link sites per length. If the spacing between cross-link sites is 20 nm and the binding energy is equal to kBT, then the two filaments would each experience a force of around 0.2 pN, roughly ten times less than the maximum force from a single molecular motor. A model for cell division estimates that the force required to constrict a bacterium during cell division may be as small as 10 pN [13], which would then only require around 50 filaments.
The forces driving eukaryotic cell crawling are significantly larger. For example, the force required to halt a crawling keratocyte is on the order of 10 nN [14]. Can bundling and/or depolymerization account for this scale of force production? To describe the behavior of large numbers of filaments, it is easiest to work in terms of the stress (which describes the force per area that is exerted on the surface of a volume containing the filaments). The free energy discussed in this review leads to a stress that is roughly proportional to the difference between the actual cytoskeletal density and the preferred density [15]; i.e., the cytoskeleton behaves like a spring (see Box 1 for the equation relating stress to force). A rough estimate of the maximum force that can be generated is 10 nN, which can lead to cytoskeletal velocities of up to a few microns per second (Box 1).
Cytokinesis and Cell Motility Without Molecular Motors
A number of recent experiments across different organisms support this view of force generation without molecular motors. Take, for example, bacterial cell division. Bacterial cells grow, replicate their DNA, partition the two copies of the genome to opposite sides of the cell, and then constrict the cell envelope while building new cell-wall material, which divides the cell into two daughter cells [13]. Constriction of the cell is dependent on the Z-ring, a conglomerate of proteins that forms a hoop-like structure at the center of the cell in rod-shaped bacteria and also forms a ring-like structure in coccoid-shaped cells [16,17] (Figure 1E). The major component of the Z-ring is FtsZ, a bacterial homologue of tubulin. Like tubulin, FtsZ itself forms filaments and has weak bundling activity, but microtubule-like structures have not been observed. In addition, there do not seem to be motor proteins like dyneins and kinesins that bind to FtsZ. How then does the Z-ring constrict? One hypothesis is that lateral bundling interactions between FtsZ filaments cause the contraction, and computational modeling confirms that this mechanism can produce sufficient force to drive cytokinesis [18]. An alternative mechanism is based on the possible conformational change of GTP-bound FtsZ upon GTP hydrolysis, generating curved FtsZ filaments [19,20]. But the GTP hydrolysis activity of FtsZ was not found to be essential for division [21]. It is possible, though, that multiple mechanisms are at play in the Z-ring in order to achieve robustness.
Cell division in eukaryotic cells does not always require motor proteins either. Here a ring composed of actin, myosin II, and a number of other proteins forms at the center of the cell (Figure 1D). As in bacteria, constriction of this ring separates the cell into two halves. This constriction is believed to be driven by myosin-induced contraction of the actin. In two organisms, however, there is evidence that this is not the sole mechanism driving constriction of the division site. Dictyostelium discoideum cells that are adhered to a substrate can divide even when myosin is absent; cells in suspension, however, still require myosin in order to divide [22,23]. Interestingly, the actin-bundling protein cortexillin concentrates near the division furrow and facilitates contraction [24]. In addition, cytokinesis in myosin II null Dictyostelium cells can be described by a model in which cortical tension induces contraction [25] and the dynamics of contraction correlate with perturbations in cortical cross-linking proteins [26]. Furthermore, modeling also shows that depolymerization in the presence of cross-linkers that track actin filament ends can explain cytokinesis in myosin II null cells [27]. In Saccharomyces cerevisiae, an actin–myosin division ring also carries out cytokinesis. But again, the motor activity of myosin is not required for successful division [28–30]. Instead, gradual actin depolymerization during contraction is observed. Since myosin itself is a cross-linker of actin filaments, it is possible that the cross-linking activity of myosin is more important than the motor activity and, in conjunction with regulated depolymerization, is able to generate sufficient forces.
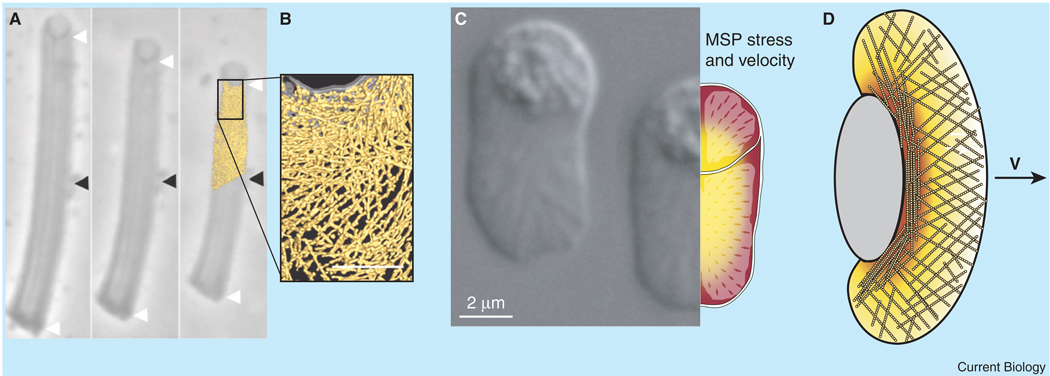
In crawling cells, the leading edge is pushed forward by polymerization of the actin cytoskeleton, and the rear of the cell is believed to be hauled forward by contraction of the cytoskeleton. The force driving this contraction has traditionally been attributed to myosin motor activity [31]; however, myosin II-null D. discoideum cells are still capable of locomotion [32,33], and myosin IIA-deficient fibroblasts migrate faster than wild-type cells [34]. Likewise, inhibition of myosin using blebbistatin or ML-7 only moderately affects the crawling speeds of fish keratocytes on 2D substrates [35] or cancer cells in 3D matrices [36,37]. So, how do cells haul themselves forward when myosin is inhibited or absent? One possibility is that the depolymerization mechanism mentioned above may play a role. Indeed, in vitro experiments using the major sperm protein (MSP) cytoskeleton of nematode sperm showed that MSP depolymerization accompanied force-producing contraction of the network [38], and a model for depolymerization-induced contraction can reproduce the dependence of crawling speed on cell size and shape [15] (Figure 2). The mechanism underlying this force production was originally explained by the entropic elasticity in the network [39]; however, more recent experiments show that the MSP in the comet tails is shorter than the persistence length of the filaments [40], which argues against the entropic elasticity model since short filaments are relatively rigid and the force from entropic elasticity depends on the flexibility of the filaments. Might depolymerization also produce forces in actin-based crawling cells? One hint that this is the case comes from traction force microscopy of D. discoideum, where cells expressing a myosin II mutant that lacks the essential light chain but retains actin cross-linking activity show only a slight reduction in traction force [41]. Therefore, transient cross-linking of depolymerizing actin by myosin may help to drive migrating cells.
Figure 2. Cell crawling driven by depolymerization of the cytoskeleton.
In nematode sperm, a major sperm protein (MSP) cytoskeleton drives motility. In vitro, MSP will polymerize behind vesicles, forming a dense network of short, fairly rigid filaments that push the vesicle. (A) Disassembly of the MSP filaments leads to a contraction of the MSP network that can pull the vesicle; however, tomographic imaging shows that the filaments are too short and rigid for the contraction to be due to entropic bundling of the MSP (B). (Note that the MSP filaments are not drawn to size in (A).) Black arrowhead points to a stationary feature at the center of the MSP comet tail. White arrowheads show the comet tail ends. Scale bar in (B) is 0.2 µm. (C) Mathematical modeling of C. elegans sperm motility, consistent with the depolymerization mechanism described in this review, has shown that depolymerization of the cytoskeleton can produce significant stress inside the cell to pull the cell forward, while also producing realistic MSP flows. The colormap and arrows on the right show the mathematical model predictions for the cytoskeletal stress and velocity. (D) Actin-based cell motility may involve similar mechanisms. Fish keratocytes crawl with a roughly constant speed V while maintaining a characteristic half-moon shape. The actin at the leading edge is dendritic; however, high concentrations of myosin at the rear of the cell (shown by the colormap) cause the actin to align and bundle in a direction perpendicular to the direction in which the cell crawls. Myosin-mediated cross-linking of actin filaments may produce some of the contractile force inside the keratocyte. Gray oval denotes the cell body. In addition, actin depolymerization may also assist. Panels (A,B) redrawn from [38,40]. Panel (C) redrawn from [15].
Conclusions
We have seen that cells can utilize a variety of physical mechanisms for generating forces during cytokinesis and cell movement. Though not directly related to force production, it should be noted that similar physical mechanisms may also play an important role in other arenas of cell biology. For example, during the development of Caenorhabditis elegans embryos, the progenitors of the germ cells contain RNA-rich cytoplasmic bodies called P-granules, whereas all other cells do not [42,43]. Recent experiments have shown that P-granules behave as a liquid droplet, held together by weak binding affinities and, presumably, spatial modulation of binding affinities causes the granules to coalesce preferentially on one side of the fertilized egg [44]. Therefore, P-granule localization, and possibly other mechanisms underlying cell differentiation, may rely on similar physical principles as the force-producing mechanisms that we described here. Indeed, a good generic mechanism (nicely described by a simple theory) can easily be subsumed to accomplish different tasks.
It is now clear that cytoskeletal proteins are much more than simple mechanical elements. Cells have a number of accessory proteins that can actively regulate the behavior of the cytoskeletal network. Taking advantage of a variety of physical mechanisms, cells can generate forces in surprising ways. Motor proteins are only a part of the story. These different available mechanisms of course contribute to the robustness and redundancy that are needed for cells to thrive in different environments.
References
- 1.Ono S, Yamakita Y, Yamashiro S, Matsudaira PT, Gnarra JR, Obinata T, Matsumura F. Identification of an actin binding region and a protein kinase C phosphorylation site on human fascin. J. Biol. Chem. 1997;272:2527–2533. doi: 10.1074/jbc.272.4.2527. [DOI] [PubMed] [Google Scholar]
- 2.Miyata H, Yasuda R, Kinosita K., Jr Strength and lifetime of the bond between actin and skeletal muscle alpha-actinin studied with an optical trapping technique. Biochem. Biophys. Acta. 1996;1290:83–88. doi: 10.1016/0304-4165(96)00003-7. [DOI] [PubMed] [Google Scholar]
- 3.Mogilner A, Keren K. The shape of motile cells. Curr. Biol. 2009;19:R762–R771. doi: 10.1016/j.cub.2009.06.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kole TP, Tseng Y, Jiang I, Katz JL, Wirtz D. Intracellular mechanics of migrating fibroblasts. Mol. Biol. Cell. 2005;16:328–338. doi: 10.1091/mbc.E04-06-0485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pollard TD, Berro J. Mathematical models and simulations of cellular processes based on actin filaments. J. Biol. Chem. 2009;284:5433–5437. doi: 10.1074/jbc.R800043200. [DOI] [PubMed] [Google Scholar]
- 6.Otto JJ. Actin-bundling proteins. Curr. Opin. Cell Biol. 1994;6:105–109. doi: 10.1016/0955-0674(94)90123-6. [DOI] [PubMed] [Google Scholar]
- 7.Edwards RA, Bryan J. Fascins, a family of actin bundling proteins. Cell Motil. Cytoskel. 1995;32:1–9. doi: 10.1002/cm.970320102. [DOI] [PubMed] [Google Scholar]
- 8.Bausch AR, Ziemann F, Boulbitch AA, Jacobson K, Sackmann E. Local measurement of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys. J. 1998;75:2038–2049. doi: 10.1016/S0006-3495(98)77646-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Keller M, Tharmann R, Dichtl MA, Bausch AR, Sackmann E. Slow filament dynamics and viscoelasticity in entangled and active actin networks. Phlios. Transact. A Math. Phys. Eng. Sci. 2003;361:699–711. doi: 10.1098/rsta.20021158. [DOI] [PubMed] [Google Scholar]
- 10.Panorchan P, Lee JS, Kole TP, Tseng Y, Wirtz D. Microrheology and ROCK signalling of human endothelial cells embedded in a 3D matrix. Biophys. J. 2006;91:3499–3507. doi: 10.1529/biophysj.106.084988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wottawah F, Schinkinger S, Lincoln B, Ananthakrishnan R, Romeyke M, Guck J, Kaes J. Optical rheology of biological cells. Phys. Rev. Lett. 2005;94:098103. doi: 10.1103/PhysRevLett.94.098103. [DOI] [PubMed] [Google Scholar]
- 12.Walcott S, Sun SX. A mechanical model of actin stress fiber formation and substrate elasticity sensing in adherent cells. Proc. Natl. Acad. Sci. USA. 2010;107:7757–7762. doi: 10.1073/pnas.0912739107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lan G, Wolgemuth CW, Sun SX. Z-ring force and cell shape during division in rod-like bacteria. Proc. Natl. Acad. Sci. USA. 2007;104:16110–16115. doi: 10.1073/pnas.0702925104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Oliver T, Lee J, Jacobson K. Forces exerted by locomoting cells. Semin. Cell Biol. 1994;5:139–147. doi: 10.1006/scel.1994.1018. [DOI] [PubMed] [Google Scholar]
- 15.Zajac M, Dacanay B, Mohler WA, Wolgemuth CW. Depolymerization-driven flow in nematode spermatozoa relates crawling speed to size and shape. Biophys. J. 2008;94:3810–3823. doi: 10.1529/biophysj.107.120980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bi EF, Lutkenhaus J. FtsZ ring structure associated with division in Escherichia coli. Nature. 1991;172:5610–5616. doi: 10.1038/354161a0. [DOI] [PubMed] [Google Scholar]
- 17.Margolin W. Spatial regulation of cytokinesis in bacteria. Curr. Opin. Microbiol. 2001;4:647–652. doi: 10.1016/s1369-5274(01)00264-8. [DOI] [PubMed] [Google Scholar]
- 18.Lan G, Daniels BR, Dobrowsky RM, Wirtz D, Sun SX. Condensation of FtsZ can drive bacterial cell division. Proc. Natl. Acad. Sci. USA. 2009;106:121–126. doi: 10.1073/pnas.0807963106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Erickson HP. Modeling the physics of FtsZ assembly and force generation. Proc. Natl. Acad. Sci. USA. 2009;106:9243–9283. doi: 10.1073/pnas.0902258106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Allard JF, Cytrynbaum EN. Force generation by a dynamic Z-ring in Escherichia coli cell division. Proc. Natl. Acad. Sci. USA. 2009;106:145–150. doi: 10.1073/pnas.0808657106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dai K, Lutkenhaus J. The proper ratio of FtsZ to FtsA is required for cell division to couur in Escherichia coli. J. Bacteriol. 1992;174:6145–6151. doi: 10.1128/jb.174.19.6145-6151.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Neujahr R, Heizer C, Gerisch G. Myosin II-independent processes in mitotic cells of Dictyostelium discoideum: redistribution of the nuclei, re-arrangement of the actin system and formation of the cleavage furrow. J. Cell Sci. 1997;110:123–137. doi: 10.1242/jcs.110.2.123. [DOI] [PubMed] [Google Scholar]
- 23.Weber I. On the mechanism of cleavage furrow ingression in Dictyostelium. Cell Struct. Func. 2001;26:577–584. doi: 10.1247/csf.26.577. [DOI] [PubMed] [Google Scholar]
- 24.Weber I, Gerisch G, Heizer C, Murphy J, Badelt K, Stock A, Schwartz JM, Faix J. Cytokinesis mediated through the recruitment of cotexillins into the cleavage furrow. EMBO J. 1999;18:586–594. doi: 10.1093/emboj/18.3.586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang W, Robinson DN. Balance of actively generated contractile and resistive forces controls cytokinesis dynamics. Proc. Natl. Acad. Sci. USA. 2005;102:7186–7191. doi: 10.1073/pnas.0502545102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Reichl EM, Ren Y, Morphew MK, Delannoy M, Effler JC, Girard KD, Divi S, Iglesias PA, Kuo SC, Robinson DN. Interactions between myosin and actin cross-linkers control cytokinesis contractility dynamics and mechanics. Curr. Biol. 2008;18:471–480. doi: 10.1016/j.cub.2008.02.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zumdieck A, Kruse K, Bringmann H, Hyman AA, Julicher F. Stress generation and filament turnover during actin ring constriction. PLoS ONE. 2007;2:e696. doi: 10.1371/journal.pone.0000696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bi E, Maddox P, Lew DJ, Salmon ED, McMillan JN, Yeh E, Pringle JR. Involvement of an actomyosin contractile ring in Saccharomyces cerevisiae cytokinesis. J. Cell Biol. 1998;142:1301–1312. doi: 10.1083/jcb.142.5.1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tolliday N, Pitcher M, Li R. Direct evidence for a critical role of myosin II in budding yeast cytokinesis and the evolvability of new cytokinetic mechanisms in the absence of myosin II. Mol. Biol. Cell. 2003;14:798–809. doi: 10.1091/mbc.E02-09-0558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pollard TD. Progress toward understanding the mechanism of cytokinesis in fission yeast. Biochem. Soc. Trans. 2008;36:425–430. doi: 10.1042/BST0360425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Huxley HE. Muscular contraction and cell motility. Nature. 1973;243:445–449. doi: 10.1038/243445a0. [DOI] [PubMed] [Google Scholar]
- 32.DeLozanne A, Spudich JA. Disruption of Dictyostelium myosin heavy chain gene by homologous recombination. Science. 1987;236:1086–1091. doi: 10.1126/science.3576222. [DOI] [PubMed] [Google Scholar]
- 33.Knecht DA, Loomis WF. Antisence RNA inactivation of myosin heavy chain gene expression in Dictysotelium discoideum. Science. 1987;236:1081–1086. doi: 10.1126/science.3576221. [DOI] [PubMed] [Google Scholar]
- 34.Even-Ram S, Doyle AD, Conti MA, Matsumoto K, Adelstein RS, Yamada KM. Myosin IIA regulates cell motility and actomyosin-microtubule crosstalk. Nat. Cell Biol. 2007;9:299–309. doi: 10.1038/ncb1540. [DOI] [PubMed] [Google Scholar]
- 35.Keren K, Yam PT, Kinkhabwala A, Mogilner A, Theriot JA. Intracellular fluid flow in rapidly moving cells. Nat. Cell Biol. 2009;11:1219–1224. doi: 10.1038/ncb1965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bastian P, Lang K, Niggemann B, Zaenker KS, Entschladen F. Myosin regulation in the migration of tumor cells and leukocytes within a three-dimensional collagen matrix. Cell. Mol. Life Sci. 2005;62:65–76. doi: 10.1007/s00018-004-4391-6. [DOI] [PubMed] [Google Scholar]
- 37.Bloom RJ, George JP, Celedon A, Sun SX, Wirtz D. Mapping local matrix remodeling induced by a migrating tumor cell using three-dimensional multiple-particle tracking. Biophys. J. 2008;95:4077–4088. doi: 10.1529/biophysj.108.132738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Miao L, Vanderlinde O, Stewart M, Roberts TM. Retraction in amoeboid cell motility powered by cytoskeletal dynamics. Science. 2003;302:1405–1407. doi: 10.1126/science.1089129. [DOI] [PubMed] [Google Scholar]
- 39.Wolgemuth CW, Miao L, Vanderlinde O, Roberts T, Oster G. MSP dynamics drives nematode sperm locomotion. Biophys. J. 2005;88:2462–2471. doi: 10.1529/biophysj.104.054270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Miao L, Vanderlinde O, Liu J, Grant RP, Woutserse A, Shimabukuro K, Philipse A, Stewart M, Roberts TM. The role of filament-packing dynamics in powering amoeboid cell motility. Proc. Natl. Acad. Sci. USA. 2008;105:5390–5395. doi: 10.1073/pnas.0708416105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lombardi ML, Knecht DA, Dembo M, Lee J. Traction force microscopy in Dictyostelium reveals distinct roles for myosin II motor and actin-cross-linking activity in polarized cell movement. J. Cell Sci. 2007;120:1624–1634. doi: 10.1242/jcs.002527. [DOI] [PubMed] [Google Scholar]
- 42.Seydoux G, Braun RE. Pathway to totipotency: lessons from germ cells. Cell. 2006;127:891–904. doi: 10.1016/j.cell.2006.11.016. [DOI] [PubMed] [Google Scholar]
- 43.Strome S, Lehmann R. Germ versus soma decisions: lessons from flies and worms. Science. 2007;316:392–393. doi: 10.1126/science.1140846. [DOI] [PubMed] [Google Scholar]
- 44.Brangwynne CP, Eckmann CR, Courson DS, Rybarska A, Hoege C, Gharakhani J, Jülicher F, Hyman AA. Germline P granules are liquid droplets that localize by controlled dissolution/condensation. Science. 2009;324:1729–1732. doi: 10.1126/science.1172046. [DOI] [PubMed] [Google Scholar]