Polarizable Simulations with Second order Interaction Model (POSSIM) force field: Developing parameters for protein side-chain analogues

Abstract

A previously introduced POSSIM (POlarizable Simulations with Second order Interaction Model) force field has been extended to include parameters for small molecules serving as models for peptide and protein side-chains. Parameters have been fitted to permit reproducing many-body energies, gas-phase dimerization energies and geometries and liquid-phase heats of vaporization and densities. Quantum mechanical and experimental data have been used as the target for the fitting. The POSSIM framework combines accuracy of a polarizable force field and computational efficiency of the second-order approximation of the full-scale induced point dipole polarization formalism. The resulting parameters can be used for simulations of the parameterized molecules themselves or their analogues. In addition to this, these force field parameters are currently being employed in further development of the POSSIM fast polarizable force field for proteins.

I. Introduction

Computer simulations have become an invaluable tool in biophysical research. Quantum mechanical calculations yield valuable data in a number of applications, but the area of their utility is limited. Therefore, simulations with empirical force fields remain the method of choice in a large majority of computational biophysical projects.

Obtaining accurate results by employing empirical force fields often require that these force fields include explicit treatment of electrostatic polarization.^1–4 Some examples of such problems include small molecule and protein pKa calculations, accurate determination of dimerization energies, modeling of sugar-protein binding, ion binding by proteins and small molecules. For instance, we have demonstrated that using a polarizable force field allows to reduce the errors in calculating pKa values of the acidic residues of the OMTKY3 protein from 3.3 to 0.6 pH units,^2a and polarization is required for predicting a thermodynamically stable structure for the complex of the CopZ protein with the Cu(I) ion.⁴

Overall, it is usually acknowledged that polarization is a crucial component in many computational studies of proteins and protein-ligand complexes, even though it is sometimes included in surrogate forms, such as, for example, conformation-specific protein charges.⁵

This is why polarizable simulations have gained a certain level of popularity inspite of the higher computational cost. Let us mention just some prominent examples in addition to those given above. MacKerell and Roux have been successful in developing and applying a polarization model based on the classical Drude oscillator, in which polarization is represented by a charge with a fictitious mass that can move away from its original position at an atomic center.^6a The model has been applied to a variety of cases, including simulations of solutions of ions, calculations of free energies of hydration and many others. The Drude oscillator model has also been incorporated into the CHARMM force field.^6b,c Ponder with co-workers have created the AMOEBA polarizable force field (included in Tinker package). It has been successfully used in applications ranging from simulations of small molecules to protein-ligand binding.^6d SIBFA polarizable methodology has been employed in modeling of ion binding to metalloproteins and hydrated metal ion systems.^6e Explicit polarization has been a part of AMBER for some time now.^6f And this list can be continued.

While the number of polarizable simulations has been growing, it is still common to see statements that the majority of biophysical simulations are carried out with nonpolarizable force fields, even in articles describing development of polarizable methodologies. There is a good reason for that. Polarizable simulations represent a growing field with unresolved questions, perhaps more so than in fixed-charges molecular modeling. We would like to emphasize the following two main issues. The first one pertains to the functional form of the polarization. For instance, one can use fluctuating charges, which offer a fast way to obtain polarizable reaction to changing electrostatic environment,^6g (even though they can be insufficient in certain situations, such as a need to reproduce a bifurcated hydrogen bond or an out-of-plane polarization). Inducible point dipoles are a popular means of representing many-body electrostatic polarization effects (and this is the technique we are using). The Drude oscillator is yet another method. And there are other techniques as well.

We are employing the inducible point dipole method, but we combine it with our fast second-order approach that has been demonstrated to decrease the amount of computational time needed for simulations by ca. an order of magnitude without any loss of accuracy.^7,8 This method also eliminated the danger of the so called polarization catastrophe (the resonance-like infinite growth of the induced dipole moment values). This second-order technique forms the basis of the polarizable part of the POSSIM framework.

The second question relates to choosing the right source of the fitting target data. High-level quantum mechanical results are very attractive in this respect,^9,10 but we have found that they have to be augmented by robust experimental data, for example, in fitting parameters for small molecular systems which then act as models for peptide and protein fragments. Therefore, we have been pursuing a balanced approach of using both quantum mechanical and experimental results in creating fitting target for force field development.

Moreover, we believe, based on our experience, that polarizable parameters fitted to represent electrostatic response to changing environment under one set of conditions should automatically work in other reasonably chosen circumstances. For example, polarizabilites fitted to reproduce three-body energies in gas-phase interactions with dipolar electrostatic probes^7,8 should perform well in liquid-state simulations where the molecule interacts with the bulk solvent. This statement has been confirmed by the good overall performance of our force fields in applications to solvation of small molecules, binding and pKa calculations.^2,7–9 The parameters are very transferable. We believe that this is a result of using a fundamentally robust underlying physical model, which makes the very exact specifics of the procedure of fitting the parameters less crucial (although we do not want to downplay the need to validate potential energy functions and parameter values).

Previously, we have successfully developed polarizable POSSIM parameters for a number of small molecules⁸ and alanine and protein backbones.¹¹ We have also simulated polyalanine peptides in their α-helical form,¹¹ as well as similar systems with an added protonated lysine residue.¹² We have demonstrated that the POSSIM framework works very well in reproducing experimentally known structure and stability properties of these systems, while also offering more detailed microscopic information about them and the processes they undergo. Following this success, we have now extended the development of the POSSIM force field to a much broader variety of small molecules which can serve as side-chain analogues for protein residues. The results are presented in this article.

The rest of the paper is organized as follows: Given in Section II is description of the methodology involved. Section III contains results and discussion. Finally, conclusions are presented.

II. Methods

A. Force Field

We employed fixed-charges OPLS-AA¹³ and polarizable POSSIM (References 8, 11 and this work) force fields. In both cases, the total energy E_tot was calculated by adding the electrostatic interactions E_{electrostatic}, the van-der-Waals energy E_vdW, harmonic bond stretching and angle bending E_stretch and E_bend and the torsional energy E_torsion terms:

$$E_{\mathit{tot}}=E_{\mathit{electrostatic}}+E_{\mathit{vdW}}+E_{\mathit{stretch}}+E_{\mathit{bend}}+E_{\mathit{torsion}}$$ (1)

Electrostatic energy

It is the electrostatic term which contains most of the differences between the POSSIM and OPLS-AA methods. In the POSSIM force field, the electrostatic polarization is manifested via inducible point dipoles μ:

$$E_{\mathit{pol}}=-\frac{1}{2}\sum _i{\mathbf{\mu }}_i{\mathbf{E}}_i^0.$$ (2)

Here E⁰ is the electrostatic field in the absence of the induced dipoles. Furthermore,

$${\mathbf{\mu }}_i={\alpha }_i{\mathbf{E}}_i^0+{\alpha }_j\sum _{j\ne i}{\mathbf{T}}_{ij}{\mathbf{\mu }}_j$$ (3)

α stands for the scalar polarizabilities and T_ij is the dipole-dipole interaction tensor. The usual way of solving Equation 3 for large molecular systems is by applying iterations in order to reach self-consistency. The first two iterations in this procedure are:

$${\mathbf{\mu }}_i^I={\alpha }_i{\mathbf{E}}_i^0$$ (4a)

$${\mathbf{\mu }}_i^{II}={\alpha }_i{\mathbf{E}}_i^0+{\alpha }_i\sum _{j\ne i}{\mathbf{T}}_{ij}{\mathbf{\mu }}_j^I={\alpha }_i{\mathbf{E}}_i^0+{\alpha }_i\sum _{j\ne i}{\mathbf{T}}_{ij}{\alpha }_j{\mathbf{E}}_j^0$$ (4b)

The fast polarization technique which forms the basis of the POSSIM formalism employs the second-order expression in Equation (4b). We have previously shown that it yields a significant increase in computational speed without loss of accuracy.^7,8 In addition to the polarization energy, the POSSIM force field also contains a pairwise-additive contribution from interactions of fixed charges with each other:

$$E_{\mathit{additive}}=\sum _{i\ne j}\frac{q_i{q}_j}{R_{ij}}{f}_{ij},$$ (5)

where the factor f_ij is set to zero for 1,2- and 1,3-pairs (atoms which belong to the same valence bond or angle), to 0.5 for 1,4-interactions (atoms in the same dihedral angle) and to 1.0 for all the other pairs.

The electrostatic part of the OPLS force field contains only the additive term given in Equation 5. In addition, the POSSIM technique contains another feature which is not present in the OPLS, a short-distance cutoff parameter R_cut = 0.8 Å. If the distance between two atoms R_ij is smaller than the sum of these parameters R_min^ij = R_cutⁱ + R_cut^j for the atoms i and j, R_ij is replaced by a smoothing function

$$R_{ij}^{\mathit{eff}}=(1-{\left(\frac{R_{ij}}{R_{min}^{ij}}\right)}^2+{\left(\frac{R_{ij}}{R_{min}^{ij}}\right)}^3)·R_{min}^{ij}$$ (6)

The approximation in Equation 4b differs from the complete physical induced-dipole electrostatic model, but we have shown that it increases the computational speed without compromising the accuracy of the simulations.^7,8 Furthermore, the second-order formalism given by Equation 4b turns the expression for the inducible dipoles into an analytical one, and the possibility of the polarization catastrophe is completely eliminated. This feature is also useful in extending this methodology to building continuum solvation models, since it permits to avoid the convergence issue which can be a problem in creation and parameterization of such techniques.

The rest of the force field

The POSSIM force field uses the same standard Lennard-Jones formalism for the van-der-Waals energy as OPLS-AA:

$$E_{\mathit{vdW}}=\sum _{i\ne j}4{\epsilon }_{ij}\left[{(\frac{{\sigma }_{ij}}{R_{ij}})}^{12}-{(\frac{{\sigma }_{ij}}{R_{ij}})}^6\right]f_{ij}$$ (7)

Geometric combining rules are applied as: (ε_ij = (ε_i·ε_j)^1/2, σ_ij (σ_i·σ_j)^1/2). Harmonic bond stretches and angle bending were used and the torsional term is obtained as a Fourier series:

$$E_{\mathit{torsion}}=\sum _i\frac{V_1^i}{2}[1+cos({\phi }_i)]+\frac{V_2^i}{2}[1-cos(2{\phi }_i)]+\frac{V_3^i}{2}[1+cos(3{\phi }_i)]$$ (8)

All the POSSIM stretch and bend parameters were adopted from the OPLS-AA force field without any change, while the torsional parameters were either fitted previously^8,11 or produced in the course of the work reported in this article.

B. Parameterization of the POSSIM Force Field

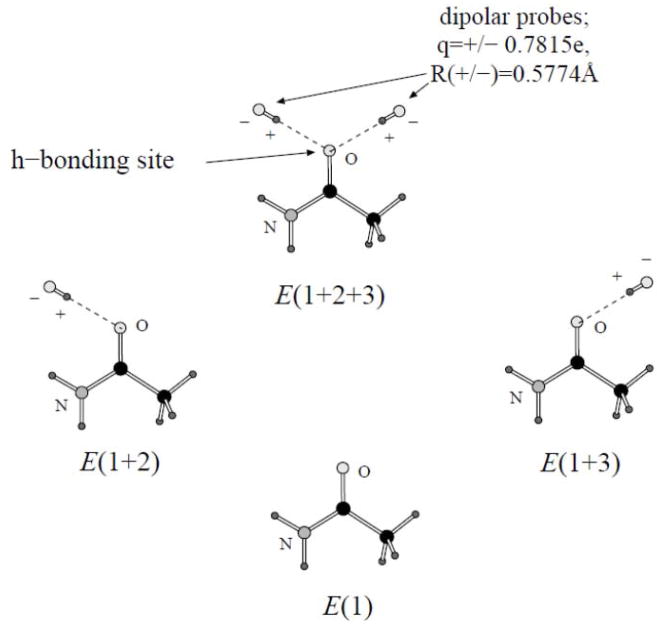
Parameters for small molecules are valuable both as such and as a basis for simulating other systems containing similar functional groups (such as protein side-chains). The first step in fitting parameters for small molecules is producing atomic polarizabilities. We used the three-body energies as targets, similarly to what we did in previous work.^8,11 Briefly, we considered the molecule in hand with two electrostatic dipolar probes composed of bare fixed charges. The positions of the probes were chosen to correspond to possible hydrogen bonds with the molecule. One such pair of probes for the CH₃CONH₂ system (used as an example) is shown on Figure 1. Each dipolar probe contains two opposite charges of magnitude 0.78 e, separated by 0.58 Å (so that the dipole moment is equal to 2.17D which is similar to that of non-polarizable SPC/E water model¹⁴). The three body energies were calculated as follows:

$$E_{3\mathit{body}}=E(1+2+3)-E(1+2)-E(1+3)-E(2+3)+E(1)+E(2)+E(3)$$ (9)

Figure 1.

Calculating two-and three-body energies of a small molecule with dipolar probes.

In the essence, this is the part of the total energy which cannot be reduced to a sum of the molecule-probe and probe-probe dimerization energies. The target quantum mechanical values of the energies were evaluated by density-functional theory (DFT) with the B3LYP method¹⁵ and cc-pVTZ(-f) basis set. Jaguar software suite¹⁶ was used. The resulting three-body energies were then employed to fit isotropic atomic polarizablities α_i, which were chosen to minimize the difference between the POSSIM and DFT three-body energies.

After this first step, atomic charges and Lennard-Jones parameters were optimized to reproduce gas-phase quantum mechanical dimerization energies. Normally, for electrostatically neutral molecules, homodimer energy and energies of binding to a single water molecule at hydrogen bonding positions were calculated. Distances between the heavy atoms in these bonds were used as a fitting target as well. For charged molecules, which were used as prototypes for ionized side-chains of corresponding protein residues, only heterodimers with water were simulated. The quantum mechanical calculations were carried out following the general extrapolation protocol involving LMP2 data with the cc-pVTZ(-f) and cc-pVQZ basis sets which has been described elsewhere.¹⁷ This protocol was found to yield very accurate results and we have been using it in developing parameters in a number of cases.^7,8,12,18

Torsional parameters were fitted to reproduce quantum mechanical torsional profiles calculated with the LMP2/c-pVTZ(-f) level of theory.

Finally, the non-bonded parts of the potential energy functions for the electrostatically neutral molecules were fine-tuned by reproducing liquid-state heats of vaporizations and molecular volumes (and thus the densities). The target accuracy in this fitting was ca. 2–3%. Once a new improved set of parameters was obtained, the dimerization energies were recomputed (and further adjustments to the parameters were made if needed), new torsional parameters were produced, and the liquid-state simulations were rerun. The whole cycle was repeated if necessary.

The empirical force field calculations, including liquid-state simulations, were carried out with the POSSIM software suite. The NPT ensemble (constant temperature, pressure and the number of molecules) was employed, and a cubic cell with 216 molecules subject to periodic boundary conditions was used for each compound. The simulations were run at 1 atm. The heats of vaporization were calculated as follows:

$$\mathrm{\Delta }{H}_{\mathit{vap}}=E(\mathit{gas})-E(\mathit{liq})+RT$$ (10)

The difference between the energy for one molecule in the gas-phase and in the condensed state had to be modified by adding the RT term to account for the Δ(PV) part of the enthalpy, in the assumption that the vapor obeys the ideal gas law, and the molecular volume of the liquid can be neglected compared to that of the gas. All the calculations consisted of at least 1 × 10⁶ Monte Carlo configurations of averaging and no less than 5 × 10⁶ configurations of averaging for the thermodynamic properties. Elements of the dipole-dipole interaction tensor were set to zero for distances beyond 7.0 Å. The other intermolecular interactions were cut off at 11.0 Å. The charge-charge interactions were switched off smoothly over the last 0.5 Å. The standard correction for the neglected Lennard-Jones energies beyond the cutoff distances was applied.

III. Results and Discussion

A. Three-Body Energies

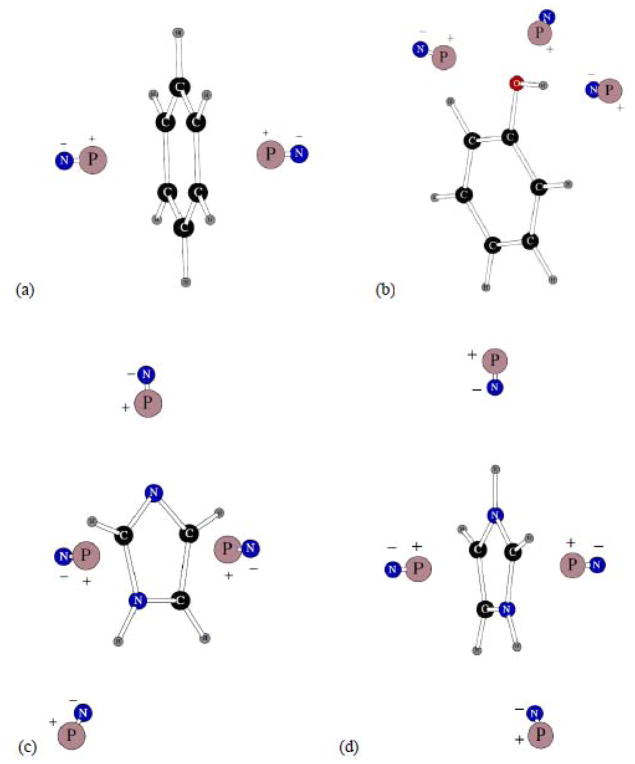
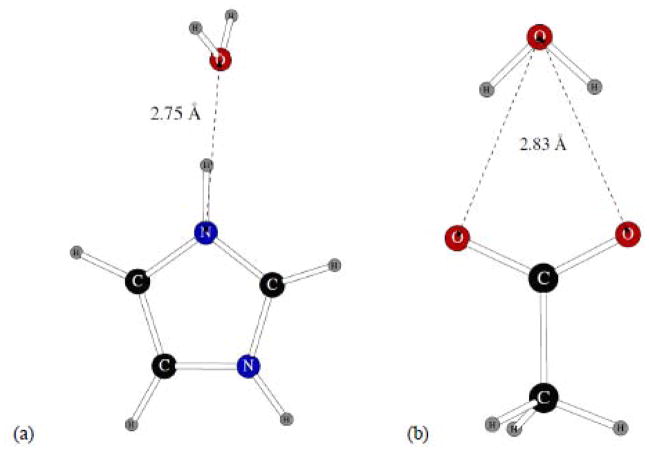
As stated in the previous section, fitting POSSIM three-body energies to the quantum mechanical target was the first step in producing the new potential energy parameters. Shown on Figure 2 are location of the dipolar probes used in calculating the three-body energies for the four aromatic compounds parameterized in this work – benzene, phenol, and neutral and protonated imidazole.

Figure 2.

Dipolar probes used in calculating three-body energy for benzene (a), phenol (b), imidazole (c) and protonated imidazole (d). Symbols “P” and “N” denote the positive and negative point charges, respectively.

There were only two probes for the benzene case (and thus only one three-body energy value), both perpendicular to the molecular plane. We used benzene carbon and hydrogen polarizabilities in the other aromatic compounds. The dipolar probes for phenol were located at the hydrogen-bonding sites for the –OH group, two at the positions to be bound to the oxygen and one to the hydrogen. The imidazole cases had both probes hydrogen bonded to the N and NH fragments and to the delocalized π-orbitals of the aromatic rings, as shown on Figure 2. The average unsigned errors in the three body energies for these compounds were 0.014, 0.276, 0.081 and 0.179 kcal/mol, respectively. All the average errors in three-body energies are given in Table 1.

Table 1.

Average unsigned errors in three-body energies, kcal/mol.

System	Error in three-body energy
Benzene	0.014
Phenol	0.276
Acetamide	0.264
Methanethiol	0.002
Acetic Acid	0.209
Imidazole	0.081
Methylamine	0.245
Imidazolium	0.179
Carboxylate (CH3COO−)	0.093
Methyl guanadinium	0.117

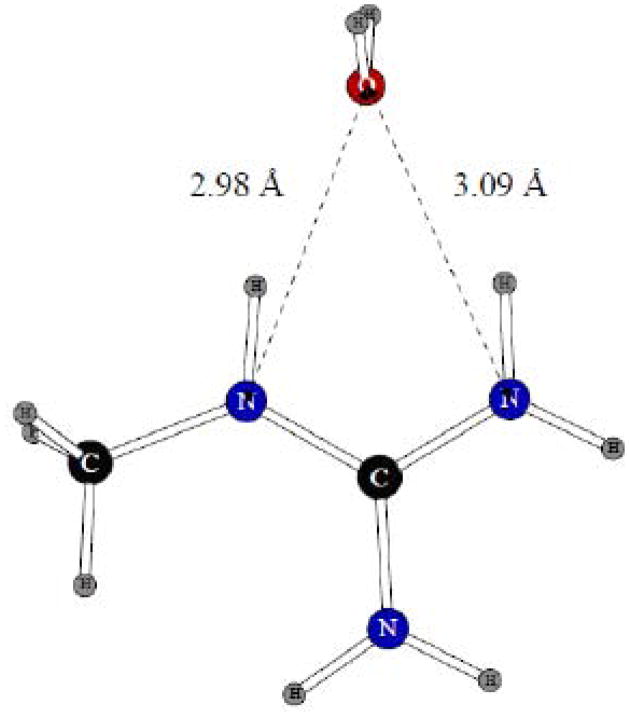
Configurations of the dipolar probes used in calculating three body energies for methyl amine and acetamide are given on Figure 3. The average errors in the three-body energies were both in the acceptable range, their values at 0.245 and 0.264 kcal/mol, respectively.

Figure 3.

Dipolar probes used in calculating three-body energy for CH₃NH₂ (a) and acetamide (b). Symbols “P” and “N” denote the positive and negative point charges, respectively.

The two compounds shown on Figure 4 served as a basis for parameters that can be used in a number of derivative molecules. First of all, all aliphatic groups have the same parameters as given in Reference 8 for saturated hydrocarbons. In the specific case of the compounds on Figure 4, the resulting parameters for the –SH and –COOH groups were used in dimethyl sulfide and dimethyl disulfide, and in propanoic and butanoic acids, respectively. The average errors in the methane thiol and acetic acid three-body energies were 0.002 and 0.209 kcal/mol.

Figure 4.

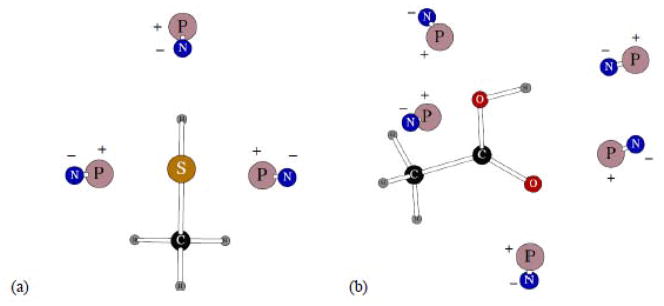
Dipolar probes used in calculating three-body energy for CH₃SH (a) and acetic acid (b). Symbols “P” and “N” denote the positive and negative point charges, respectively.

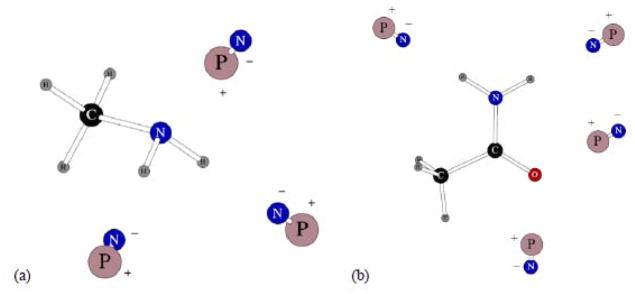
Two more charges species are shown on Figure 5. They are the CH₃COO⁻ carboxylate ion and methyl guanadinium cation needed as models for side-chains in aspartic and glutamic acid, and arginine. The fitting of the carboxylate polarizabilities gave an average unsigned error in three-body energies of 0.093 kcal/mol.

Figure 5.

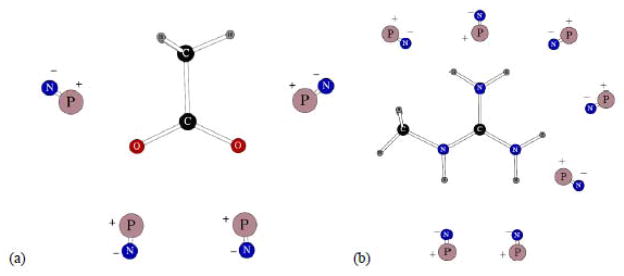
Dipolar probes used in calculating three-body energy for CH₃COO⁻ carboxylate ion (a) and methyl guanadinium cation (b). Symbols “P” and “N” denote the positive and negative point charges, respectively.

There are seven possible positions of hydrogen=bonded dipolar probes around the methyl guanadinium ion. Five of them have their negative charges pointed toward the five polar hydrogen atoms of the cation. The other two have their positive point charges at hydrogen-bonding distances from the –NH₂ nitrogens, as can be seen from Figure 5b. Therefore, there is a total of twenty-one possible three-body energies for the methyl guanadinium cation. We decided to test the level of transferability of our atomic polarizabilities and did not fit any of the values. The central carbon polarizability was exactly the same as in benzene carbons, the methyl group had standard aliphatic parameters, nitrogens and polar hydrogens had exactly the same polarization properties as in the –NH₂ group of acetamide. The result was quite remarkable. The average absolute value error in the three-body energies of methyl guanadinium was only 0.117 kcal/mol, which is a great result given that there are 21 tree-body configurations.

B. Dimerization Energies and Distances

The second step in producing the potential energy functions was in fitting charges and Lennard-Jones parameters to reproduce gas-phase dimerization energies and geometries. Wherever a water molecule was involved in the dimers, it was the H₂O model previously developed in the POSSIM framework.⁸ The water model was not refitted in the project presented here.

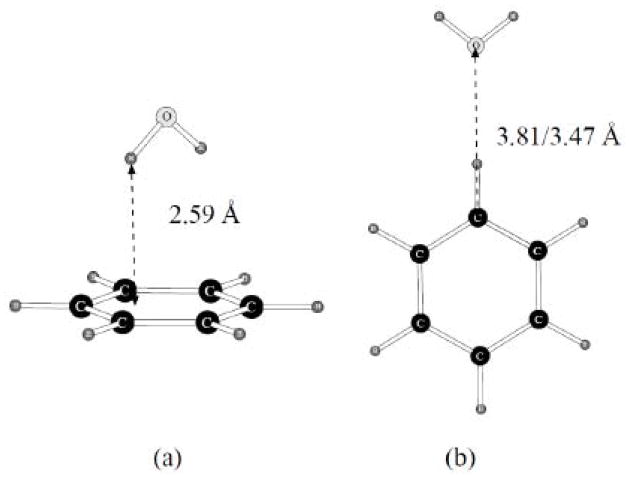
Two benzene-water dimers were considered. They are shown on Figure 6.

Figure 6.

Dimers of benzene with one water molecule.

Two values of the distance are given on the figure for the second dimer. The potential energy surface is rather flat for these dimers, and even the C…O distance change significantly in transition from the initial 6-31G** to the final cc-pVTZ(-f) optimization. Therefore, it looks like fitting this distance precisely with the POSSIM formalism might not be entirely justified. Our computed quantum mechanical (QM) and POSSIM dimerization energies and distances are shown in Table 2. The quantum mechanical energies are reproduced by POSSIM rather well (within ca. 0.25–0.35 kcal/mol) and the quality of the calculated POSSIM distances is also good if we take into the account the range of the quantum mechanical distances which we saw in this case for the second benzene-water dimer.

Table 2.

Computed dimerization energies (in kcal/mol) and distances (in Å).

Dimer	Energy		Distance
	QM	POSSIM	QM	POSSIM
C6H6…H2O (a)	−2.97	−3.33	2.59	2.66
C6H6…H2O (b)	−1.21	−0.96	3.47/3.81	3.85
C6H5OH x 2	−5.68a	−5.16	2.98a	3.01
C6H5OH…H2O (H2O)		−3.77	3.13b	3.12
C6H5OH…H2O (OH2)		−8.12	2.81b	2.80
CH3CONH2 x 2	−12.8	−12.96	2.94	2.82
CH3CONH2…H2O (NF)	−3.72	−5.54	3.03	2.94
CH3CONH2…H2O (OF)	−4.29	−3.84	2.96	2.96
CH3SH x 2	−1.56a	−2.72	4.27a	3.80
CH3SH… H2O (SH)		−4.34		3.28
CH3SH… H2O (OH)		−4.34		3.44
CH3COOH x 2	−15.64	−15.60	2.68	2.67
CH3COOH…H2O (H2O)	−4.33	−4.16	2.91	3.02
CH3COOH…H2O (OH2)	−9.17	−9.15	2.75	2.66
imidazole x 2	−9.19c/−7.70e	−7.59	3.00c,e	2.81
imidazole…H2O (H2O)	−6.73/−6.59d	−6.18	2.85/2.92d	2.86
imidazole…H2O (OH2)	−6.37/−6.11e	−5.45	2.91/2.99e	2.89
CH3NH2 x 2	−3.09	−2.62	3.18	3.07
CH3NH2…H2O	−6.48	−5.68	2.84	2.87
protonated imidazole…H2O	−15.76	−16.00	2.80	2.80
CH3COO−…H2O	−20.21	−20.17	2.83	2.93
methyl guanadinium…H2O	−17.86	−18.09	2.98, 3.09	2.98, 3.04

^aReference 18.

^bLMP2/cc-pVTZ(-f).

^cLMP2/cc-pVQZ for energy, LMP2/cc-pVTZ(-f) for distance.

^dReferences 20 and 21.

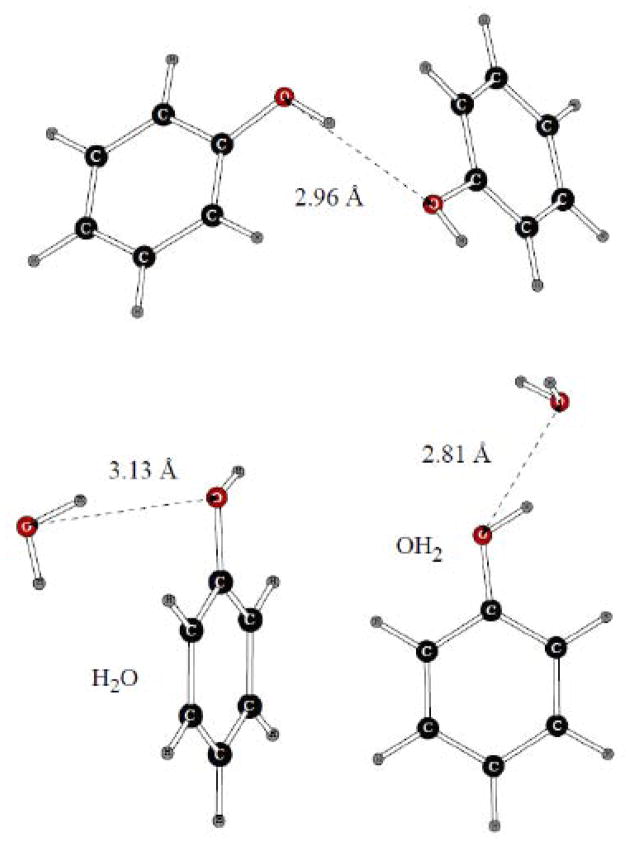
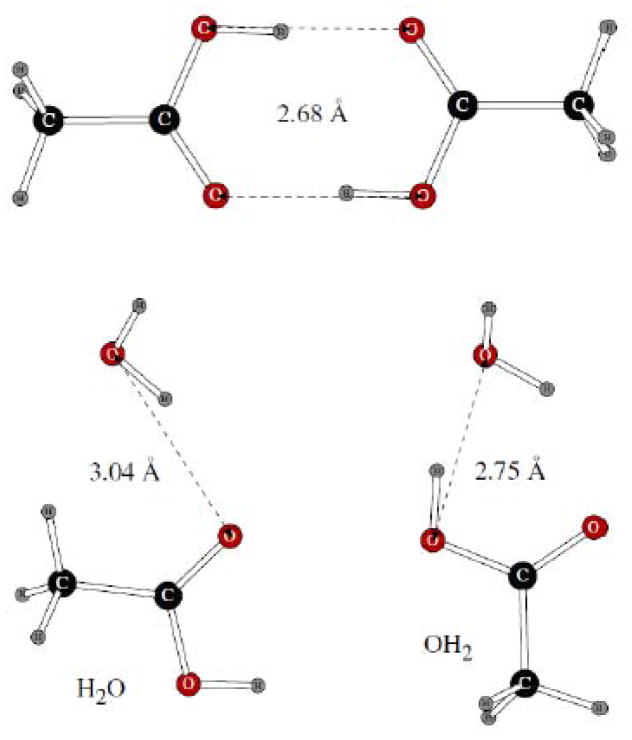
In case of phenol, both the homodimer and two dimers with water were considered (Figure 7). At this stage, we fitting charges on the atoms of the –OH group and on the adjacent carbon. The polar hydrogen has zero Lennard-Jones parameters, and the Lennard-Jones σ and ε values of the carbon and oxygen atoms were the same as in their benzene and alcohol⁸ counterparts, respectively. Comparison of our dimerization results calculated with the POSSIM software and force field was done with literature¹⁸ quantum mechanical values of binding energy and oxygen-oxygen distance in phenol homodimer and to O…O distances in the phenol-water dimers, as calculated at our standard LMP2/cc-pVTZ(-f) geometry optimization level. As can be seen from the results in Table 2, the energy was reproduced within ca. 0.5 kcal/mol accuracy, and errors in the distances were only 0.01 – 0.03Å.

Figure 7.

Dimers of phenol with another benzene molecule and with water.

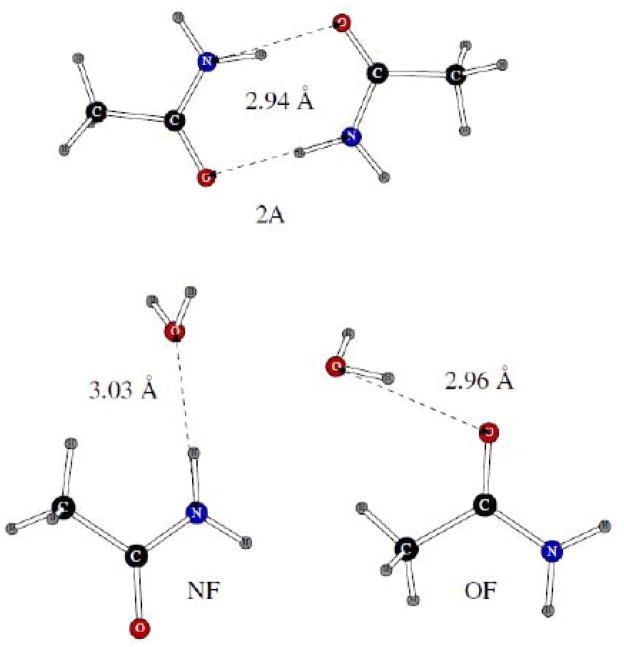
Acetamide represented another case for which both homo- and heterodimers were considered. Their geometries are shown on Figure 8. As can be seen from Table 2, all the quantum mechanical distances are reproduced very well, with errors ranging from less than 0.01Å for the OF acetamide-water dimer to about 0.1Å for the other two dimers. The POSSIM dimerization energies are not very far from the quantum mechanical data except for the NF heterodimer. The error is significant in this case, but it is not unusual to have such a deviation for amides, and some other groups are even known to disregard such gas-phase dimerization energies altogether in some cases.⁸

Figure 8.

Dimers of acetamide with another acetamide molecule and with one water molecule.

For the sulfur-containing compounds, we considered dimers of methanethiol only. We had previously shown that quantum mechanical simulations of such system give results which are less robust than those obtained for other hydrogen-bonded dimers.¹⁸ Therefore, the only comparison of the POSSIM results for these dimers (shown on Figure 9) with quantum mechanics was done for the methanthiol homodimer, and the quantum mechanical results are taken from Reference 18.

Figure 9.

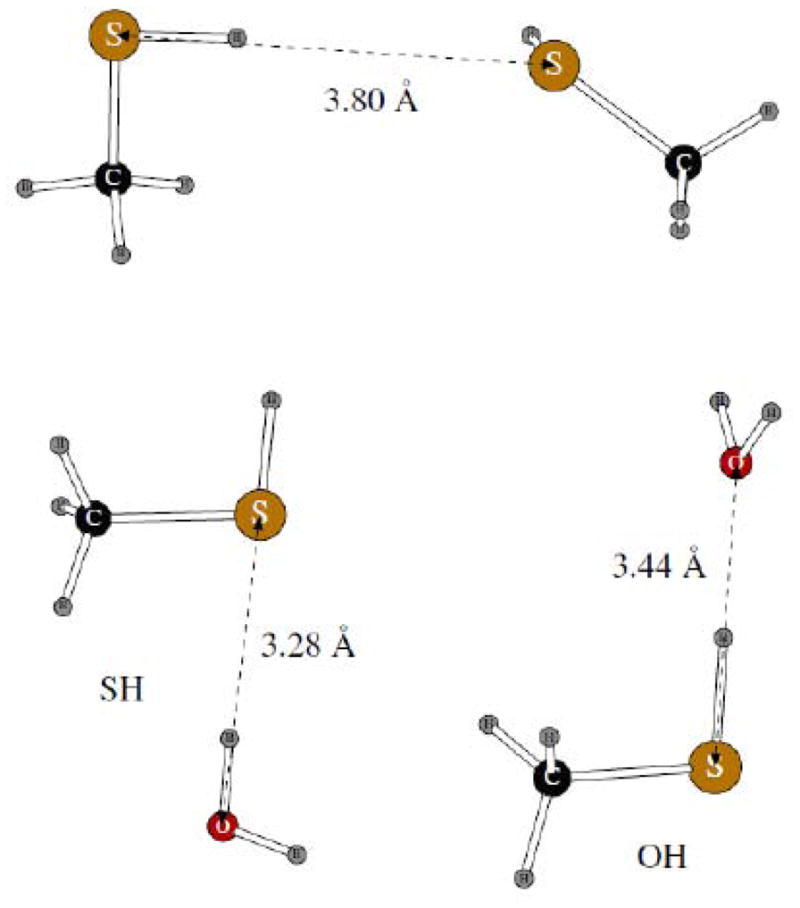
Dimers of methanethiol with another methanethiol molecule and with one water molecule. POSSIM distances are shown.

Dimerization properties of carboxylic acids were studied with the systems shown on Figure 10. Charges and Lennard-Jones parameters of the acid atoms were adjusted (we kept the methyl group with the standard aliphatic parameter set). The dimers with water were labeled as shown on Figure 10. The OH group of the water molecule in the H₂O structure was restricted to be in the plane of the heavy atoms of CH₃COOH. It can be seen from the data in Table 2 that the results of this parameter fitting were very good, with the O…O distances produced by POSSIM being within 0.1 – 0.2 Å of the quantum mechanical results, and the energy being within 0.1 – 0.2 kcal/mol from the quantum extrapolated data.

Figure 10.

Dimers of acetic acid with another acetic acid molecule and with one water molecule.

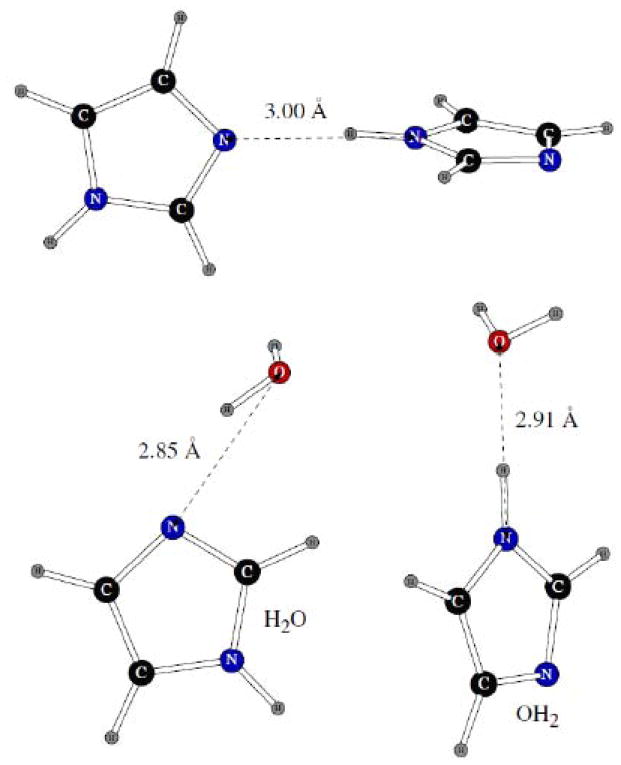
We considered three imidazole dimers shown on Figure 11. The homodimer has the NH group of one molecule hydrogen bonded to the nitrogen atom of the other one, with the LMP2/cc-pVTZ(-f) distance between the two nitrogens of 3.00Å. The H₂O and OH₂ heterodimers with a water molecule had hydrogen and oxygen atoms of the water bonded to the imidazole molecule, respectively.

Figure 11.

Dimers of imidazole with another imidazole molecule and with one water molecule.

As we have already observed in fitting POSSIM parameters for other systems containing nitrogen, the uncertainty in dimerization energies for such molecules can be significant, and some research groups even omit comparison with quantum mechanical dimerization energies altogether.⁸ In the particular case of imidazole, the range of reported homodimer energies can be ca. 1.5 kcal/mol, with the energies for the imidazole – water dimers varying by several tenths of a kcal/mol, as can be seen from the data presented in Table 2. Given these differences, the accuracies of the POSSIM dimerization energies are satisfactory. The interatomic distances are correct within 0.1 – 0.2Å, which is also acceptable.

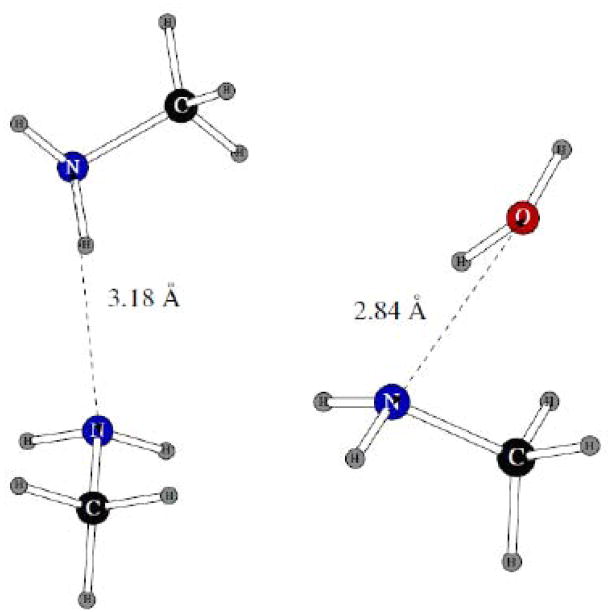
The two dimers used in fitting the nitrogen Lennard-Jones σ and ε and the charge distribution are shown on Figure 12. We have managed to fit the parameters so that the distances between the heavy atoms are reproduced within ca. 0.1Å. At the same time, the errors in the binding energies are once again somewhat higher than could be expected from molecules with no nitrogen atoms. The same rational as the one for the imidazole dimerization results presented above is applicable here.

Figure 12.

Methylamine-methylamine dimer and dimer of methylamine with one water molecule.

Dimers of ionic species with water displayed higher values of their binding energies (and no stable homodimers were possible). Only one dimer was considered for each ion. The dimers for the protonated imidazole and the carboxylate ion are shown on Figure 13, and the methyl guanadinium dimer with one water molecule is given on Figure 14.

Figure 13.

Dimer of the protonated imidazole (a) and carboxylate (b) ions with water.

Figure 14.

Dimer of the methyl guanadinium ion with one water molecule.

Lennarg-Jones parameters and charges of the aromatic C and H atoms in imidazolium were kept at the same values as for the benzene molecule which served as the basis for all the aromatic systems. Following the usual protocol, all the polar hydrogen atoms were kept with zero Lennard-Jones parameters. For the carboxylate, the methyl group Lennard-Jones (and the hydrogen charges on the same group) were kept at their standard values. While fitting the methyl guanadinium parameters, the N – H charge distribution and nitrogen Lennard-Jones σ were fitted. As can be seen from the results presented in Table 2, the fitting was successful, with the dimerization energy errors being within 0.5 kcal/mol, and the distances reproduced with an accuracy level of 0.1Å or better.

C. Torsional Fitting

We followed the validation procedure established by both other researchers and ourselves^8,13 to fit the V₁ – V₃ coefficients in the torsional energy term. We carried out fitting of the POSSIM energies to LMP2/cc-pVTZ(-f) quantum mechanical energies at key conformational (equilibrium) and non-equilibrium rotamer points. The improper torsional parameters were adopted from the OPLS-AA¹⁹ without changes. The torsional parameters produced for benzene were used as the basis for the other aromatic systems. For phenol, V₂ coefficients for the H–O–C–C rotation and O–C–C–C out-of-plane bending were parameterized. In acetamide, the C–C–N–H parameters were created. All the necessary torsional parameters for the thiols and carboxylic acids were fitted, and O–C–C–H was the torsion fitted for the carboxylate ion. N–C–C–N, C–C–N–H and H–C–N–H torsional parameters were considered for imidazole C–C–N–H for the protonated version of this molecule. H–C–N–H was the only angle for methylamine. Several torsional parameters were produced for the methyl guanadinium.

All the resulting POSSIM and reference quantum mechanical energies are given in Table 3. It can be seen that in almost all of the cases the deviations were no more than ca. 0.1 kcal/mol, and in many cases much smaller. Overall, we believe that the quality of the torsional fitting was very adequate.

Table 3.

Torsional energies in kcal/mol

Molecule	Dihedral	Angle Values	Energy, QMa	Energy, POSSIM
C6H6	C–C–C–C	15°	1.748	1.654
		0°	0.000	0.000
	H–C–C–C	150°	5.190	5.089
		180°	0.000	0.000
C6H5OH	C–C–O–H	90°	3.187	3.238
		60°	2.461	2.389
		30°	0.763	0.770
		0°	0.000	0.000
	C–C–C–O	165°	1.505	1.505
		180°	0.000	0.000
CH3CONH2	C–C–N–H	135°	12.244	12.361
		150°	7.147	6.917
		180°	1.845	1.850
		0°	0.000	0.000
CH3SH	H–C–S–H	0°	1.19	1.19
		60°	0.000	0.000
CH3SCH3	H–C–S–C	120°	1.753	1.742
		150°	0.832	0.857
		180°	0.000	0.000
CH3SSCH3	C–S–S–C	120°	−3.469	−3.469
		150°	−0.869	−0.866
		180°	0.000	0.000
	H–C–S–S	120°	1.248	1.242
		150°	0.616	0.627
		180°	0.000	0.000
CH3COOH	C–C–O–H	0°	5.486	5.490
		150°	2.923	2.938
		135°	6.125	6.119
		180°	0.000	0.000
C2H5COOH	C–C–C–O	90°	0.032	0.032
		60°	0.000	0.000
	H–C–C–C	150°	1.406	1.406
		180°	0.000	0.000
C3H7COOH	C–C–C–C	0°	4.363	4.363
		135°	2.746	2.747
		150°	1.516	1.513
		180°	0.000	0.000
C3H4N2	N–C–C–N	5°	0.453	0.224
		0°	0.000	0.000
	C–C–N–H	175°	0.061	0.140
		180°	0.000	0.000
	H–C–N–H	5°	0.067	0.107
		0°	0.000	0.000
CH3NH2	H–C–N–H	0°	2.017	2.116
		30°	0.830	0.716
		60°	0.011	0.018
		180°	0.000	0.000
C3H5N2+	C–C–N–H	150°	3.492	3.608
		165°	0.864	0.928
		170°	0.380	0.415
		175°	0.091	0.104
		180°	0.000	0.000
CH3COO−	O–C–C–H	150°	0.020	−0.316
		180°	0.000	0.000
C2N3H8+	H–N(H2)–C–N	30°	0.242	0.146
		15°	−0.049	−0.025
		0°	0.000	0.000
	C–N–C–N(H2)	30°	0.517	0.540
		15°	0.034	0.102
		0°	0.000	0.000
	H–C(sp3)–N–C	180°	0.076	0.001
		60°	0.954	0.969
		0°	0.000	0.000

^aLMP2/cc-pVTZ(-f)

D. Heats of Vaporization and Molecular Volumes of Pure Liquids

Following the common procedure,^7,8,13,18 we assessed the quality of reproducing condensed-phase properties of the parameterized neutral compounds by simulating the corresponding pure liquids and determining their molecular volumes. The results are shown in Table 4. Overall, these data demonstrate that our fitting of the parameters has been successful, with the average errors in the heats of vaporization and molecular volumes (and thus the densities) being 3.0% and 1.4%, respectively. A couple of specific things to note here are as follows.

Table 4.

Heats of vaporization (in kcal/mol) and molecular volumes (in ų).

System	ΔHvap		Molecular volume
	Reference	POSSIM	Reference	POSSIM
C6H6, 25°C	8.09a	7.85	148.4a	149.3
C6H5OH, 25°C	13.8a	14.2	147.8a	148.4
CH3CONH2, 100°C		15.32	99.9b	97.15
CH3CONH2, 221°C	13.4b	13.22		109.28
CH3SH, 5.96°C	5.87c	6.023	90c	90.41
CH3SCH3, 25°C	6.61c	6.663	122.5c	125.74
CH3SSCH3, 25°C	9.18c	9.616	148c	151.77
CH3COOH, 25°C	12.49b	13.08	95.5b	95.47
CH3COOH, 100°C	11.30b	12.01	104.1b	103.28
C3H4N2, 25°C	14.94e	15.41	100.9e	102.1
CH3NH2, −6.30 °C	6.17e	6.18	73.9e	72.18

^aReference 18.

^bReference 13.

^cReference 18.

^dReference 13.

^eReference 7.

It can be seen that the methanethiol error in the enthalpy of vaporization is about 2.5%, while the error in molecular volume/density is less than 0.5%. For the CH₃SCH₃ molecule, the error in the heat of vaporization is only 0.8%, while the density is off by about 2.6%. For CH₃SSCH₃, the errors in the ΔH_vap and V are about 4.8% and 2.6%, respectively. Overall, the accuracy of these results is quite adequate. This does not only mean that our fitting of POSSIM parameters yielded good results, but also confirmed once again that the quantum mechanical results for the methanethiol dimer are not entirely reliable given that our polarizable POSSIM dimer is bound noticeably tighter than its quantum mechanical counterpart, and yet the most reliable part of the target data which are the liquid-state heats of vaporization and densities are reproduced correctly.

Acetic acid heat of vaporization and molecular volumes are reported in Table 4. At 25°C, the calculated ΔH_vap is equal to 13.08 kcal/mol, which is within ca. 0.6 kcal/mol from the experimental result of 12.49 kcal/mol. Errors of this relative magnitude are slightly greater than the average for our force field development, but certainly not out of the range of what has been deemed adequate before.¹⁸ At the same time, the molecular volume computed with POSSIM (95.46ų) coincides with the experimental result of 95.5 Å ³ within the reported precision. We have also simulated pure liquid acetic acid at 100°C. While this temperature is far outside of the characteristic range of biophysical simulations, the error in the enthalpy of vaporization was only about 0.7 kcal/mol, and the molecular volume was less than 1% off. Thus, our model appears to robustly reproduce the physical properties of the carboxylic acid system at a broad range of conditions.

IV. Conclusions

We have extended our previously introduced POSSIM (POlarizable Simulations with Second order Interaction Model) framework to include a potential energy parameters for a number of electrostatically neutral and charged small molecules. These parameters are important as permitting to model the molecules as such and as side-chain analogues intended as the basis for development of the POSSIM force field for proteins. The POSSIM force field includes explicit treatment of the electrostatic polarization. Moreover, this is done with the second-order approximation which permits to reduce computational cost associated with the polarizable calculations and to avoid the possibility of the polarization catastrophe by making the expressions for the induced dipole moments essentially analytical. Both experimental and quantum mechanical data has been used as fitting target for the newly introduced parameters. The accuracy of the POSSIM results is adequate and consistent with the acceptable standards of the field.

We hope that these newly developed parameters will permit applications of POSSIM to new systems and further development of the force field and its application to simulating peptides, proteins and protein-ligand complexes.