The mechanical consequences of load bearing in the equine third metacarpal across speed and gait: the nonuniform distributions of normal strain, shear strain, and strain energy density

Abstract

Distributions of normal strain, shear strain, and strain energy density (SED) were determined across the midshaft of the third metacarpal (MCIII, or cannon bone) of 3 adult thoroughbred horses as a function of speed and gait. A complete characterization of the mechanical demands of the bone made through the stride and from mild through the extremes of locomotion was possible by using three 3-element rosette strain gauges bonded at the diaphyseal midshaft of the MCIII and evaluating the strain output with beam theory and finite element analysis. Mean ± sd values of normal strain, shear strain, and SED increased with speed and peaked during a canter (−3560±380 microstrain, 1760±470 microstrain, and 119±23 kPa, respectively). While the location of these peaks was similar across animals and gaits, the resulting strain distributions across the cortex were consistently nonuniform, establishing between a 73-fold (slow trot) to a 330-fold (canter) disparity between the sites of maximum and minimum SED for each gait cycle. Using strain power density as an estimate of strain history across the bone revealed a 154-fold disparity between peak and minimum at the walk but fell to ∼32-fold at the canter. The nonuniform, minimally varying, strain environment suggests either that bone homeostasis is mediated by magnitude-independent mechanical signals or that the duration of stimuli necessary to establish and maintain tissue integrity is relatively brief, and thus the vast majority of strain information is disregarded.—Rubin, C. T., Seeherman, H., Qin, Y.-X., Gross, T. S., The mechanical consequences of load bearing in the equine third metacarpal across speed and gait: the nonuniform distributions of normal strain, shear strain, and strain energy density.

The primary role of the axial and appendicular skeleton is to withstand the loads and moments that arise during both the mundane and extremes of functional activity. At a continuum level, these loads and moments result in deformation of the bone tissue, which can be described using the dimensionless parameter strain. In 1 dimension, strain is defined by the change in length of an object divided by its original length. Whether in a mandible in a macaque, a humerus in a tennis player, a femur in a kangaroo, or a vertebra in a whale, the osteoblast/osteocyte syncytium is subject to the functionally induced distortion of the bone matrix (e.g., chewing, serving, hopping, or swimming; ref. 1). The ubiquitous presence of skeletal strain identifies it as a generic, and efficient, means of translating the demands of functional activity into a site-specific signal relevant to the cells responsible for the regulation of bone morphology (2). The increased cortical thickness of the humerus in the serving arm of tennis players (3), or the rapid decline of bone mineral in the postcranial skeleton that parallels bed rest (4) or spaceflight (5), qualitatively emphasizes the potent morphological influence of mechanical signals on the skeleton (6). However, inferring bone's strain environment from bone morphology postmortem demands a range of presumptions about loading conditions and optimization criteria and is fraught with potential error (7).

To determine the role of functionally induced strain in establishing a structurally appropriate skeleton, it is first essential to quantify the range and type of mechanical signals the skeleton is subject to. This goal can be achieved by attaching strain gauges directly to a bone in vivo (8). The use of a single, single-element gauge is somewhat limited, as it permits an evaluation of the bone strain only at the site to which the gauge is attached and only in the direction in which the gauge is oriented, while the degree of shear cannot be established. Increasing to 2 strain gauges allows the manner of loading (e.g., axial loading vs. bending) to be approximated yet still requires presumptions be made about the critical locomotory planes of bending before the gauges are even attached (9, 10). Using 3 gauge attachment sites in conjunction with beam theory, Rybicki and Mills (11) were able to characterize the distribution of normal strains acting on a particular cortical cross-section. Their efforts, however, relied on single-element gauges, and, as a result, they were unable to calculate bending planes, principal strains, shear strain, or strain energy density (SED) at any point across the cortex.

A full characterization of the strain environment requires a minimum of three 3-element rosette strain gauges to be attached in a given plane around the bone's perimeter. This strategy permits the distribution of normal and shear strain, as well as the sites of greatest (and least) strain information to be quantified (12). The neutral axis of normal strain within the cortex as caused by bending can also be determined without a priori assumptions of the manner in which the bone is loaded, and the sites of peak tensile and compressive strain can be identified without presupposition. Further, resolving the strain environment throughout a stride permits the determination of how peak strain locations may vary during activity, and thus a more complete strain history of the bone can be established (13, 14). Thus a three 3-element strain gauge design permits a more comprehensive examination of how the bone is challenged by functional activity and the degree to which strain signals are, or are not, homogeneous about the cortex.

In the work reported here, the mechanical demands made on the equine third metacarpal (MCIII) from mild to strenuous locomotion were established using three 3-rosette gauges attached around the midshaft cross-section in conjunction with combined beam theory and finite element analysis. These protocols allowed a comprehensive characterization of the entire normal and shear strain environment acting on that cross-section without a priori assumptions of how the bone was actually loaded. Importantly, these characterizations were not restricted to a single point in time but were extended through the stance and swing phase of gait. As a result, SED distributions throughout the gait cycle were determined, providing a measure of the bone's strain history during locomotion [strain power density (SPD)]. The characterization of a long bone's strain environment throughout the gait cycle enables new insight into the association between functional strain and bone morphology.

MATERIALS AND METHODS

All animal procedures were reviewed and approved by Tufts University (North Grafton, MA, USA) and Stony Brook University Laboratory Animal User Committees and met or exceeded U.S. Department of Agriculture guidelines for animal safety and welfare. Three thoroughbred horses (ages 3, 4, and 5 yr, mean weight of 456±32 kg), donated from local racetracks, were used for this study. After a thorough examination to establish that they had no musculoskeletal injuries or lameness, the horses were trained to walk, trot, canter, and gallop on a motorized treadmill (Sato 1; Equispeed Technologies, Raymore, MO, USA) at speeds up to 9.2 m/s (33 kph).

Following induction and maintenance of halothane general anesthesia, 1 medial and 1 anterior/lateral skin incision, each 3 cm in length, were made on the midshaft of the right MCIII diaphysis using aseptic technique. Access to the medial, anterior, and lateral aspects of the cortex of MCIII could be obtained by retracting the skin incisions to expose the appropriate location of the cortex. The medial, anterior, and lateral aspects of the diaphysis were chosen for placement of the strain gauges because exposure of the bone surface required only minimal retraction of the skin and essentially no interference with adjacent extensor or flexor tendon systems. At each of these 3 sites, 1 cm² of periosteum was removed, and the bone surface was degreased using swabs soaked in diethyl ether.

Triple-rosette strain gauges (FCA-2, 120 Ω, gauge factor 2; Kenkyojo Co., Tokyo, Japan) were glued to the 3 prepared surfaces using 2-isobutyl cyanoacrylate “superglue” (Tissue Adhesive, Ethicon Inc., Livingston, UK). Each gauge backing was flooded with the glue, and the gauge was pressed onto the surface with firm digital pressure for ∼2 min (9). Gauge leads were strain-relieved 2 cm from the attachment sites by fixing an epoxy flange to the bone with a tapped 2.0-mm surgical screw. The 18 gauge leads (6 from each 3-element gauge) were then fed into a 3-mm tube, which was passed subcutaneously from the strain gauge site to a remote incision 40 cm proximal to the site of the gauges. The tube was then retracted through the remote stab incision, leaving the leads exiting the newly created subcutaneous tunnel. The skin incisions over the strain gauge sites were sutured using a routine 2-layer closure.

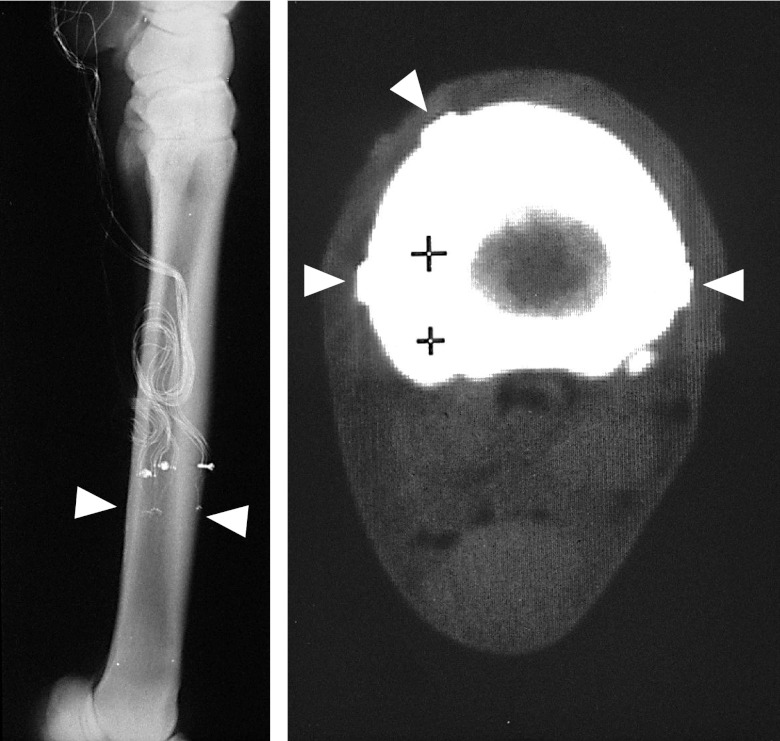
The alignment of each rosette relative to the metacarpal long axis, and confirmation of their attachment in the same transverse plane was determined from postop radiographs (Fig. 1, left panel). Cross-sectional strain gauge locations were established from a postoperative computerized axial tomography (CAT) scan (Delta 2010; in-plane pixel size 0.4×0.4 mm; Technicare, Solon, OH, USA), made while the horse was still anesthetized (Fig. 1, right panel).

Figure 1.

Left panel: Radiograph of the horse MCIII, showing the level of attachment of the three 3-element rosette strain gauges (arrow showing plane of three gauges, evident by small solder dots visible as small white dots). Approximately 2.5 cm proximal to the gauge site, a plastic flange is used relieve strain on the wires, anchored to the bone via a 2.0-mm screw tapped into the cortex. These radiographs also determine the orientation of the gauge placement (visible at higher magnification) relative to the longitudinal axis of the bone. Right panel: areal properties of the bone, as well as the relative location of the 3 gauges around the cortex (rectangular gauge backing shown by arrows), is determined by CAT scan, performed immediately following surgery while the animal remains anesthetized. The soft tissue (e.g., muscle, skin, and tendons) can be seen as an elliptical silhouette surrounding the bone. Posterior (ventral) surface of the MCIII is toward the bottom, and the medial aspect is to the left. The + symbols on the scan are provided by the computed topography instrument to establish a scale of 1 cm.

The limb was bandaged to protect the exposed lead wires, and the horses were allowed to recover from general anesthesia. Phenylbutazone (2 g) was administered intravenously to provide postoperative analgesia. Phenylbutazone analgesia was continued orally at a dose of 2 g 2×/d for 5 d following surgery.

Recovery for the minimally invasive strain gauge application procedure was routine, allowing for data collection on days 1 and 2 following surgery. Musculoskeletal evaluation before data collection confirmed that the horses did not exhibit any signs of lameness. As each horse was exercised through a range of gaits and speeds on the treadmill, analog strain gauge data were sampled digitally for 13.5-s intervals at 200 Hz/channel (Metrabyte DASH-16 12-bit A/D converter). Data were initially stored in laptop computer and transferred to a workstation for analysis. With these strain gauges, this amplifier and calibration system, and with data collected at this speed, the precision of the strain measurement was estimated at ±10 microstrain (με; ref. 14).

Areal properties based on the position of the strain gauges on radiographs and CAT scans for each horse were determined using custom image analysis software developed using a visual analysis software package (PV-WAVE, Precision Visuals, Boulder, CO, USA). For each animal, digital data from 10 consecutive complete cycles of a given gait and speed (stance and subsequent swing phase) were averaged to determine normal and shear strain data at each gauge site. Many of the analysis techniques used to characterize the cross-sectional normal and shear strain environment of the equine MCIII have been previously described in detail (12). In brief, strain and stress distributions through the MCIII midshaft induced by speed and gait were evaluated using a 3-dimensional linear elastic finite element analysis (FEA) model. The geometry of the FEA was established from CAT scan cross-sectional images of the MCIII, creating a model with a total of 15 layers in the longitudinal direction, 20 sectors in circumferential direction, and 5 sections in the radial direction, bounded by the endosteal and periosteal perimeters. This established a FEA model consisting of ∼1000 8-noded linearly elastic elements, based on convergence studies sufficient to obtain converged and stable strain outcomes (15). Cortical bone material properties of the MCIII were assumed to be an isotropic continuum (E=18 GPa, υ=0.3; ref. 16).

To approximate the end-loading conditions generated by locomotion, boundary conditions were applied in the FEA by constraining nodes at the most proximal section of the bone. FEA loading was iteratively adjusted by changing the displacement amplitudes at the distal end of bone until calculated strains matched measured strain at the corresponding location. Normal strains acting at any point on the cross-section (ε_zz) were determined by modeling the metacarpal as a prismatic beam of irregular cross-section subjected to a combination of axial loading and bending moments that resulted in normal strains as measured at all 3 gauge sites. To extend shear strains from measurements at gauge sites to shear strain distributions acting on the midshaft cross-section, the MCIII was modeled as a prismatic cantilever subjected to end shearing forces and a torsional moment.

Shear strains were determined at each gauge element center using an initial arbitrary loading condition consisting of all possible resolved forces and moments contributing to shear strains acting on the cross-section (F_x, F_y, T). Predicted strains at the gauge sites were compared with those measured experimentally, and the end loads and moment conditions were scaled so that the numerically determined strains at elements corresponding to the strain gauge sites matched the strains measured in vivo at these sites (<2% of difference). The normal and shear strains were then combined to determine SED (SED=1/2τ_ijε_ij). The distribution of SED acting on the midshaft cross-section was also resolved for each sampling point within the gait cycle.

Strain data were characterized with two objectives: determining peak values for a given gait, and the distribution of strain parameters around the midshaft cross-section through the stride. While the transition from trot to canter was readily identified, during data collection it became evident that the transition from a walk to a trot, as well as canter to gallop, was more difficult to delineate. For that reason, the trotting data were analyzed at two speeds, a slow trot (encompassing the walk/trot transition) and a fast trot. Strain evaluated at the highest speeds, whether canter or gallop, are also reported. All data are presented as means ± sd.

RESULTS

Peak normal strains

The peak magnitude of normal and shear strain, as well as SED acting on the midshaft cross-section, varied as a function of gait and speed. The peak normal strain was always compressive and occurred during the stance phase. Maximum compressive strains varied little during the walk (−1770±70 με), despite speeds ranging from 1.8 to 2.8 m/s (Fig. 2). Peak compressive strains increased when the horses changed gait to a trot (Fig. 3).At a slow trot (2.8±0.4 m/s; range: 2.3 to 3.3 m/s), peak compressive strains increased 18% compared with the walk (−2080±380 με), while at a faster trot (4.6±0.9 m/s; range: 3.5 to 6.0 m/s) peak compressive strains were 61% greater than at a walk (−2850±520 με). Maximal compressive strains were observed during the canter (7.1±0.8 m/s; range: 6.0 to 8.8 m/s, which were 2-fold greater than that measured in the walk (−3560±380 με).

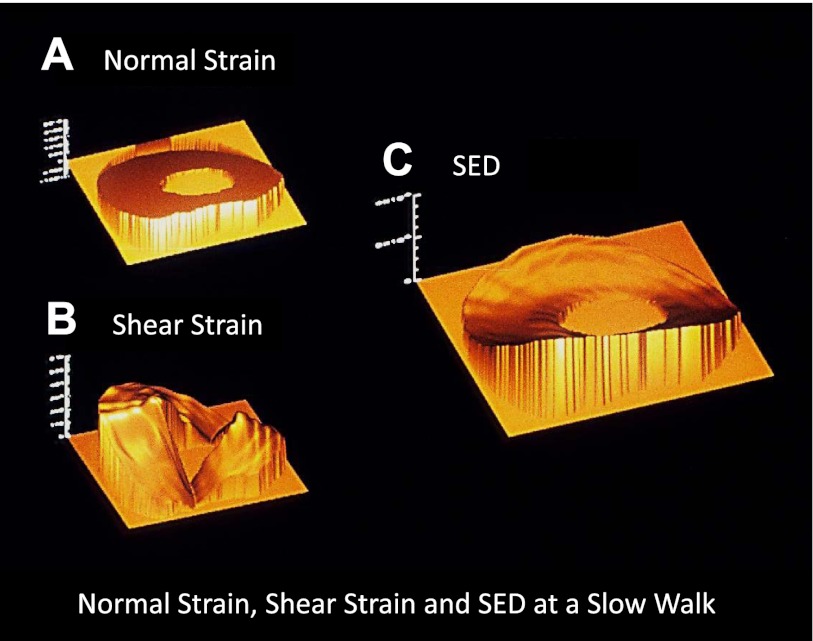
Figure 2.

Spatial distribution of normal and shear strain, as well as SED, in the MCIII during a 2 m/s walk. A) The nonuniform distribution of strain is evident in the profile of normal strain, ranging from the neutral axis (+13 με in tension) to −1048 με in compression. B) Shear strain ranges from 54 to −360 με. C) At this specific point in the stride, SED spans 2 orders of magnitude, from 117 to 10,602 Pa. Posterior (ventral) surface of the MCIII is toward the bottom; medial aspect is to the left.

Figure 3.

Shear strain due to bending [f(Vx), f(Vy)], as well as torsion [f(T)] were used to determine total shear strain around the cortex. As direction is arbitrary, shear strain only shown in absolute values. Posterior (ventral) surface of the MCIII is toward the bottom; medial aspect is to the left.

Maximum tensile strains also increased with speed, but the relative increases with gait changes differed. Maximum tensile strains during the walk (670±40 με) were identical at the slow trot (670±86 με). Peak tension increased 35% during the fast trot compared with the walk (900±220 με) and nearly doubled during the canter (1300±255 με; 94% vs. walk).

Peak shear strain

Peak shear was lowest during the walk (670±160 με; Fig. 2). In contrast to normal strains, shear increased substantially between both the walk and slow trot (1110±180 με; 66%) and the walk and fast trot (1600±220 με; 136%). Maximal shear strains were observed during the canter, but these peaks only slightly exceeded that of the fast trot (1760±470 με; 164% vs. walk).

Peak SED

Peak SED was lowest during the walk (33±6.7 kPa; Fig. 2) but rose rapidly beyond this condition. Maximal SED increased 31% for a slow trot (43±13.8 kPa) and 145% for a fast trot as relative to a walk (80±23 kPa). Peak SED was greatest during the canter (119±23 kPa; 260% vs. walk), at 6.9 m/s, a level that was not surpassed even at the fastest gallop (9.2 m/s). The minimum SED recorded across the cross-section also increased with gait speed, rising from 0.3 ± 0.3 kPa at a walk to 2.3 ± 2.2 kPa at a slow trot and 2.9 ± 3.5 kPa at a fast trot. The minimum SED was greatest during the canter (3.7±4.6 kPa).

Distributions of normal strain, shear strain, and SED

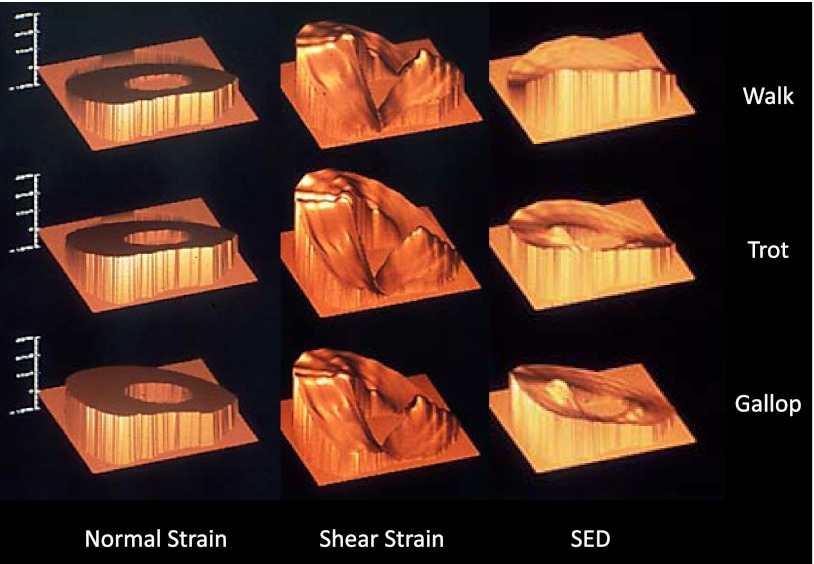
The distribution of normal and shear strain as a function of speed and gait were highly nonuniform across both speed and gait. The posterior/lateral cortex was consistently exposed to the greatest magnitude normal and shear strain, while the anterior/medial cortex was consistently exposed to the lowest strain environment (Fig. 4). As a result, at any given point in time, SED was also highly nonuniform across the cortex. For context, a SED distribution that was uniform across the cortex would be indicated by a ratio of 1.0 between the maximum and minimal sites of SED, a condition achieved in a beam exposed to uniform axial compression. In contrast, at the time in which peak SED was reached, the mean ratio of maximum to minimum SED exceeded 2 orders of magnitude (188±206x) across all horses and speeds. These ratios were high at the walk (280±195), were least for the slow (73±78x) and fast trots (120±104x), and greatest at the canter (330±330x). While the locations of the maximums and minimums were consistent, the ratios varied substantially, with the greatest range observed in the canter (10–815x). Given the minimal variation in maximal SED and its location (Fig. 4), variations in the minimum SED at any site within the cortex at a given point in time were most likely the cause of these shifts.

Figure 4.

Spatial distribution of normal and shear strain, as well as SED, in the MCIII during a 2 m/s walk, 5 m/s trot, and 8 m/s canter. Despite the large changes in strain magnitude and speed, the patterns of strain components about the cortex remain relatively stable, with only slight shifts in SED evident from walk to trot to canter. Posterior (ventral) surface of the MCIII is toward the bottom; medial aspect is to the left.

Strain history: integration of SED through the gait cycle

When the SED data were integrated through the entire stance phase, the distribution of SPD (kPa·s) remained highly nonuniform (Fig. 5). The sites of maximum SPD (posterior/medial cortex) and minimum SPD (anterior/lateral cortex) were consistent with those determined at the time of peak SED (Fig. 4). Unlike other assessed strain parameters, the maximum magnitude of SPD varied little and was maximal during walking (9.4±1.2 kPa·s). SPD was least for the slow (7.2±1.5 kPa·s) and fast trots (7.6±1.2 kPa·s), with a slight increase measured during the canter (9.0±2.6 kPa·s). The mean ratios of maximum to minimum averaged SPD were greatest for the walk (154±30x) and were reduced but >30-fold disparity was observed for the slow trot (41±35x), fast trot (34±22x), and canter (32±25x). Like the other mechanical parameters, the locations of maximal/minimal SPD shifted very little.

Figure 5.

Spatial distribution of SED integrated over an entire stride (SPD), for a 7 m/s canter. The maximum magnitude of SPD varied little with gait, while mean SPD was similar across gaits, implying the amount of power was normalized by the differences in time the hoof made contact with the ground. To better visualize the 32-fold disparity between peak and minimal SPD during the canter, the posterior (ventral) aspect of the MCIII is toward the left; lateral aspect is toward the bottom.

DISCUSSION

In the study reported here, the use of three 3-element rosette strain gauges made it possible to quantify the magnitude and distribution of normal and shear strain acting on the MCIII midshaft throughout a wide range of speeds and gaits. No a priori assumptions as to the manner of loading were required to enable resolution of the normal and shear strain distributions. An advantage of the combined beam theory and finite element analysis, as compared with a higher resolution full-field FEA, was that our approach enabled SED distributions to be determined at each sampling point (200 Hz) through the gait cycle with modest computational requirements. These measurements provided a full in vivo determination of normal, shear, and SED values and the first full characterization of the way bones are loaded during a complete locomotory gait cycle, including a comprehensive map of strain history in the bone matrix.

These data indicate that normal and shear strain, as well as SED, are highly nonuniform through the stance phase, emphasizing that mechanical signals induced by functional loading are far from homogeneous within the cortex at any given point in time, a condition that remains nonuniform through the stride. While peak strain magnitudes may be similar between animals and different species, (1, 17) the bone is subject to a disparate range of deformations that exceeds 2 orders of magnitude within a given cortical cross-section. In addition, the conservation of the sites of minimum and maximum normal strain, shear strain, and SED suggest that during strenuous functional activity, as best approximated by treadmill locomotion, bone cells within different portions of the cortex are subject to vastly different magnitudes of strain information.

The MCIII is a prismatic bone whose lack of midshaft muscle attachments makes it an ideal model to pursue experimental measurement and analytical characterization of in vivo strains. However, there are several clear limitations with our study. First, the small sample size was limited by the extreme fiscal and physical demands of the protocols, including the training of the animals, the surgical procedures, and the data analysis. With this in mind, we have focused on complete characterization of the strain environment of the MCIII to a descriptive extent rather than attempting to identify statistical difference between experimental conditions (e.g., across gait; refs. 1, 9). Second, our modeling approach assumed homogeneous material properties. This choice arose from a lack of direct available measurement of the material properties of the strain assessed bones. While better defined material properties may have changed the end loading conditions required for the model strain predictions to converge to measured strains at the gauge sites, we believe that the distributions of strain would be minimally influenced given that these distributions were, in essence, defined by in vivo strain measurements at each sampling point within the gait cycle, which are inevitably a product of end loading conditions, architecture, and material properties in the first place. Further, as the peak normal and shear strains recorded in the study are consistent with the literature (9, 11, 18, 19), the likelihood of error associated with strain measurement profoundly influencing the strain distributions is somewhat diminished.

Another significant limitation of this study lies with the use of a treadmill to control speed and gait, which inherently confines the induced strain environment compared with unconstrained ambulation in a field, including rapid acceleration/deceleration and changes in direction. A recent study in pygmy goats assessed whether strains induced in the metacarpus and radius vary between treadmill gait and outdoor activity when the goats were chased in an outdoor enclosure (20). While strain distributions across the cortex were not determined in that study, the attachment of gauges on 3 surfaces enabled the authors to assess the frequency distribution of peak strains at each gauge site. The data indicated that while outdoor activity had a slight tendency toward more frequent high-strain events, signs of profound change in strain distribution across surface (e.g., strain at a gauge site changing from compression to tension or vice versa) were not evident. Given that goats are known for their acrobatic behavior, we interpret these data to suggest that changes in bone strain distributions as may be provoked by unconstrained activity are, to a certain degree, limited by the cross-sectional morphology and longitudinal curvature of the bone.

Along these lines, this study does not afford insight into the possibility that turns at a racetrack further confound the mechanical challenge to the bone (21, 22). This limitation is amplified when the higher incidence of left front metacarpal stress fractures is considered, hypothesized to arise due to the tendency of galloping racehorses to go through counterclockwise turns using a left lead gait pattern. While on the left lead, the left leg contacts the ground first in the single limb stance phase following the aerial transition from the hind limbs to the front limbs. Interestingly, most galloping thoroughbreds will immediately switch to the right lead when they come out of the turn and into straight running, perhaps to share the musculoskeletal burden of the lead leg.

As noted above, the peak normal strains measured in this study were consistent with those reported in the literature (1). To our knowledge, however, these data represent the first full characterization of normal and shear strain across a long bone cross-section during a wide range of gaits and speeds. Further, given our approach, we were able to readily extend this analysis to assess the entire SED input at a given cross-sectional site through the entire stance phase of gait. The maximal SED in this study (119 kPa) was recorded during a 6.9 m/s canter, a level that was not surpassed even during a gallop at speeds up to 9 m/s. When this maximal SED was attained, the ratio between maximum and minimum SED exceeded 300-fold. In addition to providing a measure of the extreme nonuniformity of the strain environment, this ratio also provides general insight into the loading environment that causes the strain. For example, an end loading condition of pure compression (peak longitudinal normal strain: −300 με) superimposed on bending (peak longitudinal normal strain: −1500 με) would generate a SED ratio of 36. If pure torsion was also superimposed (peak shear: 100 με), this ratio would be reduced to 6.6. Since the mean ratio achieved across the walk, trot, and canter was in excess of 2 orders of magnitude, this strain heterogeneity could only be achieved if the bone was loaded primarily in bending with a nonuniform shear environment created by superimposed end shear and torsion. As SED was minimal in the anterior/medial cortex, these complex end-loading conditions were oriented such that the sites of minimal shear strain coincided with the location of the neutral axis of bending in this area.

Summing SED over the gait cycle indicated that, during a single gait cycle, portions of the midshaft cortex were exposed to, on average across all speeds and gaits, a 60-fold greater strain energy compared with the minimal SPD sites within the same cross-section. As the data indicate, the specific functional loading milieu of this bone persists through and across gaits, meaning that the SED disparities occurring at the time of peak loading are not normalized across the cross-section of bone over the remainder of the gait cycle. Indeed, using 200 cycles of trotting to represent a conservative estimate of daily activity (13), portions of the same cross-section experience daily strain energy inputs that differ by >1000-fold. Given that walking generated the greatest differences in SED input, a daily activity count skewed toward modest locomotion events would induce an even greater disparity of strain information (and perhaps supersede any differences in loading distribution, if they indeed exist, as caused by occasional acceleration/deceleration or rapid turns). As the MCIII persists, to some degree, in a healthy remodeling balance, these data suggest that either bone homeostasis is achieved via perception of nonmagnitude related strain parameters or that a vast majority of strain information is disregarded at the cellular and tissue levels.

The similarity in peak strains in long bones attained across a range of vertebrates and during strenuous activities lends support to bone remodeling being governed by a “mechanostat” (23). Simply stated, this paradigm anticipates that bone tissue will adapt its mass, up or down, to remain within a range of safe strain magnitudes and that this desired range is equivalent regardless of location in the skeleton. Other theories, as well, anticipate bone morphology to reflect the predominant characteristics of the bone's mechanical challenges; including peak strain magnitude and peak SED (24–26). While the goal of these theoretical predictions of bone remodeling is to best explain functionally induced changes in bone morphology, they are often based on an incomplete estimate of bone's strain history. In other words, over the course of a step or stride, many models predict that each area of the cortex is ultimately subject to the same strain or SED. Resulting from such a strain-driven paradigm, the bone would change its morphology such that each bone cell would ultimately be subject to the same mechanical stimulus, and the osteoblast-osteocyte syncytium would only have to coordinate formation-resorption to retain that optimal strain target. To a certain extent, this notion has grown out of the premise that morphological aspects of bone, such as curvature, girth, and cross-sectional design, arise to resist strain (“flexural neutralization”) with the goal being the avoidance of tensile strain in the bone (27). Because of the lack of a complete set of data describing the bone's actual mechanical environment, which must include both normal and shear strain, this presumption of a uniform strain environment has been difficult to either support or refute.

These data support the idea that parameters, such as strain distribution (28), strain frequency (29), strain rate (30), interstitial fluid flow (31), and strain gradients (32), may be as likely as magnitude as candidates for the control of skeletal adaptation, perhaps signaling adaptive cell responses independent of matrix distortion or damage. Lending some support to this perspective, high-frequency components of strain history (>10 Hz) are relatively uniform about the bone as a function of time (14). If bone were preferentially sensitive to strains in this high frequency domain (33), it would share the adaptive “responsibility” of mechanical signaling driving bone morphology with the highly nonuniform, sporadic, and relatively rare peak strain distribution described here.

In summary, this work provides a complete characterization of the mechanical environment of the equine MCIII through a range of speed and gait. The results indicate that the loading milieu of this bone is extremely complex, including end-shear, axial loads, and torsional moments. Critically, the bone cortex is subject to widely disparate levels of strain information, a nonuniformity that is stable through speed and gait and over time. Despite the resulting wide disparity in strain history that one area of the cortex is subject to relative to another, the bone manages to remain, to a large extent, in a homeostatic remodeling equilibrium, raising the possibility that the resident bone cell population is either synthesizing this mechanical information across the cortex (34) or saturating to mechanical signals past a given point of input (35) or that parameters other than peak strain control the adaptive response (36).