Abstract
The impact of ocean acidification on benthic habitats is a major preoccupation of the scientific community. However, the natural variability of pCO2 and pH in those habitats remains understudied, especially in temperate areas. In this study we investigated temporal variations of the carbonate system in nearshore macrophyte meadows of the western Baltic Sea. These are key benthic ecosystems, providing spawning and nursery areas as well as food to numerous commercially important species. In situ pCO2, pH (total scale), salinity and PAR irradiance were measured with a continuous recording sensor package dropped in a shallow macrophyte meadow (Eckernförde bay, western Baltic Sea) during three different weeks in July (pCO2 and PAR only), August and September 2011.The mean (± SD) pCO2 in July was 383±117 µatm. The mean (± SD) pCO2 and pHtot in August were 239±20 µatm and 8.22±0.1, respectively. The mean (± SD) pCO2 and pHtot in September were 1082±711 µatm and 7.83±0.40, respectively. Daily variations of pCO2 due to photosynthesis and respiration (difference between daily maximum and minimum) were of the same order of magnitude: 281±88 µatm, 219±89 μatm and 1488±574 µatm in July, August and September respectively. The observed variations of pCO2 were explained through a statistical model considering wind direction and speed together with PAR irradiance. At a time scale of days to weeks, local upwelling of elevated pCO2 water masses with offshore winds drives the variation. Within days, primary production is responsible. The results demonstrate the high variability of the carbonate system in nearshore macrophyte meadows depending on meteorology and biological activities. We highlight the need to incorporate these variations in future pCO2 scenarios and experimental designs for nearshore habitats.
Introduction
Human activities since the 19th century led to an increase of atmospheric pCO2 from 280 to 392 μatm [1] and the trend is rising. Some scenarios expect an elevation of atmospheric pCO2 up to 1000 μatm during the 21th century, peaking around 1400 μatm in the year 2300 [2], [3]. As oceans equilibrate with the atmosphere, dissolution of CO2 in water induces a decrease in pH. Global change has already led to an average seawater “acidification” of 0.1 pH units in the world ocean [4]. Acidification is enhancing the corrosiveness of seawater to calcite and aragonite, the two isoforms of calcium carbonates composing the shells and skeletons of marine organisms. Corrosiveness is expressed by the saturation states Ωarag and Ωcalc. A saturation state below 1 indicates a tendency towards dissolution of the crystal. Aragonitic structures (e.g. scleratinian corals, nacre of bivalve shells) are more soluble than calcitic (e.g. outer shell of oyster) [4]–[5].
Once dissolved, CO2 becomes part of the carbonate system, almost entirely composed of bicarbonate (HCO3 −) and carbonate ions (CO3 2−). Under actual atmospheric concentrations of CO2, CO2(aq) in the surface ocean represents less than 1% of the dissolved inorganic carbon (DIC) while HCO3 − represents ∼90% and CO3 2− ∼10%. The carbonate system in open oceanic environments is well known and most of the data forming the basis for the predictive models (see GLODAP database, [5], [6]) are derived from the open ocean. Those oceanic actual and future pCO2/pH values are the ones referred to when designing ocean acidification studies [7]. However, the biogeochemistry of nearshore ecosystems features more variations and differs widely than offshore conditions [8], [9]. Shallow nearshore and estuarine areas are the habitat of numerous benthic calcifiers. As highlighted by Andersson and Mackenzie (2012) [10], investigations on the effects of ocean acidification on calcifiers are neglecting this natural variability.
In nearshore habitats, the few available investigations were conducted on: (1) estuaries, salt marshes, mangroves and mudflats where transfers of carbon from land are occurring (e.g. [11]–[13]) and (2) reefs formed by corals or calcifying algae because of the direct effect of calcification on the carbonate system (e.g. [14], [15]). The carbonate chemistry of nearshore habitats dominated by macrophytes (kelp forests and seagrass and/or seaweed meadows) is almost unknown, even though they represent ∼5% of the primary production in the ocean and ¾ of the vegetal biomass [16], [17]. In these habitats, the carbonate system is driven by the photosynthetic physiology of the macrophytes, taking up carbon during the day and releasing it by respiration during the night [18], [19]. Since CO2 is a minor component of DIC and its diffusion rate in seawater is 10,000 times lower than in air [20], most macrophytes are relying on HCO3 − for photosynthesis [21]–[24]. Macrophyte meadows are highly productive and net autotrophic (carbon sink) [25], [26] exporting their excess production to the neighboring ecosystems under the form of litter or dissolved organic carbon [27]. Microbial degradation of exported organic carbon leads to elevated pCO2 and hypoxia of deeper offshore waters [28]. This phenomenon is particularly important in eutrophied ecosystems like the Baltic Sea [29]. In the inner bays of the western Baltic, local upwelling of hypercapnic water masses is regularly observed, increasing the surface pCO2 up to 2500 μatm. This typically happens at the end of summer when offshore winds are upwelling deep waters after long periods of stratification [30]–[32].
The aim of this study, conducted in the western Baltic Sea over three weeks of summer 2011, was to measure (1) the day/night variations of pCO2 due to photosynthesis and respiration of a macrophyte bed, (2) the evolution of the baseline pCO2 over summer and (3) the effect of local upwellings on the carbonate system and its diel variations. The variations of DIC, measured in the macrophyte meadow, were modeled with a statistical model considering wind direction and speed together with photosynthetically active radiation (PAR).
Materials and Methods
2.1 Study site
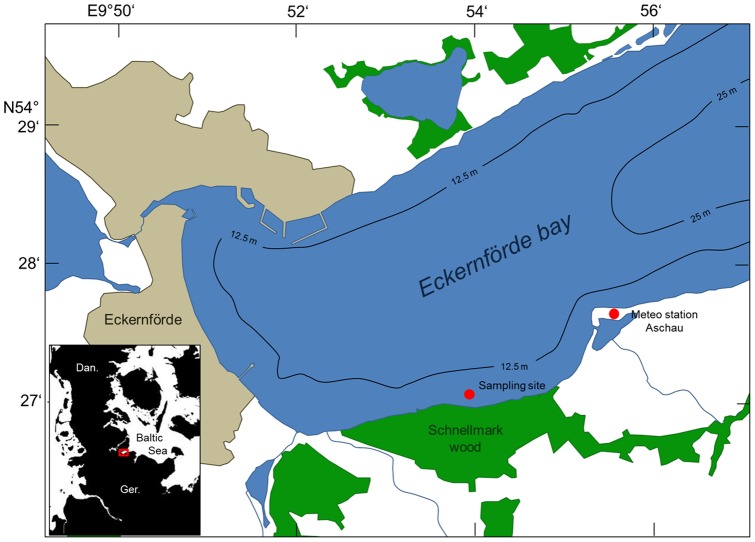
Physico-chemical parameters of seawater were recorded in a macrophyte meadow (3 m depth) in Eckernförde Bay (western Baltic Sea, Germany, 54°27′ N, 9°54′ E, see Fig. 1), during 3 weeks of summer 2011: July: 29.06−08.07, August: 29.07–05.08 and September: 09.09–16.09. In July, only pCO2 and PAR irradiance were recorded by two independent sensors. For the August and September deployments, a multimeter recording pH, salinity and temperature was added to the CO2 and PAR sensor. Wind speed (m s−1) and direction (rad) with a resolution of 10 min were provided by the meteorological station of Aschau in Eckernförde Bay (54°27′40 N, 9°55′30 E) belonging to the division of marine technology and research of the German Navy. The nearshore habitat of Eckernförde is a mixed bottom type dominated by macrophyte vegetation. The macrophyte vegetation covers approximately 75% of the surface. Dominant species are the brown algae Fucus serratus (40–60% of the macrophytes), growing on stones and rocks and the seagrass Zostera marina (<10% of the macrophytes) growing on sandy bottoms [33]. The inner basin reaches a maximum depth of 28 m in gentle slope. The water column is stratified in summer, with a pycnocline around 15 m depth [34]. September is the period of maximal stratification and hypoxia in the deep water. Hence, O2 reaches minimal concentrations of about 30 μM, associated with peaks of pCO2 up to 2500 μatm and accumulation of dissolved methane [29], [35]. No specific permits were required for the study, the location is not privately-owned or protected in any way and the study did not involve endangered or protected species.
Figure 1. Study site.
Map of the inner Eckernförde Bay indicating the locations of the survey site and the meteorological station, urban area (brown) and forests area (green).
2.2 The autonomous measuring system
The pCO2 was measured with a HydroC™ underwater sensor (CONTROS Systems & Solutions, Germany). The instrument measures the CO2 mole fraction in a headspace behind a membrane equilibrator with a two-wavelength non-dispersive infra-red detector (NDIR). The equilibrator is composed of a flat silicone composite membrane, the NDIR unit and additional sensors for pressure, temperature and relative humidity used to correct the NDIR signal and calculate the partial pressure. A small internal pump insures the continuous circulation of air in the equilibrator. To correct the drifting of the instrument with time, regular zeroings are automatically performed by scrubbing the CO2 from the internal gas stream. The zeroings are accounted during post processing of the data. A first description of the instrument can be found in [36] and deployments on various platforms are presented in [37]. The instrument was calibrated by the manufacturer prior to every deployment in the range of 100–1000 µatm at 17°C, 18°C and 18°C for the first, second and third deployment respectively. An overall accuracy of better than ±1% of the upper range value is assumed for post processed data. In order to achieve a constant and sufficiently short response time of the instrument, the HydroC™ is equipped with a water pump (Sea-Bird Electronics, USA) that provides a continuous water flow of approx. 35 ml sec−1 to the membrane, leading to a response time T63% of 3 min and a T99% of approximately 15 min. These response times are sufficiently fast to resolve the observed signal changes without the need for signal deconvolution. To correct the pCO2 series for the instrument drift, the zerooing signals were regarded as nodes and linearly interpolated in time to result in a smooth signal drift correction throughout the deployment time.
Salinity (psu), voltage (analogue signal from the pH measurement) and temperature (°C) were recorded automatically every 45 min with a pH-meter/conductimeter Mettler-Toledo SG 7/8 (Mettler Toledo, Switzerland). For the measurement of pH on total scale, seawater TRIS pH buffers for 15 psu were made according to the SOP 6a of Dickson et al. (2007) [38]. A combined electrode with a solid polymer electrolyte reference, equipped with an NTC (negative temperature coefficient) thermistor was used (Inlab expert pro, Mettler Toledo, Switzerland). The calibration of a new electrode was made 24 h before each deployment. To do so, the TRIS buffer was immersed in a thermostatic bath and the voltage of the pH electrode was measured with an accuracy of ±0.1 mV. The temperature of the buffer was varied by 1.5°C around seawater temperature. The temperature corresponding to every mV change was recorded with accuracy better than 0.01°C with a Fluke 5658 reference thermometer doted of a 5608 platinum resistance sensor (Fluke, USA). This process was repeated by increasing and decreasing the temperature to get an average voltage (mV) versus T (°C) reference curve for the electrode in the buffer. The NTC sensor of the pH sensor, of resolution 0.1°C, was calibrated against a reference thermometer and the resulting regression was achieved with a R2 >0.99. The resulting equation was used to correct the sampled temperature. The sampled voltage and corrected temperature were converted to pHtot by making use of the initial TRIS buffer calibration of the electrode and by using the equations given in the SOP 6a. In the lab, work conducted on Certified Reference Material (CRM) (Andrew Dickson, Scripps Institution of Oceanography) together with 35 psu buffers demonstrated an accuracy of 0.003 to 0.005 pH units and a precision better than 0.001 pH unit. However, this accuracy was not reached in the field and therefore the pH series were not used to derive the carbonate system but instead the alkalinity from discrete samples (see 2.3 for method and 4.4 for discussion on the method).
Salinity was measured within 0.01 psu by a Mettler Toledo Inlab 738 conductivity probe after calibration at 25°C with KCl 0.1 mol L−1 (Fischer Scientific, USA). The PAR irradiance (400 to 700 nm) was recorded every 5 min using a LI-192 quantum sensor connected to a LI-1400 data logger (Li-Cor Biosciences, USA). All series were extended to one minute interval series by linear interpolation.
2.3 Calculation of the carbonate system
Samples for alkalinity were taken at the beginning, middle and end of the measurement periods of August (the 29.07, 02.08 and 05.08, no replication) and September (the 09.09, 13.03 and 16.09, one replicate). Alkalinity was measured with an accuracy of ±5 µmol kg−1 using an open cell potentiometric titrator as described in the SOP 3b of [38] (Titrando 888, Methrom, Switzerland). A regression was calculated between the total alkalinity and salinity of the samples from August and September pooled together. The regression was highly significant (F-statistic: p<0.001, R2 = 0.83, n = 9): Alkalinity = 905.17 * Salinity +59. 83, with both slope and intercept significant at p<0.001 and p<0.01 (t-test, n = 9). Therefore, the alkalinity for the entire period was estimated from the salinity series. The DIC, Ωarag and Ωcalc were derived from calculated alkalinity and the measured pCO2 according to the equations described in [39] with the R package Seacarb [40] using first and second carbonate system dissociation constants for estuarine systems from [41] and the dissociations constants of HF and HSO4− of [42], [43].
2.4 Statistical modeling
The calculated DIC series of August and September was explained through a statistical model. It considered that (1) the weekly trend of the DIC series is caused by the upwelling of DIC-rich bottom water, (2) the diel variation of the DIC series is caused by primary production and respiration of the meadow. The weekly trends of DIC (Cw) were separated from the diel oscillations (Cd) by a central running average with a time frame of 24 h. Upwelling was assumed to be driven by wind. Cw was fit by a function of wind speed weighted by wind direction (WWt).
With Wup being a parameter between 0 and 2π, corresponding to the wind direction for which wind-induced upwelling is maximal. As examples, if Wup = 0 or 2π, maximal weights are given to northern winds, if Wup = π maximal weights are given to Southern winds. A “left-sided” running integration was performed on the weighted wind time series over a period kw:
Where Cwt is the 24 h running-average series of DIC at time t, WWt is the weighted wind speed at time t, μw and αw are regression parameters and kw is determined as the integration period yielding the best fit. Parameters in the regression were chosen to minimize residual variance. In the regression between time series, formal hypothesis tests, F-statistics and regression coefficients were not considered as they would be biased due to auto-correlation.
The within-day variations of DIC, Cd were modeled by exponentially weighted running integration of the PAR series over a period of 12 hours with an exponential decay rate λ (min−1):
In a final step, the irradiance and wind sub-models were summed to obtain the final model. The standard deviation of the residuals between model and DIC observation were considered for the parameterization of Wup, kw and λ.
Results
3.1 Measures
The three weeks revealed important day/night oscillations of pH and pCO2. The pCO2 increased during the night and decreased during the day reaching minima and maxima at 18∶00 and 6∶00 respectively. The pH inversely mirrored these pCO2 variations.
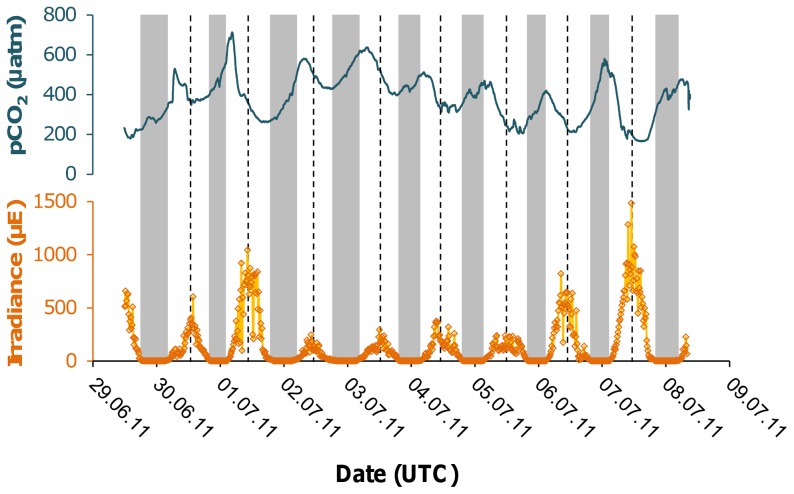
In July, only pCO2 and light was recorded. The mean pCO2 of the week was 390 μatm (mean ± SD), corresponding to the atmospheric CO2. However, diel oscillations of 281±88 μatm (mean ± SD) were recorded, with a phase shift of ∼6 h between light and pCO2 cycles. This shift, common to all three measurement periods is illustrated for July in Fig. 2.
Figure 2. Comparison between Light and pCO2 series in July.
Dark bands: period of darkness. Dashed lines: estimated center of the daylight distribution.
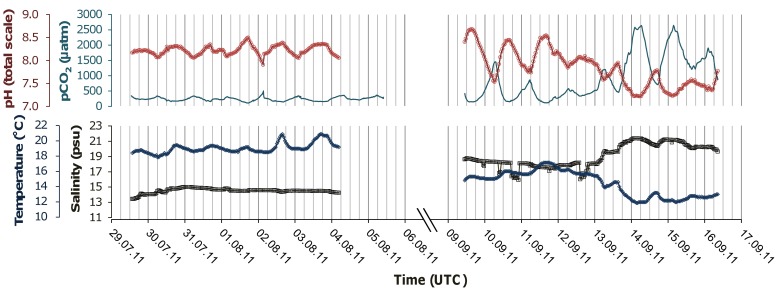
In August, seawater was undersaturated for CO2 compared to the atmosphere with a week mean of 239 μatm only. However, the diel variations remained comparable to those of July with a mean of 219±24 μatm (± SD) (Fig. 3, top left panel). The mean ± SD daily maximal and minimal pCO2 values were 374±67 and 155±32, respectively. The maximal amplitude was 416 μatm. The pH variations mirrored fluctuations in pCO2 with a weekly mean of 8.21, mean diel amplitude of 0.34±0.15 (± SD) and mean daily minimum and maximum of 8.03±0.07 and 8.37±0.08 (± SD). The average salinity and temperature during the week were 14.5±0.3 psu and 19.1±0.7°C, respectively (Fig. 3, lower left panel).
Figure 3. In situ measurements for August and September.
pCO2 (cyan), pH (red) Salinity (black) and temperature (dark blue) recorded in August (left) and September (right). The recording frequency was one minute for pCO2 and 45 minutes for the 3 other parameters. Symbols in the plots mark the recording events; linkage between the measurements every 45 min was achieved by linear interpolation. Secondary vertical gridlines unit: 6 h.
The recordings of September exhibit a strong difference between the beginning (09.09 to 13.09) and the end of the week (13.09 to 16.09). The mean ± SD salinity and temperature during the first three days were 17.8±0.6 psu and 15.9±0.6°C while during the three last days they increased and decreased to 20.7±0.5 psu and 12.4±0.4°C respectively (Fig. 3, lower right panel). This sudden decrease in seawater density is revealing an upwelling occurring in the middle of the week. Consequently, we observed a large discrepancy of the pCO2/pH between those two periods with means of 426 μatm/8.14 and 1593 μatm/7.46 respectively (Fig. 2, top right panel). In that second part of the week, oscillations of pCO2 became extreme. The maximal daily amplitudes recorded were 2184 μatm pCO2 and 1.15 pH units. The night peaks (mean ± SD) of pCO2 were 2397±425 μatm, with drops of pH to (mean ± SD) 7.26±0.07. During daytime, minimum pCO2 levels were still much higher than atmospheric concentrations with minima of (means ± SD) 681±211 μatm and corresponding maxima of pH of 7.77±0.18.
3.2 Carbonate system
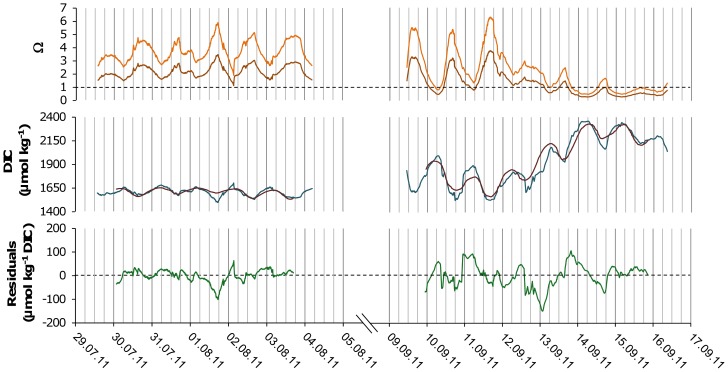
In August, means ± SD of the week and day/night variations of DIC were 1609±37 μmol kg−1 and 131±45 μmol kg−1 respectively (Fig. 4 central left panel). The seawater was always supersaturated with respect to both aragonite and calcite with diel means ± SD of 2.2±0.2 and 3.7±0.3 and means ± SD day/night variations of 1.4±0.6 and 2.4±0.9 respectively (see Fig. 4, top left panels).
Figure 4. Calculated and modeled carbonate chemistry.
Top panels: Saturation states for calcite (light brown) and aragonite (dark brown) for August (left) and September (right). Dashed line: Saturation threshold. Central panels: Observed (cyan) and modeled (red) DIC for August (left) and September (right). The residuals between model and observations are presented in bottom left and right for August and September respectively. Secondary vertical gridlines unit: 6 h.
In September the daily mean ± SD DIC concentrations preceding and during the upwelling event were 1829±45 and 2158±27 μmol kg−1, respectively (Fig. 4 central right panel). The diel variations of DIC were higher before than during the upwelling, with mean ± SD of 259±10 μmol kg−1 against 205±91 μmol kg−1, respectively.
Before the upwelling, the seawater was almost always supersaturated for aragonite and calcite (see Fig. 4 top right panel, 09.09 to 13.09). However at the hours of maximal pCO2 (6∶00), aragonite saturation dropped below 1: mean Ωarag: 0.8±0.3 (± SD). Oppositely, seawater reached maxima for Ωarag and Ωcalc around 18∶00. The resulting diel oscillations were of 4.3±0.3 and 2.6±0.2 for calcite and aragonite, respectively.
During the upwelling event the seawater was constantly undersaturated with mean ± SD Ωcalc and Ωarag of 1±0.5 and 0.6±0.3, exception made of the hours around 18 h, were modest maxima (mean ± SD) of 1.9±0.6 and 1.1±0.4 were reached (see Fig. 4 top right panel, 13.09 to 16.09).
3.3 Model
The DIC calculated from pCO2 and alkalinity and the DIC predicted by the statistical model for August and September are presented in Fig. 4 central panels. The differences between both are presented in Fig. 4. lower panels (residuals). In August, the model predicted a diel DIC mean (± SD) of 1610±16 µmol kg−1 and diel amplitudes of DIC of 86±14 µmol kg−1 (mean ± SD). The differences between modeled and calculated DIC is 1 µmol kg−1 for the diel average and 44 µmol kg−1 for the diel amplitude.
In September, the model predicted a diel DIC mean (± SD) of 1852±83 µmol kg−1 before the upwelling and 2143±47 µmol kg−1 during the upwelling. The differences with the calculated DIC are 23 µmol kg−1 and 15 µmol kg−1, respectively. Before and during upwelling, the diel amplitudes of DIC predicted by the model are 141±61 µmol kg−1 and 150±107 µmol kg−1 (mean ± SD), respectively. The difference from the calculated DIC is 117 µmol kg−1 and 55 µmol kg−1.
The set of parameters producing the best fitting models are Wup = 3π/2, corresponding to westerly wind, a period of integration kw of 55 h and λ of 0.0025 min−1and 0.001 min−1 for August and September respectively. The standard deviation of the residuals between modeled and calculated DIC are 25 μmol kg−1 and 49 μmol kg−1, corresponding to percentages of unexplained variation of 1.6% and 2.5% for August and September respectively (Fig. 3 lower panels). Fig. 5 presents, for September only, the evolution of the model residuals as function of the wind direction (Wup) and the integration period (kw). Easterly winds as maximal weights produce the worst fitting models while westerly winds the best fitting ones, southerly and northerly winds are intermediate. The parameter λ had less influence on the outcome of the model (Fig. 6), increasing its accuracy by a maximum of 2 to 4 μmol kg−1. Despite its poor effect on the model, the presence of this parameter is justified by the consideration of the decrease of the day length between August and September (the period of integration of the irradiance is fixed to 12 h in both).
Figure 5. Sensitivity of the model to the integration period ks and wind direction Wup.
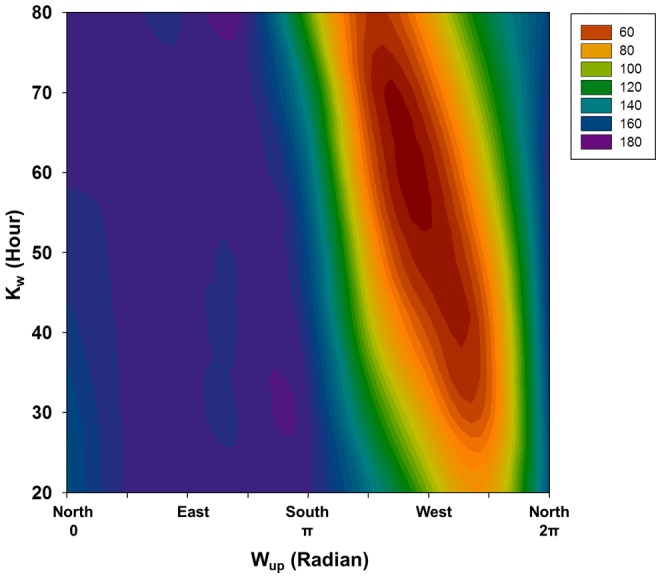
Contour plot of the standard deviation of the residuals between model and observation in µmol kg−1 DIC (color palette) for the September series as a function of Wup, the azimuth of reference used as maximal weight, and the kw, the period of the running integration of the weighted wind series.
Figure 6. Sensitivity of the model to λ.
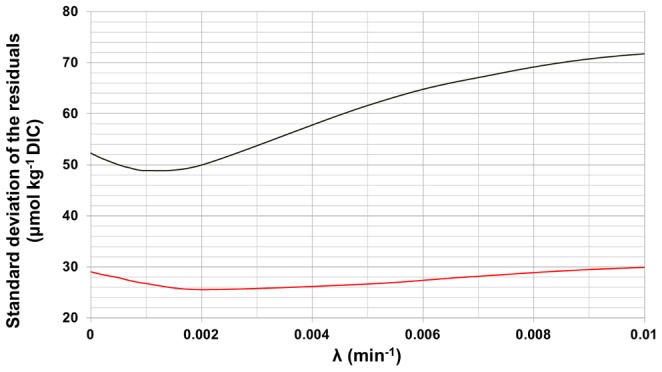
Evolution of the standard deviation of the residuals between model and observation in µmol kg−1 DIC in August (red) and September (black) as a function of λ (min−1), the instantaneous rate of increase used for the exponentially weighted running integration of the irradiance series.
Discussion
In our study, we showed the importance of the diel variations of pCO2 and pH due to photosynthesis and the importance of the variations of the carbonate chemistry baseline over summer. We demonstrated the interactive effects of upwelling and algal metabolism on the carbonate chemistry with a simple statistical model.
4.1 Inter-weekly dynamics
The pCO2 of our measurement site exhibited very different weekly trends over the summer. In August, we observed an important and stable pCO2 undersaturation. This reflects the conditions of the whole Baltic at this period, generated by the succession of blooms of phytoplankton and cyanobacteria [44], [45]. In September this stable condition is interrupted by the strengthening of the westerly winds, leading to the upwelling of the water masses isolated until then below the pycnocline. The chemistry of the deep waters of Eckernförde bay are monitored since 1957 and pCO2 of about 2500 μatm, linked to heterotrophic processes, are yearly observed in summer (Boknis Eck time series: [46]). Our study shows that the nearshore biota in shallow water is exposed to these high concentrations during upwelling events. The deep-water pCO2 is presumed to increase in the future by the conjunction of higher atmospheric pCO2 and reduced salinity and alkalinity of the Baltic Sea [32]. Melzner et al. (2012) [29] are expecting this deep water body to reach pCO2 of 4000 to 5000 μatm and the hypercapnic events of September to increase in magnitude. Besides, the frequency and duration of those upwelling events could also increase as a reinforcement of the westerly winds in the Baltic region is expected with global warming [47].
4.2 Daily oscillations
Diel oscillations, related to photosynthesis and respiration, are superimposed to the week scale dynamics. In normal summer conditions (without upwelling), the mean (± SD) amplitudes of the diel variations were 243±95 μatm CO2 (July, August) and 0.34±0.15 pH units (August only). Such diel variations have already been observed in macrophyte stands worldwide: in seagrass beds of Australia [16], Mediterranean [48] and Zanzibar [19], in tidal rocky-shores of the northeastern Pacific [49] and in algal meadows of the Danish islands [18]. Among nearshore ecosystems, the highest diel variations are occurring in macrophyte dominated ecosystems, upwelling areas and estuaries [50]. Our study site cumulates those three characteristics: brackish, weakly buffered and eutrophied ecosystem dominated by macrophytes and submitted to upwelling. We recorded diel oscillations of 1604.9±795.7 μatm (mean ± SD) during the upwelling event of September. To our knowledge only near-shore mangroves exhibit wider diel variations with 3500 μatm recorded in the Bermuda [10].
However, the importance of these variations is relative, as the fraction of DIC present as CO2(aq) in high pCO2/low pH seawater is higher than in low pCO2/high pH seawater (see Bjerrum plot in e.g. [39]). Thus, in September, the diel variations of CO2 are stronger during the upwelling than before but we observe the opposite for DIC (mean ± SD DIC: 258.6±10.5 μmol kg−1 against 205.1±90.7 μmol kg−1), possibly revealing a reduction of photosynthesis during the upwelling. This could be explained by an osmotic stress engendered by a rapid increase of salinity [51], [52] rather than by the elevated pCO2. Indeed, any increase in DIC and pCO2 is presumed to be beneficial to marine macrophytes [53], even if this have never been formally proven [54].
4.3 Model
We were able to explain the DIC variations of August and September to an accuracy of±50 μmol kg−1 with a simple statistical model (three parameters only), based on wind and PAR. The weighing procedure of the wind speed, although simple in its geometric approach, appeared to work very well as an explanation of the multi-day trends.
Our model designates westerly winds as responsible for upwelling. This result is slightly different from previous observations and simulations in other regions of the Baltic Sea identifying southwesterly winds as being the most effective [30]. This small discrepancy is certainly due to the east-west orientation of Eckernförde bay compared to the general north-east/south-west orientation of the Baltic Sea. The use of exponentially weighted integration of irradiance as a proxy for primary production was less effective than the similar approach used for the upwelling. Indeed, while the daily DIC means are quite accurately predicted (<20 µmol kg−1), the diel amplitude is systematically underestimated by 40 to 70 µmol kg−1 DIC. This variation, unexplained by the model, could be due to heterotrophic respiration, air-sea exchange of CO2 [17] or diel variation of alkalinity as discussed in 4.1. However, despite the simplistic nature of our model, it is a first step in the understanding and prediction, in a context of global change, of the carbonate system dynamics in the Baltic nearshore areas.
4.4 Measurement reliability
The accuracy of the post-processed pCO2 data is expected to be <±10 μatm for values within the calibrated measuring range of 100–1000 µatm. An additional error can be expected when the pCO2 exceeds the measuring range as in this case the calibration polynomial of the instrument is extrapolated. We expect this error to be ±150 μatm at maximum for the highest pCO2 recorded in September at around 2600 μatm.
Despite our efforts, we did not achieve in the field the pH accuracy necessary to use it as input parameter for the derivation of the carbonate system, as we are able to in laboratory. We estimate the error in pH of the order of 0.01 due to uncorrectable drift during the measurement periods. In the conditions of temperature and salinity of the western Baltic, such inaccuracy in pH produces anomalies in derived alkalinity of the order of 10–100 μmol kg–1 at pH/pCO2 inferior to 7.8/800 μatm and up to 1000 at higher pH/lower pCO2. For future field studies, Durafets sensors [55] or spectrophotometric sensors [56] represent promising alternatives to glass electrodes, both capable of reaching accuracies of 0.001 to 0.0001 pH units. We had to perform alkalinity titrations and rely on a salinity to alkalinity relationship to achieve the calculations. This method is relevant [57], [58] and we estimate the error on the derived DIC to be <15 µmol kg−1 DIC. However, it ignores any changes of alkalinity at constant salinity. This phenomenon is very important in coral and shellfish reefs due to the uptake or release of Ca2+ by calcification or dissolution [59], [60]. However, in macrophyte ecosystems, we expect very marginal diel variations of alkalinity due to photosynthesis and respiration [61].
4.5 Effect on fauna
The daily oscillations of pCO2 generated by photosynthesis could be of prime importance for calcifiers, creating at daytime periods of high saturation states favourable to CaCO3 precipitation. Such coupling between photosynthesis and calcification has already been observed in a Hawaiian coral reef by Drupp et al. (2011) [59] and Shamberger et al. (2011) [60] where calcification is maximal at midday when the pCO2 is minimal due to planktonic photosynthesis. In that reef, the intensity of the photosynthesis is modulated by wind driven inputs of nutrients from the flume of a neighboring estuary.
In general, studies conducted on western Baltic populations of animals, calcifying or not, tend to demonstrate their tolerance to acidic conditions [62]. Also, the Baltic population of the mussels Mytilus edulis experiences reduced growth and dissolution of the shell only when Ωarag ≤0.15 corresponding to a pCO2 of ∼ 4000 μatm [31]. Despite this weakening of their shells, the predation by sea stars Asterias rubens and crabs Carcinus maenas maintained at similar pCO2 are reduced by 56% and 41% respectively [63]. Besides, the growth of the Baltic brackish barnacle Amphibalanus improvisus, competitor of Mytilus for space, remains unaffected at both larval and adult stage at pCO2 >3000 μatm [64]. Macrophyte meadows are also transient habitats, sheltering early life stages of numerous animal species. Those might exhibit more tolerance to ocean acidification as well. As example, the spawns of Baltic herrings Clupea harengus, deposited on macrophyte beds [65], are not affected in their embryonic development by high pCO2/low pH [66]. The volatility of the carbonate system and the extreme acidic events we observed could have exerted a selective pressure on Baltic populations, explaining the resistance of the local fauna to acidification stress in laboratory. Nevertheless, all the studies quoted previously were conducted under stable elevated pCO2. None coupled elevated pCO2 baseline and the diel variations we observed.
Conclusion
Our study represents one of the first attempts of high resolution continuous measurement of the carbonate system in the highly variable environment that is the Baltic Sea's nearshore. The three weeks showed quite different results related to the dynamics of the whole Baltic carbonate system, to the meteorological condition and to very local processes of photosynthesis and respiration. This study highlights the importance of the natural variations of pCO2 and pH and emphasizes the consideration of these in ocean acidification studies on nearshore organisms.
Acknowledgments
We thank M. Fischer, C. Hiebenthal, C. Howe, B. Huang Xuan, C. Lieberum, K. Maczassek and C. Pansch, Y. Sawall and the crew of the F. B. Polarfuchs for their field assistance.
Funding Statement
This work was funded by the European community, Marie Curie ITN CALMARO (PITN-GA-2008-215157). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.NOAA – ESRL (2011) Available: http://www.esrl.noaa.gov/gmd/ccgg/trends.
- 2.Solomon S, Qin D, Manning M, Chen Z, Marquis M, et al. (2007) IPCC, 2007: Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge: Cambridge University Press. 996 p.
- 3. Ridgwell A, Zondervan I, Hargreaves J, Bijma J, Lenton T (2007) Assessing the potential long-term increase of oceanic fossil fuel CO2 uptake due to CO2 – calcification feedback. Biogeosciences 4: 481–492. [Google Scholar]
- 4. Orr JC, Fabry VJ, Aumont O, Bopp L, Doney SC, et al. (2005) Anthropogenic ocean acidification over the twenty-first century and its impact on calcifying organisms. Nature 437: 681–686. [DOI] [PubMed] [Google Scholar]
- 5. Feely RA, Sabine CL, Lee K, Berelson W, Kleypas JA, et al. (2004) Impact of anthropogenic CO2 on the CaCO3 system in the oceans. Science 305: 362–363. [DOI] [PubMed] [Google Scholar]
- 6. Key RM, Kozyr A, Sabine CL, Lee K, Wanninkhof R, et al. (2004) A global ocean carbon climatology: Results from Global Data Analysis Project (GLODAP). Glob Biogeochem Cy 18: 1–23. [Google Scholar]
- 7.Riebesell U, Fabry VJ, Hansson L (2010) Guide to best practices for ocean acidification research and data reporting. Luxembourg: Publication office of the European Union. 260 p.
- 8. Borges AV, Delille B, Frankignoulle M (2005) Budgeting sinks and sources of CO2 in the coastal ocean: Diversity of ecosystems counts. Geophys Res Lett 32: 1–6. [Google Scholar]
- 9. Chen CTA, Borges AV (2009) Reconciling opposing views on carbon cycling in the coastal ocean: Continental shelves as sinks and near-shore ecosystems as sources of atmospheric CO2 . Deep Sea Res Pt II 56: 578–590. [Google Scholar]
- 10. Andersson AJ, Mackenzie FT (2012) Revisiting four scientific debates in ocean acidification research. Biogeosciences 9: 893–905. [Google Scholar]
- 11. Brasse S, Reimer A, Seifert R, Michaelis W (1999) The influence of intertidal mudflats on the dissolved inorganic carbon and total alkalinity distribution in the German Bight, southeastern North Sea. J Sea Res 42: 93–103. [Google Scholar]
- 12. Gattuso JP, Frankignoulle M, Wollast R (1998) Carbon and carbonate metabolism in coastal aquatic ecosystems. Annu Rev Ecol Syst 29: 405–434. [Google Scholar]
- 13. Gazeau F, Borges AV, Barrón C, Duarte CM, Iversen N, et al. (2005) Net ecosystem metabolism in a micro-tidal estuary (Randers Fjord, Denmark): evaluation of methods. Mar Ecol Prog Ser 301: 23–41. [Google Scholar]
- 14. Rees SA, Opdyke BN, Wilson PA, Henstock TJ (2006) Significance of Halimeda bioherms to the global carbonate budget based on a geological sediment budget for the Northern Great Barrier Reef, Australia. Coral Reefs 26: 177–188. [Google Scholar]
- 15. Kleypas JA, Anthony KRNN, Gattuso JP (2011) Coral reefs modify their seawater carbon chemistry – case study from a barrier reef (Moorea, French Polynesia). Glob Change Biol 17: 3667–3678. [Google Scholar]
- 16. Smith S (1981) Marine macrophytes as a global carbon sink. Science 211: 838–840. [DOI] [PubMed] [Google Scholar]
- 17. Gattuso JP, Payri CE, Pichon M, Delsalle B, Frankignoulle M (1997) Primary production, calcification and air-sea CO2 fluxes of a macroalgal-dominated coral-reef community (Moorea, French Polynesia). J Phycol 33: 729–738. [Google Scholar]
- 18. Middelboe AL, Hansen PJ (2007) High pH in shallow-water macroalgal habitats. Mar Ecol Prog Ser 338: 107–117. [Google Scholar]
- 19. Semesi IS, Beer S, Björk M (2009) Seagrass photosynthesis controls rates of calcification and photosynthesis of calcareous macroalgae in a tropical seagrass meadow. Mar Ecol Prog Ser 382: 41–48. [Google Scholar]
- 20.Lobban CS, Harrison PJ (1994) Seaweed Ecology and Physiology. Cambridge: Cambridge University Press. 366 p.
- 21. Beer S, Rehnberg J (1997) The acquisition of inorganic carbon by the seagrass Zostera marina . Aquat Bot 56: 277–283. [Google Scholar]
- 22. Badger MR (2003) The roles of carbonic anhydrases in photosynthetic CO2 concentrating mechanisms. Photosynth Res 77: 83–94. [DOI] [PubMed] [Google Scholar]
- 23. Giordano M, Beardall J, Raven JA (2005) CO2 concentrating mechanisms in algae: mechanisms, environmental modulation, and evolution. Annu Rev Plant Biol 56: 99–131. [DOI] [PubMed] [Google Scholar]
- 24. Hepburn CD, Pritchard DW, Cornwall CE, McLeod RJ, Beardall J, et al. (2011) Diversity of carbon use strategies in a kelp forest community: implications for a high CO2 ocean. Glob Change Biol 17: 2488–2497. [Google Scholar]
- 25. Barrón C, Marbà N, Duarte CM, Pedersen MF, Lindblad C, et al. (2003) High Organic Carbon Export Precludes Eutrophication Responses in Experimental Rocky Shore Communities. Ecosystems 6: 144–153. [Google Scholar]
- 26. Duarte CM, Marbà N, Gacia E, Fourqurean JW, Beggins J, et al. (2010) Seagrass community metabolism: Assessing the carbon sink capacity of seagrass meadows. Glob Biogeochem Cy 24: 1–8. [Google Scholar]
- 27. Barrón C, Duarte CM (2009) Dissolved organic matter release in a Posidonia oceanica meadow. Mar Ecol Prog Ser 374: 75–84. [Google Scholar]
- 28. Gray JS, Wu RS, Or YY (2002) Effects of hypoxia and organic enrichment on the coastal marine environment. Mar Ecol Prog Ser 238: 249–279. [Google Scholar]
- 29.Melzner F, Thomsen J, Koeve W, Oschlies A, Gutowska MA, et al. (2012) Future ocean acidification will be amplified by hypoxia in coastal habitats. Mar Biol. Available:http://www.springerlink.com/index/10.1007/s00227-012-1954-1. Accessed 5 June 2012.
- 30. Myrberg K, Andrejev O (2003) Main upwelling regions in the Baltic Sea – a statistical analysis based on three-dimensional modelling. Boreal Environ Res 8: 97–112. [Google Scholar]
- 31. Thomsen J, Gutowska MA, Saphörster J, Heinemann A, Trübenbach K, et al. (2010) Calcifying invertebrates succeed in a naturally CO2-rich coastal habitat but are threatened by high levels of future acidification. Biogeosciences 7: 3879–3891. [Google Scholar]
- 32. Gräwe U, Burchard H (2011) Global Change and Baltic Coastal Zones. In: Schernewski G, Hofstede J, Neumann T, editors. Global Change and Baltic Coastal Zones. Dordrecht: Springer Netherlands, Vol. 1: 3–22. [Google Scholar]
- 33.Karez R (2008) Kartierung mariner Pflanzenbestände im Flachwasser der Ostseeküste – Schwerpunkt Fucus und Zostera: Außenküste der schleswig-holsteinischen Ostsee und Schlei. Landesamt für Landwirtschaft, Umwelt und ländliche Räume. 310 p.
- 34. Krey J, Koske P, Szekielda K (1965) Produktionsbiologische und hydrographische untersuchungen in der Eckernförder Bucht. Kieler Meeresforschungen 21: 135–143. [Google Scholar]
- 35. Bange H, Bergmann K, Hansen H, Kock A, Koppe R, et al. (2010) Dissolved methane during hypoxic events at the Boknis Eck Time Series Station (Eckernförde Bay, SW Baltic Sea). Biogeosciences 7: 1279–1284. [Google Scholar]
- 36.Fietzek P, Körtzinger A (2010) Optimization of a membrane-based NDIR sensor for dissolved carbon dioxide. In: Harrison DE, Stammer D, editors. OceanObs′09: Sustained Ocean Observations and Information for Society Conference. venice: ESA publication. 1–4.
- 37.Fietzek P, Kramer S, Esser D (2011) Deployment of the HydroCTM (CO2/CH4) on stationary and mobile platforms – Merging the trends in the field of platform and sensor development. Oceans 11 MTSIEEE Conference. 1–9.
- 38.Dickson AG, Sabine CL, Christian JR (2007) Guide to Best Practices for Ocean CO2 Measurements. PICES spec. Dickson AG, Sabine CL, Christian JR, editors. 191 p.
- 39.Zeebe RE, Wolf-Gladrow DA (2001) CO2 in seawater: equilibrium, kinetics, isotopes. Dordrecht: Elsevier. 346 p.
- 40.Lavigne H, Gattuso JP (2010) seacarb: seawater carbonate chemistry with R. R package version 2.3. 3. Software. Available: http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:seacarb:seawatercarbonatechemistrywithR.Rpackageversion2.3#0.
- 41. Millero FJ (2010) Carbonate constants for estuarine waters. Mar Freshwater Res 61: 139–142. [Google Scholar]
- 42. Perez FF, Fraga F (1987) The pH measurements in seawater on the NBS scale. Mar Chem 21: 315–327. [Google Scholar]
- 43. Dickson AG (1990) Standard potential of the reaction: AgCl(s) + ½H2(g) = Ag(s) + HCl(aq), and the standard acidity constant of the ion HSO4 - in synthetic sea water from 273.15 to 318.15 K. Chem Thermodyn. 22: 113–127. [Google Scholar]
- 44. Thomas H, Schneider B (1999) The seasonal cycle of carbon dioxide in Baltic Sea surface waters. J Mar Syst 22: 53–67. [Google Scholar]
- 45. Schneider B (2011) The CO2 system of the Baltic Sea: Biogeochemical control and impact of anthropogenic CO2 . In: Schernewski G, Hofstede J, Neumann T, editors. Global Change and Baltic Coastal Zones. Dordrecht: Springer Netherlands, Vol. 1: 33–49. [Google Scholar]
- 46.Bange H, Hansen H, Malien F, Laß K, Karstensen J, et al. (2011) Boknis Eck time series station (SW Baltic Sea): Measurements from 1957 to 2010. LOICZ inprint: 16–22.
- 47. Neumann T (2011) Climate Change Impacts on the Baltic Sea. In: Schernewski G, Hofstede J, Neumann T, editors. Global Change and Baltic Coastal Zones. Dordrecht: Springer Netherlands, Vol. 1: 23–32. [Google Scholar]
- 48. Invers O, Romero J, Pérez M (1997) Effects of pH on seagrass photosynthesis: a laboratory and field assessment. Aquat Bot 59: 185–194. [Google Scholar]
- 49. Wootton JT, Pfister CA, Forester JD (2008) Dynamic patterns and ecological impacts of declining ocean pH in a high-resolution multi-year dataset. P Natl Acad Sci USA 105: 18848–18853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hofmann GE, Smith JE, Johnson KS, Send U, Levin LA, et al. (2011) High-frequency dynamics of ocean pH: a multi-ecosystem comparison. PloS one 6: e28983. Available: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3242773&tool=pmcentrez&rendertype=abstract. Accessed 6 March 2012. [DOI] [PMC free article] [PubMed]
- 51. Ohno M (1976) Some observations on the influence of salinity on photosynthetic activity and chloride ion loss in several seaweeds. Internationale Revue der gesamten Hydrobiologie und Hydrographie 61: 665–672. [Google Scholar]
- 52. Bäck S, Collins JC, Russel G (1992) Comparative ecophysiology of Baltic and Atlantic Fucus vesiculosus . Mar Ecol Prog Ser 84: 71–82. [Google Scholar]
- 53. Beer S, Koch E (1996) Photosynthesis of marine macroalgae and seagrasses in globally changing CO2 environments. Mar Ecol Prog Ser 141: 199–204. [Google Scholar]
- 54. Israel A, Hophy M (2002) Growth, photosynthetic properties and Rubisco activities and amounts of marine macroalgae grown under current and elevated seawater CO2 concentrations. Glob Change Biol 8: 831–840. [Google Scholar]
- 55. Martz TR, Connery JG, Johnson KS (2010) Testing the Honeywell Durafet for seawater pH applications. Limnol Oceanogr -Meth 8: 172–184. [Google Scholar]
- 56. Aßmann S, Frank C, Körtzinger A (2011) Spectrophotometric high-precision seawater pH determination for use in underway measuring systems. Ocean Sci 7: 597–607. [Google Scholar]
- 57. Beldowski J, Löffler A, Schneider B, Joensuu L (2010) Distribution and biogeochemical control of total CO2 and total alkalinity in the Baltic Sea. J Mar Syst 81: 252–259. [Google Scholar]
- 58. Hjalmarson S, Wesslander K, Anderson LG, Omstedt A, Perttila M, et al. (2008) Distribution, long-term development and mass balance calculation of total alkalinity in the Baltic Sea. Cont Shelf Res 28: 593–601. [Google Scholar]
- 59. Drupp P, De Carlo EH, Mackenzie FT, Bienfang P, Sabine CL (2011) Nutrient inputs, phytoplankton response, and CO2 variations in a semi-enclosed subtropical embayment, Kaneohe bay, Hawaii. Aquat Geochem 17: 473–498. [Google Scholar]
- 60. Shamberger KEF, Feely RA, Sabine CL, Atkinson MJ, DeCarlo EH, et al. (2011) Calcification and organic production on a Hawaiian coral reef. Mar Chem 127: 64–75. [Google Scholar]
- 61. Chisholm J, Gattuso JP (1991) Validation of the alkalinity anomaly technique for investigating calcification and photosynthesis in coral reef communities. Limnol Oceanogr 36: 1232–1239. [Google Scholar]
- 62. Thomsen J, Melzner F (2010) Moderate seawater acidification does not elicit long-term metabolic depression in the blue mussel Mytilus edulis . Mar Biol 157: 2667–2676. [Google Scholar]
- 63. Appelhans Y, Thomsen J, Pansch C, Melzner F, Wahl M (2012) Sour times: seawater acidification effects on growth, feeding behaviour and acid–base status of Asterias rubens and Carcinus maenas . Mar Ecol Prog Ser 459: 85–98. [Google Scholar]
- 64. Pansch C, Nasrolahi A, Appelhans YS, Wahl M (2012) Impacts of ocean warming and acidification on the larval development of the barnacle Amphibalanus improvisus . J Exp Mar Biol Ecol 420–421: 48–55. [Google Scholar]
- 65. Aneer G (1989) Herring (Clupea harengus L.) spawning and spawning ground characteristics in the Baltic Sea. Fish Res 8: 169–195. [Google Scholar]
- 66. Franke A, Clemmesen C (2011) Effect of ocean acidification on early life stages of Atlantic herring (Clupea harengus L.). Biogeosciences 8: 3697–3707. [Google Scholar]