An Optical Super-Microscope for Far-field, Real-time Imaging Beyond the Diffraction Limit

Abstract

Optical microscopy suffers from a fundamental resolution limitation arising from the diffractive nature of light. While current solutions to sub-diffraction optical microscopy involve combinations of near-field, non-linear and fine scanning operations, we hereby propose and demonstrate the optical super-microscope (OSM) – a superoscillation-based linear imaging system with far-field working and observation distances – which can image an object in real-time and with sub-diffraction resolution. With our proof-of-principle prototype we report a point spread function with a spot size clearly reduced from the diffraction limit, and demonstrate corresponding improvements in two-point resolution experiments. Harnessing a new understanding of superoscillations, based on antenna array theory, our OSM achieves far-field, sub-diffraction optical imaging of an object without the need for fine scanning, data post-processing or object pre-treatment. Hence the OSM can be used in a wide variety of imaging applications beyond the diffraction limit, including real-time imaging of moving objects.

The diffractive nature of light poses a fundamental limitation on the resolution of electromagnetic wave-based imaging systems. This "diffraction limit" has been well understood since the times and contributions of Abbé and Rayleigh¹,². While overcoming the diffraction limit has been a problem of great interest for more than a century, it also takes on increasing importance as scientific instrumentation and fabrication reaches ever deeper into the nanoscale, and the scientific community requires imaging tools with unprecedented resolution. Heretofore, solutions to sub-diffraction optical microscopy involve combinations of near-field, non-linear and fine scanning operations.

Of the various proposals in the past century to surpass the diffraction limit, the near-field scanning optical microscope (NSOM), which scans a sharp optical probe across a plane nanometers away from an object and collects near-field information to form an image, has become an essential technology in obtaining sub-wavelength image resolution³,⁴. More recently, several creative imaging devices (namely, the metamaterial superlens, the hyperlens, the radiationless interference screen, the metascreen and the sub-wavelength grating⁵,⁶,⁷,⁸,⁹,¹⁰,¹¹,¹², amongst others) have been conceived which utilize the evanescent spectrum in clever ways to achieve sub-wavelength resolution imaging, and improve the device working distance (the distance between the object and the component of the imaging device, including its illumination module, which is closest to the object) to the approximate range of 0.1λ to 0.25λ, where λ is the imaging wavelength. However, the strong confinement of the evanescent near-field prevents these imaging devices from achieving further extension of the working distance. In addition to near-field imaging devices, a plethora of non-linear imaging devices also exist, which make use of non-linear optical phenomena, chemically labeled objects, and/or prior information about the object target to perform sub-diffraction imaging¹³,¹⁴,¹⁵,¹⁶,¹⁷. While these devices have important niche applications primarily in life sciences, their reliance on particular material systems or object properties preclude their widespread use as tools for general-purpose microscopy. Clearly a linear way to circumvent the diffraction limit at a working distance beyond the evanescent near-field of light will be of great benefit towards scientific research and instrumentation.

In related developments, the past century has also seen proposals of “slightly sub-diffraction” devices, which provide modest resolution improvements to the diffraction limit through trade-offs with parameters such as the side-lobe level or the power confinement ratio¹⁸,¹⁹,²⁰. Superoscillation-based imaging can be viewed as a significant advancement along this direction. Superoscillation is a phenomenon whereby over a finite interval, a waveform oscillates faster than its highest constituent frequency component. Hence a superoscillatory lightwave can, over a finite spatial duration, oscillate faster than its largest spatial frequency component, and thus holds promise for bringing sub-diffraction imaging capabilities into the far-field of an imaging system. The mathematical groundwork for superoscillatory waves was laid by Slepian et al.²¹, and later emphasized by Aharonov et al. and Berry²²,²³, citing its manifestation in quantum physical and optical systems. Sub-wavelength superoscillatory foci and vortices have been demonstrated by various groups²⁴,²⁵,²⁶; in particular an important recent work by Rogers et al.²⁷ illuminated a sub-wavelength superoscillatory spot upon an object, and scanned the spot in sub-wavelength steps to construct a super-resolution image. The operational principle of this so-called super-oscillatory lens is similar to that of the NSOM. However the probe-object proximity requirement is lifted since the sub-wavelength illumination is achieved using superoscillatory waves. While this represents important progress in sub-wavelength imaging at an extended working distance, we aim to show that superoscillatory waves can be further utilized in a significant way with our proposal and demonstration of the optical super-microscope (OSM) – a superoscillation-based imaging system which achieves linear, far-field, sub-diffraction imaging in a direct, single-capture mode. The operation of the OSM harnesses a new understanding of the phenomenon of superoscillations which directly links it to antenna superdirectivity in a subtle way (see Methods). The resulting OSM alleviates the needs for sample pre-treatment, non-linear and near-field interactions, sub-wavelength scanning and data post-processing, and hence can perform real-time general purpose imaging on a wide-variety of objects, including moving objects.

Results

Superoscillatory point spread function design

In departure from ref. 27, which illuminated a test object with a scanning superoscillatory lightwave, we aim to design a linear imaging system which has a superoscillatory point spread function (PSF). This way, when a pinhole is imaged through this system, the image becomes a superoscillatory waveform with a sub-diffraction spot size; by extension, when a more complicated object is imaged through this system, a high-resolution image forms. A superoscillatory PSF desirable for far-field sub-diffraction imaging would feature a 2-dimensional sub-diffraction peak, as well as a region of low illumination (hereafter termed “region of silence”) which spatially separates the peak from its superoscillatory sideband. Previous works²⁸,²⁹ have deemed such waveforms impractical, citing the unrealistic signal dynamic range required to faithfully generate the waveform along with its high intensity sidebands, which were thought to inevitably exist alongside the desired superoscillation. However, in our work we conclude to the contrary. While it has been proven²⁸, in conformity to the Shannon limit, that a tradeoff is unavoidable between the sharpness of the sub-diffraction peak and the percentage of waveform energy residing therein, we find that requirements on sideband intensity and signal dynamic range can be alleviated when one suitably controls the sidebands of the superoscillatory function. To obtain systematic control to both the superoscillatory region and the sidebands, we leveraged a recently-established relationship between superoscillation and superdirective antennas³⁰, and adapted a superoscillatory function design method from the field of antenna-array synthesis. Using this method, we designed a superoscillatory PSF with a sub-diffraction peak, an acceptable region of silence and sidebands which are controlled to a reasonable level. The PSF design process and key parameters of the final design can be found in the Methods section of this paper. As the PSF design algorithm resulted to a set of modulation coefficients in the spatial frequency domain (which are analogous to current excitations on an antenna array), we found it natural to implement the modulation as a spatial frequency filter at the Fourier plane of a folded 4F imaging system, as shown in Figure 1. Details on implementing this optical transfer function are included in the Methods section. The modulation represents the Fourier transform of the superoscillatory PSF, which when spatially mapped can be viewed as a class of super-resolving apertures. Super-resolving apertures were first proposed by Toraldo di Francia through inspiration drawn from superdirective antennas³¹, but later theoretical and numerical works³² have deemed them impractical for the same reasons which appeared to undermine the practicality of superoscillations. However, as explained above, we have bypassed this hurdle by careful considerations from the perspective of antenna array design.

Figure 1. A schematic of the optical super-microscope (OSM).

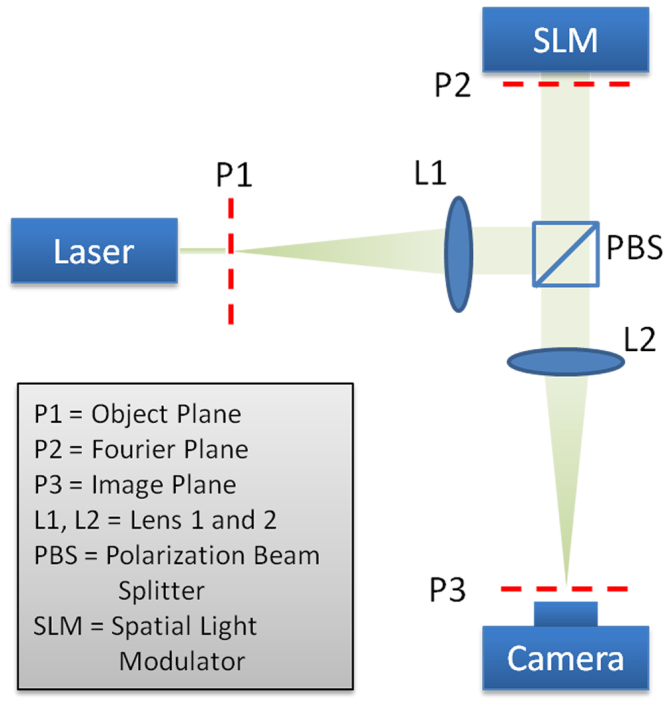
The distance between the five labeled planes: P1, L1, P2, L2 and P3 are 40 cm apiece.

Experimental apparatus

In our experiment as depicted in Figure 1, a HeNe laser of wavelength 632.8 nm illuminated the object. The first lens L1 transformed the light field at the object into its spectrum at the Fourier plane, where an SLM performed reflective filtering. The SLM used in our experiment featured a 1,024 × 768 pixel array and a pitch size of 9 μm. Thereafter, the second lens L2 performed an inverse Fourier transform, producing a final image in the spatial domain. Both lenses in our experiment had focal lengths of 40 cm (this also set the working and observation distances), while the width of the SLM was 7 mm. This translates into a system with a numerical aperture of NA = 0.00864, and a corresponding diffraction-limited spot width of

While obviously a high NA system would be desired for high-resolution imaging, we have chosen to work with a low NA system in our proof-of-principle experiment, so that sub-diffraction images can be well resolved by a CMOS camera placed at the image plane, 40 cm away from L2.

PSF comparison

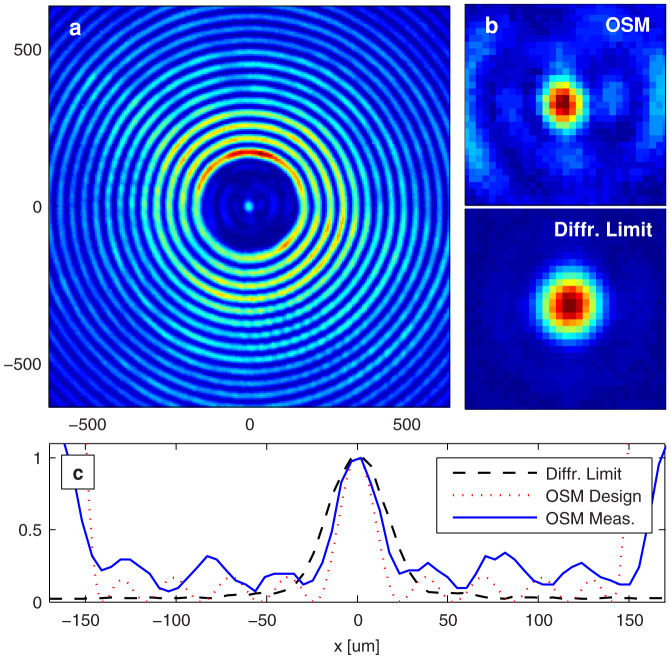
Figure 2a and Figure 2b compare the PSF of the OSM with a diffraction-limited imaging system of the same numerical aperture. The PSFs were obtained by imaging a small circular aperture 10 μm in diameter; the PSF of the diffraction-limited system was obtained by replacing the superoscillatory filter with a uniform reflection filter. We have shown that the 10 μm aperture was sufficiently small to have negligible effect on the PSF (see Supplementary Information). The PSF of the superoscillation imaging system contained a sub-diffraction spot size 28 μm in intensity FWHM. This was clearly reduced from the spot size of the diffraction-limited system, which was measured to be 39 μm, in agreement with equation (1) to within the camera pixel pitch of 5.3 μm. This superoscillatory sub-diffraction spot was 150 μm separated from the high-intensity sideband. The inner half of the region of silence formed the OSM's field of view: as long as the object's spatial extent fell within this field of view, a sub-diffraction image could be achieved without contamination from overlapping with high-intensity sidebands of the superoscillatory PSF. Figure 2c compares the horizontal cross-section of the intensity profile with theoretical calculation and shows a good agreement between the two. Slight deviations in focal width probably originated from the discrete and rectangular pixilation of the SLM which was used to implement the desired (circular) filter. Nonetheless, the measured focal width remained clearly narrower than the diffraction-limited peak. This improvement would translate into sub-diffraction imaging for more complicated objects.

Figure 2. A comparison of measured PSFs for the OSM and the diffraction-limited system.

(a) An image of a 10 μm hole obtained by the OSM, which approximates the system's PSF. (b) A close up of the focal point (top), which clearly shows a reduced size compared to the diffraction-limited focal point (bottom). (c) A horizontal cross-section plot of the detected intensity across the center of the superoscillatory image waveform, showing reasonable agreement with the theoretical PSF, and clear spot-size reduction from the diffraction-limited focus.

Two-point resolution comparison

Next we characterize the two-point resolution capability of the OSM. The inset of Figure 3 shows a diffraction-limited image obtained for two 15 μm circular apertures, separated 55 μm center-to-center. Clearly, at this separation the two apertures could not be resolved with a diffraction-limited imaging system, as predicted by the diffraction theory on coherent imaging (see Supplementary Information). However, Figure 3 shows that the same apertures were well resolved by the OSM and were well separated from the high-intensity sidebands. An interference pattern formed at the high-intensity sidebands and generated regions of constructive and destructive interference, which caused an angular modulation on the sideband intensity. Figure 4 compares the imaging capability of the OSM and the diffraction-limited system for two circular apertures separated by a varied set of distances. To improve clarity, we display a close-up of the waveforms, neglecting the high-intensity sideband. Corresponding figures for vertical and diagonal apertures are shown in Supplementary Figures S1 and S2. The comparisons in Figure 3 and Figure 4 demonstrate the OSM's ability to achieve far-field sub-diffraction imaging. It can resolve two apertures spaced 45 μm apart horizontally and vertically, and 42 μm apart diagonally. This is clearly improved from the diffraction-limited system, which has an experimental two-point resolution distance of 60 μm. Further resolution improvements can be obtained with filters with finer pixilation, which will faithfully implement PSF designs containing more degrees of freedom. The present work nonetheless successfully demonstrates the OSM's sub-diffraction imaging capability at the long working distance of 40 cm.

Figure 3. Comparison in resolving closely spaced apertures (I).

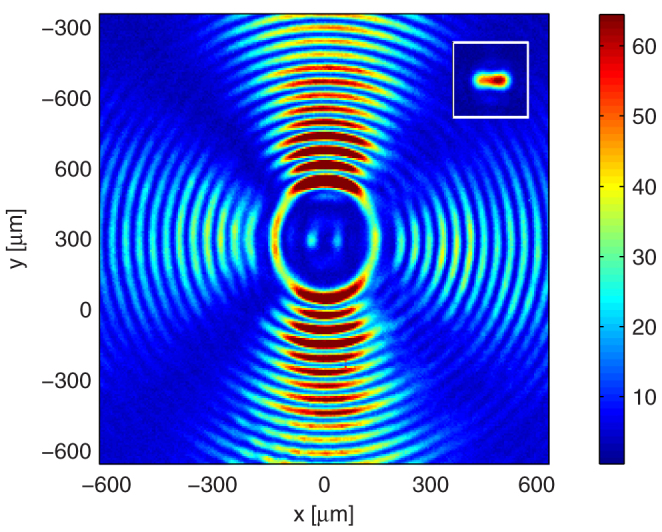
The main panel shows that the OSM resolves two 15 μm apertures, separated 55 μm center-to-center. The inset shows the corresponding (unresolved) image for the diffraction-limited system.

Figure 4. Comparison in resolving closely spaced apertures (II).

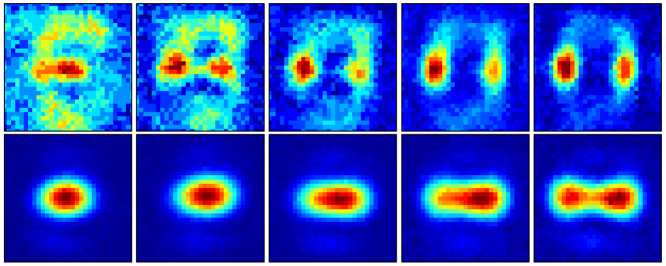
Close ups of 2-point resolution images, for two 15 μm apertures, separated by distances of 40 μm, 45 μm, 50 μm, 55 μm and 60 μm respectively, from left to right. The top row shows a close up of the superoscillatory image, while the bottom row shows the corresponding view with the diffraction-limited system.

Real-time imaging for moving objects

The OSM's ability to directly image an object without scanning brings attractive advantages and enables novel functionalities in comparison to scanned-imaging solutions to sub-diffraction imaging⁴,¹¹,²⁷. Firstly, we have dramatically simplified the imaging system by alleviating needs for sub-wavelength scanning stages and subsequent post-processing overhead. Furthermore, since an image can be formed in real-time, the system can be used to image time-varying objects. To demonstrate this, Supplementary Video S1 shows a real-time capture of our object as it laterally moved in the object plane. We emphasize that each frame in this video came directly from a camera capture. No data or image processing was performed. The ability to perform real-time imaging further distinguishes the OSM from previously-proposed superoscillation-based imaging systems²⁷,³³, and allows attractive potential applications such as in vivo sub-diffraction biomedical microscopy.

Discussion

Experimental results on PSF measurement and two-point resolution investigation have convincingly proven the viability of performing sub-diffraction imaging using the OSM. We have reduced our optical system's spot width to 72% of the diffraction limit, and improved its minimal resolvable distance to 75% of the equivalent Rayleigh criterion (see Supplementary Information) While this work has successfully provided a proof of principle for our proposed concept of optical super-microscopy, we envision that further improvements from the diffraction limit can be achieved with increasing degrees of freedom in the spectral domain. While we were limited from achieving higher degrees of freedom by the finite pixilation of our SLM (18 μm per superpixel), such limitations can be alleviated by using a custom fabricated mask as the superoscillation filter. Contemporary fabrication technologies can reliably produce masks with feature sizes on the order of 100 nm. Using masks with a feature size on this length scale will enable one to encode more degrees of freedom into the superoscillation filter, and thereby achieve further resolution improvement with the OSM.

While the field of view of the OSM can be restrictive in certain cases, to image a large object, an illumination beam occupying the OSM's field of view (which for our case is a circular area with a diameter of approximately 2λ/NA) can be scanned across the object, and the image of adjacent fields of view can be stitched together, much like stitching together views from a conventional microscope. We emphasize that this large-step scanning procedure differs fundamentally from a sub-wavelength scanning procedure in near-field probes, spatially shifted-beam based imaging or the super-oscillation lens⁴,¹¹,²⁷, in that the step size is on the order of the field of view, which for our case is more than six times the resolution limit of the system. Thus this scan modality does not contribute to resolution enhancement; it only increases the overall field of view of the system. Further, with a large-step scan, a sub-diffraction image of a large object can be obtained in lesser time, avoiding mechanical drifts and other slow time artifacts such as those observed in ref. 27.

Besides large object imaging, we also discuss the potential for the OSM to perform sub-wavelength imaging. We have chosen a low NA in this work to enable the measurement of sub-diffraction features with a CMOS camera. By increasing the numerical aperture to close to, or beyond unity, the OSM can easily be adapted to perform far-field imaging at sub-wavelength resolution. Further, the sub-wavelength image can be observed in real-time through conventional microscopy, with no loss of resolution. In such case, one will need to replace the SLM with a custom-fabricated transmission and/or reflection filter, which contains finer feature sizes than the 9 μm pitch resolution for the SLM used in this work. As explained above, a spatial amplitude and phase filter with much reduced feature sizes can be reliably produced with present custom fabrication methods. Further, with the combined amplitude and phase modulation capability of a custom-fabricated mask, one might be able to do away with Fourier transformation lenses, and arrive at a single-element super-resolution imaging device. Such enhanced simplicity can lead to widespread applicability.

We have presented an OSM capable of linear, far-field imaging beyond the diffraction limit. Adapting methods of antenna array design, we mitigated impractical sensitivity requirements that were thought to inevitably accompany superoscillations, and constructed a superoscillatory function suitable for sub-diffraction imaging. Through implementing this superoscillatory function as the PSF of a 4F imaging system, we have demonstrated clear resolution improvements over a diffraction-limited system with the same NA. The usage of superoscillations removes the reliance on evanescent waves or non-linear effects, and thus enables the OSM to perform imaging without the presence of near-field scatterers or other device components, and without the need for florescent labels or material-based restrictions. Furthermore, the OSM's single-capture operation allows it to form real-time images of moving objects. All these benefits are available at very long working distances (40 cm in this experiment) which, in addition to microscopy, makes the OSM very desirable for super-resolution standoff imaging (e.g. in a "super-camera" mode), imaging objects embedded in transparent dielectrics or objects having a rough surface. These properties should make the OSM an attractive tool for general purpose imaging beyond the diffraction limit.

Methods

1D superoscillatory function design

We designed the 2D superoscillatory filter used in this work through an extension from a corresponding 1D filter, which was designed with a substantial adaptation from established methods in the field of antenna design. This design method represented a slight extension from our previous work³⁰. We considered a periodic function F(x) with Bloch period Λ, which was composed of N complex exponentials.

Here k_x0 and 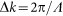respectively represent the component with the lowest (most negative) spatial frequency, and the spacing between adjacent spatial frequency components. The factorization of the polynomial F(z) allowed us to visually represent it as a function with N-1 zeros in the complex z-plane. On this z-plane, F(x) traced a path along the unit circle, with every Bloch period Λ representing one traverse along the unit circle. Thus choosing the zeros of the complex function F(z) represented an intuitive way to design the function F(x).

One simple design for a fast varying F(x) would be to evenly distribute all N-1 zeros on the unit circle. In this case, evaluating equation (2) would yield a sinusoid of the highest frequency:

Where A₀ and φ₀ signified arbitrary amplitude and phase constants. To construct a function with more rapid oscillations (i.e. superoscillations), we borrowed an idea from antenna superdirectivity: we close-packed a portion of the available zeros along a section of the unit circle, and hence constructed a waveform F(x) which super-oscillated along that interval. While the energy content of F(x) outside the superoscillatory region inevitably increased, we controlled the amplitude in this non-superoscillatory region by an appropriate (albeit sparser) placement of zeros.

In our design we used N = 63 complex exponentials, evenly spaced between ±2πNA/λ, where λ = 632.8 nm and NA = 0.00864 were the illumination wavelength and numerical aperture of our experimental system. We specified a superoscillatory design region of 4λ/NA, in which 10 zeros were placed through a Tschebyscheff expansion to form the narrowest possible peak, and equi-ripple sidelobes with intensity of 21% that of the peak. After this initial placement of zeros, the remaining zeros were placed to minimize the sideband amplitude, and all zero locations were slightly modified to optimize the equi-ripple performance. Figure S3 shows the final location of zeros.

2D radially symmetric superoscillatory function design

For constructing 2D superoscillatory functions with radial symmetry, we used as our basis a set of Bessel functions within the same transverse spatial frequency range as the complex exponentials in equation (3):

Due to the similarity between Bessel functions and sinusoids (which were used to construct the 1D superoscillatory function), we determined the weights 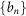for a function G(r) which would produce the same nulls in r as F(x) would in x:

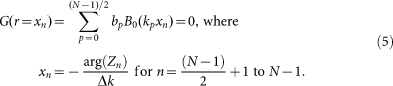Here we assumed that the zeros are listed in ascending phase, from -π to π, and only involved zeros on the positive x-axis, as they directly corresponded to the radial co-ordinate r. Choosing b₀ as a normalization constant, we arrived at

After solving equation (6), we arrived at a 2D superoscillatory function G(r) whose radial cross-section was very much similar to its 1D counterpart. Figure S4 shows a comparison of both the 1D and 2D superoscillatory functions. In experimental implementations, we implemented the Bessel functions on the SLM as rings of width Δk. An image of this optical transfer function is shown in Figure S5. We found that this increased the power throughput while contributing negligible affects to salient features of the superoscillatory PSF.

Using an SLM as a real-valued transmission filter

We worked with the SDE1024 SLM kit from Cambridge Correlators – a reflective SLM with a 1028 × 724 pixel array, of pitch size 9 μm. Following a calibration procedure described in ref. 34, we found the SLM's complex reflection coefficient 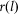, where was the input signal level ranging from 25 to 255.

While 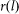was in general complex, we operated the SLM in a superpixel mode to effectively form a real-valued reflection filter t_RE(x,y), where (x,y) were the lateral directions. Figure S6 shows a normalized plot of 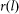for our SLM. The considered superpixel consisted of an SLM pixel and its immediate neighbor in the x-direction. We rotated the SLM along the y-axis such that the first diffraction order undergoes retro-reflection. At this angle, the rotation incurred an extra path length of π between adjacent SLM pixels (in the x-direction). Hence, when we excited the superpixel with signal levels 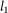and 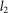the total complex reflection coefficient became

Where the subtraction came from the π-phase shift. It is now trivial to observe that

We charted large set of values for 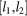for which the corresponding values for 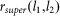were real. Working with this set of signal levels, we were able to synthesize a real reflection-filter with near-continuous refelection coefficients, albeit at the cost of reduced pixel resolution. We have adapted this method from ref. 35, where 4 × 1 superpixels were used to achieve a full complex reflection filter with an SLM.

Author Contributions

The authors jointly conceived the main ideas in this work and developed the theory. A.M.H.W. designed and performed the experiment, and performed related calculations. G.V.E. provided overall guidance to the project. Both authors discussed the results and contributed to the manuscript.

Supplementary Material

Supplementary Information

Supplemental Information

Supplementary Information

Sub-diffraction Imaging for Moving Objects