Parametric Bayesian priors and better choice of negative examples improve protein function prediction

Abstract

Motivation: Computational biologists have demonstrated the utility of using machine learning methods to predict protein function from an integration of multiple genome-wide data types. Yet, even the best performing function prediction algorithms rely on heuristics for important components of the algorithm, such as choosing negative examples (proteins without a given function) or determining key parameters. The improper choice of negative examples, in particular, can hamper the accuracy of protein function prediction.

Results: We present a novel approach for choosing negative examples, using a parameterizable Bayesian prior computed from all observed annotation data, which also generates priors used during function prediction. We incorporate this new method into the GeneMANIA function prediction algorithm and demonstrate improved accuracy of our algorithm over current top-performing function prediction methods on the yeast and mouse proteomes across all metrics tested.

Availability: Code and Data are available at: http://bonneaulab.bio.nyu.edu/funcprop.html

Contact: shasha@courant.nyu.edu or bonneau@cs.nyu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The rate of new protein discovery has, in recent years, outpaced our ability to annotate and characterize new proteins and proteomes. To combat this functional annotation deficit, many groups have successfully turned to computational techniques, attempting to predict the function of proteins to guide experimental verification. Specifically, there has been a surge of interest in applying machine learning methods to the problem of protein function prediction (FP), to take advantage of the wealth of biological data available for each protein beyond its sequence, such as computationally predicted tertiary structure, which has already been shown to aid FP (Drew et al., 2011). While traditional approaches to FP mainly involved either homology (with limitations of accuracy) or manual curation (dependent on rare expertise), these new methods present new evaluation and comparative challenges. The MouseFunc competition (Peña-Castillo et al., 2008) was organized to test the ability of machine learning methods to take advantage of large integrated datasets and provide useful predictions of gene function.

The validity of integrative approaches to FP was first demonstrated by the works of Marcotte et al. (1999) and Troyanskaya et al. (2003), which respectively used linkage graphs and a Bayesian network to predict function. By the time of the MouseFunc competition, FP methods had become diverse, including Support Vector Machines, Random Forests, Decision Trees and several composite methods (Guan et al., 2008; Lee et al., 2006; Obozinski et al., 2008; Tasan et al., 2008), but a recurring theme was to use protein–protein networks of various types to determine function based on guilt by association (Kim et al., 2008; Leone et al., 2005; Qi et al., 2008; Zhang et al., 2008). In such a method, genes are represented by nodes in a network, with weighted edges defined by a similarity metric obtained from raw data (often the Pearson correlation coefficient of feature vectors). Predictions are then formed by propagating information from genes known to have a function, through the network to unlabeled genes.

While providing unprecedented accuracy, the methods of the MouseFunc competition exposed several general challenges still remaining for the FP problem: (i) choosing a set of high-confidence negative examples, (ii) using available data to form prior beliefs about the biological functions of a gene and (iii) effectively combining disparate data sources. As no comprehensive database of functional negative examples currently exists, and nearly all major machine learning methods require a negative class for the training of a classifier, the selection of high-confidence negative examples is especially important for the FP problem.

In this work, we begin to address these challenges by presenting a parameterizable Bayesian technique for computing prior functional biases for each gene, and a novel method for selecting negative examples using these biases. To apply our method, we use the framework of the GeneMANIA algorithm (Mostafavi et al., 2008), one of the highest-performing competitors in MouseFunc. In addition to our new priors and negative examples, we present a framework for tuning our Bayesian parameters and other parameters in the original GeneMANIA algorithm. To facilitate this parameter tuning, we incorporate new optimization techniques that take advantage of the structure of the optimization problem. We also integrate our novel negative examples into the GeneMANIA network combination algorithm that synthesizes heterogeneous data into one affinity network.

While well-established procedures exist for the comparison of machine learning methods, recent work (Greene and Troyanskaya, 2012; Pavlidis and Gillis, 2012) has exposed and discussed problems that can be introduced into these comparisons by the nature of biological data. To mitigate these biases, we heed the suggestions of Greene and Troyanskaya (2012), and focus on evaluation with a temporal holdout (an evaluation set of annotations obtained later in time than the training data, referred to in this article and in the MouseFunc competition as the ‘novel evaluation setting’). We also include one of the few available gold standard evaluation sets (an exhaustive experimental evaluation of the presence of a particular protein function across an entire genome), obtained from Huttenhower et al. (2009). Our goal is to demonstrate the performance improvements of our new algorithm over the existing state of the art in a fair (apples-to-apples) comparison across several datasets. We expect that these comparative results will generalize to other datasets as they become available.

2 PREVIOUS WORK

We present our novel methods using the framework of the GeneMANIA FP algorithm of Mostafavi et al. (2008), which incorporates prior beliefs and an intelligent network combination algorithm into its guilt-by-association framework. GeneMANIA is a form of Gaussian Random Field (GRF) label propagation, a semi-supervised technique pioneered by Zhou et al. (2004) and Zhu et al. (2003), and provides predictions for genes one function at a time. Given a set of nodes (genes) in a network the edges of which define pairwise similarity, and a vector 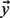of prior label biases for the nodes, given the current function being examined, the GRF algorithm assigns a discriminant value 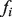to each node, which can be ranked to produce predictions. The label biases 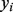take values in (−1,1), with −1 representing known negative labels, 1 representing known positive labels and values in between reflecting prior belief about the likelihood of a gene having the function in question. The final discriminant vector 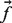is obtained by solving the optimization problem:

(1)

This equation has an analytical solution in the form of a linear system: 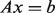(see Supplementary Material for details), and also guarantees that the discriminant values 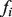will lie in the range (−1,1), with larger values indicating greater likelihood of an unlabeled node being a positive example of the function in question.

Intuitively, this algorithm allows prior information to flow through the network until equilibrium is reached. The objective function propagates known labels through the similarity network via the second ‘smoothness’ term in Equation (1), weighted by the strength of similarity between nodes as specified by the network, and also enforces adherence to the prior bias through the first ‘consistency’ term in Equation (1). Thus, the label biases, both the positive and negative examples as well as biases used for unlabeled nodes, play an important role in the algorithm. Mostafavi and Morris (2009) explore variations on techniques to choose the label bias vector, but we expand on this work to improve accuracy in our algorithm by using more of the information contained in current functional annotations to determine functional biases and negative examples (see Section 3.1).

The other key component of the GRF algorithm is the composite network defining similarity between all pairs of genes. Mostafavi et al. (2008) proposed a method to combine disparate data sources, each represented as an affinity matrix, into one composite matrix, based on the work of Tsuda et al. (2005). This algorithm, for each Gene Ontology (GO) category of interest, maximizes the similarity between pairs of positively labeled genes and minimizes the similarity between genes of opposite labels (see Supplementary Material for details).

This network combination algorithm is prone to overfitting in cases with few positive examples. The original GeneMANIA algorithm addressed this problem by introducing a regularization term, but later work (Mostafavi and Morris, 2010) instead attempts to fit the composite data network for multiple GO categories simultaneously. Our algorithm expands on this second approach by directly incorporating our negative examples (see Section 3.3).

3 ALGORITHM

We propose novel techniques focusing on several key aspects of protein FP: choosing negative examples, forming label biases for unlabeled genes with some known annotations and an issue specific to GRF-based methods, namely, combining heterogeneous data types into one affinity network. In addition, we suggest a new optimization algorithm tailored to our techniques, and provide a framework for tuning parameters using the training data.

3.1 Label biases

Mostafavi and Morris (2009) showed that significant performance gain could be achieved by allowing existing GO annotations to inform the priors applied to genes in GRF FP, using a technique called Hierarchical Label Bias (HLBias). This idea is supported by the work of King et al. (2003), which showed that patterns of GO annotations alone provided enough signal to predict future annotations. HLBias specified that genes which possessed annotations for functions ancestral to the function of interest received a prior bias equal to the proportion of genes with the ancestral function that also are known to have the function in question.

However, owing to the difficulty of defining a functional hierarchy, the structure of the GO tree is often altered by its curators, with terms being moved to different parents, virtually guaranteeing that there exist functional relationships that are non-ancestral. When considering the complexity of functional interactions, it would seem likely that the presence of some functions might influence the likelihood of a gene possessing other functions, regardless of whether the relationship between the two is ancestral. This is especially true when considering annotations in all three branches of the GO hierarchy simultaneously. Accordingly, we extend HLBias to include the likelihood of a given function co-occurring with all other existing annotations [across all three branches of the GO tree: Biological Process (BP), Molecular Function (MF) and Cellular Component (CC)], in the following manner:

Let 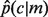denote the empirical conditional probability of seeing annotation c, given the presence of annotation m, then 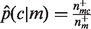, where 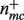is the number of gene products where both m and c appear, and 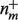is the number of gene products that have annotation m. For a protein i, let 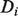be the set of all GO terms annotated to i. For a given function c, we approximate the conditional prior probability of gene i having function c by the following score:

(2)

The label biases are then scaled to the range .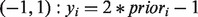

Owing to the hierarchical nature of GO categories, some of the conditional probabilities in this calculation will contain redundant information, and so when considering a protein with annotations 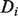, we remove from 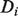all GO terms that have a child in 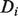, leaving a set of only the most specific annotations of protein i to use in calculating the bias.

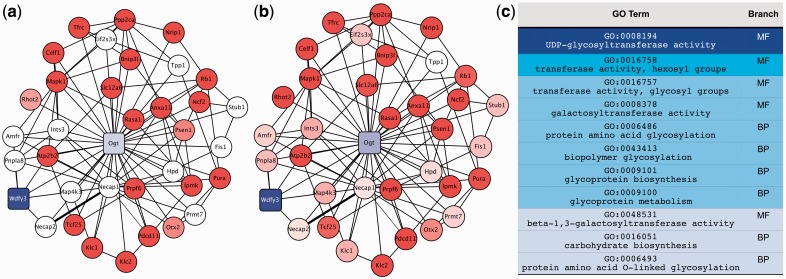
Figure 1c provides an example of the most predictive GO terms for the GO function UDP-glycotransferase activity (UDPGA), which include many terms that have no ancestral relationship to UDPGA. Examining a specific prediction example, we find that the annotations informing the prior bias for gene Ogt (pictured in Fig. 1a), are all non-ancestral terms, and contribute to the algorithm making a correct positive prediction (Fig. 1b).

Fig. 1.

(a) A subsection of the association network before the algorithm is run, showing prior beliefs for genes for the function: GO:0008194, UDP-glycotransferase activity, focusing on gene Ogt. The shading of the nodes represents the degree of positivity compared with the mean of all prior biases, with blue indicating greater likelihood of possessing the function in question, red representing lesser likelihood and white representing genes that had no GO annotations to use for a prior. Square nodes represent validated true positives (including the training positive example Wdfy3). (b) The same subsection of the association network as (a), but after label propagation, showing the final discriminant values of the genes. (c) The GO categories that are most predictive of the function GO:0008194, with darker shades of blue representing stronger predictors. Network visualized with Cytoscape (Smoot et al., 2011)

Lastly, we observe a large bias introduced by categories with small sample size, where one category appears to be a perfect predictor of another. To reduce the potential for overfitting stemming from this phenomenon, we introduce a weighted pseudocount into the calculation of the empirical conditional probability, whereby 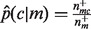is replaced by the following:

(3)

This idea is motivated by the hypotheses that no two GO categories ‘c1’ and ‘c2’ should both appear in every protein where one appears, unless ‘c1’ and ‘c2’ have an ancestral relationship, and also that the number of undiscovered occurrences of a function is related to the number of currently known occurrences. This equation (via the two parameters 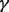and 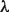) allows us to smoothly transition between two extreme assumptions about how missing and currently known annotations are distributed: (i) the number of observations in the data is a proxy for how well a function has been studied, and so the number of missing counts in the data should be inversely proportional to the number already seen, and (ii) the number of currently known occurrences is a better representation of the specificity of a function, and so the undiscovered occurrences should be directly proportional to the number already seen.

To allow the data itself to choose one of these hypotheses, we sample from a range of combinations of parameters, including the potential for no pseudocounting (see Supplementary Material). The final value of the parameters is chosen by tuning with cross-validation over the training set, as described in Section 3.5.

For genes with no previous annotations in GO, we follow Mostafavi et al. (2008) and set the label bias to the mean of all the label biases calculated for genes with GO annotations, including the positive and negative example genes with values of 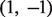respectively. We refer to our label bias algorithm hereafter as ALBias.

3.2 Negative examples

The choice of negative training examples for use in supervised machine learning algorithms is a recurring problem for FP methods. While the GO database does include negative annotations, the number of such annotations is currently small. Thus, it is necessary to infer negative examples for each function (typically using a heuristic). Past heuristics include (i) designating all genes that do not have a particular label as being negative for that label (Guan et al., 2008), (ii) randomly sampling genes and assuming the probability of getting a false negative is low (often done when predicting protein–protein interactions, as in Gomez et al., 2003) and (iii) using genes with annotations in sibling categories of the category of interest as negative examples (Mostafavi and Morris, 2009). Mostafavi and Morris (2009) note in discussion that this last technique may often break down, as some genes are annotated to more than one sibling category, and many genes have few siblings to use.

We present a new technique for choosing negative examples based on the label biases calculated for each function. Namely, all genes with an annotation in the same branch of GO as the term being predicted, and which have a 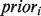score of 0 for the function in question (with the prior score computed across all three branches of GO), are treated as negative examples for that function. Intuitively, this amounts to treating a gene ‘g’ as a negative for annotation ‘c’ if no annotation ‘s’ among the most specific annotations of ‘g’ ever appeared alongside annotation ‘c’ in any other gene (note that the choice of pseudocounting parameters does not impact the negative examples, as only the magnitude of the label bias will be affected and not whether a bias is non-zero).

Restricting the negative examples to having an annotation in the same branch as the GO term being predicted, rather than simply having an annotation in any branch, decreases the number of negative examples, and also more significantly decreases the number of validated true positives that were misclassified as negatives. The number of negatives in mouse decreased by 14.9% owing to this restriction, while the number of verifiable misclassified negatives dropped by 22.5%; in yeast, the number of negative examples decreased by 23.2%, while the verifiable misclassified negatives dropped by 91.5%.

3.3 Network weighting

As mentioned in our description of previous work, one essential component of the GRF algorithm is synthesizing heterogeneous data sources into one pairwise affinity matrix. Mostafavi and Morris (2010) found that fitting this matrix for multiple GO functions simultaneously significantly decreased overfitting, especially in low-annotation categories. The authors simplified the calculation of this simultaneous fit by considering negative–negative pairs of labels as well as the positive–positive and positive–negative pairs used by the original network-weighting algorithm of Mostafavi et al. (2008). This simplification also requires the treatment of all non-positive genes as negative genes for each GO category (see Supplementary Material).

Mostafavi and Morris (2010) showed that these simplifications do not hamper performance, and also found that fitting the combined network to all GO categories in a particular branch (GO-BP, GO-CC or GO-MF) worked better than any other subset or grouping of functions. We concur that fitting to all categories performs better than any of the subsets we attempted, but propose that the apparent indifference of this algorithm to the assumption that all non-positive nodes are negative was most likely due to a lack of any satisfactory alternative for choosing negative examples.

We return to the unsimplified version of the simultaneous fit proposed by Mostafavi and Morris (2010), and use our more specific negative examples that are unique to each GO category (see Supplementary Material for details of the calculation). We refer to our modified network combination algorithm as Simultaneous Weights with Specific Negatives (SWSN).

3.4 Successive block conjugate gradient optimization

The network-weighting scheme defined above creates a single combined matrix W for all functional categories within the same GO branch. Thus, the coefficient matrix is identical for the optimization problem that is solved for each function, and so we are faced only with the issue of a different right-hand side (RHS) per function. In such cases, computational costs can be decreased by methods that solve all of the problems simultaneously, rather than iteratively solving each problem without using any of the information obtained by other solutions. We propose a modified version of the Successive Block Conjugate Gradient algorithm (SBCG) proposed by Suarjana and Law (1994).

In this algorithm, the search direction is obtained simultaneously for all of the distinct RHS vectors in the problem. If at any point, the search direction matrix becomes rank deficient, dependent RHS vectors are moved to a secondary system, but are still updated with steps obtained from the search direction in the primary system, and so still proceed toward convergence. The speed of this secondary convergence is dependent on the angle between the vectors in the primary system and secondary system.

Our algorithm differs from the original one proposed by Suarjana and Law (1994) in several ways. Firstly, not all solutions converge to the desired tolerance in the same number of iterations, and so we save computation by removing already-converged RHS vectors from the block calculation rather than updating the entire system until all RHS vectors converge. Secondly, when the RHS vectors in the secondary system are nearly orthogonal to those in the primary system, waiting for secondary convergence can require a large number of iterations. Instead, once all primary system RHS vectors are converged, we restart the algorithm in a second phase, with the secondary system as the primary system, but using the latest residuals as our starting point. Lastly, empirical observation has shown some low condition numbers can occur in the secondary phase when the number of dependent RHS vectors is large. We find that splitting up the total number of RHS vectors into a few smaller blocks alleviates this problem without significantly increasing computational cost. For the problem at hand, we chose to divide the FP problems into subproblems with a maximum of 500 RHS vectors. Pseudocode for our algorithm is presented in the Supplementary Material.

3.5 Parameter tuning

The multiple RHS framework described in Section 3.4 lends itself well to parameter tuning, as the different combinations of the parameters 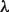and 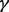described in Section 3.1 simply yield more RHS label bias vectors to solve for with the same coefficient matrix.

The original formulation of the GRF objective function in Zhou et al. (2004) included the parameter 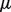, which describes the relative weight to be placed on each component of the objective function, which we formulate as follows:

(4)

This parameter was ignored by the GeneMANIA algorithm, but we reintroduce it here, and test its impact on FP by adding it to our tuning methodology.

To choose performance-maximizing parameters, we create a synthetic learning problem from the training data, which is characteristically similar to the original learning problem, and choose parameters that yield the best performance on this subproblem. Details are presented in the Supplementary Details.

4 METHODS

4.1 Evaluation datasets

We evaluate our algorithm on three datasets: the MouseFunc benchmark, yeast data and a gold standard dataset of yeast genes. With regard to MouseFunc data, we focus on the Molecular Function branch of the GO hierarchy. For fair comparison with prior work, we use only data available to participants at the time of the MouseFunc exercise: these data include 10 networks (Interpro data, PFAM data, three Gene Expression networks, Protein–Protein Interaction data, Phenotype, two Conservation Profile networks, Disease Association data), 1874 molecular function categories, and 21 603 mouse genes, with all data gathered in 2006 (see Peña-Castillo et al., 2008). Predictions are made, as in MouseFunc, only for functional categories with between 3 and 300 annotations in the genome, but all functional categories are used in the bias calculation and negative example choice described in Sections 3.1 and 3.2.

For our performance evaluation in yeast, we focus on the Biological Process branch of the GO tree, using data obtained from Mostafavi and Morris (2010), which includes 44 networks of data obtained from BIOGRID (Stark et al., 2006), covering 3904 genes with 1188 biological process categories (categories with between 3 and 300 annotations). We augment this yeast data with experimentally confirmed gold standard annotations in the BP category of GO:0007005, mitochondrion organization and biogenesis (MOB), obtained from Huttenhower et al. (2009; see Section 4.3).

4.2 Functional association data

Association networks are created from feature-based data types using the Pearson correlation coefficient, after a frequency transform as described in Mostafavi et al. (2008). Only the top 100 interactions are used for each gene in the training set to keep the networks sparse, and a normalization scheme of 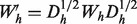is applied to each network and to the final combined network, where 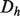is again the diagonal matrix containing the row sums of .

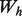4.3 Evaluation frameworks

We categorize protein function through GO ontology annotations, observing the common convention of excluding annotations denoted as 'Inferred Electronic Annotations' (IEA).

As in the MouseFunc competition, performance is evaluated in two different scenarios: (i) a test set where all GO annotations are removed from a subset of data (1718 genes in mouse) and then predictions are made from the remaining training data, and (ii) a novel set where predictions are made for proteins that have received new annotations at a later date. The member genes of this second set consist of the intersection of all proteins that have received at least one new annotation in any of the GO categories for which we are attempting predictions (1954 genes in mouse, 362 genes in yeast), and so include many proteins that already had some annotations in the training set, as well as proteins with no annotations in the training set.

We treat the novel scenario as the more important evaluation scheme for this work, as we believe it better reflects the true task facing computational biologists, and is less prone to evaluation biases (Greene and Troyanskaya, 2012). The test set approach suffers from biases stemming from the underlying use of sequence-similarity methods in both input data and GO labeling (discussed in greater detail in the Supplementary Material), which likely explains the better performance of all algorithms in the test scenario versus the novel scenario. Error results are presented for the test scenario as well, to facilitate comparison with MouseFunc algorithms. For both the novel and test MouseFunc evaluations, predictions are made for the same set of GO Molecular Function categories as the original competition: 488 and 442 categories, respectively. For yeast, we show results only in the novel scenario, with data from June 2007, 1 year after the training data, which includes 511 GO BP categories with at least one new annotation.

Any comparison of computational methods using GO annotations as the ground truth suffers from the lack of delineation between negative and absent annotation. This drawback is discussed at length in Huttenhower et al. (2009), and can create significant difficulty in evaluating computational prediction methods, as observed false-positive predictions may simply be a function of a lack of study rather than incorrect prediction. It is for this reason that performance evaluation in the novel scenario ignores any false positives for genes outside the novel set, as it is likely that these genes were not studied at all in the time interval between the annotation date for training and for testing. To further alleviate some of the uncertainty caused by incomplete annotation, we present performance evaluation metrics on a ‘gold standard’ benchmark of yeast genes experimentally verified by Huttenhower et al. (2009) for GO:0007005 MOB. These gold standard annotations include 148 additional positive annotations that match genes in our yeast gene set, and are also added to the novel set used for the general yeast benchmark. Lastly, when calculating performance statistics on the MOB gold standard, we add an additional 2473 genes to the 342 comprising the yeast novel set. These additional genes are the negative examples from Huttenhower et al. (2009) that are present in our gene set.

4.4 Evalutation metrics: precision-recall versus receiver-operator characteristic curve, TopScore

The performance of discriminant-based classification algorithms is most often represented by two plots: The receiver-operator characteristic (ROC) curve, and the precision-recall (PR) curve, each of which can be summarized by their AUC, the area that the curve encompasses. While both performance measures attempt to describe how well the ordering of discriminant values captures the true-positive and -negative labels, each has different strengths and weaknesses. Precision tends to be more easily interpretable for an experimentalist, but averaging 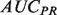numbers over many classifiers can be misleading owing to the non-linear nature of precision scores (see Supplementary Fig. S1). Conversely 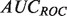provides a better global view of the rankings, but lacks a meaningful interpretation for experimentalists, and its magnitude depends on the skew of the dataset. See the Supplementary Material for a more detailed description of the pitfalls of each metric.

When presented with computational predictions, experimentalists must determine the number of predictions to assay, as well as which functions to focus on … a task made more difficult by complicated performance metrics. To create a metric more robust to averaging than PR, but which still enjoys easy interpretability for experimentalists, we propose 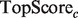, defined as 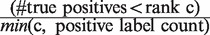. This score represents the fraction of a fixed number of experiments expected to yield a positive result, normalized by the maximum number of positive results possible. In this article, we present results for 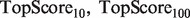and 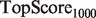for mouse, an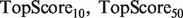d and 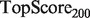for yeast, providing insight into the usefulness of computational predictions at three different scales of experimental testing (see Supplementary Material for more details on TopScore).

4.5 Algorithm component exploration

Uncovering which component of our algorithm is responsible for what performance changes is a challenging undertaking, as many of our algorithmic changes are interlinked. For example, our choice of negative examples affects both the bias value of selected genes and the network combination algorithm. Additionally, our bias calculation can also produce genes with a prior of −1, but which were not chosen as negative examples for the purposes of network combination (owing to our restriction that a gene must have annotations in the branch of interest to be declared an official negative). We have performed additional experiments to isolate the performance contributions of each of our algorithm subcomponents, presented in Sections 5.1, 5.2 and 5.3.

5 RESULTS AND DISCUSSION

We present results for our proposed techniques based on the evaluation metrics and datasets described in Section 4, along with analysis of the different components of our algorithm: negative example choice, network combination and parameter tuning.

Our tuned ALBias algorithm shows clear advantages over the current GeneMANIA methods in the majority of evaluations, with these differences being especially striking in the novel evaluation scenarios, where prior biases play a more important role in the algorithm than in the test scenario. In the yeast proteome, our algorithm achieved a performance increase of 11–26% points in every metric in the novel scenario, whereas in the mouse proteome, we improved all evaluation scores by 2–6% points in the novel scenario.

5.1 Negative example choice

To investigate the impact of our novel negative example choice, we evaluate the SW network combination algorithm with no label bias method, using three different negative example methods: the sibling negative examples, setting all non-positive genes with GO annotations to negative examples and our new negative example approach. As shown in Table 1, our negative example choice outperforms previous choices in all three full-organism evaluations, sometimes even approaching the performance of our full SWSN with ALBias and tuned parameters algorithm, indicating that our choice of negative examples is responsible for a significant part of our algorithm’s final performance.

Table 1.

Performance metrics for different negative example choices: sibling negatives (SibNeg) as in Mostafavi et al. (2008), using all non-positive genes with GO annotations as negative (AllNeg), and negative examples based on our ALBias method (ALBNeg)

Algorithm		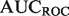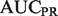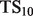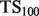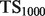		a	a
Mouse novel
SibNeg	0.7347	0.3236	0.4103	0.5342	0.7411
AllNeg	0.8155	0.3420	0.4318	0.5783	0.8354
ALBNeg	0.8366	0.3447	0.4314	0.5793	0.8705
Mouse test
SibNeg	0.8573	0.5019	0.6136	0.7622	0.8725
AllNeg	0.9232	0.5168	0.6207	0.7994	0.9530
ALBNeg	0.9330	0.5171	0.6160	0.8014	0.9745
Yeast novel
SibNeg	0.7566	0.3090	0.3674	0.6014	0.8094
AllNeg	0.7563	0.2865	0.3299	0.5284	0.8405
ALBNeg	0.8711	0.3387	0.4133	0.7127	0.9633
Yeast gold standard
SibNeg	0.7936	0.3729	0.8	0.54	0.5068
AllNeg	0.8679	0.4685	1	0.74	0.4932
ALBNeg	0.8413	0.3896	0.7	0.6	0.4865

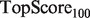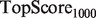Note: All algorithms were run using the SW network combination method, and the GRF label propagation algorithm of Mostafavi et al. (2008). ^aFor the yeast scenarios, and are replaced by 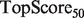and .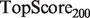

On the yeast gold standard, even though our algorithm decreases the number of validated true positives that are misclassified as negatives from 110 to 6, our negative example choice results in lower evaluation metrics than the AllNeg selection. We attribute the counterintuitive decrease in predictive performance when using ALBNeg in this setting, to the fact that the particular category MOB is specific enough to have small prevalence in the genome (only 5.3% of yeast genes possess this function), yet it is common enough that many genes have shared an annotation with it, resulting in our algorithm only selecting 691 negative examples. Thus, AllNeg yields high precision by virtue of having so many more negative examples, whereby it avoids false positives, while the rarity of the category means that there are not many true positives, and thus the mislabeling of true positives is outweighed by the decrease in predicted false positives.

Despite the success of our method in increasing performance in most evaluations, and reducing the instances of mislabeling validated true positives as negatives, in some GO categories, this mislabeling still occurs. Accordingly, we believe there is more potential for refined methods that correctly define high-confidence negative examples, and that these methods will have significant impact in the performance of machine learning algorithms. Indeed, we hypothesize that part of the performance gain demonstrated by the earlier HLBias algorithm was because the authors adjusted the labels for all non-positive genes, effectively turning any gene without a label in an ancestral category of the function in question into a negative example.

5.2 Network combination algorithm SWSN

To examine the effect of our network combination algorithm, SWSN, we performed a comparison with the SW network weight algorithm, using no label biases and our negative examples, yielding mixed results across evaluation scenarios and metrics. SWSN slightly outperforms SW on the mouse novel set; the two algorithms are virtually tied on the mouse test set; and SW outperforms SWSN on the yeast novel and gold standard evaluations. Yet, we believe that further refinement of negative example choice will show SWSN to be a more successful method. To demonstrate this, we add to the comparison of the two algorithms in Table 2 a third algorithm (SWSNOracle) in which our negative examples are granted access to a negative oracle, namely, the validation annotations, to ensure we do not select any negative examples that are demonstrated positives (there are almost certainly others among our negative examples that are true positives, but not yet studied at the time of the collection of validation data). This results in stronger performance on the mouse novel set and yeast gold standard, but makes no difference on the mouse test or yeast novel sets, as there were no instances of negative examples that were demonstrated positives in the mouse test and only 11 in the yeast novel benchmark.

Table 2.

Performance metrics for network combination algorithms: simultaneous weights (SW) from Mostafavi and Morris (2010), our own SWSN algorithm and SWSN with a negative oracle (SWSNOracle)

Algorithm		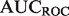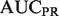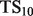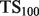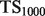		a	a
Mouse novel
SW	0.8366	0.3447	0.4315	0.5793	0.8705
SWSN	0.8376	0.3460	0.4396	0.5878	0.8755
SWSNOracle	0.8775	0.3491	0.4433	0.6027	0.9366
Mouse test
SW	0.9330	0.5171	0.6160	0.8014	0.9745
SWSN	0.9315	0.5177	0.6211	0.8041	0.9684
SWSNOracle	0.9315	0.5177	0.6211	0.8041	0.9684
Yeast novel
SW	0.8711	0.3387	0.4133	0.7127	0.9633
SWSN	0.8632	0.3139	0.3796	0.6294	0.9649
SWSNOracle	0.8636	0.3139	0.3796	0.6294	0.9656
Yeast gold standard
SW	0.8413	0.3896	0.7	0.6	0.4865
SWSN	0.8315	0.3729	0.7	0.52	0.5135
SWSNOracle	0.8569	0.3871	0.7	0.54	0.5270

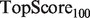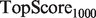Note: All algorithms were run using the GRF label propagation method of Mostafavi et al. (2008). ^aFor the yeast scenarios, and are replaced by 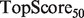and .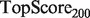

We believe this result indicates the promise of our SWSN algorithm, although it was likely not a significant factor in the current performance increase of our algorithm as a whole. Therefore, we submit SWSN as a logical extension of SW, as it uses the more accurate and specific negative example information now available. We hypothesize the likelihood of future performance gain from using SWSN, once even better negative example methods are uncovered.

5.3 Parameter-tuning results

From the performance measurements presented in Section 5.1, we see that while the tuned parameters performed significantly better than the null parameters in the mouse novel and yeast MOB benchmarks, their performance was on par with, or occasionally worse than, the null guess in the mouse test and yeast novel benchmarks. We attribute the decrease in performance, primarily in the yeast novel set, to the inherent difference between the state of annotation in yeast and mouse. Our parameter-tuning algorithm was designed to re-create a learning problem where annotations are only partially known, yet in yeast, a well-studied organism, this type of learning problem was most likely not as representative of the true learning problem as it was in mouse, a less-studied organism.

In general, adapting the tuning process to be representative of the original learning problem is a more intricate problem than first anticipated, and requires further exploration. For detailed analysis of the parameter-tuning results, and future avenues of approach, please refer to the Supplementary Material.

5.4 Prediction evaluations

We present the performance, evaluated by 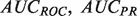and TopScore metrics, of five algorithms: the original MouseFunc GeneMANIA algorithm, the SW GeneMANIA algorithm presented in Mostafavi and Morris (2010) using sibling negative examples, the SW algorithm combined with the HLBias algorithm of Mostafavi and Morris (2009) and two versions of our algorithm: SWSN with ALBias and naive parameters 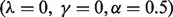and SWSN with ALBias and tuned parameters. Results are averaged over all categories, with an analysis of results broken down by function specificity available in Supplementary Figure S2a in the Supplementary Material.

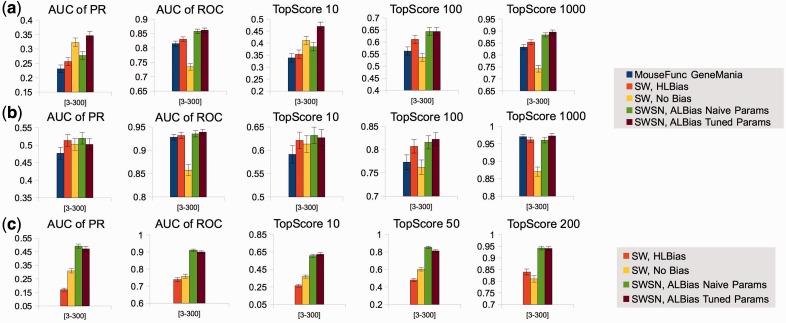
In the novel scenario for MouseFunc, our algorithms show a strong increase in performance across all metrics, especially our version with tuned parameters, as seen in Figure 2a. We see here a large difference in performance between ALBias with tuned parameters and ALBias with naive parameters, indicating that some of our algorithmic performance increase in mouse is due to the ability of our parametric pseudocounting procedure to prevent undue bias influence from understudied GO categories in mouse.

Fig. 2.

Performance metrics in (a) the novel scenario in mouse (488 functions, 1954 genes), (b) the test scenario in mouse (442 functions, 1718 genes) and (c) the novel scenario in yeast (511 functions, 342 genes). Metrics are averaged over all GO functions (each with between 3 and 300 counts per genome), and error bars are 1 SD of the error in the mean

For the mouse test set, the difference in performance is much smaller, as the test set is stripped of all labels, thus negating a key advantage of ALBias (see Fig. 2b for mouse test results). Yet, we still see a performance increase from our algorithm across most metrics, owing to better biases for genes sharing edges with test genes.

In the yeast novel set, we compare all algorithms except the original MouseFunc GeneMANIA algorithm, and observe a striking performance advantage of our algorithms across all evaluation metrics (see Fig. 2c). Further analysis indicates that much of this performance gain is due to our algorithm’s incorporation of information from all branches of GO into the label bias calculation. Examining an example GO term, ‘DNA packaging’, where our algorithm boosted performance in 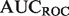from 0.722 to 0.989 and 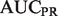from 0.467 to 0.803, we find the primary cause to be the improvement in rankings of two true-positive genes with useful Cellular Component annotations. YBR090C-A moved from rank 102 to rank 5, owing to the Cellular Component term ‘nuclear chromatin’, which has a high joint probability with ‘DNA packaging’, and YCL060C moved from rank 298 to 18, owing to the terms ‘nuclear chromosome’, and ‘chromosomal part’. Further examples are provided in the Supplementary Material.

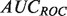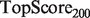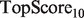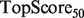Lastly, on the yeast MOB gold standard (results in Table 3), we see strong performance from our tuned SWSN ALBias algorithm, which achieved significantly higher and scores, and also from the SW, HLBias algorithm, which achieved the highest and scores, as well as a marginally higher 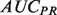score. Thus, our algorithm provided a better global ranking of true positives, while the current GeneMANIA algorithm ranked the top true predictions more highly.

Table 3.

Performance metrics on the yeast gold standard (GO:0007005), with experimental data from Huttenhower et al. (2009), composed of 148 positive examples in 2815 genes

Algorithm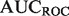
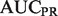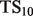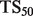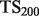SW, HLBias	0.8679	0.4685	1.0	0.74	0.4932
SW, No bias	0.7908	0.3729	0.8	0.54	0.5068
SWSN, naive parameters	0.8842	0.4076	0.8	0.56	0.5068
SWSN, tuned parameters	0.9032	0.4634	0.7	0.70	0.5608

Note: For both algorithms using the SW network combination algorithm, negative examples were chosen according to the sibling technique discussed in Section 3.2.

5.5 Computational cost

A theoretical complexity analysis of the SBCG algorithm is not possible (see Supplementary Material), but empirical testing shows a 30% reduction in the number of flops required for the prediction task on original MouseFunc data, with SBCG converging to a solution with smaller residuals as well. On the yeast benchmark, the reduction in flops was less, at 22%, as the ratio between the number of genes and the number of functions to predict is much smaller (see Table 3 in the Supplementary Material). As expected, there was an observable increase in computation saved as the number of categories increased, but this is bounded by the fact that our algorithm splits the categories into subsets with a maximum size of 500. This suggests that further computation could be saved by devising a suitable strategy to deal with low condition numbers for larger sets of RHS vectors. Suarjana and Law (1994) suggest that a pre-conditioner applied to the data might help reduce the number of iterations required as well.

6 CONCLUSION

We have addressed several of the key problems encountered by protein function prediction efforts by proposing novel algorithms, including a method of choosing negative examples, and a parameterized Bayesian methodology for computing prior functional biases from existing annotation data. These methods, applied using the framework of the GeneMANIA algorithm, have resulted in a significant performance increase across three large benchmarks. We also introduced a new optimization methodology, which significantly decreased computational costs.

We devised a framework for tuning parameters in a synthetic novel set, which added further performance gain in the novel scenario in mouse, but it requires additional work to be more broadly applicable to other evaluation scenarios. Our new SWSN network combination algorithm shows even more promise in settings with more extensive negative example information. Finally, we presented a new evaluation metric designed to be easily interpretable by experimentalists, even when averaged over many function categories.

When comparing performance statistics of different algorithms, a difference of a few percentage points can mean hundreds of new true annotations when applied across all functions. For example, a 1% increase in 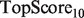would result in 187 new true annotations were an experimentalist to use that metric to guide experiments over the 1874 GO MF categories in the mouse genome (at the time of MouseFunc publication). Thus, we believe the algorithms presented here have the potential to guide experimentalists to a large number of fruitful assays, and are in general aligned with current biological understanding of how genes are functionally related to each other through different data types.

We have shown that our algorithm can perform function prediction through data integration and guilt by association with substantially more accuracy and efficiency than previously published algorithms, and provided insight into some of the inherent difficulties encountered by the development and evaluation of protein function prediction algorithms.