Joint Modeling of Longitudinal Change and Survival

Abstract

Joint longitudinal-survival models are useful when repeated measures and event time data are available and possibly associated. The application of this joint model in aging research is relatively rare, albeit particularly useful, when there is the potential for nonrandom dropout. In this article we illustrate the method and discuss some issues that may arise when fitting joint models of this type. Using prose recall scores from the Swedish OCTO-Twin Longitudinal Study of Aging, we fitted a joint longitudinal-survival model to investigate the association between risk of mortality and individual differences in rates of change in memory. A model describing change in memory scores as following an accelerating decline trajectory and a Weibull survival model was identified as the best fitting. This model adjusted for random effects representing individual variation in initial memory performance and change in rate of decline as linking terms between the longitudinal and survival models. Memory performance and change in rate of memory decline were significant predictors of proximity to death. Joint longitudinal-survival models permit researchers to gain a better understanding of the association between change functions and risk of particular events, such as disease diagnosis or death. Careful consideration of computational issues may be required because of the complexities of joint modeling methodologies.

Introduction

Longitudinal studies often collect both repeated measures and time-to-event data. For instance, aging studies interested in cognitive change repeatedly collect information about participants’ cognitive function and date of death or dementia diagnosis. Repeated measures and time-to-event data are often analyzed independently using growth curve models (e.g., linear mixed, multilevel, or random coefficients) for the investigation of change as well as survival analysis methods such as the Cox proportional hazard models for the time-to-event data.

Although independent analyses of repeated measures and time-to-event data inform about each process separately, they do not account for the possible association between the longitudinal measures and the event data. Joint longitudinal–time-to-event models have been developed to explicitly account for the dependency between the longitudinal change functions and event time data.

A second context in which a joint modeling approach may be appropriate is when one is interested in the longitudinal outcome and the dropout is nonrandom, that is, when the probability of dropout depends on unobserved longitudinal data. Here, ignoring dropout may result in biased results (Little & Rubin, 1987). A shared parameter model that models the joint distribution of the longitudinal outcome and the event data has been proposed to overcome this limitation (Follman & Wu, 1995). Technical overviews of the joint modeling literature can be found in Tsiatis and Davidian (2004) and Neuhaus and Heuman (2006).

In the health literature, the association between repeated measures and time-to-event data has been modeled in various ways. Wang and Taylor (2001) modeled the association between CD4 counts and the hazard of AIDS by including CD4 counts as a time-dependent covariate in a proportional hazards model considered for modeling the hazard of AIDS. Lin, Turnbull, McCulloch, and Slate (2002) described prostate-specific antigen change and prostate cancer diagnosis, fitting a latent class model and including each person’s class membership as a covariate in a survival model. Henderson, Diggle, and Dobson (2000) combined a random effects model for the longitudinal data and a semiparametric proportional hazards model for the survival data. Joint modeling occurs by including the random effects from the longitudinal model singly or in combinations in the survival model. A distinguishing feature of this modeling approach is that the model is estimated in a single simultaneous step, not as a two-stage model.

Henderson et al.’s model (2000) has been applied to examine the association between changes in episodic memory and early Alzheimer’s diagnosis (McArdle, Small, Backman, & Fratiglioni, 2005). McArdle et al. fitted an age-based latent growth model to memory scores and a Cox proportional hazards model to data about the age of onset of Alzheimer’s disease. They reported that level of memory function – but not its change – was a predictor of age of disease onset. Ghisletta, McArdle, and Linderberg (2006) examined the association of a range of cognitive abilities and mortality, reporting that, when cognitive variables were analyzed separately, their level was predictive of mortality, but that after controlling for sensory and motor performance and for broad personality characteristics, verbal knowledge and one of the episodic memory indicators considered in the analysis were no longer associated with mortality: Only change in speed and verbal fluency were found to be associated with mortality. Ghisletta (2008) later extended the longitudinal submodel to a multivariate model that allowed him to describe change in several cognitive abilities simultaneously.

Henderson et al.’s model is becoming increasingly popular in health research despite its considerable complexity and the fact that fitting the model may require sophisticated modeling skills and the use of specialized software packages. Statistical packages such as JM and JoineR (Philipson, 2011; Rizopoulos, 2010) were recently developed to fit joint longitudinal-survival models using R.¹ Both packages use maximum likelihood estimation techniques for model estimation.

Guo and Carlin (2004) compared results obtained from fitting Henderson et al.’s model using SAS, which estimates the model using maximum likelihood estimation via the EM algorithm and WinBUGS (Lunn, Thomas, Best, & Spiegelhalter, 2000), which estimates the model using a Bayesian approach implemented via Markov Chain Monte Carlo methods. They concluded that the Bayesian approach offered significantly improved and enhanced estimation, simpler coding, and comparable runtimes. Following Guo and Carlin’s recommendation and an estimating technique applied in previous publications in the aging literature (Ghisletta, 2008; Ghisletta et al., 2006; McArdle et al., 2005), we illustrate the fit of a joint longitudinal-survival model and discuss some of the challenges that may arise when fitting these models considering a Bayesian approach, though the issues discussed are not exclusive to the Bayesian paradigm.

With this purpose in mind, we examine the association between change in memory and death in older individuals using data from a Swedish longitudinal study of aging.

Methods

Data

We analyzed data from participants of a population-based study of aging, the “Origins of Variance in the Old-Old” study (OCTO-Twin) (McClearn et al., 1997). Initially, 351 intact aged twin pairs (702 individuals: 149 monozygotic and 202 same-sex dizygotic pairs) were sampled from the Swedish Twin Registry. These individuals were first interviewed between 1991 and 1993 and then in four further interview waves conducted at 2-year intervals. Sociodemographic information such as sex, years of education, and marital status were also collected during the study. Date, cause of death, and dementia diagnosis were collected throughout and beyond the study from the Swedish Death Registry and medical records. Dementia was diagnosed by consensus according to the 3rd edition of the Diagnostic and Statistical Manual of Mental Disorders (APA, 1980). After accounting for mortality, only 10% of the missing data are due to refusal to participate that has been reported to be associated with ill health (Johansson & Zarit, 1997). Given the low intraclass correlation previously reported for these data (Johansson & Berg, 1989), the twins were treated as unrelated singletons.

We examined scores from the Prose Recall test of 618 study participants who were not demented at baseline. The Prose Recall test is a verbal memory test in which participants are asked for immediate free recall of a brief (100 words) story that has a humorous point. Responses are coded for the amount of information recalled in a manner similar to the Wechsler Memory Scale. The maximum score is 16; Figure 1 shows Prose Recall scores of a randomly selected OCTO participants plotted against time in study.

Figure 1.

Prose scores from a randomly selected subsample of participants of the OCTO Twin longitudinal study who were nondemented at baseline plotted as a function of time in study.

Of the 618 participants with available Prose Recall scores, 410 were women and 208 men. They had an average of 7.2 years of education (SD = 2.3) and at baseline were, on average, aged 83.4 years (SD = 3.1). The average age at death of the 577 individuals who died during the duration of the study (93% of sample) was 90 years (SD = 4.3). About 30% of the sample (180 individuals) received a dementia diagnosis during the study.

Statistical Analysis

We fitted a series of joint longitudinal-survival models with several options for the longitudinal and survival submodels and their combination.

We modeled the longitudinal outcome using random effects models as they permit the investigation of mean change while allowing for between-individual variability about population average parameters. To identify the best fitting model of change in the Prose Recall scores, we considered a series of random effects models structured as a function of individual’s time in study. Models considered were (1) a model where rate of decline was assumed to be constant (Model 1, linear); (2) a model where the rate of decline was assumed to change with increasing age (Model 2, quadratic); (3) a piecewise linear model with an inflection point estimated from the data and common to all individuals and with constant rate of decline before and after the inflection point (Model 3, fixed change point; Hall, Lipton, Sliwinski, & Stewart, 2000); and (4) a model with individual inflection points (Model 4, random change point; Hall et al., 2000) with constant rate of decline before and after the inflection point. Mathematical formulations of these models are presented in Table 1.

Table 1.

List of random effects model considered for the independent and joint analyses and frailty terms

Random effects models fitted
Linear random effects model (Model 1)	${\text{Prose}}_{it}={\alpha }_{0i}+{\alpha }_{1i}{T}_{it}+{\epsilon }_{it}$ (1) ${\alpha }_{0i}={\alpha }_{00}+{\gamma }_{01}B.{\mathit{age}}_i+{\gamma }_{02}{\mathit{Educ}}_i+{\gamma }_{03}{\mathit{Gender}}_i+{\gamma }_{04}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{0i}$ (1.1) ${\alpha }_{1i}={\alpha }_{11}+{\gamma }_{11}B.{\mathit{age}}_i+{\gamma }_{12}{\mathit{Educ}}_i+{\gamma }_{13}{\mathit{Gender}}_i+{\gamma }_{14}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{1i}$ (1.2)
Quadratic random effects model (Model 2):	${\text{Prose}}_{it}={\alpha }_{0i}+{\alpha }_{1i}{T}_{it}+{\alpha }_{2i}{T}_{it}^2+{\epsilon }_{it}$ (2) ${\alpha }_{0i}={\alpha }_{00}+{\gamma }_{01}B.{\mathit{age}}_i+{\gamma }_{02}{\mathit{Educ}}_i+{\gamma }_{03}{\mathit{Gender}}_i+{\gamma }_{04}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{0i}$ (2.1) ${\alpha }_{1i}={\alpha }_{11}+{\gamma }_{11}B.{\mathit{age}}_i+{\gamma }_{12}{\mathit{Educ}}_i+{\gamma }_{13}{\mathit{Gender}}_i+{\gamma }_{14}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{0i}$ (2.2) ${\alpha }_{2i}={\alpha }_{22}+{\gamma }_{21}B.{\mathit{age}}_i+{\gamma }_{22}{\mathit{Educ}}_i+{\gamma }_{23}{\mathit{Gender}}_i+{\gamma }_{24}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{0i}$ (2.3)
Fixed change point model (Model 3)	${\text{Prose}}_{it}={\alpha }_{0i}+{\alpha }_{1i}{T}_{it}\text{I}(T_{it}\le \tau )+[{\alpha }_{0i}+{\alpha }_{1i}\tau +{\alpha }_{2i}(T_{it}-\tau )]\text{I}(T_{it}>\tau )+{\epsilon }_{it}$ (3) ${\alpha }_{0i}={\alpha }_{00}+{\gamma }_{01}B.{\mathit{age}}_i+{\gamma }_{02}{\mathit{Educ}}_i+{\gamma }_{03}{\mathit{Gender}}_i+{\gamma }_{04}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{0i}$ (3.1) ${\alpha }_{1i}={\alpha }_{11}+{\gamma }_{11}B.{\mathit{age}}_i+{\gamma }_{12}{\mathit{Educ}}_i+{\gamma }_{13}{\mathit{Gender}}_i+{\gamma }_{14}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{0i}$ (3.2) ${\alpha }_{2i}={\alpha }_{22}+{\gamma }_{21}B.{\mathit{age}}_i+{\gamma }_{22}{\mathit{Educ}}_i+{\gamma }_{23}{\mathit{Gender}}_i+{\gamma }_{24}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{0i}$ (3.3)
Random change point model (Model 4)	${\text{Prose}}_{it}={\alpha }_{0i}+{\alpha }_{1i}{T}_{it}\text{I}(T_{it}\le {\tau }_i)+[{\alpha }_{0i}+{\alpha }_{1i}{\tau }_i+{\alpha }_{2i}(T_{it}-{\tau }_i)]\text{I}(T_{it}>{\tau }_i)+{\epsilon }_{it}$ (4) ${\alpha }_{0i}={\alpha }_{00}+{\gamma }_{01}B.{\mathit{age}}_i+{\gamma }_{02}{\mathit{Educ}}_i+{\gamma }_{03}{\mathit{Gender}}_i+{\gamma }_{04}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{0i}$ (4.1) ${\alpha }_{1i}={\alpha }_{11}+{\gamma }_{11}B.{\mathit{age}}_i+{\gamma }_{12}{\mathit{Educ}}_i+{\gamma }_{13}{\mathit{Gender}}_i+{\gamma }_{14}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{0i}$ (4.2) ${\alpha }_{2i}={\alpha }_{22}+{\gamma }_{21}B.{\mathit{age}}_i+{\gamma }_{22}{\mathit{Educ}}_i+{\gamma }_{23}{\mathit{Gender}}_i+{\gamma }_{24}\mathit{Inc}.{\mathit{Dem}}_i+{\nu }_{0i}$ (4.3)
Frailty terms	$\begin{array}{l}{W}_i(t)=R_0{\nu }_{0i};W_i(\text{t})=R_1{\nu }_{1i};W_i(t)=R_2{\nu }_{2i}\\ W_i(t)=R_0{\nu }_{0i}+R_1{\nu }_{1i}\\ W_i(t)=R_0{\nu }_{0i}+R_2{\nu }_{2i}\\ W_i(t)=R_2{\nu }_{2i}+R3{\nu }_{3i}\\ W_i(t)=R_0{\nu }_{0i}+R_1{\nu }_{1i}+R_2{\nu }_{2i}\end{array}$

All models were adjusted for baseline age, education (considered as a continuous variable measured as years of education), sex (men = 0, women = 1), and a dementia indicator (1 = incident case, 0 = dementia free). Continuous variables were centered at their mean values.

To model the hazard of death, we considered a Weibull and an exponential model. Under a Weibull model, the hazard of death at time t, was modeled as:

$${\lambda }_i(t)={\lambda }_0(t){\mu }_i(t)$$

with μ_i(t) = exp(δ₀Bage_i + δ₁Educ_i + δ₂Gender_i + δ₃Inc.Dem_i) (1) and λ₀(t) = kt^(k−1), where t is the number of years past age 79 and k > 0. The term λ₀(t) = kt^(k−1) represents the baseline hazard model for an individual with values of zero in all covariates. The parameter k is such that, when k > 1, the risk of death increases with time, while if 0 < k < 1, the risk of death decreases with time. The exponential model is a special case of the Weibull model and can be obtained from equation (1) by taking k = 1. Under the exponential model the risk of death remains constant over time. Parameters for δ_i for i = 1,2, 3, represent the effect of age at study entry, education, sex, and incident dementia, respectively, on the hazard of death after age 79.

To link both submodels, we included an extra term W_i(t) in the model presented in equation (1). This new term, often called frailty, took different forms to represent relevant aspects of the random effects model, including single individual random effects from the longitudinal submodel and various combinations of them.

The mean hazard of death modeled in the joint model formulation was then represented as:

$${\mu }_i(t)=exp({\delta }_0{\mathit{Bage}}_i+{\delta }_1{\mathit{Educ}}_i+{\delta }_2{\mathit{Gender}}_i+{\delta }_3\mathit{Inc}.{\mathit{Dem}}_i+W_i(t)).$$

For instance, for a linear random effects model with random effects ν_0i and ν_1i correspond to baseline memory performance and rate of change, respectively. Possible formulations of the frailty term W_i(t) include W_i(t) = R₀ν_0i, W_i(t) = R₀ν_0i, and where R₀ and R₁ are normally distributed parameters. Where both random effects were included, R₀ and R₁ were modeled as bivariate normals. R₀ and R₁ in W_i(t) represent the effect of individual variations in memory performance and its annual rate of change on the mean hazard of death. (See bottom row of Table 1 for other possible formulations of frailty terms W_i(t).)

To compare results from an independent analysis and the joint models proposed, independent analyses were also conducted fitting the same longitudinal random effects and survival models previously described but excluding the linking terms W_i(t) from the survival model.

Model Implementation

All models were fitted in a Bayesian framework following Guo and Carlin’s model specification. WinBUGS performs MCMC simulations to construct Markov chains that converge toward a stationary distribution.

Convergence was assessed graphically after discarding an initial burn-in of 7,000 iterations and by inspection of the Brooks and Gelman (Brooks & Gelman, 1997) method implemented in WinBUGS. Monte Carlo standard errors of all parameters of interest were examined, and we verified that they were below 5% of the sample standard deviation as usually recommended.

Vague prior distributions were considered. Sensitivity analyses were conducted to assess the impact of the prior distributions on model estimates. Model selection was performed by comparison of deviance information criterion (DIC) values (Spiegelhalter, Best, Carlin, & vander Linde, 2002), a generalization of Akaike’s information criterion. Models with small DIC values are preferred as small values of DIC identify a parsimonious model with good fit.

Results

Joint Model

A joint model consisting of a quadratic random effects model and a Weibull survival model with linking termsthat included random effects corresponding to baseline memory performance (intercept), annual rate of change in memory performance (linear slope), and acceleration in change (quadratic slope) was identified as the model with the lowest DIC.

Results from the model are presented in Table 2 (left columns). Mean Prose Recall scores at baseline for a reference individual (nondemented man aged 83 years at baseline with 7 years of education) was estimated at 9.69 (SD = 0.57) points. Annual rate of change was estimated at 0.11 (SD = 0.47) points per year, and its change at −0.15 (SD = 0.13) (quadratic slope), although these estimates did not reach statistical significance.

Table 2.

Results from a joint longitudinal-survival model, where the longitudinal model was a quadratic model and the survival model a Weibull model that included the random intercept, the random slopes before and after the change point, and the random change point as linking terms

	Joint model		Independent analysis
	Mean (SD)	95% credible interval	Mean (SD)	95% credible interval
Random effects model
Fixed effects
Memory performance	9.69 (0.57)	[8.57, 10.82]	9.86 (0.60)	[8.70, 11.02]
Baseline age	−0.30 (0.10)	[−0.51, −0.10]	−0.32 (0.10)	[−0.53, −0.11]
Education	0.52 (0.12)	[0.28, 0.76]	0.52 (0.12)	[0.28, 0.76]
Sex	0.32 (0.55)	[−0.77, 1.40]	0.20 (0.57)	[−0.91, 1.33]
Incident case	−3.52 (0.53)	[−4.52, −2.47]	−3.47 (0.52)	[−4.51, −2.43]
Rate of change	0.11 (0.47)	[−0.81, 1.03]	−0.11 (0.48)	[−1.04, 0.82]
Baseline age	0.01 (0.07)	[−0.14, 0.15]	0.00 (0.07)	[−0.14, 0.16]
Education	−0.07(0.408)	[−0.24, 0.09]	−0.08 (0.08)	[−0.2, 0.08]
Sex	0.22 (0.46)	[−0.68, 1.10]	0.31 (0.42)	[−0.51, 1.22]
Incident case	−0.60 (0.35)	[−1.29, 0.08]	−0.63 (0.34)	[−1.33, 0.01]
Change in rate of change	−0.15 (0.13)	[−0.42, 0.10]	−0.01 (0.12)	[−0.26, 0.23]
Baseline age	0.01 (0.01)	[−0.03, 0.04]	0.00 (0.01)	[−0.04, 0.04]
Education	−0.00 (0.02)	[−0.04, 0.04]	0.00 (0.02)	[−0.04, 0.04]
Sex	0.02 (0.12)	[−0.22, 0.27]	−0.04 (0.12)	[−0.27, 0.19]
Incident case	−0.03 (0.08)	[−0.20, 0.13]	−0.02 (0.08)	[−0.18, 0.14]
Random effects
Res. Variance intercept	3.15 (0.23)	[2.70, 3.63]	3.15 (0.23)	[2.70, 3.63]
Res. Variance random slope before change point	1.04 (0.20)	[0.69, 1.48]	1.04 (0.20)	[0.69, 1.48]
Res. Variance random slope before change point	0.31 (0.02)	[0.26, 0.37]	0.27 (0.02)	[0.22, 0.34]
Error	4.55 (0.02)	[3.57, 5.88]	4.54 (0.02)	[3.57, 5.88]
DIC	9488.0		9810.8
Survival model
Baseline risk (p)	3.72 (0.22)	[3.34, 4.23]	3.32 (0.10)	[3.11, 3.52]
Constant	−9.04 (0.54)	[−10.25, −8.11]	−8.13 (0.28)	[−8.70, −7.57]
Baseline age	−0.20 (0.02)	[−0.25, −0.15]	−0.17 (0.01)	[−0.20, −0.14]
Education	0.01 (0.02)	[−0.03, 0.06]	0.02 (0.01)	[−0.01, 0.05]
Sex	−0.47 (0.11)	[−0.70, −0.26]	−0.40 (0.08)	[−0.56, −0.21]
Incident case	0.37 (0.11)	[0.15, 0.59]	0.29 (0.09)	[0.11, 0.47]
Random effects intercept	−0.07 (0.02)	[−0.11, −0.01]
Random effects linear slope	−0.21 (0.13)	[−0.48, 0.05]
Random effects quadratic slope	−1.77 (0.68)	[−3.15, −0.44]

Individuals who entered the study at an older age performed poorer compared to those who entered the study at a younger age. Incident dementia cases scored 3.52 points lower at study entry than individuals who were never diagnosed with dementia. Better educated individuals also had better performance at study entry than individuals with poorer education. None of the variables considered as possible predictors of change were found to be significant predictors of linear or quadratic rate of memory change.

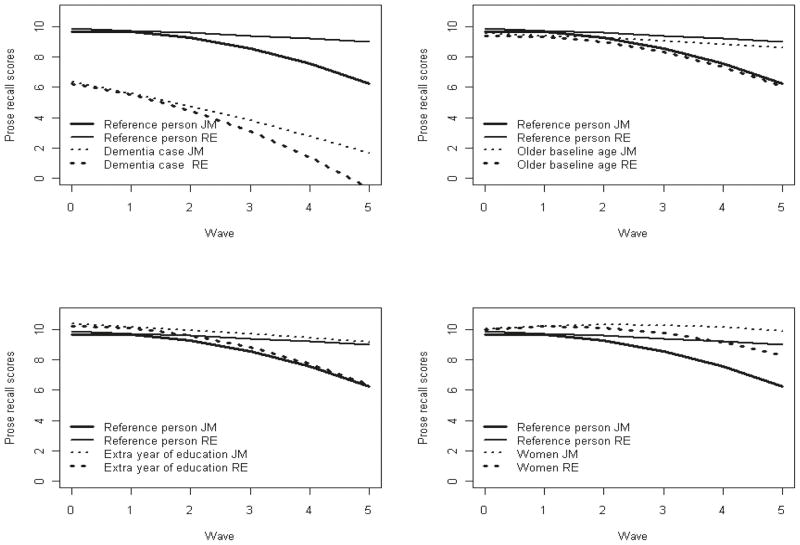
Figure 2 shows estimated mean curves obtained from the joint and independent models fitted to the data and the effect of risk factors on them. The thick solid line represents the trajectory estimated by the joint model for a person with reference values in all covariates (nondemented man with 7 years of education and aged 83.4 years at study entry) and the thin solid line the trajectory estimated by the random effects model. They illustrate the bias induced in the independent model by the missing at random assumption and show how the independent analysis underestimates the decline experienced by individuals.

Figure 2.

Estimated mean trajectories for a reference individual (nondemented man, aged 83 years at study entry, with 7 years of education) obtained fitting a joint model and a random-effects model and the effect of covariates of these trajectories.

Results from the survival model indicate that the risk of death increased with time (k = 3.72 > 1). Women were found to have lower hazard of death after age 79 years than men, incident dementia cases had a higher hazard of death than those who stayed dementia free during the study, and individuals who joined the study at an older age had lower hazard of death after age 79 years than those who joined the study at a younger age. Our results identified poorer memory function at study entry and a faster change in rate of decline (acceleration) as associated with an increasing hazard of death after age 79.

The results obtained from the joint analysis illustrates that, even after the inclusion of the covariates, the residual random effects of both the linear and quadratic slopes are still significant. This demonstrates that the lack of prediction of the random effects by the covariates is not due to lack of variance to begin with.

Independent Analyses

Longitudinal Model

Mean Prose Recall scores at baseline for a reference individual were estimated at 9.86 (SD = 0.59), with an annual rate of change (linear slope) of −0.11 (SD = 0.47) points per year, and a change in rate of change of −0.01 (SD = 0.13) points per year (quadratic slope). Per extra year of age at study entry (relative to 83 years), memory performance was 0.30 points lower. Incident dementia cases scored 3.52 points lower at study entry than individuals who were never diagnosed with dementia. Better educated individuals also had better performance at study entry than individuals with poorer education.

Survival Model

Results from the independent survival model were similar to those obtained from the joint analyses, though the effects of predictors were attenuated when the linking terms that conveyed information about the longitudinal model were excluded from the survival model (see right columns of Table 1).

Discussion

Our results support the hypothesis of an association between mortality and memory changes. We found that the hazard of death increases with poorer cognitive function and a faster change in rate of memory decline after accounting for dementia.

Only baseline age, incident dementia, and education reached statistical significance as predictors of memory performance. Being male, being diagnosed with dementia, and being younger at baseline were identified as predictors of higher hazard of death. These results agree with previous publications (Lavery, Dodge, Snitz, & Ganguli, 2009; Oksuzyan et al., 2010). Although initially it may seem counterintuitive that individuals who joined the study at a younger age have higher hazard of death, we believe our results reflect a survivor effect (Mendes de Leon, 2007). That is, individuals who joined the study at an older age are likely to be healthier than those who reach that same age during the duration of the study.

Initially, it may be thought that inferences about the association between death and memory changes similar to the ones obtained from a joint analysis can be obtained by fitting time to death linear mixed models (or possibly other independent longitudinal analysis conducted using linear mixed models where time is structured differently). However, one must bear in mind that, although time to death mixed models represent an interesting modeling alternative, inferences obtained from these models are affected by the same issues as other linear mixed model independent analysis. Specifically, inferences are likely to be biased in the presence of nonrandom dropout. Moreover, in order to fit these models it is necessary to calculate the time elapsed between each interview and death, so only data from individuals with known dates of death can be included for analysis. This may result in a smaller sample size and biased inferences because they are produced using data from a selected subsample of individuals.

The joint modeling approach considered here was specifically developed to avoid biases induced by nonrandom dropout. Where date of death is unknown, it is treated as censored, so that nondeceased individuals are not excluded from the analyses.

The comparison of results obtained from a separate analysis of the repeated measures models and survival models illustrates the differences in the fixed effects estimates obtained under the assumption of an “immortal cohort” and when death is modeled explicitly as in the joint longitudinal-survival model. A 2-step analysis (that is, an analysis where a linear mixed model is first fitted and random effects are then extracted and included in a time-to-event model) will have similar problems as the ones discussed previously, since results from the longitudinal model will be biased being produced under a missing at random assumption. Estimates of change produced by an independent random effects model will be likely to underestimate change as in the example we considered. Random effects produced will also be affected by bias. Because these will then inform the time-to-event part of the model, this second model will in and of itself produce biased estimates of hazard of death.

Differences between estimates obtained from an independent analysis of the longitudinal data and time-to-event data and estimates obtained from their joint analysis were also reported by McArdle et al. (2005) in an investigation of the association between episodic memory and the onset of Alzheimer’ disease. Estimates of memory performance and annual rate of change reported by McArdle from the independent analysis conducted fitting an age-based latent growth model were 6.18 (SD = 0.18) and −1.15 (SD = 0.16), whereas the corresponding estimates from a joint growth-survival model were 7.10 (SD = 0.41) and −0.95 (SD = 0.18). These results demonstrate the biased estimates obtained from the growth model when not accounting properly for possible informative dropout.

The fitting of joint models is a time-consuming task for several reasons. First, a range of measurement and intensity models must be considered if sufficient data are available to explore longitudinal models that would allow researchers to obtain gain better knowledge about the shape of the change in the longitudinal outcome. For instance, we had five waves of data from the OCTO study, which allowed us to examine the possibility of nonlinear change. We considered four different random effects submodels in addition to two survival submodels, but restricted our analysis to four longitudinal models with directly interpretable parameters without considering more complex parametric shapes or nonparametric alternatives. Within each combination of longitudinal-survival model, several options for linkage should be considered. The consideration of other longitudinal models would have considerably increased the number of possible combinations of longitudinal-survival models and ways of linking them. For instance, where a model with constant rate of decline is considered, the survival model may include a set of covariates in addition to the random intercept and the random slope as single terms, and combinations thereof, resulting in at least three possible models. Although it may be tempting to identify the best-fitting longitudinal and survival models separately and then combine them in a second-stage analysis, we do not encourage researchers to do so as results from independent models may be misleading since they ignore the association of the longitudinal and survival data may produce biased results.

Second, analyses performed in a Bayesian framework require the assessment of the impact of the choice of prior distributions on estimates of model parameters. In a Bayesian modeling framework, inferences are based on estimates obtained from the posterior distribution of model parameters, a combination of the data likelihood and the prior distribution of the parameters. Prior distributions are chosen by the researcher based on knowledge about the parameters of interest, before the data are seen. Consequently, sensitivity analyses of the prior distributions considered in the models fitted are a necessary condition to ensure that results are consistent. Although this further step in the analysis is necessary only when models are fitted in a Bayesian framework, other issues arise when fitting joint models using maximum likelihood and the EM algorithm. When fitting joint models using the EM algorithm, numerical integration is required and convergence problems have been reported (Ghisletta et al., 2006). Convergence problems have been reported to affect the number of covariates that could be included in the model, as with an increasing number of covariates, problems became more acute.

Finally, caution in the choice of the number of covariates to be included in the two submodel may be needed. Ghisletta et al. (2006) reported limitations in the number of covariates they could include in their analysis; when they tried to include an additional number of covariates, they encountered convergence problems. We did not encounter these problems in our work, though we included only a reduced number of core covariates in our analysis.

The Bayesian approach considered in this paper offers a flexible modeling framework that does not require sophisticated code-writing skills, though familiarity with Bayesian inference is necessary. Model selection was conducted via comparison of DIC values. Unlike other fit indices like the Bayesian information criterion or Akaike’s information criterion, there is no rule of thumb for model comparison using the DIC. Models with small DIC values are considered to be parsimonious and fit the data well. Yet, in models of considerable complexity like the one discussed here, the DIC may not be an appropriate index, and researchers may need to use alternative indices of fit (Celeux, Forbes, & Robert, 2006; Spiegelhalter et al., 2002). Model fit in Bayesian statistics is an active area of research that is continuously evolving and where alternative measures of model fit are currently being investigated.

To conclude, joint models provide researchers with a promising modeling alternative in the presence of nonrandom dropout and where the focus of interest is on both the longitudinal and the survival processes and their association. Yet, these are complex models, so that researchers need to be aware of some of the issues that may arise when joint models are employed.

Appendix

Statistical assumptions of longitudinal submodels presented in Table 1 model include the following:

$${\epsilon }_{\text{it}}~N(0,{\sigma }^2);{\nu }_{\text{i}}=({\nu }_{0\text{i}},{\nu }_{1\text{i}}~N(0,{\mathrm{\sum }}_{\nu })\text{or}\text{where}\text{appropriate}{\nu }_{\text{i}}=({\nu }_{0\text{i}},{\nu }_{1\text{i}},{\nu }_{2\text{i}})~N(0,{\mathrm{\sum }}_{\nu }).$$

Errors are assumed to be independent.

Survival Submodels

Under a Weibull proportional hazards model, the hazard of death at time t, for individual i can be formulated as: λ_i(t) = kt^(k−1) μ_i(t) with

$$\mu (t)=exp({\delta }_0{\mathit{Bage}}_i+{\delta }_1{\mathit{Educ}}_i+{\delta }_2{\mathit{Gender}}_i+{\delta }_3\mathit{Inc}{\mathit{Dem}}_i)$$

The exponential model can be obtained from the expression of the formulation of the Weibull model by taking k = 1.

Joint Models Fitted

For each of the longitudinal submodels and survival models, a set of frailty terms W_i(t) were used. These are listed in Table 1. The association parameters R₀, R₁, R₂ were modeled as Gaussian variables with mean zero and constant variance.