Abstract
The genotype–phenotype map (GP map) concept applies to any time point in the ontogeny of a living system. It is the outcome of very complex dynamics that include environmental effects, and bridging the genotype–phenotype gap is synonymous with understanding these dynamics. The context for this understanding is physiology, and the disciplinary goals of physiology do indeed demand the physiological community to seek this understanding. We claim that this task is beyond reach without use of mathematical models that bind together genetic and phenotypic data in a causally cohesive way. We provide illustrations of such causally cohesive genotype–phenotype models where the phenotypes span from gene expression profiles to development of whole organs. Bridging the genotype–phenotype gap also demands that large-scale biological (‘omics’) data and associated bioinformatics resources be more effectively integrated with computational physiology than is currently the case. A third major element is the need for developing a phenomics technology way beyond current state of the art, and we advocate the establishment of a Human Phenome Programme solidly grounded on biophysically based mathematical descriptions of human physiology.
 |
Arne B. Gjuvsland is a researcher at the Centre for Integrative Genetics at the Norwegian University of Life Sciences. He did his PhD on linking genetic theory and gene regulatory network models. Currently he is investigating genotype–phenotype relation- ships in the Virtual Physiological Rat project and a project on experimental evolution in yeast. Jon Olav Vik is a researcher at the same centre. With a broad background in quantitative biology ranging from ecology to climate effects to cardiac modelling, he is now working on causally cohesive genotype–phenotype modelling and the analysis and comparison of virtual physiology models. Daniel A. Beard is a Professor of Physiology and Director of the Center for Computational Medicine at the Medical College of Wisconsin and coordinator of the NIH-supported Virtual Physiological Rat project. His research interests are in cardiovascular physiology, energy metabolism, and in using computational modelling and simulation to study multiple-scale process in physiology. Peter J. Hunter is Professor of Engineering Science and Director of the Auckland Bioengineering Institute at the University of Auckland in New Zealand. His major research interests have been the interrelated electrical, mechanical and biochemical functions of the heart. As the recent co-Chair of the Physiome Committee of the International Union of Physiological Sciences (IUPS) he has been helping to lead the international Physiome Project using computational methods for understanding the integrated physiological function of the body in terms of the structure and function of tissues, cells and proteins. Stig W. Omholt is Research Professor in the Faculty of Medicine at the Norwegian University of Science and Technology (NTNU) and Director of its new cross-campus biotechnology programme ‘NTNU Biotechnology – the Confluence of Life Sciences, Mathematical Sciences and Engineering’. His current research interests include the etiology of hypertension, aspects of the astroglia–neuron interaction in the brain, model-guided drug targeting, and the linking of genetics with systems dynamics and multiscale modelling.
Introduction
We use DNA information in at least four explanatory settings: as a pure marker where we do not make a direct link to any particular phenotype; when we by statistical means establish an association between one or more chromosomal regions and phenotypic variation; when we can document that a particular DNA variation (natural or imposed) does indeed cause a phenotype; and finally in a causally cohesive setting where we can also explain how the genetic variation causes the observed phenotype in terms of biophysical mechanism at the cell, tissue and organ system levels. Even though there are several challenges associated with the first three types of explanation, they are all dwarfed by those facing us in connection with the fourth type. But these are the ones to be overcome if we are to bridge the gap between the genotype and the phenotype with real understanding, and thus realize the disciplinary goals of both genetics (Bateson, 1906, p. 190) and physiology (Gove, 1981).
The terms genotype and phenotype were introduced by the Danish plant physiologist and geneticist Wilhelm Johannsen in 1909. An individual's genotype denotes the constitution of parts or all of its genetic material, while its phenotype may comprise anything from a single observable characteristic or trait to all conceivable ones. Thus any morphological, developmental, biochemical or physiological property all the way down to the subcellular level (including epigenetic marks), as well as any of the individual's behaviour and products of behaviour, is a phenotypic characteristic and belongs to the individual's phenome (Soulé, 1967; Houle et al. 2010).
The relation between genotype and phenotype can be conceptualized as a genotype–phenotype map (GP map), assigning a phenotype to each possible genotype. Even though the term physiological genetics pointing to the genotype–phenotype relation has at least a 75 years history (Goldschmidt, 1938), the mathematically oriented GP map concept was coined only 40 years ago (Burns, 1970). The concept is highly instrumental for physiological research and concords well with the disciplinary goals of physiology as they are laid out in the standard definition of the discipline: “the study of the functions and activities of living matter (as of organs, tissues, or cells) as such and of the physical and chemical phenomena involved” (Webster's Third New International Dictionary). Fulfilling these goals demands an understanding of the mechanisms underlying the GP map.
The GP map concept applies to any time point in the ontogeny of a living system and it is an abstraction of a relation that is the outcome of very complex dynamics that include environmental effects. The concept does not imply that DNA has a privileged place in the chain of causality authorizing the current zoo of anthropomorphic concepts we attribute to it (Noble, 2012; Omholt, 2012). As described in more detail by Omholt (2012), DNA allows a system to induce perturbations of its own dynamics as a function of its own system state or phenome. Thus the presence of DNA is a systems structure that enables living systems to self-transcend – not beyond the dictums of physics and chemistry, but beyond those morphogenetic limits that exist for non-living open physical systems in general. Thus there is no direct causal arrow from genotype to phenotype in the sense that DNA is responsible for exerting a direct effect as a sub-system on the system dynamics. The causality flows from the system state through a change in use of DNA (as an inert system component) that results in a change in the production of RNA and protein, which in turn perturbs the system's dynamics. In those cases where variations in DNA cause changes in the perturbation regime it may lead to different system dynamics and thus physiological variation. This way of perceiving the function of DNA in a GP map context brings physiology back as the major arena for understanding the manifestation and propagation of genetic variation.
Our view is that without the massive, combined use of existing and new mathematics, high-dimensional data analysis, computer science and advanced engineering methodology, biological research will not be able to probe very deeply into the genotype–phenotype relation. In the following we elaborate on a few selected topics associated with what it takes to bridge the genotype–phenotype gap through this merging of life sciences, mathematical sciences and engineering.
Causally cohesive genotype–phenotype modelling
The subject matter of physiological research is to understand the mechanisms and principles underlying biological systems behaviour. Computational physiology has a long and effective track record of applying systems dynamics models to dissect biological function. The efficacy of computational models in physiology arises from their capacity to connect a comprehensive amount of empirical data into a functional whole, by enforcing explicit formulations of various hypotheses, by precisely framing the prediction space of hypotheses, by initiating and canalizing experimental or empirical work by pointing out key questions and the type of data needed, and last but not least, by functioning as highly efficient synthesizers of intellectual capital from various disciplines. But however complex they may be, such models do not link with the genetic realm unless we embed them in a model setting that maintains an explicit relation to genetic variation.
If a dynamic model of a physiological system is capable of accounting for the phenotypic variation in a population, the causative genetic variation will manifest in the model parameters (Rajasingh et al. 2008), i.e. those model elements that are constant over the time scale of an individual instance of the particular model being studied. However, even the lowest-level model parameters are themselves phenotypes, whose genetic basis may be mono-, oligo- or polygenic, and whose physiological basis and variation can be mechanistically modelled at ever deeper levels of detail (Rajasingh et al. 2008; Vik et al. 2011). The term causally cohesive genotype–phenotype (cGP) modelling describes an approach where low-level parameters have an articulated relationship to the individual's genotype, and higher-level phenotypes emerge from the mathematical model describing the causal dynamic relationships between these lower-level processes (Rajasingh et al. 2008). Such cGP models bridge the gap between standard population genetic models that simply assign phenotypic values directly to genotypes, and mechanistic physiological models without an explicit genetic basis (Fig. 1).
Figure 1. Decomposition of the genotype-phenotype map.
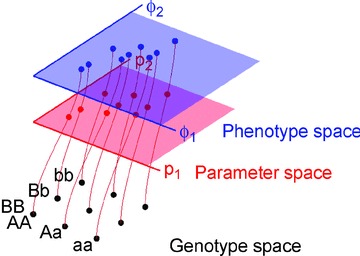
In causally cohesive genotype–phenotype (cGP) models, the mapping from genotypes to phenotypes can be decomposed into two separate mappings. Mathematical models describing the dynamics of a biological system typically contain two types of elements, state variables that change with time and parameters that remain constant over the time scale of the study. This scheme applies to any level of biological resolution. A phenotype is any observable characteristic of interest, such as the trajectory of a state variable or a summary thereof. Because the parameters in a physiological model can be conceived as aggregated summaries of finer-scale underlying models, parameters are phenotypes too. In a causally cohesive multiscale model, this leads to layers of models. The mapping from genotypes to parameters can in principle be experimentally measured. With current technology this is in most cases a daunting task, but considerable insight can be obtained even if one does not have detailed information about this mapping.
This research programme idea was stated explicitly by Jim Burns (1970) in one of the symposia led by Conrad Waddington that resulted in the three-volume work Towards a Theoretical Biology: “It is the quantitative phenotype, arising from the genotypic prescriptions and the environment, which is of critical importance for the cell's survival and which therefore features in population genetic theory. A study of this synthetic problem would thus, by providing genotype–phenotype mappings for simple synthetic systems, help to connect two major areas of biological theory: the biochemical and the population genetic.”
By linking genetics with computational physiology, the cGP programme opens up a research field whose explanatory domain in principle encompasses all phenotypic patterns associated with the genotype–phenotype relation. This includes the description of phenotypic plasticity as a function of genetic variation in mechanistic terms, i.e. how a given genotype may produce different phenotypes due to environmental change. Even though it is early days, this research programme has already provided results that go well beyond the explanatory domains of traditional statistically oriented genetics theory construction.
Over the last 30 years there have been several studies on the genetics of generic models of metabolic networks (e.g. Kacser & Burns, 1981; Keightley & Kacser, 1987; Keightley, 1989; Bagheri & Wagner, 2004; Fiévet et al. 2010). From the late 1990's, several groups reported various quantitative genetic properties of generic models of gene regulatory systems (e.g. Wagner, 1994; Gibson, 1996; Frank, 1999; Johnson & Porter, 2000; Omholt et al. 2000; Gilchrist & Nijhout, 2001; Bergman & Siegal, 2003). In the last 10 years a number of organism-specific studies have revealed novel insights; e.g. on galactose metabolism (Peccoud et al. 2004), sporulation efficiency (Gertz et al. 2010) in yeast, control of flowering time in Arabidopsis thaliana (Welch et al. 2005), signal transduction in the invertebrate phototransduction system (Pumir & Shraiman, 2011) and action potentials and calcium dynamics in mammalian myocytes (Silva et al. 2009; Vik et al. 2011; Wang et al. 2012). These studies exemplify the insights and patterns to be discovered. In the following sections we provide a few illustrations of how such studies lead to new understanding of the link between non-linear dynamics models of biological systems and classical genetic theory.
Illustrations of insights provided by cGP modelling
Link between single locus genetics and physiology
In this era of genomics one may easily get the impression that single-locus genetics is a bygone activity. But this is far from being the case as much of current experimental physiology is devoted to understanding the physiological implications of variation at a single locus. In standard genetics theory additive and dominant gene action in diploids are defined by comparing heterozygote and homozygote phenotypes. Because these concepts just compare the phenotypes of three different genotypes they cannot serve directly as mediators between genetics theory and physiology. Gjuvsland et al. (2010) introduced the concept of allele interaction for studying non-additivity in each diploid genotype based on monoallelic knockouts (so-called hemizygotes). By targeting the degree of functional dependency between the two alleles composing each genotype of a given locus, allele interaction allows a straightforward link between regulatory biology and single locus genetics. This enriches single locus genetics with a number of new features, and leads to the conclusion that in terms of biological mechanism, genetic dominance is given by a specific relationship between the allele interactions of all the three genotypes. This represents, to the best of our knowledge, the first real epistemic refinement of the genetic dominance concept since it was introduced by Gregor Mendel 150 years ago.
The study demonstrates how the allele interaction in each genotype is directly quantifiable in gene regulatory models, and that there is a unique, one-to-one correspondence between the sign of regulatory feedback loops and the sign of the allele interactions. This can be used as an intellectual torch to search for feedback loops across a whole range of physiological systems in any diploid organism where allele-specific knockouts or knockdowns are feasible.
Thus a closer look at one of the oldest concepts in genetics in a computational physiology setting appears to have disclosed a new experimental approach on how to identify intricate intra- and inter-locus feedback relationships in eukaryotes as well as providing a most needed directly operational conceptual link between genetics theory and regulatory biology.
Describing and analysing high-dimensional multiscale genotype–phenotype maps
The study by Vik et al. (2011) on an in silico heart cell summarized in Box 1 showed that the cGP framework is useful for understanding how different genetic phenomena, such as intralocus dominance, interlocus epistasis and varying degrees of phenotypic correlation, arise in physiological systems. Of particular biomedical relevance, the study showed how the cGP approach can be used to disclose penetrance features as a function of regulatory anatomy and genetic background. Thus here we have a tool to systematically study the phenotypic masking and release of genetic variation and thus understand how, without any change in the regulatory anatomy of a physiological system, traits may appear monogenic, oligogenic or polygenic depending on which genotypic variation is actually present in a population.
Box 1. A cGP model of the action potential of a heart muscle cell
Vik et al. (2011) explored, characterized and analysed the GP map for a detailed model of a mouse heart cell (Li et al. 2010).
Biological system. The heart cell model describes the flow of ions across the cell membrane and between different compartments of the cell. This flow of ions achieves the two main functions of the cell: To contract the heart muscle, and to propagate an electrical signal. The cell ‘charges its battery’ by moving many positive ions out of the cell fluid. Once it is charged, an electrical impulse will cause the cell to ‘fire’, as ion channels open to allow rapid depolarization, producing a signal that propagates to neighbouring cells. Muscle contraction, on the other hand, is triggered by the release of calcium into the cytosol. Initially, calcium is sequestered into special compartments, until depolarization triggers its release.
Multilevel phenotypes. The main cell-level phenotypes of this model are the action potential and calcium transient, i.e. the time courses of the transmembrane potential and cytosolic calcium concentration, respectively. However, many subcellular phenotypes can be observed and studied experimentally, in particular the ion currents that make up the action potential and calcium transient and are carried by specialized protein complexes called ion channels (see Box 2), of which there are many types and many instances of each type within a given cell. Ion channels help or hinder the passage of ions (particularly calcium, sodium, and potassium) across the cell membrane, opening or closing in response to conditions such as ion concentrations or transmembrane potential. Ion channels differ in their thresholds, as well as in how fast they switch between states. The structure and function of ion channels is well understood, and can be observed and experimentally manipulated (Molleman, 2002). In particular, stepwise changes in transmembrane voltage can be induced to study the voltage-dependent conformation switching behaviour and ‘memory’ of ion channels, offering a common basis for comparing the ion-channel behaviour of different cell types, models, or parameter scenarios.
Disease phenotype. Normal heart function requires both relaxation (to fill the heart chambers with blood) and contraction (to pump blood out to the body). Using the calcium transient as a proxy for contraction and relaxation, cell dynamics was categorized as ‘failed’ if the peak was below 50% of baseline (illustrating failure to contract), if the base was more than 200% of baseline (failure to relax), if amplitude was less than 50% of baseline, or if dynamics failed to converge within 10 min of simulated time.
Virtual experiments. Muscle cells require external stimuli to exhibit their characteristic dynamics, and different experiments are designed bring out different aspects of the behavioural repertoire of the system. The simulated heart cells were subjected to four different protocols: Pacing at regular intervals, to mimic the normal function of the heart; two-step voltage clamping to observe the voltage-dependent activation of ion currents; variable-gap voltage clamping to study the recovery from inactivation; and quiescence as a ‘null experiment’ (no stimulus).
Genotype to parameter map. For purposes of illustration, it was assumed that each model parameter was determined by one biallelic locus, with genotypic values of aa = 50%, Aa = 100%, and AA = 150% of the baseline parameter estimate.
Genotype generation. The effects of the hypothetical genes were estimated by an initial sensitivity analysis describing the percentage change in each scalar phenotype per percentage change in each model parameter. For a subset of the parameters, all possible combinations (i.e. a full factorial design) were generated to study higher-order parameter interactions.
The relationship between inputs (initial conditions and model parameters) and outputs (measures of model dynamics and behaviour) in computational physiological models may be high-dimensional and complex. In this study, however, sensitivity analysis showed that the effects of genetic parameter variation on higher-level phenotypes such as action potential duration and calcium transient amplitude were quite sparse. Furthermore, the study showed that sensitivity analysis together with virtual experiments can disclose biologically important parameter variation that would otherwise go undetected. This implies that cGP models may be used to suggest experimental perturbations and measurements to reveal important context-dependent genetic variation.
The study described above shows how cGP modelling can be used to gain important new insights, and in fact build theory on, for example, the relationship between penetrance and regulatory anatomy, even without being able to describe the genotype to parameter map in causal terms. In some cases, however, it is already possible to make a direct link between specific genetic variation and high-level phenotypes. An epistemically very important first step in this direction has been made by combining molecular dynamics models of individual ion channels with channel Markov models that can then be introduced into single cell models and from there into whole organ simulations (Silva et al. 2009; Box 2 and Fig. 2). This strategy links genetic variation in the coding parts of genes to variation in the properties of protein channels up to variation in whole organ phenotypes (Fig. 1). This represents a significant achievement and provides a very strong framework for linking genetic variation with whole organ function, and it points to a future where not only many more ion channels can be addressed in this way, but where also gene regulatory models will link a much wider class of genetic variation to cellular phenotypes that have impact on higher-level function. This will lead us toward a long term goal of cGP research, namely to combine high-resolution physiological models with the complex genetic variation found in human populations. The next section describes one preliminary step in that direction.
Box 2. Refining the genotype-to-parameter map: From nucleotide mutation to protein conformation to state switching in ion channels
Cardiac ion channels are prime candidates for realistic genotype-to-parameter mapping, being quite low-level parameters whose genetic variation has been well studied (Roberts & Brugada, 2003; Roepke & Abbott, 2006; Sanguinetti & Tristani-Firouzi, 2006). Silva et al. (2009) used protein folding models to predict effects of amino acid substitutions on conformation stability and transition rates in ion channels, developed Markov models as a higher-level approximation, and verified the results experimentally for some mutations (Fig. 2). For small perturbations in overall structure, and particularly for the voltage-sensing region of voltage-sensitive ion channels, this marks a major advance in the state of the art in mapping genetic variation to physiological parameters.
Whole-cell models of cellular electrophysiology usually lump together the combined activity of many instances of an ion channel. Thus, they describe how transmembrane voltage changes due to ion currents:
Rate of change in voltage = (Capacitance of cell membrane) × (Current 1 + Current 2 +…)
What drives the current is the difference in ion concentration between the inside and outside of the cell, as well as differences in electrical charge concentration. At a certain transmembrane voltage, those forces cancel and there can be no net current. Thus, a typical ion current is modelled as:
Current = (Amount of ion channel) × (Proportion of channels that are open) × (Voltage – Equilibrium voltage)
As indicated, not all ion channels are open at any given time. The ion-channel proteins flicker between open and closed states. In voltage-sensing ion channels, the opening and closing rates depend on transmembrane voltage in a way that depends on the amino acid side chains of the ion channel's voltage-sensing domain. Thus, the sequence of DNA that codes for this protein domain has a very direct effect on model parameters.
Figure 2. Bridging the genotype–phenotype gap with data and models at multiple phenotypic levels.
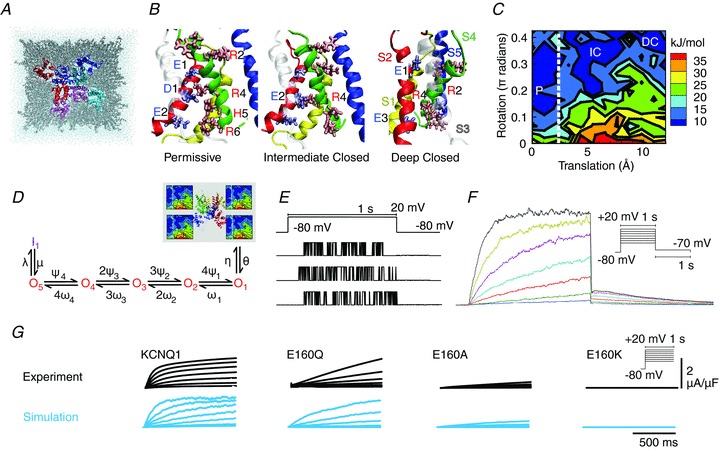
A, three-dimensional structure of KCNQ1 potassium channel, looking in from outside the cell. The channel consists of four subunits with six segments (colour-coded). Pore regions (S5–S6) of one subunit interact with the adjacent subunit voltage-sensing region (S1–S4). B, alternative metastable conformations of the subunits, only one of which permits ions to pass. C, energy landscape of conformations as characterized by translation and rotation of the S4 segment, shown here for transmembrane voltage Vm= 0 mV. Labels P, IC, DC refer to conformations in B. D, Markov model that simplifies the state space of the ion channel into discrete states. Only when all 4 subunits are in the permissive state (P) on the energy landscape, can the channel open (transition to O1) to generate current. E, recorded traces from single ion channels, showing stochastic switching between open and closed states. F, macroscopic current; the sum of 1000 single channels. Both individual traces and macroscopic current can be directly simulated from the Markov model. G, effects of mutation on macroscopic current, as observed and as simulated via protein conformation stability and the Markov model. Modified from Silva et al. (2009), with permission.
GWAS: Model parameters are containers of missing heritability
Genome-wide association studies (GWAS) of human traits have generally failed to explain more than a small proportion of the heritable variation. This so-called ‘missing heritability’ is perhaps the major challenge in current biomedical genetics (Maher, 2008; Manolio et al. 2009; Allen et al. 2010; Eichler et al. 2010; Park et al. 2010; Makowsky et al. 2011), and the realization that the genotype–phenotype map is more complex than expected necessitates the development of new methodology. The cGP framework offers a promising approach by exploiting the fact that parameters of physiological models are intermediate-level phenotypes linked by a causal mathematical structure.
Wang et al. (2012) introduced this approach by doing genome-wide association studies on virtual populations of heart cell models. Parameter values for an individual were generated by randomly sampled effects of simulated SNPs. Genotypes with realistic linkage disequilibrium between SNPs were derived from the HapMap database (Fig. 3). The GWAS was much more successful when it targeted variation in model parameters than the cell-level phenotypes directly. Furthermore, the GWAS results for the cellular phenotype groups were predominantly a consequence of the sensitivity structure of the dynamic model. SNPs associated with traits that were sensitive to few parameters had a higher penetrance than SNPs associated with traits that were sensitive to many parameters for a given model resolution. This shows how sensitivity analysis can be used to systematically reveal hotspots for genetic variation underlying a complex trait, focusing attention on the SNP variation that affects the parameters to which the trait is most sensitive, and thus identify those parameters (i.e. phenotypes) that should be priority targets of phenotypic screening programmes (see below).
Figure 3. Virtual genome-wide association analysis, looking for DNA variation to predict phenotypic variation.
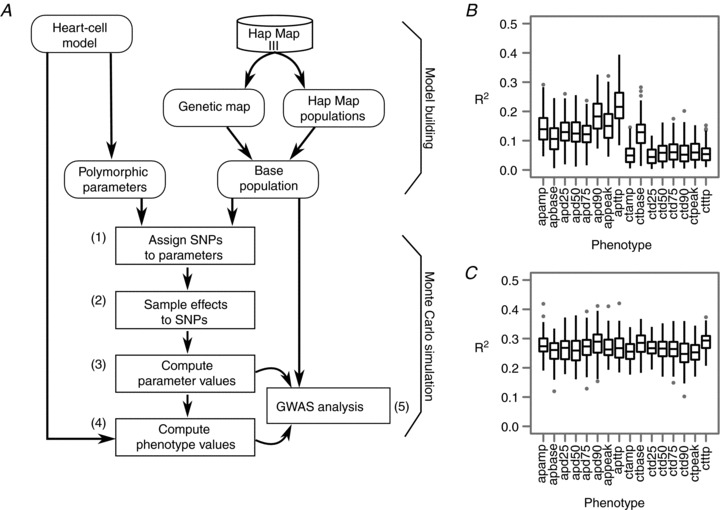
Targeting model parameters as intermediate phenotypes (C) proved more efficient than targeting top-level phenotypes alone (B). Panel A shows how a heart cell model, a genetic map and a virtual population are tied together by selecting heart model parameters assumed to be under the influence of genetic variation and associating the parameter variation to DNA variation (single nucleotide polymorphisms, SNPs) on virtual genomes. Individual genotypes are mapped into heart model parameters (steps 1–3), and by running the heart cell model parameters are mapped into cell-level phenotypes (step 4). Finally, GWAS analysis is then performed on the virtual population (step 5). (Fig. 1 of Wang et al. 2012). Panel B shows the variance in cellular phenotypes that could be explained using causal SNPs detected in GWAS targeting these phenotypes directly. Panel C shows improved results when using causal SNPs obtained from GWAS targeting all genetically controlled parameters. Each boxplot summarizes total explained variance by GWAS for 100 Monte Carlo runs. (Modified from Wang et al. 2012).
Thus, letting GWAS studies be guided by computational physiology can reveal much more of the variation underlying phenotypic variation of complex traits and at the same time disclose how this genetic variation actually influences the high-level phenotypic variation in causally cohesive terms. Even though we will most likely see improvements in statistical genetics methodology to reveal causal genetic variation in coming years, we claim that in terms of gaining biological understanding the impact of such methodology will be substantially enhanced by combining it with computational physiology.
Accounting for the influence of environment
Statistical genetics acknowledges the effects of environment on the genotype–phenotype relationship by estimating the so-called ‘genotype × environment interaction’. This measure serves several purposes well, but it does not convey underlying causal mechanisms and can thus only identify phenomena in need of explanation. In contrast, because the effects of environment can be directly built into computational physiology models, the cGP approach provides both an explanatory and a predictive framework. The environment-phenotype map for a given genotype (or ecotype or species) has been extensively studied in ecological genetics, where it is called a reaction norm (Pigliucci, 2001). This concept is important because the fitness of a parent depends on the undetermined environment of its future offspring. Hence, many organisms are phenotypically plastic, so that the same genotype can result in strikingly different behaviours, morphologies or life histories depending on both abiotic (e.g. temperature, pH, nutrient availability) and biotic factors (e.g. predation risk, competition for mates).
Plant physiology in particular has pioneered the explicit incorporation of environmental effects in cGP studies. Factors such as temperature, pH, humidity and nutrients are often highly variable, easily logged, and have obvious physiological effects that are already well understood and modelled. Good illustrations are models of crop yield whose parameters are linked to genomic variation and where temperature and vapour pressure are environmental inputs (Hammer et al. 2006) and a model describing how the photoperiod works through gene regulatory networks to determine flowering time in pea (Wenden et al. 2009). A conceptually similar, but arguably more difficult challenge is to account for lifestyle and environmental factors in models seeking to describe the etiology of complex disease.
The biomedical utility of cGP modelling
There is in principle no limit to the complexity of biological models that can be used in a cGP context. In the not too distant future, the cGP programme in a multiscale and multiphysics context will probably give us an extensive understanding of how different types of genetic variation propagate and manifest in different environmental and physiological settings and genetic backgrounds. Investigation of the GP map associated with high-level phenotypes manifest at the level of the whole organism requires computational models integrating molecular-, cellular-, tissue-, and organ-level processes to high-level function. Developing such models is the goal of the IUPS Physiome Project (Hunter & Borg, 2003) and a number of related efforts organized under the Physiome banner. The Virtual Physiological Rat (VPR) Project represents one international effort recently organized along these lines, using the laboratory rat as a model physiome (Beard et al. 2012).
If we are to probe deep into the etiology of complex disease and develop efficient therapies, where the genetic dimension is included, we will most likely be forced to deal with quite complex multiscale models in most cases. However, one should not underestimate the importance of simple models. Such models have proved very useful when the goal is to unravel unifying principles underlying specific biological phenomena (Alon, 2006), and can also have direct clinical relevance, e.g. cancer chronotherapy (Altinok et al. 2007). But in general, we think the predominant role of such models in a biomedical GP map context is to contribute to the epistemic foundation for integrative models of wider clinical utility.
Considering what computational physiology has already achieved with relatively moderate resources, we are confident that cGP models of practical utility for personalized medicine are within reach. However, how long this will take, and how far-reaching and transformative cGP models will become, depends very much on the broader biomedical community and its ability to start collaborating on defining, financing and pursuing the wide array of concerted theoretical-experimental R&D programmes that are needed to bring the necessary knowledge, methodology and technology to the table.
Ontogeny: the ultimate cGP modelling challenge
Hopefully, the emergence of multiscale and multiphysics modelling will also put us in position to start to make real headway in what may be considered to be the ultimate cGP modelling challenge, namely the description of the ontogeny (and associated themes) of organisms where the genetic and environmental dimensions are fully incorporated (Alberch, 1991; Pigliucci, 2010).
A particularly illustrative step in this direction is a dynamic model of tooth shape in ringed seals (Salazar-Ciudad & Jernvall, 2010; Fig. 4), where dentitions show a high degree of variation. Despite the complexity of dental variation in ringed seals, the model is able to mimic the range of variation by simple changes to the parameters describing the functioning of the signalling network and cell and tissue biomechanical properties known to underlie the morphological development of teeth. Changes in single parameters regulating signalling during cusp development were shown to explain shape variation among individuals, whereas a parameter regulating epithelial growth was shown to explain serial, tooth-to-tooth variation along the jaw. As variations of these parameters are partly under genetic control, this insight accords very well with the general scheme depicted in Fig. 1. What the genotype-to-parameter map looks like in this case we do not know, and even though the physics involved in tooth development was modelled in a quite rudimentary way, the results show that the cGP programme can successfully target developmental phenomena long before all the biological details are in place.
Figure 4. Linking genotype to phenotype through gene networks and tissue mechanics.
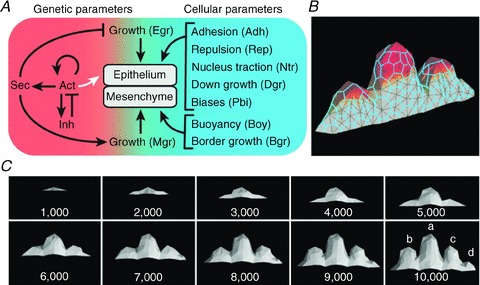
A, cell behaviour is characterized by a combination of parameters for gene network properties and cellular properties. B, tissue morphology emerges from a model where the mesenchyme is a three-dimensional space in which molecules and mechanical stresses diffuse (mesh connects cell centres; colour indicates the diffusing inhibitor). C, the developing tooth shape at regular time intervals, starting from seven cells representing the tip of the oral epithelium invagination, where A–D in the last panel identify seal tooth cusps. From Salazar-Ciudad & Jernvall (2010) with permission.
Considering the ongoing efforts to model developmental processes in several model organisms based on comprehensive phenotyping and experimentation (Tomlin & Axelrod, 2007; Band et al. 2012) and the fact that the bioengineering community is now increasing its efforts to develop sophisticated conceptual and methodological machinery for describing biological growth (Humphrey & Rajagopal, 2002; Lubarda & Hoger, 2002; Taber, 2006; Lage et al. 2010; Jones & Chapman, 2012), we are quite confident that causally cohesive explanatory bridges for developmental systems will be successfully constructed in ever more detail in the years to come. However, these efforts, and several others, would benefit substantially from a tighter connection between cGP modelling and bioinformatics.
Linking bioinformatics with cGP modelling
The analysis of -omics data routinely produces vast networks of associations, e.g. between genetic variability, protein expression, and disease-related phenotypes (Joyce & Palsson, 2006). Analyses of network structure have yielded many valuable biological insights. Cause and effect can to some extent be identified by Bayesian network analysis, though this framework struggles to incorporate time and feedback, the main characteristics of dynamical systems (Sieberts & Schadt, 2007). Several other modelling frameworks have been applied to infer features of the underlying dynamic processes (Machado et al. 2011), e.g. Boolean networks and simple Petri nets. However, utilizing -omics data in models of physiological mechanism, such as differential equations or continuum mechanics, poses fundamental challenges in parameter identifiability (Tarantola, 2004, 2006; Aster et al. 2012) as well as computation. We suspect that the realization will emerge that current physiological models are often much more complex than existing phenomics data can support. Being able to iterate between different levels of model complexity, recognizing pattern and focusing in on mechanism, will be essential in making use of the best data we are likely to get (Tenazinha & Vinga, 2011).
We believe many important next steps can be made using existing data and models. The immediate obstacle is that model components are not properly annotated. It is currently an overwhelming task to browse through genomics databases for polymorphisms related to a given model parameter, to extract candidate models for a given cell type in a repository, or to confront models with commensurable experimental data. However, this situation is about to change, as the standardization of ontologies is giving precise technical meaning to data and model resources (De Bono et al. 2011). Many -omics databases are already ontologically annotated, whereas the annotation of model repositories is in its infancy. Making model and data resources speak the same language enables large-scale machine processing of biologically meaningful queries. For bioinformatics, this is a major step forward and it will transform computational physiology by facilitating faster and more relevant confrontation with data.
The need for dramatically improved phenomics
Phenotype space is a vast place, and the development of phenomics will always demand prioritizing what to measure (Houle et al. 2010). We claim that this prioritization will benefit tremendously from being guided by computational models of how phenotypes are created and maintained in causal terms and not by simple conceptual models. At the same time, for this modelling work to really become transformative, it is mission critical that it becomes nourished and confronted by massive amounts of data that only a mature phenomics technology can provide.
Full understanding of how genetic variation causes phenotypic variation of a complex trait requires a mathematical representation that extends from cells to tissues, organs and the whole-organism level. Such representations will have to encompass a hierarchy of descriptions at different length and time scales spanning 9 and 15 orders of magnitude, respectively (Hunter & Borg, 2003). A much improved phenomics may quantitatively and qualitatively enrich the intimate relationship that exists between experimental measurement and multiscale model construction and validation. For example, a model ensemble of the mammalian heart is now emerging, incorporating electrical activation, mechanical contraction, fluid mechanics, energy supply and utilisation, cell-signalling and many other biochemical processes capable of linking gene sequences and protein pathways to the integrative function of cardiac cells, tissues and the intact organ (Fink et al. 2011). Much of the experimental data needed requires time-consuming, expensive efforts by highly trained personnel. For example, standard phenotyping of a mouse heart to obtain a minimal set of data for model parameterization, may involve in vivo MRI measurements of volume, surface area and velocity, magnitude and direction of the myocardium left ventricular volume (Pautler, 2004) but also several other high-resolution features (Sosnovik et al. 2007): mounting of the heart in a Langendorff rig to obtain left ventricle pressure–volume data (How et al. 2005); the mounting of dissected right ventricle trabeculae in another rig to measure force and heat generation, to do calcium imaging, and perform patch clamping (Han et al. 2009); and finally fixation and slicing of the heart to obtain fibre orientation and other structural data by confocal imaging (Young et al. 1998). This laborious ‘business-as-usual’ phenotyping provides a very modest amount of information compared to the high-dimensional spatiotemporal phenotypic data from several individuals that is really needed for making fast progress.
It is an embarrassing fact that age is still the best predictor for many complex diseases. A major reason for this is that biological ageing (senescence) leads to frailty, a syndrome of decreased reserve and resistance to stressors causing vulnerability to adverse outcomes (Fried et al. 2001). This implies that we sorely need to understand frailty in quantitative terms if we are really going to get a grip on the etiology and treatment of complex diseases. That is, we need to make the physiology of the ageing individual a mathematical object. The data requirements for this endeavour may be much more complex than for understanding the physiology of the young, because ageing is a stochastic process and manifests in many different ways and anatomical locations (Wilkinson, 2009). New phenomics technology will be essential for the making of multiscale physiological models of the effects of ageing.
Engineers can take much of the credit for the very fast improvements in genome sequencing technology we are now witnessing. Considering the diversity of technologies required, the development of a mature phenomics technology will need to involve far wider sectors of the engineering community than we have seen up to now for genomics. To the gain sufficient momentum in this direction it would have been most helpful with an internationally funded Human Phenome Programme solidly grounded on biophysically sound mathematical descriptions of human physiology.
Concluding remarks
So what does it take to the bridge the genotype–phenotype gap? Our message is in principle quite simple. The functional genomics community should stop applying misconceived anthropomorphic metaphors for how DNA works in biological systems, and instead start to acknowledge that it is completely dependent on adapting the vocabulary of physiology to understand gene function. The physiological research community, on the other hand, should to a greater extent embrace the fact that the disciplinary goals of physiology demand an understanding of the mechanisms underlying the genotype–phenotype map. Biology is par excellence the realm where we observe the most varied and complex manifestation of non-linear system dynamics on the planet. To hope for a deep causal understanding of the genotype–phenotype relation without making use of the vocabularies designed for describing and analysing such dynamics is wishful thinking. A thorough mathematically phrased and biophysically based understanding of what causes the variation of phenomes as a function of genetic and environmental variation will not only transform drug design, personalized medicine, production biology and biotechnology, but also foster very sophisticated engineering in several technology areas. We think this level of understanding is within reach, even though it awaits several technological, conceptual and methodological breakthroughs.
Acknowledgments
This work has been supported in part by The Research Council of Norway, project number 178901/V30, Bridging the gap: disclosure, understanding and exploitation of the genotype–phenotype map, and by the Virtual Physiological Rat Project funded through NIH grant P50-GM094503.
References
- Alberch P. From genes to phenotype: dynamical systems and evolvability. Genetica. 1991;84:5–11. doi: 10.1007/BF00123979. [DOI] [PubMed] [Google Scholar]
- Allen HL, et al. Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature. 2010;467:832–838. doi: 10.1038/nature09410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alon U. An Introduction to Systems Biology: Design Principles of Biological Circuits. Boca Raton, FL, USA: Chapman and Hall/CRC; 2006. [Google Scholar]
- Altinok A, Lévi F, Goldbeter A. A cell cycle automaton model for probing circadian patterns of anticancer drug delivery. Adv Drug Deliv Rev. 2007;59:1036–1053. doi: 10.1016/j.addr.2006.09.022. [DOI] [PubMed] [Google Scholar]
- Aster RC, Borchers B, Thurber CH. Parameter Estimation and Inverse Problems, Second Edition. 2nd edn. New York: Academic Press; 2012. [Google Scholar]
- Bagheri HC, Wagner GP. Evolution of dominance in metabolic pathways. Genetics. 2004;168:1713–1735. doi: 10.1534/genetics.104.028696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Band LR, Fozard JA, Godin C, Jensen OE, Pridmore T, Bennett MJ, King JR. Multiscale systems analysis of root growth and development: modeling beyond the network and cellular scales. Plant Cell. 2012 doi: 10.1105/tpc.112.101550. DOI: 10.1105/tpc.112.101550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bateson W. The progress of genetic research: an inaugural address to the Third Conference on Hybridisation and Plant-Breeding. In: Punett RS, editor. Scientific Papers of William Bateson (1928) Cambridge, UK: Cambridge University Press; 1906. pp. 142–151. [Google Scholar]
- Beard DA, Neal ML, Tabesh-Saleki N, Thompson CT, Bassingtwaighte JB, Shimoyama M, Carlson BE. Multiscale modeling and data integration in the virtual physiological rat project. Ann Biomed Eng. 2012;40:2365–2378. doi: 10.1007/s10439-012-0611-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergman A, Siegal ML. Evolutionary capacitance as a general feature of complex gene networks. Nature. 2003;424:549–552. doi: 10.1038/nature01765. [DOI] [PubMed] [Google Scholar]
- Burns J. The synthetic problem and the genotype-phenotype relation in cellular metabolism. In: Waddington CH, editor. Towards a theoretical biology. 3. Drafts. An I.U.B.S. symposium. Chicago, USA: Aldine Publishing Company; 1970. pp. 47–51. [Google Scholar]
- De Bono B, Hoehndorf R, Wimalaratne S, Gkoutos G, Grenon P. The RICORDO approach to semantic interoperability for biomedical data and models: strategy, standards and solutions. BMC Res Notes. 2011;4:313. doi: 10.1186/1756-0500-4-313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichler EE, Flint J, Gibson G, Kong A, Leal SM, Moore JH, Nadeau JH. Missing heritability and strategies for finding the underlying causes of complex disease. Nat Rev Genet. 2010;11:446–450. doi: 10.1038/nrg2809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiévet JB, Dillmann C, Vienne D. Systemic properties of metabolic networks lead to an epistasis-based model for heterosis. Theor Appl Genet. 2010;120:463–473. doi: 10.1007/s00122-009-1203-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fink M, Niederer SA, Cherry EM, Fenton FH, Koivumäki JT, Seemann G, Thul R, Zhang H, Sachse FB, Beard D, Crampin EJ, Smith NP. Cardiac cell modelling: Observations from the heart of the cardiac physiome project. Prog Biophys Mol Biol. 2011;104:2–21. doi: 10.1016/j.pbiomolbio.2010.03.002. [DOI] [PubMed] [Google Scholar]
- Frank S. Population and quantitative genetics of regulatory networks. J Theor Biol. 1999;197:281–294. doi: 10.1006/jtbi.1998.0872. [DOI] [PubMed] [Google Scholar]
- Fried LP, Tangen CM, Walston J, Newman AB, Hirsch C, Gottdiener J, Seeman T, Tracy R, Kop WJ, Burke G, McBurnie MA. Frailty in older adults: evidence for a phenotype. J Gerontol A Biol Sci Med Sci. 2001;56:M146–M157. doi: 10.1093/gerona/56.3.m146. [DOI] [PubMed] [Google Scholar]
- Gertz J, Gerke JP, Cohen BA. Epistasis in a quantitative trait captured by a molecular model of transcription factor interactions. Theor Popul Biol. 2010;77:1–5. doi: 10.1016/j.tpb.2009.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson G. Epistasis and pleiotropy as natural properties of transcriptional regulation. Theor Popul Biol. 1996;49:58–89. doi: 10.1006/tpbi.1996.0003. [DOI] [PubMed] [Google Scholar]
- Gilchrist MA, Nijhout HF. Nonlinear developmental processes as sources of dominance. Genetics. 2001;159:423–432. doi: 10.1093/genetics/159.1.423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gjuvsland AB, Plahte E, Ådnøy T, Omholt SW. Allele interaction – single locus genetics meets regulatory biology. PLoS ONE. 2010;5:e9379. doi: 10.1371/journal.pone.0009379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldschmidt RB. Physiological Genetics. New York: McGraw-Hill; 1938. [Google Scholar]
- Gove PB(ed), editor. Webster's Third New International Dictionary of the English Language, Unabridged. Springfield, MA, USA: Merriam; 1981. [Google Scholar]
- Hammer G, Cooper M, Tardieu F, Welch S, Walsh B, Van Eeuwijk F, Chapman S, Podlich D. Models for navigating biological complexity in breeding improved crop plants. Trends Plant Sci. 2006;11:587–593. doi: 10.1016/j.tplants.2006.10.006. [DOI] [PubMed] [Google Scholar]
- Han J-C, Taberner AJ, Kirton RS, Nielsen PM, Smith NP, Loiselle DS. A unique micromechanocalorimeter for simultaneous measurement of heat rate and force production of cardiac trabeculae carneae. J Appl Physiol. 2009;107:946–951. doi: 10.1152/japplphysiol.00549.2009. [DOI] [PubMed] [Google Scholar]
- Houle D, Govindaraju DR, Omholt S. Phenomics: the next challenge. Nat Rev Genet. 2010;11:855–866. doi: 10.1038/nrg2897. [DOI] [PubMed] [Google Scholar]
- How O-J, Aasum E, Kunnathu S, Severson DL, Myhre ESP, Larsen TS. Influence of substrate supply on cardiac efficiency, as measured by pressure-volume analysis in ex vivo mouse hearts. Am J Physiol Heart Circ Physiol. 2005;288:H2979–2985. doi: 10.1152/ajpheart.00084.2005. [DOI] [PubMed] [Google Scholar]
- Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Math Models Methods Appl Sci. 2002;12:407–430. [Google Scholar]
- Hunter PJ, Borg TK. Integration from proteins to organs: The Physiome Project. Nat Rev Mol Cell Biol. 2003;4:237–243. doi: 10.1038/nrm1054. [DOI] [PubMed] [Google Scholar]
- Johnson N, Porter A. Rapid speciation via parallel, directional selection on regulatory genetic pathways. J Theor Biol. 2000;205:527–542. doi: 10.1006/jtbi.2000.2070. [DOI] [PubMed] [Google Scholar]
- Jones GW, Chapman SJ. Modeling Growth in Biological Materials. SIAM Rev Soc Ind Appl Math. 2012;54:52–118. [Google Scholar]
- Joyce AR, Palsson BØ. The model organism as a system: integrating “omics” data sets. Nat Rev Mol Cell Biol. 2006;7:198–210. doi: 10.1038/nrm1857. [DOI] [PubMed] [Google Scholar]
- Kacser H, Burns JA. The molecular basis of dominance. Genetics. 1981;97:639–666. doi: 10.1093/genetics/97.3-4.639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD. Models of quantitative variation of flux in metabolic pathways. Genetics. 1989;121:869–876. doi: 10.1093/genetics/121.4.869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD, Kacser H. Dominance, pleiotropy and metabolic structure. Genetics. 1987;117:319–329. doi: 10.1093/genetics/117.2.319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lage K, et al. Dissecting spatio-temporal protein networks driving human heart development and related disorders. Mol Syst Biol. 2010;6:381. doi: 10.1038/msb.2010.36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L, Niederer SA, Idigo W, Zhang YH, Swietach P, Casadei B, Smith NP. A mathematical model of the murine ventricular myocyte: a data-driven biophysically based approach applied to mice overexpressing the canine NCX isoform. Am J Physiol Heart Circ Physiol. 2010;299:H1045–1063. doi: 10.1152/ajpheart.00219.2010. [DOI] [PubMed] [Google Scholar]
- Lubarda VA, Hoger A. On the mechanics of solids with a growing mass. Int J Solids Struct. 2002;39:4627–4664. [Google Scholar]
- Machado D, Costa RS, Rocha M, Ferreira EC, Tidor B, Rocha I. Modeling formalisms in Systems Biology. AMB Expr. 2011;1:1–14. doi: 10.1186/2191-0855-1-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maher B. Personal genomes: the case of the missing heritability. Nature. 2008;456:18–21. doi: 10.1038/456018a. [DOI] [PubMed] [Google Scholar]
- Makowsky R, Pajewski NM, Klimentidis YC, Vazquez AI, Duarte CW, Allison DB, De los Campos G. Beyond missing heritability: prediction of complex traits. PLoS Genet. 2011;7:e1002051. doi: 10.1371/journal.pgen.1002051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA, et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molleman A. Patch Clamping: An Introductory Guide to Patch Clamp Electrophysiology. New York: Wiley; 2002. [Google Scholar]
- Noble D. A theory of biological relativity: no privileged level of causation. Interface Focus. 2012;2:55–64. doi: 10.1098/rsfs.2011.0067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omholt SW, Plahte E, Oyehaug L, Xiang K. Gene regulatory networks generating the phenomena of additivity, dominance and epistasis. Genetics. 2000;155:969–980. doi: 10.1093/genetics/155.2.969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Omholt SW. From sequence to consequence and back. Prog Biophys Mol Biol. 2012 doi: 10.1016/j.pbiomolbio.2012.09.003. DOI: 10.1016/j.pbiomolbio.2012.09.003. [DOI] [PubMed] [Google Scholar]
- Park J-H, Wacholder S, Gail MH, Peters U, Jacobs KB, Chanock SJ, Chatterjee N. Estimation of effect size distribution from genome-wide association studies and implications for future discoveries. Nat Genet. 2010;42:570–575. doi: 10.1038/ng.610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pautler RG. Mouse MRI: concepts and applications in physiology. Physiology. 2004;19:168–175. doi: 10.1152/physiol.00016.2004. [DOI] [PubMed] [Google Scholar]
- Peccoud J, Velden KV, Podlich D, Winkler C, Arthur L, Cooper M. The selective values of alleles in a molecular network model are context dependent. Genetics. 2004;166:1715–1725. doi: 10.1534/genetics.166.4.1715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pigliucci M. Phenotypic Plasticity: Beyond Nature and Nurture. Baltimore, MD, USA: The Johns Hopkins University Press; 2001. [Google Scholar]
- Pigliucci M. Genotype–phenotype mapping and the end of the “genes as blueprint” metaphor. Phil Trans R Soc B. 2010;365:557–566. doi: 10.1098/rstb.2009.0241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pumir A, Shraiman B. Epistasis in a Model of Molecular Signal Transduction. PLoS Comput Biol. 2011;7:e1001134. doi: 10.1371/journal.pcbi.1001134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajasingh H, Gjuvsland AB, Våge DI, Omholt SW. When parameters in dynamic models become phenotypes: a case study on flesh pigmentation in the chinook salmon (Oncorhynchus tshawytscha) Genetics. 2008;179:1113–1118. doi: 10.1534/genetics.108.087064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts R, Brugada R. Genetics and Arrhythmias. Annu Rev Med. 2003;54:257–267. doi: 10.1146/annurev.med.54.073002.182112. [DOI] [PubMed] [Google Scholar]
- Roepke TK, Abbott GW. Pharmacogenetics and cardiac ion channels. Vascul Pharmacol. 2006;44:90–106. doi: 10.1016/j.vph.2005.07.013. [DOI] [PubMed] [Google Scholar]
- Salazar-Ciudad I, Jernvall J. A computational model of teeth and the developmental origins of morphological variation. Nature. 2010;464:583–586. doi: 10.1038/nature08838. [DOI] [PubMed] [Google Scholar]
- Sanguinetti MC, Tristani-Firouzi M. hERG potassium channels and cardiac arrhythmia. Nature. 2006;440:463–469. doi: 10.1038/nature04710. [DOI] [PubMed] [Google Scholar]
- Sieberts SK, Schadt EE. Moving toward a system genetics view of disease. Mamm Genome. 2007;18:389–401. doi: 10.1007/s00335-007-9040-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva JR, Pan H, Wu D, Nekouzadeh A, Decker KF, Cui J, Baker NA, Sept D, Rudy Y. A multiscale model linking ion-channel molecular dynamics and electrostatics to the cardiac action potential. Proc Natl Acad Sci U S A. 2009;106:11102–11106. doi: 10.1073/pnas.0904505106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sosnovik DE, Nahrendorf M, Weissleder R. Molecular Magnetic Resonance Imaging in Cardiovascular Medicine. Circulation. 2007;115:2076–2086. doi: 10.1161/CIRCULATIONAHA.106.658930. [DOI] [PubMed] [Google Scholar]
- Soulé M. Phenetics of natural populations I. Phenetic relationships of insular populations of the side-blotched lizard. Evolution. 1967;21:584–591. doi: 10.1111/j.1558-5646.1967.tb03413.x. [DOI] [PubMed] [Google Scholar]
- Taber LA. Biophysical mechanisms of cardiac looping. Int J Dev Biol. 2006;50:323–332. doi: 10.1387/ijdb.052045lt. [DOI] [PubMed] [Google Scholar]
- Tarantola A. Inverse Problem Theory and Methods for Model Parameter Estimation. Philadelphia, PA, USA: SIAM: Society for Industrial and Applied Mathematics; 2004. [Google Scholar]
- Tarantola A. Popper, Bayes and the inverse problem. Nat Phys. 2006;2:492–494. [Google Scholar]
- Tenazinha N, Vinga S. A survey on methods for modeling and analyzing integrated biological networks. IEEE/ACM Trans Comput Biol Bioinform. 2011;8:943–958. doi: 10.1109/TCBB.2010.117. [DOI] [PubMed] [Google Scholar]
- Tomlin CJ, Axelrod JD. Biology by numbers: mathematical modelling in developmental biology. Nat Rev Genet. 2007;8:331–340. doi: 10.1038/nrg2098. [DOI] [PubMed] [Google Scholar]
- Vik JO, Gjuvsland AB, Li L, Tøndel K, Niederer SA, Smith NP, Hunter PJ, Omholt SW. Genotype–phenotype map characteristics of an in silico heart cell. Front Physioly. 2011;2:106. doi: 10.3389/fphys.2011.00106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner A. Evolution of gene networks by gene duplications: a mathematical model and its implications on genome organization. Proc Natl Acad Sci U S A. 1994;91:4387–4391. doi: 10.1073/pnas.91.10.4387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Gjuvsland AB, Vik JO, Smith NP, Hunter PJ, Omholt SW. Parameters in dynamic models of complex traits are containers of missing heritability. PLoS Comput Biol. 2012;8:e1002459. doi: 10.1371/journal.pcbi.1002459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch SM, Dong Z, Roe JL, Das S. Flowering time control: gene network modelling and the link to quantitative genetics. Austr J Agric Res. 2005;56:919–936. [Google Scholar]
- Wenden B, Dun EA, Hanan J, Andrieu B, Weller JL, Beveridge CA, Rameau C. Computational analysis of flowering in pea (Pisum sativum) New Phytol. 2009;184:153–167. doi: 10.1111/j.1469-8137.2009.02952.x. [DOI] [PubMed] [Google Scholar]
- Wilkinson DJ. Stochastic modelling for quantitative description of heterogeneous biological systems. Nat Rev Genet. 2009;10:122–133. doi: 10.1038/nrg2509. [DOI] [PubMed] [Google Scholar]
- Young AA, Legrice IJ, Young M, Smaill BH. Extended confocal microscopy of myocardial laminae and collagen network. J Microsc. 1998;192:139–150. doi: 10.1046/j.1365-2818.1998.00414.x. [DOI] [PubMed] [Google Scholar]


