Abstract
Background Mammographic breast density is a strong breast cancer risk factor but is not used in the clinical setting, partly because of a lack of standardization and automation. We developed an automated and objective measurement of the grayscale value variation within a mammogram, evaluated its association with breast cancer, and compared its performance with that of percent density (PD).
Methods Three clinic-based studies were included: a case–cohort study of 217 breast cancer case subjects and 2094 non-case subjects and two case–control studies comprising 928 case subjects and 1039 control subjects and 246 case subjects and 516 control subjects, respectively. Percent density was estimated from digitized mammograms using the computer-assisted Cumulus thresholding program, and variation was estimated from an automated algorithm. We estimated hazards ratios (HRs), odds ratios (ORs), the area under the receiver operating characteristic curve (AUC), and 95% confidence intervals (CIs) using Cox proportional hazards models for the cohort and logistic regression for case–control studies, with adjustment for age and body mass index. We performed a meta-analysis using random study effects to obtain pooled estimates of the associations between the two mammographic measures and breast cancer. All statistical tests were two-sided.
Results The variation measure was statistically significantly associated with the risk of breast cancer in all three studies (highest vs lowest quartile: HR = 7.0 [95% CI = 4.6 to 10.4]; OR = 10.7 [95% CI = 7.5 to 15.3]; OR = 2.6 [95% CI = 1.6 to 4.2]; all P trend < .001). In two studies, the risk estimates and AUCs for the variation measure were greater than those for percent density (AUCs for variation = 0.71 and 0.76; AUCs for percent density = 0.65 and 0.65), whereas in the third study, these estimates were similar (AUC for variation = 0.60 and AUC for percent density = 0.61). A meta-analysis of the three studies demonstrated a stronger association between variation and breast cancer (highest vs lowest quartile: RR = 3.6, 95% CI = 1.9 to 7.0) than between percent density and breast cancer (highest vs lowest quartile: RR = 2.3, 95% CI = 1.9 to 2.9).
Conclusion The association between the automated variation measure and the risk of breast cancer is at least as strong as that for percent density. Efforts to further evaluate and translate the variation measure to the clinical setting are warranted.
Mammographic breast density—the proportion of fibroglandular tissue pictured on the mammogram—is an established risk factor for breast cancer (1,2). Women who have high mammographic breast density have approximately 3–4 times the risk of breast cancer compared with women who have low mammographic breast density (1,3). The consistent association seen in epidemiological studies and the magnitude of risk associated with high breast density support the use of mammographic breast density in the clinical management of women at risk of breast cancer. Such translation of mammographic density to the clinic is most likely to occur in the breast cancer screening environment. For example, baseline and serial breast cancer risk estimates that incorporate mammographic density measures could be used to inform the frequency and type of screening or specific interventions. However, mammographic density is not currently used in clinical practice for these purposes, partly because of the lack of measurement standardization and automation from mammographic images (4,5).
The successful incorporation of mammographic density into the clinical setting relies on an algorithm to accurately and reliably quantify density independent of a reader and in a manner that does not disrupt clinic flow or patient management. The ideal density measure would apply across mammography screening centers and imaging platforms, preferably in an automated and standardized manner. Operator-assisted (ie, nonautomated) percent density measures have shown associations with the risk of breast cancer (1). However, automated measures of mammographic density developed to date are not widely used or known to be validated (5). These measures include methods that compensate for (ie, calibrate) interpatient differences in the image acquisition technique (6–9) that have produced mixed findings regarding their associations with breast cancer. In many studies, calibrated density measures have not proven to be stronger, or even equivalent, risk factors for breast cancer compared with percent density (10,11).
We recently developed an automated method to estimate mammographic density using full-field digital mammography; the method assesses the variation in the grayscale values underlying the image in a calibrated mammogram (12–17). This variation measure is the standard deviation of the calibrated pixel values (12). In a study of 160 case subjects and matched control subjects, the associations between the variation measure and the risk of breast cancer were similar to those between percent density and the risk of breast cancer (18). The goals of this study were to examine associations between the variation measure and the risk of breast cancer in three independent epidemiological studies and to compare the magnitude of the associations with breast cancer for the variation measure and the well-established percent density measure.
Methods
Data from three studies conducted at the Mayo Clinic (Rochester, MN) were used in this analysis. All three studies were approved by the Mayo Clinic Institutional Review Board.
The Mayo Mammography Health Study (MMHS)
The MMHS is an ongoing cohort study of women living in Minnesota, Wisconsin, or Iowa who are older than 35 years, had screening mammography at the Mayo Clinic between 2003 and 2006, and have no personal history of breast cancer. Participants completed a questionnaire and provided written informed consent to use their mammograms, medical records, and blood samples and to link their data to state cancer registries. The 19924 subjects who participated (51% of the 38883 subjects who were eligible) were followed up for incident cancer events through the tri-state cancer and Mayo Clinic tumor registries. Through December 31, 2008, a total of 290 incident and histologically confirmed primary breast cancers were identified; we excluded 59 women who were diagnosed breast cancers within 60 days of the enrollment mammogram and 14 women with a digital mammogram, leaving 217 case subjects eligible for analyses. We used a case–cohort design to efficiently target our mammogram collection efforts to a random sample (or subcohort) of 2300 women from the entire MMHS cohort (control subjects) and all women with incident breast cancer. A total of 217 case subjects (155 of whom were diagnosed with invasive breast cancer) and 2094 subcohort members were available for these analyses.
The Mayo Clinic Breast Cancer Study (MCBCS)
The MCBCS is an ongoing clinic-based breast cancer case–control study initiated in February 2001 at the Mayo Clinic as described previously (19,20). Case subjects were recruited within 6 months of their date of breast cancer diagnosis from a six-state region in the Midwestern United States (Minnesota, Iowa, Wisconsin, North Dakota, South Dakota, and Illinois). Women with no history of cancer other than nonmelanoma skin cancer (control subjects) were recruited from the internal medicine practices at Mayo Clinic and frequency matched to case subjects on age (5-year age category), race, and state of residence. Case and control subjects provided written informed consent. Analyses are based on 1870 case subjects and 1628 control subjects enrolled in MCBCS through October 1, 2008; participation rates were 69% and 71% among case and control subjects, respectively. Mammograms were available and digitized for 940 (50%) case subjects (748 with invasive breast cancer) and 1087 (65%) control subjects.
The Mayo Clinic Mammography (MCMAM) Study
The MCMAM study is a matched breast cancer case–control study nested within the Mayo Clinic mammography screening practice in Rochester, Minnesota, as described previously (21). Written informed consent was not provided for this study; however, all subjects had provided written permission for their Mayo Clinic medical records to be used for research purposes as provided for in the Minnesota Statutes (Minnesota State Privacy Law, Statute 144.335, 1997). Case subjects (n = 373) and control subjects (n = 713) had a screening mammogram between 1997 and 2001, were aged 50 years or older, lived within a 120-mile radius of Rochester, and were required to have had at least two screening mammograms before their breast cancer diagnosis (case subjects) or screening examination (control subjects). Thus, the case and control subjects represented a regularly screened population. Control subjects (ie, women without breast cancer) were matched to each case subject on age (within 5 years), date of screening examination (within 4 months), menopausal status, interval between first and last mammograms (within 8 months), number of previous screening mammograms (within one mammogram), and county of residence. Mammograms were available for 246 case subjects (193 with invasive breast cancer) and 522 control subjects for this study.
Mammogram Retrieval, Digitization, and Percent Density Estimation
We used the earliest available mammogram before diagnosis for case subjects (or before enrollment or screening date for control subjects) for the primary analyses. The mean time between that mammogram and the dates of diagnosis (or screening or enrollment) were 4.7 years for the MMHS and 3.7 years for the MCMAM study. This interval was considerably shorter (mean time = 22 days) in the MCBCS because the majority of the case subjects only had mammograms available at the time of diagnosis. The craniocaudal mammogram view for the contralateral breast was digitized and analyzed for case subjects across all studies. For control subjects, we digitized and analyzed the left craniocaudal view (MCBCS and MMHS) or the craniocaudal view for the same side as the case subject (MCMAM).
For secondary analyses that evaluated the influence of acquisition parameters on the associations between percent density and the variation measures and the risk of breast cancer, we used the enrollment mammograms in the MMHS case–cohort study, because the earlier mammograms used for the primary analyses did not have information about the acquisition technique printed on the image. All mammograms from the MMHS and the majority of those from the MCBCS (80%) were digitized on an Array 2905 laser digitizer (Array Corporation, Hampton, NH) that had 50-μm (limiting) pixel spacing with a 12-bit grayscale depth. All mammograms from the MCMAM study and the remaining 20% of those from the MCBCS were digitized on a Kodak Lumiscan 85 scanner (Eastman Kodak Co, Rochester, NY) that had 50-μm (limiting) resolution with 12-bit grayscale depth.
Percent Mammographic Density Measure
Percent density (calculated as the dense area divided by the total area, multiplied by 100%) was estimated from the craniocaudal mammogram view in all three studies by one expert reader (F. F. Wu) using the Cumulus program ( 21,22). Briefly, two thresholds are set: the first separates the breast tissue from the background and the second separates dense from nondense tissue. Operator reliability across all three studies was high: The intraclass correlation was greater than 0.93 for more than 1500 duplicate images read across the different study time frames.
The Variation Measure
The automated algorithm for estimating the variation measure includes three steps. First, the breast area on the craniocaudal mammogram view is automatically segmented from the background using a method we developed previously (J. J. Heine, E. E. Fowler [H. Lee Moffitt Cancer Center & Research Institute], C. M Vachon, unpublished observation) to remove image artifacts and detect the breast area. This method detects the breast orientation in craniocaudal view images and removes extraneous information from the off-breast portion of the image, resulting in a half-hemispherical shaped binary mask. Before estimating the variation measure, we visually inspected all segmented images from the three studies (more than 5000 images) and found that less than 0.08% were unacceptable (ie, too much breast area was removed). These incorrectly segmented images were segmented manually and included in the analysis. Examples of four segmented mammograms are shown in Figure 1. As shown in this figure, the dark area exterior to the visible breast region for a given breast image shows the pixel values that were set to zero in the automated segmentation process. This segmentation step constrains the image processing to the breast region used in the second step. Because the breast was not compressed uniformly during the image acquisition, the second step reduces the breast area to approximate the portion of the breast that coincides with the uniformly compressed breast region. In the outer region, the breast thickness changes rapidly from the fully compressed breast thickness to close to zero thickness. Thus, the second step reduces unwanted spatial variation by eliminating the portion of the projected breast area corresponding to large variations in compressed breast thickness during imaging and retaining that which is approximately of uniform thickness. For craniocaudal view mammograms, the breast area is well approximated as a semicircle (or half-moon). This binary half-moon silhouette image is eroded by 25% along a radial direction using an algorithm described previously (23). This process removes those regions that could potentially interfere with the variation measure (18). The erosion border is marked on each of the images shown in Figure 1. In the third step, the variation measure is calculated as the standard deviation of the pixel values within the eroded breast region for each study image. All mammograms were processed with the same algorithm.
Figure 1.
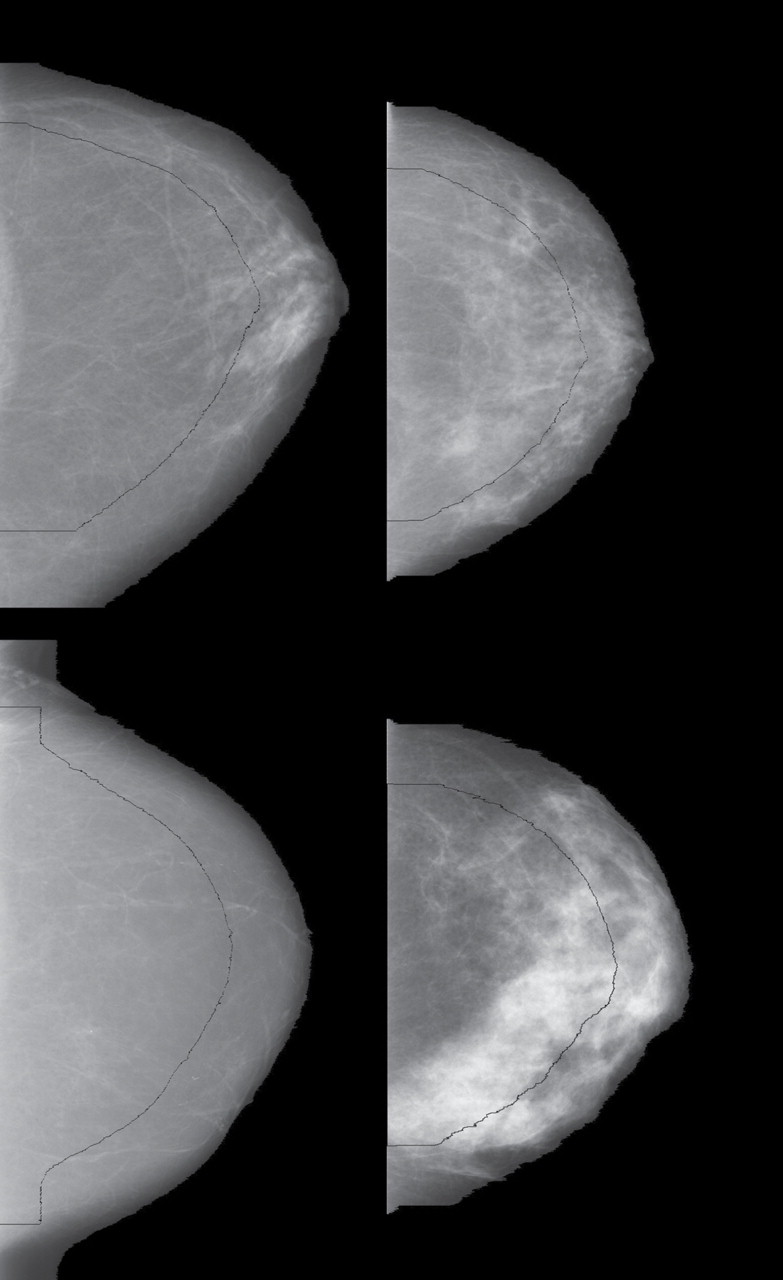
Image processing examples of the variation measure (V) representing four combinations of the first (lowest) and fourth (highest) quartiles of variation and percent density (PD) distributions. Top left: first quartile V (V = 205) and first quartile PD (PD = 7%); top right: first quartile V (V = 208) and fourth quartile PD (PD = 44%); bottom left: fourth quartile V (V = 394) and first quartile PD (PD = 0%); bottom right: fourth quartile V (V = 571) and fourth quartile PD (PD = 42%). The breast is segmented from the background of the mammogram image. The curved black line indicates erosion of the breast by 25%. The variation measure is calculated using the pixels bound by this curved black line and the image border on the left.
The variation measure and percent density have different properties. The variation measure cannot be zero, and unlike PD, which ranges from 0% to 100%, it has no upper bound. We have also shown that these two measures have a nonlinear relationship (12).
Acquisition Technique Parameters
The image acquisition technique varies from one mammogram to the next, and variation due to these differences has the potential to interfere with mammographic density measures. To evaluate the influence of these differences on associations between the variation measure and percent density and the risk of breast cancer, we abstracted the values of the important acquisition technique parameters from mammograms digitized from the MMHS case–cohort. Abstracted parameters included the compressed breast thickness in millimeters, compression force in pounds, x-ray tube voltage in kilovoltage peak, and beam current–time in milliampere-seconds (a surrogate for x-ray generation).
Statistical Methods
We summarized the data for each study by case and control (or subcohort) subject status, including presenting mean values and standard deviations for mammographic measures by categories of age, body mass index (BMI), and menopausal status at mammogram. Age (per 10 years) and BMI (per 5 kg/m2) categories were chosen for convenience as well as to ensure that a sufficient number of case and control subjects were within each category for comparison purposes. Associations between the variation measure and percent density were visualized using scatter plots, and Spearman correlation coefficients with 95% confidence intervals (CIs) were used to summarize the strength of the linear association between the two measures. The magnitude of the associations between the variation measure or percent density and the risk of breast cancer was estimated using odds ratios (ORs) or hazard ratios (HRs). For the quantitatively scaled density measures, the odds ratios and hazard ratios reflect the relative risk (RR) of breast cancer for a woman whose measurement was one standard deviation higher than that of another woman; for quartiles of the density measures, the odds ratios and hazard ratios reflect the risk of breast cancer for women in the second, third and fourth quartiles relative to the risk for women in the first (lowest) quartile. For the case–cohort study (MMHS), hazard ratios were estimated by Cox proportional hazards regression using sampling weights to account for the subsampling that was performed in this case–cohort design (24). In the Cox regression, age at study enrollment was used as the starting age and age at breast cancer diagnosis or at the last follow-up was used as the stopping age. The proportional hazards assumption was evaluated by examination of Schoenfeld residuals over age; no violations of the proportional hazards assumption were noted. For the case–control studies (MCBCS and MCMAM), odds ratios were estimated using logistic regression.
Ordinal tests of trend were performed to assess the association between each density measure and the risk of breast cancer.Analyses of data from all three studies were adjusted for age at mammogram alone, as well as for age, BMI (in kg/m2), and menopausal status (pre- vs postmenopausal) at mammogram. Both age and BMI were included in all models as continuous covariates. A transformed version of BMI (inverse BMI = 1/BMI) was used in the regression models because it provided a better fit compared with the untransformed version. All tests of statistical significance were two-sided, and all analyses were performed using SAS statistical software (version 9.2; SAS Institute, Cary, NC). Statistical significance was defined as P less than .05.
We also performed a meta-analysis to obtain pooled estimates across the three studies. Before combining the study-specific estimates, we used Poisson regression models to analyze the data from the case–control studies and estimate approximations of the log-relative risks and their standard errors (25). The pooled estimates were then obtained using a meta-analysis with a random study effect (26). We used the Cochran Q test to test for heterogeneity of study effects in the meta-analysis (27).
To compare the ability of the two density measures to identify women at increased risk of breast cancer, we estimated the area under the receiver operating characteristic curve (AUC), that is, the concordance statistic (28,29). This statistic can be estimated as the proportion of case–control pairs for which a risk factor predicts a higher risk for the case subject than for the control subject. A concordance statistic value of 0.5 indicates that the risk factor(s) cannot discriminate between case and control subjects, whereas a value of 1.0 indicates that the model provides perfect discrimination between case subjects and control subjects. We used a bootstrap resampling approach (with 5000 bootstrap samples) to obtain 95% confidence intervals for these AUC estimates and to test the statistical significance of their differences between models that included percent density and the variation measure. In addition, we used the bootstrap samples to obtain tests of statistical significance for the comparisons of quartile-specific hazard ratio estimates between the percent density and variation measures.
We assessed the extent to which the variation measure might improve clinical breast cancer risk assessment over what might be achieved with the clinical use of percent density for risk assessment in a simulation study. We based this simulation study on the MMHS study, by using the baseline breast cancer incidence rates, the joint distribution of the quartiles of the percent density and variation measures, and the hazard ratio estimates that were observed in the MMHS cohort to simulate breast cancer incidence in a hypothetical collection of 19924 women (ie, the same size as the MMHS cohort). We estimated the 5-year absolute risk of breast cancer and the numbers of observed breast cancers, overall and in quartiles defined by the percent density and variation measures. Differences in these quantities were compared across quartiles within each of the measures and between percent density and the variation measure in each of the quartiles to quantify the potential improvements in risk prediction that might be made through the use of the variation measure in place of percent density.
Finally, we examined the potential influence of acquisition technique (ie, the machine settings unique to each individual when her mammogram was acquired) on the associations of percent density and the variation measure with the risk of breast cancer within the MMHS study. To do so, we assessed the degree to which the relative risk and AUC estimates were affected when the acquisition parameters were included as covariates in the proportional hazards regression models.
Results
The characteristics of the study subjects are summarized, by study population, in Table 1. The MCMAM study subjects were mostly postmenopausal (91%) and had the oldest mean ages at mammogram (64.9 years for case subjects and 64.1 years for control subjects), whereas the MMHS study had the largest number of premenopausal case and control (ie, subcohort) subjects (43% and 54%, respectively), which was reflected in their younger mean ages at mammogram (55.3 and 51.6 years, respectively). BMI was comparable across all study populations. The mean percent density and the mean variation were higher in case subjects compared with control subjects (Table 1).
Table 1.
Characteristics of subjects by study and case–control status*
| Variable | MMHS | MCBCS | MCMAM study | |||
|---|---|---|---|---|---|---|
| Case subjects | Subcohort (Control subjects) | Case subjects | Control subjects | Case subjects | Control subjects | |
| Number of women | 217 | 2094 | 928 | 1039 | 246 | 515 |
| Mean age at mammogram, y (SD) | 55.3 (10.7) | 51.6 (11.0) | 59.3 (11.8) | 61.4 (11.0) | 64.9 (10.1) | 64.1 (10.2) |
| Mean BMI at mammogram, kg/m2 (SD) | 28.2 (5.7) | 27.7 (6.7) | 27.6 (5.6) | 27.0 (5.3) | 27.9 (5.0) | 27.5 (5.2) |
| Menopausal status at mammogram, No. (%) | ||||||
| Premenopausal | 93 (43) | 1121 (54) | 238 (25) | 201 (19) | 21 (8) | 40 (8) |
| Postmenopausal | 124 (57) | 973 (46) | 676 (73) | 831 (80) | 223 (91) | 471 (91) |
| Unknown | 0 (0) | 0 (0) | 14 (2) | 7 (1) | 2 (1) | 4 (1) |
| Invasive cancer, No. (%) | 155 (71) | – | 748 (81) | – | 193 (78) | – |
| Mean density, % (SD) | 21.6 (15.3) | 19.7 (15.1) | 27.4 (15.1) | 21.4 (14.0) | 22.5 (15.0) | 18.3 (13.6) |
| Mean variation† (SD) | 383.3 (145.1) | 305.33 (125.1) | 435.3 (146.5) | 311.5 (109.3) | 320.4 (126.3) | 285.0 (115.8) |
* MMHS = Mayo Mammography Health Study; MCBCS = Mayo Clinic Breast Cancer Study; MCMAM = Mayo Clinic Mammography; BMI = body mass index; – = not applicable.
† In grayscale units.
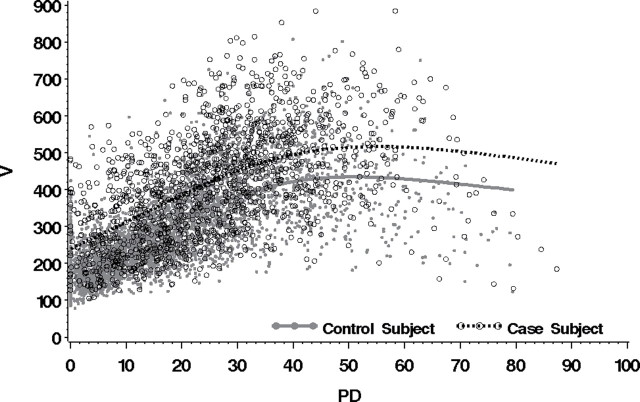
A scatter plot of the variation measure vs percent density for case and control subjects illustrates that these measures were moderately correlated (R 2 = .64 for all three studies combined [range = .64–.66]) (Figure 2). The nonlinear relationship between percent density and the variation measure (Figure 2) is consistent with our previous findings (12). There was also large variation in the variation measure at low values of percent density, which is partly a function of the greater potential for operator error at low values of percent density and also reflects the fact that the variation measure can never be zero in practice.
Figure 2.
Scatter plot of variation (V) vs percent density (PD) for each case and control subject from all three studies. Lines represent fit of cubic spline applied separately to case (dashed line) and control (solid line) subjects to show overall trend of association between V and PD.
Supplementary Table 1 (available online) presents the mean percent density and mean variation for case and control subjects by categories of age, BMI, and menopausal status at mammogram. In all three studies, premenopausal women, women younger than 50 years, and women with a BMI less than 25 kg/m2 had the highest mean values for both percent density and the variation measure.
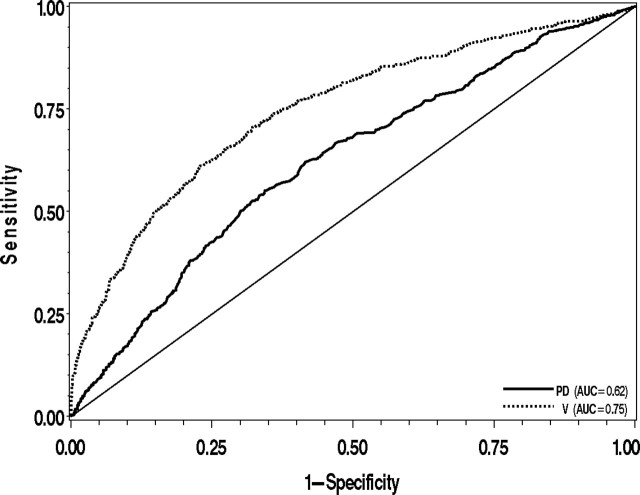
In all three studies, the variation measure was positively associated with the risk of breast cancer both in a model adjusted for age alone and in a model adjusted for age, BMI, and menopausal status (Table 2). The associations and discrimination (AUC) were slightly stronger with the fully adjusted model, and these results are presented below. Among the 217 case subjects and 2094 subcohort subjects from the MMHS, the variation measure was associated with the risk of developing breast cancer (HRs for increasing quartiles of variation: 1.0 [referent], 0.92 [95% CI = 0.5 to 1.6], 2.1 [95% CI = 1.3 to 3.3], and 7.0 [95% CI = 4.6 to 10.4]; P trend < .001). The corresponding findings for percent density were, by comparison, attenuated in the top two quartiles (HRs for increasing quartiles of percent density: 1.0 [referent], 1.5 [95% CI = 1.0 to 2.2], 1.6 [95% CI = 1.1 to 2.5], and 3.1 [95% CI = 2.0 to 4.8]; P trend < .001), and the risk estimate for the top quartile of percent density was statistically significantly different from that of the top quartile of variation (P < .001). The variation measure was also positively associated with the risk of breast cancer among the 928 case subjects and 1039 control subjects from the MCBCS (ORs for increasing quartiles of variation: 1.0 [referent], 1.3 [95% CI = 0.92 to 1.9], 3.0 [95% CI = 2.1 to 4.3], and 10.7 [95% CI = 7.5 to 15.3]; P trend < .001). Again, the corresponding findings for percent density were, by comparison, attenuated in the top two quartiles (ORs for increasing quartiles of percent density: 1.0 [referent], 1.6 [95% CI = 1.2 to 2.2], 2.1 [95% CI = 1.5 to 2.8], and 4.4 [95% CI = 3.1 to 6.1]; P trend < .001), and there was a statistically significant difference between the risk estimates for the top quartiles of percent density and variation (P < .001). Importantly, in these two studies, the estimates of discriminatory accuracy for the variation–breast cancer association were greater than the estimates of discriminatory accuracy for the percent density–breast cancer association (MMHS, AUC variation vs AUC percent density: 0.71 [95% CI = 0.68 to 0.75] vs 0.65 [95% CI = 0.62 to 0.69], P < .001; MCBCS, AUC variation vs AUC percent density: 0.76 [95% CI = 0.74 to 0.79] vs 0.65 [95% CI = 0.63 to 0.67], P < .001). The receiver operating characteristic curves for the percent density–breast cancer and variation–breast cancer associations in the MCBCS illustrate the distinct contrast in the ability of these measures to distinguish between the breast cancer case subjects and the control subjects (Figure 3). Among the 246 case subjects and 515 control subjects in the MCMAM study, increasing quartiles of percent density and of the variation measure showed similar associations with the risk of breast cancer (OR for highest quartile of percent density: 3.1 [95% CI = 1.9 to 5.1] and OR for highest quartile of variation: 2.6 [95% CI = 1.6 to 4.2]) and similar AUCs (0.61 [95% CI = 0.58 to 0.66] and 0.60 [95% CI = 0.58 to 0.66], respectively), and the differences were not statistically significant (all P > .20) (Table 2). We obtained similar results when the analyses were restricted to the case subjects with invasive breast cancer and when analyses were stratified by age groups using cut points that provided sufficient case and control subjects in each stratum (<50 years, 50–59 years, or ≥60 years) (data not shown).
Table 2.
Associations between percent density and variation measures and the risk of breast cancer (with corresponding AUCs)*
| Variable | MMHS | MCBCS | MCMAM study | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No. of case subjects | Age-adjusted HR (95% CI) | Full model† HR (95% CI) | No. of case subjects | Age-adjusted OR (95% CI) | Full model† OR (95% CI) | No. of case subjects | Age-adjusted OR (95% CI) | Full model† OR (95% CI) | |
| Percent density: | |||||||||
| Quartile 1 (0–8.3%) | 51 | 1.0 (referent) | 1.0 (referent) | 91 | 1.0 (referent) | 1.0 (referent) | 50 | 1.0 (referent) | 1.0 (referent) |
| Quartile 2 (8.4–17.6%) | 52 | 1.3 (0.9 to 1.9) | 1.5 (1.0 to 2.2) | 179 | 1.5 (1.1 to 2.0) | 1.6 (1.2 to 2.2) | 50 | 1.0 (0.6 to 1.6) | 1.2 (0.73 to 1.8) |
| Quartile 3 (17.7–28.3%) | 43 | 1.3 (0.9 to 2.0) | 1.6 (1.1 to 2.5) | 253 | 1.7 (1.2 to 2.3) | 2.1 (1.5 to 2.8) | 68 | 1.5 (1.0 to 2.3) | 1.8 (1.1 to 2.8) |
| Quartile 4 (28.4–79.4%) | 71 | 2.3 (1.6 to 3.3) | 3.1 (2.0 to 4.8) | 405 | 3.0 (2.2 to 4.1) | 4.4 (3.1 to 6.1) | 78 | 2.2 (1.4 to 3.6) | 3.1 (1.9 to 5.1) |
| AUC (95% CI) | 0.63 (0.60 to 0.67) | 0.65 (0.62 to 0.69) | 0.62 (0.59 to 0.64) | 0.64 (0.62 to 0.67) | 0.59 (0.55 to 0.63) | 0.61 (0.58 to 0.66) | |||
| Per 1 SD increase in percent density‡ | 217 | 1.4 (1.2 to 1.6) | 1.6 (1.3 to 1.8) | 928 | 1.5 (1.4 to 1.7) | 1.8 (1.6 to 2.0) | 246 | 1.4 (1.2 to 1.7) | 1.6 (1.3 to 2.0) |
| AUC (95% CI) | 0.63 (0.59 to 0.66) | 0.65 (0.62 to 0.69) | 0.62 (0.60 to 0.65) | 0.65 (0.63 to 0.67) | 0.59 (0.55 to 0.64) | 0.61 (0.58 to 0.66) | |||
| Variation measure§ | |||||||||
| Quartile 1 (0–212) | 36 | 1.0 (referent) | 1.0 (referent) | 53 | 1.0 (referent) | 1.0 (referent) | 48 | 1.0 (referent) | 1.0 (referent) |
| Quartile 2 (213–280) | 22 | 0.9 (0.5 to 1.5) | 0.92 (0.5 to 1.6) | 109 | 1.3 (0.9 to 1.8) | 1.3 (0.9 to 1.9) | 65 | 1.6 (1.0 to 2.5) | 1.7 (1.1 to 2.6) |
| Quartile 3 (281–380) | 44 | 1.8 (1.2 to 2.8) | 2.1 (1.3 to 3.3) | 184 | 2.6 (1.8 to 3.6) | 3.0 (2.1 to 4.3) | 63 | 1.8 (1.2 to 2.9) | 1.9 (1.2 to 3.0) |
| Quartile 4 (381–809) | 115 | 5.8 (3.9 to 8.7)║ | 7.0 (4.6 to 10.4)║ | 582 | 8.2 (5.8 to 11.5)║ | 10.7 (7.5 to 15.3)║ | 70 | 2.4 (1.5 to 3.8) | 2.6 (1.6 to 4.2) |
| AUC (95% CI) | 0.70 (0.66 to 0.74)║ | 0.71 (0.68 to 0.75)║ | 0.72 (0.70 to 0.74)║ | 0.75 (0.73 to 0.77)║ | 0.58 (0.55 to 0.63) | 0.60 (0.57 to 0.65) | |||
| Per 1 SD increase in variation¶ | 217 | 2.3 (2.0 to 2.6)║ | 2.4 (2.1 to 2.7)║ | 928 | 2.8 (2.5 to 3.1)║ | 3.1 (2.8 to 3.5)║ | 246 | 1.4 (1.2 to 1.7) | 1.5 (1.2 to 1.8) |
| AUC (95% CI) | 0.70 (0.66 to 0.74)║ | 0.71 (0.68 to 0.75)║ | 0.75 (0.73 to 0.77)║ | 0.76 (0.74 to 0.79)║ | 0.58 (0.55 to 0.63) | 0.60 (0.58 to 0.66) | |||
* AUC = area under the receiver operating curve; MMHS = Mayo Mammography Health Study; MCBCS = Mayo Clinic Breast Cancer Study; MCMAM = Mayo Clinic Mammography; HR = hazard ratio; CI = confidence interval; OR = odds ratio; SD = standard deviation.
† Full model adjusted for age, body mass index, and menopausal status at mammogram.
‡ SD = 15.0.
§ In grayscale units.║ P < .001(two-sided) bootstrap-based comparison of variation estimates (either HR, OR, or AUC) to the corresponding percent density estimates.
¶ SD = 136.5.
** Variation measure in grayscale units.
Figure 3.
Receiver operating characteristic curves and area under the curve (AUC) for unadjusted associations between percent density (PD) and variation (V) and the risk of breast cancer in the Mayo Clinic Breast Cancer Study. The diagonal line represents a model with no predictive value (AUC = 0.5).
In a meta-analysis of the three studies, both the variation measure and percent density were positively associated with the risk of breast cancer (approximate RRs for increasing quartiles of variation: 1.0 [referent], 1.2 [95% CI = 0.98 to 1.5], 1.9 [95% CI = 1.5 to 2.3], and 3.6 [95% CI = 1.9 to 7.0]; approximate RRs for increasing quartiles of percent density: 1.0 [referent], 1.3 [95% CI = 1.1 to 1.6], 1.5 [95% CI = 1.3 to 1.8], and 2.3 [95% CI = 1.9 to 2.9]) (Table 3). Even though all three studies showed a positive trend for the association between increasing quartiles of the variation measure and the risk of breast cancer, there was evidence of heterogeneity among the studies for the association between the top quartile of variation and the risk of breast cancer (P heterogeneity < .001), which was likely driven by the high risk estimate for the MCBCS. We examined the influence of several factors, including age, menopausal status, mammogram time period, type of digitizer, and type of cancer (invasive vs all), on the association between the variation measure and the risk of breast cancer across all studies, but we found no explanation for the heterogeneity between studies (data not shown).
Table 3.
Estimated relative risk of breast cancer by quartiles of percent density and variation in each of the three studies and from a meta-analysis of the three studies*
| Variable | MMHS | MCBCS | MCMAM study | Meta-analysis | |||
|---|---|---|---|---|---|---|---|
| HR (95% CI) | OR (95% CI) | RR† (95% CI) | OR (95% CI) | RR† (95% CI) | RR (95% CI) | P heterogeneity‡ | |
| Percent density (%) | |||||||
| Quartile 1 (0–8.3) | 1.0 (referent) | 1.0 (referent) | 1.0 (referent) | 1.0 (referent) | 1.0 (referent) | 1.0 (referent) | |
| Quartile 2 (8.4–17.6) | 1.5 (1.0 to 2.2) | 1.6 (1.2 to 2.2) | 1.3 (1.0 to 1.7) | 1.2 (0.73 to 1.8) | 1.1 (0.7 to 1.6) | 1.3 (1.1 to 1.6) | .57 |
| Quartile 3 (17.7–28.3) | 1.6 (1.1 to 2.5) | 2.1 (1.5 to 2.8) | 1.5 (1.2 to 1.9) | 1.8 (1.1 to 2.8) | 1.5 (1.0 to 2.1) | 1.5 (1.3 to 1.8) | .93 |
| Quartile 4 (28.4–79.4) | 3.1 (2.0 to 4.8) | 4.4 (3.1 to 6.1) | 2.2 (1.7 to 2.8) | 3.1 (1.9 to 5.1) | 2.1 (1.4 to 3.1) | 2.3 (1.9 to 2.9) | .28 |
| Variation measure§ | |||||||
| Quartile 1 (0–212) | 1.0 (referent) | 1.0 (referent) | 1.0 (referent) | 1.00 (referent) | 1.0 (referent) | 1.00 (referent) | |
| Quartile 2 (213–280) | 0.92 (0.5 to 1.6) | 1.3 (0.9 to 1.9) | 1.2 (0.9 to 1.7) | 1.7 (1.1 to 2.6) | 1.4 (0.99 to 2.1) | 1.2 (0.98 to 1.5) | .49 |
| Quartile 3 (281–380) | 2.1 (1.3 to 3.3) | 3.0 (2.1 to 4.3) | 2.0 (1.5 to 2.8) | 1.9 (1.2 to 3.0) | 1.6 (1.1 to 2.3) | 1.9 (1.5 to 2.3) | .75 |
| Quartile 4 (381–809) | 7.0 (4.6 to 10.4) | 10.7 (7.5 to 15.3) | 3.5 (2.7 to 4.7) | 2.6 (1.6 to 4.2) | 1.9 (1.3 to 2.8) | 3.6 (1.9 to 7.0) | <.001 |
* Estimates adjusted for age, body mass index, and menopausal status at mammogram. MMHS = Mayo Mammography Health Study; MCBCS = Mayo Clinic Breast Cancer Study; MCMAM = Mayo Clinic Mammography; HR = hazard ratio; CI = confidence interval; OR = odds ratio; RR = relative risk.
† RR approximation using Poisson regression models.
‡ Pheterogeneity calculated from the Cochran Q statistic.
§ In grayscale units.
We next examined whether the association between the variation measure and the risk of breast cancer persisted when examining mammograms taken years before the diagnosis of breast cancer. Only the MMHS and the MCMAM study were used for these analyses because the participants in these studies had mammograms that were taken years before a breast cancer diagnosis (or index date). In this analysis, we stratified the subjects by the median time between the dates of the earliest mammogram and the breast cancer diagnosis or last follow-up (4 years for MCMAM and 8 years for MMHS). In the MCMAM study, there were essentially no differences in the associations between percent density or the variation measure and the risk of breast cancer with regard to the timing of the mammogram (<4 vs ≥4 years). However, in the MMHS, the risk estimates for the percent density and variation measures were somewhat attenuated when assessed from mammograms taken 8 or more years before diagnosis vs mammograms taken within 8 years of diagnosis (Supplementary Table 2, available online). Importantly, the positive associations between the variation measure and the risk of breast cancer remained statistically significant even for mammograms taken 8 or more years before diagnosis.
We also assessed the influence of interpatient differences in mammographic acquisition parameters on the associations between the density measures and the risk of breast cancer in the MMHS. Adjustment for these factors had little effect on the association between either percent density or variation and the risk of breast cancer (Supplementary Table 3, available online).
We next assessed the extent to which the variation measure might improve clinical breast cancer risk assessment compared with percent density by performing a simulation based on data from the MMHS cohort. In this study, the AUC for the variation measure was 0.71 and the AUC for percent density was 0.65 (Table 2). Overall, the average absolute 5-year risk of breast cancer in this cohort was 1.1%. For women in the lowest and highest quartiles of percent density, the average absolute 5-year risks of breast cancer were 0.7% and 1.6%, respectively. For women in the lowest and highest quartiles of variation, the average absolute 5-year risks were 0.4% and 2.6%, respectively. When using these estimates in 1000 simulations, we found that the median number of breast cancers after 5 years among those in the highest quartile of percent density was 84 (95% CI = 67 to 103), whereas the median number of breast cancers after 5 years among those in the highest quartile of variation was 136 (95% CI = 113 to 159). The number of breast cancers observed in the highest quartile of the variation measure was 1.6 times higher (95% CI = 1.4 to 1.9 times ) than the number observed in the highest quartile of percent density. Thus, the improved risk prediction provided by the variation measure when compared with percent density, as reflected in the difference between the values of their AUCs, results in a large difference in expected number of breast cancers among women in the highest quartiles of these mammographic measures.
Discussion
We found that an automated estimate of mammographic density—the variation measure—was associated with the risk of breast cancer in three epidemiological studies. The association between the variation measure and breast cancer was at least as strong as the association between percent density and breast cancer in all three studies, as reflected by estimates of risk and discriminatory accuracy. The variation measure–breast cancer association was not materially influenced by mammographic acquisition parameters, and this association was similar to that seen in a recent study of a calibrated variation measure and breast cancer that used full-field digital mammography (18). Taken together, these results suggest that the variation measure is a viable automated mammographic density measure that is consistent across film and digital imaging platforms and may be useful in the clinical setting for risk assessment.
Several of our findings support incorporation of the variation measure into future breast cancer risk models. First, the association between variation and the risk of breast cancer remained strong when it was assessed on mammograms taken at least 4 years before diagnosis. Second, the associations reported here between variation measured on film mammograms and the risk of breast cancer are similar to our previously published results using full-field digital mammography (18). Thus, the variation measure appears to be an important risk factor across the imaging platforms evaluated to date. Third, the variation measure provided better discrimination between breast cancer case subjects and control subjects relative to percent density in two of the three studies we examined. In addition, the magnitude of the AUC for these two studies (which was calculated from models that included age, BMI, and menopausal status together with the density measure) was 0.70 or higher; by contrast, the concordance statistic for the current Gail model (30) is 0.596, and the breast cancer risk models to date that incorporate percent density estimates have concordance statistics that range from 0.62 to 0.68 ( 31–34). Finally, we used a simulation study to quantify the likely differences in breast cancer risk associated with either percent density or the variation measure and found substantially different absolute risks of breast cancer for women in the highest quartiles of percent density and variation. The 5-year absolute risk of breast cancer for women in the highest quartile of percent density was less than the Gail model cut-off of 1.66% that is often used to classify women as being at high risk, whereas the 5-year absolute risk of breast cancer for women in the highest quartile of the variation measure exceeded this threshold.
Although the variation measure performed at least as well as percent density for risk discrimination in the three studies included in this analysis, there was heterogeneity in the results. Two studies—MCBCS and MMHS—showed better discrimination of risk and higher risk estimates for the variation measure relative to percent density, whereas the MCMAM study showed similar performance for both measures. Formal tests of heterogeneity showed differences in the risk estimates for the variation measure across the three studies, but only for the top quartile of variation. We also examined the influence of several factors, including age, menopausal status, mammogram time period, type of digitizer, and type of cancer (invasive vs all), on the association between the variation measure and the risk of breast cancer across all studies, but none of these factors explained the differences seen between studies. Study design might have contributed to heterogeneity given that MCMAM was a closely matched case–control study; there is the potential that we overmatched on some factors related to the variation measure. Also, subjects in the MCMAM study were sampled from a regularly screened population of women who were required to have had at least two mammograms at least 2 years before breast cancer diagnosis. Thus, although the variation measure performed as well as percent density in all three studies, additional research is required to determine whether the variation measure is superior to percent density.
If we assume that percent density and variation show similar associations with risk, the fact that the variation measure is automated may make it preferable to percent density for use in the clinical setting. Methods of automating breast density measurements are not widely used or have not been well validated (5,35). These automated methods range from calibrated approaches, including both planar and volumetric measures (6,7,36), to texture features of the underlying mammogram images (37). As noted above, the process for measuring variation is not analogous to that for measuring percent density and thus is not directly related to methods that are intended to capture percent density or volumetric breast density in an automated fashion. The variation measure is most closely related to automated texture measures (37), which can be alternatively described as Fourier measures. Importantly, initial evidence from full-field digital mammography shows that variation can be measured with or without calibration (18), which will simplify the use of this measure in the clinical setting.
Even though mammographic density has consistently been assessed as the amount or proportion of bright tissue in an image (1,5), we found that a measure of variation of dense tissue is also relevant to breast cancer. These findings are consistent with recent calibration work (18) and texture analyses (37). First, the calibrated variation measure in full-field digital mammography was found to be a function of the percent density measure as well as of the other relevant calibrated tissue parameters (12). Thus, the variation measure and percent density have been shown to be related. Second, the variation measure includes both the low-frequency features and fractal texture measures that were previously found to be associated with the risk of breast cancer (37). Thus, the variation measure is indirectly associated with existing mammographic density measures.
The strengths of this study include the evaluation and validation of a novel breast density measure across three well-designed epidemiological studies. We were able to compare this novel measure with an established percent density measure that was also available for all studies. The magnitude of the association between the variation measure and the risk of breast cancer was comparable to the magnitude of the association between percent density and the risk of breast cancer and in two of three studies, the variation measure resulted in improved risk discrimination, with AUCs of 0.70 or higher. Furthermore, two of the included studies had mammograms available that were taken years before diagnosis, which allowed us to show that the variation–breast cancer association was present at least 4 years, and even more than 8 years, before breast cancer diagnosis.
Weaknesses of this study include limited risk factor data for the MCMAM study and limited follow-up in the MCBCS between mammograms and cancer diagnosis. Even though we did not have prediagnostic mammograms for the MCBCS, we did evaluate the variation measure in the noncancerous breast to ensure that the cancer abnormalities were not responsible for the associations we observed. In addition, estimation of the variation measure requires a consistent breast segmentation preprocessing stage. The segmentation processing may have removed too much or too little breast area in some images. The degree of breast erosion was set as a static parameter (25%), which may not be optimal (ie, may not be the optimal breast region to examine) and will require further investigation. A larger degree of erosion produced stronger associations in a recent study (18). Our analysis was restricted to craniocaudal view images because of processing concerns related to the inclusion of the chest wall or pectoral muscle in the mediolateral oblique mammogram views limiting the evaluation of the variation measure from these views. Finally, pixel dynamic range, digital resolution, and varying digital detector technologies may influence the estimation of the variation measure. Reducing the allowable pixel dynamic range (ie, the bit rate or bit depth used for film digitization) below some critical value can interfere with the image information and display and, therefore, the variation measure. However, in this study, we used an accepted pixel value dynamic range for mammography (38), thereby limiting the influence on the variation measure.
The variation measure will require further evaluation with data collected under varying conditions to ensure its consistency across diverse settings. The robustness of this measure across a variety of imaging platforms, equipment, and technicians remains to be determined. In addition, alternative metrics for the variation measure, such as total variation within a given mammogram or region of interest, will also need to be examined as they may prove to be equivalent or stronger risk factors for breast cancer.
The variation measure holds promise for use as a mammographic density measure in the clinical setting because of its simplicity and the ability to standardize and automate this measure across sites. The variation measure is automated and is generated without subjective thresholds or other detection-related parameters. Variation can be measured in film as well as in full-field digital mammography, and the corresponding associations have now been shown to be similar. Evidence that the variation measure is associated with breast cancer in different study populations and across imaging conditions would support incorporation of this measure into clinical risk assessment practices.
Funding
This work was supported by the Department of Defense (DAMD 17-00-1-0331), National Cancer Institute (R01 CA 128931; R01 CA 128931Z1; R01 CA 122340; R01 CA97396 and P50 CA116201).
Notes
The authors declare that they have no relevant conflicts of interest to report. The study sponsor had no role in the design of the study; the collection, analysis, and interpretation of the data; the writing of the article; or the decision to submit the article for publication.
References
- 1. McCormack VA, dos Santos Silva I. Breast density and parenchymal patterns as markers of breast cancer risk: a meta-analysis. Cancer Epidemiol Biomarkers Prev. 2006;15 6):1159 1169 [DOI] [PubMed] [Google Scholar]
- 2. Cummings SR, Tice JA, Bauer S, et al. Prevention of breast cancer in postmenopausal women: approaches to estimating and reducing risk. J Natl Cancer Inst. 2009;101 6):384 398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Boyd NF, Martin LJ, Bronskill M, et al. Breast tissue composition and susceptibility to breast cancer. J Natl Cancer Inst. 2010;102 16):1224 1237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Brower V. Breast density gains acceptance as breast cancer risk factor. J Natl Cancer Inst. 2010;102 6):374 375 [DOI] [PubMed] [Google Scholar]
- 5. Yaffe MJ. Mammographic density. Measurement of mammographic density. Breast Cancer Res. 2008;10 3):209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Highnam R, Brady M. Mammographic Image Analysis Boston, MA: Kluwer Academic Publishers; 1999. [Google Scholar]
- 7. Pawluczyk O, Augustine BJ, Yaffe MJ, et al. A volumetric method for estimation of breast density on digitized screen-film mammograms. Med Phys. 2003;30 3):352 364 [DOI] [PubMed] [Google Scholar]
- 8. van Engeland S, Snoeren PR, Huisman H, et al. Volumetric breast density estimation from full-field digital mammograms. IEEE Trans Med Imaging. 2006;25 3):273 282 [DOI] [PubMed] [Google Scholar]
- 9. Malkov S, Wang J, Kerlikowske K, et al. Single x-ray absorptiometry method for the quantitative mammographic measure of fibroglandular tissue volume. Med Phys. 2009;36 12):5525 5536 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Ding J, Warren R, Warsi I, et al. Evaluating the effectiveness of using standard mammogram form to predict breast cancer risk: case-control study. Cancer Epidemiol Biomarkers Prev. 2008;V 5):1074 1081 [DOI] [PubMed] [Google Scholar]
- 11. Boyd N, Martin L, Gunasekara A, et al. Mammographic density and breast cancer risk: evaluation of a novel method of measuring breast tissue volumes Cancer Epidemiol Biomarkers Prev. 2009;18 6):1754 1762 [DOI] [PubMed] [Google Scholar]
- 12. Heine JJ, Cao K, Rollison DE. Calibrated measures for breast density estimation. Acad Radiol. 2011;18 5):547 555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Kaufhold J, Thomas JA, Eberhard JW, et al. A calibration approach to glandular tissue composition estimation in digital mammography. Med Phys. 2002;29 8):1867 1880 [DOI] [PubMed] [Google Scholar]
- 14. Heine JJ, Behera M. Effective x-ray attenuation measurements with full field digital mammography. Med Phys. 2006;33 11):4350 4366 [DOI] [PubMed] [Google Scholar]
- 15. Heine JJ, Thomas JA. Effective x-ray attenuation coefficient measurements from two full field digital mammography systems for data calibration applications. Biomed Eng Online. 2008;7:13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Heine JJ, Cao K, Beam C. Cumulative sum quality control for calibrated breast density measurements. Med Phys. 2009;36 12):5380 5390 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Heine JJ, Cao K, Thomas JA. Effective radiation attenuation calibration for breast density: compression thickness influences and correction. Biomed Eng Online. 2010;9:73 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Heine JJ, Fowler EE, Flowers CI. Full field digital mammography and breast density: comparison of calibrated and noncalibrated measurements. Acad Radiol. 2011;18 11):1430 1436 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Kelemen LE, Couch FJ, Ahmed S, et al. Genetic variation in stromal proteins decorin and lumican with breast cancer: investigations in two case-control studies. Breast Cancer Res. 2008;10 6):R98 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Wang X, Goode EL, Fredericksen ZS, et al. Association of genetic variation in genes implicated in the beta-catenin destruction complex with risk of breast cancer. Cancer Epidemiol Biomarkers Prev. 2008;17 8):2101 2108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Vachon CM, Brandt KR, Ghosh K, et al. Mammographic breast density as a general marker of breast cancer risk. Cancer Epidemiol Biomarkers Prev. 2007;16:43 49 [DOI] [PubMed] [Google Scholar]
- 22. Byng JW, Boyd NF, Fishell E, Jong RA, Yaffe MJ. The quantitative analysis of mammographic densities. Phys Med Biol. 1994;39 10):1629 1638 [DOI] [PubMed] [Google Scholar]
- 23. Heine JJ, Cao K, Rollison DE, et al. A quantitative description of the percentage of breast density measurement using full-field digital mammography. Acad Radiol. 2011;18 5):556 564 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Langholz B, Jiao J. Computational methods for case-cohort studies. Comput Stat Data Anal. 2007;51:3737 3748 [Google Scholar]
- 25. McNutt LA, Wu C, Xue X, et al. Estimating the relative risk in cohort studies and clinical trials of common outcomes. Am J Epidemiol. 2003;157 10):940 943 [DOI] [PubMed] [Google Scholar]
- 26. DerSimonian R, Laird N. Meta-analysis in clinical trials. Control Clin Trials. 1986;7:177 188 [DOI] [PubMed] [Google Scholar]
- 27. Cochran WG. The combination of estimates from different experiments. Biometrics. 1954;10:101 129 [Google Scholar]
- 28. Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143 1):29 36 [DOI] [PubMed] [Google Scholar]
- 29. Hanley JA, McNeil BJ. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology. 1983;148 3):839 843 [DOI] [PubMed] [Google Scholar]
- 30. Costantino JP, Gail MH, Pee D, et al. Validation studies for models projecting the risk of invasive and total breast cancer incidence. J Natl Cancer Inst. 1999;91 18):1541 1548 [DOI] [PubMed] [Google Scholar]
- 31. Tice JA, Cummings SR, Smith-Bindman R, et al. Using clinical factors and mammographic breast density to estimate breast cancer risk: development and validation of a new predictive model. Ann Intern Med. 2008;148 5):337 347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Barlow WE, White E, Ballard-Barbash R, et al. Prospective breast cancer risk prediction model for women undergoing screening mammography. J Natl Cancer Inst. 2006;98 17):1204 1214 [DOI] [PubMed] [Google Scholar]
- 33. Chen J, Pee D, Ayyagari R, et al. Projecting absolute invasive breast cancer risk in white women with a model that includes mammographic density. J Natl Cancer Inst. 2006;98 17):1215 1226 [DOI] [PubMed] [Google Scholar]
- 34. Tice JA, Cummings SR, Ziv E, et al. Mammographic breast density and the gail model for breast cancer risk prediction in a screening population. Breast Cancer Res Treat. 2005;94 2):115 122 [DOI] [PubMed] [Google Scholar]
- 35. Assi V, Warwick J, Cuzick J, et al. Clinical and epidemiological issues in mammograhic density. Nat Rev Clin Oncol. 2012;9:33 40 [DOI] [PubMed] [Google Scholar]
- 36. Shepherd JA, Kerlikowske K, Ma L, et al. Volume of mammographic density and risk of breast cancer. Cancer Epidemiol Biomarkers Prev. 2011;20 7):1473 1482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Manduca A, Carston MJ, Heine JJ, et al. Texture features from mammographic images and risk of breast cancer. Cancer Epidemiol Biomarkers Prev. 2009;18 3):837 845 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. ACR Technical Standard for Electronic Practice of Medical Imaging. 2007. Res. 13 - 2007. Amended 2009 (Res. 11). http://www.acr.org/Quality- Safety/Standards-Guidelines/Technical-Standards-by-Modality.