Abstract
Dripping and jetting regimes in microfluidic multiphase flows have been investigated extensively, and this review summarizes the main observations and physical understandings in this field to date for three common device geometries: coaxial, flow-focusing and T-junction. The format of the presentation allows for simple and direct comparison of the different conditions for drop and jet formation, as well as the relative ease and utility of forming either drops or jets among the three geometries. The emphasis is on the use of drops and jets as templates for microparticle and microfiber syntheses, and a description is given of the more common methods of solidification and strategies for achieving complex multicomponent microparticles and microfibers.
1. Introduction
Microfluidic techniques are now well established as tools for fundamental research in chemistry, biology and physics, as well as facilitating new advancements in fields as diverse as biotechnology, materials engineering and food science [1–2]. At the micron length scale, interfacial and viscous effects dominate over bulk forces, and fluid inertia is often negligible. As a consequence of these physical constraints, the characteristic features of multiphase flows in microfluidic environments are unique. One major aspect of this field of study is the formation of droplets and fluid threads. Drop and thread formation have rich dynamics that are affected by many parameters, including the flow rates of the different fluid phases, their viscosities, densities and interfacial tension, surface chemistry, and device geometry [3–5].
As microfluidic methods offer controlled environments for the production of droplets, they have become established as reliable alternatives to more conventional bulk emulsification methods for the generation of monodisperse emulsions. The droplets themselves can be used as discrete reactors for investigating chemical and biochemical reactions [6–7]. Both droplets and jets can also be used as templates for the synthesis of highly uniform monodisperse micro-objects [8–9], which include novel multicomponent and non-spherical microparticles, as well as large aspect ratio microfibers. Applications of these micro-objects include particle-based display technologies [10–11], photonic materials [12–13], field-responsive rheological fluids [14], tissue engineering scaffolds [15], therapeutics [16], high performance composite filler materials [17], consumer and personal care products [18], and food additives [19]. In these applications, monodispersity and uniformity are highly desired properties to ensure that the micro-objects exhibit constant, controlled and predictable behavior. Monodispersity and 3Current address: Department of Mechanical and Industrial Engineering, Ryerson University, Toronto, Ontario, Canada M5B 2K3 uniformity are major advantages of microfluidic methods for generating high value materials, and as such the mechanism of formation of these micro-objects has been an active field of research. The first step in the formation of such materials is the generation of uniform droplets, to obtain spherical or nearly spherical particles, and jets, which may be a precursor to fibers.
Due to the wide range of applications, researchers have realized that a detailed understanding of the dripping and jetting regimes is important, and there are many studies geared towards a more comprehensive and unified understanding of the various flow regimes [20–24]. Drop formation is known to be the result of fluid instabilities. When one immiscible fluid is introduced into another, generally one of two events will occur: the formation of droplets (or bubbles) or the formation of a continuous jet. This response is a consequence of the inner or dispersed fluid becoming unstable due to surface tension forces seeking to minimize the interfacial area (Rayleigh-Plateau instability). Opposing this action are viscous forces which suppress the growth of deformations of the jet that lead to pinch off, and, if present, inertial forces, which promote the formation of a long fluid thread. It is the balance of these forces that determine whether droplets or jets form for a given set of conditions.
The theory of absolute and convective instabilities provides a convenient framework to understand jet stability in flowing systems [22–25]. An absolute instability corresponds to disturbances growing and propagating both in the downstream and upstream directions; the perturbations grow from a fixed point in space. In this case, a continuous fluid jet cannot exist, but breaks up into drops. In contrast, a convective instability corresponds to perturbations propagating downstream while they grow, which allows for a long continuous fluid thread to persist. This response usually occurs in the high velocity limit, when fluid inertia effects become more important than surface tension effects.
In this review, we focus on what is understood about drop and jet formation in microfluidic multiphase flows. Both fluid configurations are very interesting from the perspective of using the droplet or jet as a template for particle or fiber synthesis, so our interest is two-fold. We are interested in the instabilities that drive droplet formation and the ability to control droplet size and production rate for a wide range of parameters. On the other hand, we are also interested in the suppression of instabilities (or the downstream propagation of disturbances) to encourage jet formation and the ability to control jet dimensions for a wide parameter space. Both drop and jet formation are dependent on a number of factors. In the simplest sense though, in the dripping regime, drops detach from the injection source and are convected downstream by the continuous outer flow of a second fluid. In the jetting regime, the dispersed fluid can flow out of the source as a single thread or jet, the length of which may be several times the dimensions of the nozzle before the jet destabilizes and droplets pinch off from the tip. These regimes have been studied extensively and a great deal of progress has been made in understanding the physical mechanisms involved. Moreover, droplet size, jet diameter and frequency of droplet production can be predicted for certain conditions. Thus we summarize what, to date, is understood about dripping and jetting for three of the most prevalent geometries in the microfluidic droplet generation literature: coaxial, flow-focusing and T-junction.
There is an overwhelming body of literature on drop and, to a lesser extent, jet formation in microfluidics for a wide range of parameters: flow rates, viscosities, surface tension, surface chemistry, channel aspect ratios and channel geometry. However, what is often found is that no single study, regardless of how comprehensive, spans all of the available parameter space. We wish to explore the degree of commonality among the geometries, considering both what has been observed experimentally and predicted theoretically. Thus, our review may aid in the process of selecting the most appropriate geometry and set of conditions for a specific drop or jet application, thereby making it less arbitrary and time-intensive.
We focus on the passive generation of drops and jets in closed microchannels without the integration of moving parts or external actuation; thus the formation relies on the growth or suppression of interfacial instabilities. All of the examples presented are systems where, with respect to the channel walls, the dispersed phase liquid is non-wetting relative to the continuous phase liquid [26]. If this were not the case, inverted emulsions, as well as other multiphase regimes beyond the scope of this review may be observed [26–28]. It should be noted however, that wetting is an important consideration in drop and jet formation, and researchers have employed clever selective wetting strategies to make multiple emulsions in a single device through selective modification of the wetting properties of the channel walls [29–31].
Also, for the sake of conciseness, the examples discussed herein are concerned with all liquid phases only; we have not included microfluidic bubble generation [32–36] in this discussion, though much of the physics applies and studies on bubble formation have contributed greatly to our general understanding of breakup mechanisms of the dispersed phase. Specifically, we present a summary of the physical mechanisms of the drop to jet transition for the coaxial, flow-focusing and T-junction microfluidic geometries, in terms of important dimensionless parameters, which are defined in section 2. There is an extensive and rich literature on drop formation in microfluidics, and we do not presume to cover all of it in detail in this review. We briefly overview the major points concerning the scaling laws for stable drop formation in section 3, then focus in more detail on understanding the transition between dripping and jetting in section 4, and the conditions for the formation of ‘stable jets’ in section 5. We concentrate primarily on immiscible liquid phases, though we do include a brief note in section 5 on flows of partially miscible phases. This review is prepared with particular emphasis on particle and fiber synthesis, where the steps and considerations involved in transforming a liquid drop or jet to a solid microparticle or microfiber are discussed in section 6.
2. Channel geometry and dimensionless numbers
In two-phase microfluidic systems, dispersed and continuous phase fluids generally flow into the device from two separate microchannels. The channels typically meet at a junction, which depends on the specific microfluidic device geometry, and the shape of the junction helps define the local flow fields that deform the two-fluid interface. When the free surface instabilities between the phases are sufficiently large, drops emerge and eventually break off from the dispersed phase. For steady flows, the formation of droplets in microfluidic channels is usually periodic and monodisperse. To form jets, it is necessary to minimize the free surface instabilities. Such instabilities derive from the competition between stabilizing and destabilizing forces at the interface between the two phases. Common examples of stabilizing forces that promote the formation of jets are shear stresses and fluid inertia, while capillary pressure is often the main contributor to the destabilization of the interface and the formation of drops.
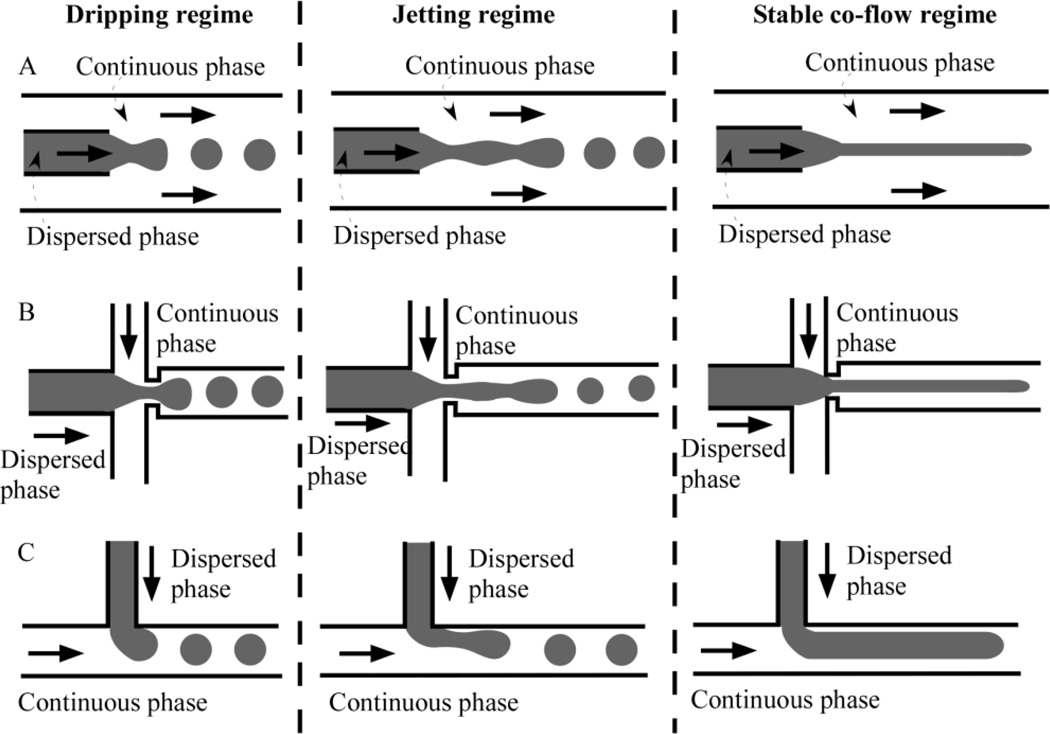
There are numerous microfluidic device geometries; however, three of the most common microfluidic configurations that have been developed to produce droplets passively are the coaxial, flow-focusing and T-junction designs. These configurations are shown schematically in Figure 1. Other common geometries that have been developed for the generation of droplets, but which will not be focused on in this review, include double glass microcapillary devices that hydrodynamically focus coaxial flows [37] and step emulsification devices that employ step changes in channel dimensions to trigger drop formation [38–39].
Figure 1.
Schematic of different flow regimes in (A) coaxial, (B) flow-focusing, and (C) T-junction microfluidic devices (not to scale). Solid arrows indicate the flow direction.
For the coaxial geometry (Fig. 1A), which is commonly referred to as co-flow, the inner dispersed phase fluid is driven in the same direction as the outer continuous phase fluid, inside concentric channels. Experimental devices using the coaxial geometry are often made by inserting a smaller circular inner glass capillary tube into a larger square capillary tube [20, 23, 40]. The inner capillary has a tapered tip, such that flow of fluid around the tip is approximately axisymmetric. More recently, researchers have been able to design all-PDMS coaxial channels for more rapid prototyping of devices [41].
There are many variations of flow-focusing microfluidic devices. Most of these devices have the consistent structural feature of an intersection of two channels to form a cross. The dispersed phase flows through the central channel with the continuous phase flowing in the two side channels. The fluids meet at the cross-junction, where droplets or jets of the dispersed phase form as the fluids flow into the main channel. Flow-focusing geometries create approximately extensional flows at the junction, for example due to hydrodynamic focusing or the presence of a contraction in the channel width (or orifice) at the junction (Fig. 1B).
T-junction microfluidic devices typically have the continuous phase flowing through a straight main channel, with the dispersed phase entering the main channel through a cross flowing side channel (Fig. 1C). The three geometrical parameters in T-junction microfluidic devices are wc, the width of the continuous phase channel, wd, the width of the dispersed phase channel, and h, the channel height.
The production of droplets in microfluidics requires at least two fluid phases, where physical variables of the fluids, such as interfacial tension (γ) and viscosities of the dispersed (µd) and continuous phases (µc) are necessary to characterize the generation of droplets. In addition, external parameters such as flow rates of the dispersed (Qd) and continuous phases (Qc), and channel dimensions (w and h) play important roles. In the case of large flow velocities where inertia starts to have an effect, the densities of the dispersed (ρd) and continuous phases (ρc) also become relevant. To understand the dynamics of the generation of droplets and particularly to obtain quantitative scaling laws of the droplet volume and generation frequency for a specific flow regime, a suitable choice of dimensionless numbers, which are typically the product or ratio of the physical parameters mentioned above, is desired.
The balance between local shear stresses and capillary pressure is conveniently captured by the dimensionless continuous phase and dispersed phase capillary numbers, Cac = µc Uc/γ and Cad = µd Ud/γ, and the relative dominance of fluid inertia to capillary pressure is similarly modeled using the dimensionless Weber number, . Here, Uc and Ud are the flow speeds, and dd is the characteristic diameter of the dispersed phase as it penetrates into the continuous phase. Ca is the most important dimensionless number for microfluidic droplet formation and its value is typically around 10−3–10. We is an important dimensionless number when inertial effects start to matter, for example at the onset of jetting in coaxial devices. These dimensionless parameters help in the prediction of resulting drop or jet formation and are also useful for designing experiments. For example, to suppress instabilities in a two-phase microfluidic system and produce jets, it is possible to increase the flow speeds or the ratio of viscosity to interfacial tension in the system to increase the capillary numbers.
In addition to the capillary and Weber numbers, the ratio of volumetric flow rates between the dispersed phase and the continuous phase, Qd/Qc, the viscosity ratio of the two phases, µd/µc, and the geometrical aspect ratios of the dispersed and continuous phase channel width and height, h/w, are often cited in the literature to capture the various dynamics that promote or inhibit instabilities.
3. Droplet formation
Active and passive technologies have been used to generate droplets in microfluidic channels. Compared to the active approach, which involves the use of valves, the passive approach takes advantage of the characteristic flow field in microfluidics to control the interface and capillary instability, and consequently to produce droplets. Therefore, external actuation is not necessary in the passive generation of droplets via microfluidics. Moreover, the droplets obtained using passive methods are typically highly monodisperse; for example the droplet polydispersity can be as small as 1–3% [42]. The sizes of the droplets can be estimated using scaling laws and analytical models [43–44] that have been developed for some of the channel geometries and flow regimes. As the fundamental understanding of the breakup processes that form droplets in the coaxial, flow-focusing, and T-junction geometries have been recently reviewed intensively [3–5, 45–46], we will only introduce the main findings briefly and emphasize the scaling laws that control the sizes of droplets.
In the coaxial configuration, the continuous phase fluid surrounds the dispersed phase fluid and dispersed phase droplets are produced mainly due to the Rayleigh–Plateau instability. Therefore, the size of the droplets scales linearly with the diameter of the liquid thread in the jetting regime. For the dripping regime, the diameter of the droplets is comparable with the diameter of the inlet of the dispersed phase.
During flow-focusing, the continuous phase fluid flows on either side of the dispersed phase fluid to an orifice fabricated in a microfluidic device, where the elongational velocity field in the continuous phase fluid stretches the dispersed phase to a thin jet, which eventually breaks into droplets (Fig. 1B). Although the physical mechanisms are complicated and no simple models have been developed to predict the dependence of the size of droplets on the operating parameters, dripping and jetting regimes have been observed in the flow-focusing configuration [47]. For the dripping regime, a combination of capillary instability and viscous drag is proposed to argue the mechanism of the generation of drops because observations showed that the droplet size does not scale purely with either a capillary instability or viscous drag [4]. Two models that have been proposed for droplet formation in flow-focusing geometries include the shearing model, where the diameter of the droplet is related to the reciprocal of the capillary number, and the rate-of-flow-controlled breakup model, where the size of the droplet is only related to the ratio of the flow rates of the dispersed and continuous phases [34, 48]. In the jetting regime, the droplets are generated not only due to the natural growth of an interfacial instability but also because of the viscous forces exerted by the continuous phase fluid.
Two regimes are commonly observed for the production of droplets in the T-junction geometry: 1) the squeezing regime where the generated droplet blocks the channel of the continuous phase fluid and creates a pressure drop across the droplet, and 2) the dripping regime where the size of the droplets is much smaller than the dimensions of the channel of the continuous phase fluid. In the squeezing regime, because droplets restrict the flow of continuous phase fluid, there is an increased pressure upstream, which plays an essential role in the droplet pinch-off. The droplet size scales as , where V is the droplet volume, D is the equivalent diameter of the channel and α is a constant of the order of unity. In the dripping regime, on the other hand, the droplets are small and do not disturb the continuous flow significantly, thus the size of the droplets is controlled mainly by the local shear stresses. Typically, the ratio of Ddrop/D, where Ddrop is the diameter of droplets, scales inversely with Ca. At high flow rates of the continuous and dispersed phases, a jetting regime or co-flow regime occurs, which is explained generally by the competition of different time scales. For example, when the pinch-off time scale is longer than the time scale to form a blob of the dispersed phase, the jetting regime appears [5]. It is believed, however, that both the pinching pressure and shear stresses are important for the transition region between the squeezing and dripping regimes [4].
Although physical mechanisms for the generation of droplets are different for the various types of microfluidic configurations, one common feature exists: the interplay between viscous stresses and capillary pressure. For example, for a coaxial geometry, a force balance between the viscous drag force and the capillary force, i.e., 6πRµcUc ≈ 2πwγ can give a quantitative relation between the size of the droplets (R), the dimension of the channel (w) and interfacial tension (γ) [5].
4. Transition from droplets to jets
Since the mechanisms for the transition from droplet to jet formation can vary depending on the geometry of the microfluidic system, we will describe the results of several experimental observations and theoretical models from the literature for coaxial, flow-focusing and T-junction microfluidic geometries. To aid in this description, we compiled data from numerous publications on dripping and jetting regimes in microfluidics. Table 1 compares order of magnitude estimates of the dimensionless numbers reported for the three geometries for dripping and jetting regimes (and squeezing for the T-junction geometry). Wherever possible, we used the values reported explicitly in the literature. When explicit values of the dimensionless numbers were not provided, but sufficient data was available, we used the data to estimate the dimensionless numbers of interest. Similarly, Figures 2–4 are phase diagrams for each of the three geometries, which were plotted to compare experimental observations from different research groups obtained for different ranges of parameters.
Table 1.
A comparison of estimated dimensionless numbers compiled from experimental data for drop and jet formation in coaxial, flow-focusing and T-junction microfluidic devices. For each geometry, data is ordered according to the regime, whether squeezing (for T-junctions), dripping or jetting to easily compare the dimensionless numbers within a regime from different studies.
| Regime | Capillary number (Cac) |
Capillary number (Cad) |
Weber number (Wed) |
Viscosity ratio (µd/µc) |
Flow rate ratio (Qd/Qc) |
Aspect ratio1 |
Ref. |
|---|---|---|---|---|---|---|---|
| Coaxial | |||||||
| Dripping | 10−3 – 10−1 | - | 10−3 – 10−1 | 10−2 – 10 | - | 10−2 – 10−1 | [20] |
| Dripping | 10−2 – 1 | - | 10−2 – 1 | 10−1 | 10−3 – 10 | 10−1 | [23] |
| Jetting | 10−3 – 1 | - | 10−1 – 103 | 10−2 – 10 | - | 10−2 – 10−1 | [20] |
| Jetting | 10−1 – 10 | - | 1 | 10−1 | 1 – 102 | 10−1 | [23] |
| Jetting | 10−2 – 1 | - | 1 – 10 | 10−2 – 10−1 | 10 | 10−1 | [40] |
| Jetting | 10−3 – 10−2 | 1 | 10−1 – 10 | 10−1 – 10 | 10−2 – 10−1 | 10−1 | [49] |
| Flow-focusing | |||||||
| Dripping | 10−3 – 10−2 | - | - | 10−1 | 10−3 – 10−1 | 10−1 | [55] |
| Dripping | 10−1 | - | - | 10−2 | 10−1 – 1 | 1 | [70] |
| Dripping | 10−1 | - | - | 10−2 | 10 – 103 | 10−1 | [47] |
| Dripping | 10−1 | - | - | 10−1 | 10−1 | - | [71] |
| Dripping | 10−2 – 10−1 | - | - | 10−1 | 10−2 – 1 | 1 | [65] |
| Dripping | 10−3 | - | - | 10−2 | 10−1 – 1 | 1 | [68] |
| Dripping | 10−1 – 1 | - | - | 10−3 – 10−2 | 10−2 | 10−1 | [61] |
| Dripping | 10−4 – 10−1 | 10−2 – 10−1 | - | 10−3 | 10−2 – 1 | 1 | [57] |
| Dripping | 10−1 – 10 | - | - | 10−3 – 10−1 | 10−2 | 10−1 | [62] |
| Dripping | 10−3 – 10−1 | - | - | 10 | 10−1 | 1 | [59] |
| Dripping | 10−2 – 1 | - | - | 1 | 10−1 – 1 | 10−1 | [21] |
| Dripping | - | 10−4 – 10−2 | - | 10−2 – 1 | 10−1 | 10−2 | [72] |
| Dripping | 10−6 – 10−5 | - | - | 10 – 102 | 10−1 – 1 | 1 | [56] |
| Dripping | 10−2 – 101 | - | - | 10−1 | 10−1 | 10−1 | [66] |
| Dripping | 10−2 – 10−1 | - | - | 10−2 | 10−1 – 1 | - | [60] |
| Dripping | 10−3 – 10−2 | - | - | 10−2 – 102 | 10−2 – 1 | 10−1 | [67] |
| Dripping | 10−1 | - | - | 10−2 | 10−1 – 1 | 1 | [64] |
| Jetting | 10−1 | - | - | 10−1 | 10−3 – 10−1 | 10−1 | [55] |
| Jetting | 1 | - | - | 10−2 | 10 – 103 | 10−1 | [47] |
| Jetting | 1 | - | - | 10−1 | 10−2 | - | [71] |
| Jetting | 1 – 10 | - | - | 10−3 – 10−2 | 10−2 | 10−1 | [61] |
| Jetting | 10−2 – 10−1 | 10−1 – 1 | - | 10−3 | 10−2 – 1 | 1 | [57] |
| Jetting | 10−1 – 1 | - | - | 1 | 10−1 – 1 | 10−1 | [21] |
| Jetting | - | 10−3 – 10−1 | - | 10−1 | 10−1 | 10−2 | [72] |
| T-junction | |||||||
| Squeezing | 10−4 – 10−2 | - | - | 10−1 – 10 | 10−1 – 1 | - | [82] |
| Squeezing | 10−4 – 10−2 | - | - | 102 | - | 1 | [76] |
| Squeezing | 10−2 – 10−1 | - | - | 10−1 – 1 | 10−2 – 10−1 | 1 | [58] |
| Squeezing | 10−3 – 10−1 | - | - | 10−2 – 1 | 10−2 – 1 | 1 | [85] |
| Squeezing | 10−4 – 10−2 | - | - | 10−2 – 10−1 | 10−2 – 10 | 10−1 | [77] |
| Squeezing | 10−3 – 10−2 | - | - | - | 10−1 | 10−1 | [75] |
| Squeezing | 10−5 – 10−3 | - | - | 10 | 10−2 – 10 | 1 | [28] |
| Squeezing | 10−3 | - | - | 10−1 | 10−1 – 1 | 1 | [81] |
| Squeezing | 10−3 – 10−2 | - | - | 10−1 | 10−1 – 1 | 10−1 – 1 | [78] |
| Dripping | 10−1 – 1 | - | - | 10−2 – 1 | 10−2 – 1 | 1 | [85] |
| Dripping | 10−2 – 10−1 | - | - | 10−2 – 10−1 | 1 – 10 | 10−1 | [80] |
| Dripping | 10−2 – 10−1 | - | - | - | 10−1 | 10−1 | [75] |
| Dripping | 10−2 – 10−1 | - | - | 1 | 10−1 – 1 | 1 | [21] |
| Dripping | 10−2 – 10−1 | - | - | 10−2 – 10−1 | 10−1 – 1 | 10−1 | [84] |
| Dripping | 10−3 – 10−1 | - | - | 10 | 10−2 – 10−1 | 1 | [28] |
| Dripping | 10−2 | - | - | 10−1 | 1 | 1 | [81] |
| Jetting | 10−2 – 10−1 | - | - | 10−1 – 10 | 10−1 – 1 | - | [82] |
| Jetting | 10−1 | - | - | 1 | 1 | 1 | [21] |
| Jetting | 10−3 – 10−1 | - | - | 10 | 10−1 – 1 | 1 | [28] |
| Jetting | 10−1 | - | - | 10−1 | 1 | 1 | [81] |
For coaxial devices, the aspect ratio is defined as the ratio of the radius of inner capillary tip to the radius of outer channel, while for flow-focusing and T-junction devices, the aspect ratio is defined as the ratio of channel height, h, and main channel width, w, i.e. h/w.
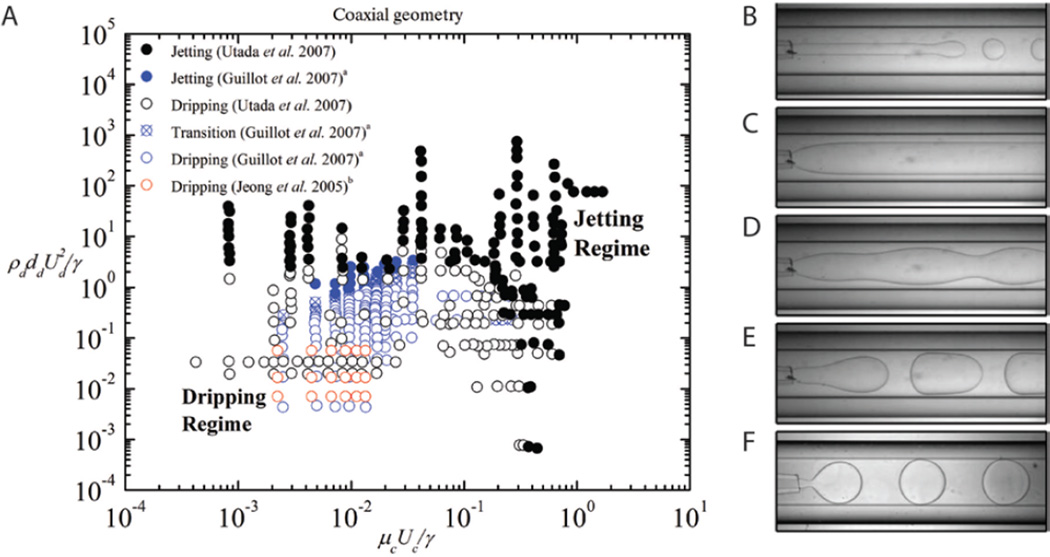
Figure 2.
(A) Phase diagram for microfluidic coaxial geometry comparing data from Utada et al. (modified with permission from [20]. Copyright 2007 by the American Physical Society), Guillot et al. (modified with permission from [23]. Copyright 2007 by the American Physical Society) and Jeong et al. (modified with permission from [51]. Copyright 2005 American Chemical Society), and examples of observed flow patterns where (B–D) fall within the jetting regime and (E–F) are in the dripping regime of the phase diagram. ((B–F) modified from [23]. Copyright 2007 by the American Physical Society).
a Glycerol density estimated using values from [52]; inner radius of capillary, rd, approximated as 20 µm (within the range of rd reported in [23]).
b Density values estimated using densities of chemicals that compose the solution. To estimate the properties of the mineral oil continuous phase, it is assumed to be kerosene, so that the corresponding fluid properties (interfacial tension, viscosity) of kerosene are obtained from [52].
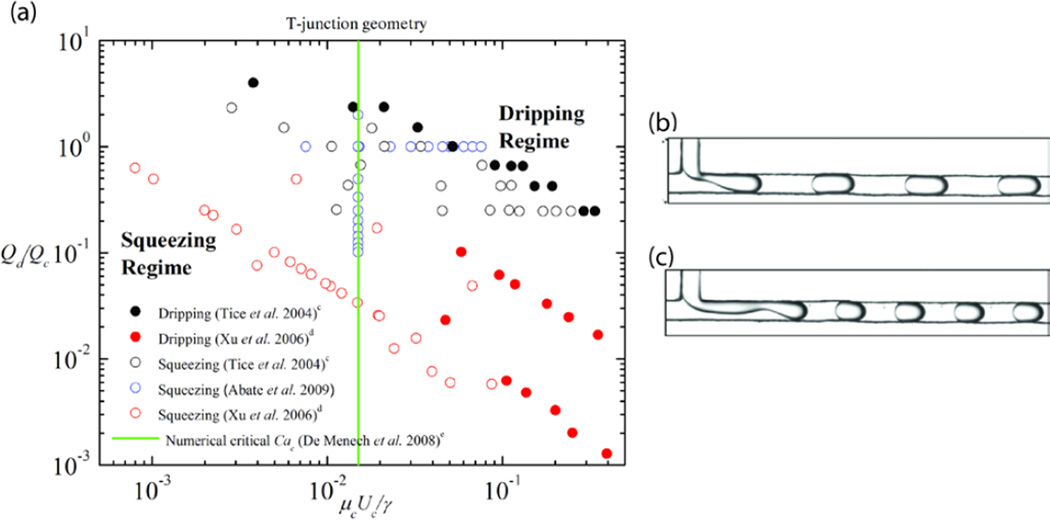
Figure 4.
(A) Phase diagram for microfluidic T-junction geometry, comparing data from Tice et al. (modified from [82]. Copyright 2004, with permission from Elsevier), Xu et al. (modified with permission from [85]. Copyright 2006 Wiley-VCH), and Abate et al. (modified with permission from [21]. Copyright 2009 by the American Physical Society), and examples of observed flow patterns (B) in the squeezing regime and (C) in the dripping regime of the phase diagram ((B–C) adapted from [82]. Copyright 2004, with permission from Elsevier).
c Data from [82] used so that viscosity ratio is 1. The capillary number of the continuous phase is calculated using data from [82].
d We assume the squeezing-to-dripping transition occurs when the average drop size becomes less than the width of the microchannel, and the scaling of the drop size with the capillary number abruptly changes.
e Numerical data obtained from [90].
4.1. Coaxial geometry
A number of studies [20, 22–24, 40, 49–50] have made use of the coaxial configuration to generate droplets (Fig. 2E–F) and jets (Fig. 2B–D). Utada et al. [20] used an inner capillary that had a tip diameter, dd = 20 µm, inserted into a 1 mm inner diameter square capillary, and observed two classes of the dripping to jetting transition. In one class, they found that as the flow rate of the outer continuous phase increased, drops that formed at the tip of the inner capillary decreased in size until a jet is formed. Downstream from the capillary tip, the jet destabilizes due to the Rayleigh-Plateau instability and eventually forms drops. The authors found that the formation of drops or jets depends on the competition between the viscous shear stress from the outer continuous phase, which is trying to stretch the emerging dispersed phase liquid, and interfacial tension, which tries to break the dispersed phase into drops immediately as the liquid flows out of the capillary tip. The authors determined a critical outer phase capillary number, Cac = µc Uc/γ = O(1) above which the formation of jets occurs.
Utada et al. [20] identified a second class of the dripping to jetting transition, at higher flow rates, which is controlled by the relative inertia of the dispersed phase fluid to the capillary pressure. The inertia of the dispersed phase fluid pushes the dripping location downstream, away from the capillary tip, so that a jet is formed at the tip itself. In this regime, the authors capture the relationship between inertial forces and capillary forces with the dispersed phase Weber number, and find that above a critical value, Wed = O(1) jets are formed.
Castro-Hernandez et al. [49] extended the understanding of the dripping to jetting transition in coaxial devices by observing that the criteria Wed > O(1) for jet formation is valid only if the Reynolds number of the dispersed phase liquid, Red = 2 ρd Qd/(πµddd) > O(1). When Red < O(1), the Weber number does not accurately capture the transition from dripping to jetting. They found, instead, that in these cases, jetting occurs when the Cad > O(1).
The phase diagram results from Utada et al. [20] are re-plotted in Figure 2A, along with other experimental results [23, 51] that are chosen because they share similar ranges of viscosity ratios and channel aspect ratios; in addition, some typical flow patterns are shown in Figure 2B–F. Figure 2A shows that, indeed, consistent among the different studies, there is a critical continuous phase capillary number and a critical dispersed phase Weber number, above which jet formation occurs. Similarly, the estimates of the dimensionless numbers in Table 1 presented for different studies using the coaxial geometry show that for different viscosity ratios, flow rate ratios and channel aspect ratios, dripping has been observed in the range O(10−3) < Cac < O(1) and O(10−3) < Wed < O(1), while jetting has been observed in the range O(10−3) < Cac < O(10) and O(10−1) < Wed < O(103). The results displayed in Figure 2A, along with the results presented in Table 1, illustrate the importance of the balance of viscous shear stresses and fluid inertia with capillary pressure. We note that the transition from dripping to jetting in coaxial geometries has also been explored in other works within the context of absolute and convective instabilities [23, 40].
4.2. Flow-focusing geometry
The flow-focusing geometry, which was introduced by Gañán-Calvo and coworkers [53–54] with the capillary flow-focusing technique for the generation of microbubbles and droplets, was first implemented in microfluidic two-phase flows to control the formation of dispersions by Anna et al. [55]. Flow-focusing microfluidic devices have since become popular and appear in a number of studies on monodisperse drop formation [47, 56–71]. A few of these studies also observe the formation of jets [21, 47, 57, 61, 71–72], the effect of the addition of surfactants [47], the influence of changing the viscosity ratio between the two phases [57], and the suppression of instabilities by geometrical confinement [72] among other mechanisms.
In the dripping regime, the dispersed phase entering the two-phase junction immediately breaks up into droplets and the resulting drops are carried downstream by the continuous phase. In the jetting regime, the shear from the outer continuous phase in the post-junction channel results in the elongation of the inner dispersed stream, and undulations that appear on the interface between the two fluids get carried downstream. A quasi-stable co-flow regime can be achieved with higher continuous phase flow rates, such that all interfacial instabilities are convected downstream.
In the flow-focusing geometry, the dimensionless capillary number is once again important in controlling the transition between dripping and jetting as the competition between viscous stresses and interfacial tension is significantly more important than inertia [4]. Here the capillary numbers of the continuous and dispersed phases are both relevant in controlling the transition [57] and are commonly described as Cac = µcQc/γh2 and Cad = µdQd/γh2 respectively, for flow-focusing geometries where the aspect ratio between the channel height and width is O(1).
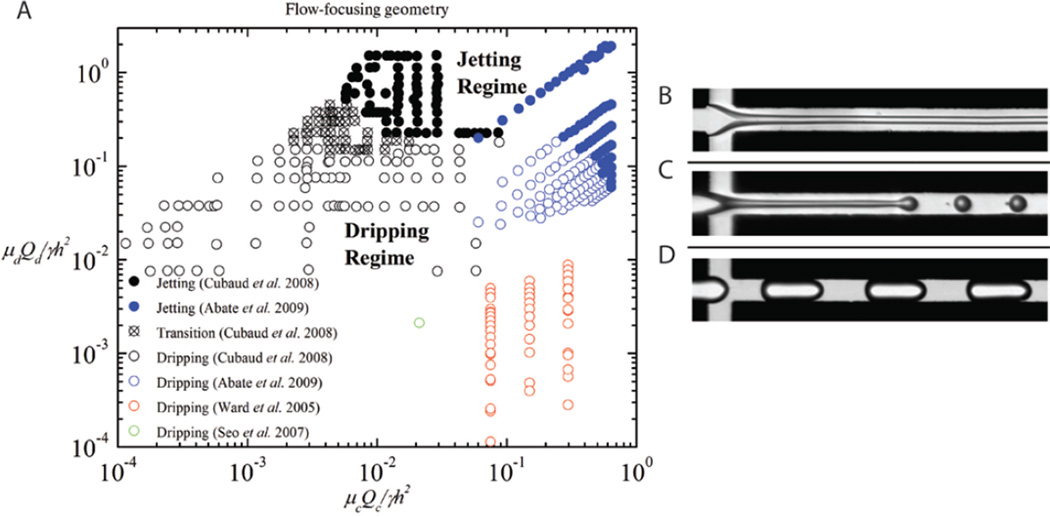
Figure 3A is a phase diagram of the dripping and jetting regions observed in experiments from four different flow-focusing studies [21, 57, 70, 73]; some typical flow patterns are shown in Figure 3 B–D. The phase diagram is plotted using the capillary numbers of the two phases, and indicates a transition from dripping to jetting above the critical capillary numbers.
Figure 3.
(A) Phase diagram for microfluidic flow-focusing geometry comparing results from Cubaud et al. (modified with permission from [57]. Copyright 2008, American Institute of Physics), Abate et al. (modified with permission from [21]. Copyright 2009 by the American Physical Society), Ward et al. [70] and Seo et al. ([73] – reproduced by permission of The Royal Society of Chemistry), and examples of observed flow patterns (B, C) in the jetting regime, and (D) in the dripping regime of the phase diagram ((B–D) modified with permission from [57]. Copyright 2008, American Institute of Physics).
There exists a few competing models that describe the conditions for the dripping to jetting transition. The models are summarized neatly in the review article by Christopher and Anna [4], but in principal, the transition occurs close to the lines, Cac = µcQc/γh2 ≈ 1 and Cad = µdQd/γh2 ≈ 1, which suggests that the competition between viscous stresses and capillary pressures predicts the formation of drops and jets.
4.3. T-junction geometry
The T-junction geometry in a microfluidic system was first introduced by Thorsen et al. [74], and was later adopted by others to form drops [21, 28, 75–85], characterize mixing in liquid-liquid systems [83], and form liquid-gas plugs [86] and double emulsions [87]. Studies that have applied T-junctions to microfluidic systems can be approximately categorized into either confined or unconfined T-junctions [4]. In unconfined T-junction systems, the dispersed phase entering the main channel is not significantly affected by the walls of the main channel because the width of the main channel is large relative to the dispersed phase channel, wc >> wd, and large compared to the jets and drops. In most unconfined T-junction microfluidic systems, the width of the continuous phase channel wc is at least a factor of five larger than the dispersed phase channel width wd [4, 80, 88]. Since unconfined T-junction microfluidic systems appear much less frequently than confined devices in the literature, this review will limit its scope to confined geometries for T-junction devices. Information on the predicted drop sizes and the transition between dripping and jetting regimes for unconfined systems can be found in [80] and [89].
In confined microfluidic T-junctions, the widths of dispersed and continuous phases are similar in size, wd ≈ wc. The dispersed phase enters the main channel and quickly fills the width of the main channel, which causes the pressure gradient across the drop to build-up. When this pressure overcomes the pressure inside the tip of the dispersed phase, the interface is deformed and necks. The neck thins and eventually breaks, which results in drop formation. Formed drops and jets are confined by the side walls of the main channel (for example, the drops are often oblong shaped rather than spherical because of confinement from the walls). When the flow is of the low capillary number type, as is common in microfluidic systems (Cac = µcUc/γ < O(10−2)), the buildup of pressure upstream of the penetrated dispersed phase squeezes the liquid such that it breaks into drops, and the length of the resulting slug scales with the flow rate ratio, Qd/Qc [35, 77]. This low capillary number formation of drops is typically referred to as “squeezing.”
Above a critical capillary number, Cac > O(10−2) the two-phase T-junction drop formation becomes shear-dominated [90], where the length of the resulting slug can be predicted with the capillary number, Cac. The high capillary number regime is often called the “dripping” regime in T-junction microfluidics because of its similarities with the dripping regime in coaxial flows. Here the dispersed fluid only occupies a portion of the main channel, flow fields from the continuous phase shear the portion of the dispersed phase protruding into the continuous phase, and droplets are formed and convected downstream. Figure 4A shows a phase diagram that describes the transition from squeezing to dripping for a range of capillary numbers Cac = µcUc/γ and flow rate ratios, Qd/Qc; representative experimental images are shown in Figure 4B–C. The data plotted are from different studies [21, 82, 85] that have similar viscosity and aspect ratios, and includes a numerically estimated critical capillary number, Cac ≈ 0.015 for the squeezing to dripping transition calculated by De Menech et al. [90]. This critical capillary number, which is not strongly affected by viscosity, was determined numerically from a phase-field model, where wd = wc = h, ρd = ρc, and the Reynolds number, Re < 1 [90].
There was insufficient experimental data available for the transition from dripping to jetting in T-junctions to include in the phase diagram (Fig. 4A). Although not as well studied, the transition from dripping to jetting has been found by measurement and calculation to be in the range Cac = O(10−2 – 10−1), with some dependence on factors such as viscosity ratios, flow rate ratios and geometry [89–91].
From the estimates of different experimental studies presented for the T-junction in Table 1, it is clear that as the capillary number of the continuous phase increases, the flow transitions from squeezing (O(10−4) < Cac < O(10−2)) to dripping (O(10−3) < Cac < O(10−1)) to jetting (O(10−2) < Cac < O(10−1)). A few published studies involving the formation of oil-in-water emulsions in hydrophilic T-junctions do not observe the transitions occurring in similar ranges of Cac. Their observation may be related to different wetting characteristics of the phases and hysteretic behavior [28].
4.4. Strategies that promote or prevent instability
In addition to the primary parameters (capillary number, Weber number, and flow rate ratio) that control the product of two-phase flows in microchannels – either drops or jets – a number of studies have focused on other factors that promote or prevent instabilities in microfluidic two-phase flows. Specifically, parameters related to channel geometry [72], fluid viscoelasticity [92], fluid viscosity [48, 82], and surface chemistry [67] all contribute to making drops or jets.
Geometric confinement can be used to suppress instabilities and thus encourage jet formation. Thus, it follows that the removal of geometric confinement can trigger the instabilities that lead to drop formation; this effect has been employed to generate drops in step emulsification devices [38–39]. Using a flow-focusing microfluidic geometry, Humphry et al. [72] found that instabilities can be suppressed when the width of the dispersed phase jet is comparable to or larger than the height of the channel. In addition, non-Newtonian polymer dispersed phase solutions that shear thin have been shown to suppress instabilities in a flow-focusing system [92]. Instabilities can be initiated and the dispersed phase emulsified with the addition of a chaperoning fluid around the dispersed phase that is Newtonian and easy to emulsify. The report of Tice et al. [82] shows, using a microfluidic T-junction system, that threshold capillary numbers can be lowered when the viscosities of the two phases differ significantly. A separate study also shows that higher viscosity liquids produce larger drops when emulsified in a flow-focusing device [48]. Roberts et al. [67] demonstrate, for a shallow aspect ratio flow-focusing device, that the instabilities are suppressed when the dispersed phase wets the channel surface and the thread has a height that is on the same order or larger than the channel height.
5. Jet or thread formation
5.1. Jet diameter
Typically in the dripping regime, drops are formed with diameters comparable to the source dimensions (dispersed phase channel inlet), but jet diameters are typically independent of the size of the source [24]. Moreover, a steady jet can be reduced to a very small diameter compared to the source [24]. Such jets can be used to make long fibers.
Castro-Hernandez et al. [49] showed that the jet diameter, dj, can be estimated for both the narrowing and widening regimes of unconfined jetting flow in a coaxial device. For the narrowing regime, the dispersed and continuous phase velocities become equal some distance downstream of the inlet tube and dj = (4Qd/(πUc))1/2, where Uc, the average speed of the continuous phase depends on the flow rate, Qc, and the geometry of the device. For the widening regime, the dispersed phase velocity never reaches the continuous phase velocity because the flow is locally absolutely unstable and the jet breaks before the dispersed phase velocity can become equal to the continuous phase velocity. In this case, dj can be estimated from , where Oh is the Ohnesorge number, defined as , and ω*, which is also a function of dj, is the maximum value of the growth rate of capillary sinusoidal perturbations.
To estimate the jet radius for their core-sheath coaxial experiments, Jeong et al. [93] used a simple model first introduced by Zarrin and Dovichi [94], where the jet radius is described as a function of the volume flow rates of the sample and sheath streams, where both streams have equal viscosities. Assuming laminar flow and the jet is circular within a circular channel, the velocity is given as a function of the distance to the jet center, r, where R is the channel radius, and Q is the total volumetric flow rate, . Integrating V(r) over the area of the jet, and solving for the jet radius yielded an expression for Rj as a function of dispersed and continuous flow rates, Jeong et al. [93] used the expression for Rj to estimate the diameters of fibers synthesized at different flow rate conditions, and found that the expression estimated their measured fiber diameters well, with small differences they attributed to measurement error, fluctuations in flow rate and shrinkage during polymerization.
5.2. Jet length
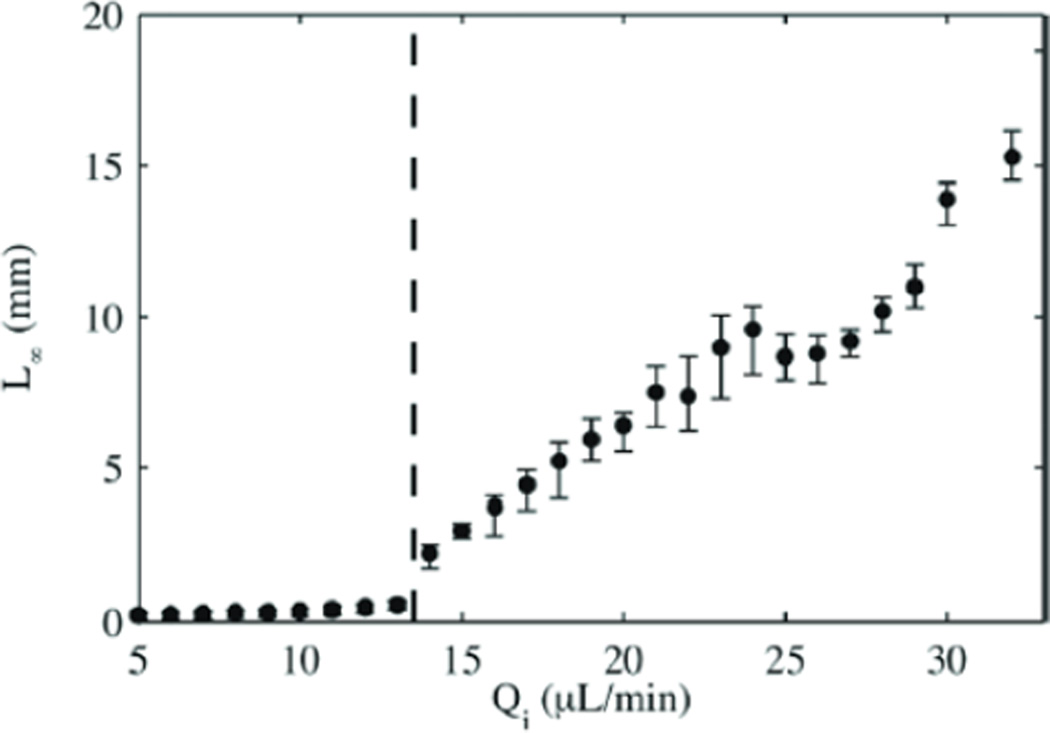
Cordero et al. [50] studied dripping and jetting regimes in confined coaxial flows. They measured the length of the jet (from inlet tip to pinch off), L∞, as a function of dispersed phase flow rate, Qd, as shown in Figure 5. They found that for low Qd, L∞ was small and grew only slightly with Qd. This response corresponds to the dripping regime. At a specific value of Qd, the jet starts to grow indicating that the flow is in the jetting regime. The large scatter in the L∞ data in the jetting regime reflects that the position of drop pinch off was not as well defined and thus not regular in time. The authors confirmed this conclusion with measurements of the frequency of the oscillations of the dispersed fluid jet. Moreover, they showed that while the dripping regime was independent of external forcing by a pulsing IR laser, the jetting regime showed synchronization between the laser frequency and the drop formation frequency, where the length of the jet decreased with increasing laser frequency.
Figure 5.
Length of the dispersed phase fluid jet as a function of the dispersed phase flow rate for an continuous phase flow rate fixed at Qc = 30 µL/min (Reprinted with permission from [50]. Copyright 2011, American Institute of Physics).
5.3. Factors affecting jet formation
Guillot and coworkers [22–24] studied in detail, both experimentally and theoretically, the stability of jets in confined pressure-driven flows at low Reynolds numbers. Their studies first focused on the coaxial geometry, with a cylindrical main channel [23]. They used the lubrication approximation to obtain a dispersion relation for the growth rate of perturbations, and were able to identify three key parameters that controlled the behavior of their system: the viscosity ratio, µd/µc, the degree of confinement of the unperturbed jet, and the continuous phase capillary number, Cac. They determined a simple analytical prediction for the transition between dripping and jetting, and though they made a number of approximations in their analysis, they found impressive agreement between experiment and theory. The major findings of their model are that decreasing µd/µc increases the dripping regime, and for a given µd/µc, there can be a transition from dripping to jetting by increasing the capillary number or the degree of confinement. The researchers interpreted their results in terms of suppressing perturbations: increasing Ca, corresponds to convecting away the perturbations faster and increasing the confinement decreases the rate of development of the perturbations because of the proximity of the channel walls. Another important feature of their study was the observation of what they referred to as “reentrant” behavior. As the continuous phase flow rate, Qc, was increased, they observed transitions from jets to drops then jets again, given that all other parameters were fixed. This result is because at low Qc, increasing Qc tends to reduce the strong confinement of the jet, promoting the formations of drops. At high Qc, where confinement is not significant, increasing Qc increases the jet velocity and the downstream convection of any growing perturbations, promoting the formation of continuous jets.
Guillot et al. [22] extended their investigations on jet stability to different geometries beyond the cylindrical case. They found that the stability of the jet is a function of the channel geometry with the circular cross-section channel being the most favorable for jetting, followed by the square cross-section, with the rectangular cross-section being the least favorable for the jetting regime, and in fact, it promotes dripping. For square and rectangular cross-section channels, they also consider the case of a jet squeezed by the geometry (the continuous phase completely wets the walls). They found that these 2D jets are absolutely stable and thus will not break up into drops, as has been observed by others [72]. While Guillot’s model agreed very well with experiments for a wide range of conditions, it failed for low degrees of confinement due to the assumptions made in the model. Instead of using the simplified model of Guillot et al. [23], Herrada et al. [24] presented an axisymmetric model, with an analytical solution for negligible inertia and a numerical solution when inertia could not be neglected. Their model was more successful at predicting the dripping to jetting transition for high external flow rates.
5.4. Ultra-low interfacial tension systems and partially miscible fluid phases
As has been discussed in previous sections, jet formation is generally favored at high capillary numbers. This limit can be achieved by reducing the interfacial tension between the two phases. Examples of such systems are aqueous two-phase systems (ATPS) [95], which typically have interfacial tension values ≤ 10−1 mN m−1 [96–97]. The fluids are formed from polymer solutions or polymer and salt solutions that demix into immiscible aqueous phases according to their phase separation dynamics [95–96]. Often, small amounts of one polymer remain in the second phase, and vice-versa. Such low interfacial tension facilitates the formation of long threads or jets of the dispersed phase, and do not typically destabilize readily to the dripping regimes without some form of external force integrated with the microfluidic device [97–99]. For example, Ziemecka et al. [97] were able to generate droplets of dextran solution in a poly(ethylene glycol) (PEG) continuous phase, but this required very low flow rates consistent with that predicted by Guillot et al. [22] for square cross-section channels. For a wide range of their flow rate conditions, the dextran solution formed very stable threads. The conditions for the passive formation of droplets in these systems are not practical for typical droplet generation applications, for example to synthesize microparticles for the delivery of drugs and cells. Thus, researchers have developed methods using either electric fields or mechanical actuation to generate droplets from ATPS at higher flow rates [97–102].
6. Solidification of drops and jets
Once drops or jets have formed, they can be used, for example, as liquid templates for particle and fiber synthesis. In order to efficiently use the drops or jets as templates, there must be some understanding of how the system (the choice of device geometry, flow rates) and material parameters (viscosity, density, interfacial tension) affect the reproducible formation of drops and jets with predictable dimensions. This understanding was the focus of the previous sections, where the conditions leading to dripping and jetting in common microfluidic device geometries were described.
In this section, we summarize the factors involved in converting the liquid template to a solid micro-object, taking into account that often, prior to designing a particle or fiber synthesis experiment, the experimentalist has already identified one or more desired particle properties. These properties may include size, shape, mechanical properties, optical properties, surface properties, and chemical and geometrical anisotropy. These desired properties may limit the choice of composition of the dispersed phase, and therefore also limit some of the material parameters, such as µd. The device geometry and composition of the continuous phase should then be chosen such that conditions for the appropriate flow regime(s) – whether squeezing (for T-junctions), dripping or jetting – are easily achievable. For example, if the target regime is stable dripping in a passive coaxial device where the diameter of the droplets is comparable to the diameter of the dispersed phase inlet, a continuous phase that would yield an ultra-low interfacial tension may likely be a poor choice because there would only be a small flow rate range (at low flow rates) where dripping is possible.
There are numerous examples of microparticles and microfibers generated by solidifying the drop or jet templates in microfluidic multiphase flows. Table 2 and Figures 6 and 7, discussed further below, illustrate the wide ranging compositions, solidification methods, geometries and complex structures achieved by different research groups.
Table 2.
A comparison of the different microfluidic device geometries, solidification methods and dispersed phase chemical compositions used to synthesize particles and fibers, indicating the relative prominence of the different procedures in the field for particle and fiber synthesis.
| Device Geometry |
Solidification method |
Particle composition | Fiber composition |
|---|---|---|---|
| Coaxial | UV-triggered reactions on-chip | 4-hydroxybutyl acrylate [51], Norland optical adhesive [37], isobornyl acrylate [137], 2-phenoxyethyl acrylate + 1,6-hexanediol diacrylate [137] | 4-hydroxybutyl acrylate[93] |
| Thermally triggered reactions off-chip | Hyperbranched polyglycerols [151] | ||
| Phase separation, solvent extraction | Mixed metal oxide hollow spheres [160], poly(butyl acrylate)-b-poly(acrylic acid)[37], alumina + iron oxide composite hollow spheres [161], silica + iron oxide composite hollow spheres [161], clay hollow spheres [161], | Poly(lactic-co-glycolic acid) (PLGA) [121,158], polysulfone [122], polyacrylonitrile [122], polystyrene [122], poly(p-dioxanone-co-caprolactone)-block-poly(ethylene oxide)-block-poly(p-dioxanone-co-caprolactone) amphiphilic triblock copolymer [123] | |
| Room temperature redox-initiated crosslinking | N-isopropylacrylamide [162] | ||
| Polycondensation | Polyethyleneimine + sebacoyl chloride + trimesoyl chloride [106] | ||
| Solvent evaporation | Polystyrene [163] | ||
| Ionic crosslinking | Alginate [111, 113], chitosan + sodium triphosphate pentabasic [159, 164] | ||
| Flow-focusing | Self-assembly | Polystyrene-polymethylmethacrylate block copolymer [165] | |
| Thermally triggered reactions off-chip | Poly(dimethylsiloxane) [166] | ||
| UV triggered reactions off-chip | Dextran-hydroxyethyl methacrylate [167] | ||
| UV triggered reactions on-chip | Divinylbenzene [103], ethyleneglycol diacrylate [103], ethyleneglycol dimethacrylate [128, 143], benzyl methacrylate + 1,6-hexanediol dimethacrylate [168], methacryloxypropyl dimethylsiloxane [169], poly(ethylene glycol) diacrylate + pentaerythritol triacrylate [169], pentaerythritol triacrylate [103, 128], pentaerythritol tetraacrylate [128], tripropyleneglycol diacrylate [103,143], N-isopropylacrylamide [92, 105], acrylamide + silica particles [127], dimethacrylate oxypropyldimethylsiloxane [103], Janus-perfluoropolyether + allylhydridopolycarbosilane [126], Janus poly(NIPAAm-co-fluorophore) [170] | Poly(ethylene glycol) diacrylate [130, 171], norland optical adhesive [131], 4-hydroxybutyl acrylate [17] | |
| Click reactions | Dithiolated poly(ethylene glycol) + acrylated hyperbranched polyglycerol [108], hydrazide-functionalized carboxymethyl cellulose + aldehydefunctionalized dextran [172] | ||
| Solvent extraction | 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) [173], silica [174] | polymethylmethacrylate [124] | |
| Solvent evaporation off-chip | Poly(DL-lactide-co-glycolide) [175], polyfluorene [176] | ||
| Room temperature redox-initiated crosslinking | N-isopropylacrylamide [177] | ||
| Ionic crosslinking | Alginate [109, 112, 114–115, 178], chitosan [179] | Alginate [41, 110, 116] | |
| Phase change (cooling) | Bismuth alloy [103], agarose [103], κ-carrageenan [119], hydrogenated coco glycerides [92], gelatin-maltodextrin [120], agar [180] | ||
| Polycondensation | Polyurethane-polybutadienediol [92], 1,6-diaminohexane + adipoyl chloride [69] | ||
| T-junction | Self-assembly | Organosilane [181] | |
| Thermally triggered reactions off-chip | Polydivinylbenzene [182], polystyrene [183], 1,6-hexanediol diacrylate [91, 144], isobornyl acrylate [144] | ||
| UV triggered reactions on-chip | Norland optical adhesive 60 [76] | ||
| UV triggered reactions off-chip | Poly(methylacrylic acid) + ethyleneglycol dimethacrylate [184], 1,6-hexanediol diacrylate [91], isobornyl acrylate [91] | ||
| Ionic crosslinking | Alginate [185] | ||
| Solvent evaporation | Poly(D,L-lactide-co-glycolide) [125] | ||
| Phase change (cooling) | Agarose [186] |
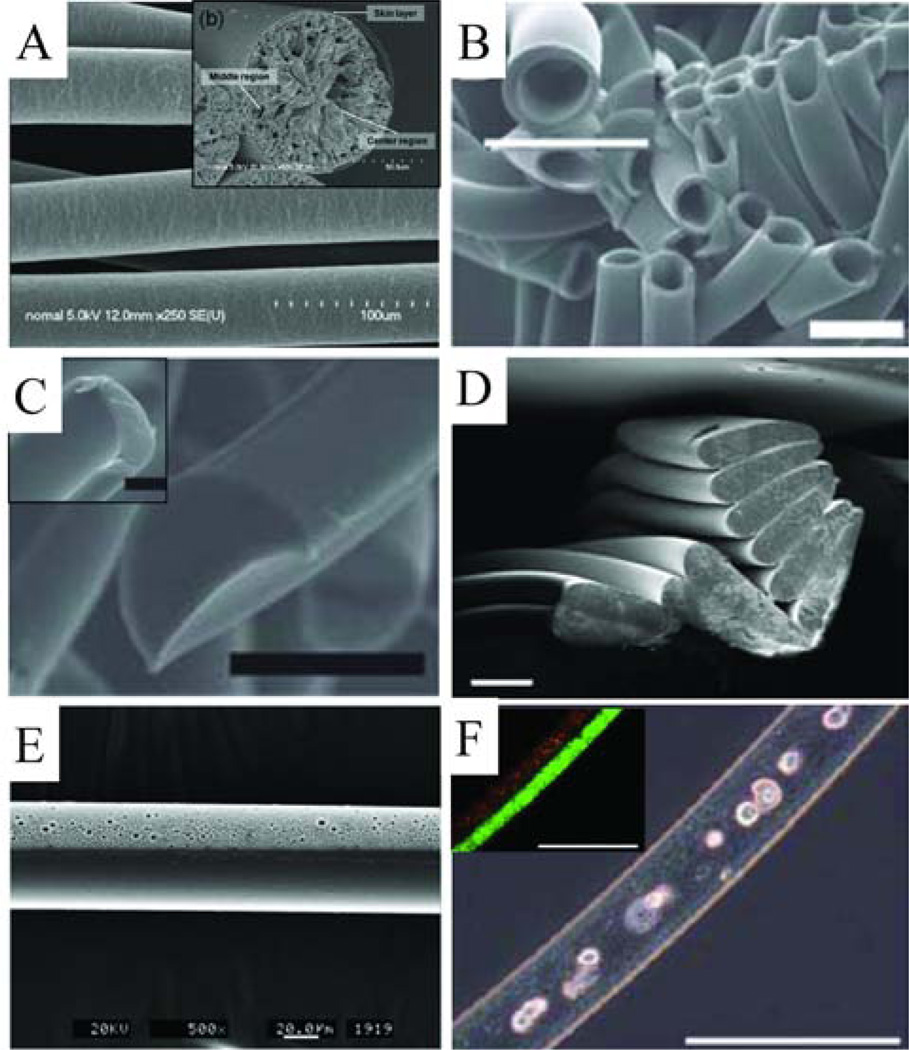
Figure 6.
Examples of microfluidic generated microparticles. (A) Tripropyleneglycol diacrylate microrods (reprinted from [103]); (B) bismuth alloy ellipsoids (reprinted from [103]); (C) Norland optical adhesive hollow microspheres (reprinted from [37]); (D) dumbbell-shaped Janus microparticles (perfluoropolyether/allylhydride polycarbosilane), scale bar represent 100 µm (reprinted with permission from [126]. Copyright 2009 Wiley-VCH); (E) Microparticles composed of gelatin and maltodextrin, scale bar represent 100 µm (reprinted from [120]. Copyright 2012, with permission from Elsevier); (F) Janus colloid-filled acrylamide microparticles, scale bar represents 100 µm (reprinted with permission from [127]. Copyright 2006 American Chemical Society).
Figure 7.
Examples of microfluidic synthesized microfibers. (A) Scanning electron microscope image (SEM) of PLGA microfibers with inset image showing cross-section (reprinted with permission from [121]. Copyright 2008 American Chemical Society). (B) SEM of hollow PEG diacrylate microfibers with a higher magnification inset image, scale bars represent 50 µm ([130] – reproduced by permission of The Royal Society of Chemistry). (C) Two examples of non-circular cross-section PEG diacrylate microfibers, scale bar represents 50 µm ([130] – reproduced by permission of The Royal Society of Chemistry). (D) Non-circular cross-section crosslinked 4-hydroxybutyl acrylate microfibers, scale bar represents 100 µm ([17] – reproduced by permission of The Royal Society of Chemistry). (E) Janus polyurethane microfiber, with one solid and one porous side ([131] – reproduced by permission of The Royal Society of Chemistry). (F) Janus ‘sandwiched’ structure alginate microfibers with fibroblast cells cultured in the core, inset fluorescence image shows the two halves of the sandwich structure, scale bar represents 200 µm ([116] – reproduced by permission of The Royal Society of Chemistry).
6.1 Solidification methods
There are a number of synthetic methods for the solidification of drop and jet precursor liquids. The more frequently used methods include free radical polymerization (photo- and thermally initiated), polycondensation reactions, ionic crosslinking, cooling, solvent extraction and self-assembly. The choice of method depends on the properties of the precursor liquid, the desired particle or fiber composition and physical properties, as well as the final application of the micro-objects. For example, if the microparticles or microfibers are to be synthesized with UV- or heat-sensitive cargo encapsulated, photo- and thermally initiated methods would not be appropriate. For spherical particle synthesis, depending on the method of solidification, the droplets can be collected off-chip and solidified at a later time. Thus, the microfluidic device is used solely for emulsification and not for particle synthesis. One factor to consider is that following the emulsification step and prior to solidification, it is possible for the dimensions of the droplets to change due to coalescence or partial dissolution of the monomer in the continuous phase for partially miscible systems, and thus this may affect the polydispersity of the microparticles [9]. Naturally, it is not possible to perform off-chip solidification for the synthesis of non-spherical particles or fibers because of relaxation of the shapes.
A common method for solidifying particles and fibers in microfluidic devices is free-radical polymerization. Typically in free-radical systems, an initiator produces highly reactive free radical species that initiate the chain reaction that ultimately results in linear polymers for monofunctional monomers or crosslinked networks for multifunctional monomers; this process may be initiated thermally or by light. For example, Nisisako et al. generated polymer particles from 1,6-hexanediol diacrylate via both UV-initiation and thermal initiation off-chip [91]. Xu et al. [103] developed a continuous microfluidic reactor for particles synthesis, where both the emulsification and the polymerization compartments were integrated into a single planar microfluidic device. Various diacrylate, triacrylate and divinyl monomers were crosslinked on-chip using UV light. For particles synthesized from monofunctional monomers with small quantities of multifunctional crosslinkers, it was observed that the chemical composition of the particles was not always well-controlled. In an effort to improve the properties of these microgel particles, researchers developed methods to better control the chemical homogeneity of the particles [104–105]. They prepared well characterized uncrosslinked polymer chains with sites for subsequent crosslinking. Semi-dilute solutions of these macromolecular precursors are emulsified on-chip and the crosslinking reaction is triggered; for example, poly(N-isopropylacrylamide) (pNIPAM) microparticles were synthesized in this manner with UV light triggering the reaction. The authors refer to this method as a polymer-analogous crosslinking process [105].
Step polymerization reactions are not as popular as free-radical polymerizations for microfluidic synthesis [69, 106]. Takeuchi et al. synthesized Nylon-6,6 capsules via a polycondensation reaction in a coaxial flow-focusing device [69]. The particles were formed from the rapid interfacial polymerization between adipoyl chloride (dissolved in the continuous phase) and 1,6-diaminohexane (dissolved in the dispersed phase).
Many of the crosslinking reactions used for particle solidification are not ideal for the encapsulation of fragile cargo, such as cells and nucleic acids, due to harsh conditions - UV exposure, high temperatures or the presence of free radicals. Researchers have developed gentler cross-linking methods, such as using click chemistry [107]. For example, Rossow et al. [108] used a radical- and catalyst-free crosslinking reaction to form microparticles containing cells via a nucleophilic Michael addition of dithiolated poly(ethylene glycol) to acrylated hyperbranched polyglycerol.
Ionic crosslinking is a solidification method often used with biological polymers. The reaction typically proceeds via the crosslinking of polyelectrolyte polymer chains with multivalent ions or small ionized molecules. One of the most common examples of this reaction is the gelation of anionic alginate with Ca2+ ions, which crosslink the guluronic acid blocks. Alginate gelation is commonly used for both particle and fiber synthesis [41, 109–117]. For fiber synthesis, an aqueous sodium alginate solution is flowed as the dispersed phase in a continuous phase of aqueous Ca2+ solution. When the two solutions come into contact, the alginate jet rapidly gels and flows out of the device. It is not possible to make spherical alginate particles if both solutions are aqueous because the jet will not destabilize, so different approaches have been used, such as the coalescence of droplets separately containing alginate and Ca2+ [112, 115, 117–118]. Simpler approaches, however, include the formation of sodium alginate droplets in an immiscible continuous phase, then flow of the emulsion into a bath of aqueous Ca2+ to solidify off-chip [109], or dissolution of the Ca2+ ions in the immiscible continuous phase to solidify on-chip [41, 114–115].
Solidification of precursor drops via a temperature induced phase change is typically used for biological polymers, such as agarose [103], κ-carrageenan [119], gelatin [120], maltodextrin [120] and pectin [9], but can also be used for inorganic precursors, such as low melting point alloys (Fig. 6B) [103]. Though there are some examples of this method being used for spherical droplets and deformed droplets [96], we are unaware of any examples of this method being used for microfiber synthesis.
Methods that involve solvent extraction, phase inversion and/or solvent evaporation are useful for particles and fibers composed of uncrosslinked polymeric systems [121–124]. Solvent evaporation methods are used off-chip to solidify droplets of a polymer solution (usually dissolved in a volatile solvent) [125]. This method provides a second step with which to control the size of the microparticle because the final size of the particle is dependent on the volume of solvent in the droplets. For the case of phase inversion methods for fiber generation, the polymer solution is used as the dispersed phase and a solution containing a non-solvent for the polymer is flowed as the outer continuous phase. At the interface there is diffusion of solvent molecules, which causes the polymer in the jet to precipitate and form a solid fiber. This method has been used to generate fibers of different compositions, including polymethylmethacrylate [124], poly(lactic-co-glycolic acid) [121], polyacrylonitrile, polysulfone and polystyrene [122].
6.2. Particle shape asymmetry
There are different methods for synthesizing non-spherical particles using two-phase microfluidics. For example, Dendukuri et al. used a T-junction device to synthesize plugs and disks [76]. At low Ca (in the squeezing regime), plugs were formed where the length of the plug decreased with increasing Ca. In their experiments, they were able to synthesize objects with aspect ratios ≈ 2.4. Longer plugs were not possible in their experiments because at even lower Ca, there was a transition from plugs to what the authors referred to as ‘wetting’, where the dispersed phase liquid flowed as one phase through the channel because the shear forces were not sufficiently large to cause the polymer to pinch off at the T-junction. This result may be due to the wetting properties of the channel or the very large viscosity ratio between the Norland optical adhesive dispersed phase and the water continuous phase, µd/µc ≈ 300. There are few examples in the literature where this co-flow wetting regime is observed and studied at such low Ca [28].
For less viscous dispersed phase liquids, higher aspect ratio plugs are possible; for example, Garstecki et al. were able to achieve aspect ratios approaching 10, though these liquid plugs were not solidified [77]. Others have used similar approaches to generate asymmetrically shaped particles [96, 103, 128]. Once precursor droplets form, they can be deformed by hydrodynamics and or by varying the droplet volume and channel cross-sectional area [103], and rapidly solidified to preserve the shape. In this manner, rods, disks, ellipsoids, and other more complex anisotropic shapes can be synthesized (Fig. 6A, B) [103].
Two-phase microfluidics can also be used to synthesize asymmetric cross-section microfibers [17, 124, 129]. Thangawng et al. [124] demonstrated that the incorporation of diagonal grooves or chevron-shaped grooves on the top and bottom surfaces of the microchannel forces the continuous phase to completely surround the core stream. With this method, they were able to successfully generate ribbon-like polymethylmethacrylate fibers by a solvent extraction method [124] and crosslinked hydroxybutyl acrylate fibers (Fig. 7D) [17, 129].
6.3. Effect of dispersed phase viscosity
Not all fluid precursors are compatible with typical microfluidic methods of drop formation. If the precursor does not meet the required material properties for stable dripping, i.e. relatively low viscosity, negligible viscoelasticity and moderate interfacial tension, it is difficult to form uniform monodisperse particles. Seo et al. [128] sought to investigate the effect of monomer viscosity on the quality of polymeric particles synthesized in flow-focusing devices. They used different multifunctional monomers with viscosities ranging from 3.5 to 1813 cP. They found that at low Ca, all monomers formed relatively large droplets. As the Ca increases, the droplet diameter of the low viscosity monomers decreased until the droplet size became independent of Ca. On the other hand, the high viscosity monomers showed a different trend. With increasing values of Ca, the drop diameter of the 586 cP monomer increased slightly then remained constant. For the highest viscosity monomer (1813 cP), the droplet size increased slightly with increasing Ca, but upon further increase the monomer jet did not break up into droplets [9, 128]. The authors performed rheological measurements on the monomers and showed that the viscosity of all the monomers did not change with increasing shear rate, verifying that the monomers were Newtonian. Thus, the authors concluded that the differences in drop formation were due to differences in viscosity. Their observations can be interpreted in terms of the flow-focusing breakup models mentioned in Section 3: 1) a shearing mechanism, where the diameter of the droplet is inversely related to the capillary number, and 2) a rate-of-flow-controlled mechanism, where the droplet volume is proportional only to the flow rate ratio, Qd/Qc. Furthermore, Nie et al. [48] observed similar behavior in their experiments, where they studied the effect of the viscosities of the phases in a microfluidic flow-focusing device. They concluded that while the drop formation of fluids with low viscosities can be described by the rate-of-flow-controlled breakup mechanism, other effects have to be considered for high viscosity fluids, such as the retardation of the speed of breakup due to high viscosity.
Particle synthesis from non-Newtonian fluids, such as lipid melts, high molecular weight polymers and copolymers, can be very difficult. The extensional viscosity of the fluids resists the pinching needed to form drops, leading to the formation of long jets that break into drops of uncontrolled size due to the Rayleigh-Plateau instability. Thus, these liquids are more compatible with microfluidic fiber synthesis. Abate et al. [92] developed a clever method for forming uniform drops of non-Newtonian fluids, which could be solidified to form particles. They used a one-step double emulsification technique to form a coaxial jet of the non-Newtonian fluid sheathed by an immiscible chaperoning fluid that is easy to emulsify. In this way, they avoid having to rely only on the Rayleigh-Plateau instability of the viscoelastic jet. By increasing the dimensions of the channel, an instability is triggered in the chaperoning fluid, which causes the chaperoning fluid to pinch into equal sized drops, which in turn causes the inner non-Newtonian fluid to also pinch off, thereby creating double emulsion drops. They were then able to solidify the core of the double emulsion droplets by different methods. The authors studied three difficult to emulsify precursor fluids: a viscoelastic UV-crosslinkable poly(N-isopropylacrylamide) (pNIPAM), a very viscous thermally crosslinkable solution of polyurethane and polybutadienediol (pU-pBDO), and a low interfacial tension lipid melt (hydrogenated coco glycerides) that was cooled to solidify.
6.4. Length and time scales relevant for in-situ solidification of jets or deformed droplets
For most of the solidification methods discussed, especially those used for on-chip generation of micro-objects, it is advantageous that the process occurs rapidly. For example, UV-initiated free radical polymerizations can typically produce solid particles in less than 100 ms, making that class of reactions very suitable to on-chip microfluidic synthesis [132–133]. Thus, if we consider a typical microfluidic experiment with a microchannel length, L ≈ 3 cm and a flow speed, U ≈ 1 cm/s, the monomer droplet or jet flows through the microchannel for L/U ≈ 3 s. This time scale is approximately an order of magnitude larger than the typical reaction time, and so is more than sufficient for typical on-chip syntheses. For solidification methods, such as ionic crosslinking and phase inversion, which rely on the diffusion of small ions or molecules, the time to form a solid micro-object is dependent on the diffusion time scales for the specific system. For example, poly(lactic-co-glycolic acid), PLGA, is a biodegradable polymer useful in different life science applications, such as fibrous scaffolds for guided cell growth [121] and biodegradable porous particles for cell encapsulation or drug delivery applications [125]. Hwang et al. 121] synthesized PLGA fibers in a coaxial device with a dispersed phase solution composed of 10 % PLGA in dimethylsulfoxide (DMSO) and a continuous phase solution of 1:1 glycerol and water. At the interface between the two solutions, there is rapid exchange of DMSO and water due to short-range diffusion, and a dense skin layer is formed. This layer reduces additional diffusion of solvent molecules, thus PLGA precipitation in the middle and central regions of the jet occurs more slowly, and voids are formed. Figure 7(A) inset shows the variations in the cross-sectional morphology of the synthesized PLGA fibers caused by the different stages in the diffusion process. The entire precipitation process, however, proceeds quickly, within 250 ms [121].
For cases where transient droplet deformations are used as the template for non-spherical particle synthesis, it is important that the solidification timescale is much shorter than that of shape relaxation. Erni et al. [96] presented scaling arguments for the deformation and solidification of droplets. The authors proposed that with a good understanding of both the flow and solidification kinetics it should be possible to define a suitable ratio of the respective capillary and gelation time scales, tcap = µ0 R/γ and tgel to define a ‘capillary gelation number’, µ0 R/γtgel, which is the ratio of the viscocapillary time to a characteristic gelation time.
6.5. Multicomponent or multiphase microparticles and microfibers
While the majority of this review focuses on two-phase flows, some of the more interesting and complex particle and fiber morphologies are achieved with three or more fluid phases, in the formation of multiple emulsions and multicomponent jets [134–142]. The controlled generation of multiple emulsions has been accomplished in different channel geometries, for example, double coaxial devices and double flow-focusing planar devices. Core-shell, Janus or multicomponent particles are readily prepared from multiple emulsions using microfluidic devices [37, 104, 126, 143–144]. Utada et al. [37] generated monodisperse double emulsions from coaxial jets. They showed control of the inner droplet size, as well as the number of inner droplets. The emulsions were solidified by polymerization of the outer shell. Hollow particles were thus prepared (Fig. 6C). Hollow fibers [93, 122, 130] can also be readily prepared using microfluidic approaches. For example, Lan et al. used a double coaxial microdevice to generate polymer microtubes by a solvent extraction method. They successfully prepared tubes in three polymer compositions, polyacrylonitrile, polysulfone and polystyrene. Choi et al. [130] used a somewhat different approach where they relied on the spreading coefficients of three liquid phases to determine whether core-shell, stratified jetting or separated jetting would occur. They used this approach to synthesize hollow crosslinked poly(ethylene glycol) fibers, where they could control the location of the core, and microribbons with different cross-sections (Fig. 7B, C).
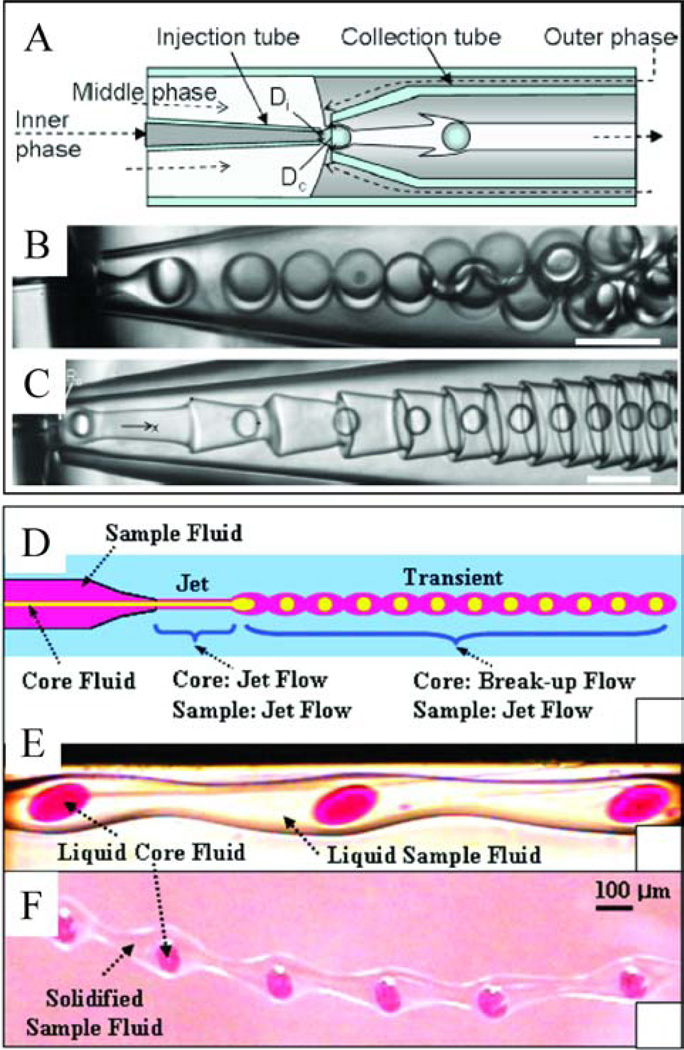
Shum et al. [145] used double coaxial devices (Figure 8A), in which the breakup of the inner phase and the middle phase can occur simultaneously or in two steps, where inner drops are first formed and trigger the breakup of the middle jet. If however, the middle phase has a very low interfacial tension, stable double emulsion generation may not be possible. In the example studied by Shum et al., the inner fluid was in the dripping regime while the middle fluid was in the jetting regime. They observed the formation of interfacial corrugations triggered by advection of the innermost drops within the jet. For their system, the interfacial tension between the middle fluid and the outermost phase was 30 µN/m, resulting in very large capillary and Weber numbers (Ca ≈ 37, We ≈ 600). As has been described in section 4.1 for coaxial devices, when Ca, We ≥ O(1), the dispersed phase is in the jetting regime. This result is illustrated in Figure 8A–C. The authors propose that the formation of such corrugated jets can potentially be a novel route to the creation of fibers with high surface area for possible biomedical and catalytic applications [145].
Figure 8.
Examples of complex multiphase flows; (A–C) Corrugated interfaces (reprinted from [145]) and (D–F) transient flows (reprinted with permission from [146]). (A) Schematic of the experimental setup for the formation of double emulsions, (B) generation of uniform double emulsion droplets, where the inner, middle and outer fluids are water, 10 % Span 80 in dodecane and water, respectively (γ between middle and outer fluids is 2.7 ± 0.2 mN/m). (C) Formation of corrugations when the interfacial tension between the middle and outer phases is significantly reduced, where the inner, middle and outer fluids are water, 2 % Span 80 in dodecane and water with 4 mM SDS, respectively (γ between middle and outer fluids is 30 ± 4 µN/m). Scale bars represent 100 µm. (D) Schematic of transient flow generation. (E) Optical microscopy images of transient liquid flow, where the inner, middle and outer fluids are dyed water, a polymerizable 4-hydroxybutyl acrylate solution and 25 % poly(vinyl alcohol) in water, respectively. (F) Solidified fiber containing liquid core droplets.
Another example of a complex, unique fiber morphology evolving from the dispersed phase fluids existing in different regimes was presented by Oh and coworkers [146], who studied the formation of core-shell microparticles from a double coaxial system. They observed the formation of a transient flow where the core jet destabilizes into droplets but the surrounding outer jet remains intact, though there were undulations along its length corresponding to the core liquid droplet distribution within the jet. They were able to solidify the jet in this transient regime to form a solid jet with liquid droplets spaced evenly along its length [146], as shown in Figure 8D–F. We note that an alternative route (not using microfluidics) to achieving a similar structure was recently reported, where a pre-formed multi-core fiber was heated to induce the Raleigh-Plateau instability in the core to form a uniform distribution of droplets within a polymer fiber [147].
6.6. Biotechnological applications of microparticles and microfibers
Important applications of microparticles and microfibers are in the fields of tissue engineering, cell biology and cell-based therapeutics [15–16, 148]. Encapsulation of cells in micro-sized hydrogels has led to applications in clinical diagnostics, pharmaceutical research and regenerative medicine [16]. Encapsulation provides an environment that allows control of the shear forces on the cells, facilitates straightforward cell visualization and control the transport of oxygen, nutrients, growth and signaling factors and metabolic products to and from the cells [16]. There are a number of important considerations when encapsulating cells in particles. These include the particle size, morphology and composition, which determine the matrix elasticity and permeability to different chemical species, the number of cells per particle and spatial configuration of cells within the particles [148]. Microfluidics has been used to successfully encapsulate cells in particles in a range of hydrogel compositions, including agarose [149], alginate [150], poly(ethylene glycol) [151], gelatin [152] and polyglycerol [151]. While microfluidics offers significant advantages in cell encapsulation over other approaches, one of the major limitations researchers are striving to improve is control over the number of cells per droplet [153–157].
Microfibers have been synthesized using microfluidics in a range of compositions conducive to cell growth, including alginate, PLGA and chitosan, for use as tissue engineering substrates. Alginate microfibers have been used as scaffolds onto which cells are seeded (Fig. 7F). For example, alginate microfibers were synthesized in a coaxial microfluidic device, where both cells and proteins were encapsulated in the fibers [113]. PLGA fibers were used to control cellular orientation of mouse fibroblast cells [158]. Chitosan microfibers were also synthesized in a coaxial device and used as the scaffold in a bio-artificial liver chip. It was found that when human hepatocarcinoma cells were seeded on the chitosan microfibers, the cells showed higher liver-specific functions [159].
The release properties of microfibers can be controlled by controlling the porosity of fibers, as for example demonstrated by Marimuthu et al. [123], who studied the protein and drug release characteristics of amphiphilic triblock copolymer-based microfibers. Fibers can be synthesized with increasing degrees of complexity in composition and morphology. For example, Janus polyurethane fibers were synthesized with porous and non-porous sides (Fig. 7E), which caused selective cell adhesion [131]. Cells can also be encapsulated in the fibers; for example endothelial cell-laden alginate hollow fibers were synthesized in a coaxial microfluidic device [111].
7. Summary
We have reviewed the main ideas and mechanisms of dripping and jetting in microfluidic multiphase flows. Using solely passive microfluidic methods, it is possible to take advantage of the behavior of multiphase flows to reproducibly form drops and jets with a significant level of control by understanding the effects of all the parameters of the system, which include the flow rates, fluid viscosities, interfacial tension, channel geometry and surface wettability. Furthermore, the dimensionless numbers, which include the capillary number and Weber number, have been shown to be both essential and convenient in describing the properties of drop and jets, as well as the transition from dripping to jetting. The field has progressed to a point where passive microfluidic methods for drop generation have become standard and widely used for specific research applications, providing reliable and consistent results.
For each of the three geometries discussed in this review, there are benefits and drawbacks to their use depending on the desired outcome. Coaxial devices are currently less convenient to rapidly prototype, as the typical method involves fitting pulled glass capillary tubes. All-PDMS coaxial devices have been demonstrated, but they require precise alignment of layers, and so are not as straightforward to assemble as the planar devices. Coaxial devices, however, are the most commonly used microfluidic geometry for microfiber synthesis. By contrast, T-junction devices are never used for fiber synthesis; in fact, as mentioned in Section 4.2, the jetting regime for this geometry is the least studied of the three geometries described in this review. The squeezing regime in T-junctions, however, is very useful for the production of liquid slugs that can be used to template elongated particles. In terms of spherical (or nearly spherical) particle synthesis, the flow-focusing geometry has been the most prevalent, possibly due to the wide range of drop sizes achievable with this geometry. Even though passive microfluidic methods can allow for significant control of the drop and jet formation processes, there are limits to their capabilities, for example in the case of non-Newtonian fluids and all-aqueous systems. Thus, for an even greater degree of control and increased flexibility in the procedure, active devices, where there is some externally controlled force such as through the use of valves and external fields, can be used [100–101, 110, 171, 187–189].
There are many applications of the drops and fluid threads generated in microfluidic devices. We chose to focus on the use of drops and jets as templates for microparticle and microfiber synthesis. Of the techniques available for the synthesis of such materials, microfluidics offers the combined advantages of monodispersity, uniformity, composition flexibility and continuous rapid production. These micro-objects are especially attractive for biologically relevant applications, which is the most dominant application studied in the literature for these classes of materials.
Acknowledgments
We thank the National Science Foundation (via grant CBET-8854046), the National Institutes of Health (via grant R01 CA155061-01) and the Grand Challenges Initiative at Princeton University for partial support of this research.
References
- 1.Whitesides GM. Nature. 2006;442:368–373. doi: 10.1038/nature05058. [DOI] [PubMed] [Google Scholar]
- 2.Stone HA, Stroock AD, Ajdari A. Annu. Rev. Fluid Mech. 2004;36:381–411. [Google Scholar]
- 3.Baroud CN, Gallaire F, Dangla R. Lab Chip. 2010;10:2032–2045. doi: 10.1039/c001191f. [DOI] [PubMed] [Google Scholar]
- 4.Christopher GF, Anna SL. J. Phys. D: Appl. Phys. 2007;40:R319–R336. [Google Scholar]
- 5.Seemann R, Brinkmann M, Pfohl T, Herminghaus S. Rep. Prog. Phys. 2012;75:016601. doi: 10.1088/0034-4885/75/1/016601. [DOI] [PubMed] [Google Scholar]
- 6.Song H, Chen DL, Ismagilov RF. Angew. Chem. Int. Ed. 2006;45:7336–7356. doi: 10.1002/anie.200601554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Theberge AB, Courtois F, Schaerli Y, Fischlechner M, Abell C, Hollfelder F, Huck WTS. Angew. Chem. Int. Ed. 2010;49:5846–5868. doi: 10.1002/anie.200906653. [DOI] [PubMed] [Google Scholar]
- 8.Wang J-T, Wang J, Han J-J. Small. 2011;7:1728–1754. doi: 10.1002/smll.201001913. [DOI] [PubMed] [Google Scholar]
- 9.Kumacheva E, Garstecki P. Microfluidic Reactors for Polymer Particles. UK: Wiley; 2011. [Google Scholar]
- 10.Comiskey B, Albert JD, Yoshizawa H, Jacobson J. Nature. 1998;394:253–255. [Google Scholar]
- 11.Oh SW, Kim CW, Cha HJ, Pal U, Kang YS. Adv. Mater. 2009;21:4987–4991. doi: 10.1002/adma.200901595. [DOI] [PubMed] [Google Scholar]
- 12.Kim S-H, Lee SY, Yang S-M, Yi G-R. NPG Asia Mater. 2011;3:25–33. [Google Scholar]
- 13.Sacanna S, Pine DJ. Curr. Opin. Colloid Interface Sci. 2011;16:96–105. [Google Scholar]
- 14.Stanway R. Mater. Sci. Technol. 2004;20:931–939. [Google Scholar]
- 15.Chung BG, Lee K-H, Khademhosseini A, Lee S-H. Lab Chip. 2012;12:45–59. doi: 10.1039/c1lc20859d. [DOI] [PubMed] [Google Scholar]
- 16.Velasco D, Tumarkin E, Kumacheva E. Small. 2012;8:1633–1642. doi: 10.1002/smll.201102464. [DOI] [PubMed] [Google Scholar]
- 17.Thangawng AL, Howell JPB, Spillmann CM, Naciri J, Ligler FS. Lab Chip. 2011;11:1157–1160. doi: 10.1039/c0lc00392a. [DOI] [PubMed] [Google Scholar]
- 18.Pardeike J, Hommoss A, Müller RH. Int. J. Pharm. 2009;366:170–184. doi: 10.1016/j.ijpharm.2008.10.003. [DOI] [PubMed] [Google Scholar]
- 19.Gouin S. Trends Food Sci. Technol. 2004;15:330–347. [Google Scholar]
- 20.Utada AS, Fernandez-Nieves A, Stone HA, Weitz DA. Phys. Rev. Lett. 2007;99:094502. doi: 10.1103/PhysRevLett.99.094502. [DOI] [PubMed] [Google Scholar]
- 21.Abate AR, Poitzsch A, Hwang Y, Lee J, Czerwinska J, Weitz DA. Phys. Rev. E. 2009;80:026310. doi: 10.1103/PhysRevE.80.026310. [DOI] [PubMed] [Google Scholar]
- 22.Guillot P, Colin A, Ajdari A. Phys. Rev. E. 2008;78:016307. doi: 10.1103/PhysRevE.78.016307. [DOI] [PubMed] [Google Scholar]
- 23.Guillot P, Colin A, Utada AS, Ajdari A. Phys. Rev. Lett. 2007;99:104502. doi: 10.1103/PhysRevLett.99.104502. [DOI] [PubMed] [Google Scholar]
- 24.Herrada MA, Gañán-Calvo AM, Guillot P. Phys. Rev. E. 2008;78:046312. doi: 10.1103/PhysRevE.78.046312. [DOI] [PubMed] [Google Scholar]
- 25.Eggers J, Villermaux E. Rep. Prog. Phys. 2008;71:036601. [Google Scholar]
- 26.Dreyfus R, Tabeling P, Willaime H. Phys. Rev. Lett. 2003;90:144505. doi: 10.1103/PhysRevLett.90.144505. [DOI] [PubMed] [Google Scholar]
- 27.Xu JH, Luo GS, Li SW, Chen GG. Lab Chip. 2006;6:131–136. doi: 10.1039/b509939k. [DOI] [PubMed] [Google Scholar]
- 28.Zagnoni M, Anderson J, Cooper JM. Langmuir. 2010;26:9416–9422. doi: 10.1021/la1004243. [DOI] [PubMed] [Google Scholar]
- 29.Nisisako T, Okushima S, Torii T. Soft Matter. 2005;1:23–27. doi: 10.1039/b501972a. [DOI] [PubMed] [Google Scholar]
- 30.Abate AR, Krummel AT, Lee D, Marquez M, Holtze C, Weitz DA. Lab Chip. 2008;8:2157–2160. doi: 10.1039/b813405g. [DOI] [PubMed] [Google Scholar]
- 31.Bauer W-AC, Fischlechner M, Abell C, Huck WTS. Lab Chip. 2010;10:1814–1819. doi: 10.1039/c004046k. [DOI] [PubMed] [Google Scholar]
- 32.Cubaud T, Tatineni M, Zhong X, Ho C-M. Phys. Rev. E. 2005;72:037302. doi: 10.1103/PhysRevE.72.037302. [DOI] [PubMed] [Google Scholar]
- 33.Garstecki P, Gitlin I, DiLuzio W, Whitesides GM, Kumacheva E, Stone HA. Appl. Phys. Lett. 2004;85:2649–2651. [Google Scholar]
- 34.Garstecki P, Stone HA, Whitesides GM. Phys. Rev. Lett. 2005;94:164501. doi: 10.1103/PhysRevLett.94.164501. [DOI] [PubMed] [Google Scholar]
- 35.van Steijn V, Kleijn CR, Kreutzer MT. Phys. Rev. Lett. 2009;103:214501. doi: 10.1103/PhysRevLett.103.214501. [DOI] [PubMed] [Google Scholar]
- 36.Dollet B, van Hoeve W, Raven J-P, Marmottant P, Versluis M. Phys. Rev. Lett. 2008;100:034504. doi: 10.1103/PhysRevLett.100.034504. [DOI] [PubMed] [Google Scholar]
- 37.Utada AS, Lorenceau E, Link DR, Kaplan PD, Stone HA, Weitz DA. Science. 2005;308:537–541. doi: 10.1126/science.1109164. [DOI] [PubMed] [Google Scholar]
- 38.Priest C, Herminghaus S, Seemann R. Appl. Phys. Lett. 2006;88:024106–024113. [Google Scholar]
- 39.Sugiura S, Nakajima M, Tong J, Nabetani H, Seki M. J. Colloid Interface Sci. 2000;227:95–103. doi: 10.1006/jcis.2000.6843. [DOI] [PubMed] [Google Scholar]
- 40.Utada AS, Fernandez-Nieves A, Gordillo JM, Weitz DA. Phys. Rev. Lett. 2008;100:014502. doi: 10.1103/PhysRevLett.100.014502. [DOI] [PubMed] [Google Scholar]
- 41.Kang E, Shin S-J, Lee KH, Lee S-H. Lab Chip. 2010;10:1856–1861. doi: 10.1039/c002695f. [DOI] [PubMed] [Google Scholar]
- 42.Link DR, Anna SL, Weitz DA, Stone HA. Phys. Rev. Lett. 2004;92:054503. doi: 10.1103/PhysRevLett.92.054503. [DOI] [PubMed] [Google Scholar]
- 43.Erb RM, Obrist D, Chen PW, Studer J, Studart AR. Soft Matter. 2011;7:8757–8761. [Google Scholar]
- 44.van Steijn V, Kleijn CR, Kreutzer MT. Lab Chip. 2010;10:2513–2518. doi: 10.1039/c002625e. [DOI] [PubMed] [Google Scholar]
- 45.Gu H, Duits MHG, Mugele F. Int. J. Mol. Sci. 2011;12:2572–2597. doi: 10.3390/ijms12042572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhao C-X, Middelberg APJ. Chem. Eng. Sci. 2011;66:1394–1411. [Google Scholar]
- 47.Anna SL, Mayer HC. Phys. Fluids. 2006;18:121512–121513. [Google Scholar]
- 48.Nie Z, Seo M, Xu S, Lewis P, Mok M, Kumacheva E, Whitesides G, Garstecki P, Stone H. Microfluid. Nanofluid. 2008;5:585–594. [Google Scholar]
- 49.Castro-Hernández E, Gundabala V, Fernández-Nieves A, Gordillo JM. New. J. Phys. 2009;11:075021. [Google Scholar]
- 50.Cordero ML, Gallaire F, Baroud CN. Phys. Fluids. 2011;23:094111–094118. [Google Scholar]
- 51.Jeong WJ, Kim JY, Choo J, Lee EK, Han CS, Beebe DJ, Seong GH, Lee SH. Langmuir. 2005;21:3738–3741. doi: 10.1021/la050105l. [DOI] [PubMed] [Google Scholar]
- 52.White FM. Fluid Mechanics. New York: McGraw-Hill; 2003. [Google Scholar]
- 53.Gañán-Calvo AM. Phys. Rev. Lett. 1998;80:285–288. [Google Scholar]
- 54.Martín-Banderas L, Flores-Mosquera M, Riesco-Chueca P, Rodríguez-Gil A, Cebolla Á, Chávez S, Gañán-Calvo AM. Small. 2005;1:688–692. doi: 10.1002/smll.200500087. [DOI] [PubMed] [Google Scholar]
- 55.Anna SL, Bontoux N, Stone HA. Appl. Phys. Lett. 2003;82:364–366. [Google Scholar]
- 56.Berthier J, Le Vot S, Tiquet P, David N, Lauro D, Benhamou PY, Rivera F. Sens. Actuators, A. 2010;158:140–148. [Google Scholar]
- 57.Cubaud T, Mason TG. Phys. Fluids. 2008;20:053302–053311. [Google Scholar]
- 58.Cygan ZT, Cabral JT, Beers KL, Amis EJ. Langmuir. 2005;21:3629–3634. doi: 10.1021/la0471137. [DOI] [PubMed] [Google Scholar]
- 59.Funfschilling D, Debas H, Li HZ, Mason TG. Phys. Rev. E. 2009;80:015301. doi: 10.1103/PhysRevE.80.015301. [DOI] [PubMed] [Google Scholar]
- 60.Lapierre F, Wu N, Zhu Y. Proc. SPIE. 2011;8204:82040H-7. [Google Scholar]
- 61.Lee W, Walker LM, Anna SL. AIP Conf. Proc. 2008;1027:994–996. [Google Scholar]
- 62.Lee W, Walker LM, Anna SL. Phys. Fluids. 2009;21:032103–032114. [Google Scholar]
- 63.Morimoto Y, Tan W-H, Takeuchi S. Biomed. Microdevices. 2009;11:369–377. doi: 10.1007/s10544-008-9243-y. [DOI] [PubMed] [Google Scholar]
- 64.Mulligan M, Rothstein J. Microfluid. Nanofluid. 2012:1–9. [Google Scholar]
- 65.Ong W-L, Hua J, Zhang B, Teo T-Y, Zhuo J, Nguyen N-T, Ranganathan N, Yobas L. Sens. Actuators, A. 2007;138:203–212. [Google Scholar]
- 66.Peng L, Yang M, Guo S-S, Liu W, Zhao X-Z. Biomed. Microdevices. 2011;13:559–564. doi: 10.1007/s10544-011-9526-6. [DOI] [PubMed] [Google Scholar]
- 67.Roberts CC, Rao RR, Loewenberg M, Brooks CF, Galambos P, Grillet AM, Nemer MB. Lab Chip. 2012;12:1540–1547. doi: 10.1039/c2lc21197a. [DOI] [PubMed] [Google Scholar]
- 68.Tafti EY, Law K, Kumar R, Cho HJ. Proc. ECTC, ASME. 2008 [Google Scholar]
- 69.Takeuchi S, Garstecki P, Weibel DB, Whitesides GM. Adv. Mater. 2005;17:1067–1072. [Google Scholar]
- 70.Ward T, Faivre M, Abkarian M, Stone HA. Electrophoresis. 2005;26:3716–3724. doi: 10.1002/elps.200500173. [DOI] [PubMed] [Google Scholar]
- 71.Yobas L, Martens S, Ong W-L, Ranganathan N. Lab Chip. 2006;6:1073–1079. doi: 10.1039/b602240e. [DOI] [PubMed] [Google Scholar]
- 72.Humphry KJ, Ajdari A, Fernández-Nieves A, Stone HA, Weitz DA. Phys. Rev. E. 2009;79:056310. doi: 10.1103/PhysRevE.79.056310. [DOI] [PubMed] [Google Scholar]
- 73.Seo M, Paquet C, Nie Z, Xu S, Kumacheva E. Soft Matter. 2007;3:986–992. doi: 10.1039/b700687j. [DOI] [PubMed] [Google Scholar]
- 74.Thorsen T, Roberts RW, Arnold FH, Quake SR. Phys. Rev. Lett. 2001;86:4163–4166. doi: 10.1103/PhysRevLett.86.4163. [DOI] [PubMed] [Google Scholar]
- 75.Christopher GF, Noharuddin NN, Taylor JA, Anna SL. Phys. Rev. E. 2008;78:036317. doi: 10.1103/PhysRevE.78.036317. [DOI] [PubMed] [Google Scholar]
- 76.Dendukuri D, Tsoi K, Hatton TA, Doyle PS. Langmuir. 2005;21:2113–2116. doi: 10.1021/la047368k. [DOI] [PubMed] [Google Scholar]
- 77.Garstecki P, Fuerstman MJ, Stone HA, Whitesides GM. Lab Chip. 2006;6:437–446. doi: 10.1039/b510841a. [DOI] [PubMed] [Google Scholar]
- 78.Glawdel T, Elbuken C, Ren CL. Phys. Rev. E. 2012;85:016322. doi: 10.1103/PhysRevE.85.016322. [DOI] [PubMed] [Google Scholar]
- 79.Guillot P, Colin A. Phys. Rev. E. 2005;72:066301. doi: 10.1103/PhysRevE.72.066301. [DOI] [PubMed] [Google Scholar]
- 80.Husny J, Cooper-White JJ. J. Non-Newtonian Fluid Mech. 2006;137:121–136. [Google Scholar]
- 81.Li X-B, Li F-C, Yang J-C, Kinoshita H, Oishi M, Oshima M. Chem. Eng. Sci. 2012;69:340–351. [Google Scholar]
- 82.Tice JD, Lyon AD, Ismagilov RF. Anal. Chim. Acta. 2004;507:73–77. [Google Scholar]
- 83.Tice JD, Song H, Lyon AD, Ismagilov RF. Langmuir. 2003;19:9127–9133. [Google Scholar]
- 84.Wang K, Lu YC, Xu JH, Tan J, Luo GS. AIChE J. 2011;57:299–306. [Google Scholar]
- 85.Xu JH, Li SW, Tan J, Wang YJ, Luo GS. AIChE J. 2006;52:3005–3010. [Google Scholar]
- 86.Gunther A, Khan SA, Thalmann M, Trachsel F, Jensen KF. Lab Chip. 2004;4:278–286. doi: 10.1039/b403982c. [DOI] [PubMed] [Google Scholar]
- 87.Okushima S, Nisisako T, Torii T, Higuchi T. Langmuir. 2004;20:9905–9908. doi: 10.1021/la0480336. [DOI] [PubMed] [Google Scholar]
- 88.Husny J, Jin H, Harvey EC, Cooper-White J. Smart Mater. Struct. 2006;15:S117–S123. [Google Scholar]
- 89.Gupta A, Kumar R. Phys. Fluids. 2010;22:122001–122011. [Google Scholar]
- 90.De Menech M, Garstecki P, Jousse F, Stone HA. J. Fluid Mech. 2008;595:141–161. [Google Scholar]
- 91.Nisisako T, Torii T, Higuchi T. Chem. Eng. J. 2004;101:23–29. [Google Scholar]
- 92.Abate AR, Kutsovsky M, Seiffert S, Windbergs M, Pinto LFV, Rotem A, Utada AS, Weitz DA. Adv. Mater. 2011;23:1757–1760. doi: 10.1002/adma.201004275. [DOI] [PubMed] [Google Scholar]
- 93.Jeong W, Kim J, Kim S, Lee S, Mensing G, Beebe DJ. Lab Chip. 2004;4:576–580. doi: 10.1039/b411249k. [DOI] [PubMed] [Google Scholar]
- 94.Zarrin F, Dovichi NJ. Anal. Chem. 1985;57:2690–2692. doi: 10.1021/ac00286a010. [DOI] [PubMed] [Google Scholar]
- 95.Hardt S, Hahn T. Lab Chip. 2012;12:434–442. doi: 10.1039/c1lc20569b. [DOI] [PubMed] [Google Scholar]
- 96.Erni P, Cramer C, Marti I, Windhab EJ, Fischer P. Adv. Colloid Interface Sci. 2009;150:16–26. doi: 10.1016/j.cis.2009.05.005. [DOI] [PubMed] [Google Scholar]
- 97.Ziemecka I, van Steijn V, Koper GJM, Rosso M, Brizard AM, van Esch JH, Kreutzer MT. Lab Chip. 2011;11:620–624. doi: 10.1039/c0lc00375a. [DOI] [PubMed] [Google Scholar]
- 98.Ziemecka I, van Steijn V, Koper GJM, Kreutzer MT, van Esch JH. Soft Matter. 2011;7:9878–9880. [Google Scholar]
- 99.Sauret A, Shum HC. Appl. Phys. Lett. 2012;100:154106–154114. [Google Scholar]
- 100.Choi YH, Song YS, Kim DH. J. Chromatogr., A. 2010;1217:3723–3728. doi: 10.1016/j.chroma.2010.04.015. [DOI] [PubMed] [Google Scholar]
- 101.Song YS, Choi YH, Kim DH. J. Chromatogr., A. 2007;1162:180–186. doi: 10.1016/j.chroma.2007.06.032. [DOI] [PubMed] [Google Scholar]
- 102.Shum HC, Varnell J, Weitz DA. Biomicrofluidics. 2012;6:012808–012809. doi: 10.1063/1.3670365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Xu S, Nie Z, Seo M, Lewis P, Kumacheva E, Stone HA, Garstecki P, Weibel DB, Gitlin I, Whitesides GM. Angew. Chem. Int. Ed. 2005;44:724–728. doi: 10.1002/anie.200462226. [DOI] [PubMed] [Google Scholar]
- 104.Seiffert S, Romanowsky MB, Weitz DA. Langmuir. 2010;26:14842–14847. doi: 10.1021/la101868w. [DOI] [PubMed] [Google Scholar]
- 105.Seiffert S, Weitz DA. Soft Matter. 2010;6:3184–3190. [Google Scholar]
- 106.Quevedo E, Steinbacher J, McQuade DT. J. Am. Chem. Soc. 2005;127:10498–10499. doi: 10.1021/ja0529945. [DOI] [PubMed] [Google Scholar]
- 107.Kolb HC, Finn MG, Sharpless KB. Angew. Chem. Int. Ed. 2001;40:2004–2021. doi: 10.1002/1521-3773(20010601)40:11<2004::AID-ANIE2004>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- 108.Rossow T, Heyman JA, Ehrlicher AJ, Langhoff A, Weitz DA, Haag R, Seiffert S. J. Am. Chem. Soc. 2012;134:4983–4989. doi: 10.1021/ja300460p. [DOI] [PubMed] [Google Scholar]
- 109.Huang K-S, Lai T-H, Lin Y-C. Lab Chip. 2006;6:954–957. doi: 10.1039/b606424h. [DOI] [PubMed] [Google Scholar]
- 110.Kang E, Jeong GS, Choi YY, Lee KH, Khademhosseini A, Lee S-H. Nat Mater. 2011;10:877–883. doi: 10.1038/nmat3108. [DOI] [PubMed] [Google Scholar]
- 111.Lee KH, Shin SJ, Park Y, Lee S-H. Small. 2009;5:1264–1268. doi: 10.1002/smll.200801667. [DOI] [PubMed] [Google Scholar]
- 112.Liu K, Ding H-J, Liu J, Chen Y, Zhao X-Z. Langmuir. 2006;22:9453–9457. doi: 10.1021/la061729+. [DOI] [PubMed] [Google Scholar]
- 113.Shin S-J, Park J-Y, Lee J-Y, Park H, Park Y-D, Lee K-B, Whang C-M, Lee S-H. Langmuir. 2007;23:9104–9108. doi: 10.1021/la700818q. [DOI] [PubMed] [Google Scholar]
- 114.Zhang H, Tumarkin E, Peerani R, Nie Z, Sullan RMA, Walker GC, Kumacheva E. J. Am. Chem. Soc. 2006;128:12205–12210. doi: 10.1021/ja0635682. [DOI] [PubMed] [Google Scholar]
- 115.Zhang H, Tumarkin E, Sullan RMA, Walker GC, Kumacheva E. Macromol. Rapid Commun. 2007;28:527–538. [Google Scholar]
- 116.Yamada M, Sugaya S, Naganuma Y, Seki M. Soft Matter. 2012;8:3122–3130. [Google Scholar]
- 117.Tan WH, Takeuchi S. Adv. Mater. 2007;19:2696–2701. [Google Scholar]
- 118.Sugiura S, Oda T, Izumida Y, Aoyagi Y, Satake M, Ochiai A, Ohkohchi N, Nakajima M. Biomaterials. 2005;26:3327–3331. doi: 10.1016/j.biomaterials.2004.08.029. [DOI] [PubMed] [Google Scholar]
- 119.Walther B, Cramer C, Tiemeyer A, Hamberg L, Fischer P, Windhab EJ, Hermansson A-M. J. Colloid Interface Sci. 2005;286:378–386. doi: 10.1016/j.jcis.2005.01.054. [DOI] [PubMed] [Google Scholar]
- 120.Wassén S, Rondeau E, Sott K, Lorén N, Fischer P, Hermansson A-M. Food Hydrocolloids. 2012;28:20–27. [Google Scholar]
- 121.Hwang CM, Khademhosseini A, Park Y, Sun K, Lee S-H. Langmuir. 2008;24:6845–6851. doi: 10.1021/la800253b. [DOI] [PubMed] [Google Scholar]
- 122.Lan W, Li S, Lu Y, Xu J, Luo G. Lab Chip. 2009;9:3282–3288. doi: 10.1039/b913247c. [DOI] [PubMed] [Google Scholar]
- 123.Marimuthu M, Kim S, An J. Soft Matter. 2010;6:2200–2207. [Google Scholar]
- 124.Thangawng AL, Howell PB, Jr, Richards JJ, Erickson JS, Ligler FS. Lab Chip. 2009;9:3126–3130. doi: 10.1039/b910581f. [DOI] [PubMed] [Google Scholar]
- 125.Choi S-W, Zhang Y, Xia Y. Adv. Funct. Mater. 2009;19:2943–2949. doi: 10.1002/adfm.200900763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Prasad N, Perumal J, Choi C-H, Lee C-S, Kim D-P. Adv. Funct. Mater. 2009;19:1656–1662. [Google Scholar]
- 127.Shepherd RF, Conrad JC, Rhodes SK, Link DR, Marquez M, Weitz DA, Lewis JA. Langmuir. 2006;22:8618–8622. doi: 10.1021/la060759+. [DOI] [PubMed] [Google Scholar]
- 128.Seo M, Nie Z, Xu S, Mok M, Lewis PC, Graham R, Kumacheva E. Langmuir. 2005;21:11614–11622. doi: 10.1021/la050519e. [DOI] [PubMed] [Google Scholar]
- 129.Shields AR, Spillmann CM, Naciri J, Howell PB, Thangawng AL, Ligler FS. Soft Matter. 2012;8:2656–2660. [Google Scholar]
- 130.Choi C-H, Yi H, Hwang S, Weitz DA, Lee C-S. Lab Chip. 2011;11:1477–1483. doi: 10.1039/c0lc00711k. [DOI] [PubMed] [Google Scholar]
- 131.Jung J-H, Choi C-H, Chung S, Chung Y-M, Lee C-S. Lab Chip. 2009;9:2596–2602. doi: 10.1039/b901308c. [DOI] [PubMed] [Google Scholar]
- 132.Dendukuri D, Doyle PS. Adv. Mater. 2009;21:4071–4086. [Google Scholar]
- 133.Dendukuri D, Pregibon DC, Collins J, Hatton TA, Doyle PS. Nat. Mater. 2006;5:365–369. doi: 10.1038/nmat1617. [DOI] [PubMed] [Google Scholar]
- 134.Seiffert S. Macromol. Rapid Commun. 2011;32:1600–1609. doi: 10.1002/marc.201100342. [DOI] [PubMed] [Google Scholar]
- 135.Pannacci N, Bruus H, Bartolo D, Etchart I, Lockhart T, Hennequin Y, Willaime H, Tabeling P. Phys. Rev. Lett. 2008;101:164502. doi: 10.1103/PhysRevLett.101.164502. [DOI] [PubMed] [Google Scholar]
- 136.Zhang Q, Lin B, Qin J. Microfluid. Nanofluid. 2012;12:33–39. [Google Scholar]
- 137.Chen PW, Erb RM, Studart AR. Langmuir. 2011;28:144–152. doi: 10.1021/la203088u. [DOI] [PubMed] [Google Scholar]
- 138.Chen H, Zhao Y, Li J, Guo M, Wan J, Weitz DA, Stone HA. Lab Chip. 2011;11:2312–2315. doi: 10.1039/c1lc20265k. [DOI] [PubMed] [Google Scholar]
- 139.Wang W, Xie R, Ju X-J, Luo T, Liu L, Weitz DA, Chu L-Y. Lab Chip. 2011;11:1587–1592. doi: 10.1039/c1lc20065h. [DOI] [PubMed] [Google Scholar]
- 140.Zhao Y, Shum HC, Chen H, Adams LLA, Gu Z, Weitz DA. J. Am. Chem. Soc. 2011;133:8790–8793. doi: 10.1021/ja200729w. [DOI] [PubMed] [Google Scholar]
- 141.Wan J, Bick A, Sullivan M, Stone HA. Adv. Mater. 2008;20:3314–3318. [Google Scholar]
- 142.Wan J, Stone HA. Langmuir. 2011;28:37–41. doi: 10.1021/la203824f. [DOI] [PubMed] [Google Scholar]
- 143.Nie Z, Xu S, Seo M, Lewis PC, Kumacheva E. J. Am. Chem. Soc. 2005;127:8058–8063. doi: 10.1021/ja042494w. [DOI] [PubMed] [Google Scholar]
- 144.Nisisako T, Torii T, Takahashi T, Takizawa Y. Adv. Mater. 2006;18:1152–1156. [Google Scholar]
- 145.Shum HC, Sauret A, Fernandez-Nieves A, Stone HA, Weitz DA. Phys. Fluids. 2010;22:082002–082005. [Google Scholar]
- 146.Oh H-J, Kim S-H, Baek J-Y, Seong G-H, Lee S-H. J. Micromech. Microeng. 2006;16:285. [Google Scholar]
- 147.Kaufman JJ, Tao G, Shabahang S, Banaei E-H, Deng DS, Liang X, Johnson SG, Fink Y, Abouraddy AF. Nature. 2012 doi: 10.1038/nature11215. advance online publication. [DOI] [PubMed] [Google Scholar]
- 148.Wan J. Polymers. 2012;4:1084–1108. [Google Scholar]
- 149.Eun Y-J, Utada AS, Copeland MF, Takeuchi S, Weibel DB. ACS Chem. Biol. 2010;6:260–266. doi: 10.1021/cb100336p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Kim C, Chung S, Kim YE, Lee KS, Lee SH, Oh KW, Kang JY. Lab Chip. 2011;11:246–252. doi: 10.1039/c0lc00036a. [DOI] [PubMed] [Google Scholar]
- 151.Steinhilber D, Seiffert S, Heyman JA, Paulus F, Weitz DA, Haag R. Biomaterials. 2011;32:1311–1316. doi: 10.1016/j.biomaterials.2010.10.010. [DOI] [PubMed] [Google Scholar]
- 152.Sakai S, Ito S, Inagaki H, Hirose K, Matsuyama T, Taya M, Kawakami K. Biomicrofluidics. 2011;5:013402–013407. doi: 10.1063/1.3516657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Chabert M, Viovy J-L. Proc. Natl. Acad. Sci. USA. 2008;105:3191–3196. doi: 10.1073/pnas.0708321105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Clausell-Tormos J, Lieber D, Baret J-C, El-Harrak A, Miller OJ, Frenz L, Blouwolff J, Humphry KJ, Köster S, Duan H, Holtze C, Weitz DA, Griffiths AD, Merten CA. Chem. Biol. 2008;15:427–437. doi: 10.1016/j.chembiol.2008.04.004. [DOI] [PubMed] [Google Scholar]
- 155.Tumarkin E, Tzadu L, Csaszar E, Seo M, Zhang H, Lee A, Peerani R, Purpura K, Zandstra PW, Kumacheva E. Integr. Biol. 2011;3:653–662. doi: 10.1039/c1ib00002k. [DOI] [PubMed] [Google Scholar]
- 156.Abate AR, Chen C-H, Agresti JJ, Weitz DA. Lab Chip. 2009;9:2628–2631. doi: 10.1039/b909386a. [DOI] [PubMed] [Google Scholar]
- 157.Edd JF, Di Carlo D, Humphry KJ, Koster S, Irimia D, Weitz DA, Toner M. Lab Chip. 2008;8:1262–1264. doi: 10.1039/b805456h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Hwang C, Park Y, Park J, Lee K, Sun K, Khademhosseini A, Lee S. Biomed. Microdevices. 2009;11:739–746. doi: 10.1007/s10544-009-9287-7. [DOI] [PubMed] [Google Scholar]
- 159.Lee KH, Shin SJ, Kim C-B, Kim JK, Cho YW, Chung BG, Lee S-H. Lab Chip. 2010;10:1328–1334. doi: 10.1039/b924987g. [DOI] [PubMed] [Google Scholar]
- 160.Kim JH, Choi WC, Kim HY, Kang Y, Park Y-K. Powder Technol. 2005;153:166–175. [Google Scholar]
- 161.Sander JS, Studart AR. Langmuir. 2011;27:3301–3307. doi: 10.1021/la1035344. [DOI] [PubMed] [Google Scholar]
- 162.Kim J-W, Utada AS, Fernández-Nieves A, Hu Z, Weitz DA. Angew. Chem. Int. Ed. 2007;46:1819–1822. doi: 10.1002/anie.200604206. [DOI] [PubMed] [Google Scholar]
- 163.Liu S, Deng R, Li W, Zhu J. Adv. Funct. Mater. 2012;22:1692–1697. [Google Scholar]
- 164.Yeh C-H, Lin P-W, Lin Y-C. Microfluid. Nanofluid. 2010;8:115–121. [Google Scholar]
- 165.Abraham S, Jeong EH, Arakawa T, Shoji S, Kim KC, Kim I, Go JS. Lab Chip. 2006;6:752–756. doi: 10.1039/b518006f. [DOI] [PubMed] [Google Scholar]
- 166.Shojaei-Zadeh S, Morris JF, Couzis A, Maldarelli C. J. Colloid Interface Sci. 2011;363:25–33. doi: 10.1016/j.jcis.2011.06.073. [DOI] [PubMed] [Google Scholar]
- 167.De Geest BG, Urbanski JP, Thorsen T, Demeester J, De Smedt SC. Langmuir. 2005;21:10275–10279. doi: 10.1021/la051527y. [DOI] [PubMed] [Google Scholar]
- 168.Barnes SE, Cygan ZT, Yates JK, Beers KL, Amis EJ. Analyst. 2006;131:1027–1033. doi: 10.1039/b603693g. [DOI] [PubMed] [Google Scholar]
- 169.Nie Z, Li W, Seo M, Xu S, Kumacheva E. J. Am. Chem. Soc. 2006;128:9408–9412. doi: 10.1021/ja060882n. [DOI] [PubMed] [Google Scholar]
- 170.Lone S, Kim SH, Nam SW, Park S, Joo J, Cheong IW. Chem. Commun. 2011;47:2634–2636. doi: 10.1039/c0cc04517a. [DOI] [PubMed] [Google Scholar]
- 171.Nunes JK, Sadlej K, Tam JI, Stone HA. Lab Chip. 2012;12:2301–2304. doi: 10.1039/c2lc40280g. [DOI] [PubMed] [Google Scholar]
- 172.Kesselman LRB, Shinwary S, Selvaganapathy PR, Hoare T. Small. 2012;8:1092–1098. doi: 10.1002/smll.201102113. [DOI] [PubMed] [Google Scholar]
- 173.Teh S-Y, Khnouf R, Fan H, Lee AP. Biomicrofluidics. 2011;5:044113–044212. doi: 10.1063/1.3665221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Fang A, Gaillard C, Douliez J-P. Chem. Mater. 2011;23:4660–4662. [Google Scholar]
- 175.Lin Y-S, Yang C-H, Wang C-Y, Chang F-R, Huang K-S, Hsieh W-C. Sensors. 2012;12:1455–1467. doi: 10.3390/s120201455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.Kuehne AJC, Weitz DA. Chem. Commun. 2011;47:12379–12381. doi: 10.1039/c1cc14251h. [DOI] [PubMed] [Google Scholar]
- 177.Huang S, Lin B, Qin J. Electrophoresis. 2011;32:3364–3370. doi: 10.1002/elps.201100340. [DOI] [PubMed] [Google Scholar]
- 178.Lin Y-S, Huang K-S, Yang C-H, Wang C-Y, Yang Y-S, Hsu H-C, Liao Y-J, Tsai C-W. PLoS ONE. 2012;7:e33184. doi: 10.1371/journal.pone.0033184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179.Yang C-H, Huang K-S, Chang J-Y. Biomed. Microdevices. 2007;9:253–259. doi: 10.1007/s10544-006-9029-z. [DOI] [PubMed] [Google Scholar]
- 180.Lin Y-S, Yang C-H LuK, Huang K-S, Zheng Y-Z. Electrophoresis. 2011;32:3157–3163. doi: 10.1002/elps.201100343. [DOI] [PubMed] [Google Scholar]
- 181.Steinbacher JL, Moy RWY, Price KE, Cummings MA, Roychowdhury C, Buffy JJ, Olbricht WL, Haaf M, McQuade DT. J. Am. Chem. Soc. 2006;128:9442–9447. doi: 10.1021/ja0612403. [DOI] [PubMed] [Google Scholar]
- 182.Cho S-H, Jun J-B, Ryu J-H, Suh K-D. Colloids, Surfaces A: Physicochem. Eng. Aspects. 2005;254:1–7. [Google Scholar]
- 183.Groß GA, Hamann C, Günther PM, Köhler JM. Chem. Eng. Technol. 2007;30:341–346. [Google Scholar]
- 184.Kubo A, Shinmori H, Takeuchi T. Chem. Lett. 2006;35:588–589. [Google Scholar]
- 185.Yeh C-H, Zhao Q, Lee S-J, Lin Y-C. Sens. Actuators, A. 2009;151:231–236. [Google Scholar]
- 186.Kumachev A, Greener J, Tumarkin E, Eiser E, Zandstra PW, Kumacheva E. Biomaterials. 2011;32:1477–1483. doi: 10.1016/j.biomaterials.2010.10.033. [DOI] [PubMed] [Google Scholar]
- 187.Churski K, Michalski J, Garstecki P. Lab Chip. 2010;10:512–518. doi: 10.1039/b915155a. [DOI] [PubMed] [Google Scholar]
- 188.Lin Y-H, Lee C-H, Lee G-B. J. Microelectromech. Syst. 2008;17:573–581. [Google Scholar]
- 189.Abate AR, Romanowsky MB, Agresti JJ, Weitz DA. Appl. Phys. Lett. 2009;94:023503. [Google Scholar]