Comparing adaptive procedures for estimating the psychometric function for an auditory gap detection task

Abstract

A subject’s sensitivity to a stimulus variation can be studied by estimating the psychometric function. Generally speaking, three parameters of the psychometric function are of interest: the performance threshold, the slope of the function, and the rate at which attention lapses occurs. In the current study, three psychophysical procedures were used to estimate the three-parameter psychometric function for an auditory gap detection task. They were an up-down staircase (up-down) procedure, an entropy-based Bayesian (entropy) procedure, and an updated maximum-likelihood (UML) procedure. Data collected from four young, normal-hearing listeners showed that while all three procedures provided similar estimates of the threshold parameter, the up-down procedure performed slightly better in estimating the slope and lapse rate for 200 trials of data collection. When the lapse rate was increased by mixing random responses into the three adaptive procedures, the larger lapse rate was especially detrimental to the efficiency of the up-down procedure, and the UML procedure provided better estimates of the threshold and slope than the other two procedures.

Many psychophysical experiments measure people’s ability to detect a change in one or more aspects of a physical stimulus. As the magnitude of the change, or the signal strength, increases, the probability of detecting the change typically increases as well. Psychometric functions describe the dependence of detectability on signal strength, making psychometric functions an important tool for the study and modeling of perceptual sensitivity. Typically, a psychometric function takes the form of a sigmoidal function, which can be described using three parameters: (1) the detection threshold, i.e. the signal strength at the center of the psychometric function’s dynamic range; (2) the slope of the psychometric function; and (3) the lapse rate, i.e. the distance between 100 percent correct and the function’s upper asymptote. The lapse rate is named so because attentional lapses provide an explanation for the observation that measured psychometric function may not reach 100 percent correct response.

A classic procedure for estimating the psychometric function utilizes the method of constant stimuli. In this procedure, the percent correct is estimated at each of several pre-selected signal strengths. The psychometric function is obtained by fitting the resulting percent-correct data to a pre-specified function. Although a widely accepted procedure, the method of constant stimuli can lead to very time consuming data collection. Consequently, adaptive tracking procedures have been proposed with the goal of more efficient estimation of either threshold, or more generally, psychometric functions. Most of these procedures use information gained from previous trials to determine the stimulus placement on the following trials, and can be roughly classified into three categories: (1) up-down staircase adaptive tracking procedures (e.g., Levitt, 1971), (2) min-variance Bayesian procedures (e.g., Green, 1990), and (3) min-entropy Bayesian procedures (e.g., Kontsevich & Tyler, 1999).

Non-parametric staircase procedures are typically used to estimate the signal strength at a predetermined percent correct (i.e. threshold). Typically, signal strength is reduced following a correct response or increased following an incorrect response. To ensure that the signal strength converges rapidly towards the target percent correct, many procedures adaptively adjust the step size by which the signal strength is manipulated following each trials (e.g., PEST procedure, Taylor & Creelman, 1967; Kaernbach, 1991), while others use fixed step size and modulate the probability of increasing versus decreasing the signal strength after each trial (e.g., Derman, 1957; Durham & Flournoy, 1995). Levitt (1971) described a transformed up-down procedure, in which different rules for increments and decrements of signal strength yield different target percent correct convergences. For instance, given a fixed step size, if an increment of signal strength takes place following one incorrect response and a decrement occurs after one correct response (1-down, 1-up track), the procedure would place the signal strength at the 50-% correct point on the psychometric function. On the other hand, if two consecutive correct responses are required for a decrement but a single incorrect response leads to an increment (2-down, 1-up track), the signal strength would be placed at the 70.7% point.

Although staircase procedures were originally proposed to estimate one point on the psychometric function (i.e. the threshold), several studies have been conducted to explore their usefulness in estimating the slope of the psychometric function using maximum-likelihood algorithms. Leek et al. (1992) investigated the reliability and accuracy of using transformed up-down procedures for slope estimation and found that accurate psychometric function slope estimates can be achieved using these procedures, however, when the number of experimental trials is small (e.g., less than 100 trials), the slope estimates could be biased, particularly when the slope of the true psychometric function is relatively shallow. In a simulation study, Kaernbach (2001) studied the origin of this type of bias in the slope estimates and found that the staircase procedures that estimate thresholds at a certain percentage correct on the psychometric function would introduce sequential dependency between adjacent trials. However, the maximum-likelihood estimation of the psychometric-function requires independent data across trials. As a result, the estimated slopes using maximum-likelihood algorithms are usually steeper than the true psychometric-function slopes. The author suggested that to prevent biases in the slope estimates, experimenters could either use interleaved staircase tracks targeting two different points on the psychometric function or Bayesian adaptive procedures that provide interim estimation of the psychometric-function slope during the run. Unlike the slope parameter, there has been no study systematically addressing the question of whether the lapse rate can be reliably estimated using transformed up-down procedures.

In addition to staircase procedures, Bayesian adaptive procedures have been proposed (e.g., QUEST, Watson & Pelli, 1983; ZEST, King-Smith & Rose, 1997), and, with increasingly fast computers, are gaining popularity. These procedures update the posterior distributions of the psychometric-function parameters on a trial-by-trial basis according to Bayes’ rule. Closely related to these Bayesian procedures are maximum-likelihood procedures (Green, 1990, 1993) that follow the same procedure, although rather than posteriors, they use the likelihood functions for parameter estimation¹. On a given trial, a current best estimate of the psychometric function is obtained based on either posterior distributions or likelihood functions. The signal strength of the following trial is then chosen, based on a pre-defined sampling strategy, at one of a few specific points on the best-fitted psychometric function. These special locations for stimulus placement, the so-called “sweet points”, are derived to minimize the expected variances in the parameter. It has been found that for psychometric functions taking the form of a logistic function, there exists one sweet point optimized for the estimation of the threshold parameter (Green, 1990), and two sweet points for the slope parameter (King-Smith & Rose, 1997; Brand & Kollmeier, 2002). In a recent study, Shen and Richards (2012) also showed that the best sampling strategy for estimating the lapse rate is to present stimuli at the upper limit of signal strength. Therefore, several sweet points might co-exist and rules must be implemented to select the appropriate sweet point on each trial. In their ZEST procedure, King-Smith and Rose (1997) used an alternating sweet-point selection rule; the stimulus was placed alternatingly at one of the two sweet points for the slope parameter.

To enable the inclusion of more than two sweet points for concurrent estimation of multiple parameters of the psychometric function, Shen and Richards (2012) described a sweet-point selection rule based on the transformed up-down procedure, in which the signal strength was shifted down to the next highest sweet point after n consecutive correct responses and shifted up to the next lower sweet point after a single incorrect response. Note that the signal strength might change even though the same sweet point was visited on two different trials because sweet point estimates are changed as the estimate of the psychometric function is updated trial-by-trial. This n-down, 1-up sweet-point selection rule has the potential advantage of making the experiment easy to follow for naïve listeners, allowing subjects to maintain performance at a certain percent correct. Using this sweet-point selection rule, Shen and Richards (2012) investigated the efficiency of an updated maximum-likelihood procedure (UML) that utilized four sweet points in a simulation study. Results suggested that extending the stimulus placement to four sweet points improved the estimation of the psychometric-function parameters, especially for the slope and lapse rate.

The procedures described above use sampling strategies that minimize the variances of the parameter estimates. Criteria other than variance minimization have also been used in Bayesian adaptive procedures. Kontsevich and Tyler (1999) described a procedure that determines signal strength by performing a one-step-ahead search that minimized the expected entropy function. For example, after a trial, the parameter posterior distributions might be concentrated into narrow regions exhibiting low entropies, or widely spread across the parameter space exhibiting high entropies. Depending on the signal strength on the following trial, the total entropies might be expected to increase or decrease. According to Kontsevich and Tyler (1999), the optimal place to sample is at the signal strength that minimizes overall expected entropy, thereby maximizing expected information gain. Both computer simulations and psychophysical experiments suggested that the entropy-based Bayesian procedure with a two-alternative forced-choice task yielded accurate threshold estimates (within 2 dB) with as few as 30 trials, while a good estimate of the psychometric-function slope takes, on average, 300 trials.

The current study compared three adaptive procedures: the up-down staircase procedure (Levitt, 1971), the entropy-based Bayesian procedure (Kontsevich & Tyler, 1999), and the UML procedure (Shen & Richards, 2012) in auditory gap detection experiments. In Experiment I, the three procedures were evaluated in terms of the variability of the parameter estimates, test-retest repeatability and rates of convergence. Experiment II evaluated the performance of these procedures when frequent lapses of attention occur.

Experiment I: Estimating the psychometric function using three adaptive procedures

Participants

Four normal-hearing listeners (S1-4) participated in the current experiment. All listeners were between 18 and 35 years of age and had audiometric thresholds equal or better than 15 dB HL between 250 and 8000 Hz in both ears. The left ears of the listeners were tested in the experiment. The subjects practiced the gap detection task for at least two hours before the data collection began. Listeners were paid for their participation. The experiment was conducted in 2-hour sessions. For each listener, no more than one session was run on a single day.

Stimuli

The ability to detect a silent gap in an otherwise continuous sound is a measure of the auditory system’s sensitivity to intensity fluctuations over time (e.g,. Plomp, 1964; Penner, 1975; Fitzgibbons & Wightman, 1982; Shailer & Moore, 1983). In the current study, the detection of a silent gap in a broadband noise carrier was measured for four young, normal-hearing listeners. Four sound intervals were presented on each trial, separated by 500-ms inter-stimulus intervals. Each interval contained a broadband noise, presented at 70 dB SPL. The duration of the noise was 500 ms including 5-ms cosine-squared onset/offset ramps. In either the second or the third interval, a brief silent gap was introduced to the temporal center of the noise. The gap was ramped on and off using 5-ms cosine-squared ramps. The duration of the gap was defined from the half-amplitude point of its onset to that of its offset. The listeners were instructed to select the interval that contained the gap with the understanding that it would only occur in one of the middle two intervals.

All stimuli were generated digitally at a sampling frequency of 44100 Hz and were presented to the left ear of each listener via a 24-bit soundcard (Envy23 PCI controller, VIA Technologies, Inc., Taipei, Taiwan) installed on the experimental computer, a programmable attenuator (PA4, Tucker-Davis Technologies, Inc., Alachua, FL), a headphone buffer (HB6, Tucker-Davis Technologies, Inc., Alachua, FL), and a headphone (HD410 SL, Sennheiser, Old Lyme, CT). Each stimulus presentation was followed by a visual feedback indicating the correct response. The experiment was conducted in a double-walled, sound-attenuating booth.

Procedure

For the gap detection task, the psychometric function was assumed to take the form of a logistic function:

$$p=\gamma +(1-\gamma -\lambda )/(1+e^{-\beta (x-\alpha )}),$$ (1)

where p indicates proportion correct; x is the gap duration in decibel unit ( $x=20log\frac{\text{gap}\text{duration}}{1\times {10}^{-3}}$); α, β, and λ are the threshold, slope, and lapse rate of the psychometric function; =0.5 is the chance performance level for the two-alternative forced-choice paradigm.

Three procedures were used for data collection: (1) the up-down staircase procedure, (2) the entropy-based Bayesian procedure, and (3) the UML procedure. For the staircase procedure, 200 trials were run, which consisted of four adaptive tracks of 50 trials. On the first trial, the gap duration was 35 dB (56.2 ms in the physical scale), which was reduced after two consecutive correct responses and increased after a single incorrect response. The initial step size of 8 dB was reduced to 5 dB after the first two reversals. It was reduced further to 2 dB after the first four reversals.

For the entropy procedure, the parameter space was a grid of α, β, and λ values. The α parameter took 18 values ranging from −3 to 31 dB (0.7 to 35.5 ms) with 2 dB spacing. The β parameter took 11 log-spaced values ranging from 0.1 to 10. The λ parameter took five values, linearly spaced between 0 and 0.2. Flat, uninformative priors were used for the three parameters. The signal strength, i.e. the gap duration, took 21 potential values, linearly spaced between −9 and 35 dB (logarithmically spaced between 0.35 and 56.2 ms). Each adaptive track consisted of 200 trials, which were divided into four blocks of 50 trials. Following the procedure described by Kontsevich and Tyler (1999), before each trial, the posterior parameter distributions were calculated for each potential gap duration and each potential response (correct or incorrect). The entropies of these parameter distributions were calculated, and the expected total entropy was then derived for each potential gap duration. The gap duration that led to the minimum expected entropy was used in the following stimulus presentation. After obtaining the listener’s response, the posterior parameter distributions were updated, and the procedure was repeated to select the gap duration for the next trial.

The parameter space for the UML procedure was the same as the one used in the entropy procedure. Each adaptive track consisted of 200 trials, which were divided into four blocks of 50 trials. The initial gap duration was 35 dB (56.2 ms). Following each trial, the posterior parameter distributions were calculated based on the listener’s response, which updated the best-fitted psychometric function. Then, the signal strength was place at one of the four sweet points based on a 2-down, 1-up sweet-point selection rule (Shen & Richards, 2012). From short to long gap duration on the psychometric function, the four sweet points were the lower β sweet point, the α sweet point, the upper β sweet point, and the λ sweet point. The sweet points for the α, β parameters were re-estimated on a trial-by-trial basis, while the sweet point for the λ parameter was fixed at 35 dB². The gap duration was shifted to the adjacent lower sweet point after two consecutive correct responses and was shifted to the adjacent higher sweet point after a single incorrect response. When the gap duration was already at the lowest sweet point (i.e. the lower β sweet point), the gap duration remained the same even if two correct responses were collected. Similarly, when the gap duration was at the highest sweet point (i.e. the λ sweet point), the gap duration stayed at that sweet point, even an incorrect response was collected.

For each listener, gap detection data were collected using the three procedures in random order³. This included four adaptive tracks for the up-down procedure, and one track for each of the entropy and UML procedures⁴. When completed, the process was repeated with the three procedures tested in the reverse order.

Psychometric functions for individual listeners were estimated from data collected for each procedure, one function for each repetition, yielding six psychometric functions per listener. This was done using the psignifit routine developed by Witchmann and Hill (2001a, b). Flat priors were used for all parameters. The ranges of the parameters were from −20 to 20 for α, from 0.1 to 10 for β, and from 0 to 0.3 for λ. To provide a best estimate of the true underlying psychometric function, all data collected from each listener were pooled (1200 trials), and the parameter estimates were calculated using the psignifit routine.

For each procedure and for each of the α, β, and λ parameters, let φ_k denote the best parameter estimate using the pooled data for the kth listener and let φ_r,k,n denote the parameter estimate obtained from the kth listener in the rth repetition and after the nth trial. The goodness of the parameter estimate for the kth listener, rth repetition, and after n=200 trials was quantified by a deviation |φ_r,k,200 -φ_k |. When

$$\left|{\phi }_{r,k,200}-{\phi }_k\right|>0.5{\phi }_k,$$ (2)

the parameter estimate for the kth listener in the rth repetition was considered poor. Besides the accuracy of the parameter estimates, two additional aspects of the experimental procedures, repeatability and rate of convergence, were also estimated. To quantify the repeatability, an across-repetition deviation R (at the end of 200 trials and averaged across listeners) was calculated as:

$$R=\sqrt{\frac{{\displaystyle \sum _k}{\left({\phi }_{1,k,200}-{\phi }_{2,k,200}\right)}^2}{4}}.$$ (3)

Smaller values of R indicated better repeatability. To investigate the rate of convergence, the root-mean-squared (rms) deviation from the best estimate after the nth trial was calculated as:

$$D_{\text{n}}=\sqrt{\frac{{\displaystyle \sum _r}{\displaystyle \sum _k}{\left({\phi }_{r,k,n}-{\phi }_k\right)}^2}{8}}.$$ (4)

Note that D_n was defined for each trial, averaged across listeners and repetitions. The rate of convergence was reflected in how rapidly the value of D_n dropped with increasing number of trials⁵.

Results and discussion

The best parameter estimates (from the pooled data) and the estimates from the two repetitions of the three procedures are listed in the different columns of Table 1. Results are shown for each individual listener and for the three parameters of the psychometric function in rows. Previous works have suggested that for broadband noise carriers, the gap detection threshold is about 2 ms (for 71-% correct, e.g., Forrest and Green, 1987), which corresponds to 6 dB on the stimulus parameter scale used in the present study. The α estimates obtained here are approximately the same.

Table 1.

The threshold (α), slope (β), and lapse rate (λ) parameters estimated for individual listeners for the two repetitions of Experiment I. Parameters were estimated using three different procedures: (1) the up-down staircase procedure (up-down), (2) the entropy-based Bayesian procedure (entropy), and (3) the updated maximum-likelihood procedure (UML). The asterisks indicate the poor estimates (see the criterion of Equation 2).

		pooled	up-down		entropy		UML
			rep1	rep2	rep1	rep2	rep1	rep2
α	S1	5.90	5.78	5.84	3.77	7.32	4.37	5.61
	S2	4.92	5.41	5.05	4.88	5.28	3.69	5.18
	S3	6.96	8.00	5.72	6.97	6.40	9.00	6.42
	S4	6.81	5.25	7.86	4.57	7.70	5.85	7.17
β	S1	0.53	0.84*	0.32	2.44*	0.67	0.32	1.94*
	S2	0.63	0.91	0.43	0.48	0.68	1.80*	0.94*
	S3	0.64	0.57	0.96	1.24*	0.83	1.10*	0.50
	S4	0.78	0.81	1.27*	0.54	0.71	0.58	1.22*
λ	S1	0.12	0.06	0.08	0.25*	0.15	0.11	0.12
	S2	0.03	0.02	0.03	0.00*	0.02	0.04*	0.03
	S3	0.04	0.02	0.03	0.00*	0.13*	0.02	0.08*
	S4	0.04	0.09	0.00*	0.00*	0.00*	0.07*	0.03

Using the criterion specified in Equation 2, the poor parameter estimates are indicated in Table 1 by asterisks. Comparing across the three procedures, poor parameter estimates occurred less frequently for the up-down procedure (4 out of 24 occasions) than the entropy (8 out of 24 occasions) and UML (8 out of 24 occasions) procedures. All three procedures provided fairly reliable estimates of the α parameter, no poor estimate was observed. The up-down and entropy procedures seemed to provide better estimation of the β parameter than the UML procedure, while the up-down and UML procedures out-performed the entropy procedure in terms of the λ estimation.

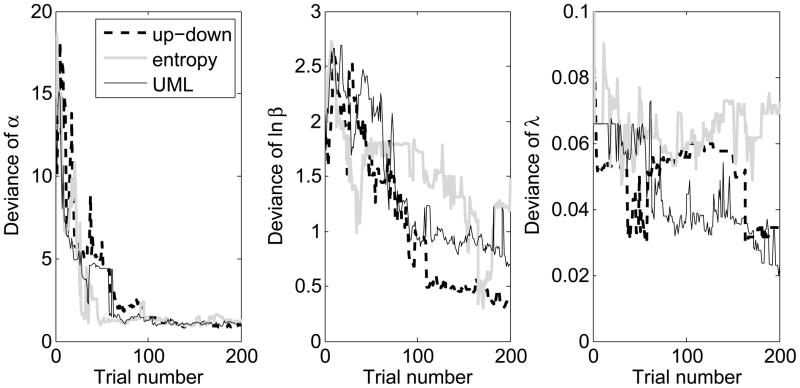
Table 2 lists the values of R (Equation 3) for α, lnβ, and λ and for the three procedures. Recall that R is a summary statistic, and smaller values of R mean better test-retest reliability. The values of R were comparable across different procedures, suggesting similar repeatability for the three procedures tested. Figure 1 plots the rms deviation from the best estimate, D_n, as a function of trial number. For the α parameter (left panel), fast convergence of the estimates over the first 100 trials was observed. The rates of convergence were comparable across the three procedures. In contrast, the value of ln β converged gradually. The rates of convergence were initially similar among the three procedures; after 100 trials, the up-down procedure began to converge more rapidly than the other two procedures and ultimately provided the best estimate of β. For the λ parameter, the rms deviations did not decrease with the trial number in a systematic fashion for the up-down and entropy procedures. On the other hand, a generally monotonic decreasing D_n was observed for the UML procedure.

Table 2.

The across-repetition deviations R for the up-down, entropy, and updated maximum-likelihood (UML) procedures in Experiment I. Smaller values indicate smaller difference in parameter estimates across replicates.

	up-down	entropy	UML
α	1.74	2.39	1.74
ln β	0.30	0.31	0.48
λ	0.05	0.08	0.03

Figure 1.

The rms deviations between the parameter estimates and the best parameter estimates of the psychometric function as a function of the number of trials for Experiment I. Changes in the functions indicate the rate at which the parameters converge for three parameters, α, ln β, and λ (left to right panels). The up-down staircase procedure, the entropy-based Bayesian procedure, and the updated maximum-likelihood (UML) procedure are plotted with different line styles.

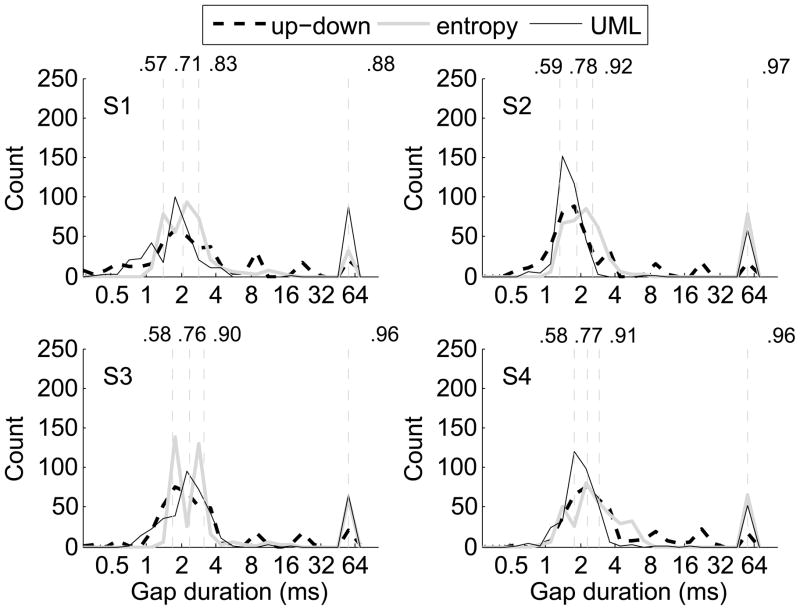
Figure 2 illustrates the differences in stimulus placement for the three procedures. Each panel of Fig. 2 plots histograms of the gap durations presented to one of the listeners. The vertical dashed lines mark the sweet points according to the best parameter estimate for this listener. These sweet points are the optimal places to sample in order to minimize the variances in the threshold, slope, and lapse rate estimates, assuming a logistic psychometric function (e.g., Shen & Richards, 2012). For all three procedures, significant numbers of trials had signal strengths near the α and β sweet points (the left-most three dashed lines). In this regard, the distributions of the gap durations were similar across procedures and listeners, except that listeners S2 and S4 showed more concentrated distribution for the UML procedure than the other two procedures. Moreover, all three procedures visited the λ sweet point (the right-most dashed line), though the entropy and UML procedures spent more trials at the λ sweet point than the up-down procedure. It is worth pointing out that although the λ sweet point was the best place (within the defined parameter space) to sample the stimuli for the estimation of λ, all gap durations associated with high percent-correct (see the labels above the dashed lines) contributed to the λ estimate. Although the up-down procedure visited the λ sweet point less frequently than the other two procedures, it spent a significant proportion of trials at other gap durations in the high-percentage-correct region. Therefore, a reasonable estimate of λ was achieved using the up-down procedure, even though it did not specifically sample the stimuli at the λ sweet point.

Figure 2.

The histograms of the gap durations tested for the up-down staircase procedure, the entropy-based Bayesian procedure, and the updated maximum-likelihood (UML) for Experiment I. Results for individual listeners are plotted in separate panels. Within each panel, the vertical lines mark the sweet points derived from the best estimate of the psychometric function using the pooled data across procedures and repetitions. The proportions correct at the sweet points are labeled above the vertical lines.

Results from the current experiment suggested that although the algorithms in updating the stimulus placement were different for these procedures, the resulting distributions for the stimulus presentation were strikingly similar (Fig. 2). The up-down procedure, despite of its simplicity, provided better estimates of the β parameter than the UML procedure and better estimates of the λ parameter than the entropy procedure. The success of the up-down procedure was consistent with the findings of Leek et al. (1992). These authors showed that when the lapse rate was assumed to be zero, the transformed up-down procedure provided accurate estimates of the psychometric function threshold and slope using 200 experimental trials.

For both entropy and UML procedures, their performance would likely to be improved if appropriate prior parameter distributions were implemented. Informative prior distributions might help preventing the placement of the stimuli to extreme signal strengths during the entropy procedure, enhancing its efficiency. It is not clear, however, whether the introduction of priors would cause the entropy procedure to out-perform the UML procedure, or vice versa. A systematic investigation of the effect of the prior distribution is needed to explore this question.

In the current experiment, the quanlity of the parameter estimates was evaluated by comparing individual estimates to the best estimate φ_k based on the pooled data across the three procedures (see Equations 2-4). However, if φ_k provided a biased estimate of the true psychometric function, the usefulness of these quality measures could be undermined. As pointed out by Kaernbach (2001), biases in parameter estimates could be a consequence of the sequential dependency inherent in adaptive procedures. Therefore, it is important to check whether φ_k agrees with the estimates from procedures in which the sampling of stimuli is independent of responses in previous trials. For this purpose, the estimation of the psychometric function was repeated for one of the listeners (S4) using the method of constant stimuli. Five blocks were run, each of which contained 60 trials. Within the 60 trials, six gap durations (3, 5, 7, 9, 11, and 13 dB) were tested in quasi-random manner with ten responses being collected at each of the gap durations. Following the data collection, the 300 trials of data were used to estimate the psychometric function using the psignifit routine. The resulting estimates were 6.48 for α, 0.75 for β, and 0.01 for λ. These estimates using the method of constant stimuli matched very closely to the best estimates from the pooled data listed in Table 1 for listener S4. No obvious bias was observed, except that the λ estimate was smaller using the method of constant stimuli. The close agreement between procedures with and without sequential dependency in stimulus sampling provided support for the validity of the best estimates φ_k.

Experiment II: Effect of inattention on the estimates of the psychometric function

When estimating the threshold, slope, and lapse rate simultaneously, one of the major difficulties faced by the estimation algorithm (such as the psignifit routine) is that a shallow slope is easily confused with a high lapse rate, causing a bimodal instability. This occurs frequently when the lapse rate is high. This problem severely prohibits the reliable measurement of the psychometric function in subjects who typically exhibit high lapse rates, such as naive participants, subjects from clinical populations, infants, young children, and laboratory animals. The current experiment investigates whether this difficulty of estimating the psychometric function associated with the lapse of attention can be alleviated by the sampling strategies used by the three procedures.

Methods

The same four listeners participated in Experiment II. The stimuli and procedure used in the current experiment were identical to Experiment I except that on one fourth of the trials, determined at random, the listeners’ responses were discarded and random responses were assigned. This manipulation was introduced as a simulation of frequent inattention during the experiment. Because during these inattention trials the correctness was determined at random, the maximum proportion correct was bounded by 0.875 instead of 1. Therefore, the λ parameter was expected to be at least 0.125.

For each listener, best estimates of the psychometric-function parameters were calculated, which were used as references to assess the accuracy provided by the three procedures. In contrary to Experiment I, these best estimates were not obtained using the pooled data across procedures and repetitions. Because the expected lapse rates were very high, even pooling all the collected data for each listener (1200 trials) would not guarantee a reliable estimate of the psychometric function. When fitting the logistic psychometric function to the pooled data from Experiment II using the psignifit routine, the confidence intervals of the parameters were sometimes extremely large. On the other hand, when performing the same analyses to the pooled data from Experiment I, much narrower confidence intervals were obtained. Therefore, the best parameter estimates of Experiment II were derived from the best estimates obtained using the pooled data in Experiment I. Let p₁ be the best estimated psychometric function in Experiment I, the best psychometric-function estimate in Experiment II was given by:

$$p_2({\alpha }_2,{\beta }_2,{\lambda }_2,x)=0.75·p_1({\alpha }_1,{\beta }_1,{\lambda }_1,x)+0.25·\mathrm{0.5.}$$ (5)

Consequently, the best parameter estimates for the two experiments followed the relationship: α₂ = α₁, β₂ = β₁, and λ₂ = 0.75λ₁+0.125. To assess the goodness of the estimates, repeatability, and rate of convergence (|φ_r,k,200 -φ_k |, R, and D_n) were calculated, respectively, following the same procedure as in Experiment I.

Results and Discussion

The derived best parameter estimates and the estimates from the three procedures for the two repetitions are listed in different columns in Table 3. Results are arranged as in Table 1. Comparing across the three procedures, poor parameter estimates (asterisks) occurred less frequently for the UML procedure (4 out of 24 occasions) than the entropy (6 out of 24 occasions) and up-down (12 out of 24 occasions) procedures. The UML procedure was more successful in estimating the α and β parameters compared to the other two procedures. Compared to the results from Experiment I (Table 1), the parameter estimates were more variable and the total number of the poor estimates was higher in Experiment II. For example, for listener S1, the estimates provided by the up-down procedure in the current experiment did not at all resemble the best estimates. The α estimates were about 20 dB and 13 dB in the two repetitions while the expected α value based on the results from Experiment I was approximately 6 dB. These results suggested that introducing frequent lapses of attention brought difficulties to the procedures. Among the three procedures tested, the UML procedure seemed to be the most resistant to inattention.

Table 3.

The threshold (α), slope (β), and lapse rate (λ) parameters estimated for individual listeners for the two repetitions of Experiment II. Parameters were estimated using three different procedures: (1) the up-down staircase procedure (up-down), (2) the entropy-based Bayesian procedure (entropy), and (3) the updated maximum-likelihood procedure (UML). The asterisks indicate the poor estimates (see the criterion of Equation 2).

		predicted	up-down		entropy		UML
			rep1	rep2	rep1	rep2	rep1	rep2
α	S1	5.90	19.90*	13.28*	19.93*	6.63	3.45	6.94
	S2	4.92	5.02	7.60*	4.86	5.16	5.01	4.90
	S3	6.96	8.04	8.95	4.82	5.85	4.63	6.03
	S4	6.81	6.80	8.12	6.96	9.00	8.86	9.01
β	S1	0.53	0.10*	0.10*	0.10*	0.27	0.67	7.18*
	S2	0.63	0.76	4.94*	5.30*	0.44	0.59	1.96*
	S3	0.64	0.24*	0.15*	7.29*	0.27*	0.38	0.49
	S4	0.78	1.25*	1.71*	6.45*	1.02	1.11	2.55*
λ	S1	0.21	0.01*	0.22	0.21	0.19	0.21	0.26
	S2	0.14	0.08	0.14	0.19	0.08	0.10	0.14
	S3	0.16	0.12	0.00*	0.22	0.10	0.16	0.14
	S4	0.15	0.15	0.12	0.16	0.13	0.10	0.08*

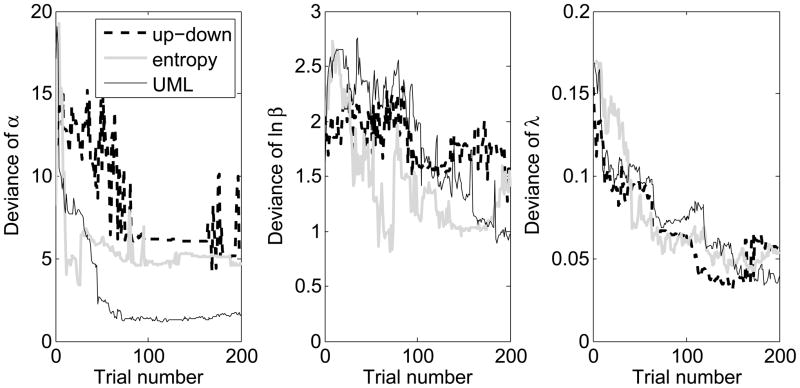
Table 4 lists the across-repetition deviations R for Experiment II. The UML procedure exhibited smaller values of R, hence better repeatability, for the α and λ parameters, whereas the up-down procedure had smaller values of R for lnβ. Figure 3 plots the values of D_n as a function of trial number. For the α parameter (left panel), fast convergence of the estimates over the first 100 trials was observed for all three procedures. However, only the α estimate in the UML procedure converged to a value that was close to the expected value. The up-down and entropy procedures gave biased estimates for the α parameter. These biases were largely associated with a single listener (S1). For this listener, the α estimates obtained from the up-down procedure and from the first repetition of the entropy procedure were much larger than the best estimate predicted using the data from Experiment I (see Table 3). The convergence of ln β was fairly unstable for all procedures, but for the UML procedure, the convergence was somewhat more consistent. After 200 trials, the UML procedure provided the best estimates of β. For the λ parameter, all three procedures showed rapid convergence with the values of D_n comparable across procedures throughout the 200 trials.

Table 4.

The across-repetition deviations R for the up-down, entropy, and updated maximum-likelihood (UML) procedures in Experiment II.

	up-down	entropy	UML
α	3.64	6.75	1.88
ln β	0.42	1.00	0.61
λ	0.12	0.08	0.03

Figure 3.

The rms deviations between the parameter estimates and the best parameter estimates of the psychometric function as a function of the number of trials for Experiment II. Changes in the functions indicate the rate at which the parameters converge for three parameters, α, ln β, and λ (left to right panels). The up-down staircase procedure, the entropy-based Bayesian procedure, and the updated maximum-likelihood (UML) procedure are plotted with different line styles.

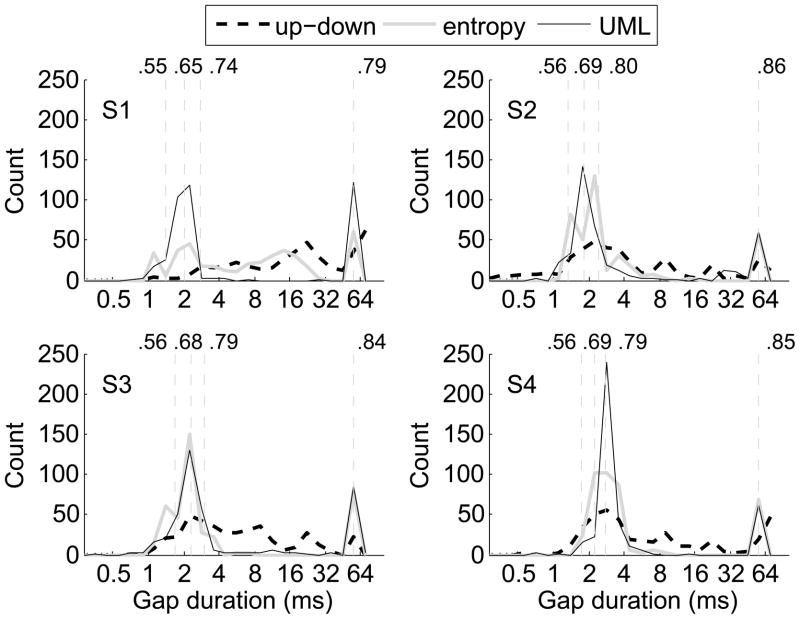
Figure 4 illustrates the differences in stimulus placement for the three procedures tested. For the UML procedure, the distributions of gap durations were very similar to those obtained in Experiment I (see Fig. 2). The stimuli were concentrated into two areas: one was near the α and β sweet points, and the other was at the upper limit of the gap durations (56.2 ms). The stimulus distributions for the entropy procedure were similar to those for the UML procedure in three of the listeners (S2, S3, and S4). For listener S1, however, the stimuli were broadly distributed across all gap durations. This was also the listener who exhibited the largest lapse rate in Experiment I. Therefore, it seems possible that listeners who naturally have high lapse rates would be more likely to exhibit sub-optimal sampling of stimuli and poor psychometric-function estimates when additional lapses of attention are artificially introduced. In such situations, the dynamic range of the psychometric function, from the chance performance level to the upper asymptote, would be very narrow, which makes the identification of the optimal place to sample the stimuli extremely difficult. However, it is not clear why a large lapse rate would affect the entropy procedure more than the UML procedure. Broad distributions of gap durations were observed for the up-down procedure for all four listeners. Listeners S2, S3, and S4 had the highest concentration of the stimuli near the the α and β sweet points, while for listener S1, almost all stimuli were presented at gap durations above the α and β sweet points. These results indicated that when lapse rate was high, it would take large numbers of trials for the stimuli in an up-down track to approach its targeting percent correct (e.g., 70.7% correct for a 2-down, 1-up track, Levitt, 1971).

Figure 4.

The histograms of the gap durations tested for the up-down staircase procedure, the entropy-based Bayesian procedure, and the updated maximum-likelihood (UML) for Experiment II. Results for individual listeners are plotted in separate panels. Within each panel, the vertical lines mark the sweet points derived from the best estimate of the psychometric function using the pooled data across procedures and repetitions. The proportions correct at the sweet points are labeled above the vertical lines.

In summary, the current experiment introduced random responses to simulate lapses of attention. Among the three procedures tested, the UML procedure seemed to be less affected by this manipulation, demonstrating similar accuracy, repeatability, and rate of convergence compared to Experiment I, where no artificial inattention was introduced. On the other hand, the frequent lapses of attention had detrimental effects on the performance of the up-down procedure. Poor estimates of the α and β parameters and poor convergence of ln β were found in the current experiment. The entropy procedure gave reasonable estimates of the psychometric function, except for one listener, who also had the highest lapse rate. For the up-down and entropy procedures, the failures in the estimation of the psychometric function were associated with poor sampling strategies.

Conclusions

Three adaptive procedures were compared against one another in estimating the psychometric function for an auditory gap detection task. The psychometric function was modeled as a logistic function, which was described by three parameters: threshold, slope, and lapse rate. Results from four listeners showed that the up-down staircase procedure (up-down procedure, Levitt, 1971), the entropy-based Bayesian procedure (entropy procedure, Kontsevich & Tyler, 1999), and the updated maximum-likelihood procedure (UML procedure, Shen & Richards, 2012) performed similarly in estimating the threshold of the psychometric function for this task. The up-down procedure provided more efficient estimation of the slope and the lapse rate than other two procedures. When the lapse rates of the listeners were elevated through experimental manipulations, the up-down procedure gave poor estimates of the threshold and slope of the psychometric function presumably because it failed to optimize the stimuli for estimating these parameters. The UML procedure was less sensitive to the increased occurrences of inattention compared to the entropy procedure. Therefore, if low lapse rates are expected, the up-down procedure could be a simpler and slightly superior method for estimating the parameters of the psychometric function simultaneously. However, when high lapse rates are expected or the lapse rates are unknown, the UML procedure is more likely to provide reliable estimates of the psychometric function.