Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 Mar 25;7(4):3276–3286. doi: 10.1021/nn305987x

Tensile Lattice Strain Accelerates Oxygen Surface Exchange and Diffusion in La1–xSrxCoO3−δ Thin Films

Markus Kubicek †,*, Zhuhua Cai ‡, Wen Ma ‡, Bilge Yildiz ‡, Herbert Hutter †, Jürgen Fleig †
PMCID: PMC3635458  PMID: 23527691

Abstract

graphic file with name nn-2012-05987x_0011.jpg

The influence of lattice strain on the oxygen exchange kinetics and diffusion in oxides was investigated on (100) epitaxial La1–xSrxCoO3−δ (LSC) thin films grown by pulsed laser deposition. Planar tensile and compressively strained LSC films were obtained on single-crystalline SrTiO3 and LaAlO3. 18O isotope exchange depth profiling with ToF-SIMS was employed to simultaneously measure the tracer surface exchange coefficient k* and the tracer diffusion coefficient D* in the temperature range 280–475 °C. In accordance with recent theoretical findings, much faster surface exchange (∼4 times) and diffusion (∼10 times) were observed for the tensile strained films compared to the compressively strained films in the entire temperature range. The same strain effect—tensile strain leading to higher k* and D*—was found for different LSC compositions (x = 0.2 and x = 0.4) and for surface-etched films. The temperature dependence of k* and D* is discussed with respect to the contributions of strain states, formation enthalpy of oxygen vacancies, and vacancy mobility at different temperatures. Our findings point toward the control of oxygen surface exchange and diffusion kinetics by means of lattice strain in existing mixed conducting oxides for energy conversion applications.

Keywords: strain, oxygen exchange, diffusion, mixed ionic electronic conductor, isotope exchange, secondary ion mass spectrometry

One of the main goals of research in solid oxide fuel cells (SOFCs) is to lower the operation temperatures to 500–700 °C.1,2 At these temperatures, the slow kinetics of the oxygen reduction reaction (ORR) at the cathode is usually responsible for the biggest part of resistive losses of SOFCs, which makes improving the cathode crucial.3,4 The use of mixed ionic and electronic conducting (MIEC) cathodes helps to enhance the reaction rates of ORR by increasing the electrochemically active area, but still further improvement is desired. Recent research efforts have focused not only on finding new cathode materials but also on improving existing ones. The kinetics of the ORR can be influenced in numerous ways such as by microstructural optimization,5,6 surface decoration layers,7 dc-polarization pulses,8 and chemical surface treatment,9,10 thus achieving strong enhancements of exchange current densities up to several orders of magnitudes. Among the relevant factors is also lattice strain, which was shown recently to strongly influence many important material properties such as the electronic structure and charge transfer,11−13 phase transitions,14 interface cation chemistry,15−19 surface and bulk oxygen transport,20−22 and the concentration of oxygen vacancies at the surface.11,23 Also an influence on the oxygen surface exchange and transport has been indirectly shown.24,25 The reasons for these effects on the atomistic scale can be found in changes in interatomic bond lengths and bond strengths. Simulations on the LaCoO3 system22 revealed that these changes can influence the activation barriers of the curved path26−28 of oxygen migration in perovskite oxides and can strongly enhance mobility in distinct directions and thus also chemical diffusion of oxygen in MIECs. These promising results, demonstrating that modification of lattice strain can lead to significant kinetic improvements at the elementary process level, provided the motivation to study these effects at a collective level experimentally.

Isotope exchange depth profiling (IEDP) was chosen as the measurement technique, due to the simple underlying methodology29 and its direct way of investigating the oxygen exchange reaction and diffusion kinetics. While in literature IEDP is often performed on bulk samples, it should be emphasized that establishing and measuring tracer concentration variations in very thin films of 20 nm is far from trivial and rarely done. For LSC this is particularly challenging since critical lengths (Lcrit = D/k) in the μm range up to 150 μm are reported for bulk LSC samples.30−33 Accordingly, in this paper we determined the experimental conditions for which a significant 18O concentration gradient within LSC exists, and those were restricted to a very limited temperature window and short diffusion times of mostly only around 5 min. Further the effect of chemically induced tracer incorporation, which could not be avoided, and its effect on the accuracy of the determined values for k* and D* are discussed.

The lattice strain of La1–xSrxCoO3−δ (LSC) was tailored by depositing epitaxial thin films of about 20 nm thickness on different substrates SrTiO3 (STO) and LaAlO3 (LAO). The sample preparation and strain analysis was based on a recent work11 investigating the influence of lattice strain on surface electronic and chemical states of La0.8Sr0.2CoO3−δ. For different strain states we probed the temperature dependence of the collective kinetic parameters (coefficients of oxygen surface exchange, k*, and oxygen tracer diffusion, D*). Our results demonstrate that tensile strain can strongly enhance oxygen exchange rates and diffusion coefficients compared to the compressive state. This enhancement was consistently found across various samples that included the effect of chemical surface modification and the LSC composition (La0.8Sr0.2CoO3−δ, LSC82, and La0.6Sr0.4CoO3−δ, LSC64).

Results and Discussion

Structure and Strain State of the LSC Thin Films

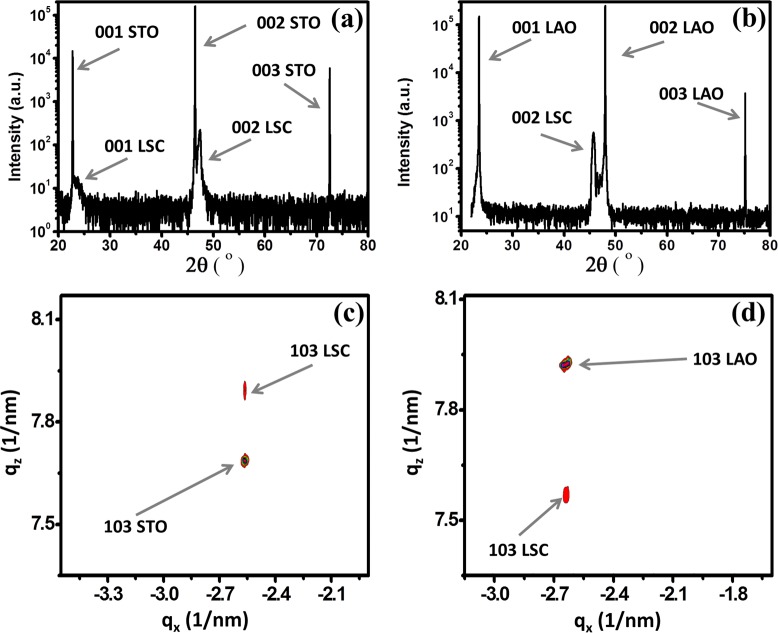
The perovskite LSC82 has a rhombohedral unit cell with a pseudocubic lattice constant of apc = bpc = cpc = 3.851 Å. Two different single-crystal substrates, STO (100) (a = 3.905 Å) and LAO (100) (a = 3.793 Å), were used to produce a tensile and compressive planar strain within the pseudocubic LSC82, respectively. At room temperature, based on the lattice mismatch between the film and the substrates, STO introduces 1.4% tensile and LAO introduces −1.5% compressive planar strain into the LSC82 films. At experimental temperatures up to 475 °C, the expected tensile strains induced by STO decrease to 1.0%, while the compressive stains induced by LAO increase to −1.9% due to the different thermal expansion coefficients of the film and substrates. Normal XRD scans (Figure 1a and b) of the as-deposited LSC films grown on both substrates, hereafter denoted as LSC/LAO and LSC/STO, clearly showed only (001) diffraction peaks, which indicates single-phase (001) LSC//(001) STO and (001) LSC//(001) LAO. X-ray diffraction (XRD) reciprocal space maps measured at room temperature around the (103) Bragg reflection of the pseudocubic LSC thin films (Figure 1c and d) confirm that the LSC film is fully strained by the STO and LAO substrates respectively since the in-plane components of the reciprocal lattice vectors for both the film and the substrate are matching well. While some strain relaxation away from the interface can be expected, the sharp film peaks aligning with substrates peaks in reciprocal space maps indicate that the films are mostly uniformly strained without significant relaxations in them. This is reasonable because the films are very thin, ∼20 nm, and can sustain a high quality of epitaxy with the substrate. In addition, we expect that these films retained their strain states at the elevated temperatures in the experiments reported here, as we demonstrated in our previous work using the same type of strained LSC films with in situ XRD up to 500 °C.11

Figure 1.

Figure 1

Open in a new tab

The 2θ–ω scans in logarithmic intensity scale of (a) LSC/STO and (b) LSM/LAO show only 00l diffraction peaks of LSC. X-ray diffraction reciprocal space maps for (c) LSC/STO and (d) LSC/LAO thin films. The arrows in (c) and (d) show the 103 reflections of the LSC thin films and the substrates.

The LSC films grown on STO and LAO exhibited a smooth surface (Figure 2a and b) with an overall root-mean-square roughness (RMS) of 0.64 ± 0.06 and 0.56 ± 0.05 nm, respectively. The color contrast shown in the atomic force microscopy (AFM) images for both films corresponds to a peak-to-valley height difference of only 1–2 nm. The surfaces of these two sets of films are similar to each other, enabling a comparison of oxygen exchange kinetics between them that may have only minimal (if any) artifacts due to the surface morphology differences.

Figure 2.

Figure 2

Open in a new tab

LSC morphology on (a) STO and (b) LAO showed smooth surfaces with RMS roughnesses of 0.64 ± 0.06 and 0.56 ± 0.05 nm, respectively, imaged by atomic force microscopy.

SIMS Depth Profiles

Poisson-corrected secondary ion counts of 16O– and 18O– were used to calculate the 18O tracer fraction c:

graphic file with name nn-2012-05987x_m001.jpg 1

17O– (natural abundance 0.038%) was ignored due to interference with the stronger 16OH– secondary ion signal. The tracer fraction c was then normalized according to

graphic file with name nn-2012-05987x_m002.jpg 2

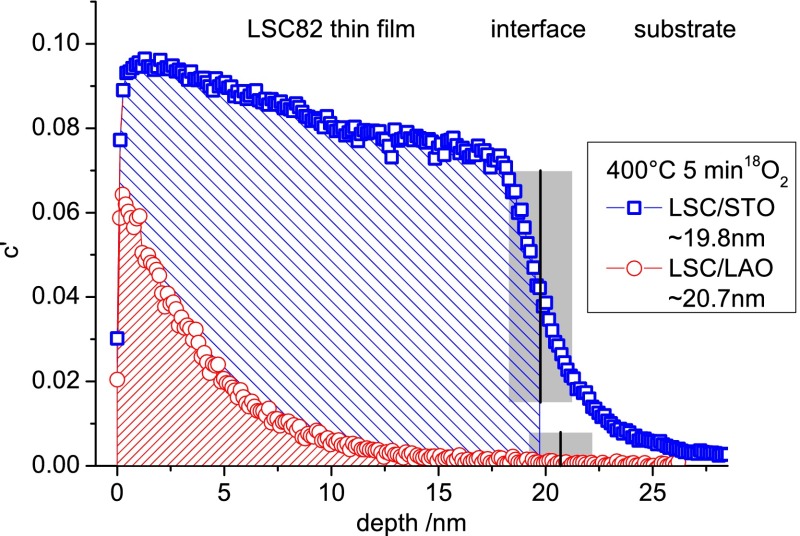
By this normalization step the experimental boundaries of tracer fraction, given by the natural abundance of 18O (0.205%) and its isotope fraction in the annealing gas (97.1%), are taken into account. Thin film thicknesses were calculated from SIMS measurements by using the Cs+ ion current and sputter time, assuming the same sputter coefficient for all LSC films. The sputter coefficient was determined in our previous work from multiple LSC films sputtered in secondary ion mass spectrometry (SIMS), with their thicknesses being measured by cross-section-SEM and digital holography microscopy (DHM, Lyncee Tec, Switzerland). The same normalization was used to transfer sputter times into depths. For location of the LSC|substrate interface, the secondary ion signals of CoO–, AlO–, and TiO–, respectively, were used. The sharpness of the interface in SIMS measurements was characterized by the drop of the CoO– counts from 90% to 10% of the CoO– counts measured in the center of the LSC film, yielding typical values of 2–3 nm (a very low value for SIMS depth profiling34−36). Profiles of CoO– are shown for different annealing temperatures in the Supporting Information. At the interface, several effects such as ionic mixing during sputtering, surface roughness, and sputter-induced roughness add up to spread the almost atomically sharp interface. The center of this “interface zone” was treated as “the interface” and used for film thickness calculation. Thickness calculations from SIMS depth profiles were in good agreement with XRR measurements of the films. Typical depth profiles are shown in Figure 3 for LSC82 thin films on STO and LAO. The main features of all profiles are a surface value in the tracer fraction of a few percent up to 30%—below the 18O fraction of 97.1% in the annealing gas, a pronounced decrease of the tracer fraction throughout the LSC film, and a final sharp decrease close to the film/substrate interface. Details of the profile such as the sharp drop in the very first nanometer as well as the temperature/time settings and the influence on the error margins of k* and D* will be discussed later.

Figure 3.

Figure 3

Open in a new tab

Tracer depth profiles of 20 nm epitaxial (100) LSC82 films with tensile strain on STO and compressive strain on LAO. Profiles resulted from oxygen tracer exchange for 5 min at 400 °C. Obvious differences in amount of tracer incorporated as well as in slope are pointing to strong differences in oxygen exchange kinetics in connection with the strain state.

In Figure 3 it is also exemplarily shown that the resulting tracer depth profiles in LSC82 thin films strongly depend on the substrate and thus on the strain states of the films. It is apparent that the total amount of tracer exchanged is much higher for the tensile strained LSC/STO system, indicating a significantly higher surface exchange coefficient there. Besides that, also the gradient of the two tracer profiles is very different. While LSC/LAO drops to half the near-surface level within about 3 nm, the slope of the 18O fraction in LSC/STO is much smaller. This points to LSC/STO having also the higher diffusion coefficient.

Determination of k* and D*

Depth profiles of the normalized tracer fraction c′ were used to calculate the tracer surface exchange coefficient k* and the tracer diffusion coefficient D*. Assuming the substrates to be ideally blocking for oxide ions, the LSC thin film can be considered as a thin sheet with tracer incorporation from a source of constant tracer concentration on one side (the surface). For symmetry reasons, the profiles resulting from this geometry are exactly one-half of a profile generated in a plane sheet of twice the thickness and tracer incorporation on both sides. The corresponding solution of Fick’s second law,

graphic file with name nn-2012-05987x_m003.jpg 3

for a change from c1 to c2 can therefore be applied for our films, and the transient of tracer fraction with depth and time is given by37

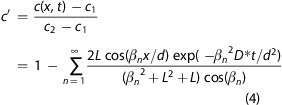graphic file with name nn-2012-05987x_m004.jpg 4

In this equation, d denotes the film thickness, t is the time, and L is the quotient of film thickness and critical length that is derived from d, k*, and D*:

graphic file with name nn-2012-05987x_m005.jpg 5

The βn factors are solutions of the equation

graphic file with name nn-2012-05987x_m006.jpg 6

and can only be numerically analyzed for each L. A procedure for determining βn is given in ref (38). In our analysis we performed a recursive fitting of eqs 4 and 6 to the experimental data and thus of L, k*, and D* using 12 roots βn (n = 1–12).

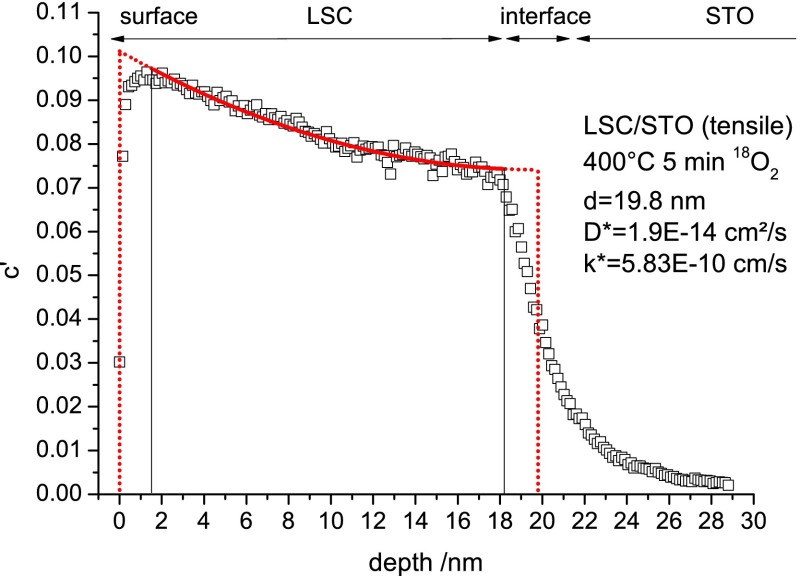
Because of nonidealities of real samples and measurement-related limitations, the real depth profiles differ from calculated profiles especially at the surface and at the interface. In all measurements, in the first 1–1.5 nm, close to the thin film surface, a lower 18O fraction than expected from the main part of the depth profile was found (cf. Figure 3). This might be caused by 18O tracer back-diffusion, while keeping the samples in ambient air (<80 °C). However, tracer exchange and diffusion at temperatures below 80 °C (between annealing and SIMS analysis) are considered to be negligible; reference samples were measured immediately after and 6 months after annealing, and almost no differences in their tracer depth profiles were found. Only the very first data points of <1 nm showed a minimally lower 18O fraction after 6 months at room temperature. Hence, it is more likely that this effect occurs due to 16O-rich adsorbates from ambient air (−O2, −OH) at the surface.

A sharp drop of the 18O fraction takes place within the interfacial zone already observed for the CoO– signal (cf. Figure 3). 18O fractions in this zone are a mixture of the values in the thin film and in the substrate. Owing to these nonidealities, on both sides of the depth profiles in LSC—at the surface and toward the interface—1.5 nm was ignored for fitting but included for length calculation. Any significant effect of interfacial cation diffusion on the determined k* and D* values can thereby be neglected. This interface zone of 3 nm should not be confused with the depth resolution of the 18O fraction, which is significantly higher. Figure 4 illustrates this fitting procedure, showing the measured depth profile (squares), the actual fit within the set boundaries (solid line), and the idealized tracer depth profile (dotted line) for k*, D*, and thin film thickness d (d is evaluated from the CoO– signal; evaluation is not shown here). Applying this procedure to the two profiles in Figure 3 yields k* = 9.67 × 10–11 cm/s, D* = 8.0 × 10–16 cm2/s for LSC/LAO and k* = 5.83 × 10–10 cm/s, D* = 1.9 × 10–14 cm2/s for LSC/STO and thus a much faster oxygen exchange and diffusion in the tensile LSC film at 400 °C.

Figure 4.

Figure 4

Open in a new tab

Tracer depth profile of tensile strained LSC82/STO after annealing in 18O2 for 5 min at 400 °C illustrating the fitting method. The solid line denotes the actual fit, and the dotted line shows the idealized profile for the film thickness d and fitting parameters D* and k*.

For a completely blocking substrate the normalized tracer fraction is expected to be constant in LSC close to the interface and to be zero beyond the interface throughout the substrate (compare dotted line in Figure 4). To represent an ideally blocking substrate, the undoped substrates (LAO, STO, MgO) were used. Although these oxides can show significant oxygen diffusion at temperatures above 600 °C,39,40 for given experimental conditions (below 500 °C, a few minutes), tracer profiles extended only very slightly into the substrate. The effect is measurable for all substrates and is more pronounced for samples with higher tracer levels in LSC. Ionic mixing from SIMS doubtlessly also contributes to tracer being carried over into the substrates. However, some residual tracer diffusion in the single-crystalline substrates seems to be present, which is most probably caused by impurities. Significant tracer incorporation into the substrate would lead to falsely too low values of k* and D* when analyzing by means of eqs 4 and 6. For all investigated profiles relevant in this work, however, the 18O level in the substrate is very low, with the total 18O amount being always less than 3% of that in LSC even at the highest temperatures. Therefore, analysis using eqs 4 and 6 is assumed to lead to reliable k* and D* values.

Temperature and Strain Dependence of k* and D*

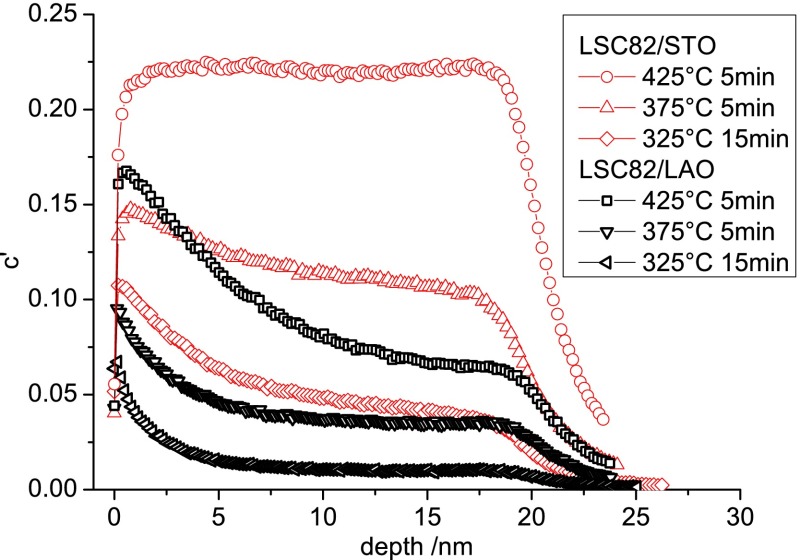
Several annealing temperatures in the interval 280–475 °C were selected for oxygen tracer exchange in order to investigate the temperature dependence of k* and D* from tracer depth profiles. Different time settings were necessary, depending on the temperature (summarized in S4 in the Supporting Information), to keep errors of k* and D* as small as possible. For each temperature/time setting an LSC/STO and LSC/LAO pair was annealed in one run to ensure that differences in the tracer profiles are only due to differences in the properties of the thin films. Figure 5 shows typical 18O depth profiles for both strain states and different temperatures. For all annealing temperatures, tensile LSC/STO was found to have both a higher k* and a higher D* value than compressively strained LSC/LAO. At temperatures above 400 °C, tracer profiles for LSC/STO are very flat, due to high values of D*. For such flat profiles the determination of D* becomes very erroneous or even impossible.

Figure 5.

Figure 5

Open in a new tab

18O depth profiles in 20 nm LSC82 thin films at different temperatures. For each temperature/time setting, both strain states LSC/STO and LSC/LAO were annealed together in 18O2. Tensile LSC/STO incorporates more 18O and has the flatter drop of the 18O fraction toward the interface.

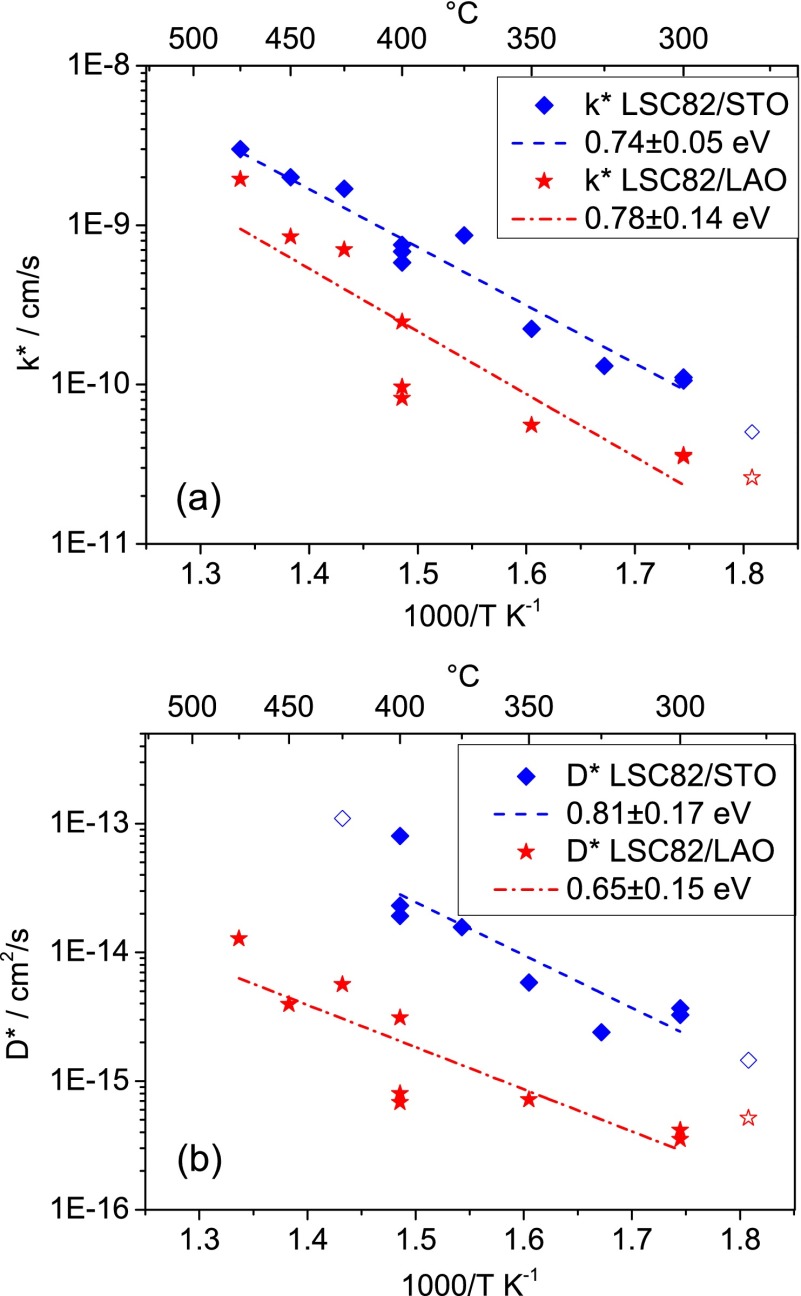
Mathematical errors of the entire fitting process were difficult to determine as a consequence of the two-step-iterative fitting procedure. As k* and D* are determined in a step for given βn and a given/self-consistent L, the system is under-parametrized and calculated errors for k* and D* are consequently too low. These calculated errors would be below 1% for k* and about 1–10% for D* for low values of D*; they are increasing to undefined values for very high D* (flat tracer profiles). Another approach would be to estimate errors by calculating the standard deviation of the measurement points considered for the linear regression lines of the temperature dependence (Figure 6). This would yield relative errors of ±9% for k* and ±16% for D* in the respective temperature range.

Figure 6.

Figure 6

Open in a new tab

Arrhenius-type diagrams showing the temperature dependence of the coefficients k* (a) and D* (b) for LSC82 thin films extracted from fittings of tracer depth profiles.

Figure 6 displays Arrhenius-type plots of the parameters k* and D* that were determined for LSC82. k* and D* at the lowest temperature and D* of LSC/STO at the highest temperature (open or missing symbols) are not reliable or are very ill defined, an issue that will be discussed in more detail later. A linear regression line is shown for the reliable data points. The average differences between the kinetic properties of the strained films are about a factor of 4 in k* and about a factor of 10 in D*, with the tensile strained LSC/STO having the higher values. For the temperature range covered here, 280–475 °C, the values of the activation energies for k* are almost the same for both strain states, 0.74 ± 0.05 eV for tensile and 0.78 ± 0.14 eV for compressive strain. Also activation energies of D* are similar for both strain states (0.81 ± 0.17 eV tensile, 0.65 ± 0.15 eV compressive); because of the uncertainty of individual D* values (flat profiles), the significance of the slight difference in activation energies is uncertain.

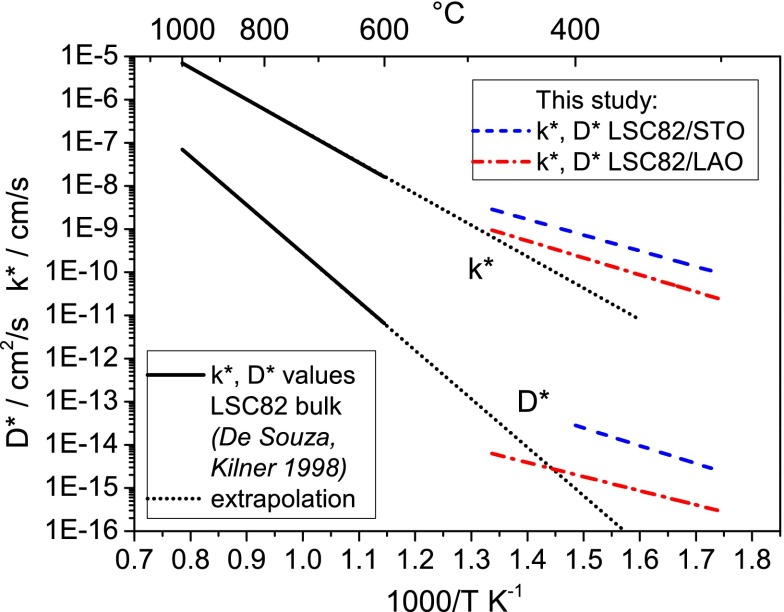
We have two important observations about these activation energies found in the thin films: the first is related to their comparison to those reported for bulk LSC samples, and the second is related to their seemingly negligible sensitivity to strain. First, very different activation energies of 1.32 eV for k* and 2.21 eV for D* are reported in the literature30 for LSC82 bulk samples above 600 °C. This very strong difference becomes obvious in Figure 7, where literature data are extrapolated to the temperature regime investigated in this study. Interestingly, the extrapolated lines of high-temperature (bulk sample) measurements and low-temperature (thin film) measurements of LSC82/LAO for k* and D* both intersect at temperatures close to 450 °C and for LSC82/STO close to 550 °C. This is an indication that the very different activation energies from bulk and thin films are caused by an intrinsic change within LSC at about 500 °C (for the strain-neutral state) rather than an artifact of the preparation of the samples. Unfortunately, measurements at higher temperatures could not be performed on the thin films in this work (as discussed later) to finally prove this interpretation. However, literature data on the temperature dependence of the oxygen vacancy concentration in LSC indicate a change of the kinetic parameters and of the activation energy at about 500 °C.32 This reported transition behavior is in excellent agreement with our findings on the thin film LSC at temperatures lower than 500 °C, as explained below.

Figure 7.

Figure 7

Open in a new tab

Arrhenius-type diagram comparing literature values of k* and D* obtained on bulk LSC8230 to values of differently strained LSC82 thin films investigated in this study.

First we note that the temperature dependency of D* arises both from the enthalpy of oxygen vacancy formation, ΔH0, and from the activation energy for oxygen vacancy migration, Ea. D* is proportional to the product of the oxygen vacancy diffusion coefficient, DV, and the concentration of oxygen vacancies, [VO••],

graphic file with name nn-2012-05987x_m007.jpg 7

Therefore, the change of both DV and [VO••] with temperature contributes to the calculated values of the activation energy here. In eq 7fc denotes the correlation factor related to crystal structure, typically 0.69 for perovskite-type materials,41k is Boltzmann’s constant, T is the temperature, z is the charge number, e0 is the elementary charge, and uv is the vacancy mobility. At temperatures below 500 °C almost no change of δ was observed in LSC64 bulk samples (with nonzero values of δ), while for temperatures above 500 °C δ increases strongly with temperature.32 This reflects that the enthalpy of oxygen vacancy formation in LSC is very small below 500 °C.

Assuming very little change of the oxygen vacancy concentration with temperature (with a very small formation enthalpy) below 500 °C not only in bulk samples32 but also in thin films, our relatively low activation energy should then reflect almost solely the temperature dependence of the oxygen vacancy diffusion coefficient. This is in good agreement with activation energies of vacancy transport of 0.78–1.08 eV in La0.6Sr0.4CoO3−δ42 and LaCoO3−δ43,44 and in other perovskite-type oxides: 0.6 eV in SrTiO3,45 0.86 eV in Sr(Ti,Fe)O3,46 0.74 eV in La1–xCaxAlO3-δ,47 0.6–0.8 eV in (La,Sr)(Ga,Mg)O3−δ.48,49 At temperatures where there is a strong change in δ (>500 °C, with a nonzero formation enthalpy), a higher activation energy is observed for D* than in our study (280–475 °C).

In order to quantify this difference, the formation of oxygen vacancies VO•• is described by

graphic file with name nn-2012-05987x_m008.jpg 8

and the corresponding mass-action law leads to

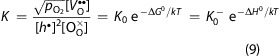graphic file with name nn-2012-05987x_m009.jpg 9

with ΔG0 denoting the standard Gibbs energy and ΔH0 the standard reaction enthalpy for vacancy formation. At high temperatures and sufficiently high oxygen partial pressures, the hole concentration can be assumed to be fixed by the Sr-doping level and thus is constant. The vacancy concentration is then given by

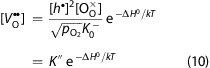graphic file with name nn-2012-05987x_m010.jpg 10

and depends on the enthalpy of the vacancy formation reaction eq 8. Accordingly, the tracer diffusion coefficient becomes

graphic file with name nn-2012-05987x_m011.jpg 11

with

graphic file with name nn-2012-05987x_m012.jpg 12

From eq 11 it is apparent that experimentally determined values of the activation energies of D* are the sum of Ea and ΔH0 at high temperatures >500 °C. The difference of ∼1.5 eV between the high-temperature literature value and our activation energy should therefore be close to the activation energy of oxygen vacancy formation ΔH0. Literature values for ΔH0 exist for bulk LSC64 (0.89 eV)50 and are also similar for bulk La0.6Sr0.4Co1–xFexO3−δ ranging from 0.8 eV51 for x = 0.2 to 1.0 eV52 for x = 1. Interestingly, for LSC64 thin films an even higher value of 1.29 eV is reported,53 which is observed together with a smaller oxygen vacancy concentration compared to bulk samples. In this approximate model, activation energies of D* on the order of 2 eV are very realistic at high temperatures, and the differences in activation energies can be explained quite well.

As mentioned above, the discrepancies between activation energies at high and low temperatures are higher for D* (av 1.48 eV) than for k* (av 0.56 eV). Because the oxygen vacancies are thought to play an important role in the surface reactivity of perovskites in oxygen reduction,54,55 the activation energy change of k* may also depend on the temperature dependence of δ on the surface. Furthermore, the vacancy formation energy on the surface of oxides, including LSC, is generally lower than that in the bulk.22,56,57 However, it would be necessary to know the exact rate-determining step of the reaction as well as the temperature dependencies of all involved charge carriers or surface species. The concentration of minority electrons, for example, which are considered crucial for ORR,58,59 would be showing a different increase with temperature than oxygen vacancies. At this point, it can only be speculated what the reason is for the lower discrepancy between the activation energies of k* on bulk LSC at high temperature and on thin film LSC at the lower temperatures.

Although the exact temperature for the proposed change of regimes at around 500 °C could not be measured, further reports exist in the literature about transitions of bulk LSC82 in the same temperature range. A semiconductor to metal transition60 as a result of a change of the rhombohedral angle,35 a proposed transition of the cobalt spin state (intermediate-high),61 and a change of thermal expansion62 are reported. We assume that one or more of these transitions are connected to the regime change in the temperature dependence of oxygen nonstoichiometry32 in LSC and to the low activation energies of k* and D* in the thin film LSC samples in this study.

Second, we note that the activation energies for k* and D* do not present a change with strain beyond the uncertainty margins. In a previous work, it was shown theoretically that the lattice strain alters the oxygen vacancy formation and migration energies,22,23 with a trend of increasing tensile strains associated with lower energies of vacancy formation and migration. Moreover, prior experiments demonstrated a strain effect on the oxygen vacancy content and charge transfer properties11 in LSC. In this work, the effective activation energies of k* and D* are relatively insensitive to strain, while the magnitude of k* and D* increases when strain varies from compressive to tensile state. In light of eqs 9–12, the impact of planar lattice strain in the LSC/LAO and LSC/STO thin films is either on the oxygen vacancy content or on their mobility, or both. The tensile strain could be favoring a lower vacancy formation enthalpy, but also equally a lowering of the migration barrier. One order of magnitude increase in tracer diffusion coefficient at about 400 °C would arise from a 0.14 eV reduction in the vacancy formation enthalpy and/or in the migration barrier (eq 11). While this is reflected in the magnitude of D*, a reduction of 0.14 eV is not detectable in our measured activation energies because of the uncertainty margins being close to 0.15 eV (Figure 6).

Using k* and D* to calculate the critical length (film thickness for which L = 1) leads to different values for the two strain states with 100–150 nm for LSC/LAO and 300–400 nm for LSC/STO in the investigated temperature range. Both values are much smaller than values of 3–150 μm reported for bulk LSC in the literature.30−33 However, due to the different activation energies of k* and D* in the literature, critical lengths strongly depend also on temperature. Critical lengths of more than 50 μm are found at 1000 °C, while 3–5 μm are reported at 600 °C for LSC82 bulk samples.30 Extrapolating those data (as shown in Figure 7) to 400 °C, without considering the activation energy change, leads to a critical length of about 150 nm, which is well in the range of the measured values in this study for thin films.

Three sets of additional measurements were performed on (i) surface-etched strained films of which about 3 nm were removed from the surface, (ii) LSC thin films on MgO as a strain-neutral reference state, and (iii) strained thin films of a different composition, La0.6Sr0.4CoO3−δ (LSC64). Key findings from these experiments are the following. Experiment (i) shows the same activating effect of tensile compared to compressive strain, and we therefore exclude that differences in surface cation chemistry affect the measured strain dependence of k*. An enhancing effect of chemical etching on k* is found for both strain states and attributed to the removal of a surface layer that is enriched with Sr. From (ii) we get evidence that tensile strain enhances and compressive strain reduces oxygen exchange kinetics compared to films without a predominant strain state, despite the likely presence of extended defects in this system. With (iii) we can show that the acquired results on the effect of strain are consistent also when varying the thin film composition, and as expected k* and D* are higher for LSC64. The quantitative consistency among all the measurements in this work demonstrate that indeed planar lattice strain can affect the kinetics of oxygen surface exchange and diffusion in LSC, and likely in other similar perovskite oxides. Details on these experiments and results are presented as Supporting Information.

Limitations of the Method and the Temperature Range

Although it is desired to measure only the profiles caused by tracer diffusion, chemical diffusion could not be avoided under the given experimental conditions. It was particularly challenging to realize very short diffusion times of only 4 or 5 min to still obtain reasonable concentration gradients in LSC. In the literature30,63,64 it is often suggested to extensively preanneal the films either in oxygen or in ambient air before tracer experiments in order to chemically equilibrate the material and thus to avoid chemical diffusion. Here this procedure would not improve the situation, because further stoichiometry changes during evacuation before tracer exposure are hardly avoidable. Trying to avoid the problem by a very fast evacuation and refilling process would here be in vain, as the time constant of chemical equilibration is too short. This time constant can be estimated from impedance measurements performed on similar thin films on YSZ (time constant of the semicircle featuring the chemical capacitance) and is about 1–5 s at 400 °C. Extrapolating the time constant for the lower temperatures yields higher values, but they are yet still below one minute at 280 °C. One might pre-equilibrate the sample, quench it to room temperature, perform the tracer exchange at room temperature, and heat the sample back to annealing temperature. Then, however, the heating step would have to be much faster than the annealing time (typically 5 min here), which was not possible in our setup. Hence, a simultaneous occurrence of tracer and chemical diffusion could not be avoided in this study. The only viable way to completely avoid a chemical contribution in 18O profiles would be to use continuous gas flows at high flow rates with fast changes from ambient to tracer-enriched oxygen retaining the same p(O2) during the whole procedure, which would be extremely 18O2 consuming and costly.

Oxygen nonstoichiometry of La1–xSrxCoO3−δ adapts to evacuation by increasing δ. After refilling with 18O2 to 200 mbar, δ returns to the original value by incorporation of oxygen into LSC. As only the 18O isotope is available for this readjustment of δ, an 18O tracer profile from chemical diffusion is created. This “chemical” tracer profile depends in size and shape on the change of δ and the coefficients kchem and Dchem. Simultaneous with the formation of this chemical tracer profile, and also continuing after the usually fast chemical incorporation/diffusion process, tracer exchange and tracer diffusion take place in the system governed by k* and D*. As both processes have different driving forces and different time constants, a very complex combined diffusion profile is generated over time.

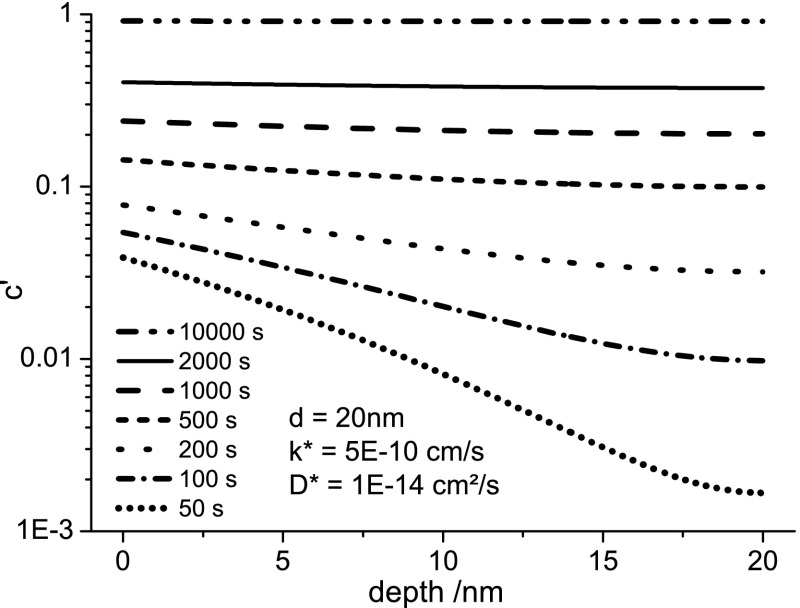
A way to handle this problem and to still measure meaningful values for k* and D* is to keep the amount of 18O incorporated by chemical driving forces very low compared to the amount of 18O incorporated via pure tracer exchange. Then resulting profiles are still very close to profiles generated by only tracer exchange and diffusion, while chemical incorporation/diffusion can be neglected. For annealing at low temperatures this can only be realized by long annealing times. For very long annealing times, though, another limiting effect becomes relevant: Longer annealing times inevitably lead to profiles with smaller relative drops of tracer fraction, as shown in Figure 8. Due to the flatter profiles, D* becomes more and more ill-defined. For even higher annealing times, finally also k* becomes undefined as the thin film gets almost completely filled with tracer. Therefore, an ideal time setting has to be found for each temperature, for which the influence of chemical tracer incorporation is negligible, but not too much tracer is incorporated so that simultaneous determination of k* and D* remains possible with acceptable errors.

Figure 8.

Figure 8

Open in a new tab

Simulated depth profiles using eqs 4 and 6 for different annealing times with typical values of d, k*, and D*. A logarithmic y-scale is used to show that the relative drop in the profiles decreases with annealing time, leading to higher errors in D*.

The influence of chemical tracer incorporation at low temperatures could be clearly shown in additional experiments at 280 °C and different annealing times (1–36 min). The amount of tracer incorporated into LSC for small times does not follow the expected behavior for pure tracer diffusion. Rather, a bigger amount of tracer than expected is incorporated in the first minutes. Furthermore it was observed that tracer profiles in which an influence of chemical tracer incorporation is expected (low temperatures/times) could not be fitted satisfactorily with the formulas valid for tracer diffusion (eqs 4 and 6). A steep drop in tracer fraction at the surface followed by a flat diffusion tail toward the interface was observed, features that could not be adjusted simultaneously. From variation of annealing time in these measurements we concluded that the tracer close to the surface followed by a steep drop is incorporated by chemical driving forces. Therefore, k* and D* values for LSC82/LAO (see Figure 6) at 280 °C for which these effects could be observed were also not included in activation energy calculations (the open symbols in Figure 6 (a,b)).

Conclusions

Oxygen tracer profiles generated in differently strained epitaxial 20 nm (La,Sr)CoO3−δ thin films were measured after annealing in 18O2 atmosphere. Both the surface exchange coefficient k* and the diffusion coefficient D* were extracted simultaneously from depth profiles, despite the very small thickness. Within the entire temperature interval of 280–475 °C and for two compositions (LSC82 and LSC64), both k* and D* are always found to be higher for tensile strained LSC on STO compared to compressively strained LSC on LAO. An enhancing effect of chemical etching on k* is measured for both strain states and attributed to the removal of a surface Sr enrichment. Activation energies of both k* and D* in the range 280–475 °C are much lower than those reported for bulk LSC at higher temperatures. We suggest this difference is due to the temperature independence of the oxygen nonstoichiometry, δ, at temperatures lower than 500 °C, causing higher activation energies above 500 °C and much lower ones in this study below 500 °C. While the enhancements in k* and D* of tensile LSC films with respect to the compressively strained LSC thin films are highly reproducible, the exact values of k* and D* and their temperature dependence are prone to some errors. The reason is that the investigation method is close to its geometrical limit: the sample thickness of 20 nm is very small to extract a well-evaluable SIMS depth profile on a good mixed conducting oxide such as LSC. In addition, the temperature/time settings for annealing have to be well adjusted to extract both k* and D* and to minimize the influence of chemically driven tracer incorporation. The consistency of the strain dependence of k* and D* across all samples that were systematically surveyed here, together with the previous theoretical predictions, suggests that lattice strain is an important parameter to control the reactivity of perovskite cathodes to oxygen reduction reaction.

Methods

Sample Preparation

LSC films with thicknesses of about 20 nm on single-crystal SrTiO3 and LaAlO3 were prepared by pulsed laser deposition (PLD), using a KrF excimer laser at λ = 248 nm, 10 Hz pulse rate, and 400 mJ pulse energy under a pO2 of 10 mTorr at 700 °C. After deposition, the sample was cooled at 10 °C/min to room temperature for ∼2 h under a pO2 of 2 Torr. The target used for LSC82 film deposition is purchased from MTI Corporation, USA. LSC64 target was prepared using the (Pecchini) nitrate/citrate route, and materials we used were Co 99.995%, SrCO3 99.995%, La2O3 99.999%, HNO3 99.999%, and citric acid monohydrate 99.9998% (all Sigma-Aldrich)

Structural Characterization

A Veeco/Digital Instrument Nanoscope IV was used to perform tapping mode atomic force microscopy for characterizing the surface morphology before and after chemical etching. X-ray diffraction 2θ–ω scans and reciprocal space mapping were performed to characterize the crystal structure and strain states of the LSC films, respectively. The measurements were performed using a high-resolution four-circle Bruker D8 Discover diffractometer, equipped with a Göbel mirror, 4-bounce Ge (022) channel-cut monochromator, Eulerian cradle, and a scintillation counter, using Cu Kα1 radiation.

18O Tracer Exchange

For 18O tracer exchange experiments, single-crystalline substrates (10 × ∼3 × 0.5 mm3) with LSC thin films on top were placed inside a quartz tube and heated (12 K/min) to the specified annealing temperature. Then the quartz tube was evacuated (0.02 mbar) and filled with 200 mbar of tracer oxygen (97.1% 18O isotope enriched, Campro Scientific, Germany). The evacuation process was performed in about 5 min, and the tracer filling took 10 s. After annealing for a certain time (4–36 min), the sample holder was removed from the tube furnace and the quartz tube was cooled (ca. 60 K/min) while retaining the gas pressure at 200 mbar 18O2. At 80 °C the tube was opened and the sample was removed and quenched to room temperature in ambient air.

SIMS Depth Profiling

Time-of-flight secondary ion mass spectrometry (ToF-SIMS) measurements were performed on a TOF.SIMS 5 (ION-TOF, Germany) instrument. Bi+ primary ions of 25 kV were used in a novel operation mode optimized for oxygen tracer experiments [Holzlechner, G., Kubicek, M., Hutter, H., Fleig, J.; submitted to J. Anal. At. Spectrom.], thus allowing a <100 nm beam diameter and an exact determination of the oxygen isotope fraction (measured natural abundance 18O value 0.206% ± 0.004). Areas of 100 × 100 μm2 were investigated using a raster of 512 × 512 or 1024 × 1024 measured points. Negative secondary ions were analyzed. For depth profiling, 2 kV Cs+ ions (500 × 500 μm2, ca. 105 nA) were employed for sequential ablation of the surface between measuring mass spectra, resulting in average depth steps of ca. 0.2 nm. This distance was chosen as the smallest meaningful step size for sputtering: 0.2 nm is about the distance of adjacent oxide-ion layers in the (100) direction of LSC. For charge compensation, a low-energy electron flood gun (10 V) was used.

Acknowledgments

Financial support by Austrian Science Fund (FWF) project F 4509-N16 is gratefully acknowledged by M.K., H.H., and J.F. B.Y., Z.C., and W.M. thank NSF-CAREER Award for financial support, and Carolyn Ross and Harry Tuller for the use of their PLD system at MIT.

Supporting Information Available

In section 1 the effect of chemical etching of the surface of strained LSC films on k* and D* is shown. Section 2 compares the k* and D* of the strained LSC films to LSC films on MgO without a predominant epitaxial strain state. Section 3 shows that the enhancing effect of tensile strain over compressive strain is present for different La1–xSrxCoO3−δ compositions (x = 0.2, x = 0.4). Section 4 gives a sample overview of the temperature/time settings for tracer exchange. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

nn305987x_si_001.pdf (2MB, pdf)

References

  1. Steele B. C. H.; Heinzel A. Materials for Fuel-Cell Technologies. Nature 2001, 414, 345–352. [DOI] [PubMed] [Google Scholar]
  2. Jacobson A. J. Materials for Solid Oxide Fuel Cells. Chem. Mater. 2009, 22, 660–674. [Google Scholar]
  3. Fleig J. Solid Oxide Fuel Cell Cathodes: Polarization Mechanisms and Modeling of the Electrochemical Performance. Annu. Rev. Mater. Res. 2003, 33, 361–382. [Google Scholar]
  4. Adler S. B. Factors Governing Oxygen Reduction in Solid Oxide Fuel Cell Cathodes. Chem. Rev. 2004, 104, 4791–4843. [DOI] [PubMed] [Google Scholar]
  5. Peters C.; Weber A.; Ivers-Tiffee E. Nanoscaled (La0.5Sr0.5)CoO3-δ Thin Film Cathodes for SOFC Application at 500°C < T < 700°C. J. Electrochem. Soc. 2008, 155, B730–B737. [Google Scholar]
  6. Hayd J.; Dieterle L.; Guntow U.; Gerthsen D.; Ivers-Tiffee E. Nanoscaled La0.6Sr0.4CoO3-δ as Intermediate Temperature Solid Oxide Fuel Cell Cathode: Microstructure and Electrochemical Performance. J. Power Sources 2011, 196, 7263–7270. [Google Scholar]
  7. Crumlin E. J.; Mutoro E.; Ahn S. J.; La O G. J.; Leonard D. N.; Borisevich A.; Biegalski M. D.; Christen H. M.; Shao-Horn Y. Oxygen Reduction Kinetics Enhancement on a Heterostructured Oxide Surface for Solid Oxide Fuel Cells. J. Phys. Chem. Lett. 2010, 1, 3149–3155. [Google Scholar]
  8. Baumann F. S.; Fleig J.; Konuma M.; Starke U.; Habermeier H. U.; Maier J. Strong Performance Improvement of La0.6Sr0.4Co0.8Fe0.2O3-δ SOFC Cathodes by Electrochemical Activation. J. Electrochem. Soc. 2005, 152, A2074–A2079. [Google Scholar]
  9. Jiang S. P.; Love J. G. Origin of the Initial Polarization Behavior of Sr-Doped LaMnO3 for O2 Reduction in Solid Oxide Fuel Cells. Solid State Ionics 2001, 138, 183–190. [Google Scholar]
  10. Kubicek M.; Limbeck A.; Frömling T.; Hutter H.; Fleig J. Relationship between Cation Segregation and the Electrochemical Oxygen Reduction Kinetics of La0.6Sr0.4CoO3−δ Thin Film Electrodes. J. Electrochem. Soc. 2011, 158, B727–B734. [Google Scholar]
  11. Cai Z.; Kuru Y.; Han J. W.; Chen Y.; Yildiz B. Surface Electronic Structure Transitions at High Temperature on Perovskite Oxides: The Case of Strained La0.8Sr0.2CoO3 Thin Films. J. Am. Chem. Soc. 2011, 133, 17696–17704. [DOI] [PubMed] [Google Scholar]
  12. Rata A. D.; Herklotz A.; Nenkov K.; Schultz L.; Dorr K. Strain-Induced Insulator State and Giant Gauge Factor of La0.7Sr0.3CoO3 Films. Phys. Rev. Lett. 2008, 100. [DOI] [PubMed] [Google Scholar]
  13. Hou F.; Cai T. Y.; Ju S.; Shen M. R. Half-Metallic Ferromagnetism via the Interface Electronic Reconstruction in LaAlO3/SrMnO3 Nanosheet Superlattices. ACS Nano 2012, 6, 8552–8562. [DOI] [PubMed] [Google Scholar]
  14. Cantoni C.; Gao Y. F.; Wee S. H.; Specht E. D.; Gazquez J.; Meng J. Y.; Pennycook S. J.; Goyal A. Strain-Driven Oxygen Deficiency in Self-Assembled, Nanostructured, Composite Oxide Films. ACS Nano 2011, 5, 4783–4789. [DOI] [PubMed] [Google Scholar]
  15. Estrade S.; Rebled J. M.; Arbiol J.; Peiro F.; Infante I. C.; Herranz G.; Sanchez F.; Fontcuberta J.; Cordoba R.; Mendis B. G.; Bleloch A. L. Effects of Thickness on the Cation Segregation in Epitaxial (001) and (110) La2/3Ca1/3MnO3 Thin Films. Appl. Phys. Lett. 2009, 95, 072507–3. [Google Scholar]
  16. Estradé S.; Arbiol J.; Peiró F.; Infante I. C.; Sánchez F.; Fontcuberta J.; De La Peña F.; Walls M.; Colliex C.. Cationic and Charge Segregation in La2/3Ca1/3MnO3 Thin Films Grown on (001) and (110) SrTiO3. Appl. Phys. Lett. 2008, 93. [Google Scholar]
  17. Estradé S.; Arbiol J.; Peiró F.; Abad L.; Laukhin V.; Balcells L.; Martínez B.. Cationic Diffusion in La2/3Ca1/3MnO3 Thin Films Grown on LaAlO3 (001) Substrates. Appl. Phys. Lett. 2007, 91. [Google Scholar]
  18. Lussier A.; Dvorak J.; Stadler S.; Holroyd J.; Liberati M.; Arenholz E.; Ogale S. B.; Wu T.; Venkatesan T.; Idzerda Y. U. Stress Relaxation of La1/2Sr1/2MnO3 and La2/3Ca1/3MnO3 at Solid Oxide Fuel Cell Interfaces. Thin Solid Films 2008, 516, 880–884. [Google Scholar]
  19. Jalili H.; Han J. W.; Kuru Y.; Cai Z. H.; Yildiz B. New Insights into the Strain Coupling to Surface Chemistry, Electronic Structure, and Reactivity of La0.7Sr0.3MnO3. J Phys Chem Lett 2011, 2, 801–807. [Google Scholar]
  20. Schichtel N.; Korte C.; Hesse D.; Janek J. Elastic Strain at Interfaces and Its Influence on Ionic Conductivity in Nanoscaled Solid Electrolyte Thin Films-Theoretical Considerations and Experimental Studies. Phys. Chem. Chem. Phys. 2009, 11, 3043–3048. [DOI] [PubMed] [Google Scholar]
  21. Kushima A.; Yildiz B. Oxygen Ion Diffusivity in Strained Yttria Stabilized Zirconia: Where Is the Fastest Strain?. J. Mater. Chem. 2010, 20, 4809–4819. [Google Scholar]
  22. Han J. W.; Yildiz B. Enhanced One Dimensional Mobility of Oxygen on Strained LaCoO3(001) Surface. J. Mater. Chem. 2011, 21, 18983–18990. [Google Scholar]
  23. Kushima A.; Yip S.; Yildiz B.. Competing Strain Effects in Reactivity of LaCoO3 with Oxygen. Phys. Rev. B 2010, 82. [Google Scholar]
  24. Burriel M.; Garcia G.; Santiso J.; Kilner J. A.; Richard J. C. C.; Skinner S. J. Anisotropic Oxygen Diffusion Properties in Epitaxial Thin Films of La2NiO4+δ. J. Mater. Chem. 2008, 18, 416–422. [Google Scholar]
  25. Ji H. I.; Hwang J.; Yoon K. J.; Son J. W.; Kim B. K.; Lee H. W.; Lee J. H. Enhanced Oxygen Diffusion in Epitaxial Lanthanum-Strontium-Cobaltite Thin Film Cathodes for Micro Solid Oxide Fuel Cells. Energ. Environ. Sci. 2013, 6, 116–120. [Google Scholar]
  26. Yashima M.; Nomura K.; Kageyama H.; Miyazaki Y.; Chitose N.; Adachi K. Conduction Path and Disorder in the Fast Oxide-Ion Conductor (La0.8Sr0.2)(Ga0.8Mg0.15Co0.05)O2.8. Chem. Phys. Lett. 2003, 380, 391–396. [Google Scholar]
  27. Gunter M. M.; Boysen H.; Corte C.; Lerch M.; Suard E. In-Situ Investigation of Oxygen Diffusion in Sr, Mg-Doped LaGaO3 Superionic Conductors with a Simultaneously Applied Electric Field. Z. Kristallogr. 2005, 220, 218–224. [Google Scholar]
  28. Islam M. S. Ionic Transport in ABO3 Perovskite Oxides: A Computer Modelling Tour. J. Mater. Chem. 2000, 10, 1027–1038. [Google Scholar]
  29. Kilner J. A.; Skinner S. J.; Brongersma H. H. The Isotope Exchange Depth Profiling (IEDP) Technique Using SIMS and LEIS. J. Solid State Electrochem. 2011, 15, 861–876. [Google Scholar]
  30. De Souza R. A.; Kilner J. A. Oxygen Transport in La1-xSrxMn1-yCoyO3±δ Perovskites Part I. Oxygen Tracer Diffusion. Solid State Ionics 1998, 106, 175–187. [Google Scholar]
  31. van Doorn R. E.; Fullarton I. C.; de Souza R. A.; Kilner J. A.; Bouwmeester H. J. M.; Burggraaf A. J. Surface Oxygen Exchange of La0.3Sr0.7CoO3−δ. Solid State Ionics 1997, 96, 1–7. [Google Scholar]
  32. Sitte W.; Bucher E.; Preis W. Nonstoichiometry and Transport Properties of Strontium-Substituted Lanthanum Cobaltites. Solid State Ionics 2002, 154–155, 517–522. [Google Scholar]
  33. van der Haar L. M.; den Otter M. W.; Morskate M.; Bouwmeester H. J. M.; Verweij H. Chemical Diffusion and Oxygen Surface Transfer of La1–xSrxCoO3−δ Studied with Electrical Conductivity Relaxation. J. Electrochem. Soc. 2002, 149, J41–J46. [Google Scholar]
  34. Wang J. Y.; Starke U.; Mittemeijer E. J. Evaluation of the Depth Resolutions of Auger Electron Spectroscopic, X-ray Photoelectron Spectroscopic and Time-of-Flight Secondary-Ion Mass Spectrometric Sputter Depth Profiling Techniques. Thin Solid Films 2009, 517, 3402–3407. [Google Scholar]
  35. Escobar Galindo R.; Gago R.; Albella J. M.; Lousa A. Comparative Depth-Profiling Analysis of Nanometer-Metal Multilayers by Ion-Probing Techniques. TrAC 2009, 28, 494–505. [Google Scholar]
  36. Pergolesi D.; Fabbri E.; Cook S. N.; Roddatis V.; Traversa E.; Kilner J. A.. Tensile Lattice Distortion Does Not Affect Oxygen Transport in Yttria-Stabilized Zirconia–CeO2 Heterointerfaces. ACS Nano 2012. [DOI] [PubMed] [Google Scholar]
  37. Crank J.The Mathematics of Diffusion, 2nd ed.; Oxford University Press: Oxford, 1979. [Google Scholar]
  38. den Otter M. W.; van der Haar L. M.; Bouwmeester H. J. M. Numerical Evaluation of Eigenvalues of the Sheet Diffusion Problem in the Surface/Diffusion Mixed Regime. Solid State Ionics 2000, 134, 259–264. [Google Scholar]
  39. Schneider C. W.; Esposito M.; Marozau I.; Conder K.; Doebeli M.; Hu Y.; Mallepell M.; Wokaun A.; Lippert T.. The Origin of Oxygen in Oxide Thin Films: Role of the Substrate. Appl. Phys. Lett. 2010, 97. [Google Scholar]
  40. De Souza R. A.; Metlenko V.; Park D.; Weirich T. E.. Behavior of Oxygen Vacancies in Single-Crystal SrTiO3: Equilibrium Distribution and Diffusion Kinetics. Phys. Rev. B 2012, 85. [Google Scholar]
  41. Ishigaki T.; Yamauchi S.; Kishio K.; Mizusaki J.; Fueki K. Diffusion of Oxide Ion Vacancies in Perovskite-Type Oxides. J. Solid State Chem. 1988, 73, 179–187. [Google Scholar]
  42. Teraoka Y.; Nobunaga T.; Okamoto K.; Miura N.; Yamazoe N. Influence of Constituent Metal Cations in Substituted LaCoO3 on Mixed Conductivity and Oxygen Permeability. Solid State Ionics 1991, 48, 207–212. [Google Scholar]
  43. Tsvetkov D. S.; Zuev A. Y.; Vylkov A. I.; Petrov A. N. Oxide Ion Transport in Undoped and Cr-Doped LaCoO3-δ. Solid State Ionics 2007, 178, 1458–1462. [Google Scholar]
  44. Ishigaki T.; Yamauchi S.; Mizusaki J.; Fueki K.; Tamura H. Tracer Diffusion Coefficient of Oxide Ions in LaCoO3 Single Crystal. J. Solid State Chem. 1984, 54, 100–107. [Google Scholar]
  45. De Souza R. A.; Metlenko V.; Park D.; Weirich T. E.. Behavior of Oxygen Vacancies in Single-Crystal SrTiO3: Equilibrium Distribution and Diffusion Kinetics. Phys. Rev. B 2012, 85. [Google Scholar]
  46. Denk I.; Munch W.; Maier J. Partial Conductivities in SrTiO3: Bulk Polarization Experiments, Oxygen Concentration Cell Measurements, and Defect-Chemical Modeling. J. Am. Ceram. Soc. 1995, 78, 3265–3272. [Google Scholar]
  47. Mizusaki J.; Yasuda I.; Shimoyama J.-i.; Yamauchi S.; Fueki K. Electrical Conductivity, Defect Equilibrium and Oxygen Vacancy Diffusion Coefficient of La1-xCaxAlO3-δ Single Crystals. J. Electrochem. Soc. 1993, 140, 467–471. [Google Scholar]
  48. Lybye D.; Poulsen F. W.; Mogensen M. Conductivity of A- and B-Site Doped LaAlO3, LaGaO3, LaScO3 and LaInO3 Perovskites. Solid State Ionics 2000, 128, 91–103. [Google Scholar]
  49. Nomura K.; Tanase S. Electrical Conduction Behavior in (La0.9Sr0.1)MIIIO3-δ (MIII = Al, Ga, Sc, In, and Lu) Perovskites. Solid State Ionics 1997, 98, 229–236. [Google Scholar]
  50. Mizusaki J.; Mima Y.; Yamauchi S.; Fueki K.; Tagawa H. Nonstoichiometry of the Perovskite-Type Oxides La1-xSrxCoO3-δ. J. Solid State Chem. 1989, 80, 102–111. [Google Scholar]
  51. Kuhn M.; Fukuda Y.; Hashimoto S.; Sato K.; Yashiro K.; Mizusaki J. Oxygen Nonstoichiometry of Perovskite-Type La0.6Sr0.4Co1-yFeyO3-δ (y=0, 0.2, 0.4, 0.5, 0.6, 0.8, 1) SOFC Cathode Materials. ECS Trans. 2011, 35, 1881–1890. [Google Scholar]
  52. Kuhn M.; Hashimoto S.; Sato K.; Yashiro K.; Mizusaki J. Oxygen Nonstoichiometry, Thermo-Chemical Stability and Lattice Expansion of La0.6Sr0.4FeO3-δ. Solid State Ionics 2011, 195, 7–15. [Google Scholar]
  53. Kawada T.; Suzuki J.; Sase M.; Kaimai A.; Yashiro K.; Nigara Y.; Mizusaki J.; Kawamura K.; Yugami H. Determination of Oxygen Vacancy Concentration in a Thin Film of La0.6Sr0.4CoO3-δ by an Electrochemical Method. J. Electrochem. Soc. 2002, 149, E252–E259. [Google Scholar]
  54. De Souza R. A.; Kilner J. A. Oxygen Transport in La1–xSrxMn1–yCoyO3±δ Perovskites: Part II. Oxygen Surface Exchange. Solid State Ionics 1999, 126, 153–161. [Google Scholar]
  55. Mastrikov Y. A.; Merkle R.; Heifets E.; Kotomin E. A.; Maier J. Pathways for Oxygen Incorporation in Mixed Conducting Perovskites: A DFT-Based Mechanistic Analysis for (La,Sr)MnO3-δ. J. Phys. Chem. C 2010, 114, 3017–3027. [Google Scholar]
  56. Kuru Y.; Marrocchelli D.; Bishop S. R.; Chen D.; Yildiz B.; Tuller H. L. Anomalous Chemical Expansion Behavior of Pr0.2Ce0.8O2-δ Thin Films Grown by Pulsed Laser Deposition. J. Electrochem. Soc. 2012, 159, F799–F803. [Google Scholar]
  57. Lee Y. L.; Kleis J.; Rossmeisl J.; Shao-Horn Y.; Morgan D. Prediction of Solid Oxide Fuel Cell Cathode Activity with First-Principles Descriptors. Energ. Environ. Sci. 2011, 4, 3966–3970. [Google Scholar]
  58. Nørskov J. K.; Rossmeisl J.; Logadottir A.; Lindqvist L.; Kitchin J. R.; Bligaard T.; Jónsson H. Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar]
  59. Jung W.; Tuller H. L. A New Model Describing Solid Oxide Fuel Cell Cathode Kinetics: Model Thin Film SrTi1-xFexO3-δ Mixed Conducting Oxides-A Case Study. Adv. Energy Mater. 2011, 1, 1184–1191. [Google Scholar]
  60. Mizusaki J. Nonstoichiometry, Diffusion, and Electrical-Properties of Perovskite-Type Oxide Electrode Materials. Solid State Ionics 1992, 52, 79–91. [Google Scholar]
  61. Señarís-Rodríguez M. A.; Goodenough J. B. LaCoO3 Revisited. J. Solid State Chem. 1995, 116, 224–231. [Google Scholar]
  62. Chen X.; Yu J.; Adler S. B. Thermal and Chemical Expansion of Sr-Doped Lanthanum Cobalt Oxide (La1-xSrxCoO3-δ). Chem. Mater. 2005, 17, 4537–4546. [Google Scholar]
  63. Kawada T.; Horita T.; Sakai N.; Yokokawa H.; Dokiya M.; Mizusaki J. A Novel Technique for Imaging Electrochemical Reaction Sites on a Solid Oxide Electrolyte. Solid State Ionics 2000, 131, 199–210. [Google Scholar]
  64. Sakai N.; Yamaji K.; Horita T.; Kishimoto H.; Brito M. E.; Yokokawa H.; Uchimoto Y. Application of SIMS Analyses on Oxygen Transport in SOFC Materials. Appl. Surf. Sci. 2006, 252, 7045–7047. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn305987x_si_001.pdf (2MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES