A new residual for ordinal outcomes

Abstract

We propose a new residual for regression models of ordinal outcomes, defined as E{sign(y,Y)}, where y is the observed outcome and Y is a random variable from the fitted distribution. This new residual is a single value per subject irrespective of the number of categories of the ordinal outcome, contains directional information between the observed value and the fitted distribution, and does not require the assignment of arbitrary numbers to categories. We study its properties, describe its connections with other residuals, ranks and ridits, and demonstrate its use in model diagnostics.

1. Introduction

Residuals are an important component of regression analysis. The most basic residual, from linear regression, has many nice features. Specifically, the residual

• (a)results in only one value per subject;
• (b)reflects the overall direction of the observed value compared with the fitted value;
• (c)is monotonic with respect to the observed value for those with the same covariates;
• (d)has a range of possible values that is symmetric about zero; and
• (e)has expectation zero.

This list is by no means comprehensive, and some of these features are more important than others. But these combined features make the linear regression residual popular and useful for diagnostics and tests of conditional independence.

Residuals exist for ordinal outcomes, notably Pearson, cumulative Pearson and deviance residuals (McCullagh & Nelder, 1989). Although these residuals have some use for checking model assumptions and fit, they do not satisfy (a)–(e). Liu et al. (2009) proposed some new residuals; their residual based on the sum of cumulative residuals satisfies (a)–(e), but it implicitly assigns equal-distance scores to the categories; see the Supplementary Material. For ordinal outcomes, in addition to (a)–(e), the ideal residual

• (f)should preserve order without assigning arbitrary scores to the categories.

A residual satisfying (a)–(f) could permit the application of diagnostic tools developed for linear regression to ordinal models, and could provide a framework for testing conditional independence with ordinal variables. Here we study a new residual for ordinal data. It was introduced as a tool for constructing tests of association between ordinal variables (Li & Shepherd, 2010). However, its properties and other uses have not been studied.

2. New residual for ordinal outcomes

2.1. Definition

Consider a set of s ordered categories, S = {1, . . . , s}, with order 1 < ⋯ < s. For a category y in S and a distribution F over S, we define a residual

$$r(y,F)=E\{\text{sign}(y,Y)\}=\text{pr}(y>Y)-\text{pr}(y<Y),$$

where Y is a random variable with distribution F, and sign(a, b) is −1, 0 and 1 for a < b, a = b and a > b, respectively.

In ordinal regression models, we fit an ordinal outcome variable Y on covariates Z. Some common models include continuation ratio, proportional odds and other cumulative link models (Agresti, 2002). For subject i, let Y_i be the outcome and let F_Zi;θ be the distribution of Y_i given covariates Z_i under a model with parameters θ. We define

$$R_i=r(Y_i,F_{Z_i;\theta }).$$ (1)

Given data (y_i, z_i) and a fitted model with parameter estimates θ̂, the residual for subject i is r̂_i = r(y_i, F_zi;θ̂). Notice that r̂_i is not a realization of R_i, but of the random variable R̂_i = r(Y_i, F_Zi;θ̂). If θ̂ → θ in probability, then F_Zi;θ̂ → F_Zi;θ̂ and R̂_i → R_i in distribution. Therefore, moment properties of R_i are applicable to R̂_i asymptotically.

Our residual has all the desirable features listed in § 1; (a), (b) and (f) are obvious and (c)–(e) will result from Properties 1 and 8 below. Proofs of all the properties are given in the Appendix.

2.2. Properties of r(y, F), R_i and r̂_i

First consider a distribution F = (p₁, . . . , p_s) over S. The corresponding cumulative probabilities are γ_j = ∑_k⩽jp_k, with γ_s = 1. For convenience, we define γ₀ = 0. Then for category j ∈ S, r(j, F) = γ_j−1 − (1 − γ_j) = γ_j−1 + γ_j − 1. The following properties hold:

Property 1. −1 ⩽ r(1, F) ⩽ ⋯ ⩽ r(s, F) ⩽ 1;

Property 2. when s = 1, r(1, F) = r(1, 1) = 0, where F = (1) is a point mass;

Property 3. r(j, F) = −r(s − j + 1, G), where G = (q₁, . . . , q_s) = (p_s, . . . , p₁) with q_j = p_s−j+1;

Property 4. as functions of (γ₁, . . . ,γ_s−1), ∂r(j, F)/∂γ_j = ∂r(j + 1, F)/∂γ_j.

Property 1 implies (c) and (d). Property 3 means that when the order of the categories is reversed the residual has the same magnitude but the opposite sign. Property 4 implies that when all probabilities are fixed except for p_j and p_j+1, the residuals for categories j and j + 1 change at the same rate as γ_j, or equivalently, p_j, changes.

If two adjacent categories t and t + 1 are merged, with distribution G = (q₁, . . . , q_s−1), where q_j = p_j for j < t, q_t = p_t + p_t+1 and q_j = p_j+1 for j > t, then the branching property (Brockett & Levine, 1977),

Property 5. $r(j,G)=\{\begin{array}{ll}r(j,F)\hfill & (j<t),\hfill \\ r(j+1,F)\hfill & (j>t),\hfill \\ \{p_{t}r(t,F)+p_{t+1}r(t+1,F)\}/(p_t+p_{t+1})\hfill & (j=t),\hfill \end{array}$ensures robustness to the number of categories, that is, the residual for the new category is a weighted average of those of the merged categories with weights proportional to their probabilities, and the residual remains the same for the other categories.

Properties 1–5 are sensible for a residual measure for ordinal outcomes. Our residual is the only measure, up to a constant factor, that satisfies Properties 1–5. In fact, Properties 2, 5, and simpler versions of Properties 3 and 4, are sufficient for deriving our residual. Specifically, when s = 2, consider:

Property 3^′. r{1, (p, 1 − p)} = −r{2, (1 − p, p)};

Property 4^′. dr{1, (p, 1 − p)}/dp = dr{2, (p, 1 − p)}/dp.

Then the following uniqueness property holds.

Property 6. The function r(j, F) satisfies Properties 2, 3^′, 4^′ and 5 if and only if r(j, F) = c{γ_j−1 −(1 − γ_j)}, where c is an arbitrary constant.

A similar uniqueness property was proved by Brockett & Levine (1977) while studying the properties of ridits (Bross, 1958; Agresti, 1984). In fact, our residual is closely related to ridits, which have been used for scoring levels of an ordinal variable. The ridit for level j is ridit_j = γ_j−1 + p_j/2 = (γ_j−1 + γ_j)/2, and the mean ridit is 1/2. The following property holds:

Property 7. r(j, F)/2 = ridit_j − 1/2.

Now consider a random variable Y over S, with distribution F = (p₁, . . . , p_s). Then R = r(Y, F) is a random variable, for which the following hold:

Property 8. E(R) = 0;

Property 9. $\text{var}(R)=(1-{\sum }_{j=1}^s{p}_j^3)/3$, or alternatively, $\text{var}(R)={\sum }_{j=1}^s{p}_j{\gamma }_{j-1}{\gamma }_j$;

Property 10. when p₁ = ⋯ = p_s = 1/s var(R) reaches its maximum (1 − 1/s²)/3.

Property 9 provides alternative ways of calculating var(R) and implies that var(R) does not depend on the order of the probabilities. The maximum of var(R) is an increasing function of s and it approaches the cap 1/3 fairly quickly, being 0.25, 0.30, 0.32, 0.33, for s = 2, 3, 5, 10, respectively.

Now consider a random sample of n subjects, with n_j subjects in category j (j = 1, . . . , s). Their empirical distribution is F̂ = (p̂₁, . . . , p̂_s), where p̂_j = n_j/n, with cumulative probabilities γ̂_j = ∑_k⩽jn_k/n. Since there are no covariates, we can think of a constant predictor for all subjects. Then F̂ is the fitted distribution and for subjects in category j, their residual is r_j = r(j, F̂) = γ̂_j−1 + γ̂_j − 1 = (∑_k<j 2n_k + n_j − n)/n. If we rank these subjects their midrank is rank_j = ∑_k<jn_k + (n_j + 1)/2 and,

Property 11. rank_j = T (r_j), where T (r) = (n/2)r + (n + 1)/2.

The function T (r) can be viewed as a translation from the residual scale to the rank scale. Li & Shepherd (2010) presented statistics for testing the association between two ordinal variables, X and Y, while adjusting for covariates Z. One statistic was the correlation coefficient between the residuals from models for X | Z and Y | Z. Property 11 implies that when there are no covariates, our statistic is Spearman’s rank correlation coefficient between X and Y. When covariates exist, T (r) will yield adjusted ranks of the subjects, and our statistic can be interpreted as an adjusted rank correlation.

We now focus on models for an ordinal outcome Y on covariates Z with parameters θ. For subject i (i = 1, . . . , n) and category j (j = 1, . . . , s), let γ_i,j = pr(Y_i ⩽ j | Z_i; θ); for convenience, we define γ_i,0 = 0. Let p_i,j = pr(Y_i = j | Z_i) = γ_i,j − γ_i,j−1. The following moment properties hold:

Property 12. E(R_i | Z_i; θ) = 0;

Property 13. $\text{var}(R_i|Z_i;\theta )=E(R_i^2|Z_i;\theta )={\sum }_{j=1}^s{p}_{i,j}{({\gamma }_{i,j-1}+{\gamma }_{i,j}-1)}^2$.

Let p̂_i,j and γ̂_i,j be the maximum likelihood estimates of p_i,j and γ_i,j. Then r̂_i = γ̂_i,yi−1 + γ̂_{i, yi}− 1. The variance of R_i can be consistently estimated by inserting these estimates into Property 13, $\widehat{\text{var}}(R_i)=\text{var}(R_i|z_i;\widehat{\theta })={\sum }_{j=1}^s{\widehat{p}}_{i,j}{({\widehat{\gamma }}_{i,j-1}+{\widehat{\gamma }}_{i,j}-1)}^2$. One could therefore calculate a standardized residual as r̂_i/{vâr(R_i)}^1/2, which for binary Y is the Pearson residual (I_{Yi=2} − p̂_i,2)(p̂_i,1p̂_i,2)^−1/2 (McCullagh & Nelder, 1989).

Now consider a proportional odds model (McCullagh, 1980), logit{pr(Y ⩽ j | Z)} = α_j + Z^Tβ (j = 1, . . . , s − 1), with parameters θ = (α₁, . . . , α_s−1, β). Under this model, our residuals are related to score residuals (Therneau et al., 1990). Let l_i be the loglikelihood for subject i, and U_i = U_i (θ) = ∂l_i/∂θ. Because E_θ (U_i) = 0, U_i is called the score residual. For proportional odds models, the following properties hold:

Property 14. ${\widehat{r}}_i=-{\sum }_{j=1}^{s-1}(\partial l_i/\partial {\alpha }_j){|}_{\widehat{\theta }}$, where θ̂ is the maximum likelihood estimate;

Property 15. ${\sum }_{i=1}^n{\widehat{r}}_i=0$.

Property 14 implies that our residual is a partially aggregated score residual over the α components of U_i (θ̂), and Property 15 is analogous to that of linear regression residuals.

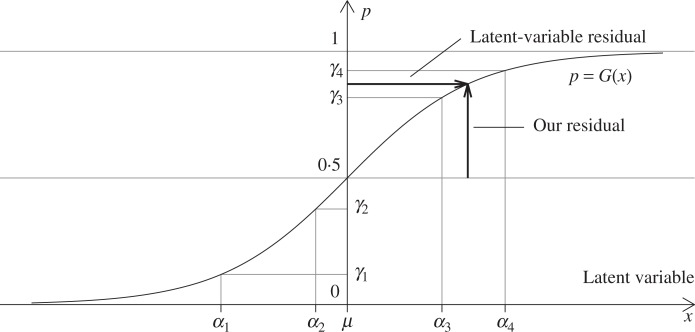
2.3. Connection to residuals on a latent variable scale

In cumulative link regression models, the cumulative probability γ_i,j is modelled through a link function G⁻¹ (γ_i,j) = α_j + $z_i^{\text{T}}$β, where G is a cumulative distribution function over the real line. The ordinal outcome Y_i can be viewed as the result of applying thresholds α₁, . . . , α_s−1 to a latent random variable U_i that has cumulative distribution function G_i (u) = G(u + $z_i^{\text{T}}$β). Then E(U_i) = μ − $z_i^{\text{T}}$β, where μ is the mean of G. For convenience, let α₀ = −∞ and α_s = +∞.

If we observed U_i, the usual residual on the latent variable scale would be U_i,res = U_i − E(U_i) = U_i + $z_i^{\text{T}}$β − μ. Since U_i + $z_i^{\text{T}}$β ∼ G, U_i,res follow the same distribution for all subjects and E (U_i,res) = 0. As U_i is latent, we do not know its value but only that α_j−1< U_i< α_j if Y_i = j. One may want to replace U_i with

$$E(U_i|Y_i=j)=\frac{1}{p_{i,j}}{\int }_{\alpha j-1}^{{\alpha }_j}u\text{d}{G}_i(u)=\frac{1}{p_{i,j}}{\int }_{{\gamma }_{i,j-1}}^{{\gamma }_{i,j}}{G}_i^{-1}(p)\text{d}p=\frac{1}{p_{i,j}}{\int }_{{\gamma }_{i,j-1}}^{{\gamma }_{i,}{}_j}{G}^{-1}(p)\text{d}p-z_i^{\text{T}}\beta ,$$

and define a residual on the latent variable scale as

$$L_{i,\text{res}}=E(U_i|Y_i=j)+z_i^{\text{T}}\beta -\mu =\frac{1}{p_{i,j}}{\int }_{{\gamma }_{i,j-1}}^{{\gamma }_{i,j}}{G}^{-1}(p)\text{d}p-\mu ,$$

where E(L_i,res) = E{E(U_i,res | Y_i)} = E(U_i,res) = 0.

If the mean of G is its median, which is true for logit and probit link functions, then μ = G⁻¹(1/2). And if the interval (γ_i,j−1,γ_i,j) is small, then

$$\frac{1}{p_{i,j}}{\int }_{{\gamma }_{i,j-1}}^{{\gamma }_{i,j}}{G}^{-1}(p)\text{d}p-\mu \approx G^{-1}(m_{i,j})-G^{-1}\left(\frac{1}{2}\right),$$

where m_i,j = (γ_i,j−1 + γ_i,j)/2. Since $R_i/2=m_{i,j}-\frac{1}{2}$, our residual is equivalent to comparing m_i,j with 1/2 on the probability scale. Therefore, our residual captures information similar to that of a latent-variable residual, but on a probability scale irrespective of the choice of link function; see Fig. 1.

Fig. 1.

Connection between our residual and a latent-variable residual.

3. Use of the residual in model diagnostics

3.1. Residual-by-predictor plots

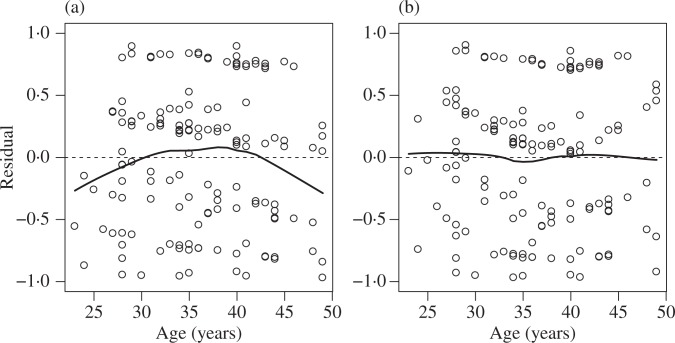
When an ordinal regression model is correct, E(L_i,res) = 0 and L_i,res = E(U_i,res | Y_i) is a categorization of U_i,res, which follows the same distribution across all subjects. Therefore, L_i,res may have similar distributions across subjects. In addition, we have shown that E(R_i) = 0, the range of R_i is symmetric about zero, and R_i and L_i,res are closely related. Therefore, a plot of r̂, or its latent-variable version l̂_res, versus a predictor can be useful for visually detecting if there is any additional effect of that predictor, such as nonlinearity, on the outcome. This plot is referred to as a residual-by-predictor plot.

We use data from a study of HIV-infected women in Zambia (Parham et al., 2006) to demonstrate an application of residual-by-predictor plots. Cervical specimens from 145 women were examined using cytology and categorized into five ordered stages. We fit proportional odds models to assess the association between stage of cervical lesions and age after adjusting for CD4 count. Under the assumption of a linear relationship of age with the log-odds of severity of lesions, the model tends to overpredict severity of lesions at low and high ages, as shown in Fig. 2. If age is put into the model with linear and quadratic terms, the residuals are much more uniform across ages. The plots are similar using standardized or latent-variable residuals, shown in the Supplementary Material.

Fig. 2.

Residual-by-predictor plots with age included in proportional odds models with a linear term (a) and with linear and quadratic terms (b). Lowess curves (solid) are added. A horizontal line (dashed) at zero is included for reference.

3.2. Partial regression plots

When fitting a regression model of an ordinal outcome Y on a covariate X and other covariates Z, we may want to examine whether X is associated with Y after adjusting for the effects of Z. To do this, we first fit an ordinal regression model of Y on Z to obtain residuals r̂_y, then fit an appropriate regression model of X on Z to obtain residuals r̂_x, and plot r̂_y versus r̂_x. This plot is called a partial regression plot. Let R_Y be the random variable as defined in (1) and R_X be the residual random variable for the model for X | Z, of which r̂_x is a realization. When the model for Y | Z is correct and Y and X are independent conditional on Z, R_Y and R_X are independent given Z. Thus, E (R_YR_X) = E{E(R_YR_X | Z)} = E{E(R_Y | Z)E(R_X | Z)} = 0 by Property 12, E(R_Y) = E{E(R_Y | Z)} = 0 and cov(R_Y, R_X) = E(R_YR_X) − E(R_Y) E(R_X) = 0; that is, R_Y and R_X are uncorrelated. Hence, the partial regression plot can provide a visual inspection on whether X remains a useful predictor of Y after the effects of Z have been adjusted for. Although the validity of this plot does not depend on the type of residual for X, its effectiveness might.

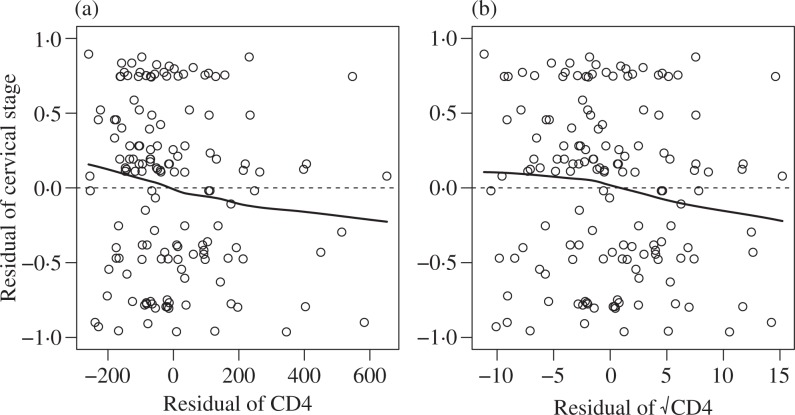
We use the same dataset as that in § 3.1 to demonstrate partial regression plots. Figure 3(a) is a partial regression plot for the association between cervical lesions and CD4 T-cell count. Residuals from a proportional odds regression of cervical lesions on age and squared age are plotted against residuals from a linear regression of CD4 count on age and squared age. There appears to be correlation between these residuals, so it may be useful to include CD4 count in the model for cervical lesions. Partial regression plots may also be useful for detecting outliers: no single observation appears to be overly influential in this analysis, although the skewed nature of the CD4 residuals suggests that a square root transformation of this variable may lead to a better fit, as suggested by Fig. 3(b). Additional examples of partial regression plots using our residuals are in Li & Shepherd (2010).

Fig. 3.

Partial regression plots looking at the residual association of cervical lesions with (a) CD4 and (b) square-root transformed CD4 after adjusting for age, with both linear and quadratic terms. Lowess curves (solid) are added. A horizontal line (dashed) at zero is included for reference.

4. Discussion

Our residual is effectively defined on the probability scale of the fitted distribution, and can be extended to any regression analysis in which fitted distributions are calculated. One potential advantage of probability-scale residuals is that they can be defined for regression analyses in which the fitted distributions are not completely determined, such as in models of censored data or quantile regression.

Our new residual offers a general solution for how to include an ordinal predictor in a regression model. Traditional approaches treat an ordinal predictor as either numerical, enforcing a linearity assumption, or categorical, ignoring order information. An alternative approach would be to fit an appropriate regression model of the outcome on other covariates Z and an ordinal regression model of the ordinal predictor on Z, and test for correlation between the residuals of the models. The partial regression plot is the graphical counterpart of this approach. We have shown this approach to be robust and powerful when the outcome variable is also ordinal (Li & Shepherd, 2010), and we are studying this approach for other outcome types.

One limitation of our residual is that it seems not useful for checking the proportional odds assumption in proportional odds models, as the cell-wise information necessary for investigating this assumption is collapsed into a single value.

Appendix. Proofs of properties

Properties 2, 4, 7, 11–13 are obvious.

Proof of Property 1. Since r(j + 1, F) − r(j, F) = γ_j+1 − γ_j−1 ⩾ 0, we have r(j, F) ⩽ r(j + 1, F). Since γ₁ ⩾ 0 and γ_s−1 ⩽ 1, r(1, F) = γ₁ − 1 ⩾ −1 and r(s, F) = γ_s−1 ⩽ 1.

Proof of Property 3. Let γ_j|F and γ_j|G be the cumulative probabilities for distributions F and G, respectively. Let t = s − j + 1. Then γ_t−1|G = 1 − γ_j|F and γ_t|G = 1 − γ_j−1|F. Therefore, r (t, G) = γ_t−1|G +γ_t|G − 1 = 1 − γ_j|F − γ_j−1|F = −r(j, F).

Proof of Property 5. The results for j < t and j > t are obvious. For j = t, since r(t + 1, F) = r(t, F) + (p_t + p_t+1) and r(t, F) = 2γ_t−1 + p_t − 1, we have {p_tr (t, F) + p_t+1r (t + 1, F)}/(p_t + p_t+1) = r(t, F) + p_t+1 = 2γ_t−1 + (p_t + p_t+1) − 1 = r(t, G).

Proof of Property 6. Let f (p) = r{2, (p, 1 − p)} for 0 < p < 1. We first show that f (p)/ p is a constant. By Property 3^′, r{1, (p, 1 − p)} = − f (1 − p). By Property 4^′, f^′(1 − p) = f^′(p) and thus f (1 − p) + f (p) ≡ c is a constant as its derivative is always zero. By Properties 2 and 5, 0 = r(1, p + 1 −p) = − p f (1 − p) + (1 − p) f (p), and thus f (1 − p) = f (p)(1 − p)/ p. Then, c ≡ f (1 − p) + f (p) = f (p)/ p and f (p) = cp.

By Property 5, r(j, F) = r{2, (a, p_j, b)}, where a = γ_j−1 and b = 1 − γ_j. By Properties 2 and 5,

$$\begin{array}{l}0=a\times r\{1,(a,p_j,b)\}+p_j\times r\{2,(a,p_j,b)\}+b\times r\{3,(a,p_j,b)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=a\times r\{1,(a,1-a)\}+p_j\times r\{2,(a,p_j,b)\}+b\times r\{2,(1-b,b)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=-af(1-a)+p_{j}r(j,F)+bf(1-b).\end{array}$$

Thus, r(j, F) = {af (1 − a) − bf (1 − b)}/ p_j = c{a(1 − a) − b(1 − b)}/ p_j = c{a(p_j + b) − b(a + p_j)}/ p_j = c(a − b) = c{γ_j−1 − (1 − γ_j)}. It is easy to show the reverse.

Proof of Property 8. Since ∑_jp_jγ_j−1 = ∑_jp_j (∑_k<jp_k) = ∑_{j1< j2} p_j1 p_j2 and ∑_jp_j (1 − γ_j) = ∑_jp_j(∑_k>jp_k) = ∑_{j1 < j2} p_j1p_j2, we have E (R) = ∑_jp_j (γ_j−1 − (1 − γ_j)} = 0.

Proof of Property 9. Since E(R) = 0 and γ_a−1 − (1 − γ_a) = ∑_b:b≠ap_b × sign(a − b),

$$\begin{array}{ll}\text{var}(R)\hfill & =E(R^2)=\sum _{a=1}^s{p}_a{\{{\gamma }_{a-1}-(1-{\gamma }_a)\}}^2\hfill \\ \hfill & =\sum _{a=1}^s{p}_a\left\{\sum _{b:b\ne a}{p}_b^2+\sum _{b,c:b<c,b\ne a,c\ne a}2p_b{p}_c\times \text{sign}(a-b)\text{sign}(a-c)\right\}\hfill \\ \hfill & =\sum _{a\ne b}{p}_a{p}_b^2+2\sum _{a<b<c}{p}_a{p}_b{p}_c.\hfill \end{array}$$

Since 1 = (∑_ap_a)³ = ∑_a $p_a^3$ + 3 ∑_a≠bp_a $p_b^2$ + 6 ∑_a<b<cp_ap_bp_c, var(R) = (1 − ∑_a $p_a^3$)/3.

For the alternative expression, since ∑_a<bp_ap_b = ∑_a<bp_ap_b ∑_cp_c = ∑_a<b(p_a $p_b^2$ + $p_a^2$p_b + ∑_c≠a,bp_ap_bp_c) = ∑_a≠bp_a $p_b^2$ + 3 ∑_a<b<cp_ap_bp_c,

$$\text{var}(R)=\sum _{a<b}{p}_a{p}_b-\sum _{a<b<c}{p}_a{p}_b{p}_c=\sum _{a<b}{p}_a{p}_b{\gamma }_b=\sum _{b=2}^s{p}_b{\gamma }_{b-1}{\gamma }_b=\sum _{b=1}^s{p}_b{\gamma }_{b-1}{\gamma }_b.$$

Proof of Property 10. To maximize var(R) subject to the constraint ∑p_j = 1, we employ a Lagrange multiplier in the function

$$f(p_1,\dots ,p_s,\lambda )=\text{var}(R)-\lambda \left(\sum p_j-1\right)=\frac{1}{3}\left(1-\sum p_j^3\right)-\lambda \left(\sum p_j-1\right).$$

Setting ∂f/∂λ = 0 gives the constraint ∑p_j − 1. Setting ∂f/∂p_j = − $p_j^2$ − λ = 0 for all j leads to p₁ = ⋯ = p_s = 1/s and var(R) = (1 − 1/s²)/3.

Proof of Properties 14 and 15. For proportional odds models, it can be shown that

$$\frac{\partial {\gamma }_{i,j}}{\partial {\alpha }_j}={\gamma }_{i,j}(1-{\gamma }_{i,j}),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{\partial {\gamma }_{i,j}}{\partial {\alpha }_k}=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(j\ne k).$$

For convenience, let γ_i,0 = 0. For subject i, let l_i = log(p_{i, yi}) = log(γ _{i, yi} − γ _{i, yi−1}) be the loglikelihood. Let l = ∑_il_i and θ̂ be the maximum likelihood estimate. Then

$$\begin{array}{l}\sum _{j=1}^{s-1}{\frac{\partial l_i}{\partial {\alpha }_j}|}_{\widehat{\theta }}=\frac{{\widehat{\gamma }}_{i,y_i}(1-{\widehat{\gamma }}_{i,y_i})}{{\widehat{p}}_{i,y_i}}-\frac{{\widehat{\gamma }}_{i,y_i-1}(1-{\widehat{\gamma }}_{i,y_i-1})}{{\widehat{p}}_{i,y_i}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\frac{({\widehat{\gamma }}_{i,y_i-1}+{\widehat{p}}_{y_i})(1-{\widehat{\gamma }}_{i,y_i})-{\widehat{\gamma }}_{i,y_i-1}({\widehat{p}}_{y_i}+1-{\widehat{\gamma }}_{i,y_i})}{{\widehat{p}}_{i,y_i}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=(1-{\widehat{\gamma }}_{i,y_i})-{\widehat{\gamma }}_{i,y_i-1}=-{\widehat{r}}_i\end{array}$$

and

$$\sum _{i=1}^n{\widehat{r}}_i=-\sum _{i=1}^n\sum _{j=1}^{s-1}\frac{\partial l_i}{\partial {\alpha }_j}|{}_{\widehat{\theta }}=-\sum _{j=1}^{s-1}\frac{\partial l}{\partial {\alpha }_j}|{}_{\widehat{\theta }}=0.$$

Supplementary material

Supplementary material available at Biometrika online includes additional figures and a discussion of residuals in Liu et al. (2009).