Predictive accuracy of covariates for event times

Summary

We propose a graphical measure, the generalized negative predictive function, to quantify the predictive accuracy of covariates for survival time or recurrent event times. This new measure characterizes the event-free probabilities over time conditional on a thresholded linear combination of covariates and has direct clinical utility. We show that this function is maximized at the set of covariates truly related to event times and thus can be used to compare the predictive accuracy of different sets of covariates. We construct nonparametric estimators for this function under right censoring and prove that the proposed estimators, upon proper normalization, converge weakly to zero-mean Gaussian processes. To bypass the estimation of complex density functions involved in the asymptotic variances, we adopt the bootstrap approach and establish its validity. Simulation studies demonstrate that the proposed methods perform well in practical situations. Two clinical studies are presented.

1. Introduction

In cohort studies, potentially censored times until the occurrence of a particular event, such as death or disease recurrence, are often recorded, along with data on certain covariates, including demographic, clinical and genetic factors. An important objective of such studies is to determine which set of covariates is most predictive of event times and thus can be used to select patients for targeted therapy or to refine disease prevention strategies. For example, the gene expression breast cancer study of van de Vijver et al. (2002) was designed to assess whether a 70-gene signature can improve the prediction of survival times and the selection of patients for adjuvant chemotherapy over standard clinical factors. Clinicians are extremely interested in the percentage of patients who can be spared adjuvant chemotherapy, and in the long-term survival probabilities for those patients. To address this type of question, a statistical measure directly related to survival probabilities is needed to quantify the predictive accuracy of covariates and to compare the predictive accuracy of different sets of covariates.

Several methods exist for assessing the predictive accuracy of covariates for survival time or a single event. One approach extends the proportion of variation explained by covariates, R², for the linear regression model to the proportional hazards model (Korn & Simon, 1990; Schemper, 1990; Schemper & Henderson, 2000), and a second approach is to use a suitable loss function, such as the Brier score, to measure residual variation (Graf et al., 1999). These measures, however, may lack clinical relevance. A more recent approach is to extend the receiver operating characteristic curve for binary response to survival time (Heagerty & Zheng, 2005; Uno et al., 2007). This measure is focused on classification rather than prediction and is not directly related to survival probabilities.

For a binary disease status D and a binary covariate Z, each taking values 0 and 1, standard measures of predictive accuracy include the positive predictive value and negative predictive value, which are defined as ppv = pr(D = 1 | Z = 1) and npv = pr(D = 0 | Z = 0), respectively. The predictive values pertain to the probability of disease or nondisease given a positive or negative result for a dichotomous test and are thus of direct interest to the end users of the test. When Z is continuous and a larger value of Z corresponds to a higher risk of disease, Moskowitz & Pepe (2004) defined the positive and negative predictive curves ppv(υ) = pr{D = 1 | F_Z (Z) > υ} and npv(υ) = pr{D = 0 | F_Z (Z) ⩽ υ} (0 ⩽ υ ⩽ 1), where F_Z (·) is the distribution function of Z. Using F_Z (Z) instead of Z yields two appealing properties. First, the positive and negative predictive curves do not depend on the scales upon which the continuous covariates are measured and are thus comparable among different covariates. Second, it can be shown that ppv(υ) = 1 − {pr(D = 0) − υnpv(υ)}(1 − υ)⁻¹, which means that a higher negative predictive curve corresponds to a higher positive predictive curve, so either curve is sufficient to quantify predictive accuracy. These measures were recently extended to survival data by Zheng et al. (2008), who defined time-dependent predictive curves as ppv(t, υ) = pr{T ⩽ t | F_Z (Z) > υ} and npv(t, υ) = pr{T > t | F_Z (Z) ⩽ υ}, where T is the survival time; the extension pertains to a single event with a single covariate. Uno et al. (2007) considered the predictive curves at a fixed time-point for a single event with multiple covariates by standardizing the linear predictor with a known transformation function and proposed inverse probability weighted estimators under completely-at-random censoring.

In the present paper, we propose a new concept, the generalized negative predictive function, to quantify the predictive accuracy of multiple covariates for both survival time and recurrent event times. In the special case of a single event with a single covariate, our function reduces to that of Zheng et al. (2008). We show that the proposed function is maximized at the set of covariates that is truly related to event times and thus can be used to quantify and compare the predictive accuracy of covariates. No such theoretical results are available even for a binary outcome or a single event with a single covariate. We develop nonparametric estimators for the proposed function, allowing censoring to depend on covariates, and establish their large-sample properties. Because a linear combination of covariates is obtained from a possibly misspecified working model to predict event times, the asymptotic distributions of the estimators for the case of multiple covariates are considerably more complicated than the case of a single covariate.

2. Generalized negative predictive function

Let N^*(t) be the counting process which records the number of events the subject has experienced by time t. Let X be the vector of all potential covariates, and Z be a p × 1 subset of X. We wish to quantify the ability of Z in predicting N^*(·).

We first consider the case where Z is a single covariate. Suppose that a larger value of Z corresponds to a higher event rate. Then at each time-point u ∈ (0, t], we can define a negative predictive curve, pr{dN^*(u) = 0 | Y^*(u) = 1, F_Z (Z) ⩽ υ}, for the subjects who are at risk at that time, where Y^*(u) is a process indicating whether the subject is at risk for experiencing an event at time u. By taking the product integral of these curves in the time interval (0, t], we define the generalized negative predictive function of Z as

$$G\left(t,\upsilon \right)=\prod _{0⩽u⩽t}\text{pr}\{\text{d}{N}^{*}(u)=0|Y^{*}(u)=1,\hspace{0.17em}{F}_Z(Z)⩽\upsilon \}.$$ (1)

For single-event data, N^*(·) has a single jump at the event time T and Y^*(t) = I (T ⩾ t), so that equation (1) reduces to npv(t, υ) = pr{T > t | F_Z (Z) ⩽ υ} of Zheng et al. (2008). For recurrent event data, equation (1) is equivalent to

$$G\left(t,\upsilon \right)=\text{exp}\hspace{0.17em}\left[-{\int }_0^{t}E\{\text{d}{N}^{*}(u)|Y^{*}(u)=1,\hspace{0.17em}{F}_Z(Z)⩽\upsilon \}\right],$$

which can be rewritten as exp[−E{N^*(t) | F_Z (Z) ⩽ υ}] because Y^* (·) = 1; therefore, − log{G(t, υ)} can be interpreted as the predictive number of events by time t in the subgroup with F_Z (Z) ⩽ υ. If the counting process has a Poisson structure such that the occurrence of an event is independent of the prior event history conditional on Z, then (1) can also be interpreted as the probability of no event by time t in the subgroup with F_Z (Z) ⩽ υ.

We now consider the case that Z includes multiple covariates. To use Z to predict N^*(·), a common approach is to obtain a linear combination of Z under a regression model. We consider a semiparametric working model in the form of

$$E\{N^{*}(t)|Z\}=g\left(t,{\beta }^{\text{T}}Z\right),$$ (2)

where β is a p × 1 vector of unknown regression parameters, and g(t, υ) is a strictly increasing function of υ for all t > 0. For single-event data, we can use the class of semiparametric transformation models (Dabrowska & Doksum, 1988; Zeng & Lin, 2006), which includes the proportional hazards and proportional odds models as special cases. For recurrent event data, we can use the class of semiparametric transformation mean models (Lin et al., 2001).

Let β̂ be the estimator of β described in Zeng & Lin (2006). For single-event data and recurrent events with a Poisson structure, β̂ is the nonparametric maximum likelihood estimator. For recurrent events without a Poisson structure, β̂ is viewed as a maximum pseudo-likelihood estimator. It can be shown that β̂ converges to some constant vector β^* under mild regularity conditions even when model (2) is misspecified. The predictive accuracy of Z can be quantified by the generalized negative predictive function of β^*TZ,

$$G_{Z,{\beta }^{*}}\left(t,\upsilon \right)=\prod _{0⩽u⩽t}\text{pr}\{\text{d}{N}^{*}(u)=0|Y^{*}(u)=1,\hspace{0.17em}{F}_{{\beta }^{*\text{T}}Z}\left({\beta }^{*\text{T}}Z\right)⩽\upsilon \},$$ (3)

which is equal to pr{T > t | F_β^*TZ (β^*TZ) ⩽ υ} for single-event data, and to exp[−E{N^*(t) | F_β^*TZ (β^*TZ) ⩽ υ}] for recurrent event data.

As a function of both t and υ, the generalized negative predictive function can be plotted against the cut-off percentage υ for a specific t. By comparing such plots for two sets of covariates, one can tell the difference in the event-free probability at time t between the two groups that include υ percentage of low-risk subjects as defined by the two sets of covariates. The low-risk group defined by the more predictive set of covariates has a higher survival probability. As in the case of the receiving operating characteristic curve, the area under the curve can be used as a summary measure. One can set a cut-off of survival probability to define low risk. For breast cancer patients, the low-risk group is usually defined to have a 5-year survival probability of at least 0.95. Then drawing a horizontal line at 0.95 would yield the percentage of patients who can be defined as low risk. For this type of application, the function is required to be monotone. The proposed function can also be plotted against t for a specific υ. By comparing such plots for two sets of covariates, one can tell how the difference in the event-free probability changes over time for the two low-risk groups defined by the two sets of covariates.

We now provide a formal justification for using the generalized negative predictive function to compare the predictive accuracy of different sets of covariates. Using Lemma A1 of Appendix 1, we can obtain an optimality property of G_Z,β^*(t, υ) that this function is maximized at the true linear combination of covariates and that the maximization holds uniformly for all t and υ. Specifically, suppose that Z₀ is the subset of X truly related to N^*(·) in that E{N^*(t) | X} depends on Z₀ only and that β₀ is the true value of β associated with Z₀ under model (2). Then G_Z0,β0 (t, υ) ⩾ G_Z,β (t, υ) for all t > 0 and υ ∈ (0, 1).

3. Inference procedures

3.1. Preliminaries

Let C denote the censoring time. In the presence of censoring, the observed counting process is N(t) = N^*(t ∧ C) and the at-risk process is Y (t) = Y^*(t)I (C ⩾ t), where a ∧ b = min(a, b), and I (·) is the indicator function. The data consist of n independent replicates {N_i (t), Y_i (t), X_i : t ∈ [0, τ]} (i = 1, …, n), where τ is the endpoint of the study. We use the estimator β̂ from the working model (2) to construct nonparametric estimators for G_Z,β^* (t, υ). We consider the situation that C is independent of N^*(·) and X, as well as the situation that C is independent of N^*(·) conditional on X. We refer to these two censoring mechanisms as completely-at-random censoring and covariate-dependent censoring, respectively.

3.2. Single-event data under completely-at-random censoring

Under completely-at-random censoring, pr{dN^*(u) = 0 | Y^* (u) = 1, F_β^*TZ (β^*T Z) ⩽ υ} = pr{dN(u) = 0 | Y (u) = 1, F_β^*TZ (β^*T Z) ⩽ υ}. Thus, we estimate G_Z,β^* (t, υ) by

$$\widehat{G}\left(t,\upsilon \right)=\prod _{0<u⩽t}\hspace{0.17em}\left[1-\frac{{\sum }_{i=1}^n\hspace{0.17em}I\{F_n\left({\widehat{\beta }}^{\text{T}}{Z}_i\right)⩽\upsilon \}\text{d}{N}_i(u)}{{\sum }_{i=1}^n\hspace{0.17em}I\{F_n\left({\widehat{\beta }}^{\text{T}}{Z}_i\right)⩽\upsilon \}{Y}_i(u)}\right],$$

where F_n(·) is the empirical distribution of β̂^TZ. Note that Ĝ(t, υ) is the Kaplan–Meier estimator of the survival function in the subgroup with F_n(β̂^TZ) ⩽ υ.

In Appendix 2, we show that the process n^1/2{Ĝ(t, υ) − G_Z,β^* (t, υ)} converges weakly to a zero-mean Gaussian process and is asymptotically equivalent to the process

$$n^{-1/2}\sum _{i=1}^n{\xi }_{1i}\left(t,\upsilon \right)+n^{1/2}\{\widehat{G}\left(t;{\widehat{c}}_{\upsilon },\widehat{\beta }\right)-\widehat{G}\left(t;c_{\upsilon },{\beta }^{*}\right)\},$$ (4)

where

$${\xi }_{1i}\left(t,\upsilon \right)=-G_{Z,{\beta }^{*}}\left(t,\upsilon \right)I\left({\beta }^{*\text{T}}{Z}_i⩽c_{\upsilon }\right)\hspace{0.17em}{\int }_0^t\frac{\text{d}{N}_i(u)-Y_i(u)\text{d}\mathrm{\Lambda }\left(t;c_{\upsilon },{\beta }^{*}\right)}{E\{I\left({\beta }^{*\text{T}}Z⩽c_{\upsilon }\right)Y(u)\}},$$

$$G\left(t;c,\beta \right)=\prod _{0<u⩽t}\left[1-\frac{E\{I\left({\beta }^{\text{T}}Z⩽c\right)\text{d}{N}^{*}(u)\}}{E\{I\left({\beta }^{\text{T}}Z⩽c\right)Y^{*}(u)\}}\right],$$

$$\widehat{G}\left(t;c,\beta \right)=\prod _{0<u⩽t}\left\{1-\frac{{\sum }_{i=1}^{n}I\left({\beta }^{\text{T}}{Z}_i⩽c\right)\text{d}{N}_i(u)}{{\sum }_{i=1}^{n}I\left({\beta }^{\text{T}}{Z}_i⩽c\right)Y_i(u)}\right\},$$

$c_{\upsilon }=F_{{\beta }^{*\text{T}}Z}^{-1}\left(\upsilon \right)$, ${\widehat{c}}_{\upsilon }=F_n^{-1}\left(\upsilon \right)$, and dΛ(t; c, β) = E{dN^*(t) | Y^*(t) = 1, β^TZ ⩽ c}. The second term in (4) is asymptotically equivalent to $n^{-1/2}\hspace{0.17em}{\sum }_{i=1}^n\hspace{0.17em}{\xi }_{2i}\left(t,\upsilon \right)$, where ξ_2i (t, υ) is the value of ξ₂(t, υ), defined in equation (A5) of Appendix 2, for the ith subject. Note that ξ₂(t, υ) involves conditional density functions given multi-dimensional covariates, which are difficult to estimate directly. To avoid this difficulty, we approximate the asymptotic distribution by bootstrapping the observations {N_i (t), Y_i (t), X_i : t ∈ [0, τ]} (i = 1, …, n). We recommend using 1000 bootstrap samples. The validity of the bootstrap is proved in Appendix 4.

3.3. Single-event data under covariate-dependent censoring

When censoring is not completely at random, the Kaplan–Meier type estimator for the generalized negative predictive function presented in § 3.2 is no longer consistent because pr{dN^*(u) = 0 | Y^*(u) = 1, F_β^*TZ (β^*TZ) ⩽ υ} ≠ pr{dN(u) = 0 | Y (u) = 1, F_β^*TZ (β^*TZ) ⩽ υ}. We decompose the set of all potential covariates X into two parts, U and W, where U is known to be independent of C, and C is independent of N^*(·) conditional on W. Let q be the number of continuous components in W. Note that pr{T > t | F_β^*TZ (β^*T Z) ⩽ υ} = E[E{I (T > t, β^*T Z ⩽ c_υ) | W}]/υ = E{S(t; c_υ, β*, W)I (β^*T Z ⩽ c_υ)}/υ, where S(t; c, β, w) = pr(T > t | β^T Z ⩽ c, W = w). Since the cumulative hazard function corresponding to S(t; c, β, w), denoted by Λ(t; c, β, w), is equal to ${\int }_0^t\hspace{0.17em}E\{\text{d}N(u)I\left({\beta }^{\text{T}}Z⩽c\right)|W=w\}/E\{I\left({\beta }^{\text{T}}Z⩽c\right)Y(u)|W=w\}$, we propose to estimate S(t; c, β, w) by a kernel-smoothed Kaplan–Meier type estimator

$$\widehat{S}\left(t;c,\beta ,w\right)=\prod _{0<u⩽t}\hspace{0.17em}\left[1-\frac{{\sum }_{i=1}^n\hspace{0.17em}K\{\left(W_i-w\right)/h\}I\left({\beta }^{\text{T}}{Z}_i⩽c\right)\text{d}{N}_i(u)}{{\sum }_{i=1}^n\hspace{0.17em}K\{\left(W_i-w\right)/h\}I\left({\beta }^{\text{T}}{Z}_i⩽c\right)Y_i(u)}\right],$$

where K(x) = K̃ (||x_c||) I (x_d = 0), x_d and x_c are the discrete and continuous components of x, respectively, || · || is the Euclidean norm, K̃ (·) is a kernel function for which there exists some integer l such that ∫ y^j K̃ (y) dy = 0 (j = 1, …, l − 1), ∫ y^l K̃ (y) dy ≠ 0 and 2l − q > 0, and h is a bandwidth such that nh^q → ∞ and nh^2l → 0 as n → ∞. When q ⩽ 3, we can use a symmetric smooth probability density function as the kernel function. In light of the relationship between S(t; c_υ, β^*, W) and G_Z,β^* (t, υ), we can then estimate G_Z,β^* (t, υ) by

$$\tilde{G}\left(t,\upsilon \right)={\upsilon }^{-1}{n}^{-1}\sum _{i=1}^n\widehat{S}\left(t;{\widehat{c}}_{\upsilon },\widehat{\beta },W_i\right)I\left({\widehat{\beta }}^{\text{T}}{Z}_i⩽{\widehat{c}}_{\upsilon }\right).$$

In Appendix 3, we show that the process n^1/2{G̃(t, υ) − G_Z,β^* (t, υ)} converges weakly to a zero-mean Gaussian process. As in § 3.2, the asymptotic distribution can be approximated by the bootstrap method.

Due to the curse of dimensionality and the difficulty in choosing an appropriate kernel function for q > 3, the proposed method may not be very useful when q is large. For q > 3, we suggest obtaining a linear combination of W under a proportional hazards model for the censoring time and then applying the proposed method to the linear combination of W.

3.4. Recurrent event data

Under completely-at-random censoring, the inference procedures developed in § 3.2 can be readily applied to recurrent event data because the formulae do not involve specific forms of single-event data. Under covariate-dependent censoring, the fact that Y^* (·) = 1 for recurrent event data yields

$$G_{Z,{\beta }^{*}}\left(t,\upsilon \right)=\text{exp}[-{\upsilon }^{-1}E\{\mu \left(t;c_{\upsilon },{\beta }^{*},W\right)I\left({\beta }^{*\text{T}}Z⩽c_{\upsilon }\right)\}],$$

where $\mu \left(t;c,\beta ,w\right)={\int }_0^{t}E\{\text{d}{N}^{*}(u)|W=w,{\beta }^{\text{T}}Z⩽c\}$, which can be consistently estimated by

$$\widehat{\mu }\left(t;c,\beta ,w\right)={\int }_{u⩽t}\frac{{\sum }_{i=1}^{n}K\{\left(W_i-w\right)/h\}I\left({\beta }^{\text{T}}{Z}_i⩽c\right)\text{d}{N}_i(u)}{{\sum }_{i-1}^n\hspace{0.17em}K\{\left(W_i-w\right)/h\}I\left({\beta }^{\text{T}}{Z}_i⩽c\right)Y_i(u)}.$$

Thus, we propose to estimate G_Z,β^* (t, υ) by

$$\tilde{G}\left(t,\upsilon \right)=\text{exp}\hspace{0.17em}\left\{-{\upsilon }^{-1}{n}^{-1}\sum _{i=1}^n\widehat{\mu }\left(t;{\widehat{c}}_{\upsilon },\widehat{\beta },W_i\right)I\left({\widehat{\beta }}^{\text{T}}{Z}_i⩽{\widehat{c}}_{\upsilon }\right)\right\}.$$

We show in Appendix 3 that the process n^1/2{G̃ (t, υ) − G_Z,β^* (t, υ)} converges weakly to a zero-mean Gaussian process. The asymptotic distribution can again be approximated by the bootstrap method.

4. Simulation studies

The first set of simulation studies concerns the performance of the proposed estimators under completely-at-random censoring. To mimic the breast cancer data of § 5.1, we generated survival times from the Weibull regression model λ(t | X) = kλ⁻¹(t/λ)^k−1 exp(β^T X), where λ(t | X) is the conditional hazard function of T given X, X is zero-mean trivariate normal with a covariance matrix that is the sample covariance matrix of age, tumor size and gene score of the breast cancer data, and the parameters k, λ, β are estimated from the breast cancer data. We also generated recurrent event times from the random-effect intensity model: λ(t | X, ξ) = ξkλ⁻¹(t/λ)^k−1 exp(β^TX), where λ(t | X, ξ) is the conditional intensity function of N^*(t) given X and ξ, and ξ is a gamma random variable with mean 1 and standard deviation 0.5. For completely-at-random censoring, we generated censoring times from a Weibull distribution whose parameters are estimated from the breast cancer data. Table 1 summarizes the results for the estimator Ĝ(t, υ) at υ = 0.25, 0.5, 0.75 and 1.0 for t = 5 years with n = 300. The parameter estimator has little bias. The standard error estimator reflects the true variability very well, and the confidence intervals have proper coverage probabilities. We also evaluated G̃ (t, υ), the estimator allowing covariate-dependent censoring, and found it to be nearly as efficient as Ĝ(t, υ). For survival data, we also evaluated the inverse probability weighted estimator of Uno et al. (2007). The relative efficiencies of Ĝ(t, υ) to Uno et al.’s estimator were found to be 3.80, 2.02, 1.34 and 1.0 for υ = 0.25, 0.5, 0.75 and 1.0, respectively.

Table 1.

Simulation results for the estimator Ĝ(t, υ) for data under completely-at-random censoring

υ	Survival data					Recurrent event data
	True	Bias	SE	SEE	CP	True	Bias	SE	SEE	CP
0.25	97.0	0.1	2.0	2.0	93	97.0	−0.0	2.1	2.0	91
0.50	94.9	0.1	1.8	1.9	96	94.8	−0.0	1.9	1.9	96
0.75	92.0	0.1	1.8	1.9	96	91.9	−0.0	1.9	2.0	96
1.0	85.6	−0.0	2.1	2.1	94	83.8	−0.0	2.5	2.5	94

True, the true value (×100) of G(t = 5 years, υ); Bias, the sampling bias (×100); SE, the sampling standard error (×100); SEE, the sampling mean (×100) of the standard error estimator; CP, the coverage probability (×100) of the 95% confidence interval. Each entry is based on 2000 replicates.

To assess the performance of the proposed estimators under covariate-dependent censoring, we adopted the above set-up but generated censoring times from the transformation model $\mathrm{\Lambda }\left(t|X\right)=H\{0.1t\hspace{0.17em}\text{exp}\left({\beta }_c\hspace{0.17em}{\sum }_{i=1}^m\hspace{0.17em}{X}_i\right)\}$, where Λ(t | X) is the cumulative hazard function of C conditional on X, H(·) is a specific increasing function, and X₁, …, X_m are standard normal variables with 0.3 correlations with the gene score. To compare the estimators under completely-at-random censoring and covariate-dependent censoring, we chose H(x) = x, m = 3 and β_c = 0.5 to produce a censoring rate of 70.2%, which is close to that of the breast cancer data. We used the 3-dimensional independent Gaussian kernel density and set the bandwidth to σn^−7/24, where σ is the maximum of the standard deviations of X₁, X₂ and X₃. As shown in Table 2, the estimator G̃ (t, υ) has very small bias; the variance estimator is accurate and the confidence intervals have proper coverage probabilities. In contrast, the estimator Ĝ(t, υ) has severe bias and improper confidence intervals. We also evaluated the inverse probability weighted estimator of Uno et al. (2007), which turned out to be severely biased and inefficient, the bias being −0.239, −0.138, −0.066, and −0.009 for υ = 0.25, 0.5, 0.75 and 1.0, respectively, and the corresponding standard errors being 0.086, 0.052, 0.033 and 0.025.

Table 2.

Simulation results for the estimators G̃ (t, υ) and Ĝ(t, υ) for survival data under covariate-dependent censoring

n	υ	True	G̃ (t, υ)				Ĝ(t, υ)
			Bias	SE	SEE	CP	Bias	SE	SEE	CP
300	0.25	97.0	−0.1	3.3	2.9	96	−0.1	2.7	2.6	87
	0.50	94.9	−0.0	2.7	2.6	96	−0.2	2.4	2.4	96
	0.75	92.0	−0.1	2.5	2.5	96	−0.4	2.3	2.4	96
	1.0	85.6	−0.2	2.6	2.5	94	−1.5	2.5	2.5	92
500	0.25	97.0	−0.0	2.5	2.2	95	−0.1	2.1	2.1	93
	0.50	94.9	−0.0	2.1	2.0	95	−0.2	1.8	1.9	96
	0.75	92.0	0.0	2.0	1.9	95	−0.5	1.8	1.8	96
	1.0	85.6	−0.1	2.1	2.0	94	−1.4	2.0	2.0	90

True, the true value (×100) of G(t = 5 years, υ); Bias, the sampling bias (×100); SE, the sampling standard error (×100); SEE, the sampling mean (×100) of the standard error estimator; CP, the coverage probability (×100) of the 95% confidence interval. Each entry is based on 2000 replicates.

Finally, we considered the situation that censoring depends on a large number of covariates. We increased the number of covariates in the above censoring model to 10 or 20 and set H(x) = x or H(x) = log(1 + x). We used the one-dimensional Gaussian kernel density and set the bandwidth to σn−^1/3, where σ is the standard deviation of the linear predictor in the proportional hazards model for the censoring time. The results for β_c = 0.1 and m = 10 and 20 are summarized in the Supplementary Material. The proposed method performs well even when the censoring model is incorrectly specified.

5. Examples

5.1. Gene expressions in breast cancer patients

van de Vijver et al. (2002) developed a database of 295 breast cancer patients. In this dataset, the time to death along with a 70-gene signature and some clinical factors were recorded. A total of 276 patients had complete information on the gene signature and clinical factors, and the survival times for 73.6% of them were censored. The main purpose of this study was to determine whether the 70-gene signature can improve the prediction of survival times above the clinical factors and thus be used to guide the selection of patients for adjuvant chemotherapy. We use this dataset to illustrate the generalized negative predictive function.

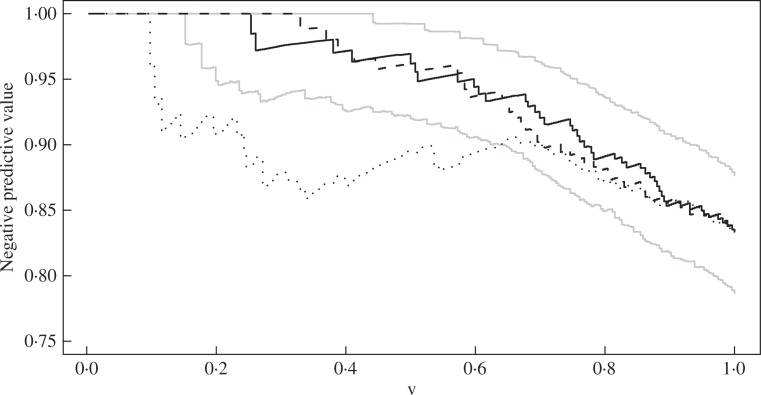
For our illustration, we compare three sets of covariates: the combination of age and tumor size, the 70-gene signature alone, and the combination of the gene signature, age and tumor size. We consider the proportional hazards models with these three sets of covariates. Because the censoring time depends on tumor size, the p-value being 0.0009, we allow censoring to depend on tumor size in our analysis. Figure 1 displays the 5-year negative predictive curves for the three sets. The gene signature indeed improves predictive accuracy above clinical factors and the gene signature alone is enough for prediction. If clinicians wish to spare 50% of the breast cancer patients adjuvant chemotheraphy, then those patients selected by the combination of the gene signature, age and tumor size will have a 5-year survival probability of 0.962, with a 95% confidence interval of (0.920, 0.992), whereas those patients selected by age and tumor size will have a 5-year survival probability of only 0.89. The area under the curve for the combination of the gene signature, age and tumor size is 0.945, which is significantly larger than that of the combination of age and tumor size and is very close to that of the gene signature alone, the two differences being 0.050 and 0.001, respectively, and the corresponding 95% confidence intervals being (0.020, 0.083) and (−0.008, 0.013). Because the effect of dependent censoring is fairly small in this case, the curves under completely-at-random censoring are very similar to their counterparts in Fig. 1 and are omitted.

Fig. 1.

Estimation of G(t, υ) at t = 5 years in the breast cancer data. The black solid, dashed and dotted curves pertain to the combination of the gene signature, age and tumor size, gene signature alone, and the combination of age and tumor size, respectively. The grey curves are the 95% pointwise confidence limits corresponding to the black solid curve.

We now demonstrate how to use the negative predictive curve to guide the selection of patients for adjuvant chemotherapy. Because of the toxicity of chemotherapy, low-risk patients should be spared adjuvant chemotherapy. Suppose that we define low risk to be a 5-year survival probability of at least 95%. Then what percentage of patients will be assigned to the low-risk group and thus spared adjuvant chemotherapy based on the 70-gene signature? The answer is given by G⁻¹ (t = 5, 0.95) = 58.0%, with a 95% confidence interval of (34.4%, 70.7%). In contrast, this percentage is only 10.5%, with a 95% confidence interval of (1.1%, 31.2%) based on age and tumor size. Thus, the use of the 70-gene signature can spare substantially more patients adjuvant chemotherapy.

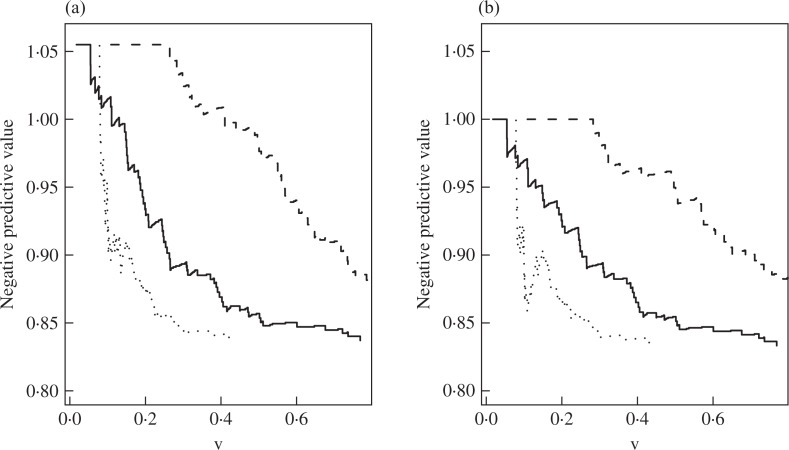
Finally, we compare our negative predictive curves with those of Uno et al. (2007). Figure 2 displays the estimates of the curves of Uno et al. (2007), for which the linear predictor is standardized by the transformation function g(y) = 1 − exp{− exp(y)}. Figure 2 shows that the x-values of the curves for different linear predictors have different ranges, although the transformation function restricts the linear predictors to the interval (0, 1). In contrast, the x-values of our curves, as shown in Fig. 1, always have the range (0, 1). In Fig. 2, the curve for the combination of the gene signature, age and tumor size is considerably lower than that of the gene signature alone. This is not sensible because the combination of the gene signature, age and tumor size should at least have the same predictive accuracy as the gene signature alone. Therefore, the negative predictive curves standardized by a known transformation function cannot be used to directly compare the predictive accuracy of different covariates. Figure 2 also shows that the inverse probability weighted estimator can yield inappropriate estimates for small cut-off values.

Fig. 2.

Estimates of the npv (t = 5 years, υ) of Uno et al. (2007) in the breast cancer data. The black solid, dashed and dotted curves pertain to the combination of the gene signature, age and tumor size, gene signature alone, and the combination of age and tumor size, respectively. (a) is based on the inverse probability weighted estimator of Uno et al. (2007); (b) is based on the Kaplan–Meier type estimator.

5.2. Exacerbations of respiratory symptoms in patients with cystic fibrosis

Patients with cystic fibrosis often suffer from repeated exacerbations of respiratory symptoms. A randomized clinical trial was conducted to evaluate the efficacy of rhDNase, a highly purified recombinant enzyme, in reducing the rate of of exacerbations (Therneau & Hamilton, 1997). By the end of the trial, 139 of 324 untreated patients and 104 of 321 treated patients had experienced at least one exacerbation; 42 untreated patients and 39 treated patients had at least two exacerbations. In addition to the times to exacerbations, the baseline level of forced expiratory volume in 1 second was recorded for each patient.

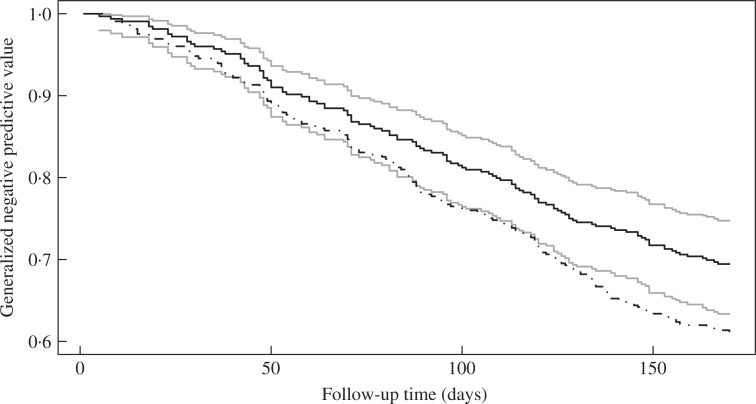
We use the proposed methods to evaluate the importance of forced expiratory volume in predicting the number of exacerbations. We compare the predictive accuracy of forced expiratory volume and treatment to that of treatment alone. We consider the class of transformation mean models for these two sets of covariates. The choices of the Box–Cox transformations H(x) = {(1 + x)^ρ − 1}/ρ with ρ = 0.5, 1, 2 and logarithmic transformations H(x) = log(1 + rx)/r with r = 0.5, 1, 2 yield highly similar estimates for G(t, υ). Since treatment is binary, G(t, υ) for the two sets of covariates are comparable only at the threshold υ = 0.498, the proportion of treated patients. Figure 3 displays the estimated G(t, υ) versus t at υ = 0.498 based on the proposed estimator under completely-at-random censoring. The model with forced expiratory volume and treatment has much higher generalized negative predictive values than the model with treatment alone, especially for large t, indicating that forced expiratory volume plays an important role in predicting the number of exacerbations. The results based on the estimator allowing the censoring to depend on forced expiratory volume and treatment are virtually the same and omitted.

Fig. 3.

Estimates of G(t, υ) at υ = 0.498 in the rhDNase study. The black solid and black dash-dotted curves pertain to the point estimates for the model with forced expiratory volume and treatment and the model with treatment alone, respectively. The grey curves pertain to the 95% pointwise confidence limits associated with the black solid curve.

6. Remarks

In the proposed methods, the working model is used only to obtain the coefficients for the linear combination of multiple covariates. The estimation of the generalized negative predictive function itself is purely nonparametric, so the predictive accuracy of different sets of covariates can be compared in a fair manner. Additional simulation studies revealed that the performance of the proposed methods is robust to misspecification of the transformation function. In real studies, the estimates of the proposed function, especially the relative magnitudes of the estimates for different sets of covariates, have been found to be similar under different transformation functions.

We have focused on the class of transformation models and its nonparametric maximum likelihood estimators (Zeng & Lin, 2006). We can also consider other survival models and other estimators provided that the influence functions for the regression parameters exist. Indeed, our methods are designed to assess the predictive accuracy of any model, whether it holds or not. If there is only a single covariate or the regression parameters are estimated from a previous study, then the influence functions for the regression parameters are set to zero in the proposed methods. Our work was partly motivated by the desire to compare the predictive accuracy of five gene-expression signatures for breast cancer (Fan et al., 2006), in which case the coefficients for each linear predictor were determined by a previous study and thus considered fixed in our estimation of the generalized negative predictive function; the results will be reported elsewhere.

Uno et al. (2007) considered the positive and negative predictive curves by thresholding the linear predictor with a known transformation function. As shown in § 5.1, such curves cannot be used to directly compare the predictive accuracy of different covariates. In addition, the inverse probability weighted estimator requires completely-at-random censoring and can yield severe bias under covariate-dependent censoring. Even under completely-at-random censoring, the inverse probability weighted estimator is less efficient than our Kaplan–Meier type estimator, especially for small cut-off values. Our proposed function thresholds the linear predictor by its distribution function and can be used to compare the predictive accuracy of different covariates. The use of the distribution function of the linear predictor creates additional challenges in deriving the asymptotic properties since the distribution function needs to be estimated and the additional variation needs to be accounted for.

The proposed function has nice connections with the receiving operating characteristic curve and overall misspecification rate. It can be shown that, for a given time t if the predictive curve of ${\beta }_1^{\text{T}}{Z}_1$ is uniformly higher than that of ${\beta }_2^{\text{T}}{Z}_2$, then the corresponding receiving operating characteristic curve is also uniformly higher, and vice versa. In addition, a uniformly higher predictive curve implies a lower overall misspecification rate. The key difference of the predictive curve from the receiving operating characteristic curve is that it depends on the patient’s survival probabilities and is thus more relevant for prediction. A main purpose of developing a prediction rule is to divide patients with low versus high survival probabilities. The prediction rule based on the receiving operating characteristic curve is not directly connected to survival probabilities, so it is difficult to determine whether the low/high risk groups determined by the prediction rule have high/low survival probabilities. As for the overall misspecification rate, it has the same problem as the receiving operating characteristic curve and does not distinguish between false positive and false negative errors.

There is a growing interest in assessing the predictive accuracy of time-dependent covariates. Henderson et al. (2002) proposed a modification of the explained variation measure of Schemper & Henderson (2000), Schoop et al. (2008) extended the Brier score, and Zheng & Heagerty (2007) extended the receiving operating characteristic method. All these extensions are confined to single-event data. The generalized negative predictive function proposed in this paper can easily incorporate time-dependent covariates by replacing Z in (3) by Z(u). It is straightforward to extend the two estimators for recurrent event data and the estimator for single-event data under completely-at-random censoring to the setting of time-dependent covariates, but the extension is difficult for single-event data under dependent censoring because our estimator relies on the equation G_Z,β^* (t, υ) = pr{T > t | F_β^*TZ (β^*T Z) ⩽ υ}, which does not hold for time-dependent covariates.

Appendix 1. Optimality of the generalized negative predictive function

Lemma A1. Let ξ(·) be a stochastic process, and Z₀ and Z be subvectors of the random vector X. Assume that the linear combinations ${\beta }_0^{\text{T}}{Z}_0$ and β^TZ are continuous and that $E\{\xi (t)|X\}=g_0\left(t,{\beta }_0^{\text{T}}{Z}_0\right)$, where g₀(t, υ) is a strictly decreasing function of υ for all t > 0. Then $E\{\xi (t)|F_{{\beta }_0^{\text{T}}{Z}_0}\left({\beta }_0^{\text{T}}{Z}_0\right)⩽\upsilon \}⩾E\{\xi \left(t\right)|F_{{\beta }^{\text{T}}Z}\left({\beta }^{\text{T}}Z\right)⩽\upsilon \}$ for all t > 0 and υ ∈ (0, 1). In addition, if there exists some t such that the equality holds for all υ, then $\text{pr}\{F_{{\beta }_0^{\text{T}}{Z}_0}\left({\beta }_0^{\text{T}}{Z}_0\right)=F_{{\beta }^{\text{T}}Z}\left({\beta }^{\text{T}}Z\right)\}=1$.

Proof. Let $Y_0=F_{{\beta }_0^{\text{T}}{Z}_0}\left({\beta }_0^{\text{T}}{Z}_0\right)$, Y = F_β^TZ (β^TZ), and $f\left(t,y\right)=g_0\{t,F_{{\beta }_0^{\text{T}}{Z}_0}^{-1}(y)\}$. Then E{I (Y₀ ⩽ υ)} = E{I (Y ⩽ υ)} = υ, E{ξ(t) | X} = f (t, Y₀), and f(t, y) is strictly decreasing in y for all t > 0. Clearly, $\upsilon E\{\xi (t)|F_{{\beta }_0^{\text{T}}{Z}_0}\hspace{0.17em}\left({\beta }_0^{\text{T}}{Z}_0\right)⩽\upsilon \}=E\{f\left(t,Y_0\right)I\left(Y_0⩽\upsilon \right)\}$, which can be written as

$$E\{f\left(t,Y_0\right)I\left(Y_0⩽\upsilon ,Y⩽\upsilon \right)\}+E\{f\left(t,Y_0\right)I\left(Y_0⩽\upsilon ,Y>\upsilon \right)\}.$$ (A1)

Since f(t, y) is strictly decreasing in y for all t > 0, the second term in (A1) is greater than or equal to f(t, υ)E{I (Y₀ ⩽ υ, Y > υ)}, where the equality holds if and only if pr(Y₀ ⩽ υ, Y > υ) = 0. Since E{I (Y₀ ⩽ υ)} = E{I (Y ⩽ υ)} = υ, we have E{I (Y₀ ⩽ υ, Y > υ)} = E{I (Y₀ > υ, Y ⩽ υ)}. This equality, together with the fact that f(t, y) is strictly decreasing in y for all t > 0, implies that the second term in (A1) is greater than or equal to E{f(t, Y₀) I (Y₀ > υ, Y ⩽ υ)}. Thus, (A1) is greater than or equal to E{f(t, Y₀) I (Y ⩽ υ)} or υ E{ξ(t) | F_β^TZ (β^TZ) ⩽ υ}. Hence, the results in Lemma A1 hold.

Remark 1. If ${\beta }_0^{\text{T}}{Z}_0$ or β^TZ is not continuous, then $E\{\xi (t)|F_{{\beta }_0^{\text{T}}{Z}_0}\left({\beta }_0^{\text{T}}{Z}_0\right)⩽\upsilon \}⩾E\{\xi (t)|F_{{\beta }^{\text{T}}Z}\left({\beta }^{\text{T}}Z\right)⩽\upsilon \}$ for all t > 0 and υ in the common range of the distribution functions of ${\beta }_0^{\text{T}}{Z}_0$ and β^TZ.

Appendix 2. Weak convergence of n^1/2{Ĝ (t, υ) − G_Z,β^* (t, υ)}

In this section, we prove the weak convergence of n^1/2{Ĝ (t, υ) − G_Z,β^* (t, υ)} for single-event data. The proof for recurrent events is similar and is omitted.

Let 𝒫_n and 𝒫 denote the empirical measure and the distribution under the true model, respectively. For a measurable function f and measure Q, the integral ∫ f dQ is abbreviated as Qf. We assume that there exists a continuous covariate in Z, denoted as Z^(k). Let Z^(−k) be the remaining components of Z, and β_k and β_(−k) be the components of β corresponding to Z^(k) and Z^(−k), respectively. Let h₁(t, x; y) and h₂(x; y) be, respectively, the conditional densities of (T, Z^(k)) and Z^(k) given Z^(−k) = y. We require that h₁(t, x; y) and h₂(x; y) are continuously differentiable. Let ψ be the influence function of β̂ in that n^1/2(β̂ − β^*) = n^1/2 𝒫_nψ + o_p(1).

Clearly,

$$n^{1/2}\{\widehat{G}\left(t,\upsilon \right)-G_{Z,{\beta }^{*}}\left(t,\upsilon \right)\}=n^{1/2}\{\widehat{G}\left(t;c_{\upsilon },{\beta }^{*}\right)-G\left(t;c_{\upsilon },{\beta }^{*}\right)\}+n^{1/2}\{\widehat{G}\left(t;{\widehat{c}}_{\upsilon },\widehat{\beta }\right)-\widehat{G}\left(t;c_{\upsilon },{\beta }^{*}\right)\}.$$ (A2)

The first term in (A2) pertains to the Kaplan–Meier estimator among the subjects with β^*TZ ⩽ c_υ and is asymptotically equivalent to n^1/2(𝒫_n − 𝒫) (t; c_υ, β^*), where

$$\xi \left(t;c,\beta \right)=-\left[G\left(t;c,\beta \right)I\left({\beta }^{\text{T}}Z⩽c\right)\hspace{0.17em}{\int }_0^t\frac{\text{d}N(u)-Y(u)\text{d}\mathrm{\Lambda }\left(u;c,\beta \right)}{E\{I\left({\beta }^{\text{T}}Z⩽c\right)Y(u)\}}\right].$$

By the result of Exercise 14 of van der Vaart & Wellner (1996, p. 152), the class of functions x ↦ I (β^Tx ⩽ c) with β and c ranging over ℛ^p and ℛ, respectively, is VC-subgraph and is thus 𝒫-Donsker by Theorems 2.6.7 and 2.5.2 of van der Vaart & Wellner (1996). In addition, the classes of functions {N(t) : t ∈ [0, τ]}, {Y (t) : t ∈ [0, τ]}, and {Λ(t; c, β) : t ∈ [0, τ]} are 𝒫-Donsker by Lemma 4.1 of Kosorok (2008). Thus, {ξ(t; c, β) : t ∈ [0, τ], c ∈ ℛ, β ∈ ℛ^p} is a 𝒫-Donsker class by the preservation properties of 𝒫-Donsker classes (van der Vaart & Wellner, 1996, § 2.10). This result, together with the fact that n^1/2{Ĝ (t; ĉ_υ, β̂) − Ĝ (t; c_υ, β^*)} = n^1/2{G(t; ĉ_υ, β̂) − G(t; c_υ, β^*)} + n^1/2{Ĝ(t; ĉ_υ, β̂) − G(t; ĉ_υ, β̂)} + n^1/2{Ĝ(t; c_υ, β^*) − G(t; c_υ, β^*)}, implies that the second term in (A2) is asymptotically equivalent to

$$n^{1/2}\{G\left(t;{\widehat{c}}_{\upsilon },\widehat{\beta }\right)-G\left(t;c_{\upsilon },{\beta }^{*}\right)\}+n^{1/2}\left({𝒫}_n-𝒫\right)\{\xi \left(t;{\widehat{c}}_{\upsilon },\widehat{\beta }\right)-\xi \left(t;c_{\upsilon },{\beta }^{*}\right)\}.$$ (A3)

As to be shown later, n^1/2(ĉ_υ − c_υ) is weakly convergent. Thus, the second term in (A3) converges uniformly to zero in probability by Lemma 19.24 of van der Vaart (1998). The first term in (A3) is asymptotically equivalent to

$${\frac{\partial G\left(t;c,{\beta }^{*}\right)}{\partial c}|}_{c=c_{\upsilon }}{n}^{1/2}\left({\widehat{c}}_{\upsilon }-c_{\upsilon }\right)+{\frac{\partial G\left(t;c_{\upsilon },\beta \right)}{\partial \beta }|}_{\beta ={\beta }^{*}}{n}^{1/2}\left(\widehat{\beta }-{\beta }^{*}\right),$$

where ∂G(t; c, β)/∂β can be obtained as follows, and ∂G(t; c, β)/∂c in the same manner. Let g₁(t, β, c) = E{I (T > t)I (β^TZ ⩽ c)}, and g₂(β, c) = E{I (β^TZ ⩽ c)}. Then for β_k > 0, $g_1\left(t,\beta ,c\right)=E[E\{I\left(T>t\right)I\left({\beta }^{\text{T}}Z⩽c\right)|Z^{\left(-k\right)}\}]=E{\int }_{-\infty }^{{\beta }_k^{-1}\left(c-{\beta }_{\left(-k\right)}{Z}^{\left(-k\right)}\right)}{\int }_t^{\infty }{h}_1\left(s,x;Z^{\left(-k\right)}\right)$ ds dx. Simple algebraic manipulations yield

$$\frac{\partial G\left(t;c,\beta \right)}{\partial \beta }=\frac{\partial g_1\left(t,\beta ,c\right)/\partial \beta -E\{I\left(T>t\right)|{\beta }^{\text{T}}Z⩽c\}\partial g_2\left(\beta ,c\right)/\partial \beta }{E\{I\left({\beta }^{\text{T}}Z⩽c\right)\}},$$

where

$$\begin{array}{l}\frac{\partial g_1\left(t,\beta ,c\right)}{\partial {\beta }_k}=-c{\beta }_k^{-2}E{\int }_t^{\infty }{h}_1\{s,{\beta }_k^{-1}\left(c-{\beta }_{\left(-k\right)}{Z}^{\left(-k\right)}\right);Z^{\left(-k\right)}\}\text{d}s,\\ \frac{\partial g_1\left(t,\beta ,c\right)}{\partial {\beta }_{\left(-k\right)}}=-{\beta }_k^{-1}E\hspace{0.17em}\left[Z^{\left(-k\right)}{\int }_t^{\infty }{h}_1\{s,{\beta }_k^{-1}\left(c-{\beta }_{\left(-k\right)}{Z}^{\left(-k\right)}\right);Z^{\left(-k\right)}\}\text{d}s\right],\\ \frac{\partial g_2\left(\beta ,c\right)}{\partial {\beta }_k}=-c{\beta }_k^{-2}E\hspace{0.17em}\left[h_2\{{\beta }_k^{-1}\left(c-{\beta }_{\left(-k\right)}{Z}^{\left(-k\right)}\right);Z^{\left(-k\right)}\}\right],\\ \frac{\partial g_2\left(\beta ,c\right)}{\partial {\beta }_{\left(-k\right)}}=-{\beta }_k^{-1}E[Z^{\left(-k\right)}{h}_2\{{\beta }_k^{-1}\left(c-{\beta }_{\left(-k\right)}{Z}^{\left(-k\right)}\right);Z^{\left(-k\right)}\}].\end{array}$$

We now establish the weak convergence of n^1/2(ĉ_υ − c_υ). Clearly,

$$\begin{array}{c}{n}^{1/2}\{F_n(c)-F_{{\beta }^{*\text{T}}Z}(c)\}=n^{1/2}\left({𝒫}_n-𝒫\right)I\left({\beta }^{*\text{T}}Z⩽c\right)+n^{1/2}𝒫\{I\left({\widehat{\beta }}^{\text{T}}Z⩽c\right)-I\left({\beta }^{*\text{T}}Z⩽c\right)\}\\ +n^{1/2}\left({𝒫}_n-𝒫\right)\{I\left({\widehat{\beta }}^{\text{T}}Z⩽c\right)-I\left({\beta }^{*\text{T}}Z⩽c\right)\}.\end{array}$$ (A4)

The second term on the right-hand side of (A4) is asymptotically equivalent to ∂g₂(β^*, c)/∂β n^1/2(β̂ − β^*), and the third term converges to zero in probability. It then follows from Lemma 12.8 of Kosorok (2008) that n^1/2(ĉ_υ − c_υ) is asymptotically equivalent to −{dF_β^*TZ (c)/dc|_c=cυ}⁻¹n^1/2(𝒫_n −𝒫){I (β^*TZ ⩽ c_υ) + ∂g₂(β^*, c_υ)/∂βψ}.

Combining the above results, we conclude that n^1/2{Ĝ(t, υ) − G_Z,βL^* (t, υ)} is asymptotically equivalent to n^1/2𝒫_n{ξ₁(t, υ) + ξ₂(t, υ)}, where ξ₁(t, υ) = ξ(t; c_υ, β^*) and

$$\begin{array}{ll}{\xi }_2\left(t,\upsilon \right)\hfill & {=-\{I\left({\beta }^{*\text{T}}Z⩽c_{\upsilon }\right)-\upsilon \}\frac{\partial G\left(t;c,{\beta }^{*}\right)/\partial c}{\text{d}{F}_{{\beta }^{*\text{T}}Z}(c)/\text{d}c}|}_{c=c\upsilon }\hfill \\ \hfill & -\left\{{\frac{\partial G\left(t;c,{\beta }^{*}\right)/\partial c}{\text{d}{F}_{{\beta }^{*\text{T}}Z}(c)/\text{d}c}|}_{c=c_{\upsilon }}{\frac{\partial g_2\left(\beta ,c_{\upsilon }\right)}{\partial \beta }|}_{\beta ={\beta }^{*}}-{\frac{\partial G\left(t;c_{\upsilon },\beta \right)}{\partial \beta }|}_{\beta ={\beta }^{*}}\right\}\hspace{0.17em}\psi .\hfill \end{array}$$ (A5)

Appendix 3. Weak convergence of n^1/2{G̃ (t, υ) − G_Z,β^* (t, υ)}

In this section, we prove the weak convergence of n^1/2{G̃ (t, υ) − G_Z,β^* (t, υ)} for single-event data. The proof for recurrent events is similar and is omitted. We express υn^1/2{G̃ (t, υ) − G_Z,β^* (t, υ)} as

$$\begin{array}{l}{n}^{1/2}\hspace{0.17em}({𝒫}_n-𝒫)\hspace{0.17em}\{S(t;\hspace{0.17em}{c}_{\upsilon },\hspace{0.17em}{\beta }^{*},\hspace{0.17em}W)I\hspace{0.17em}({\beta }^{*\text{T}}⩽c_{\upsilon })\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}{n}^{1/2}\hspace{0.17em}𝒫[\{\widehat{S}(t;\hspace{0.17em}{c}_{\upsilon },\hspace{0.17em}{\beta }^{*},\hspace{0.17em}W)-S(t;\hspace{0.17em}{c}_{\upsilon },\hspace{0.17em}{\beta }^{*},\hspace{0.17em}W)\}I\hspace{0.17em}({\beta }^{*\text{T}}\hspace{0.17em}Z⩽c_{\upsilon })]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}{n}^{1/2}\hspace{0.17em}𝒫\{\widehat{S}(t;\hspace{0.17em}{\widehat{c}}_{\upsilon },\hspace{0.17em}\widehat{\beta },\hspace{0.17em}W)\hspace{0.17em}I\hspace{0.17em}({\widehat{\beta }}^{\text{T}}\hspace{0.17em}Z⩽{\widehat{c}}_{\upsilon })-\widehat{S}(t;\hspace{0.17em}{c}_{\upsilon },\hspace{0.17em}{\beta }^{*},\hspace{0.17em}W)I\hspace{0.17em}({\beta }^{*\text{T}}Z⩽c_{\upsilon })\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}{n}^{1/2}\hspace{0.17em}({𝒫}_n-𝒫)\hspace{0.17em}[\{\widehat{S}(t;\hspace{0.17em}{\widehat{c}}_{\upsilon },\hspace{0.17em}\widehat{\beta },\hspace{0.17em}W)-S(t;\hspace{0.17em}{\widehat{c}}_{\upsilon },\hspace{0.17em}\widehat{\beta },\hspace{0.17em}W)\}I\hspace{0.17em}({\widehat{\beta }}^{\text{T}}\hspace{0.17em}Z⩽\hspace{0.17em}{\widehat{c}}_{\upsilon })]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}{n}^{1/2}\hspace{0.17em}({𝒫}_n-𝒫)\hspace{0.17em}\{S(t;\hspace{0.17em}{\widehat{c}}_{\upsilon },\hspace{0.17em}\widehat{\beta },\hspace{0.17em}W)I\hspace{0.17em}({\widehat{\beta }}^{\text{T}}Z\hspace{0.17em}⩽\hspace{0.17em}{\widehat{c}}_{\upsilon })-S(t;\hspace{0.17em}{c}_{\upsilon },\hspace{0.17em}{\beta }^{*},\hspace{0.17em}W)I\hspace{0.17em}({\beta }^{*\text{T}}Z⩽\hspace{0.17em}{c}_{\upsilon })\}.\end{array}$$ (A6)

To study the second to the fourth terms in (A6), we first study

$$\widehat{\mathrm{\Lambda }}(t;\hspace{0.17em}c,\hspace{0.17em}\beta ,\hspace{0.17em}w)\hspace{0.17em}=\hspace{0.17em}{\int }_0^t\frac{{\sum }_{i=1}^{n}K\{(W_i-w)\hspace{0.17em}/\hspace{0.17em}h\}I\hspace{0.17em}({\beta }^{\text{T}}\hspace{0.17em}{Z}_i⩽c)\hspace{0.17em}\text{d}{N}_i(s)}{{\sum }_{i=1}^{n}K\hspace{0.17em}\{(W_i\hspace{0.17em}-\hspace{0.17em}w)\hspace{0.17em}/\hspace{0.17em}h\}\hspace{0.17em}I\hspace{0.17em}({\beta }^{\text{T}}\hspace{0.17em}{Z}_i\hspace{0.17em}⩽\hspace{0.17em}c)\hspace{0.17em}{Y}_i\hspace{0.17em}(s)}.$$

Write T̃ = T ∧ C and Δ = I (T ⩽ C). Then Λ̂(t; c, β, w) − Λ(t; c, β, w) can be written as

$$\begin{array}{l}{𝒫}_n\hspace{0.17em}\left[\frac{K\left(\frac{W-w}{h}\right)I({\beta }^{\text{T}}Z⩽c)\mathrm{\Delta }I(\tilde{T}⩽t)}{{𝒫}_n\{K\left(\frac{W-w}{h}\right)I({\beta }^{\text{T}}Z⩽c)Y(u)\}{|}_{u=\tilde{T}}}\right]-𝒫\hspace{0.17em}\left[\frac{I({\beta }^{\text{T}}Z⩽c)I(\tilde{T}⩽t)}{𝒫\{I({\beta }^{\text{T}}Z⩽c)Y^{*}(u)|W\}{|}_{u=\tilde{T}}}|W\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=({𝒫}_n-𝒫)\left[\frac{K\left(\frac{W-w}{h}\right)I({\beta }^{\text{T}}Z⩽c)\mathrm{\Delta }I(\tilde{T}⩽t)}{{𝒫}_n\{K\left(\frac{W-w}{h}\right)I({\beta }^{\text{T}}Z⩽c)Y(u)\}{|}_{u=\tilde{T}}}\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-𝒫\left[\hspace{0.17em}\frac{K\left(\frac{W-w}{h}\right)I({\beta }^{\text{T}}Z⩽c)\mathrm{\Delta }I(\tilde{T}⩽t)({𝒫}_n-𝒫)\{K\left(\frac{W-w}{h}\right)I({\beta }^{\text{T}}Z⩽c)Y(u)\}{|}_{u=\tilde{T}}}{𝒫\{K\left(\frac{W-w}{h}\right)I({\beta }^{\text{T}}Z⩽c)Y(u)\}{𝒫}_n\{K\left(\frac{W-w}{h}\right)I({\beta }^{\text{T}}Z⩽c)Y(u)\}{|}_{u=\tilde{T}}}\right]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\left(𝒫\left[\frac{K\left(\frac{W-w}{h}\right)I({\beta }^{\text{T}}Z⩽c)\mathrm{\Delta }I(\tilde{T}⩽t)}{𝒫\{K\left(\frac{W-w}{h}\right)I({\beta }^{\text{T}}Z⩽c)Y(u)\}{|}_{u=\tilde{T}}}\right]-𝒫\left[\frac{I({\beta }^{\text{T}}Z⩽c)I(\tilde{T}⩽t)}{𝒫\{I({\beta }^{\text{T}}Z⩽c)Y^{*}(u)|W\}{|}_{u=\tilde{T}}}|W\right]\right).\end{array}$$ (A7)

The third term on the right-hand side of (A7) is O(h^l) by a simple transformation and Taylor expansion, together with the fact that ${\int }_0^{t}E\{\text{d}N(u)I({\beta }^{\text{T}}Z⩽c)|W\}/E\{I({\beta }^{\text{T}}Z⩽c)Y(u)|W\}={\int }_0^{t}E\{\text{d}{N}^{*}(u)|Y^{*}(u)=1,{\beta }^{\text{T}}Z⩽c,W\}.$. Thus, by the Duhamel equation and the condition that nh^2l = o(1), the second term in (A6) is asymptotically equivalent to n^1/2(𝒫_n − 𝒫)ξ_n(N, Y, Z, W; t, c_υ, β^*), where

$$\begin{array}{l}{\xi }_n(N,Y,Z,W;t,c,\beta )=-I({\beta }^{\text{T}}Z⩽c)({𝒫}_{Z,W}[I({\beta }^{\text{T}}Z⩽c)S(t;c,\beta ,W)h^{-q}K\{w-W)/h\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times M_n(N,Y;t,c,\beta ,W)]){|}_{w=W,}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{M}_n(N,Y;t,c,\beta ,w)={\int }_0^t\frac{\text{d}N(u)-Y(u)\text{d}\mathrm{\Lambda }(u;c,\beta ,w)}{{𝒫}_n[h^{-q}K\{(W-w)/h\}I({\beta }^{\text{T}}Z⩽c)Y(u)]},\end{array}$$

and 𝒫_Z,W denotes the expectation with respect to Z and W. By the condition that nh^q → ∞, it can be shown that, uniformly in t, c and β, ξ_n(t; c, β) converges in probability to

$$\xi (t;c,\beta )=-E\{I({\beta }^{\text{T}}Z⩽c)|W\}S(t;c,\beta ,W)I({\beta }^{\text{T}}Z⩽c){\int }_0^t\frac{\text{d}N(u)-Y(u)\text{d}\mathrm{\Lambda }(u;c,\beta ,W)}{E\{I({\beta }^{\text{T}}Z⩽c)Y(u)|W\}}.$$

This result, together with the fact that the class of functions ξ_n( N, Y, Z, w; t, c, β) indexed by w, t, c and β is 𝒫-Donsker, implies that, conditional on W₁, …, W_n, the process n^1/2(𝒫_n − 𝒫)ξ_n(t; c, β) is asymptotically equivalent to n^1/2(𝒫_n − 𝒫)ξ(t; c, β) by Theorem 2.11.1 of van der Vaart & Wellner (1996), which further implies the unconditional asymptotic equivalence. Therefore, the second and third terms in (A6) are asymptotically equivalent to n^1/2(𝒫_n − 𝒫)ξ(t; c_υ, β^*) and

$$\begin{array}{l}{n}^{1/2}𝒫[S(t;{\widehat{c}}_{\upsilon },\widehat{\beta },W)I({\widehat{\beta }}^{\text{T}}Z⩽{\widehat{c}}_{\upsilon })-S(t;c_{\upsilon },{\beta }^{*},W)I({\beta }^{*\text{T}}Z⩽c_{\upsilon })]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+n^{1/2}({𝒫}_n-𝒫)\{\xi (t;{\widehat{c}}_{\upsilon },\widehat{\beta })-\xi (t;c_{\upsilon },{\beta }^{*})\},\end{array}$$ (A8)

respectively. By the arguments of Appendix 2, (A8) is asymptotically equivalent to

$$\upsilon \times \left\{\frac{\partial G(t;c,{\beta }^{*})}{\partial c}{|}_{c=c_{\upsilon }}{n}^{1/2}({\widehat{c}}_{\upsilon }-c_{\upsilon })+\frac{\partial G(t;c_{\upsilon },\beta )}{\partial \beta }{|}_{\beta ={\beta }^{*}}{n}^{1/2}(\widehat{\beta }-{\beta }^{*})\right\}.$$

As in the case of n^1/2𝒫 [{Ŝ(t; ĉ_υ, β̂, W) − S(t; ĉ_υ, β̂, W)}I (β̂^TZ ⩽ ĉ_υ)], we can show that n^1/2𝒫_n[{Ŝ(t; ĉ_υ, β̂, W) − S(t; ĉ_υ, β̂, W)}I (β̂^TZ ⩽ ĉ_υ)] is asymptotically equivalent to n^1/2(𝒫_n − 𝒫) (t; ĉ_υ, β̂), which implies that the fourth term in (A6) converges uniformly to zero in probability. The fifth term in (A6) converges uniformly to zero in probability by Lemma 19.24 of van der Vaart (1998).

Combining the above results, we obtain the weak convergence of n^1/2{G̃ (t, υ) − G_Z,β^* (t, υ)}.

Appendix 4. Validity of the bootstrap method

In this section, we prove the validity of the bootstrap method for Ĝ(t, υ) for survival data. The proofs for other cases are similar and thus omitted. Define

$${\widehat{G}}^{(b)}(t;c,\beta )=\prod _{0<u⩽t}\hspace{0.17em}\left\{1-\frac{{\sum }_{i=1}^n{M}_{ni}I({\beta }^{\text{T}}{Z}_i⩽c)\text{d}{N}_i(u)}{{\sum }_{i=1}^n{M}_{ni}I({\beta }^{\text{T}}{Z}_i⩽c)Y_i(u)}\right\},$$

where M_ni is the number of times that {N_i (t), Y_i (t), X_i : t ∈ [0, τ]} is redrawn from the original sample. Let ${\widehat{c}}_{\upsilon }^{(b)}$ and β̂^(b) be the bootstrap counterparts of ĉ_υ and β̂. Our goal is to show that the distribution of n^1/2{Ĝ(t, υ) − G_Z,β^* (t, υ)} can be approximated by the conditional distribution of $n^{1/2}\{{\widehat{G}}^{(b)}\left(t;{\widehat{c}}_{\upsilon }^{(b)},{\widehat{\beta }}^{(b)}\right)-\widehat{G}\left(t,\upsilon \right)\}$ given the data.

By the arguments of Appendix 2, $n^{1/2}\{{\widehat{G}}^{(b)}\left(t;{\widehat{c}}_{\upsilon }^{(b)},{\widehat{\beta }}^{(b)}\right)-\widehat{G}\left(t,\upsilon \right)\}$ is equal to

$$n^{1/2}\{{\widehat{G}}^{(b)}(t;{\widehat{c}}_{\upsilon },\widehat{\beta })-\widehat{G}(t;{\widehat{c}}_{\upsilon },\widehat{\beta })\}+n^{1/2}\{{\widehat{G}}^{(b)}(t;{\widehat{c}}_{\upsilon }^{(b)},{\widehat{\beta }}^{(b)}-{\widehat{G}}^{(b)}(t;{\widehat{c}}_{\upsilon },\widehat{\beta })\}.$$ (A9)

Lemma S1 of the Supplementary Material implies that, given the data, the first term in (A9) has the same asymptotic distribution as n^1/2(𝒫_n − 𝒫)ξ(t; c_υ, β^*), where ξ(t; c, β) is defined in Appendix 2. It can also be shown that, given the data, n^1/2(β̂^(b) − β̂) = n^1/2(𝒫̂_n − 𝒫_n)ψ + o_p(1) under mild regularity conditions, where 𝒫̂_n is the bootstrap empirical distribution (van der Vaart & Wellner, 1996, p. 345). Combining the arguments of Appendix 2 with those of Lemma S1, we can show that the limiting distribution of $n^{1/2}\{{\widehat{G}}^{(b)}\left(t;{\widehat{c}}_{\upsilon }^{(b)},{\widehat{\beta }}^{(b)}\right)-\widehat{G}\left(t,\upsilon \right)\}$ given the data is the same as the limiting distribution of n^1/2(𝒫_n − 𝒫) {ξ₁(t, υ) + ξ₂(t, υ)}, where ξ₁(t, υ) and ξ₂(t, υ) are defined in Appendix 2.

Supplementary material

Supplementary material available at Biometrika online includes additional simulation results and Lemma S1 of Appendix 4.