Analysis of principal nested spheres

Summary

A general framework for a novel non-geodesic decomposition of high-dimensional spheres or high-dimensional shape spaces for planar landmarks is discussed. The decomposition, principal nested spheres, leads to a sequence of submanifolds with decreasing intrinsic dimensions, which can be interpreted as an analogue of principal component analysis. In a number of real datasets, an apparent one-dimensional mode of variation curving through more than one geodesic component is captured in the one-dimensional component of principal nested spheres. While analysis of principal nested spheres provides an intuitive and flexible decomposition of the high-dimensional sphere, an interesting special case of the analysis results in finding principal geodesics, similar to those from previous approaches to manifold principal component analysis. An adaptation of our method to Kendall’s shape space is discussed, and a computational algorithm for fitting principal nested spheres is proposed. The result provides a coordinate system to visualize the data structure and an intuitive summary of principal modes of variation, as exemplified by several datasets.

1. Introduction

This paper proposes a general framework for a novel decomposition of a high-dimensional sphere, which is the sample space of directions (Fisher, 1993; Fisher et al., 1993; Mardia & Jupp, 2000) and preshapes in Kendall’s statistical theory of landmark shapes (Kendall, 1984; Dryden & Mardia, 1998). The proposed decomposition method, analysis of principal nested spheres, is a flexible extension of principal component analysis to spheres. This method provides an effective means of analysing the main modes of variation of a dataset and also gives a basis for dimension reduction. There have been a number of extensions of principal component analysis to manifold-valued data, most of which find principal geodesics (Fletcher et al., 2004; Huckemann & Ziezold, 2006; Huckemann et al., 2010; Kenobi et al., 2010). A geodesic on a manifold is a shortest path between two points and can be understood as the analogue of a straight line in Euclidean space. In particular, a geodesic on a sphere is a great circle path.

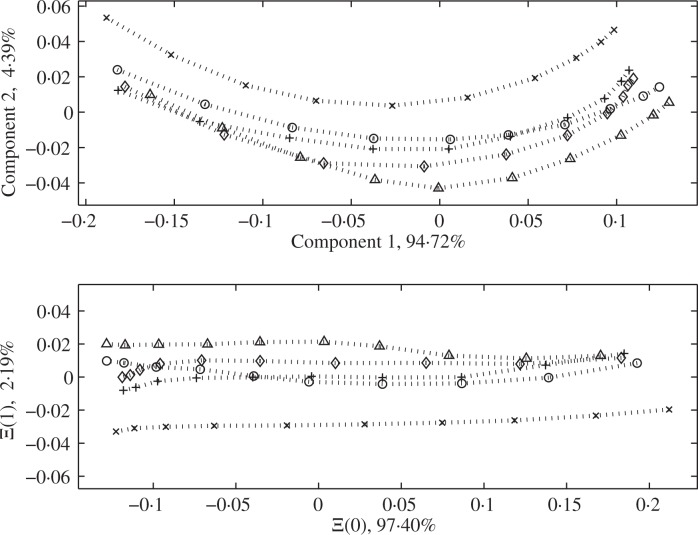
There has been a concern that when non-geodesic variation is major and apparent, geodesic-based methods do not give a fully effective decomposition of the space. As an example, a dataset of shapes representing human movements, discussed later in § 5.1 and introduced in Kume et al. (2007), is plotted in the top panel of Fig. 1 using the first two principal component directions. In this dataset the major one-dimensional mode of variation is represented as a curve lying in two components, as in the top panel of Fig. 1, and thus at least two dimensions are needed to explain the major variation. Analysis of principal nested spheres decomposes the data space so that the major one-dimensional variation is linearly represented, as shown in the bottom panel.

Fig. 1.

Plots of scores for some human movement data by two major geodesic components (top), where the different symbols represent different movements and samples for each movement are interpolated, and by the first two lowest dimensional nested spheres (bottom). The number% is the percent variance explained, defined later in § 2.4. The one-dimensional principal nested sphere captures a larger proportion of variation than the first geodesic component.

For a unit d-sphere S^d, which is the set of unit vectors in ℝ^d+1, the analysis gives a decomposition of S^d that captures the non-geodesic variation in a lower dimensional subsphere. The decomposition sequentially provides the best k-dimensional approximation 𝔄_k of the data for each k = 0, 1, . . . , d − 1. The sphere 𝔄_k is called the k-dimensional principal nested sphere and is a submanifold of the higher dimensional principal nested spheres. The sequence of principal nested spheres is

$${𝔄}_0\subset {𝔄}_1\subset \cdots \subset {𝔄}_{d-1}\subset S^d.$$ (1)

Since the preshape space of two-dimensional landmark-based shapes is also a sphere, the method can be applied to shape data lifted to and aligned on the preshape space; see § 4. The analysis provides approximations to the directional or shape data for every dimension, captures the non-geodesic variation, and provides visualization of the major variability in terms of shape changes.

The procedure of fitting principal nested spheres involves iterative reduction of the data dimension. We first fit a (d − 1)-dimensional subsphere 𝔄_d−1 of S^d that best approximates the data. This subsphere is not necessarily a great sphere, i.e., a sphere with radius 1 analogous to the great circle for S², which makes the resulting decomposition non-geodesic. Nevertheless, 𝔄_d−1 can be treated as if it were the unit (d − 1)-sphere. Each data point has an associated residual, which is the signed geodesic distance to its projection on 𝔄_d−1. Then for the data projected onto the subsphere, we continue to search for the best fitting (d − 2)-dimensional subsphere. These steps are iterated to find lower dimensional nested spheres. For visualization and further analysis, we obtain an Euclidean-type representation of the data, essentially consisting of the residuals of each level. The first two coordinates of this representation, related to 𝔄₁ and 𝔄₂, are plotted in Fig. 1 for the human movement data.

In Fig. 1 the variation of the dataset is represented linearly in a plot of scores given by principal nested spheres in the bottom panel compared to the curvy form of variation in geodesic components in the top panel. The proportion of variance contained in 𝔄₁ is almost the proportion of the sum of the first two geodesic component variances. That is, the variation explained by two geodesic components is almost attained in only the one-dimensional principal nested sphere. Moreover, the graph in the top panel is indeed obtained by a special case of our analysis, which is similar to geodesic-based principal component analysis (Fletcher et al., 2004; Huckemann et al., 2010).

Nonlinear variation like that in Fig. 1 is observed in many other datasets, where the proposed method is most useful. Such situations can be found in landmark shape analysis, examples of which are in § 5, and in computer-aided image analysis. For example, in investigations of shape variations of human organs including the lung, prostate, and hippocampus, applications of our method lead to succinct representations of the data compared to those from geodesic or linear principal component analysis (Jung et al., 2010, 2011; Pizer et al., 2012). The proposed method can also be seen as an extension of Jung et al. (2011) from S² to S^d, d > 2.

2. Principal nested spheres

2.1. Geometry of nested spheres

We begin by describing the essential geometric background for nested spheres. More detailed discussion can be found in the Supplementary Material.

For a unit sphere S^d, a geodesic joining any two points is a great circle joining the two points. A natural distance function on S^d is the geodesic distance function ρ_d (·, ·) defined as the length of the shortest great circle segment joining x, y ∈ S^d, ρ_d(x, y) = cos⁻¹(x^Ty). The shortest great circle path is unique unless x^Ty = −1, i.e., the two points are antipodal.

Definition 1. A subsphere A_d−1 of S^d is defined by an axis υ ∈ S^d and a distance r ∈ (0, π/2], as follows:

$$A_{d-1}(\upsilon ,r)=\left\{x\in S^d:{\rho }_d(\upsilon ,x)=r\right\}.$$

The subsphere A_d−1 can be viewed as an intersection of S^d ⊂ ℝ^d+1 and a d-dimensional hyperplane, {x ∈ ℝ^d+1 : υ^Tx − cos(r) = 0}. In other words, A_d−1 is identified with a slicing of S^d with the hyperplane, an example of which is illustrated as a shaded plane in Fig. 2. A subsphere A_d−1 is indeed a (d − 1)-dimensional nested sphere 𝔄_d−1 of S^d.

Fig. 2.

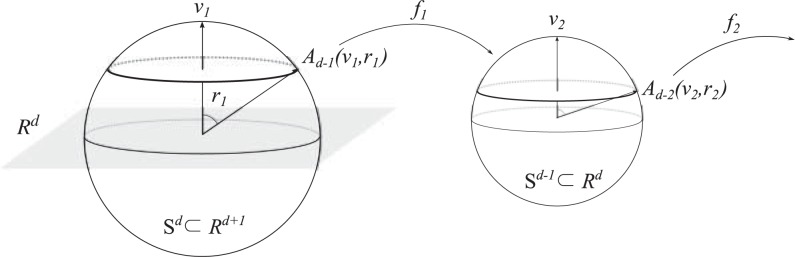
The subsphere A_d−1(υ₁, r₁) in S^d and its relation to S^d−1, through the transformation f₁. Recursively, A_d−2(υ₂, r₂) is found in S^d−1, and is identified with S^d−2 by the transformation f₂.

The subsphere A_d−1 is identified with S^d−1, so we can treat A_d−1 as a unit sphere S^d−1. This is done by a function f₁ : A_d−1 → S^d−1 and its inverse $f_1^{-1}$, defined in (2) below and depicted in Fig. 2. A subsphere A_d−2 of S^d−1 can be obtained by Definition 1 with dimension d reduced by 1. For a general subsphere A_d−k of S^d−k+1 for k = 1, . . . , d − 1, we also use the transformation f_k : A_d−k → S^d−k and its inverse $f_k^{-1}$. Let m = d − k + 1, so that the subsphere A_d−k ⊂ S^m ⊂ ℝ^m+1. The transformations are defined by υ_k ∈ S^m and r_k ∈ (0, π/2] as

$$f_k(x)=\frac{1}{\text{sin}(r_k)}{R}^{-}({\upsilon }_k)x,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{f}_k^{-1}(x^{†})=R^{\text{T}}({\upsilon }_k)\left[\begin{array}{c}\text{sin}(r_k)x^{†}\\ \text{cos}(r_k)\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x\in A_{d-k},x^{†}\in S^{d-k},$$ (2)

where R(υ_k) is a (m + 1) × (m + 1) rotation matrix that moves υ_k to the north pole, and R⁻(υ_k) is the m × (m + 1) matrix consisting of the first m rows of R(υ_k). See (A2) for a precise definition of R(υ_k).

The subspheres A_d−k are defined in different spaces S^d−k+1 for each k. A nested sphere is defined by the subsphere located in the original space S^d.

Definition 2. A (d − k)-dimensional nested sphere 𝔄_d−k of S^d is defined as

$${𝔄}_{d-k}=\{\begin{array}{ll}{f}_1^{-1}\circ \cdots \circ f_{k-1}^{-1}(A_{d-k})\hfill & (k=2,\dots ,d-1),\hfill \\ A_{d-1}\hfill & (k=1)\hfill \end{array}$$

The nested spheres 𝔄_d−k (k = 1, . . . , d − 1) satisfy the relation (1). A (d − k)-dimensional nested sphere 𝔄_d−k is indeed identified with a slicing of S^d by a (d − k + 1)-dimensional hyperplane.

2.2. The best fitting subsphere

Let x₁, . . . , x_n be a sample in S^d, d ⩾ 2. We first define the residual ξ of x from a subsphere A_d−1(υ₁, r₁) of S^d as the signed length of the minimal geodesic that joins x to A_d−1. Then ξ = ρ_d (x, υ₁) − r₁. The sign of ξ is negative if x is in the interior of the geodesic ball corresponding to A_d−1, and is positive if x is in the exterior.

The best fitting subsphere Â_d−1 = A_d−1(υ̂₁, r̂₁) is found by minimizing the sum of squares of residuals of the data points to Â_d−1. In other words, υ̂₁ and r̂₁ minimize

$$\sum _{i=1}^n{\xi }_i{({\upsilon }_1,r_1)}^2=\sum _{i=1}^n{\left\{{\rho }_d(x_i,{\upsilon }_1)-r_1\right\}}^2,$$ (3)

among all υ₁ ∈ S^d, r₁ ∈ (0, π/2].

The method can be extended using other objective functions, e.g., the sum of absolute deviations, for more robust fitting.

Each x_i can be projected on Â_d−1 along the minimal geodesic that joins x to Â_d−1. The projection of x onto A_d−1 is defined as

$$P\left\{x;A_{d-1}(\upsilon ,r)\right\}=\frac{\text{sin}(r)x+\text{sin}\left\{{\rho }_d(x,\upsilon )-r\right\}\upsilon }{\text{sin}\left\{{\rho }_d(x,\upsilon )\right\}}.$$ (4)

Denote x^P = P(x; Â_d−1) ∈ Â_d−1 for the projected x. We use the isomorphic function f̂₁ ≡ f (υ̂₁, r̂₁), as defined in (2), to transform Â_d−1 to S^d−1 so that ${\widehat{f}}_1(x_i^P)\in S^{d-1}$.

2.3. The sequence of principal nested spheres

The procedure to find the sample principal nested spheres consists of iteratively finding the best fitting subsphere and mapping to the original space.

The (d − 1)-dimensional sample principal nested sphere 𝔄̂_d−1 is the best fitting subsphere 𝔄_d−1(υ̂₁, r̂₁). The second layer 𝔄̂_d−2 is obtained from the subsphere that best fits ${\widehat{f}}_1(x_i^P)\in S^{d-1}$. The best fitting subsphere A_d−2(υ̂₂, r̂₂) ⊂ S^d−1 is then mapped to S^d by the relevant transformation ${\widehat{f}}_1^{-1}$ and becomes 𝔄̂_d−2.

In general, we recursively find the sequence of best fitting subspheres from the projected and transformed data points f̂_k{P(x; Â_d−k)} ∈ S^d−k (x ∈ S^d−k+1). At the kth level, where we fit a subsphere from S^d−k+1, we denote the best fitting subsphere as Â_d−k ≡ A_d−k(υ̂_k, r̂_k) and keep residuals defined by ξ_i,d−k (i = 1, . . . , n) for later use as analogues of principal component scores.

The lowest level best fitting subsphere Â₁ is then a small circle isomorphic to S¹. No further sphere or circle can be used to reduce the dimensionality. Instead, we find the Fréchet mean (Fréchet, 1944, 1948; Karcher, 1977; Bhattacharya & Patrangenaru, 2003) Â₀ of $x_1^{†}\dots x_n^{†}$, which are the projected and transformed data points in S¹. The Fréchet mean can be thought of as a best zero-dimensional representation of the data in our framework, and is defined as the minimizer of the sum of squared distances to the $x_i^{†}$s, i.e.,

$${\widehat{A}}_0=\underset{x\in S^1}{\text{argmin}}\sum _{i=1}^n{\rho }_1{(x,x_i^{†})}^2.$$

The Fréchet mean is unique when the support of $x_i^{†}$ is a proper subset of a half-circle in S¹ (Karcher, 1977), which is often satisfied in practice. If there are multiple Fréchet means, then the data must be carefully inspected. A typical case for having multiple means is that the data are uniformly distributed on the circle. If this is the case, then Â₀ can be chosen to be any solution of the above criterion and we may not lay much emphasis on Â₀.

The sequence of best fitting subspheres including Â₀ can be located in the original space S^d, as follows.

Definition 3. The sequence of sample principal nested spheres in S^d is {𝔄̂₀, . . . , 𝔄̂_d−1}, where

$${\widehat{𝔄}}_{d-k}=\{\begin{array}{ll}{\widehat{f}}_1^{-1}\circ \cdots \circ {\widehat{f}}_{k-1}^{-1}({\widehat{A}}_{d-k})\hfill & (k=2,\dots ,d),\hfill \\ {\widehat{A}}_{d-1}\hfill & (k=1).\hfill \end{array}$$

We call 𝔄̂₀ the principal nested spheres mean.

2.4. Euclidean-type representation

We wish to represent the data in a Euclidean space for visualization and further analysis.

Recall that in the kth level of the procedure, we have collected the signed residuals ξ_i,d−k (i = 1, . . . , n). These residuals were measured by the metric ρ_d−k of the unit sphere S^d−k, which was used to identify 𝔄̂_d−k ⊂ S^d. A natural spherical metric for 𝔄̂_d−k is defined for x, y ∈ 𝔄̂_d−k as

$${\rho }_{d-k}^{*}(x,y)=\prod _{i=1}^k\text{sin}({\widehat{r}}_i){\rho }_{d-k}\left\{{\widehat{f}}^k(x),{\widehat{f}}^k(y)\right\}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(k=1,\dots ,d-1),$$

where f̂^k(x) = f̂_k ○ ⋯ ○ f̂₁(x). The distance measured by ${\rho }_{d-k}^{*}$ is different from the great circle distance measured by ρ_d whenever any r̂_i is smaller than π/2, that is, whenever a small sphere was used in the sequence. However, it can be shown that ${\rho }_{d-k}^{*}$ (x, y) is the length of the minimal arc in 𝔄̂_d−k that joins x and y.

The residuals at the kth level are now rescaled as if they were measured by ${\rho }_{d-k}^{*}$, so that their magnitudes are commensurate. This is achieved by multiplying ${\prod }_{i=1}^{k-1}\text{sin}({\widehat{r}}_i)$ to the residuals. We put the scaled residuals in a row vector

$$\mathrm{\Xi }{(d-k)}_{1\times n}=\prod _{i=1}^{k-1}\text{sin}({\widehat{r}}_i)({\xi }_{1,d-k},\dots ,{\xi }_{n,d-k}).$$

We further define ξ_i,0 as the i th sample’s signed deviation from Â₀ measured by ${\rho }_1^{*}$. Similarly to before, rescale the deviations and let

$$\mathrm{\Xi }{(0)}_{1\times n}=\prod _{i=1}^{d-1}\text{sin}({\widehat{r}}_i)({\xi }_{1,0},\dots ,{\xi }_{n,0}).$$

These commensurate residuals are combined into a d × n data matrix

$${\widehat{X}}_{\text{PNS}}=\left[\begin{array}{c}\mathrm{\Xi }(0)\\ \mathrm{\Xi }(1)\\ ⋮\\ \mathrm{\Xi }(d-1)\end{array}\right],$$

where each column is the corresponding sample’s coordinates in terms of the sample principal nested spheres, and lies in a subset of E = [−π, π] × [−π/2, π/2]^d−1. Each entry in Ξ(k) has a role like the (k + 1)th principal component scores.

The data matrix X̂_PNS can be used to visualize the structure of the data. For example, the graph in Fig. 1 is a scatter-plot of Ξ (0) and Ξ (1). The variance of the jth component is $s_j^2={(n-1)}^{-1}{\sum }_{i=1}^n{\tilde{\xi }}_{i,j-1}^2$, where ξ̃_i,j−1 (i = 1, . . . , n) are the elements of Ξ (j − 1). The percent of variance exhibited in Fig. 1, and in the rest of the paper, is the proportion of the jth component variance of the sum of all variances, i.e., $s_j^2/{\sum }_{\ell }^d{s}_{\ell }^2$.

Moreover, conventional multivariate statistics based on Euclidean geometry can be applied to X̂_PNS for further analysis.

Remark 1. A point in S^d can be mapped to E by utilizing the projection (4) and rescaling, leading to a mapping h : S^d → E. The inverse operation h̃ : E*→ S^d can also be defined, for a subset E^*⊂ E. These transformations are built in an obvious way, details of which are contained in the Supplementary Material.

2.5. Principal arcs

In analogy with the principal component directions in Euclidean space, or the manifold extension principal geodesics, the principal arcs that represent the directions of major variation are defined. These arcs are small circles in S^d, which frequently are not equivalent to any geodesic.

Given a sequence of principal nested spheres 𝔄̂₀, . . . , 𝔄̂_d−1, the first principal arc coincides with 𝔄̂₁. This arc may be parameterized by the signed distance from 𝔄̂₀. In the space E of X̂_PNS, the first principal arc γ₁ coincides with the direction e₁ = (1, 0, . . . , 0)^T, and is parameterized by γ₁(t) = h̃(te₁), for t ∈ ℝ. See Remark 1 for the definition of h̃.

The second principal arc γ₂ lies in 𝔄̂₂ and is orthogonal to γ₁ at all points common to both. The first and second principal arcs cross at 𝔄̂₀ and also at the farthest point from 𝔄̂₀ on 𝔄̂₁. The second principal arc is in general a small circle in S^d but is identified with a great circle in S², the isomorphic space of 𝔄̂₂. The second principal arc in S² must pass through the axis υ_d−1 in order to be orthogonal to the first. This arc may be parameterized by the signed distance from 𝔄̂₀, and coincides with the direction e₂ in the space of X̂_PNS.

The higher order principal arcs are defined in the same manner. The kth principal arc γ_k can be defined and identified with the direction e_k in the space of X̂_PNS by γ_k(t) = h̃(te_k). The kth arc is then orthogonal to the principal arcs of order 1, . . . , k − 1, and passes through 𝔄̂₀.

The term principal arc was used in Jung et al. (2011), which concerns the space of direct products of two-spheres and Euclidean spaces. The principal arc γ_k used here coincides with the term in Jung et al. (2011), and both represent the path of major variation.

2.6. Principal nested spheres restricted to great spheres

An important special case of the analysis is obtained by setting r = π/2 for each subsphere fitting. This restriction leads to the nested spheres being great spheres, and the principal arcs become geodesics. We call this special case principal nested great spheres.

We conjecture that the principal geodesics, found by principal nested great spheres, are more similar to the geodesic principal components of Huckemann et al. (2010) than the usual tangent space projection methods. This is mainly because no predetermined mean, either geodesic or Procrustes, is used in our approach or in that of Huckemann et al. (2010). When r = π/2, the mean of the principal nested spheres is similar, but not identical, to the notion of mean of Huckemann et al. (2010). Although we have not yet found a significant difference between the principal nested great spheres and the geodesic-based methods in the literature, we point out that our approach as a generalization of principal components is conceptually different from the geodesic-based methods. See § 7 for discussion on this topic.

3. Computational algorithm

The computation of sample principal nested spheres involves iterative applications of minimization, projection and transformation. We have given explicit formulas for the projection (4) and the transformation (2). The least squares problem (3) is a constrained nonlinear minimization problem. It can be solved by the two-step algorithm described in Jung et al. (2011) with some modifications. The outer loop finds a point of tangency to approximate S^d by a tangent space; the inner loop solves an optimization problem in the linear space.

We make use of the exponential map and its inverse for mappings between the manifold and tangent spaces (Helgason, 2001; Buss & Fillmore, 2001). A tangent space at p ∈ S^m, T_pS^m, is an affine m-dimensional vector space and can be identified with ℝ^m. Without loss of generality, set the point of tangency as p = e_m+1 = (0, . . . , 0, 1), because one can use the rotation operator R(p) to transform p to e_m+1 while preserving all the data structure. The exponential map Exp_p : T_pS^m → S^m is defined by

$${\text{Exp}}_p(z)={\left(\frac{\text{sin}\left(\parallel z\parallel \right)}{\parallel z\parallel }{z}^{\text{T}},\text{cos}\left(\parallel z\parallel \right)\right)}^{\text{T}}\in S^m\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(z\in {ℝ}^m\cong T_p{S}^m\right).$$

The inverse exponential map or the log map Log_p : S^m → T_pS^m is defined by

$${\text{Log}}_p(x)=\frac{\theta }{\text{sin}\left(\theta \right)}{\left(x_1,\dots ,x_m\right)}^{\text{T}}\in {ℝ}^m,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}x={(x_1,\dots ,x_{m+1})}^{\text{T}}\in S^m,$$

where cos(θ) = x_m+1. These mappings preserve the distances to the point of tangency. By using the exponential mapping and its inverse, a hypersphere with radius r in the tangent space corresponds to a subsphere in S^m with distance r. In particular, A_m−1(υ, r) is equivalent to the image of {x ∈ ℝ^m : ‖x‖ = r} by Exp_υ.

The algorithm finds a suitable point of tangency υ, which is also the axis of the fitted sub-sphere. Given a candidate υ₀, the data are mapped to the tangent space T_υ0S^m by the log map. With $x_i^{†}={\text{Log}}_{{\upsilon }_0}(x_i)$, the inner loop finds

$$\underset{{\upsilon }^{†},r}{\text{min}}\sum _{i=1}^n{\left(\parallel x_i^{†}-{\upsilon }^{†}\parallel -r\right)}^2,$$

a nonlinear least-squares problem that can be solved numerically by, e.g., the Levenberg–Marquardt algorithm (Scales, 1985, Ch. 4). The solution υ^† is then mapped to S^m by the exponential map, and becomes the updated value of υ denoted by υ₁. This procedure is repeated until υ converges.

A main advantage of this approach is the reduced difficulty of the optimization task. The inner loop solves an unconstrained problem in a vector space, which is much simpler than the original constrained problem on manifolds. We have found that in many real data applications, including those not contained in the paper, the algorithm converges to at least a local minimum. The computation times for the examples in this paper on a computer with a 2.13 GHz processor are less than 2 seconds in MATLAB. In our experience with a number of datasets, the longest time required was less than 5 seconds. The computation of the principal nested great spheres is about two times faster than that of the principal nested spheres.

In modern applied problems the sample size is often less than the dimension of the manifold, i.e., x₁, . . . , x_n ∈ S^d with n ⩽ d, which is frequently referred to as the high-dimension low-sample-size situation (Hall et al., 2005; Dryden, 2005; Ahn et al., 2007). In Euclidean space, the dimension of the data can be reduced to n without losing any information. Likewise, the intrinsic dimensionality of the data on the hypersphere can be reduced to n − 1, where the additional reduction of 1 occurs because there is no origin in S^d. For the simplest example, let n = 2. Then there is a geodesic joining the two points, which is the submanifold containing all information. A generalization can be made for any n > 2.

Remark 2. For n < d, there exists an (n − 1)-dimensional nested sphere 𝔄_n−1 of S^d satisfying x_i ∈ 𝔄_n−1 for all i = 1, . . . , n. Moreover, there exist 𝔄_d−1 ⊃ ⋯ ⊃ 𝔄_n−1, all of which are great spheres with radius 1. The singular value decomposition of the data matrix [x₁, . . . , x_n] gives the appropriate 𝔄_n−1. Let ${𝒧}_1^n$ be the vector space of dimension n that all data points span. Then, the intersection of ${𝒧}_1^n$and S^d is the (n − 1)-dimensional great sphere 𝔄_n−1.

For faster computation, when n < d, we reduce the dimensionality to 𝔄_n−1 by the singular value decomposition, and use the proposed algorithm to fit 𝔄_n−2, and so on.

4. Application to planar shape space

4.1. Planar shape space

The shape of an object is what is left after removing location, scale, and rotation. The classical approach in shape analysis is to work with landmarks on the objects; see, e.g., Dryden & Mardia (1998). Each shape determined by a set of landmarks can be represented by a point in Kendall’s (1984) shape space. A useful approach to understanding the non-Euclidean shape space is through the preshape space, which is a sphere. We begin by summarizing Kendall’s framework for shape data, followed by a discussion of necessary considerations to apply our method to shape space through the preshape space.

Consider a set of k > 2 landmarks in ℝ² and the corresponding configuration matrix X, which is a k × 2 matrix of Cartesian coordinates of landmarks. The preshape of the configuration X is invariant under translation and scale, which is given by Z = H X/ ‖H X‖_F, where H is the (k − 1) × k Helmert submatrix (Dryden & Mardia, 1998, p. 34) and ‖·‖_F is the Frobenius norm. Provided that ‖H X‖_F > 0, Z ∈ S^2(k−1)−1. The unit sphere S^2(k−1)−1 in ℝ^2(k−1) is the space of all possible preshapes, and is called the preshape space.

The shape of a configuration matrix X can be represented by the equivalence set under rotation, [Z] = {ZΓ : Γ ∈ SO(2)}, where SO(2) is the set of all 2 × 2 rotation matrices. The space of all possible shapes is then a non-Euclidean space called the shape space and denoted by ${\mathrm{\Sigma }}_2^k$.

A useful notation for planar shapes, allowing much simpler mathematical development, is to represent a preshape Z = (z_ij) as a complex vector z = (z₁₁ + iz₁₂, . . . , z_k−1,1 + iz_k−1,2)^T. Let z^* denote the complex conjugate transpose of z. Then the following facts may be found in Small (1996, Ch. 3).

The horizontal subspace of the tangent space of S^2(k−1)−1 at w, with respect to the quotient map from S^2(k−1)−1 to ${\mathrm{\Sigma }}_2^k$, is expressed as H_w = {υ ∈ T_wS^2(k−1)−1 : υ^*w = 0}. The horizontal subspace is isometric to the tangent space of ${\mathrm{\Sigma }}_2^k$ at [w] (Kendall et al., 1999, p. 137). A horizontal geodesic at w in S^2(k−1)−1 is a great circle path starting at w with initial direction in H_w. Suppose that υ, w are complex preshapes satisfying υ^*w ⩾ 0, by which we mean ℜ(υ^*w) ⩾ 0 and 𝔍 (υ^*w) = 0. Then the geodesic joining υ and w is a horizontal geodesic and the spherical distance between υ and w is the same as the Riemannian distance between the corresponding shapes [υ] and [w] in ${\mathrm{\Sigma }}_2^k$, where the Riemannian distance is defined as

$${\rho }_{{\sum }_2^k}\left(\left[\upsilon \right],\left[w\right]\right)=\underset{\varphi \in \left(0,2\pi \right)}{\text{min}}{\rho }_{2(k-1)-1}\left(e^{i\varphi }\upsilon ,w\right)={\text{cos}}^{-1}\left(\left|{\upsilon }^{*}w\right|\right).$$

For υ, w that do not satisfy υ^*w ⩾ 0, one can optimally rotate υ onto w by multiplying e^iϕ, ϕ = arg(υ^*w), and treat υ^′ = e^iϕυ as if it was the υ.

Since the discussions before this section are based on real vectors, we also write the pre-shape Z as a vectorized version z = vec(Z^T), where vec(A) is obtained by stacking the columns of the matrix A on top of one another. Then the assumption υ^*w ⩾ 0 translates into υ^Tw ⩾ 0 and υ^TMw = 0, where M is the 2(k − 1) × 2(k − 1) skew-symmetric matrix consisting of k − 1 diagonal blocks

$$\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right].$$

The geodesic that joins υ to w is parametrized by Q(υ → w, θ) υ (θ ∈ ℝ) defined in (A1).

For the preshapes w, z₁, . . . , z_n, as long as the shapes of those are of interest, we assume without loss of generality that w^Tz_i ⩾ 0 and w^TMz_i = 0. These z_i s are the Procrustes fits to a common base w.

4.2. Principal nested spheres for planar shapes

The intrinsic dimension of the shape space is 2k − 4, since the degrees of freedom are reduced from 2k of the set of landmarks by 2 for translation, 1 for scale, and 1 for rotation. This is less than the dimension of the preshape space d = 2k − 3. It is thus desired that 𝔄_d−1 of S^d leaves no residuals. This is achieved by the theory and practical modifications in this section. In short, the Procrustes fit of configurations or preshapes to a common alignment base w, e.g., the Procrustes mean, results in the desired decomposition of the shape space.

Theorem 1. Suppose the preshapes w, z₁, . . . , z_n ∈ S^d satisfy w^Tz_i ⩾ 0 and w^TMz_i = 0 for i = 1, . . . , n. Let w^* = Mw. Then w, z_i ∈ A_d−1(w*, π/2). Moreover, define h A_d−1 = {z ∈ A_d−1 : z^Tw ⩾ 0} as a sub-hemisphere. Then w, z_i ∈ h A_d−1(w*, π/2).

Theorem 1 is a direct consequence of definitions and thus the proof is omitted. The h A_d−1(w*, π/2) ⊂ 𝔄_d−1 is a great sub-hemisphere of dimension d − 1. Since z_i ∈ h A_d−1(w*, π/2) for all i = 1, . . . , n, the dimension of preshape space S^d can be reduced by 1 to 𝔄_d−1 ⊃ h A_d−1(w*, π/2) without loss of any shape information. The tangent space of h A_d−1(w*, π/2) at w is in fact identical to the horizontal subspace of the tangent space of S^d at w, since the vertical geodesic at w runs through w^*. The metrics ρ_d of preshape space and ${\rho }_{{\mathrm{\Sigma }}_2^k}$ of the shape space are closely related. In particular,

$${\rho }_{d-1}^{*}(w,z)={\rho }_d(w,z)={\rho }_{{\sum }_2^k}\left(\left[w\right],\left[z\right]\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(z\in h{A}_{d-1}\right).$$

Moreover, ρ_d (z₁, z₂) for z₁, z₂ ∈ h A_d−1 is close to ${\rho }_{{\mathrm{\Sigma }}_2^k}$ ([z₁], [z₂]) when z₁, z₂ are close to w, which is justified by the following lemma, now using complex notation for simplicity of the statement and proof.

Lemma 1. For preshapes w, z₁, z₂ in complex notation satisfying w*z_i ⩾ 0,

$${\text{cos}}^2\left\{{\rho }_d(z_1,z_2)\right\}={\text{cos}}^2\left\{{\rho }_{{\sum }_2^k}\left(\left[z_1\right],\left[z_2\right]\right)\right\}+c^2,$$ (5)

where c = 𝔍{(z₁ − w)*(z₂ − w)}. Moreover, the additional term c satisfies

1. 0 ⩽ |c| ⩽ 4 sin{ρ_d (z₁, w)/2} sin{ρ_d (z₂, w)/2},

2. 0 ⩽ |c| ⩽| sin ϕ|, where $\varphi =\text{arg}(z_1^{*}{z}_2)$ is the amount of the rotation to optimally position z₁ onto z₂.

Proof. By the definitions ${\rho }_d(z_1,z_2)=\text{arccos}\{\Re (z_1^{*}{z}_2)\}$, ${\rho }_{{\mathrm{\Sigma }}_2^k}([z_1],[z_2])=\text{arccos}(|z_1^{*}{z}_2|)=\text{arccos}[{\{\Re {(z_1^{*}{z}_2)}^2+c^2\}}^{1/2}]$, we have (5) with c = 𝔍( $z_1^{*}{z}_2$) = 𝔍{(z₁ − w)*(z₂ − w) + w*z₂ + $z_1^{*}$w − w*w} = 𝔍{(z₁ − w)*(z₂ − w)}. Denote the inner product and norm of complex vectors a, b as 〈a, b〉 = a^*b and 〈a〉 = 〈a, a〉^1/2. Then we have

$$c=\parallel z_1-w\parallel \parallel z_2-w\parallel 𝔍\left\{{\left(\frac{z_1-w}{\parallel z_1-w\parallel }\right)}^{*}\frac{\left(z_2-w\right)}{\parallel \left(z_2-w\right)\parallel }\right\}⩽\parallel z_1-w\parallel \parallel z_2-w\parallel .$$

The first inequality is obtained by noting ρ_d (z, w) = 2 arcsin(‖z − w‖/2). For the second, $z_1^{*}{z}_2=\hspace{0.17em}\left|z_1^{*}{z}_2\right|e^{i\varphi }$, $\varphi =\text{arg}(z_1^{*}{z}_2)$, gives $c=𝔍(z_1^{*}{z}_2)=\hspace{0.17em}\left|z_1^{*}{z}_2\right|\text{sin}\varphi$, which in turn gives |c| ⩽ | sin ϕ|.

The hA_d−1(w*, π/2)is therefore closely related to ${\mathrm{\Sigma }}_2^k$, but is not identical to it. As previously noted our method applies to shape data that are aligned and lifted to the preshape sphere. The choice of the alignment base w is an important issue, which we discuss next.

In general, we wish to set the alignment base w as a centre of the data. We recommend using the preshape of the Procrustes mean of the data. Other reasonable candidates for w are the geodesic mean and the principal nested spheres mean 𝔄₀ as defined in Definition 3. We have tested these choices on a number of real and simulated datasets. Setting w as the principal nested spheres mean or the geodesic mean usually takes more time in computation than using the full Procrustes mean, but the resulting decompositions are virtually the same in most cases.

In the following, we describe all candidates for w in more detail, giving the advantages and disadvantages of each option.

We first considered use of the principal nested spheres mean 𝔄₀ as the alignment base. The 𝔄₀ is identified with the origin of the coordinate system for the Euclidean representation of data X̂_PNS. Since 𝔄₀ is estimated from the data, we begin with the preshape of the full Procrustes mean as an initial guess for 𝔄₀ and recursively update 𝔄̂₀ on which preshapes are aligned. The algorithm consists of the following steps.

• Step 1. Initialize w as the preshape of the Procrustes mean of z_i.

• Step 2. Align z₁, . . . , z_n to w and compute 𝔄̂₀ from aligned z_i.

• Step 3. If ρ_d (w, 𝔄̂₀) < ∊, then set w = 𝔄̂₀ and stop. Otherwise update w = 𝔄̂₀ and go to Step 2.

In practice, there is no guarantee that this algorithm will converge.

Other candidates for w are the full Procrustes mean preshape and the geodesic mean of the preshapes. These are relevant to the Fréchet mean (Fréchet, 1948; Karcher, 1977; Bhattacharya & Patrangenaru, 2003), where the geodesic mean is the Fréchet mean with the Riemannian distance and the Procrustes mean is using the full Procrustes distance, which is extrinsic to S^d. Recently, it has been observed that the curvature of the manifold S^d sometimes makes the Fréchet mean inadequate, since it can lie outside the main support of the data. See Huckemann et al. (2010). When the Fréchet mean is indeed a useful representation of the data, 𝔄̂₀ is usually found at a point close to the Fréchet mean. Even if the Fréchet mean is far from the data, 𝔄̂₀ is nevertheless located at an appropriate centre of the data.

In the next section, the Procrustes mean is used as the alignment base w.

5. Real data analysis

5.1. Human movement

A human movement dataset introduced in Kume et al. (2007) contains 50 samples of k = 4 landmarks on the lower back, shoulder, wrist, and index finger. The dataset consists of shape configurations of five different reaching movements projected in the plane of a table, each observed at ten different time-points. The raw data are plotted in Fig. 3(a), as 50 overlaid quadrilaterals, each of which is a shape configuration. Vertices of the quadrilaterals are the locations of the landmarks in two dimensions. These 50 samples have been Procrustes fitted to each other, i.e., translated, scaled, and rotated to each other so that they are as close as possible.

Fig. 3.

Human movement data. (a) Procrustes fitted human data. (b) The first principal mode of variation by principal nested spheres, showing ±2 standard deviation from Â₀. (c) The first principal mode of variation by principal nested great spheres. The curving form of variation of the lower left vertex is more precisely captured in (b) than in (c).

We applied the analysis of principal nested spheres and great spheres, with the alignment base w being the preshape of the Procrustes mean, and compared the results with the geodesic-based methods. The fitted principal nested spheres have radii 1, 0.7, 0.4, and 0.25 from the 𝔄̂₄ to 𝔄̂₁, respectively. Since the dimension of the corresponding shape space is 4, 𝔄̂₄ is a great sphere and leaves no residuals, as expected.

The quadratic form of variation in the coordinates by principal nested great spheres is captured by Â₁, the one-dimensional principal nested sphere, as illustrated in Fig. 1. The principal mode of variation found by principal nested spheres is plotted in Fig. 3(b), where the four bold dots together represent the shape at 𝔄̂₀, and those curves through 𝔄̂₀ illustrate shape changes captured in 𝔄̂₁. The nonlinear form of variation suggested by these curves can also be discerned in the raw data. Figure 3(c) shows the result of the corresponding principal nested great sphere analysis. This more conventional approach gives a less flexible mode of variation and explains less of the variation in the raw data.

Table 1 shows the proportions of variances captured in each component, as explained in § 2.4 to compare the proposed analysis with some previous methods. The first is Euclidean principal component analysis, where the usual principal component analysis is carried out for the Procrustes fitted configuration matrices. The second is called tangent coordinates at the extrinsic mean, where the Procrustes fitted preshapes are orthogonally projected to the tangent coordinates at the extrinsic mean and then the usual principal component analysis is performed for the projections. This is equivalent to carrying out principal component analysis on the partial Procrustes tangent coordinates (Dryden & Mardia, 1998, Ch. 5). The last method is principal geodesic analysis of Fletcher et al. (2004), which is the usual principal component analysis of the data mapped to the tangent space at the intrinsic mean by the inverse exponential map.

Table 1.

Proportions of variance (%), captured in the human movement data

Component	1	2	3	4	5
Euclidean principal component analysis	94.09	4.71	0.94	0.18	0.08
Tangent coordinates at the extrinsic mean	94.68	4.41	0.75	0.15	0.00
Principal geodesic analysis	94.69	4.40	0.75	0.15	0.00
Principal nested great spheres	94.72	4.39	0.74	0.15	0.00
Principal nested spheres	97.40	2.19	0.29	0.11	0.00

Principal nested spheres is clearly the best of these methods in terms of representing maximal variation using as few components as possible, showing the value of analysing this dataset with small spheres. The other manifold methods are comparable to each other, with the intrinsic method of principal nested great spheres slightly better than the two extrinsic methods. As expected, Euclidean principal component analysis, which completely ignores the manifold nature of the data, gives the worst performance. In particular, more than four components are required, compared to at most four components from manifold extensions.

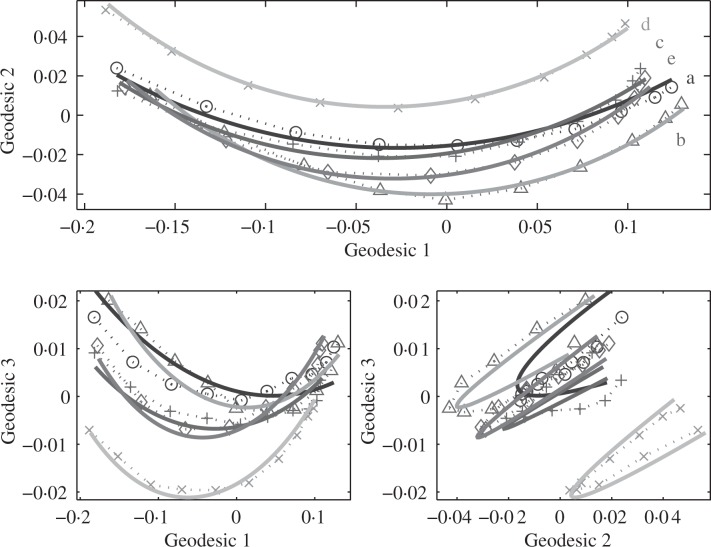
Each of the five tasks in the dataset can be modelled as a small circle in the preshape space, by separately applying the analysis of principal nested spheres to the samples corresponding to each task. The results are plotted in Fig. 4. At least three geodesic components are needed to capture the variation of each task, which is well approximated by the separately fitted 𝔄̂₁s.

Fig. 4.

Human movement data. Mode of variation represented by the small circle 𝔄̂₁ fitted to different tasks labelled a, b, c, d, and e, plotted in coordinates of principal nested great spheres, to reveal the advantage of fitting small spheres as summarized in Table 1.

5.2. Rat skull growth

The shape and size changes of rat skulls are described in Bookstein (1991) and studied by several other authors including Kenobi et al. (2010). The data are eight landmark locations for skulls of 21 laboratory rats observed at eight ages: days 7, 14, 21, 30, 40, 60, 90, and 150. We discard four X-rays with missing landmarks, and analyse the remaining 164 observations.

The results of our analysis, and comparison with previous methods, are summarized in Table 2 and Fig. 5. Table 2 shows the proportions of variances from our analyses and also from the geodesic-based methods. The corresponding shape space has dimension 12 but we present the first seven components. The analysis of principal nested spheres exhibits the best performance in terms of representing maximal variation using few components. The geodesic-based methods show similar performance to each other. We observe that the amount of variation captured in first two components by principal nested great spheres is about 89.99% which is comparable to 88.67% in the first component of principal nested spheres. Moreover, while the variances in the first three geodesic components sum up to 92.46%, the first two components by principal nested spheres contain 91.99%. This can be explained further by an inspection of Fig. 5. As for the previous example, Euclidean principal component analysis gives noticeably poorer performance than any of the manifold methods.

Table 2.

Proportions of variance (%), captured in rat skull growth data

Component	1	2	3	4	5	6	7
Euclidean principal component analysis	81.88	7.94	2.50	1.77	1.19	1.05	0.95
Tangent coordinates at the extrinsic mean	82.17	7.78	2.48	1.77	1.19	1.05	0.95
Principal geodesic analysis	82.19	7.78	2.48	1.77	1.19	1.05	0.95
Principal nested great spheres	82.22	7.77	2.47	1.76	1.19	0.89	0.77
Principal nested spheres	88.68	3.31	1.67	1.38	1.06	0.89	0.77

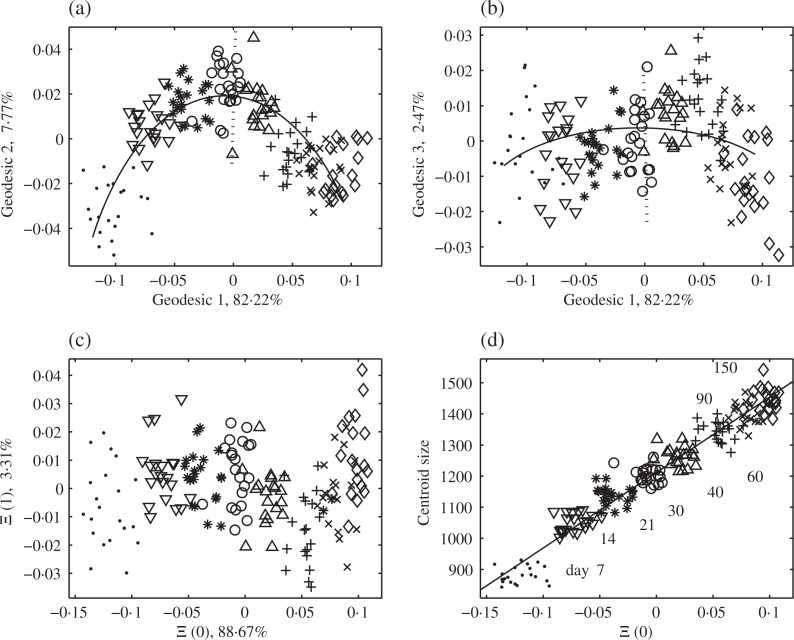
Fig. 5.

Rat skull growth: (a–b) Data plotted by the coordinates by principal nested great spheres; (—) represents the first principal arc, and (· · ·) represents the second principal arc. Different symbols represent different age groups. (c) Data plotted by the coordinates by principal nested spheres. (d) Scatter-plot with centroid size and a regression line.

In Fig. 5(a) and (b), non-geodesic variation curving through three geodesic components is illustrated. This is well captured in 𝔄̂₂, of dimension 2, as in Fig. 5(c). We then inspect the first two principal arcs γ₁ and γ₂ that represent the non-geodesic variation captured by principal nested spheres. These principal arcs are plotted in the coordinates by principal nested great spheres in Fig. 5(a–b). The quadratic variation in (a) is captured by γ₁, illustrated by the solid curve. This leads to an understanding that the non-geodesic variation, which sums up to 90% in two geodesic components, is well captured in the one-dimensional 𝔄̂₁, which contains 89% of the variance. The principal nested spheres capture more interesting variability in fewer components and give a concise and useful representation of the data.

Figure 5(d) shows that the shape change due to the growth of the rat is well captured by 𝔄̂₁, which can be checked by inspecting the relation to the size of the rat skulls. The skull size is larger for older rats. The first coordinate by principal nested spheres is strongly associated with the size, and the sample correlation coefficient is 0.97. The shape change due to the different locations of 𝔄̂₁ is illustrated in Fig. 6. The two extreme shape configurations are also overlaid, which shows the typical effect of age on shape.

Fig. 6.

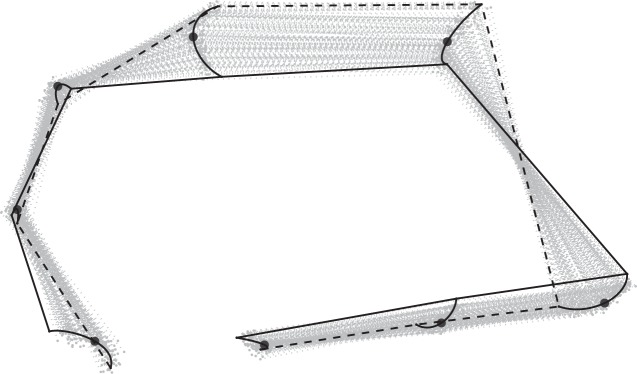
Rat skull growth: the first principal mode of variation by 𝔄̂₁. The configurations connected by (· · ·) represent the shape of a typical young skull at −2 standard deviations, and (—) represents the shape of a typical old rat skull at +2 standard deviations.

6. Problems related to overfitting of small spheres

For some datasets, there may be an overfitting issue in using small spheres instead of great spheres. We briefly examine some approaches to deal with this.

We have devised a procedure to apply sequential tests for each level of subsphere fitting, discussed in the Supplementary Material. Similar to the backward regression procedure, sequentially testing the significance of small sphere fits at each level may prevent overfitting. There are some caveats in the application of these tests. For example, they are built upon parametric assumptions. Furthermore, because they are not independent, simultaneous inference is complicated.

Another approach to the choice between small and great spheres is based upon Bayesian information criterion ideas. Formulas for implementing this approach are given in the Supplementary Material. As detailed there, we tried this on the human movement data and rat skull data and obtained reasonable results. These were quite similar to the results of the hypothesis testing approach discussed in the above paragraph.

A referee made the interesting suggestion of a soft decision rule that balances between small and great spheres using a penalization approach. A specific optimization problem for this method is described in the Supplementary Material.

7. Discussion

A classical approach to principal component analysis for manifold data is a tangent plane approach (Fletcher et al., 2004; Dryden & Mardia, 1998, Ch. 5.5). The resulting principal geodesics then pass through the point of tangency, i.e., the Procrustes mean or the geodesic mean. Huckemann et al. (2010) pointed out that the predetermined mean may not be a good representation of the data due to the curvature of the manifold. They find that the best fitting geodesics do not necessarily pass through any predetermined mean. Jung et al. (2011) proposed to use small circles to fit the non-geodesic modes of variation when the sample space is essentially S². Our method builds upon these earlier works, where principal nested spheres can be viewed as a high-dimensional extension of Jung et al. (2011), and principal nested great spheres are similar to Huckemann et al. (2010).

As noted in Marron et al. (2010) and Pizer et al. (2012), our method can be viewed as a backward generalization of principal component analysis. A conventional principal component analysis approach begins with lower dimensions and builds up, that is, finding the mean first, then the least squares line through the mean, then the second line which determines the best fitting plane and so on. We, on the other hand, sequentially reduce the dimensionality from the full data. These two approaches are equivalent in Euclidean space, because of the Pythagorean theorem, but different on manifolds. The backward approach serves as a natural viewpoint for the extension of principal component analysis to manifolds. In fact, Huckemann et al. (2010) partly used the backward approach, since their notion of mean is post-defined by two geodesic components. It should be noted that our method when applied to shape data begins with a forward approximation. This is because we pre-align preshapes with a mean, then approximate the shape space by the preshape sphere. A possible future direction of research is the development of a method for shape spaces that does not begin with any predetermined mean.

A related issue is the optimality of our fit. The fitted principal nested sphere 𝔄̂_q is not the q-dimensional small sphere that minimizes a squared loss. Specifically, 𝔄̂_q is not in general equivalent to ${\text{argmin}}_{{𝔄}_q}{\sum }_{i=1}^n{\rho }_d{(x_i,{𝔄}_q)}^2$. We believe that it is also true that other methods in the literature are not optimal under this criterion. We view this optimality issue using the analogy of variable selection in linear regression. In selecting independent variables for the regression model, one can use forward selection, backward elimination or search for the best subset. Approaches of Dryden & Mardia (1998) and Fletcher et al. (2004) can be understood as forward extensions, while the analysis of principal nested spheres can be seen as a backward extension. As the set of variables chosen by backward elimination need not be optimal under some criteria, the q-dimensional principal nested sphere may be suboptimal to a global search. A best subset search will likely be computationally heavy, even when restricting only to great spheres.

A possible issue with the proposed method is model bias. We briefly discuss this in the context of the simple S². Suppose data points or random variables are distributed along a small circle on S² with an addition of noise: x = γ₁(λ) ⊗ e ∈ S², where γ₁ is a parameterized small circle. Model bias occurs when the noise e is added at γ₁(λ) as an isotropic perturbation. For example, the noise can be added as a bivariate normal random vector with variance σ²I₂ projected onto S² by the exponential map or alternatively as a von Mises–Fisher distributed random vector with location parameter γ₁(λ). Under this noise structure, our procedure will treat this noise in a way that is biased, toward fitting a larger circle (Rivest, 1999). Hastie & Stuetzle (1989) discussed model bias in fitting principal curves to Euclidean data.

An approach to this issue is to use an alternative noise model where our method is unbiased. For example, starting with the radius of a small circle, one could add independent univariate Gaussian noise to the latitude and longitude. This corresponds to modelling e as a bivariate normal random vector with a diagonal covariance matrix in the spherical coordinate system with the centre of the circle at the north pole. The noise model in Jung et al. (2011) is a special case of this model.

Yet another model gives an opposite type of bias. This assumes the small circle distribution proposed by Bingham & Mardia (1978). It can be seen that our procedure results in a radius fit smaller than the true radius parameter, since the marginal distribution along the latitude angle of the small circle distribution is skewed to the centre of the circle.

While these bias issues deserve careful consideration, we believe that, at least in many important cases, they are of secondary concern relative to the central issue of potential large gains, relative to fitting small spheres instead of great spheres. This has been further shown in the examples of Jung et al. (2010) and Pizer et al. (2012).

Appendix

Preliminary transformations: rotation matrices

We describe a rotation matrix for moving a dataset on a sphere along a particular minimal geodesic that retains the interpoint geodesic distances after the transformation.

Suppose that a and b are unit vectors in ℝ^m and we wish to move b to a along the geodesic path on the unit sphere in ℝ^m that connects b to a. Amaral et al. (2007) showed that a rotation matrix is determined in a natural way.

Define c = {b − a(a^Tb)}/ ‖b − a(a^Tb)‖, where ‖·‖ denotes the Euclidean norm on ℝ^m. Provided that |a^Tb| < 1, c is well defined. Let A = ac^T − ca^T. Note that A² = −aa^T − cc^T and A³ = −A. Since the matrix A is skew symmetric, its matrix exponential is a rotation matrix, as summarized in the following lemma, proved in Amaral et al. (2007).

Lemma A1. Assume that a, b ∈ ℝ^m are unit vectors such that |a^Tb| < 1, and let A and c be defined as earlier. Then for θ ∈ (0, π], the matrix

$$Q(b\to a,\theta )=\text{exp}(\theta A)=I_d+\sum _{j=1}^{\infty }\frac{{\theta }^j}{j^{!}}{A}^j$$

has the following properties:

1. Q(b → a, θ) is an m × m rotation matrix;

2. Q(b → a, θ) can be written as Q(θ) = I_d + sin(θ) A + {cos(θ) − 1}(aa^T + cc^T);

3. Q(b → a, α)b = a for α = cos⁻¹(a^Tb); and

4. for any z ∈ ℝ^m such that a^Tz = 0 and b^Tz = 0, we have Q(b → a, θ)z = z for any θ ∈ (0, π].

The path given by Q(b → a, θ) is a minimal geodesic on the sphere. If b and a are orthogonal, then

$$Q(b\to a,\theta )b=b\text{cos}(\theta )+a\text{sin}(\theta )\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(-\pi /2<\theta ⩽\pi /2),$$ (A1)

which corresponds to a definition of the unit speed geodesic (Kume et al., 2007, p. 515).

We also define R(υ), for υ ∈ ℝ^m, as a rotation matrix that rotates υ to the north pole e_m = (0, . . . , 0, 1)^T, i.e.,

$$R(\upsilon )=Q(\upsilon \to e_m,{\theta }_{\upsilon }),$$ (A2)

where θ_υ = cos⁻¹(υ^Te_m). The last row of R(υ) is υ^T. If υ = e_m, then R(υ) = I_m. Finally define R⁻(υ) as the m × (m + 1) matrix consisting of the first m rows of R(υ).

Supplementary material

Supplementary material available at Biometrika online includes detailed discussion on the overfitting issue, additional data analyses, some geometric facts related to § 2, and discussion on convergence of the algorithm proposed in § 3.