Pointwise nonparametric maximum likelihood estimator of stochastically ordered survivor functions

Abstract

In this paper, we consider estimation of survivor functions from groups of observations with right-censored data when the groups are subject to a stochastic ordering constraint. Many methods and algorithms have been proposed to estimate distribution functions under such restrictions, but none have completely satisfactory properties when the observations are censored. We propose a pointwise constrained nonparametric maximum likelihood estimator, which is defined at each time t by the estimates of the survivor functions subject to constraints applied at time t only. We also propose an efficient method to obtain the estimator. The estimator of each constrained survivor function is shown to be nonincreasing in t, and its consistency and asymptotic distribution are established. A simulation study suggests better small and large sample properties than for alternative estimators. An example using prostate cancer data illustrates the method.

1. Introduction

Stochastic ordering is an important concept and has a wide range of applications, in such fields as biomedical research, economics and system reliability. We often encounter situations where there is prior knowledge of stochastic ordering among distributions. For example, in a cancer study, we expect patients with a lower stage of cancer at diagnosis to have lower death rates at all times than those with a higher stage. In addition to the natural desire for estimators of the distributions to satisfy the same expected ordering restrictions as the underlying distributions, there is the potential for improved efficiency by applying the constraints in the estimation method.

For random variables T₁ and T₂ with corresponding survivor functions S₁(t) and S₂(t), T₁ is stochastically larger than T₂, T₁ ⩾_st T₂, if S₁(t) ⩾ S₂(t) for all t (Lehmann, 1955). For G groups, the concept can be generalized to partial ordering; specifically, we say that T_g (g = 1, …, G) satisfy the partial-ordering constraints defined by the constraint set E ⊂ {1, …, G}² if for any (i, j) ∈ E, T_i ⩾_st T_j. Special cases of this are simple ordering, in which T₁ ⩾_st ⋯ ⩾_st T_G, for which E = {(1, 2), (2, 3), …, (G − 1, G)}; tree ordering, in which T₁ ⩾_st T₂, T₁ ⩾_st T₃, …, T₁ ⩾_st T_G for which E = {(1, 2), (1, 3), …, (1, G)}; umbrella ordering, in which T₁ ⩾_st ⋯ ⩾_st T_i ⩾_st T_i+1 ⩾_st ⋯ ⩾_st T_G for which E = {(1, 2), (2, 3), …, (i − 1, i), (i + 1, i), (i + 2, i + 1), …, (G, G − 1)}, and factorial ordering such as T₁ ⩾_st T₂ ⩾_st T₄, T₁ ⩾_st T₃ ⩾_st T₄, for which E = {(1, 2), (2, 4), (1, 3), (3, 4)}.

We consider independent right-censored samples of the form (Y_gi, Δ_gi) (g = 1, …, G; i =1, …, n_g), where Y_gi is the observed time and Δ_gi is the event indicator. We assume that the censoring mechanism is independent, so that the generalized likelihood is

$$L\{S_1(\cdot ),\dots ,S_G(\cdot )\}=\prod _{g=1}^G\prod _{i=1}^{n_g}{\{S_g(Y_{gi}-)-S_g(Y_{gi})\}}^{{\mathrm{\Delta }}_{gi}}{S}_g{(Y_{gi})}^{1-{\mathrm{\Delta }}_{gi}}.$$ (1)

The E-constrained nonparametric maximum likelihood estimator maximizes (1) subject to the partial-ordering constraint E. Brunk et al. (1966) studied the constrained nonparametric maximum likelihood estimator in the two-sample case without censoring. Dykstra (1982), as corrected by Park et al. (2012), extended this result to right-censored data. In the case of three or more populations with general partial-ordering constraints, Hoff (2003) and Lim et al. (2009) proposed different computational methods for obtaining the constrained nonparametric maximum likelihood estimator.

This estimator has the undesirable property that a violation of a constraint in the Kaplan–Meier estimators (Kaplan & Meier, 1958) at an earlier time affects the estimator at a later time, even if there is no violation at this later time. A number of authors have noted that the constrained nonparametric maximum likelihood estimator can have relatively large pointwise bias and mean squared error at a fixed t and have suggested alternatives (Rojo & Ma, 1996; Rojo, 2004; El Barmi & Mukerjee, 2005) that can have better mean squared error properties. Park et al. (2012) noted a correction to the constrained nonparametric maximum likelihood estimator presented by Dykstra (1982), which led to improved properties, but this corrected estimator still often has poorer pointwise properties than other estimators, some of which are relatively simple to define. In the two-sample problem, Lo (1987) suggested swapping the Kaplan–Meier estimates of the survivor functions when the constraint is violated. Rojo (2004) proposed estimating both survivor functions as the weighted average of the two Kaplan–Meier estimators at times when the constraint is violated, where the weights are based on the initial sample sizes. El Barmi & Mukerjee (2005) extended Rojo’s estimators to the simple ordering situation using isotonic regression. The simulation study in Park et al. (2012) shows that some of these estimators have smaller mean squared error than the constrained nonparametric maximum likelihood estimator when the censoring distributions are equal, but when the censoring distributions differ substantially between groups, the alternative estimators may have larger mean squared error than the constrained nonparametric maximum likelihood estimator. Moreover, these alternative estimators have not been explicitly extended to a general partial-ordering case.

When we consider finite sample properties of an estimator Ŝ(t), we typically consider point-wise criteria, such as pointwise bias or pointwise mean squared error at each fixed t. In contrast to pointwise estimators such as described in Rojo (2004) and Lo (1987), the constrained non-parametric maximum likelihood estimator estimates the whole survival curve. So it is perhaps not surprising that Rojo’s estimator typically has better properties when evaluated using metrics such as pointwise mean squared error. On the other hand, these pointwise estimators do not adapt well to unequal censoring distributions between groups, whereas the constrained nonparametric maximum likelihood estimator does. This motivated us to propose a new constrained estimator, a pointwise constrained nonparametric maximum likelihood estimator or pointwise constrained estimator for convenience.

Definition 1 (Pointwise constrained estimator). For each specified time x, let S̃_g(t; x) be the maximum likelihood estimator of S_g(t) under the constraint S_i (x) ⩾ S_j (x) for all (i, j) ∈ E. Then Ŝ_g(t) = S̃_g(t; t) (g = 1, …, G) for all t is the pointwise constrained estimator of the survivor function S_g under the partial stochastic ordering constraint E.

2. Estimation methods

2.1. Notation and likelihood

To obtain the pointwise constrained estimator as given in Definition 1, it is required to maximize the likelihood (1) subject to the constraints S_i (x) ⩾ S_j (x) for all (i, j) ∈ E for a fixed time x. This will give the estimates of S̃₁(t; x), …, S̃_G(t; x) and the constrained maximization will be repeated for all times x of interest.

Let X_gj (j = 1, …, m_g) be the distinct event times in group g and define X_g0 = 0 and X_{g(mg+ 1)} = ∞ (g = 1, …, G). Let N_g(t) be the number at risk at time t in group g and let M_g(t) be the number of distinct events in (0, t] in group g. Let d_gj and n_gj be, respectively, the number of events and the number at risk in group g at time X_gj.

It is convenient to redefine the problem in terms of hazards. Let h_g(t) = log{S_g(t)/S_g(t−)}, so that 1 − exp{h_g(t)} is the discrete hazard in group g at time t. The loglikelihood of (1) is

$$\begin{array}{l}\text{log}\hspace{0.17em}L(h_1,\dots ,h_G)=\sum _{g=1}^G\hspace{0.17em}\{\sum _{i=1}^{m_g}(d_{gi}\hspace{0.17em}\text{log}[1-\text{exp}\{h_g(X_{gi})\}]\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+(n_{gi}-d_{gi})h_g(X_{gi}))+N_g(x)h_g^{\delta }(x)\},\end{array}$$ (2)

where h_g = {h_g(X_g1), …, h_g(X_gmg), $h_g^{\delta }$(x)} (g = 1, …, G). The corresponding constraints are ${\sum }_{j=1}^{M_p(x)}{h}_p(X_{pj})+h_p^{\delta }(x)⩾{\sum }_{j=1}^{M_r(x)}{h}_r(X_{rj})+h_r^{\delta }(x)$, for all (p, r) ∈ E, and $h_g^{\delta }$(x) ⩽ 0. In this, $h_g^{\delta }$(x) = I (x ≠ X_gMg(x))h_g(x), which is included to account for the fact that if x = X_gMg(x), we do not have the extra term N_g(x)h_g(x) in the loglikelihood (2).

2.2. Linearly constrained convex minimization

There is a large literature on general approaches to linearly constrained convex minimization problems. There are essentially three types of algorithms: interior point, primal active set and dual active set methods. In general, our data contain many more observed event times than groups. Interior point and primal active set methods simultaneously optimize over the large number of quantities $h_g^{\delta }$(x) and h_g(X_gi) (g = 1, …, G; i = 1, …, m_g) at each time x of interest, and so are not computationally efficient in our setting. Dual active set methods may involve many fewer parameters, but the dual function itself is difficult to express as a function of Lagrange multipliers and the feasible range of these multipliers is difficult to specify in our problem. So the dual active set method is also difficult to implement in our context.

In § 2.4, we transform the problem of maximizing the loglikelihood (2) subject to the linear constraints to another simple concave maximization problem subject to linear constraints by using the profile likelihood. In preparation for this, we first discuss the constrained maximum likelihood estimator of the survivor function in the one-sample case.

2.3. Maximum likelihood estimator of the survivor function subject to a single constraint

In the one-sample case without constraints, the maximum likelihood estimator has probability mass only at the observed event times. The loglikelihood analogous to (2) is

$$\text{log}\hspace{0.17em}L(h)=\sum _{j=1}^m[d_j\text{log}\{1-\text{exp}\hspace{0.17em}h(X_j)\}+(n_j-d_j)h(X_j)],$$ (3)

where h = {h(X₁), …, h(X_m)} and (3) is maximized at h(X_j) = log(1 − d_j/n_j) (j = 1, …, m), which corresponds to the Kaplan–Meier estimator.

Consider now the maximum likelihood estimator subject to the constraint S(x) = exp(q). The maximum likelihood estimator of the survivor function will have positive probability mass at event times X_i and nonnegative probability mass at time x. The optimization problem is to maximize the loglikelihood of h = {h(X₁), …, h(X_m), h^δ(x)},

$$\text{log}\hspace{0.17em}L(h)=\sum _{i=1}^m[d_i\text{log}\{1-\text{exp}\hspace{0.17em}h(X_i)\}+(n_i-d_i)h(X_i)]+N(x)h^{\delta }(x),$$

subject to ${\sum }_{j=1}^{M(x)}\hspace{0.17em}h(X_j)+h^{\delta }\hspace{0.17em}(x)=q$ and h^δ(x) ⩽ 0.

Let K (q; x) = −N(x) if M(x) = 0, and otherwise let K (q; x) = max(−N(x), k̂), where k̂ is the unique solution of the equation ${\sum }_{j=1}^{M(x)}\hspace{0.17em}\text{log}\{1-d_j/(n_j+k)\}=q$. Here, k̂ = ∞ if q = 0 and k̂ = d_M(x) − n_M(x) if q = −∞. Let ${\widehat{h}}^{\delta }(q;x)=q-{\sum }_{j=1}^{M(x)}\hspace{0.17em}\widehat{h}(q;X_j)$, where

$$\widehat{h}(q;X_i)=\{\begin{array}{ll}\text{log}\hspace{0.17em}\left\{1-\frac{d_i}{n_i+K(q;x)}\right\},\hfill & i⩽M(x),\hfill \\ \text{log}\hspace{0.17em}\left(1-\frac{d_i}{n_i}\right),\hfill & i>M(x).\hfill \end{array}$$ (4)

Theorem 1. The maximum likelihood estimator of S(t) subject to constraint S(x) = exp(q) at a given x is Ŝ(t) = exp {∑_Xj⩽t ĥ(q; X_j) + I (t ⩾ x)h^δ (q; x) } (t ⩽ τ), where τ is the last observed time.

Proof. See the Appendix.

Thomas & Grunkemeier (1975) and Li (1995) considered the maximization problem described above. However, Thomas & Grunkemeier (1975) solved the problem with the equality constraint ${\sum }_{j=1}^{M(x)}\hspace{0.17em}h(X_j)=q$, which implicitly assumes that ĥ(x) = 0 if x is not an observed event time, whereas Li (1995) mistakenly proved that ĥ(x) = 0 unless x is an observed event time. In fact, the maximization problem described above involves two constraints: ${\sum }_{j=1}^{M(x)}\hspace{0.17em}h(X_j)+h^{\delta }\hspace{0.17em}(x)=q$ and h^δ (x) ⩽ 0. It is possible that ĥ^δ (x) < 0 if K (q; x) = −N(x). The inequality constraint, h^δ (x) ⩽ 0, has been neglected in these approaches. It is necessary, however, to apply the Karush–Kuhn–Tucker conditions (Kuhn & Tucker, 1951) to all possible inequality constraints, including the bounds on the parameters, and only omit the redundant constraints.

2.4. Reformulation of the problem using profile likelihood

The profile loglikelihood of S(x) = exp(q) at a given x is

$$\begin{array}{ll}\ell (q;x)\hfill & =\underset{h\in R}{\text{sup}}\hspace{0.17em}\text{log}L(h)\hfill \\ \hfill & =\sum _{i=1}^m\{d_i\text{log}[1-\text{exp}\{\widehat{h}(q;X_i)\}]+(n_i-d_i)\widehat{h}(q;X_i)\}+N(x){\widehat{h}}^{\delta }(q;x),\hfill \end{array}$$ (5)

where $R=\{h:{\sum }_{i=1}^{M(x)}\hspace{0.17em}h(X_i)+h^{\delta }(x)=q\}$, and ĥ(q; X_i) and ĥ^δ(q; x) are defined in (4).

Lemma 1. The derivative of the profile loglikelihood (5) with respect to q is − K (q; x).

Proof. See the Appendix.

For given x, maximizing the loglikelihood (2) subject to the constraints in E can be redefined as maximizing the profile loglikelihood ℓ (q₁, …, q_G; x), which equals

$$\begin{array}{ll}\sum _{g=1}^G{\ell }_g(q_g;x)=\hfill & \sum _{g=1}^G\hspace{0.17em}(\sum _{i=1}^{M_g(x)}[(n_{gi}-d_{gi})\hspace{0.17em}\text{log}\{n_{gi}+K_g(q_g;x)-d_{gi}\}\hfill \\ \hfill & -n_{gi}\hspace{0.17em}\text{log}\{n_{gi}+K_g(q_g;x)\}]+I\{K_g(q_g;x)=N_g(x)\}{N}_g(x)\hfill \\ \hfill & \times \left[q_g-\sum _{j=1}^{M_g(x)}\hspace{0.17em}\text{log}\left\{1-\frac{d_{gi}}{n_{gi}+K_g(q_g;x)}\right\}\right]),\hfill \end{array}$$ (6)

subject to constraints q_i ⩾ q_j, for all (i, j) ∈ E and q_g ⩽ 0 (g = 1, …, G). In this formulation, only G parameters q = (q₁, …, q_G) need to be estimated, and Ŝ_g(x) = exp(q̂_g), where q̂ = (q̂₁, …, q̂_G) is the maximum likelihood estimator of q.

Any of the general methods described in § 2.2 can be used to maximize the profile loglikelihood (6) under the corresponding linear constraints. The profile loglikelihood (6) and its derivative, dℓ (q; x)/dq^T = {−K₁(q₁; x), …, −K_G(q_G; x)}^T, are easily calculated.

To obtain the pointwise constrained estimator Ŝ_g(t) (g = 1, …, G) for all t, it is not necessary to maximize the profile likelihood at every t. It can be seen that the pointwise constrained estimator may jump only at observed event times and at times just after observed censoring times. Let {X′_j} be the union of all distinct times Y_gi if Δ_gi > 0 and $Y_{gi}^{+}$ if Δ_gi = 0. Here, $Y_{gi}^{+}$ can be taken as Y_gi + ∊ for a small ∊ > 0. We calculate Ŝ_g(X′_j), and then Ŝ_g(t) is a step function with jumps only at X′_j, i.e., Ŝ_g(t) = Ŝ_g(a), where a = max{X′_j : X′_j ⩽ t}.

The following theorem shows that Ŝ_g(t) (g = 1, …, G) is a valid survivor function.

Theorem 2. The pointwise constrained estimator Ŝ_g(t) obtained from maximizing the profile likelihood (6) is a nonincreasing function in t for each g = 1, …, G. That is, for any 0 ⩽ x < y ⩽ τ_g, Ŝ_g(x) ⩾ Ŝ_g(y).

Proof. See the Supplementary Material.

2.5. Generalized pool-adjacent-violators algorithm in the simple ordering case

Suppose that G survivor functions satisfy the simple stochastic ordering constraint T₁ ⩾_st ⋯ ⩾_st T_G, and we aim to estimate the pointwise constrained estimator at time x. A generalized pool-adjacent-violators algorithm can be used as developed in Best et al. (1999), because the profile loglikelihood is the sum of concave functions. The results of the generalized pool-adjacent-violators algorithm lead to a set of blocks, B₁, …, B_r, where r ⩾ 1, B_r = {u_r−1 + 1, …, u_r} and 0 = u₀ < ⋯ < u_r = G. This is described in an algorithm in the Supplementary Material. The final estimate of the survivor function for each group in a block B_r takes a common value exp(q̂_r), where q̂_r maximizes the profile loglikelihood, ℓ_Br (q; x) = ∑_i∈Br ℓ_i (q; x) and 0 ⩾ q̂₁ > ⋯ > q̂_r.

3. Consistency and asymptotic distribution

Let $S_g^{*}$(t) be the Kaplan–Meier estimator of S_g(t) and let $S_g^c$(t) be the censoring survivor function for group g. Further, let τ_g = inf{t : S_g(t) $S_g^c$(t) = 0} (g = 1, …, G). Under the condition that there are no common jumps between the event and censoring distributions, Stute & Wang (1993) showed that the Kaplan–Meier estimator $S_g^{*}$(t) is uniformly consistent for S_g(t) on [0, τ_g). A similar result holds for the pointwise constrained estimator. The following theorem is proved in the Supplementary Material.

Theorem 3. Let Ŝ_g(t) be the pointwise constrained estimator given in Definition 1. Under the condition of no common jumps of S_g(t) and $S_g^c$(t), sup_t<τg | Ŝ_g(t) − S_g(t) | → 0 with probability 1 as n_g → ∞ (g = 1, …, G).

Let W_g(V_g) be a Brownian motion on [0, ∞) with variance function V_g(t). As shown in Gill (1983), n_g^1/2( $S_g^{*}$ − S_g) $S_g^{-1}$ → W(V_g) in distribution on [0, τ_g] as n_g → ∞ where $V_g(t)=-{\int }_0^t{\{S_g^2(x-)S_g^c(x-)\}}^{-1}\text{d}{S}_g(x)$. For a fixed time x, n_g^1/2{ $S_g^{*}$(x) − S_g(x)} → N{0, ${\sigma }_g^2$(x)} in distribution, where ${\sigma }_g^2$(x) = V_g(x) $S_g^2$(x).

Let $n={\sum }_{g=1}^G{n}_g$ and assume that lim_n→∞ n_g/n = c_g > 0 and let $Z_g^{*}$(x) = n^1/2 { $S_g^{*}$(x) − S_g(x)} (g = 1, …, G). Then { $Z_1^{*}$(x), …, $Z_G^{*}$(x)}^T → {Z₁(x), …, Z_G(x)}^T in distribution, where Z_g(x) ∼ N{0, ${\sigma }_g^2$(x)/c_g} and Z₁(x), …, Z_G(x) are independent.

Theorem 4. For a fixed time x < min{τ_k : L_g(x) ⩽ k ⩽ U_g(x)} and under the simple ordering constraint T₁ ⩾_st ⋯ ⩾_st T_G,

$$n_g^{1/2}\{{\widehat{S}}_g(x)-S_g(x)\}\to c_g^{1/2}\underset{L_g(x)⩽\ell ⩽g}{\text{min}}\underset{g⩽u⩽U_g(x)}{\text{max}}\hspace{0.17em}\frac{{\sum }_{k=\ell }^u\{Z_k(x)w_k(x)\}}{{\sum }_{k=\ell }^u{w}_k(x)}$$ (7)

in distribution, where w_g(x) = c_g/ ${\sigma }_g^2$(x), L_g(x) = min{i : S_i(x) = S_g(x)} and U_g(x) = max{i : S_i(x) = S_g(x)}.

Proof. See the Supplementary Material.

In the Supplementary Material, the asymptotic distribution of the pointwise constrained estimator is discussed for situations where the number at risk in some groups is zero.

Let Š_g(x) be the estimate of S_g(x) by applying the isotonic regression algorithm to $S_g^{*}$(x) with weights w_g(x) (g = 1, …, G), subject to constraint S₁(x) ⩾_st ⋯ ⩾_st S_G(x). Then, Š_g(x) has a minimax form (Barlow et al., 1972)

$${\widehat{S}}_g(x)=\underset{1⩽\ell ⩽g}{\text{min}}\underset{g⩽u⩽G}{\text{max}}\hspace{0.17em}\frac{{\sum }_{k=\ell }^u\{S_k^{*}(x)w_k(x)\}}{{\sum }_{k=\ell }^u\hspace{0.17em}{w}_k(x)}.$$

From El Barmi & Mukerjee (2005, Theorem 2), it can be seen that

$$n_g^{1/2}\{{\widehat{S}}_g(x)-S_g(x)\}\to c_g^{1/2}\hspace{0.17em}\underset{L_g(x)⩽\ell ⩽g}{\text{min}}\underset{g⩽u⩽U_g(x)}{\text{max}}\hspace{0.17em}\frac{{\sum }_{k=\ell }^u\{Z_k(x)w_k(x)\}}{{\sum }_{k=\ell }^u\hspace{0.17em}{w}_k(x)}$$

in distribution. From (7), it follows that Ŝ_g(x) and Š_g(x) are asymptotically equivalent. We hypothesize that this equivalence to isotonic regression will also hold under the partial-ordering constraint. This yields the following conjecture for the asymptotic distribution of the pointwise constrained estimator.

Conjecture 1. For a fixed time x,

$$n_g^{1/2}\{{\widehat{S}}_g(x)-S_g(x)\}\to c_g^{1/2}\hspace{0.17em}{f}_g\hspace{0.17em}\left\{Z_1(x),\dots ,Z_G(x);\frac{c_1}{{\sigma }_1^2},\dots ,\frac{c_G}{{\sigma }_G^2},x\right\}$$

in distribution as n → ∞ for all x given S_g(x) $S_g^c$(x) > 0. Here Ψ_g(x) = {i : S_i(x) = S_g(x)}, E_g(x) = {(i, j) ∈ E : i, j ∈ Ψ_g(x)} and f_g(z₁, …, z_G; w₁, …, w_G, x) is the solution function for μ_g that minimizes ${\sum }_{i=1}^G\hspace{0.17em}{w}_i{(z_i-{\mu }_i)}^2$ subject to μ_i ⩾ μ_j for all (i, j) ∈ E_g(x).

If this conjecture is correct, inference methods developed for isotonic regression could also be useful for the pointwise constrained estimator.

4. Comparison with the Kaplan–Meier estimator when sample size is large

4.1. Simple ordering case

In the simple ordering case with no censoring, El Barmi & Mukerjee (2005) showed that their isotonic regression estimator has smaller asymptotic mean squared error than the unrestricted Kaplan–Meier estimator. A similar result holds for the pointwise constrained estimator compared with the Kaplan–Meier estimator when there is right censoring.

Theorem 5. Consider the simple ordering constraint T₁ ⩾_st ⋯ ⩾_st T_G. For a fixed x with $S_k^c$(x)S_k(x) > 0 for all k = 1, …, G, let $n_k^{1/2}$ {Ŝ_k(x) − S_k(x)} → Ẑ_k and $n_k^{1/2}$ { $S_k^{*}$(x) − S_k(x)} → Z_k in distribution. If there exists at least one g′ with S_g′(x) = S_g(x), then E( ${\widehat{Z}}_g^2$) < E( $Z_g^2$). If no such g′ exists, then Ŝ_g(x) and $S_g^{*}$(x) are asymptotically equivalent.

Thus, the pointwise constrained estimator has smaller asymptotic mean squared error than the Kaplan–Meier estimator. In fact, a stronger inequality relation holds. Namely pr(| Ẑ_g | ⩽ ∊) > pr(| Z_g | ⩽ ∊) for all ∊ > 0. In § 4.2, we calculate the asymptotic bias and asymptotic mean squared error of the pointwise constrained estimator in the two-sample case.

4.2. The two sample case, G = 2

If S₁(x) > S₂(x), then, asymptotically, the constraint is irrelevant and $n_1^{1/2}$ {Ŝ₁(x) − S₁(x)} → σ₁(x)Z̄₁ and $n_2^{1/2}$ {Ŝ₂(x) − S₂(x)} → σ₂(x) Z̄₂ in distribution, as n₁, n₂ → ∞, where Z̄₁ and Z̄₂ are independent standard normal random variables.

Let n₂/n₁ → c as n₁, n₂ → ∞. We consider asymptotic properties when S₁(x) = S₂(x). From Theorem 4, we can show that

$$\begin{array}{l}{n}_1^{1/2}\{{\widehat{S}}_1(x)-S_1(x)\}\to {\sigma }_1(x)\hspace{0.17em}\text{max}\hspace{0.17em}\left\{{\overline{Z}}_1,\frac{{\overline{Z}}_1+c{(x)}^{1/2}{\overline{Z}}_2}{1+c(x)}\right\},\\ n_2^{1/2}\{{\widehat{S}}_2(x)-S_2(x)\}\to {\sigma }_2(x)\hspace{0.17em}\text{min}\hspace{0.17em}\left\{{\overline{Z}}_2,\frac{c(x){\overline{Z}}_2+c{(x)}^{1/2}{\overline{Z}}_1}{1+c(x)}\right\},\end{array}$$ (8)

in distribution, where c(x) = c ${\sigma }_1^2$(x)/ ${\sigma }_2^2$(x). Direct calculation from (8) shows that the asymptotic mean squared errors are

$$\begin{array}{l}\underset{n_1\to \infty }{\text{lim}}\hspace{0.17em}E[n_1{\{{\widehat{S}}_1(x)-S_1(x)\}}^2]=\frac{\{2+c(x)\}{\sigma }_1^2(x)}{2\{1+c(x)\}},\\ \underset{n_2\to \infty }{\text{lim}}\hspace{0.17em}E[n_2{\{{\widehat{S}}_2(x)-S_2(x)\}}^2]=\frac{\{1+2c(x)\}{\sigma }_2^2(x)}{2\{1+c(x)\}}.\end{array}$$ (9)

These are always smaller than the unrestricted counterparts ${\sigma }_1^2$(x) and ${\sigma }_2^2$(x).

Let S̃₁(x) and S̃₂(x) be the estimators of Rojo (2004) or El Barmi & Mukerjee (2005). On the basis of definitions of their estimators, when S₁(x) = S₂(x), the asymptotic mean squared errors are given by

$$\begin{array}{l}E[n_1{\{{\tilde{S}}_1(x)-S_1(x)\}}^2]={\sigma }_1^2(x)+\frac{c\{{\sigma }_2^2(x)-(2+c){\sigma }_1^2(x)\}}{2{\{1+c\}}^2},\\ E[n_2{\{{\tilde{S}}_2(x)-S_2(x)\}}^2]={\sigma }_2^2(x)+\frac{c\{{\sigma }_1^2(x)-(1+2c){\sigma }_2^2(x)\}}{2{\{1+c\}}^2}.\end{array}$$ (10)

It can be shown that the asymptotic mean squared error of Ŝ_g(x) is less than or equal to that of S̃_g(x) (g = 1, 2), with equality only when ${\sigma }_1^2$(x) = ${\sigma }_2^2$(x), in which case S̃_g(x) and Ŝ_g(x) are asymptotically equivalent. From (10) we see that when ${\sigma }_2^2$(x)/ ${\sigma }_1^2$(x) > c₂/c₁ + 2, Rojo’s estimator S̃₁(x) is asymptotically less efficient than the Kaplan–Meier estimator $S_1^{*}$(x) and when ${\sigma }_1^2$(x)/ ${\sigma }_2^2$(x) > c₁/c₂ + 2, S̃₂(x) is asymptotically less efficient than $S_2^{*}$(x).

From (8), the asymptotic biases of Ŝ₁(x) and Ŝ₂(x) are

$$\begin{array}{ll}\underset{n_1\to \infty }{\text{lim}}\hspace{0.17em}E[n_1^{1/2}\{{\widehat{S}}_1(x)-S_1(x)\}]\hfill & ={\sigma }_1(x){\int }_{-\infty }^{\infty }{\int }_{c^{1/2}(x)}^{\infty }\frac{c^{1/2}{z}_2-c(x)z_1}{1+c(x)}{f}_{{\overline{Z}}_2}\hspace{0.17em}(z_2)f_{{\overline{Z}}_1}(z_1)\text{d}{z}_2\text{d}{z}_1\hfill \\ \hfill & ={\sigma }_1(x)\hspace{0.17em}{\left[\frac{c(x)}{2\pi \{1+c(x)\}}\right]}^{1/2}<{\sigma }_1(x)\hspace{0.17em}{\left(\frac{1}{2\pi }\right)}^{1/2},\hfill \\ \underset{n_2\to \infty }{\text{lim}}\hspace{0.17em}E[n_2^{1/2}\{{\widehat{S}}_2(x)-S_2(x)\}]\hfill & ={\sigma }_2(x)\hspace{0.17em}{\left[\frac{1}{2\pi \{1+c(x)\}}\right]}^{1/2}<{\sigma }_2(x)\hspace{0.17em}{\left(\frac{1}{2\pi }\right)}^{1/2}.\hfill \end{array}$$

5. Confidence intervals

5.1. Asymptotic approaches

While there is a substantial literature on the estimation of survivor functions under stochastic ordering constraints, there has been little discussion of constructing confidence intervals for ordered survivor functions. Rojo (2004) demonstrated weak convergence to a Gaussian process of his estimator, from which confidence bands could be constructed. For the most part, however, asymptotic results are not particularly useful since, if the true inequalities at time t are strict, then the asymptotic distribution of Ŝ_g(t) is the same as that of the Kaplan–Meier estimator and the corresponding approximate confidence interval would be unaffected by the restrictions. In our opinion, the most promising approach to constructing confidence intervals in these problems is through resampling methods that reflect the finite sample aspects. We consider some such approaches in the next section.

5.2. Bootstrap methods

We used a nonparametric resampling scheme, in which survival time and censoring indicator pairs are drawn with replacement from the data separately for each group. For each bootstrap sample, a bootstrap estimate ${\widehat{S}}_g^b$(t) (b = 1, …, B) is obtained by applying the pointwise constrained estimator. Simple confidence intervals based on these bootstrap estimates can be constructed using the percentile or the basic bootstrap method (Efron & Tibshirani, 1993; Davison & Hinkley, 1997). For a nominal level of (1 − 2α), the percentile confidence interval for S_g(t) is { ${\widehat{S}}_{g,\alpha }^B$(t), ${\widehat{S}}_{g,1-\alpha }^B$(t)}, where ${\widehat{S}}_{g,\alpha }^B$(t) is αth percentile of the bootstrap distribution. The basic bootstrap method utilizes ideas of pivotal statistics, and can also be improved by use of transformations such as h(s) = arcsin(s^1/2). The confidence interval for the basic bootstrap method is given by (h⁻¹[2h{Ŝ_g(t)} − h{ ${\widehat{S}}_{g,1-\alpha }^B$(t)}], h⁻¹[2h{Ŝ_g(t)} − h{ ${\widehat{S}}_{g,\alpha }^B$(t)}]).

While these simple methods are easy to apply, a number of different methods have been developed which have improved properties. The work in Andrews (2000) suggests that the use of the bootstrap for inference problems with order restrictions on the parameters may be particularly challenging. We investigated a number of different alternatives to the two simple bootstrap methods and present below a method which had reasonably good properties for the cases considered.

For the restricted estimation problem, the distribution of Ŝ_g(t) − S_g(t) will generally not be symmetric or centred around zero and will differ from one group g to the next. It is to be expected that the bootstrap distribution ${\widehat{S}}_g^b$(t) − Ŝ_g(t) will be similarly biased. The method we propose uses the bootstrap distribution to correct the bias, but is adjusted so as not to over-correct. Consider pointwise estimators Ŝ₁(t) and Ŝ₂(t), where S₁(t) ⩾ S₂(t). Let ${\overline{S}}_g^B$(t) be the mean of the bootstrap estimates ${\widehat{S}}_g^b$(t). The basic bootstrap method considers a pseudo estimator given by [2h{Ŝ_g(t)} − h{ ${\widehat{S}}_{g,\alpha }^B$(t)}]. While ${\overline{S}}_1^B(t)⩾{\overline{S}}_2^B(t)$, the mean of the pseudo estimator may not satisfy the order constraint, i.e., it is possible that 2h{Ŝ₁(t)} − h{ ${\overline{S}}_1^B$(t)} < 2h{Ŝ₂(t)} − h{ ${\overline{S}}_2^B$(t)}. This can be considered as an overcorrection and it might be expected that the properties of the confidence interval could be improved if this overcorrection is modified. Let ${\tilde{S}}_g^B$(t, a_g) = h{Ŝ_g(t)} + a_g[h{Ŝ_g(t)} − h{ ${\overline{S}}_g^B$(t)}], where 0 ⩽ a_g ⩽ 1. Although ${\tilde{S}}_g^B$(t, a_g) will satisfy the ordering constraint for a_g = 0, for a_g = 1, this may not be true. Given a set of a_g such that the ${\tilde{S}}_g^B$(t, a_g) (g = 1, …, G) satisfy the ordering constraints, the proposed adjusted basic bootstrap confidence interval is (h⁻¹[2h{Ŝ_g(t)} − h{ ${\widehat{S}}_{g,1-\alpha }^B$(t)} + δ_g], h⁻¹[2h{Ŝ_g(t)} − h{ ${\widehat{S}}_{g,\alpha }^B$(t)} + δ_g]), where δ_g = (a_g − 1)[h{Ŝ_g(t)} − h{ ${\overline{S}}_g^B$(t)}].

We propose the following method to obtain a set of a_g that satisfy the constraints. Let a₁ = a₂ = ⋯ = a_G = a and find the largest a that does not result in a violation of an order restriction. Use this value of a for the groups i and j for which ${\tilde{S}}_i^B$(t, a_i) = ${\tilde{S}}_j^B$(t, a_j). For the remaining groups increase a until a new violation is about to occur, and use the new value of a for the groups that have the active constraint for ${\tilde{S}}_i^B$(t, a) and have not already had a fixed value of a_i. Continue in this way, gradually increasing a, using the value of a when constraints become active, until all values of a_g have been set or a = 1. An algorithm to obtain a_g (g = 1, …, G) is given in the Supplementary Material.

5.3. Confidence interval centred on a constrained estimator

Hwang & Peddada (1994) suggested a method in which a confidence interval is computed for the unrestricted estimator and then shifted and centred on the constrained estimator. They showed that, under fairly general conditions, the coverage probability for the shifted interval will exceed the nominal level. For the survivor function, we apply this to intervals on a log transformed scale and consider the approximate 100(1 − 2α)% confidence interval, Ŝ_g(x) exp{±z_α ${\sigma }_g^{*}$(x)}, where ${\sigma }_g^{*}$(x) is the standard error estimate of log $S_g^{*}$(x) (Kalbfleisch & Prentice 2002, p. 17), and z_α is the αth percentile of the standard normal distribution.

6. Simulation studies

6.1. Two-sample case when sample size is small

We have conducted numerous simulation studies to compare the finite sample properties of three different constrained estimators, Rojo’s estimator (Rojo, 2004), the constrained nonparametric maximum likelihood estimator (Park et al., 2012) and the pointwise constrained estimator, and compared them to the unconstrained Kaplan–Meier estimator in the two-sample case. In this paper, we show results for scenarios where G = 2 and S₁(t) ⩾ S₂(t) for all t.

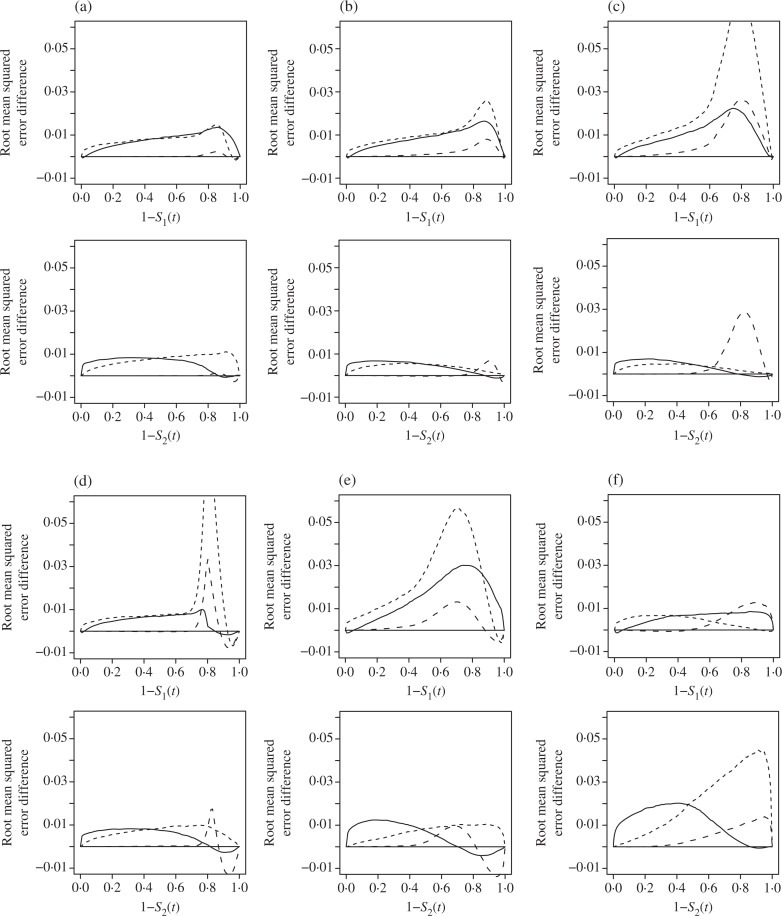
The upper and lower plots of each panel in Fig. 1 show differences of root mean squared errors of estimators of S₁(t) and S₂(t) over a range of values of t, compared with the pointwise constrained estimator. In cases with the same censoring distributions, Fig 1(a), Rojo’s estimator and the pointwise constrained estimator have smaller root mean squared error than the other estimators. However, if populations 1 and 2 have different censoring distributions, the pointwise constrained estimator has smallest root mean squared error among all estimators at almost all times. Rojo’s estimator does not adjust well to the unequal censoring distributions, Figs. 1(b)–(f), even when the censoring rates are close to each other, Fig. 1(d). The pointwise constrained estimator is the only estimator that dominates the Kaplan–Meier estimator at almost all times in all situations considered. Each simulation is based on 10 000 replications.

Fig. 1.

Difference of root mean squared errors of estimators compared with the pointwise constrained estimator. Kaplan–Meier estimator (thin dashed); constrained nonparametric maximum likelihood estimator (thick solid); Rojo’s estimator (thick dashed); pointwise constrained estimator (thin solid). Sample sizes are 80 in cases (a)–(d) and 50 in cases (e) and (f) for both groups. Event distributions are exp(1) for group 1 and exp(1.1) for group 2 in cases (a)–(d), and U(0, 1) for group 1 and U^1.1(0, 1) for group 2 in cases (e) and (f). The censoring distributions are exp(1) and exp(1) in case (a), exp(1) and no censoring in case (b), exp(2) and no censoring in case (c), U(0, 1.6) and no censoring in case (d), exp(3.2) and exp(1.6) in case (e) and exp(0.67) and exp(3.2) in case (f) for groups 1 and 2, respectively. When event random variable follows a U(0, 1) distribution, the censoring distributions exp(3.2), exp(1.6) and exp(0.67) give approximately 70, 50 and 30% censoring rates.

6.2. Two-sample case: asymptotic properties

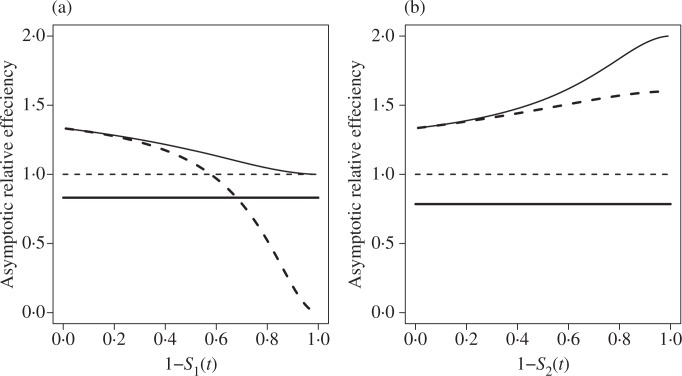
We define the asymptotic relative efficiency as the inverse ratio of the mean squared errors and compare the asymptotic relative efficiency of the three constrained estimators to the Kaplan–Meier estimator in the two sample case in Fig. 2. The underlying distributions are S₁(t) = S₂(t) = exp(−t), $S_1^c$(t) = 1 and $S_2^c$(t) = exp(−2t). The constraint is asymptotically relevant at all times. We set lim_n1,n2→∞ n₁/n₂ = 1. The asymptotic relative efficiency of the full constrained nonparametric maximum likelihood estimator is based on simulated data with a very large sample size. Asymptotic relative efficiencies of the pointwise constrained estimator and Rojo’s estimator are calculated using (9) and (10).

Fig. 2.

Comparison of asymptotic relative efficiencies under the constraint T₁ ⩾_st T₂. The underlying distributions are: S₁(t) = S₂(t) = exp(−t), $S_1^c$(t) = 1 and $S_2^c$(t) = exp(−2t). Kaplan–Meier estimator (thin dashed); constrained nonparametric maximum likelihood estimator (thick solid); Rojo’s estimator (thick dashed); pointwise constrained estimator (thin solid).

The pointwise constrained estimator dominates all other estimators for all t, whereas Rojo’s estimator could be inefficient for some t, as seen in Fig. 2(a). Compared with the Kaplan–Meier estimator, the full constrained nonparametric maximum likelihood estimator is less efficient at all times in this setting.

6.3. Simple ordering case

In this section, we compare finite sample properties of the pointwise constrained estimator with the Kaplan–Meier estimator in the simple ordering case and investigate the confidence intervals described in § 5. We consider three groups with underlying distributions T₁ ∼ exp(1), T₂ ∼ exp(1.1) and T₃ ∼ exp(1.4) and a uniform censoring distribution C ∼ U(0, 4.3), which gives an overall censoring rate of about 20%. Sample sizes are n₁ = n₃ = 40 and n₂ = 20. The simulation is based on 10 000 replicates.

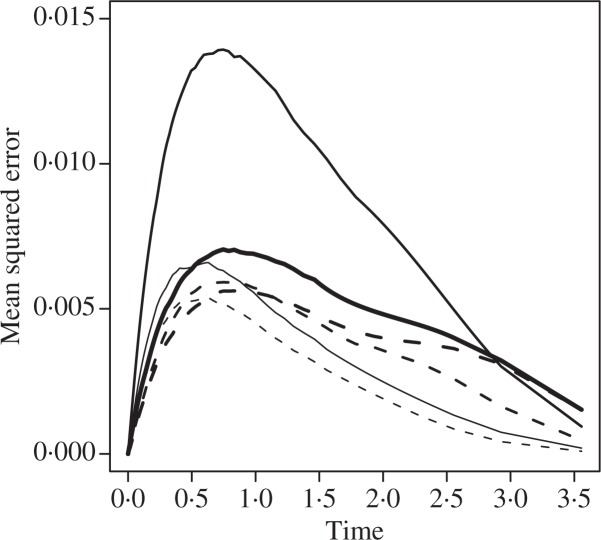
Figure 3 shows the mean squared error of the pointwise constrained estimator and the Kaplan–Meier estimator. The figure shows efficiency gains for the pointwise constrained estimator at all times for all groups, with the largest gains for the estimation of S₂(t), where the mean squared error of the pointwise constrained estimator is less than half of the mean squared error of the Kaplan–Meier estimator at almost all times.

Fig. 3.

Comparison of the Kaplan–Meier estimator and pointwise constrained estimator in the three sample case. Comparison of the Kaplan–Meier estimates for groups 1 (black solid), 2 (thick solid) and 3 (thin solid) and pointwise constrained estimator for group 1 (black dashed), 2 (thick dashed) and 3 (thin dashed) case.

Bootstrap intervals are based on 1999 bootstrap estimates. We evaluate confidence intervals at time 0.26 and 0.63, where the survival rates of group 2 are 0.75 and 0.5, respectively. In addition, we also conducted a simulation study for additional two cases with different distributions; see Table 1. The coverage rates and average widths of the confidence intervals described in § 5 are shown in Table 1. As expected, the confidence interval centred on the pointwise constrained estimator, Ŝ_g exp(±1.96 ${\sigma }_g^{*}$), is overly conservative with large average width and has higher coverage rate. The bootstrap methods give confidence intervals with significantly reduced widths, but the coverage rates can be somewhat low for some groups, especially when using the percentile or the basic bootstrap methods. The transformation and the adjusted methods described in § 5 both give slightly better coverage rates. The overall best results are obtained with the combination of the basic bootstrap with arcsin(s^1/2) transformation and controlling for bias overcorrection.

Table 1.

Percent coverage, average width, of nominal 95% confidence intervals

	t = 0.26			t = 0.63
Distribution	exp(1)	exp(1.1)	exp(1.4)	exp(1)	exp(1.1)	exp(1.4)
Percentile	91 (20.8)	95 (22.9)	95 (24.9)	94 (27.2)	95 (28.2)	94 (27.4)
Basic	89 (20.8)	90 (22.9)	91 (24.9)	91 (27.2)	88 (28.2)	90 (27.4)
With adjustment	90 (20.8)	92 (22.9)	93 (24.9)	92 (27.2)	91 (28.2)	91 (27.4)
arcsin(s1/2)	94 (22.5)	93 (23.1)	93 (24.4)	93 (27.3)	90 (28.0)	92 (27.8)
With adjustment	95 (22.4)	94 (23.2)	94 (24.5)	94 (27.3)	93 (28.1)	94 (27.8)
Ŝg exp{± 1.96 ${\sigma }_g^{*}$}	92 (26.7)	98 (37.8)	97 (28.3)	95 (33.6)	99 (46.5)	97 (31.7)
Distribution	exp(1)	exp(1.05)	exp(1.2)	exp(1)	exp(1.05)	exp(1.2)
Percentile	90 (20.2)	96 (21.5)	94 (23.4)	92 (26.2)	96 (26.5)	94 (26.6)
Basic	90 (20.2)	92 (21.5)	93 (23.4)	92 (26.2)	91 (26.5)	92 (26.6)
With adjustment	91 (20.2)	94 (21.5)	94 (23.4)	92 (26.2)	93 (26.5)	93 (26.6)
arcsin(s1/2)	95 (21.9)	94 (21.8)	94 (22.7)	94 (26.4)	93 (26.4)	94 (26.8)
With adjustment	96 (21.7)	95 (21.9)	95 (22.9)	95 (26.4)	95 (26.4)	95 (26.8)
Ŝg exp{± 1.96 ${\sigma }_g^{*}$}	93 (26.9)	98 (37.6)	98 (27.1)	95 (34)	99 (47.2)	98 (31.5)
Distribution	exp(1)	exp(1.2)	exp(1.6)	exp(1)	exp(1.2)	exp(1.6)
Percentile	92 (21.6)	95 (24.6)	95 (26.2)	94 (28.1)	95 (29.8)	94 (27.5)
Basic	90 (21.6)	87 (24.6)	90 (26.2)	91 (28.1)	86 (29.8)	89 (27.5)
With adjustment	91 (21.6)	90 (24.6)	92 (26.2)	92 (28.1)	89 (29.8)	91 (27.5)
arcsin (s1/2)	93 (23.2)	90 (24.7)	92 (25.8)	93 (28.2)	88 (29.6)	92 (28.0)
With adjustment	95 (23.1)	93 (24.8)	94 (25.9)	94 (28.2)	92 (29.7)	94 (28.0)
Ŝg exp{± 1.96 ${\sigma }_g^{*}$}	93 (26.6)	98 (38.9)	96 (29.4)	95 (33.2)	99 (47.0)	96 (31.3)

Sample sizes are n₁ = 40, n₂ = 20 and n₃ = 40 and censoring distribution is Un(0, 4.3). The five bootstrap confidence intervals are the percentile method, and the basic bootstrap method with or without arcsin(s^1/2) transformation and with or without an adjustment for bias overcorrection. Ŝ_g exp{±1.96 ${\sigma }_g^{*}$} is the centred method of Hwang & Peddada (1994). Results are based on 10 000 simulation samples.

7. Example

The data are from prostate cancer patients who received radiation therapy at the University of Michigan Hospital, a portion of the data used in Proust-Lima & Taylor (2009). Five hundred and three patients without planned hormonal therapy are used to estimate the survivor function of time to first recurrence of prostate cancer. For this analysis, recurrence is defined as the first of local recurrence, distant metastasis or initiation of salvage hormone therapy.

It is expected that patients with higher baseline prostate-specific antigen levels have a higher recurrence rate than those with lower baseline prostate-specific antigen values. The Gleason grade is a measure of the aggressiveness of the tumour cells obtained from microscopic inspection of a biopsy prior to the treatment. It is also expected that patients with a lower Gleason grade will have a lower recurrence rate. In this example, we divided the patients into six groups labelled A1, A2, A3, B1, B2 and B3 based on whether or not their baseline prostate-specific antigen is less than 10, and whether their Gleason grade is ⩽6, =7 or ⩾8. Patients with baseline prostate-specific antigen <10 and Gleason ⩽6 are labelled as A1, patients with baseline prostate-specific antigen <10 and Gleason =7 as A2 etc. The natural set of constraints for the survivor functions are A1 ⩾ A2 ⩾ A3, B1 ⩾ B2 ⩾ B3, A1 ⩾ B1, A2 ⩾ B2 and A3 ⩾ B3.

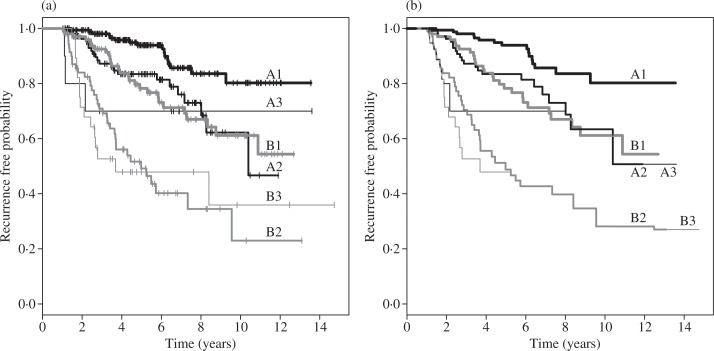
The Kaplan–Meier estimates of each groups are shown in Fig. 4(a). The unrestricted Kaplan–Meier estimates do not satisfy the stochastic ordering constraints. Specifically, between 1 and 2.5 years, the groups A2, B2 and B3 do not satisfy the ordering constraints and after 5 years the orderings of A2 and A3, and B2 and B3 are incorrect.

Fig. 4.

Estimates in the University of Michigan prostate cancer example. The vertical bars in (a) are observed censoring times. For the labels of the lines, A and B indicate, respectively, low and high baseline prostate-specific antigen; and 1, 2 and 3 indicate, respectively, low, medium and high Gleason grade. (a) Kaplan–Meier estimator and (b) pointwise constrained estimator.

The pointwise constrained estimates, shown in Fig. 4(b), satisfy the stochastic ordering constraints at all times. Between 1 and 2.5 years, the survivor functions take a common value in groups A2, B2 and B3 and after 5 years, groups A2 and A3 and groups B2 and B3 have common estimates. At around 12.5 years, there is a jump in the survivor function estimate for groups B2 and B3, even though there are no observed events at that time. This happens because the number of individuals at risk in the stochastically smaller group B3 at time t = 12.5 changes, which results in ĥ^δ(t) < 0, as discussed in § 2.3.

Detailed results of point estimates and corresponding confidence intervals for some selected times are shown in Table 2.

Table 2.

Estimates and confidence intervals (%) of survivor functions for some selected times in the prostate cancer example

	Time (years)	1.5	5	8
A1	Kaplan–Meier estimator	99.4 (97.6, 100)	93.9 (90.0, 97.2)	83.6 (76.4, 91.1)
	Pointwise constrained estimator	99.4 (97.6, 99.9)	93.9 (90.0, 97.2)	83.6 (76.4, 90.2)
A2	Kaplan–Meier estimator	99.1 (96.6, 99.9)	83.4 (75.6, 90.2)	73.0 (63.2, 82.3)
	Pointwise constrained estimator	99.1 (96.5, 99.9)	83.4 (76.6, 89.9)	73.0 (64.0, 83.0)
A3	Kaplan–Meier estimator	80.0 (36.0, 98.0)	70.0 (44.8, 92.7)	70.0 (44.8, 100)
	Pointwise constrained estimator	88.7 (70.9, 94.9)	70.0 (53.2, 91.6)	70.0 (52.6, 93.6)
B1	Kaplan–Meier estimator	98.0 (92.2, 99.7)	78.3 (71.2, 86.1)	67.0 (57.8, 77.8)
	Pointwise constrained estimator	98.0 (95.2, 99.7)	78.3 (71.2, 86.1)	67.0 (57.8, 77.8)
B2	Kaplan–Meier estimator	86.8 (79.6, 93.6)	48.8 (38.9, 62.2)	34.2 (22.9, 52.6)
	Pointwise constrained estimator	88.7 (83.0, 93.9)	48.8 (39.6, 59.9)	39.8 (30.3, 54.0)
B3	Kaplan–Meier estimator	96.4 (86.2, 99.8)	47.9 (33.4, 67.5)	47.9 (33.5, 69.4)
	Pointwise constrained estimator	88.7 (83.5, 93.8)	47.9 (38.4, 69.2)	39.8 (29.9, 54.2)

Nominal 95% bootstrap confidence intervals using arcsin(s^1/2) transformation and controlling bias overcorrection are shown in parentheses.

8. Discussion

The pointwise constrained estimator is a likelihood based pointwise estimator. Unlike the full constrained nonparametric maximum likelihood estimator, the violation of a constraint at one time does not affect the estimates at other times. The pointwise constrained estimator gives a common estimate based on maximizing the likelihood when the constraints are violated and compared with other estimators that use averaging based on initial sample sizes (Rojo, 2004; El Barmi & Mukerjee, 2005), it has better properties when censoring exists.

When there is no censoring, Rojo’s estimator in the two-sample case and El Barmi and Mukerjee’s estimator in the simple ordering case are identical to the pointwise constrained estimator. However, if censoring exists, these estimators can be quite different, especially when the censoring distributions differ significantly between groups. Another feature of El Barmi and Mukerjee’s estimator is the range of times for which the estimator is defined. Specifically, it is defined only until the minimum of the times of the last observations in all groups. Thus, if the last observed time in one group is much earlier than in other groups, then estimates in all other groups are undefined at subsequent times even though there may be a large number of observations at risk. On the other hand, the pointwise constrained estimator for a group is defined up to the last observed time of that group.

The pointwise constrained estimator can have jumps at nonevent times. Thus, the likelihood ratio statistics of the restricted survivor function, first introduced by Thomas & Grunkemeier (1975) and discussed by Li (1995) and Murphy (1995) are not exactly correct, because they assume the jumps can only occur at event times. Thus, the likelihood ratio test and confidence interval based on the likelihood ratio test may need to be revised.

Methods to construct confidence intervals in order restricted problems are not well developed. Bootstrap methods generally work better when the distributions are approximately normal after some transformations. When constraints are present, it is not clear whether there exists any such transformation. We proposed a method to control overcorrection of bias when using the basic bootstrap methods and found improved properties of confidence intervals. Further investigation of this approach on other applications could be useful.

Appendix.

Proof of Theorem 1. Let λ₁ and λ₂ be Lagrange multipliers. The corresponding Lagrangian function is

$$\begin{array}{ll}\mathrm{\Lambda }\hspace{0.17em}(h,\lambda )=\hfill & \sum _{i=1}^m[d_i\hspace{0.17em}\text{log}\{1-\text{exp}\hspace{0.17em}h(X_i)\}+(n_i-d_i)h(X_i)]+N(x)h^{\delta }\hspace{0.17em}(x)\hfill \\ \hfill & +{\lambda }_1\hspace{0.17em}\left\{\sum _{j=1}^{M(x)}h(X_j)+h^{\delta }\hspace{0.17em}(x)-q\right\}-{\lambda }_2{h}^{\delta }\hspace{0.17em}(x).\hfill \end{array}$$

The Karush–Kuhn–Tucker conditions that must be satisfied at the solution ĥ are:

$$-\frac{d_i\hspace{0.17em}\text{exp}\hspace{0.17em}\widehat{h}(X_i)}{1-\text{exp}\hspace{0.17em}\widehat{h}(X_i)}+(n_i-d_i)+{\widehat{\lambda }}_1=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i⩽M(x),$$ (A1)

$$-\frac{d_i\hspace{0.17em}\text{exp}\hspace{0.17em}\widehat{h}(X_i)}{1-\text{exp}\hspace{0.17em}\widehat{h}(X_i)}+(n_i-d_i)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i>M(x),$$ (A2)

$$N(x)+{\widehat{\lambda }}_1-{\widehat{\lambda }}_2=0,$$ (A3)

$$\sum _{j=1}^{M(x)}\widehat{h}(X_j)+{\widehat{h}}^{\delta }(x)-q=0,$$ (A4)

$${\widehat{h}}^{\delta }(x)⩽0,$$ (A5)

$${\widehat{\lambda }}_2{\widehat{h}}^{\delta }(x)=0,$$ (A6)

$${\widehat{\lambda }}_2⩾0.$$ (A7)

From (A1), we have ĥ₁ (X_i) = log{1 − d_i/(n_i + λ̂₁)} for i ⩽ M₁(x). Either λ̂₂ = 0 or ĥ^δ (x) = 0 from (A6). If λ̂₂ = 0, then λ̂₁ = −N(x) from (A3), which is only valid when ${\widehat{h}}^{\delta }\hspace{0.17em}(x)=q-{\sum }_{j=1}^{M(x)}\hspace{0.17em}\text{log}[1-d_i/\{n_i-N(x)\}]⩽0$; otherwise ĥ^δ (x) = 0 and λ̂₁ is the solution of the equation, $q-{\sum }_{j=1}^{M(x)}\hspace{0.17em}\text{log}\{1-d_i/(n_i+\lambda )\}=0$, from (A4), which is only valid when λ̂₁ ⩾ − N(x) from (A3). Since ${\sum }_{j=1}^{M(x)}\hspace{0.17em}\text{log}\{1-d_i/(n_i+k)\}$ is an increasing function in k, we can see that λ̂₁ = max{k̂, −N(x)}, where k̂ is the solution of the equation ${\sum }_{j=1}^{M(x)}\hspace{0.17em}\text{log}\{1-d_i/(n_i+k)\}-q=0$. It follows that λ̂₁ is exactly the same as K (q; x) defined in Theorem 1. Therefore, the unique solution from solving (A2)–(A7) is as given in Equation (4).

Proof of Lemma 1. We consider separately two cases where K (q; x) > −N(x) and K (q; x) = −N(x).

If K (q; x) > −N(x), then ĥ^δ (x) = 0 and ĥ(q; X_i) = log(1 − d_i/n_i) for i > M(x), which does not depend on q. For any i ⩽ M(x),

$$\begin{array}{ll}\frac{d}{d\widehat{h}(q;X_i)}[d_i\text{log}\{1-\text{exp}\hspace{0.17em}\widehat{h}(q;X_i)\}+(n_i-d_i)\widehat{h}(q;X_i)]\hfill & =\frac{-d_i\hspace{0.17em}\text{exp}\{\widehat{h}(q;X_i)\}}{1-\text{exp}\{\widehat{h}(q;X_i)\}}+n_i-d_i\hfill \\ \hfill & =n_i-\frac{d_i}{1-\text{exp}\hspace{0.17em}\widehat{h}(q;X_i)\}}\hfill \\ \hfill & =n_i-\{n_i+K(q;x)\}=-K(q;x).\hfill \end{array}$$

Thus,

$$\begin{array}{ll}\frac{\text{d}}{\text{d}q}p{l}_h(q;x)\hfill & =\frac{\text{d}}{\text{d}q}\hspace{0.17em}\left(\sum _{i=1}^m[d_i\text{log}\{1-\text{exp}\hspace{0.17em}\widehat{h}(q;X_i)\}+(n_i-d_i)\widehat{h}(q;X_i)]+N(x){\widehat{h}}^{\delta }(x)\right)\hfill \\ \hfill & =\sum _{i=1}^{M(x)}-K(q;x)\frac{\text{d}\widehat{h}(q;X_i)}{\text{d}q}=-K(q;x)\frac{\text{d}}{\text{d}q}\sum _{i=1}^{M(x)}\widehat{h}(q;X_i)=-K(q;x).\hfill \end{array}$$

If K (q; x) = −N(x), then ĥ(q; X_i) = log[1 − d_i/{n_i − N(x)}] for i ⩾ M(x) and ĥ(q; X_i) = log(1 − d_i/n_i) for i > M(x) are not functions of q. It follows that

$$\begin{array}{ll}\frac{\text{d}}{\text{d}q}\ell (q;x)\hfill & =\frac{\text{d}}{\text{d}q}\hspace{0.17em}\left(\sum _{i=1}^m[d_i\text{log}\{1-\text{exp}\hspace{0.17em}\widehat{h}(q;X_i)\}+(n_i-d_i)\widehat{h}(q;X_i)]+N(x){\widehat{h}}^{\delta }(q;x)\right)\hfill \\ \hfill & =N(x)=-K(q;x).\hfill \end{array}$$

Supplementary material

Supplementary material available at Biometrika online includes the generalized pool-adjacent-violators algorithm for the simple ordering case in § 2.5, proofs of Theorems 2–4, and an algorithm to calculate a_g described in § 5.2.