Corrected-loss estimation for quantile regression with covariate measurement errors

Abstract

We study estimation in quantile regression when covariates are measured with errors. Existing methods require stringent assumptions, such as spherically symmetric joint distribution of the regression and measurement error variables, or linearity of all quantile functions, which restrict model flexibility and complicate computation. In this paper, we develop a new estimation approach based on corrected scores to account for a class of covariate measurement errors in quantile regression. The proposed method is simple to implement. Its validity requires only linearity of the particular quantile function of interest, and it requires no parametric assumptions on the regression error distributions. Finite-sample results demonstrate that the proposed estimators are more efficient than the existing methods in various models considered.

1. Introduction

In problems relating to econometrics, epidemiology and finance, the covariates of interest are often measured with errors. The measurement error, if ignored, often leads to bias in estimating the mean and quantile functions (Carroll et al., 2006; Wei & Carroll, 2009).

Less attention has been paid to quantile regression than to mean regression with a covariate measurement error. There are two main difficulties for correcting the bias in quantile regression caused by measurement error. First, a parametric regression-error likelihood is usually not specified in quantile regression. Second, unlike the mean, quantiles do not enjoy the additivity property, that is, the quantile of the sum of two random variables is not necessarily the sum of the two marginal quantiles. He & Liang (2000) proposed an estimation procedure that minimizes the quantile loss function of orthogonal residuals. This method assumes that the random errors in the response variable y and the measurement errors in the covariate x are independent and follow the same symmetric distribution. Assuming the existence of an instrumental variable, Hu & Schennach (2008) and Schennach (2008) proposed methods that require nonparametric modelling of densities such as that of y given x, and that of x given the instrumental variable. Wei & Carroll (2009) developed an iterative estimation procedure that requires estimating the conditional density of y given x via modelling the entire quantile process, and this complicates the computation. In addition, Wei & Carroll’s method relies on a strong global assumption, that is, estimation of the τth conditional quantile of y given x depends on the assumption that all the conditional quantiles below the τth are linear. In this paper, we propose a simple and consistent estimation procedure assuming a class of measurement error distributions. The proposed method avoids the symmetry assumption used in He & Liang (2000), and requires estimation only at the quantile of interest.

Whatever the approach taken, one must resolve the identifiability issue in measurement error models. In the proposed method, it is resolved by assuming a parametric form for the measurement error distribution whose parameters such as variance can be estimated. However, we leave the quantile regression error distribution completely unspecified.

We consider the linear quantile regression model

$$Q_{\tau }(y_j|x_j)=x_j^T{\beta }_0(\tau )\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(j=1,\dots ,n),$$ (1)

where Q_τ(y_j | x_j) denotes the τth conditional quantile of the response variable y_j given by the covariate x_j, β₀(τ) ∈ ℝ^p is the coefficient vector and τ ∈ (0, 1) is the quantile level of interest. Our main interest is in estimating β₀(τ) when x_j is measured with an error. We assume an additive measurement error model, w_j = x_j + u_j, relating the surrogate w_j and x_j, where the u_j ∈ ℝ^p are the independent and identically distributed measurement errors. Throughout, we assume that u_j is independent of x_j and y_j, and we drop τ in β₀(τ) for notational simplicity.

2. Proposed methods

2.1. Corrected-loss estimator

When x_j is measured without an error, β₀ can be estimated consistently by

$${\widehat{\beta }}_x=\underset{\beta \in {ℝ}^p}{\text{argmin}}\sum _{j=1}^n\rho (y_j,x_j,\beta ),$$ (2)

where ρ(y, x, β) = ρ_τ(y – x^Tβ), ρ_τ(∊) = ∊{τ – I(∊ < 0)} is the quantile loss function and I(·) is the indicator function. The estimator β̂_x also satisfies

$$n^{-1}\sum _{j=1}^n\psi (y_j,x_j,{\widehat{\beta }}_x)=o_p(1),$$ (3)

where ψ(y, x, β) = x{I(y – x^Tβ < 0) – τ}. Under model (1), pr(y < x^Tβ₀ | x) = τ. Therefore, E{ψ(y, x, β₀)} = 0, and ψ(y, x, β) is an unbiased estimating function for β₀.

When x_j is subject to error and we observe only a surrogate w_j, naively replacing x_j with w_j in (2) or (3) usually leads to inconsistent estimators, because E{ψ(y, w, β₀)} = 0 may not hold. To account for the measurement error, we construct corrected score functions of w that are unbiased for β₀ (Stefanski, 1989; Nakamura, 1990). However, in practice, it is challenging to determine the corrected scores, especially in quantile regression, as the quantile loss function ρ_τ(∊) is not differentiable at ∊ = 0. To overcome this difficulty, we approximate ρ_τ(∊) by a smooth function ρ(∊, h) depending on a positive smoothing parameter h.

Let E^* denote the expectation with respect to w given y and x. Unless otherwise specified, we use E to denote the global expectation. We aim to find a corrected loss function ρ^*(y, w, β, h) such that E^*{ρ^*(y, w, β, h)} = ρ(y, x, β, h) → ρ(y, x, β) pointwise in (y, x, β) as h → 0. Under some regularity conditions, β₀ is the unique minimizer of E{ρ(y, x, β)}. Therefore, minimizing the sample analog of E{ρ^*(y, w, β, h)} leads to a consistent estimator of β₀, if h goes to zero at a suitable rate. Motivated by this idea, we define the corrected-loss quantile estimator as

$${\widehat{\beta }}_w=\underset{\beta \in {ℝ}^p}{\text{argmin}}\sum _{j=1}^n{\rho }^{*}(y_j,w_j,\beta ,h).$$

In the next two subsections, we develop corrected-loss estimators for two measurement error models, normal and Laplace, because these two measurement error distributions provide reasonable error models in many applications. Our simulation study in § 3 suggests that the proposed estimators are robust against misspecification of the measurement error distribution. The extension to a wider class of distribution families is discussed in § 5.

2.2. Normal measurement error

Assume ${\left\{y_j,w_j\right\}}_{j=1}^n$ is a random sample with w_j = x_j + u_j, where u_j ∼ N(0, Σ) is a p-dimensional normal random vector that is independent of y_j and x_j; see Fuller (1987) and Carroll et al. (2006) for reviews on normal measurement errors in mean regression models.

We first review a useful result for normal random variables. Suppose that ∊ ∼ N(μ, σ²) and that g(·) is a sufficiently smooth function. Let u ∼ N(0, 1) be independent of ∊. Stefanski & Cook (1995) showed that E[E{g(∊ + iσu) | ∊}] = g(μ), where i = √–1, the outer expectation is with respect to ∊ and the inner one is with respect to u given ∊.

Motivated by the above result, we propose to approximate the quantile loss function ρ_τ (∊) by an infinitely smooth function

$${\rho }_N(∊,h)=∊\left\{\tau -1/2+G_N(∊/h)\right\},$$

where $G_N(x)={\pi }^{-1}\text{Si}(x)={\pi }^{-1}\hspace{0.17em}{\int }_0^x\hspace{0.17em}\text{sin}(t)/t\hspace{0.17em}\text{d}t$ is the sine integral function, which satisfies $\underset{x\to \infty }{\text{lim}}\hspace{0.17em}\text{Si}(x)=\pi /2$ and $\underset{x\to \infty }{\text{lim}}\hspace{0.17em}\text{Si}(x)=-\pi /2$. By such an approximation, we have the following theorem.

Theorem 1. Suppose that ∊ ∼ N(μ, σ²). Define A(∊, σ², h) = E{ρ_N(∊+iσu, h) | ∊}, where u ∼ N(0, 1) is independent of ∊. Then

1. A(∊, σ², h) = ∊(τ – 1/2) + π⁻¹ ${\int }_0^{1/h}$ {y⁻¹ ∊ sin(y∊) – σ² cos(y∊)} exp(y²σ² /2) dy;

2. E{A(∊, σ², h)} = ρ_N (μ, h).

Since (y – w^Tβ) | (y, x) ∼ N(y – x^Tβ, β^TΣβ), we define the corrected quantile loss function as

$${\rho }_N^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h)=A(y-w^T\beta ,\hspace{0.17em}{\beta }^T\mathrm{\Sigma }\beta ,\hspace{0.17em}h).$$

By Theorem 1, E^*{ ${\rho }_N^{*}$(y, w, β, h)} = ρ_N(y – x^Tβ, h) ≐ ρ_N(y, x, β, h) → ρ(y, x, β) pointwise in (y, x, β) as h → 0. Let ℬ denote a compact subset of ℝ^p that contains β₀. The corrected quantile estimator is then defined as

$${\widehat{\beta }}_N=\underset{\beta \in ℬ}{\text{argmin}}\sum _{j=1}^n{\rho }_N^{*}(y_j,\hspace{0.17em}{w}_j,\hspace{0.17em}\beta ,\hspace{0.17em}h).$$

In applications, often only one or two covariates are measured with an error. Our proposed method accommodates such scenarios as special cases. Throughout the paper, we let the first component of x be 1, corresponding to the intercept, so there is no measurement error in the first component. For example, if we assume that only the pth component of x is subject to measurement error u ∼ N(0, σ²), then we have

$$\mathrm{\Sigma }=\left(\begin{array}{cc}{0}_{q\times q}& 0_q\\ 0_q^T& {\sigma }^2\end{array}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(q=p-1),$$

where 0_q and 0_q×q denote a q-dimensional vector and a q × q matrix with zero elements, respectively. Consequently, the corrected quantile loss function becomes ${\rho }_N^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h)=A(y-w^T\beta ,\hspace{0.17em}{\beta }_p^2{\sigma }^2,\hspace{0.17em}\hspace{0.17em}h)$, where β_p is the pth element of β. The same parameterization applies to the correction for a Laplace measurement error described in § 2.3.

2.3. Laplace measurement error

We consider the situation where the measurement error follows a multivariate Laplace distribution. The Laplace distribution is often used for modelling data with tails heavier than normal. We refer to Stefanski & Carroll (1990), Hong & Tamer (2003), Richardson & Hollinger (2005), Purdom & Holmes (2005), Visscher (2006) and McKenzie et al. (2008) for discussions of Laplace measurement errors. We first introduce a multivariate Laplace distribution adopted from Kotz et al. (2001, Ch. 6), and give a lemma stating some related properties.

Definition 1. A random vector X ∈ ℝ^p has a multivariate asymmetric Laplace distribution if its characteristic function is Ψ(t) = (1 + t^TΣt/2 − iμ^Tt)⁻¹ for t ∈ ℝ^p, where μ ∈ ℝ^p and Σ is a p × p nonnegative definite symmetric matrix. In the following, we write X ∼ AL_p(μ, Σ). If μ = 0, then AL_p(0, Σ) corresponds to a symmetric multivariate Laplace distribution. In addition, AL₁(0, σ²) is the classical univariate Laplace (1774) distribution L(μ, σ²) if and only if μ = 0.

Lemma 1. Let X ∼ AL_p(μ, Σ). Then

1. the mean and covariance matrix of X are E(X) = μ, and cov(X) = Σ + μμ^T;

2. if μ = 0, then for any constant a and vector b ∈ ℝ^p, the random variable a + b^TX ∼ L(a, σ²), where σ² = b^TΣb, and L(a, σ²) is the standard univariate Laplace distribution with mean a and variance σ².

Suppose that the measured covariates are w_j = x_j + u_j, where u_j ∼ AL_p(0, Σ), independent of x_j and y_j . Our corrected loss function is based on the following theorem.

Theorem 2. Suppose that the random variable ∊ follows the univariate Laplace distribution L(μ, σ²). If g(∊) is a twice-differentiable function of ∊, then

$$E\{g(∊)-({\sigma }^2/2)g^{(2)}(∊)\}=g(\mu ),$$

where g⁽²⁾(∊) is the second derivative of g(∊).

Let K (·) denote a kernel density function and define G_L (x) = ∫_u<x K (u) du. In our numerical studies, we choose K (·) as the probability density function of N(0, 1). We consider the smoothed quantile loss function ρ_L (∊, h) = ∊{τ − 1 + G_L (∊ / h)}. For Laplace measurement error, by Lemma 1, (y − w^Tβ) | (y, x) ∼ L(y − x^T β, σ²), where σ² = β^TΣβ. Let ∊ = y − w^Tβ. Define the corrected quantile loss function as

$$\begin{array}{ll}{\rho }_L^{*}(y,w,\beta ,h)\hfill & ={\rho }_L(∊,h)-\frac{{\sigma }^2}{2}\frac{{\partial }^2{\rho }_L(∊,h)}{\partial {∊}^2}\hfill \\ \hfill & =∊(\tau -1)+∊G_L\left(\frac{∊}{h}\right)-\frac{{\sigma }^2}{2}\left\{\frac{2}{h}K\left(\frac{∊}{h}\right)+\frac{∊}{h^2}{K}^{\prime }\left(\frac{∊}{h}\right)\right\}.\hfill \end{array}$$ (4)

By Theorem 2, $E^{*}\{{\rho }_L^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h)\}={\rho }_L(y-x^T\beta ,\hspace{0.17em}h)\doteq {\rho }_L(y,\hspace{0.17em}x,\hspace{0.17em}\beta ,\hspace{0.17em}h)\to \rho (y,\hspace{0.17em}x,\hspace{0.17em}\beta )$ pointwise in (y, x, β) as h → 0.

The corrected quantile estimator is therefore defined as

$${\widehat{\beta }}_L=\underset{\beta \in ℬ}{\text{argmin}}\sum _{j=1}^n{\rho }_L^{*}(y_j,w_j,\beta ,h).$$

2.4. Large sample properties

To establish the asymptotic results in this paper, we make the following assumptions.

Assumption 1. The samples {(y_j, x_j) : j = 1, . . . , n} are independent and identically distributed.

Assumption 2. The vector β₀ is an interior point of the parameter space ℬ, a compact subset of ℝ^p.

Assumption 3. The expectation E(‖x_j‖²) is bounded, and $E(x_j{x}_j^{\text{T}})$ is a positive definite p × p matrix.

Assumption 4. Let $e_j=y_j-x_j^{\text{T}}\beta (\tau )$. The conditional density of e_j, f_j (e_j | x_j), is bounded from infinity, and it is bounded away from zero and has a bounded first derivative in the neighbourhood of zero.

Assumption 5. For each j, $E(e_j^2|x_j)$ is bounded as a function of τ.

Assumption 6. The kernel function K (u) is a bounded probability density function having finite fourth moment and is symmetric about the origin. In addition, K (u) is twice-differentiable, and its second derivative K⁽²⁾(u) is bounded and Lipschitz continuous on (− ∞, ∞).

Theorem 3 states the strong consistency of the proposed estimators for normal and Laplace measurement errors, respectively.

Theorem 3. (i) Suppose that the measurement error u_j ∼ N(0, Σ), that Assumptions 1–5 hold, and that h → 0 and h = c(log n)^−δ, where δ < 1/2 and c is some positive constant. Then β̂_N → β₀ almost surely as n → ∞. (ii) If the measurement error u_j ∼ AL_p(0, Σ) and Assumptions 1–4 and 6 hold, h → 0, and (nh)^−1/2 log n → 0, then β̂_L → β₀ almost surely as n → ∞.

Assumption 2 ensures the existence of β̂_N and β̂_L, and the uniformity of the convergence of the minimand over ℬ, as required to prove the consistency. Assumptions 3 and 4 ensure that β₀ is the unique minimizer of E{ρ(y, x, β)}. With normal measurement error, because the corrected quantile loss function ${\rho }_N^{*}$ is complicated, Assumption 5 is used in the Appendix to bound the first-order expansion of ${\rho }_N^{*}$ uniformly over e_j. Assumption 5 is not needed for the Laplace measurement error. Assumption 6 specifies the conditions on the kernel function used in β̂_L for the Laplace measurement error. In Theorem 3, the rate of h differs for normal and Laplace measurement errors. This difference is related to the smoothness of the measurement error distribution. It is well known in the deconvolution literature that the rates of convergence are lower for smoother error distributions (Carroll & Hall, 1988; Fan, 1992).

We next establish asymptotic normality of the proposed estimators. For notational simplicity, let β̂ denote the proposed corrected estimator, and ρ^*(y, w, β, h) denote the corrected quantile loss function, for either normal or Laplace measurement errors. We make the following additional assumption.

Assumption 7. Let ${\psi }_1^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h)=\partial {\rho }^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h)/\partial \beta$ and ${\psi }_2^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h)={\partial }^2{\rho }^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h)/\partial \beta \partial {\beta }^{\text{T}}$. As n → ∞ and h → 0, there exist positive definite matrices D and A such that $E\left\{{\psi }_1^{*}{(y,\hspace{0.17em}w,\hspace{0.17em}{\beta }_0,\hspace{0.17em}h)}^{\otimes 2}\right\}\to D$ and $E\{{\psi }_2^{*}(y,\hspace{0.17em}w,\hspace{0.17em}{\beta }_0,\hspace{0.17em}h)\}\to A$.

Theorem 4. Suppose that Assumptions 1–7 hold, and β̂ is the consistent estimator of β₀, either β̂_N or β̂_L defined in § § 2.3 and 2.4. Then n^1/2(β̂ − β₀) → N(0, A⁻¹D A⁻¹) in distribution, as n → ∞.

2.5. Estimated measurement error covariance matrix

Thus far we have described our method under the assumption that the covariance matrix Σ is known. Applications where Σ is known exist, but are rare. The more common scenario is one in which an unbiased estimate, Σ̂, is available. Analysis then proceeds using Σ̂ as a plug-in estimator of Σ. A common design where this strategy is used is when each w_j is itself the average of m replicate measurements w_j,k (k = 1, . . . , m), each having variance Γ = mΣ. A consistent and unbiased estimator of Σ is Σ̂ = Γ̂/m, where

$$\widehat{\mathrm{\Gamma }}={\{n(m-1)\}}^{-1}\sum _{j=1}^n\sum _{k=1}^m(w_{j,k}-w_j){(w_{j,k}-w_j)}^{\text{T}}$$

is based on n(m − 1) degrees of freedom; see Liang et al. (2007). The application data in § 4 have this structure with m = 6 in which case Σ̂ is estimated on 5n degrees of freedom. In the Monte Carlo study in § 3, we simulate this situation with m = 2.

Let σ be a q-dimensional vector consisting of the elements of the upper triangle of Σ including the diagonals, where q = p(p + 1)/2. To reflect the dependence on σ, we let ρ^*(y, w, β, h, σ) denote the corrected quantile loss function, for either normal or Laplace measurement errors. We next establish the asymptotic properties of the corrected estimator,

$$\widehat{\beta }=\underset{\beta \in {ℝ}^p}{\text{argmin}}\sum _{j=1}^n{\rho }^{*}(y_j,w_j,\beta ,h,\widehat{\sigma }),$$ (5)

where $w_j=m^{-1}{\sum }_{k=1}^m{w}_{j,k}$. Let S_j be a q-vector consisting of the elements of the upper triangle of the matrix ${\sum }_{k=1}^m(w_{j,k}-w_j){(w_{j,k}-w_j)}^{\text{T}}$ including the diagonals. Define ${\psi }_{1\beta }^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h,\hspace{0.17em}\sigma )=\partial {\rho }^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h,\hspace{0.17em}\sigma )/\partial \beta$, ${\psi }_{2\beta }^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h,\hspace{0.17em}\sigma )=\partial {\psi }_{1\beta }^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h,\hspace{0.17em}\sigma )/\partial \beta$ and ${\psi }_{2\alpha }^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h,\hspace{0.17em}\sigma )=\partial {\psi }_{1\beta }^{*}(y,\hspace{0.17em}w,\hspace{0.17em}\beta ,\hspace{0.17em}h,\hspace{0.17em}\sigma )/\partial \sigma$. We replace Assumption 7 with the following Assumption 7′.

Assumption 7′. As n → ∞ and h → 0, $E\left\{{\psi }_{1\beta }^{*}{(y,\hspace{0.17em}w,\hspace{0.17em}{\beta }_0,\hspace{0.17em}h,\hspace{0.17em}\sigma )}^{\otimes 2}\right\}\to D$, $E\{{\psi }_{2\beta }^{*}(y,\hspace{0.17em}w,\hspace{0.17em}{\beta }_0,\hspace{0.17em}h,\hspace{0.17em}\sigma )\}\to A$, $E\{{\psi }_{2\sigma }^{*}(y,\hspace{0.17em}w,\hspace{0.17em}{\beta }_0,\hspace{0.17em}h,\hspace{0.17em}\sigma )\}\to ℬ$, $E[{\psi }_{1\beta }^{*}(y_j,\hspace{0.17em}{w}_j,\hspace{0.17em}{\beta }_0,\hspace{0.17em}h,\hspace{0.17em}\sigma ){\{S_j-m(m-1)\sigma \}}^{\text{T}}]\to C$, where A and D are p × p-positive definite matrices, and B and C are p × q matrices.

Theorem 5. Under the conditions of Theorem 3 and Assumption 7′, the estimator β̂ given in (5) is consistent and asymptotically normal with covariance matrix A⁻¹D^* A⁻¹, where D^* = D + {m(m − 1)}⁻²B E[{S_j − m(m − 1)σ}^⊗2]B^T + {m(m − 1)}⁻¹(C B^T + BC^T).

Remark 1. Compared with Theorem 4, the covariance of β̂ has three additional terms due to the variation in the estimated measurement error variance. For normal measurement error, (y_j, w_j) are independent of Γ̂, so the last two terms of D^* reduce to zero.

2.6. Some computational issues

Motivated by the method of Delaigle & Hall (2008), we propose a modified simulation-extrapolation-type strategy to choose the smoothing parameter h. The simulation and extrapolation method was introduced by Stefanski & Cook (1995) for estimation in a parametric setting; see also Stefanski (2000), Luo et al. (2006) among others. Delaigle & Hall (2008) showed how this strategy can be adapted to choose the smoothing parameter in nonparametric modelling.

Let β̂(h) be the corrected-loss estimator associated with smoothing parameter h. Define M(h) = E[{β̂(h) − β₀}^TΩ⁻¹{β̂(h) − β₀}] as the mean squared error of β̂(h), where Ω = cov{β̂(h)}. Ideally, we would like to find the optimal smoothing parameter h₀ = argmin M(h). However, since M(h) depends on the unknown x_j, the minimization of M(h) cannot be executed in practice. Instead, we develop two versions of M(h) by simulating higher levels of measurement errors. Let $u_{b1}^{*},\hspace{0.17em}\dots ,\hspace{0.17em}{u}_{bn}^{*}$ and $u_{b1}^{**},\hspace{0.17em}\dots ,\hspace{0.17em}{u}_{bn}^{**}(b=1,\hspace{0.17em}\dots ,\hspace{0.17em}{N}_b)$ denote independent and identically distributed random vectors from N(0, Σ) for the normal measurement error or from AL_p(0, Σ) for Laplace measurement error depending on the error model assumed. Let $w_{bj}^{*}=w_j+u_{bj}^{*}$, $w_{bj}^{**}=w_{bj}^{*}+u_{bj}^{**}$, ${\beta }_b^{*}(h)$ and ${\beta }_b^{**}(h)$ as the corrected-loss estimators based on samples (y_j, $w_{bj}^{*}$) and (y_j, $w_{bj}^{**}$), respectively. Define

$$\begin{array}{l}{M}_1(h)=N_b^{-1}\sum _{b=1}^{N_b}{\{{\beta }_b^{*}(h)-\widehat{\beta }(h)\}}^{\text{T}}{(S^{*})}^{-1}\{{\beta }_b^{*}(h)-\widehat{\beta }(h)\},\\ M_2(h)=N_b^{-1}\sum _{b=1}^{N_b}{\{{\beta }_b^{**}(h)-{\beta }_b^{*}(h)\}}^{\text{T}}{(S^{**})}^{-1}\{{\beta }_b^{**}(h)-{\beta }_b^{*}(h)\},\end{array}$$

where S^* and S^** are the sample covariance matrices of $\{{\beta }_b^{*}(h)-\widehat{\beta }(h):b=1,\hspace{0.17em}\dots ,N_b\}$ and $\{{\beta }_b^{**}(h)-{\beta }_b^{*}(h):b=1,\hspace{0.17em}\dots ,\hspace{0.17em}{N}_b\}$, respectively. Let ĥ₁ = argmin_h M₁(h) and ĥ₂ = argmin_h M₂(h). Since $w_{bj}^{**}$ measures $w_{bj}^{*}$ in the same way that $w_{bj}^{*}$ measures w_j, it is reasonable to expect that the relationship between ĥ₂ and ĥ₁ is similar to that between ĥ₁ and h₀. Therefore, back extrapolation can be used to approximate h₀. In our implementation, we use the linear extrapolation from the pair (log ĥ₁, log ĥ₂) and define the second-order approximation to h₀ as $\widehat{h}={\widehat{h}}_1^2/{\widehat{h}}_2$.

For corrected-loss approaches, one computational complication is that, in finite samples, the corrected objective function may not be globally convex in β; see also Stefanski (1989), Stefanski & Carroll (1985, 1987) and Nakamura (1990) for similar observations. If x_j is measured with a Laplace error, then $n^{-1}{\mathrm{\sum }}_j{\rho }_L^{*}(y_j-w_j^{\text{T}}\beta )\to -\infty$ or +∞ when σ² = β^TΓβ → ∞, depending on the sign of the last term in brackets in (4). In such a case, the corrected objective function has no global minimum. However, it is locally convex around a local minimizer β̂ that is the desired corrected-loss estimate. In our work, when solving the minimization problem for β̂, we adopted the common strategy of starting from the naive estimator obtained by regressing y_j on w_j, and then searched using the R (R Development Core Team, 2012) function optim with default options. This algorithm worked well in numerical studies.

3. Simulation study

We conduct a simulation study to investigate the performance of the proposed corrected-loss approaches. The data were generated from the model

$$y_j=1+x_j+(1+\eta x_j)e_j\hspace{0.17em}\hspace{0.17em}(j=1,\dots ,200),$$

where $e_j\sim N(0,{\sigma }_e^2)$. Under the above model, the τth conditional quantile of y given x is β₀₁(τ) + β₀₂(τ)x with β₀₁(τ) = 1 + σ_eΘ⁻¹(τ) and β₀₂(τ) = 1 + ησ_eΘ⁻¹(τ), and Θ(·) is the cumulative distribution function of N(0, 1). We further assume that the x _j are subject to measurement error following the model

$$w_j=x_j+u_j,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{x}_j\sim U(5,5+{12}^{1/2}).$$

We consider four different cases. The measurement errors u_j are generated from $N(0,\hspace{0.17em}{\sigma }_u^2)$ in Cases 1–2, from $L(0,\hspace{0.17em}{\sigma }_u^2)$ in Case 3, and from the normalized ${\chi }_3^2$ with mean zero and variance ${\sigma }_u^2$ in Case 4. We set η = 0 in Case 1, corresponding to a homoscedastic model, and η = 0.2 in Cases 2–4, corresponding to heteroscedastic models. We give e_j and u_j standard deviations σ_e = σ_u = 0.5, so the assumption required by He & Liang’s method is satisfied in Case 1. In Cases 2–4 with heteroscedasticity, the variances of the regression errors depends on x_j and thus are on different scales with the measurement error.

For each case, 100 simulations are performed. Focusing on τ = 0.5 and τ = 0.75, we compare five estimators, including the naive estimator obtained from regressing y_j on w_j, He & Liang’s estimator, the proposed corrected-loss estimator for normal measurement error, the proposed corrected-loss estimator for Laplace measurement error and Wei & Carroll’s estimator obtained using the R program developed by Wei and Carroll with 20 iterations.

To make a fair comparison, in the implementation of He & Liang’s method, we first transform y_i to $y_i^{*}=\lambda y$ with λ = [E{(1 + ηx_j)²}]^1/2σ_e/σ_u to match the marginal variance of regression error with the measurement error variance. The resulting coefficient estimates are then transformed back to the original scale. For the proposed corrected-loss estimators and Wei & Carroll’s approach, we generated an independent estimate ${\widehat{\sigma }}_u^2$ of ${\sigma }_u^2$ based on n degrees of freedom as explained in § 2.5 for each dataset. This simulates the situation in which each w_j is the average of two replicate measurements $w_{j,k}\sim N(x_j,\hspace{0.17em}{\gamma }_u^2)$ or $L(x_j,\hspace{0.17em}{\gamma }_u^2)\hspace{0.17em}(k=1,2)$ with ${\gamma }_u^2=2{\sigma }_u^2$.

In the implementation of the two proposed methods, we choose the smoothing parameter h following the simulation and extrapolation procedure in § 2.6 with N_b = 20. In Case 1, the mean ĥ for the corrected-loss estimators for normal and Laplace errors are 2.82 and 2.29 at τ = 0.5, and 1.04 and 1.09 at τ = 0.75, respectively.

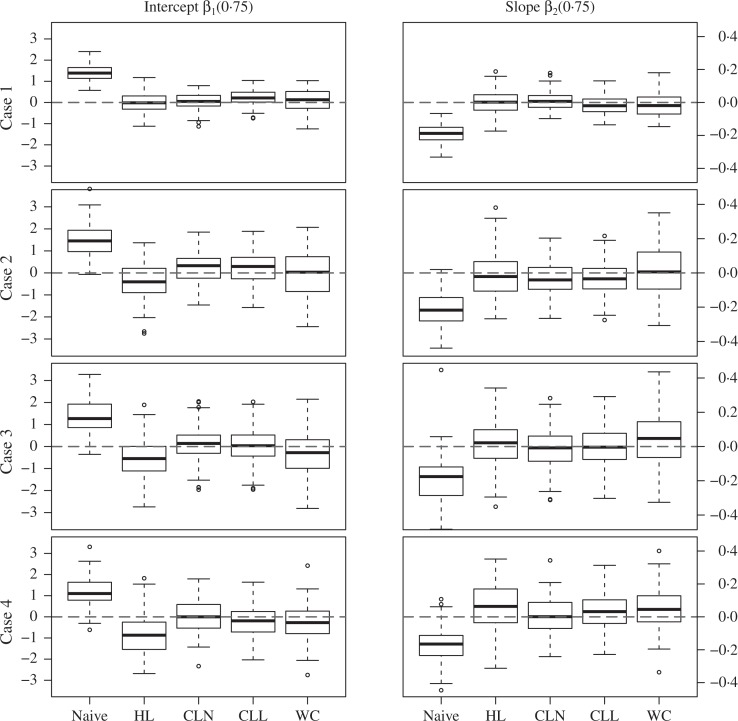
Figure 1 presents boxplots of β̂_k(τ) − β_0k(τ) (k = 1, 2) at τ = 0.75 from the five approaches. We omit the boxplots at τ = 0.5 since the main observations are similar to those at τ = 0.75. As expected, the naive estimator is seriously biased under all scenarios. He & Liang’s estimator performs well in Case 1 when e_j and u_j have the same distribution, but has considerable bias in Cases 2–4 with heteroscedastic regression errors for estimation at τ = 0.75. The two proposed estimators and Wei & Carroll’s estimator successfully correct the bias for both homoscedastic and heteroscedastic models. Even though the proposed methods require parametric assumptions on the measurement error distribution, they are quite robust against model misspecification. The two methods perform very well not only in Cases 1–3 when the normal error assumption is used for the Laplace measurement error and vice versa, but also in Case 4 when the measurement error distribution is substantially right skewed.

Fig. 1.

Boxplots of β̂_k (τ) − β_0k (τ), k = 1, 2 for different methods in Cases 1–4 at τ = 0.75. Naive, the naive method by regressing y_j on w_j; HL, He & Liang’s method; CLN, corrected-loss estimator for normal measurement error; CLL, corrected-loss estimator for Laplace measurement error; WC, Wei & Carroll’s method.

For detailed comparison, Table 1 summarizes the mean squared errors of the different estimators. The two proposed corrected-loss estimators are more efficient than Wei & Carroll’s estimator in all cases. In addition, since Wei & Carroll’s estimator requires estimation of the whole quantile process simultaneously, it is computationally much more expensive than the proposed estimators when the focus is on one or a few quantile levels. The normal corrected-loss estimator is slower than the Laplace corrected-loss estimator, as the corrected loss function ${\rho }_N^{*}(·)$ involves an integral that has no closed form and thus requires numerical integration. For one simulated dataset in Case 2 with n = 200, using R version 2.8.1 on a 3 GHz Dell computer, estimation at the median required 9.7 seconds for the Laplace corrected-loss estimator, 496 seconds for the normal corrected-loss estimator, and it took 1020 seconds for Wei & Carroll’s estimator to obtain estimates at 39 quantile levels. The number of quantile levels required by Wei & Carroll’s estimator grows with the sample size n, and thus the computation is even more challenging for larger datasets.

Table 1.

Mean squared errors of different estimators of the intercept β₁(τ) and slope β₂(τ) parameters. The values in the parentheses are the Monte Carlo standard deviations

	100 × MSE{β̂1(τ)}					100 × MSE{β̂2(τ)}
	Naive	HL	CLN	CLL	WC	Naive	HL	CLN	CLL	WC
Case 1
τ = 0.5	179 (8)	20 (4)	15 (2)	15 (2)	18 (3)	4.0 (0.2)	0.4 (0.1)	0.3 (0.1)	0.3 (0.0)	0.4 (0.1)
τ = 0.75	201 (10)	23 (3)	16 (2)	19 (2)	28 (4)	3.8 (0.2)	0.5 (0.1)	0.3 (0.1)	0.3 (0.0)	0.6 (0.1)
Case 2
τ = 0.5	192 (16)	64 (9)	47 (6)	46 (6)	67 (9)	4.4 (0.4)	1.5 (0.2)	1.1 (0.1)	1.1 (0.1)	1.6 (0.2)
τ = 0.75	275 (24)	78 (12)	58 (7)	56 (7)	105 (12)	5.8 (0.5)	1.5 (0.2)	1.1 (0.1)	1.2 (0.1)	2.3 (0.3)
Case 3
τ = 0.5	192 (19)	76 (11)	74 (12)	65 (10)	104 (19)	4.3 (0.4)	1.8 (0.3)	1.7 (0.3)	1.5 (0.2)	2.4 (0.5)
τ = 0.75	250 (24)	101 (14)	63 (10)	63 (9)	132 (21)	5.2 (0.5)	1.7 (0.3)	1.3 (0.2)	1.3 (0.2)	2.9 (0.5)
Case 4
τ = 0.5	205 (19)	69 (10)	56 (7)	53 (8)	87 (14)	4.6 (0.4)	1.6 (0.2)	1.3 (0.2)	1.2 (0.2)	1.9 (0.3)
τ = 0.75	194 (19)	157 (17)	59 (8)	58 (8)	75 (13)	4.0 (0.4)	2.5 (0.3)	1.2 (0.2)	1.2 (0.2)	1.8 (0.3)

Naive, the naive method by regressing y on w; HL, He & Liang’s method; CLN, corrected-loss estimator for normal measurement error; CLL, corrected-loss estimator for Laplace measurement error; WC, Wei & Carroll’s method.

In quantile regression, it is challenging to estimate the asymptotic covariance of the quantile coefficients directly, as the covariance matrix involves unknown density functions that are difficult to estimate in finite samples. For practical implementation, we adopt a simple bootstrap approach through resampling (y_j , w_j) with replacement. To accommodate the variation in the estimation of σ_u, for each bootstrap, we obtain the proposed estimators by using the estimated σ_u calculated with the bootstrap sample of the internal replicates w_j,k. Bootstrap confidence intervals can be constructed by using the bootstrap standard error and the asymptotic normality of the proposed estimators. In each simulation run, 200 bootstrap samples are used to obtain the confidence intervals. Table 2 summarizes the coverage probabilities of 95% confidence intervals from the two proposed estimators. The bootstrap approach performs reasonably well. The confidence intervals of the proposed methods have empirical coverage probabilities close to the nominal level 95% even in cases where the parametric measurement error distribution is misspecified.

Table 2.

Coverage probabilities, %, of bootstrap confidence intervals with a nominal level of 95%

	β1(0.5)		β2(0.5)		β1(0.75)		β2(0.75)
	CLN	CLL	CLN	CLL	CLN	CLL	CLN	CLL
Case 1	97	95	97	95	96	92	96	92
Case 2	95	96	95	96	91	94	91	94
Case 3	91	94	91	94	91	92	91	92
Case 4	98	95	98	95	92	92	92	92

CLN, the corrected-loss estimator for normal measurement error; CLL, the corrected-loss estimator for Laplace measurement error.

4. Application to a dietary data

For illustration, we analyse a dietary dataset from the Women’s Interview Survey of Health. These data are from 271 subjects, each completing a food frequency questionnaire and six 24-hour food recalls on randomly selected days. The food frequency questionnaire is a commonly used dietary assessment instrument in epidemiology studies; see Carroll et al. (1997) or Liang & Wang (2005), among others. We focus on studying the impacts of long-term usual intake, body mass index and age, on the food frequency questionnaire intake, measured as percent calories from fat. As the long-term intake cannot be observed due to measurement errors and other sources of variability, the 24-hour recalls were used to obtain error-prone measurements of intake.

We consider the following linear quantile regression and measurement error models:

$$\begin{array}{cc}{Q}_{\tau }(y_j|x_j,z_{j1},z_{j2})={\beta }_1(\tau )+{\beta }_2(\tau )x_j+{\beta }_3(\tau )z_{j1}+{\beta }_4(\tau )z_{j2},& \\ w_{j,k}=x_j+u_{j,k}& (j=1,\dots ,271;k=1,\dots ,6),\end{array}$$

where y_j, x_j, z_j1 and z_j2 are the food frequency questionnaire intake, the long-term usual intake, body mass index and age of the jth subject, w_j,k is the kth food recall intake of the jth subject u_j,k is the measurement error with mean zero and variance ${\gamma }_u^2=6{\sigma }_u^2$, and the intake measurements are on the log scale. For illustration, we study quantile levels τ = 0.2, 0.5 and 0.8. For this dataset, each subject j has six internal replicates of food recall intake, w_j,k (k =1, . . . , 6). Therefore, we estimate ${\gamma }_u^2$ by ${\widehat{\gamma }}_u^2={(5n)}^{-1}{\sum }_{j=1}^n{\sum }_{k=1}^6{(w_{j,k}-w_j)}^2=0.132$, where $w_j=1/6{\sum }_{k=1}^6{w}_{j,k}$. Thus the estimated variance of w_j as a measurement of x_j is ${\widehat{\sigma }}_u^2={\widehat{\gamma }}_u^2/6=0.022$. The attenuation factor, $1-{\widehat{\sigma }}_u^2/\text{var}(w_j)$, is estimated as 0.737. Using the simulation and extrapolation method, we chose h as 0.3, 0.55 and 0.35 for the normal corrected-loss estimator, and 0.36, 0.45 and 0.21 for the Laplace corrected-loss estimator, at τ = 0.2, 0.5 and 0.8, respectively.

Table 3 summarizes the coefficient estimates β̂(τ) from the naive method, He & Liang’s method, Wei & Carroll’s method, the normal corrected-loss and the Laplace corrected-loss methods at three quantile levels. The values in parentheses are the corresponding bootstrap standard errors, based on 200 bootstrap samples. In the implementation of He & Liang’s method, we first transform y_j to $y_j^{*}={\widehat{\sigma }}_u{y}_j/s$ to put the variances of measurement and regression errors on the same scale, where s is the standard deviation of the estimated residuals obtained from the naive method at the median. The resulting coefficient estimates are then transformed back to the original scale. According to He & Liang (2000, Theorem 2.1), their estimator β̂₁(τ) of the intercept converges to some quantity depending on β_k(τ) (k = 2, 3, 4) and the unknown τ th quantile of the regression error. Therefore, we omit β̂₁(τ) in Table 3.

Table 3.

Estimates, standard errors, of the quantile coefficients from different methods for the Womens Interview Survey of Health data: β₂(τ), β₃(τ) and β₄(τ) correspond to the effects of long-term usual intake, body mass index and age on the τ th quantile of the food frequency questionnaire intake, respectively

τ	Method	β2(τ)	β3(τ)	10 × β4(τ)
0.2	Naive	0.65 (0.12)	−0.11 (0.18)	0.28 (0.42)
	HL	0.81 (0.18)	−0.11 (0.28)	0.35 (0.38)
	WC	0.95 (0.18)	−0.19 (0.25)	0.29 (0.39)
	CLN	0.82 (0.20)	−0.01 (0.17)	0.10 (0.28)
	CLL	0.81 (0.16)	−0.05 (0.13)	0.16 (0.26)
0.5	Naive	0.51 (0.10)	0.22 (0.16)	−0.01 (0.29)
	HL	0.71 (0.13)	0.49 (0.27)	0.00 (0.30)
	WC	0.70 (0.14)	0.24 (0.16)	−0.13 (0.33)
	CLN	0.73 (0.14)	0.31 (0.13)	0.04 (0.27)
	CLL	0.71 (0.13)	0.29 (0.15)	−0.00 (0.27)
0.8	Naive	0.4 (0.17)	0.5 (0.18)	−0.06 (0.37)
	HL	0.38 (0.26)	0.75 (0.44)	0.15 (0.41)
	WC	0.62 (0.15)	0.51 (0.21)	−0.18 (0.36)
	CLN	0.70 (0.16)	0.47 (0.15)	−0.05 (0.28)
	CLL	0.78 (0.24)	0.71 (0.16)	−0.09 (0.33)

Naive, the naive method; HL, He & Liang’s method; CLN, corrected-loss estimator for normal measurement error; CLL, corrected-loss estimator for Laplace measurement error; WC, Wei & Carroll’s method.

By accounting for the measurement error, both normal and Laplace corrected-loss methods identify a stronger association between food frequency questionnaire intake and the long-term intake at all three quantiles than the naive method. For instance, the normal corrected-loss estimates of β₂(τ) increase by 26, 44 and 74% at τ = 0.2, 0.5, and 0.8, respectively, compared with the naive estimates. In contrast, He & Liang’s method gives a β₂(τ) estimate smaller than the naive estimates at τ = 0.8. Both normal and Laplace corrected-loss methods suggest that body mass index has a significantly positive effect at τ = 0.8, but He & Liang’s method gives a larger β₂(τ) estimate associated with a large standard error, which leads to insignificance. All methods show that age has no significant effect on any of the three quantiles. The effect of body mass index increases with the quantile level, and the effect of the long-term intake decreased with the quantile level, which indicate some form of heteroscedasticity. Our simulation demonstrated that He & Liang’s method gives biased estimates for such heteroscedastic data. Wei & Carroll’s method yields the same significance results as the Laplace corrected-loss method, but it is computationally much more expensive. Using the same computer, it took 218 hours to obtain the bootstrap standard error of Wei & Carroll’s estimates with 20 iterations for each of the 200 bootstrap samples, while it required only 35 minutes for the Laplace corrected-loss method.

5. Discussion

Our proposed estimation procedure has the following general structure. Since the quantile loss function cannot be corrected in the manner of Stefanski (1989) and Nakamura (1990), we projected the function into a class of suitably smooth functions via kernel smoothing. The corrected-loss method was then applied to the smoothed quantile objective function. We balanced the bias and variance by choosing the smoothing parameter using the simulation and extrapolation method of Delaigle & Hall (2008). This strategy is general and can be used in other problems where correction is possible after some smoothing of the objective functions.

We assumed a class of measurement errors, including normal and Laplace, for identification purpose. The two proposed estimators both showed robustness against misspecification of the measurement error distribution in the simulation study. Considering the finite sample performance and the computational efficiency, we recommend the Laplace corrected-loss estimator for practical usage. The corrected-loss methods developed herein can be extended to a wider class of distribution families, as long as their characteristic functions are proportional to the inverse of a polynomial; see Hong & Tamer (2003) for related discussions. The degree of the polynomial puts constraints on the smoothness of the objective function. Such an extension is beyond the scope of this paper.

Appendix

Proof of Theorem 1. We first prove (i). By the definitions of A(∊, σ², h) and ρ_N (∊, h), we get A(∊, σ², h) = ∊(τ − 1/2 + I₁/π) + I₂/π, where

$$\begin{array}{ll}{I}_1=E_z\left\{{\int }_0^{(∊+\text{i}\sigma z)/h}\text{sin}(t)/t\text{d}t\right\},\hfill & I_2=E_z\left\{\text{i}\sigma z{\int }_0^{(∊+\text{i}\sigma z)/h}\text{sin}(t)/t\text{d}t\right\}.\hfill \end{array}$$

Recall that sin(x) = (e^ix − e^−ix)/(2i) and cos(x) = (e^ix + e^−ix)/2. Then

$$I_1={\int }_{-\infty }^{\infty }{(2\pi )}^{-1}{e}^{-z^2/2}{\int }_0^{(∊+\text{i}\sigma z)/h}\text{sin}(t)/t\text{d}t\text{d}z={\int }_0^{1/h}\frac{1}{y}{e}^{{\sigma }^2{y}^2/2}\text{sin}(y∊)\text{d}y.$$

Applying similar arguments, we have

$$\begin{array}{ll}{I}_2\hfill & ={\int }_0^{1/h}\frac{1}{y}{\int }_{-\infty }^{\infty }\text{i}\sigma z{(2\pi )}^{-1}{e}^{-z^2/2}\text{sin}\{y(∊+\text{i}\sigma z)\}\text{d}z\text{ d}y\hfill \\ \hfill & =-{\int }_0^{1/h}{\sigma }^2{e}^{y^2{\sigma }^2/2}(e^{\text{i}y∊}+e^{-\text{i}y∊})/2\hspace{0.17em}\text{d}y=-{\int }_0^{1/h}{\sigma }^2{e}^{y^2{\sigma }^2/2}\text{cos}(y∊)\text{d}y.\hfill \end{array}$$

We next show (ii). For any U ∼ N(0, 1), it is easy to show that

$$\begin{array}{l}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}E\{\text{sin}(a+bU)\}={\int }_{-\infty }^{\infty }{(2\pi )}^{-1/2}{e}^{-u^2/2}{(2i)}^{-1}\{e^{\text{i}(a+bu)}-e^{-\text{i}(a+bu)}\}\text{d}u=e^{-b^2/2}\text{sin}(a),\\ E\{U\text{sin}(a+bU)\}=b{e}^{-b^2/2}\text{cos}(a),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}E\{\text{cos}(a+bU)\}=e^{-b^2/2}\text{cos}(a).\end{array}$$ (A1)

By (A1), E{∊ sin(y∊)} = E{(μ + σU) sin(yμ + yσU)} = e^{− y2σ2/2} {μ sin(yμ) + yσ² cos(yμ)}. Therefore, we have

$$\begin{array}{ll}E\{A(∊,\sigma ,h)\}\hfill & =\mu (\tau -1/2)+\frac{1}{\pi }{\int }_0^{1/h}\frac{1}{y}{e}^{y^2{\sigma }^2/2}E\{∊\text{sin}(y∊)\}-\frac{{\sigma }^2}{\pi }{\int }_0^{1/h}{e}^{y^2{\sigma }^2/2}E\{\text{cos}(y∊)\}\text{d}y\hfill \\ \hfill & =\mu (\tau -1/2)+\frac{1}{\pi }{\int }_0^{1/h}\frac{1}{y}\mu \hspace{0.17em}\text{sin}(y\mu )\hspace{0.17em}\text{d}y={\rho }_N(\mu ,h).\hfill \end{array}$$

Proof of Lemma 1. Assertion (i) can be obtained from representation (6.3.4) in Kotz et al. (2001), and (ii) is a direct conclusion of Proposition 6.8.1 in Kotz et al. (2001).

Proof of Theorem 2. Suppose that there exists a function ḡ(∊) such that E{ḡ(∊)} = g(μ). We shall show that ḡ(∊) = g(∊) − 0.5σ²g⁽²⁾(∊). First recall that if ∊ ∼ L(μ, σ²), then f (∊) = (√2σ)⁻¹e^{−√2|∊−μ|/σ}. Denote σ = √2b. Therefore

$$\begin{array}{ll}E\{\overline{g}(∊)\}\hfill & =e^{-\mu /b}{\int }_{-\infty }^{\mu }\overline{g}(∊)\frac{1}{2b}{e}^{∊/b}\text{d}∊+e^{\mu /b}{\int }_{\mu }^{\infty }\overline{g}(∊)\frac{1}{2b}{e}^{-∊/b}d∊\hfill \\ \hfill & =e^{-\mu /b}{I}_1(\mu )+e^{\mu /b}{I}_2(\mu )=g(\mu ).\hfill \end{array}$$ (A2)

Differentiating both sides of the equation (A2) with respect to μ gives

$$\begin{array}{ll}{g}^{\prime }(\mu )\hfill & =-\frac{1}{b}{e}^{-\mu /b}{I}_1(\mu )+\frac{1}{b}{e}^{\mu /b}{I}_2(\mu )\hfill \\ \hfill & =-\frac{1}{b}{e}^{-\mu /b}{I}_1(\mu )+e^{-\mu /b}\overline{g}(\mu )\frac{1}{2b}{e}^{\mu /b}+\frac{1}{b}{e}^{\mu /b}{I}_2(\mu )-e^{\mu /b}\overline{g}(\mu )\frac{1}{2b}{e}^{-\mu /b}.\hfill \end{array}$$ (A3)

Differentiating (A3) again with respect to μ, we get b⁻²{e^−μ/b I₁(μ) +e^μ/b I₂(μ)} −b⁻²ḡ(μ) = g⁽²⁾(μ). Thus, we have ḡ(μ) = g(μ) − b²g⁽²⁾(μ) = g(μ) − 0.5σ²g⁽²⁾(μ).

Proof of Theorem 3. For easy demonstration, we first show (ii). Define

$$\begin{array}{c}{M}_L^{*}(w,\beta ,h)=n^{-1}\sum _{j=1}^n\{{\rho }_L^{*}(y_j,w_j,\beta ,h)-{\rho }_L^{*}(y_j,w_j,{\beta }_0,h)\},\\ M_L(x,\beta ,h)=n^{-1}\sum _{j=1}^n\{{\rho }_L(y_j,x_j,\beta ,h)-{\rho }_L(y_j,x_j,{\beta }_0,h)\},\\ M(x,\beta )=n^{-1}\sum _{j=1}^n\{\rho (y_j,x_j,\beta )-\rho (y_j,x_j,{\beta }_0)\}.\end{array}$$

By Theorem 2, E{ $M_L^{*}$(w, β, h)} = E{M_L (x, β, h)}. Therefore,

$$\begin{array}{ll}|M_L^{*}(w,\beta ,h)-E\{M(x,\beta )\left\}\right|⩽\hfill & |M_L^{*}(w,\beta ,h)-E\{M_L^{*}(w,\beta ,h)\left\}\right|\hfill \\ \hfill & +\left|E\right\{M_L(x,\beta ,h)\}-M_L(x,\beta ,h)|+|M_L(x,\beta ,h)-M(x,\beta )|\hfill \\ \hfill & +|M(x,\beta )-E\{M(x,\beta )\left\}\right|.\hfill \end{array}$$ (A4)

Following the arguments used for proving Horowitz (1998, Lemma 1), we can show that the following relations hold almost surely as n → ∞:

$$\begin{array}{c}\underset{\beta \in ℬ}{\text{sup}}|M(x,\beta )-E\{M(x,\beta )\}|=o(n^{-1/2}\text{log}n),\\ \underset{\beta \in ℬ}{\text{sup}}|M_L(x,\beta ,h)-E\{M_L(x,\beta ,h)\left\}\right|=o(n^{-1/2}\text{log}n)+O(h).\end{array}$$ (A5)

Since the corrected loss function ${\rho }_L^{*}$(·) involves the second derivative of ρ_L(·), similar to Horowitz (1998, Lemma 3(b)), we obtain

$$\underset{\beta \in ℬ}{\text{sup}}|M_L^{*}(w,\beta ,h)-E\{M_L^{*}(w,\beta ,h)\left\}\right|=o(\text{log}n/{(nh)}^{1/2}\}+O(h)$$ (A6)

almost surely. Furthermore, under Assumption 6, sup_∊|ρ_L (∊, h) − ρ_τ (∊)| = sup_∊|∊{G_L (∊/h) − I (∊ > 0)}| = sup_t |htG_L (−t)| ⩽ hE|Z| = O(h), where t = |∊/ h|, Z ∼ G_L (·). Therefore,

$$\underset{\beta \in ℬ}{\text{sup}}|M_L(x,\beta ,h)-M(x,\beta )|=O(h)$$ (A7)

almost surely. Combining (A4)–(A7), we have that as h → 0 and (nh)^−1/2 log n → 0,

$$\underset{\beta \in ℬ}{\text{sup}}|M_L^{*}(w,\beta ,h)-E\{M(x,\beta )\left\}\right|=o(1)$$

almost surely. By Assumptions 3 and 4, β₀ uniquely minimizes E {M_N (x, β)} over ℬ. By White (1980, Lemma 2.2), β̂_L → β₀ almost surely. To prove (i), we define

$$\begin{array}{c}{M}_N^{*}(w,\beta ,h)=n^{-1}\sum _{j=1}^n\{{\rho }_N^{*}(y_j,w_j,\beta ,h)-{\rho }_N^{*}(y_j,w_j,{\beta }_0,h)\},\\ M_N(x,\beta ,h)=n^{-1}\sum _{j=1}^n\{{\rho }_N(y_j,x_j,\beta ,h)-{\rho }_N(y_j,x_j,{\beta }_0,h)\}.\end{array}$$

By Theorem 1, E{ $M_N^{*}$(w, β, h)} = E{M_N (x, β, h)}. Therefore,

$$\begin{array}{ll}|M_N^{*}(w,\beta ,h)-E\{M(x,\beta )\left\}\right|⩽\hfill & |M_N^{*}(w,\beta ,h)-E\{M_N^{*}(w,\beta ,h)\left\}\right|\hfill \\ \hfill & +\left|E\right\{M_N(x,\beta ,h)\}-E\{M_N(x,\beta ,h)\left\}\right|+|M_N(x,\beta ,h)-M(x,\beta )|\hfill \\ \hfill & +|M(x,\beta )-E\{M(x,\beta )\left\}\right|.\hfill \end{array}$$ (A8)

Denote $G_N(x)={\int }_{-\infty }^x{K}_N(u)du$, where K_N (u) = sin(u)/(uπ). For any t > 0, there exists an integer number k ⩾ 0 such that t ∈ (kπ, (k + 1)π], and

$$\begin{array}{c}|G_N(-t)|=\frac{1}{\pi }\left|{\int }_{-\infty }^{-t}\text{sin}(x)/x\hspace{0.17em}\text{d}x\right|=\frac{1}{\pi }\left|{\int }_t^{(k+1)\pi }\text{sin}(x)/x\hspace{0.17em}\text{d}x+\sum _{l=k+1}^{\infty }{\int }_{l\pi }^{(l+1)\pi }\text{sin}(x)/x\hspace{0.17em}\text{d}x\right|\\ ⩽\frac{1}{\pi }\left|{\int }_t^{(k+1)\pi }\text{sin}(x)/x\hspace{0.17em}\text{d}x\right|+\frac{1}{\pi }\left|{\int }_{(k+1)\pi }^{(k+2)\pi }\text{sin}(x)/x\hspace{0.17em}\text{d}x\right|⩽2/\left|t\right|.\end{array}$$

Therefore, we have almost surely

$$\begin{array}{ll}\underset{∊}{\text{sup}}|{\rho }_N(∊,h)-{\rho }_{\tau }(∊)|\hfill & =\underset{∊}{\text{sup}}|∊\{\tau -1+G_N(∊/h)\}-∊\{\tau -I(∊<0)\left\}\right|\hfill \\ \hfill & =\underset{∊}{\text{sup}}|∊\{G_N(∊/h)-I(∊>0)\left\}\right|\hfill \\ \hfill & =\underset{t}{\text{sup}}\{ht{G}_N(-t)\}=O(h),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t=|∊/h|,\hfill \end{array}$$ (A9)

and

$$\underset{\beta \in ℬ}{\text{sup}}|M_N(x,\beta ,h)-M(x,\beta )|=O(h).$$ (A10)

By arguments similar to Horowitz (1998, Lemma 3(a)), it is easy to see that

$$\underset{\beta \in ℬ}{\text{sup}}|M_N(x,\beta ,h)-E\{M_N(x,\beta ,h)\left\}\right|=o((\text{log}n)n^{1/2})$$ (A11)

almost surely. Let ∊ = y − w^Tβ and σ² = β^TΓβ. By Assumption 5, the compactness of ℬ and the fact that | sin(t)/t| ⩽ 1, we have

$$E\left\{{\rho }_N^{*}{(y,w,\beta ,h)}^2\right\}⩽C_1+C_{2}E{\left\{{\int }_0^{1/h}({∊}^2+{\sigma }^2)e^{t^2{\sigma }^2/2}\text{d}t\right\}}^2⩽C_1+C_2{h}^{-2}{e}^{{\sigma }^2/h^2}={\delta }_n,$$

where C₁ and C₂ are some positive constants. By Nolan & Pollard (1987, Lemma 22) and Pollard (1984, Theorem 2.37),

$$\underset{\beta \in ℬ}{\text{sup}}|M_N^{*}(w,\beta ,h)-E\{M_N^{*}(w,\beta ,h)\left\}\right|=o({\delta }_n^{1/2}{n}^{-1/2}\text{log}n)$$ (A12)

almost surely, which is o(1) if h = C(log n)^−δ, where δ < 1/2 and C is some positive constant. The above equation together with (A5), (A8) and (A9)–(A11) gives sup_β∈ℬ | $M_N^{*}$(w, β, h) − E{M(x, β)}| = o(1) almost surely The rest of the proof follows the same lines as that for Theorem 3(ii).

Proof of Theorem 4. Let ρ^*(y, w, β, h) denote the corrected quantile loss function for either normal or Laplace measurement errors. Define ${\psi }_1^{*}(y,w,\beta ,h)=\partial {\rho }^{*}(y,w,\beta ,h)/\partial \beta$, ${\psi }_2^{*}(y,w,\beta ,h)={\partial }^2{\rho }^{*}(y,w,\beta ,h)/\partial \beta \partial {\beta }^{\text{T}}$. Furthermore, let ${\rho }_n^{*}(w,\beta )=n^{-1}{\sum }_{j=1}^n{\rho }^{*}(y_j,w_j,\beta ,h)$, ${\psi }_{1n}^{*}(w,\beta )=\partial {\rho }_n^{*}(w,\beta )/\partial \beta$ and ${\psi }_{2n}^{*}(w,\beta )={\partial }^2{\rho }_n^{*}(w,\beta )/\partial \beta \partial {\beta }^{\text{T}}$. Under the conditions of Theorem 2 and 3, similar to (A6) and (A12), we have ${\text{sup}}_{\beta \in ℬ}|{\psi }_{2n}^{*}(w,\beta )-E\{{\psi }_{2n}^{*}(w,\beta )\left\}\right|=o_p(1)$. Taylor expansion gives $n^{1/2}(\widehat{\beta }-{\beta }_0)=-E\{{\psi }_{2n}^{*}(w,{\beta }_0)\}{n}^{1/2}{\psi }_{1n}^{*}(w,{\beta }_0)+o_p(1)$. By Assumption 7, we have ${\text{lim}}_{n\to \infty }E\{{\psi }_{2n}^{*}(w,{\beta }_0)\}=A$. On the other hand, $n^{1/2}{\psi }_{1n}^{*}(w,{\beta }_0)=n^{-1/2}{\sum }_{j=1}^n{\psi }_1^{*}(y_j,w_{j,}{\beta }_0,h)$. By using the results of Theorems 1–2 and methods like those used to obtain the asymptotic means and variances of kernel density estimators, we have $E\{{\psi }_1^{*}(y_j,w_j,{\beta }_0,h)\}=E\{{\psi }_1(y_j,x_j,{\beta }_0,h)\}=o(n^{-1/2})$ as n → ∞ and h → 0, where ψ₁(y, x, β, h) = ∂ρ(y, x, β, h)/∂β and ρ(y, x, β, h) is the smoothed quantile loss function. Therefore, $n^{1/2}E\{{\psi }_{1n}^{*}(w,{\beta }_0)\}=n^{1/2}E\{{\psi }_1^{*}(y_j,w_j,{\beta }_0,h)\}=o(1)$, which together with the central limit theorem gives $n^{1/2}{\psi }_{1n}^{*}(w,{\beta }_0)\to N(0,D)$ in distribution.

Proof of Theorem 5. Similar to the proof in Theorem 3, the consistency of β̂ can be proven by using the fact that Σ̂ − Σ = O_p(n^−1/2). In addition, note that minimizing the objective function in (5) with the estimated covariance matrix Σ∊ is equivalent to solving the following stacked estimating equation $[n^{-1/2}{\sum }_{j=1}^n{\psi }_{1\beta }^{*}{(y_j,w_{j,}\beta ,h,\sigma )}^{\text{T}}$, $[n^{-1/2}{\sum }_{j=1}^n{\{S_j-m(m-1)\sigma \}}^{\text{T}}]={(0_p^{\text{T}},0_{p(p+1)/2}^{\text{T}})}^{\text{T}}$. The asymptotic normality can be proven by following the same arguments as in the proof of Theorem 4 and by expanding the stacked estimating function.