Early Cohort Mortality Predicts the Cohort Rate of Aging: an Historical Analysis

Abstract

Early environmental influences on later life health and mortality are well recognized in the doubling of life expectancy since 1800. To further define these relationships, we analyzed the associations between early life mortality with both the estimated mortality level at age 40 and the exponential acceleration in mortality rates with age characterized by the Gompertz model. Using mortality data from 630 cohorts born throughout the 19^th and early 20^th century in nine European countries, we developed a multilevel model that accounts for cohort and period effects in later life mortality. We show that early life mortality, which is linked to exposure to infection and poor nutrition, predicts both the estimated cohort mortality level at age 40 and the subsequent Gompertz rate of mortality acceleration during aging. After controlling for effects of country and period, the model accounts for the majority of variance in the Gompertz parameters (about 90% of variation in estimated level of mortality at age 40 and about 78% of variation in Gompertz slope). The gains in cohort survival to older ages are entirely due to large declines in adult mortality level, because the rates of mortality acceleration at older ages became faster. These findings apply to cohorts born in both the 19^th Century and the early 20^th Century. This analysis defines new links in the developmental origins of adult health and disease in which effects of early life circumstances, such as exposure to infections or poor nutrition, persist into mid-adulthood and remain evident in the cohort mortality rates from ages 40 to 90.

Introduction

Since 1800, human life expectancy (LE) has more than doubled as a result of major decreases in mortality across the lifespan. While improving survival at early ages has historically contributed the most to increased LE, declining mortality at older ages has also contributed to the increased LE.^1,2 Eighty years ago, Kermack, McKendrick, and McKinlay³ noted associations between early and later age mortality in historical cohorts from England and Sweden, in which cohorts showed life-long benefits from the improving early environment. The developmental origins of adult health and disease have been further specified by Barker,^4,5 Bengtsson and Lindström,^6,7 Gluckman and Hanson⁸ and Fogel⁹ in relation to improvements in pre- and postnatal nutrition. Finch and Crimmins¹⁰ have further argued for a major role of infection and inflammation in outcomes of aging, finding support for this view from the fact that the level of cohort mortality at early ages, which is largely due to infections, strongly predicts mortality for the cohorts at age 70 in 19^th Century Europe.¹¹

Here we comprehensively investigate demographic associations between early cohort circumstances and later life mortality using the Gompertz exponential mortality model, using high quality data from 9 European countries to characterize later life mortality patterns of cohorts born throughout the 19^th and early 20^th Century. We analyze adult mortality at ages 40 and older assuming a Gompertz mortality model and link the resulting parameters to early life mortality. A novel statistical approach examines life-course associations while controlling for period effects. The findings provide evidence of strong associations between early life mortality with both the cohort mortality level in mid-adulthood and the rate of mortality acceleration during aging, which point to broader conclusions about the links between early life conditions and late life mortality than have been recognized.

Mortality risk in adulthood shows empirical regularities that can be approximated by mathematical models.¹² One of the most parsimonious of these models is given by the Gompertz model in which the acceleration of mortality rates with age are described by an exponential equation linking mortality at a given age x, m(x), to the parameters a and b.^13,14

$$\text{m}\left(x\right)=a\text{exp}\left(\mathit{\text{b x}}\right)$$ Eq.1

The rate of mortality acceleration at older ages (Gompertz slope, b) is considered a basic measure of the rate of population aging. Fifty years ago, Strehler and Mildvan¹⁴ analyzed age-specific mortality rates based on 1955 United Nations ‘period data’ for 32 countries, i.e. cross-sectional analysis of all ages in a given year, and found a robust inverse correlation between values of ln a (Eq. 1), the extrapolated log of mortality rate at age 0, and the Gompertz mortality acceleration parameter b calculated for ages 35-85. The Strehler-Mildvan (S-M) inverse relationship of ln a and mortality acceleration (b) has been confirmed with expanded period data from modern populations since 1955.^15,16 However, Yashin et al.¹⁷ found that S-M correlations were not stable for either periods and cohorts in Swedish mortality data from the mid-1800s to the late-1990s, again using ln a extrapolated to age 0, while Gavrilov and Gavrilova argue that S-M correlations neglect a full accounting of age-independent mortality.¹⁸

Moreover, the inverse link between ln a and mortality acceleration in the S-M relationship does not allow a life-course association when ln a is extrapolated to age 0 of the Gompertz model. For ln a to be an indicator of early life experiences, one must assume that ln a corresponds to the actual mortality rate at age 0, which is clearly not true. This issue in Gompertz models fitted to both period and cohort adult mortality rates has been largely neglected. Therefore, we fitted Gompertz models to adult cohort mortality rates for ages 40-90, where ln a represents an estimate of adult cohort mortality level at age 40 rather than an extrapolation to age 0 from the model. The Gompertz equations are fitted in a multilevel model framework to simultaneously model a and b for each cohort (Eq. 1), and link their variation with early life mortality across cohorts controlling for period and country effects.

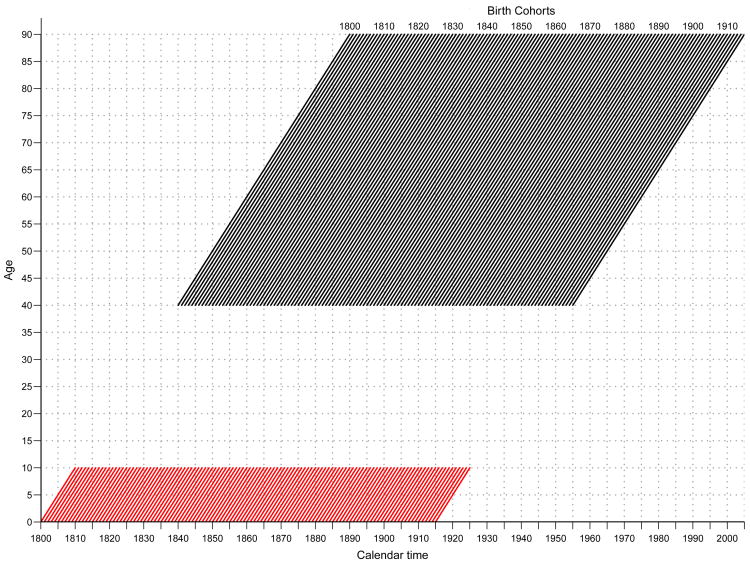
This approach allows us to statistically test the association between early life mortality (q_0-10) and both the estimated mortality level at age 40 and the acceleration in mortality rates with age across cohorts. An advantage of the multilevel approach is that it specifically models the link between q_0-10 and the Gompertz parameters across cohorts controlling for period effects and country fixed-effects to account for unobserved country differences in mortality. Specifically, this paper analyzed cohort mortality data for ages 0-10 and 40 to 90 in nine European countries (Denmark, Finland, France, Italy, Netherlands, Norway, Sweden, Switzerland, and England & Wales) using single-year cohorts born between 1800 and 1915 with mortality by single years of age from the Human Mortality Database¹⁹ (630 cohorts from nine countries) . These data allow us to capture most of the adult mortality experience from the mid-1800s throughout the late-1990s with links to early life mortality in the 19^th and early-20^th Century (Fig 1). We used the cohort life table probability of dying from ages 0 to 10 (q_0-10) as an indicator of early cohort mortality and age 40 as the onset of Gompertz mortality accelerations consistent with previous research.^14,15,17,20

Fig. 1. Lexis diagram representing cohort mortality data included in the analysis. Single–year birth cohorts aged 0–10 (red lines) and 40–90 (black lines).

Methods

Gompertz equations are fitted in a log-linear mixed-model (multilevel model) allowing us to properly account for the variation in mortality rates by age for each cohort (within cohort variation) and the variability between Gompertz slopes and intercepts across cohorts (between cohort variation) (Eq. 2). Equation 2 models the log of mortality rates for each cohort j as a function of age i (level 1), and the Gompertz intercepts and slopes as a function of early cohort mortality, q_0-10, country fixed-effects, and period effects (level 2). Adding period to level 2 allows us to parse out the variation in the cohort Gompertz parameters associated with calendar time. All models were estimated using R statistical software.

$$\begin{array}{cc}\begin{array}{c}\text{Level}1:\\ \text{Level}2:\end{array}& \begin{array}{c}\text{log}\left({\text{m}}_{\text{ij}}\right)=a_{0\text{j}}+b_{1\text{j}}({\text{Age}}_{\text{ij}}-40)+{\text{r}}_{\text{ij}},\\ a_{0\text{j}}={\gamma }_{00}+{\gamma }_{01}{\text{q}}_{0-10,\text{j}}+{\gamma }_{02\text{k}}\text{Country–fixed–effects}+{\gamma }_{03}(\text{Period}–1840)+{\text{u}}_{0\text{j}}\\ b_{1\text{j}}={\gamma }_{10}+{\gamma }_{11}{\text{q}}_{0-10,\text{j}}+{\gamma }_{12\text{k}}\text{Country–fixed–effects}+{\gamma }_{13}(\text{Period}–1840)+{\text{u}}_{1\text{j}}\end{array}\end{array}$$ Eq.2

• m_ij represents the mortality rate by age and cohort,

• Age_ij represents ages for cohort j (Age_1j= 40, Age_2j=41,…, Age_51j=90),

• Period corresponds to 1840, 1841,…, 1955,

• j is a cohort indicator (j=1800,…,1915),

• r_ij is a normally distributed error with homogeneous variance across cohorts,

• a_0j and b_1j vary across cohorts in level-2,

• γ₀₀ represents the mean Gompertz-intercept for the reference-country,

• γ₀₁ represents the average increase in Gompertz-intercept for one unit increase in q_0-10 controlling for unobserved country factors and period,

• γ_02k represents the mean difference in Gompertz-intercept between reference-country and country k controlling for q_0-10 and period,

• γ₀₃ represents the average increase in Gompertz-intercept for one unit increase in period controlling for q_0-10 and country fixed-effects,

• γ₁₀ represents the mean Gompertz-slope for reference-country,

• γ₁₁ represents the average increase in Gompertz-slope for one unit increase in q_0-10 controlling for country fixed-effects and period effects,

• γ_12k represents the mean difference in Gompertz-slope between reference-country and country k controlling for q_0-10 and period effects,

• γ₁₃ represents the average increase in Gompertz-slope for one unit increase in period controlling for q_0-10, country fixed-effects and period effects, and

• u_0j and u_1j are multivariate normally distributed with means of zero and conditional variance-covariance components after controlling for q_0-10, country and period. They represent residual dispersion in a_0j and b_1j after controlling for q_0-10, country and period.

Results

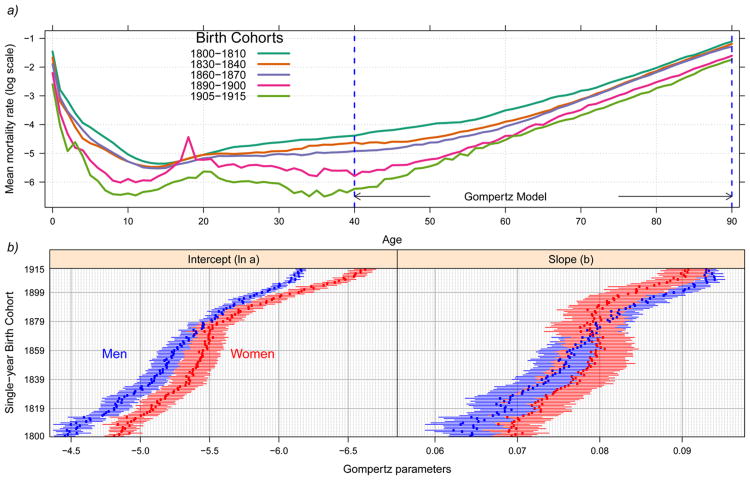
Cohort age-specific mortality rates for five Swedish cohorts are shown in Figure 2 panel a. Sweden, which has the deepest historical record of high quality data, clearly shows major mortality declines throughout life from 1800 to 1915. After age 40 mortality rates increase monotonically with age, following the Gompertz model of a linear trend in the log of mortality rates by age. Analysis of time trends in ln a and b for Swedish single-year birth cohorts for the 1800-1915 period (Fig 2 panel b) shows a five-fold decline in the mortality level at age 40 (ln a, Eq.1) for men and six-fold for women, while the Gompertz mortality acceleration (coefficient b, Eq. 1) shows increases by about 50% for men and by 35% for women.

Fig. 2.

Historical data for Sweden showing cohort mortality declines. (a) Average cohort mortality rates for the total population: selected cohorts. The spikes in mortality for the most recent two cohorts are associated with the 1918 Influenza pandemic (top panel), and (b) estimated Gompertz parameters with 95% confidence intervals for single–year birth cohorts ages 40–90 for men (blue) and women (red) (bottom panel)

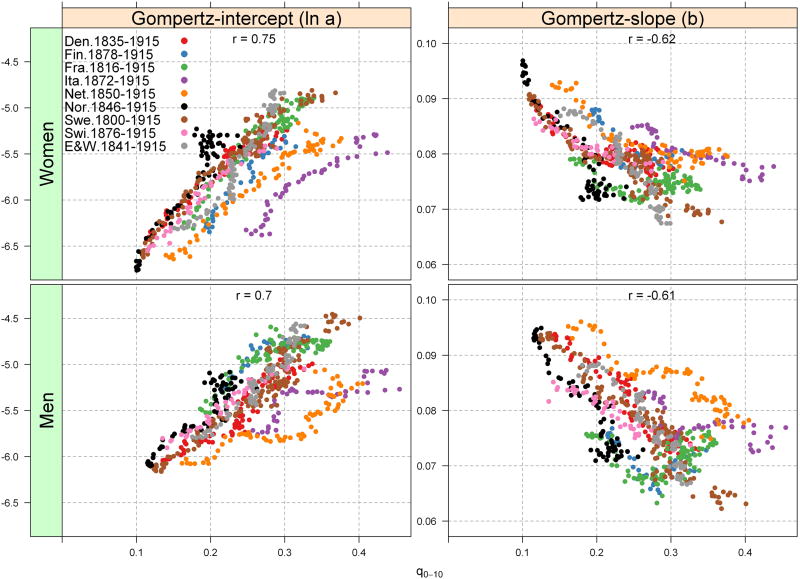
Analysis of all nine countries shows robust associations between Gompertz parameters and cohort mortality from birth to age 10 for cohorts born from 1800-1915 (Fig 3). This association, however, is stronger for the Gompertz-intercept (ln a) than for the slope (b). For example, there is a positive link between early cohort mortality (q_0-10) and the estimated adult mortality level at age 40 (ln a), suggesting that lower early cohort mortality up to age 10 is strongly linked to lower adult cohort mortality level after age 40 (in mid-adulthood), when mortality rates begin to accelerate exponentially; this result is exemplified by strong correlation coefficients between ln a and q_0-10 (0.70, men; 0.75, women) (Fig 3). On the other hand, there is an inverse association between cohort early life mortality and the Gompertz slope, such that recent cohorts with low early life cohort mortality show faster mortality acceleration in cohort mortality at older ages (correlation coefficient of -0.61 for men and -0.62 women).

Fig. 3. Gompertz parameter associations (Eq. (1)) with cohort mortality for the nine European countries ages 0–10 years (q0–10). Slope is the mortality rate acceleration, ages 40–90; In a is the log-mortality rate calculated at age 40.

According to the multilevel model (Eq. 2), across all nine countries, early age cohort mortality explains a substantial amount of the variance in the Gompertz parameters for both genders (Table 1). In the unconditional model estimating the mean Gompertz parameters across the 630 cohorts (Table 1, column a), women have slightly lower adult mortality level after age 40 (higher ln a) and slightly faster mortality rate accelerations with age than men. Men had significantly higher estimated adult mortality level at age 40 than women in 80% of the 630 birth cohorts (Supplementary figures), with the female advantage increasing progressively after the 1870 birth cohort. For example, the percentage of male cohorts having higher adult mortality level than women increased from 80% for those born in 1870-1915, to 88% in 1880-1915, 97% in 1890-1915 and 100% between 1895-1915 (Supplementary, Fig S1). However, sex differences in Gompertz slopes do not follow a consistent trend across cohorts and countries (Supplementary, Fig S2). For most countries, the cohort Gompertz slopes between men and women (France, Norway, England and Wales, Switzerland, and Italy) did not differ significantly; however, higher slope values for men may have emerged in cohorts born around 1870 in Sweden, Denmark, and the Netherlands.

Table 1. Estimated effects of early life mortality (q_0-10), country and period on Gompertz parameters and variance explained of the Gompertz parameters.

The intercept and slope were estimated from equation 2 for single year cohorts from Denmark 1835-1915, Finland 1878-1915, France 1816-1915, Italy 1872-1915, Netherlands 1850-1915, Norway 1846-1915, Sweden 1800-1915, Switzerland 1876-1915, and England and Wales 1841-1915.

Fixed effects	Men				Women
	Unconditional (a)	Conditional on q0-10 (b)	Conditional on Country & q0-10 (c)	Conditional on Country, q0-10 & Period (d)	Unconditional (a)	Conditional on q0-10 (b)	Conditional on Country & q0-10 (c)	Conditional on Country, q0-10 & Period (d)
Model for Gompertz intercept (ln a)
γ̂00	−5.290 ***	−6.4392 ***	−6.7156 ***	−5.4191 ***	−5.632 ***	−6.9011 ***	−7.3093 ***	−6.1653 ***
q0-10		4.3382 ***	5.4563 ***	2.2726 ***		5.2631 ***	7.5395 ***	4.1446 ***
Time trend (linear)				−0.0080 ***				−0.0078 ***
Country (ref=Sweden)
Denmark			−0.0840***	−0.0092			0.0074	0.0902***
Finland			0.3053 ***	0.6445 ***			−0.3082 ***	0.0361
France			0.2272 ***	0.3878 ***			−0.0449 **	0.1381 ***
Italy			−0.5256 ***	0.0225			−1.0074 ***	−0.3352 ***
Netherlands			−0.5598 ***	−0.2414 ***			−0.5368 ***	−0.2393 ***
Norway			0.1488 ***	0.0993 ***			0.1942***	0.1927 ***
Switzerland			0.0625 **	0.2320 ***			−0.0807 ***	0.0553 **
England-Wales			0.0958 ***	0.2815 ***			−0.0468	0.1205 ***
Model for Gompertz slope (b)
γ̂10	0.078 ***	0.0961 ***	0.1013 ***	0.0871 ***	0.079 ***	0.0914 ***	0.0953 ***	0.0871 ***
q0-10		−0.0686 ***	−0.0917 ***	−0.0568 ***		−0.0514 ***	−0.0723 ***	−0.0467 ***
Time trend (linear)				0.0001 ***				0.0001 ***
Country (ref=Sweden)
Denmark			0.0028 ***	0.0020 ***			0.0013 ***	0.0007
Finland			−0.0056 ***	−0.0093 ***			0.0038 ***	0.0012
France			−0.0028 ***	−0.0046 ***			−0.0013 ***	−0.0028 ***
Italy			0.0079 ***	0.0019 *			0.0089 ***	0.0036 ***
Netherlands			0.0114 ***	0.0079 ***			0.0066 ***	0.0044 ***
Norway			−0.0041 ***	−0.0036 ***			−0.0026 ***	−0.0027 ***
Switzerland			−0.0017 **	−0.0036 ***			−0.0001	−0.0011 *
England-Wales			0.0007	−0.0013 ***			−0.0004	−0.0016 ***
Random effects	Variance components				Variance components
	Variance	Variance	Variance		Variance	Variance	Variance
ln(a)	0.168702 ***	0.085212 ***	0.020590 ***	0.013120 ***	0.207147 ***	0.088606 ***	0.018566 ***	0.013158 ***
slopes	0.000054 ***	0.000033 ***	0.000012 ***	0.000011 ***	0.000026 ***	0.000015 ***	0.000006 ***	0.000006 ***
Percent of the variance explained in Gompertz-parameters by addding q0-10 and country fixed-effects
ln(a)	-----	49.49	87.79	92.22	-----	57.23	91.04	93.65
slopes	-----	38.53	77.50	79.12	-----	42.53	76.36	78.48

^*p<0.10

^**p<0.05

^***p<0.001

Source: Human Mortality Database.

The conditional models using early life cohort mortality, period effects and country fixed-effects account for most of the variation in Gompertz parameters (Table 1, columns c and d). For example, there are significant positive links between early cohort life mortality and adult mortality level after age 40: across the 630 birth cohorts, q_0-10 accounts for about half of the variation in ln a (57%, women; 50%, men; Table 1, column b). There is also a strong inverse association between early cohort mortality and the cohort Gompertz slope: q_0-10 explains about 40% of the slope variation across countries among men and women. By including country fixed-effects to the conditional model, we find that cohort early age mortality explains about 90% of the variance in the Gompertz-intercepts and about 78% of the Gompertz-slope for both genders (Table 1, column c). While controlling for period as a linear time trend (Table 1 column d) reduces the magnitude of the association of early cohort mortality and Gompertz parameters, these effects remain highly significant. Thus, the strong cohort link between early and late life mortality acts independently of period changes in mortality.

These results remain robust to alternate age limits when fitting Gompertz models (Supplementary Figures). For example, we fitted additional Gompertz models for ages 30-70, 30-80, 30-90, 40-70 and 40-80 and the results are similar to those shown in Figure 3. Among men, for instance, the correlation coefficient (r) between early cohort mortality and Gompertz-slope corresponds to -0.51, -0.54, -0.55, -0.63 and -0.63, respectively (Supplementary, Fig S3). The values are close to those estimated in Figure 3 (r = -0.61). Among women, the corresponding correlation coefficients are -0.43, -0.49, -0.60, -0.48, and -0.51, respectively, which are also similar to our result in Figure 3 (r = -0.62). Similarly, the correlation between early cohort mortality and Gompertz-intercept remains stable by fitting models to alternative age limits (Supplementary, Fig S4).

Discussion

Early life cohort mortality (q_0-10) was found strongly linked to the mortality level after age 40 and Gompertz mortality accelerations during aging in 630 cohorts born throughout the 19^th and early-20^th Century from nine European countries. When country fixed effects are included, the model accounts for 90% of variation in mortality level of estimated mortality at age 40 and 78% of variation in Gompertz slope. This link between early life mortality and Gompertz parameters is not driven by period effects (Table 1).

Early cohort mortality is assumed to reflect the early life circumstances of children in the cohort, mainly mortality due to infections and poor nutrition. Recurrent infections also impair nutrition by re-allocating energy for fever and by reducing nutrient absorption.^21,22 Reduced exposure to infection should be accompanied by lower levels of inflammation through substantial periods of life. Improved nutrition would result in better growth and organ development, as represented in the increase of adult height which is strongly linked to early mortality in those birth cohorts.¹¹ These findings on nine European countries expand the cohort associations of early exposure to infections with mortality rates in adulthood and old age^10,11 and are consistent with prior associations of early and later adult cohort mortality.^3,11,17 Thus the doubling of life expectancy since 1800 represents the developmental origins of adult health and disease, in which effects of early exposure to infections and/or poor nutrition persist throughout life, and remain evident in the cohort rate of aging

Studies addressing life-course influences on late-life mortality have typically used the first year of life as an indicator of early life circumstances. For example, historical studies using longitudinal cohort data from Sweden consistently show that higher mortality in the first year of life is positively associated with higher mortality at ages 50-80;^6,7 and historical cohort data from the Danish Twin Registry 1873-1906 show a direct link between socioeconomic conditions in the first year of life and mortality rates after age 35.²³ The 1918 Influenza Pandemic illustrates a specific exposure event from infection/inflammation in which birth cohorts with prenatal exposure to its main phase had 25% excess heart disease 60 years later.²⁴ Thus, our results extend previous findings associating cohort mortality levels in early and late-life by linking the broader prematurational interval of q_0-10 to the mortality level after age 40 and to the cohort mortality rate acceleration from ages 40 to 90. The use of q_0-10 as an indicator of early life mortality allows us to link early life mortality with Gompertz parameters, which is more appropriate for life history stage correlations than the extrapolations of the Gompertz model to age 0 used in prior modeling.^16-18

These analyses show that increases in adult survival since 1800 are entirely due to progressive declines in adult mortality levels. In fact, the increases in the Gompertz slope, keeping the intercept fixed, unambiguously predict higher mortality and shorter life expectancy.

Future lifespans are also predicted from these historical trends. Because cohort early age mortality is approaching a virtual minimum of about 1-2 deaths/10,000 people up to age 10, we can estimate the Gompertz parameters and the maximum theoretical lifespan at the lowest possible value of cohort early mortality, setting q_0-10=0 (Eq. 2). From the integrated form of equation 1 , the probability of surviving from birth to age x is S(x) = exp(a/b * (1-exp(bx))). For a population of size N, the age at which there is only one survivor, S(x)=1/N, approximates the maximum life span, t_max, of that population²⁵: t_max= ln[1+ b ln(N)/a]/b. For a population of 10 billion people (world projection for 2050) in 2005, the numbers in Table 1 predict a maximum cohort life span of about 113 years for men and 120 years for women, which only slightly underestimates the current records. Despite the continued increase of LE in many countries,²⁶ these calculations imply that these low mortality countries are fast approaching, or already have reached, the limiting life span. Also note that gender differences in mortality persist throughout this limit as shown by the larger life span of women.

Given that we are approaching the lower limit to early life mortality, the only escape from these limiting values of t_max would theoretically come from two possibilities: (1) slowing the Gompertz mortality rate acceleration or (2) delaying the mortality rate acceleration to later ages (or in some combination). Some lab animal models demonstrate these possibilities: caloric restriction extends life expectancy and t_max of some genotypes of worms and rodents by slowing the Gompertz acceleration.^22,27,28 Many of these studies also show a higher background mortality (ln a) consistent with Strehler-Mildvan relationships. The possibility of delayed mortality acceleration is modeled by the pituitary dwarf mouse (Pit-1)²⁹ and the mCAT transgenic mouse.³⁰ However, neither caloric restriction nor deficiencies in growth hormone have been shown to increase the human lifespan.