Analysis of High Throughput Screening Assays using Cluster Enrichment

Abstract

In this paper we describe implementation and evaluation of a cluster-based enrichment strategy to call hits from a high-throughput screen (HTS), using a typical cell-based assay of 160,000 chemical compounds. Our focus is on statistical properties of the prospective design choices throughout the analysis, including how to choose the number of clusters for optimal power, the choice of test statistic, the significance thresholds for clusters and the activity threshold for candidate hits, how to rank selected hits for carry-forward to the confirmation screen, and how to identify confirmed hits in a data-driven manner. While previously the literature has focused on choice of test statistic or chemical descriptors, our studies suggest cluster size is the more important design choice. We recommend clusters be ranked by enrichment odds ratio, not p-value. Our conceptually simple test statistic is seen to identify the same set of hits as more complex scoring methods proposed in the literature. We prospectively confirm that such a cluster-based approach can outperform the naive top X approach, and estimate that we improved confirmation rates by about 31.5%, from 813 using the Top X approach to 1187 using our cluster-based method.

1. Introduction

High-throughput screening (HTS) is commonly used in drug discovery to identify active compounds, or ‘hits’ with high activity levels in the assay. Several hundreds of thousands or even millions of small molecules may be assayed without replication in the primary screen and then selected ‘hits’ will be carried forward to a confirmation screen. False positive rates are high among the selected hits, and confirmation rates are correspondingly low [1]. Several cluster-based hit selection methods have been proposed to improve confirmation rates in small-molecule HTS experiments [2, 3, 4, 5], and similar methods have been proposed in siRNA screens [6, 7]. However, there are few systematic expositions of how to carry out such a cluster-based analysis in the context of a prospective screen, and there has been little discussion of the statistical issues encountered [8].

In this paper we describe the implementation and evaluation of a cluster-based enrichment strategy to call hits, developing ideas first put forward in Klekota et al [2]. The supporting idea is that compounds within the same cluster will be chemically similar, so that hits selected from a cluster containing many neighboring hits might expected to have a higher confirmation rate than hits selected on the basis of single compound activity value alone [2]. Our strategy was as follows: first, moderately sized clusters were formed according to molecular similarity between compounds. Then compounds were ranked individually by assay activity level, and compounds ranking above a relatively low threshold were identified as candidate hits. Next, each cluster was scored for enrichment with candidate hits, using Fisher’s exact test. The set of significant clusters was ranked by enrichment odds ratio, and the ranked list of clusters was walked down until the desired number of hits was identified. These were carried forward to a confirmation screen, and we identified confirmed hits using a novel data-driven method which fit a mixture of two linear models to the combined primary and confirmation screen data. As a backup strategy and to ensure compound diversity, we also called additional hits using a top X approach.

Important statistical issues remain to be clarified in implementing such a cluster-based hit selection strategy. The number of clusters is important: too many clusters means each cluster will contain relatively few compounds and so will not have much power to detect enrichment with active compounds; too few, too large clusters will not have strong similarity of compounds within the cluster, also losing power. Choosing a low activity threshold for candidate hits means there will be many candidate hits, increasing power to detect cluster enrichment, but a threshold within the activity range of no-activation controls will pick up many inactive compounds as well. As the threshold for statistical significance of a cluster is lowered, the false discovery rate on truly significant clusters will increase. The choice of test statistic to score the clusters for significant evidence about true hits should be efficient across a wide range of cluster sample sizes. Hits from the primary screen will be carried forward to a confirmation screen, but the low activity threshold used to identify candidate hits in the primary screen may not be appropriate to identify confirmed hits in the confirmation screen.

In the existing chemoinformatic literature, interest has focused on the choice of test statistic to score the clusters [2, 3, 4, 5, 6, 7], and the importance of these other design parameters has been less appreciated. Conflicting advice about how to rank the clusters appears in the literature, and standard suggested measures to select the number of clusters appear to us to be inappropriate [2, 9, 10]. Finally, the existing literature relies on retrospective analyses of existing data sets, and does not compare the actual confirmation rates achieved by the use of cluster-based and traditional hit selection. Thus a systematic description of these issues is needed.

In the remainder of the paper, we first give a short literature review. In Section 2 we describe the HTS study and the chemoinformatic descriptors we used. In Section 3 we describe the methods we use to cluster the compounds, to call hits, and to estimate confirmation rates. We validate our estimated confirmation rates using a randomly drawn pilot screen. In Section 4 we describe how to choose the number of clusters according to power considerations, and investigate odds ratios for the significant clusters in our HTS. In Section 5, we present confirmation rates, and investigate how to prioritize hits, using information from the confirmation screen. Finally, in Section 6 we conduct sensitivity studies of the number of clusters k, the activity threshold for candidate hits, and the significance threshold for enriched clusters. Section 7 contains the discussion and our summary recommendations as to how to conduct cluster-based hit calling in a HTS assay.

1.1. Review of HTS enrichment analysis methods

The standard activity-based approach (top X approach) to identifying hits from a HTS usually selects compounds above a threshold which is set using the mean and standard deviation of control compounds. For example, compounds more than 3 standard deviations above the control mean may be identified as hits [11]. Thresholds can be set either by pooling all plates in the high-throughput screen, or by considering each plate separately. However, this approach is limited in sensitivity and specificity by the practice of performing the assay without replication on each compound in the primary HTS [12].

Klekota, et al [2] were the first to propose a chemoinformatic cluster-based approach to calling hits from a HTS, attempting to improve the hit recovery rate by scoring entire structural classes. Daylight fingerprints are commercially available molecular descriptors that encode structural features of a molecule into a binary vector of 1024 bits [13]. Klekota, et al used k-mode clustering of Daylight fingerprints to classify the compound library into clusters on the basis of molecular similarity. They then selected a threshold activity level ( top 1% to 4% ) to define the set of candidate hits. Each cluster was scored for enrichment of candidate hits as compared to the remaining compounds outside the cluster, using the p-value from the hypergeometric distribution (Fisher’s exact test). This approach was used to score a set of published test compounds and activity levels, and their scoring system recovered over 80% of the known active compounds. The authors suggested that hits selected using such a cluster scoring system based on Daylight fingerprints would have higher confirmation rates than merely relying on the potency displayed by each compound separately in a primary screen.

Yan, et al [3] conducted a similar investigation, also using Daylight fingerprint-based clusters again with the goal of improving confirmation rates. Instead of using a static threshold to define the set of candidate hits, the algorithm used a data-driven and cluster-specific threshold, in a spirit similar to gene ontology or gene set enrichment analyses for gene-expression data. Compounds were sorted by decreasing activity level, and at each successive activity level in the list of compounds, the hypergeometric distribution was used to score the cluster for enrichment with candidate hits. The activity level associated with the lowest p-value for the cluster was used as the hit threshold for that cluster, and this minimum p-value was used as the cluster score. Statistical significance of the cluster enrichment score was assessed using a permutation test, separately for each cluster. A combination of cluster p-values and compound activity levels were used to rank the ‘hits’ within significant clusters. They retrospectively assessed the performance of the method on a set of existing HTS data. Importantly, in a pre-processing step, Yan, et al only considered compounds with activity levels above a filtering threshold which was specified in advance. Hence, in this approach there is still a universal activity threshold which needs to be specified prior to the analysis.

Varin, et al [5] proposed a method similar to Yan to identify active chemical series, et al, however using the Kolmogorov-Smirnov test to rank clusters, thus using the compound activity level itself rather than a binary score indicating whether the activity level is above a candidate threshold. This avoids the need to declare a candidate activity threshold, and considers enrichment for even very low levels of activity. P-values for the Kolmogorov-Smirnov test are available in closed form, avoiding the need for permutation tests. They used a multiplicity corrected significance level. They used computationally simpler scaffold tree compound classification to form the clusters, thus avoiding the computational burden of clustering the data. Tong, et al [14] used a mixture model to determine the threshold for calling hits in the primary high throughput screen, similar to our method of identifying confirmed hits using the primary and confirmation screens.

To address computational concerns about clustering very large data sets, Posner, et al [4] proposed a local hit rate analysis method similar to Klekota, et al, however scoring candidate hits against a neighborhood centered at the candidate compound with the goal to improve the confirmation rate for selected comopounds. These local neighborhoods were formed based on Daylight fingerprints and Tanimoto similarity values. Each compound was scored using a χ² test comparing the local hit rate within its neighborhood to a pre-specified background hit rate. Thus this method is similar to Klekota, et al, however avoiding the requirement to cluster the entire screening library.

Other reports have used cluster enrichment approaches to assist in design of HTS libraries, using existing HTS experiments as training data. These ‘supervised’ clustering methods [15] use existing HTS experiments as training data and include Laplacian-modified naïve Bayes models [16], recursive partitioning [17] and support vector machines [18] These studies have as a goal to identify active scaffolds. Emphasis has moved to using profiles of activity across multiple screens, for example, by using affinity fingerprints [19, 20], or by integrating chemical and genomics data base systems [21, 22]. Alternatively, the use of high content screening that has multiple variables that describe a compound, such as photographic images of cells, is being investigated to improve the quality of hits compared to single variable activity assays [23]. These sequential screening methods have focused on model-based compound selection to undergo a new HTS, rather than calling hits from the screen.

2. Overview of the HTS study

Briefly, the objective of the typical HTS assay we analyze here was to identify and characterize small molecules that might serve as novel adjuvants in human vaccines, including therapeutic anti-cancer vaccines. Compounds were to be tested for ability to stimulate immune cells in a human in vitro cell system, in the first step of a long drug discovery process. In the primary HTS, 160,000 compounds from eight commercially available libraries (Bioactive, Diversity, Kinase-targeted and RNA-targeted) were screened without replication, using a cell line which is engineered to express fluorescence when the gene of interest is stimulated. The cells were plated in 384-well plates, each with three columns of control wells (cell-free, full activation (LPS) and no activation wells (PBS)) and one column of LPS titration wells for quality control. The readout of the assay was percent activation, defined as the percent activation of compound over background, relative to the full-activation controls. Each compound was tested in one well, using high throughput robotics at a commercial HTS facility. The primary HTS was carried out continuously over 6 days. About 2,000 compounds were to be carried forward to a confirmation screen, using the same protocol as the primary screen. Confirmed positive hits from these screens were to be further triaged using cell-based toxicity screens, and then prioritized for further assays and drug development.

2.1. Design of the HTS

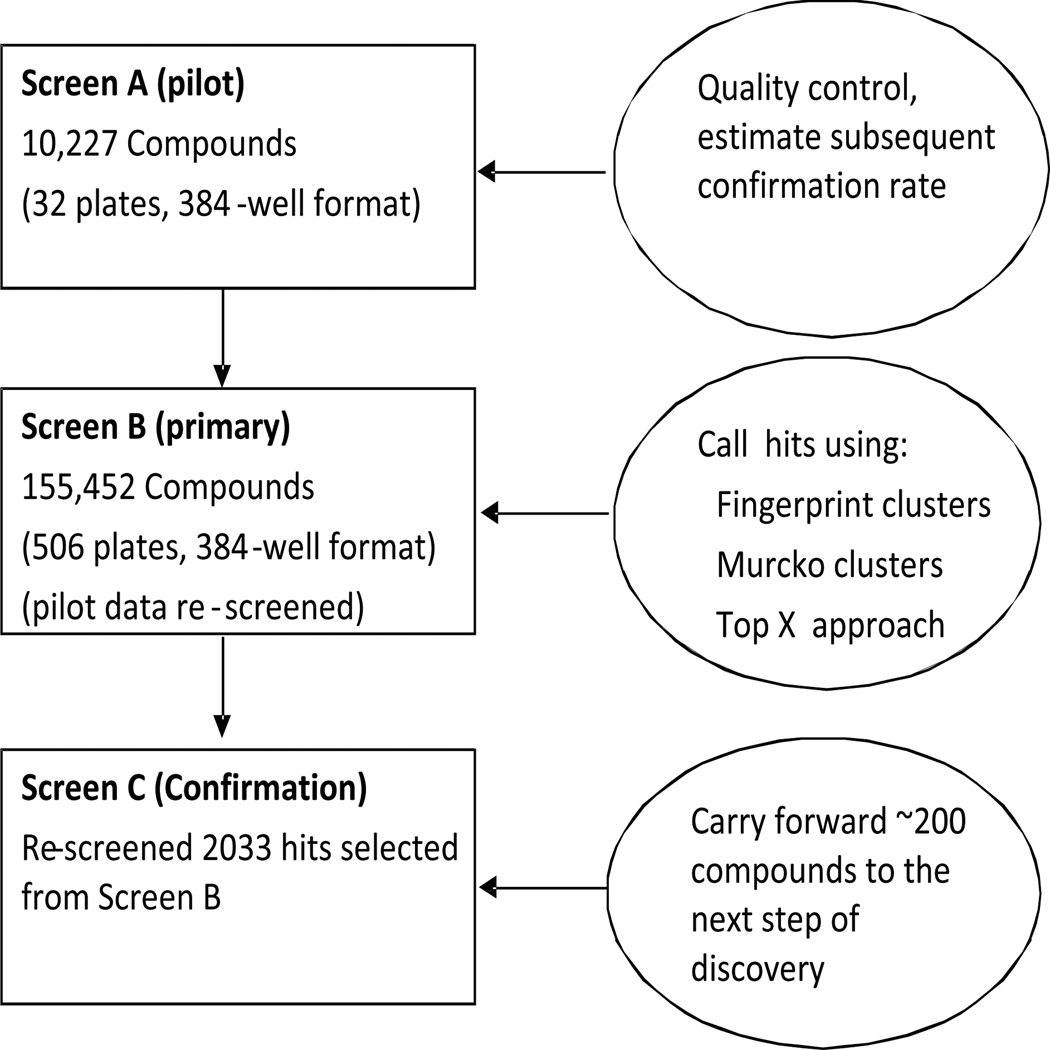
There were three sequential screens (Figure 1). A pilot screen (Screen A) of 10,000 compounds randomly chosen from the full screening library was used for quality control. Screen B was the primary screen; all the compounds of interest were screened, including those in Screen A. Screen C was the confirmation screen, carried out on 2033 hits selected from screens A and B. The number 2033 was determined by the budget and the initial estimate of the confirmation rate from screen A to screen B. Compounds identified as active (hits) in two screens are considered to be confirmed hits.

Figure 1.

Experimental Design.

2.2. Chemoinformatic descriptors used

Two distinct sets of chemoinformatic clusters were used in the enrichment strategy, one based on functional information and the other on molecular scaffolds. We expected that these two sets of descriptors would give complementary information.

Functional Class Fingerprints from Scitegic corporation (FCFP 6) are path-style fingerprints obtained by ‘walking’ the chemical structure of the molecule, and coding the component atoms as to their functional role. As each heavy (non-hydrogen) atom in the molecule is encountered, a code is assigned based on its estimated functional role relative to its neighbors [13]. The FCFP 6 algorithm results in a long bit string, which is then folded or reformatted into 1024 bits.

Murcko fragments are molecular scaffolds which form the backbone of a compound [24]. A compound is abstracted into its Murcko fragment scaffold on the basis of ring, linker, framework and side chain atoms. Each molecule is assigned to exactly one scaffold. It is computationally much simpler to abstract compounds into given Murcko scaffolds than to cluster a large library of compounds, and software Pipeline Pilot was used for our data [25].

3. The Clustering Algorithm, Test Statistic, and Confirmation Rate Model

3.1. The clustering algorithm

We applied a clustering algorithm to the functional class fingerprint descriptors, in order to assign each compound to a functional family. This was a moderately large clustering problem, of 160,000 compounds on the basis of 1024 binary variables. We used k-medoids hierarchical agglomerative clustering [26] based on Euclidian distance [2]. The R Clara function (R cluster package, v.12.0, www.r-project.org) was able to cluster this compound library into 200 clusters in approximately 142 minutes on a unix machine with 8 cores of Intel (R) Xeon (R) processor X5355 (4MB cache, 2.66GHz, 2666MHz FSB) and 16GB memory. The choice of number of clusters k was crucial, as too few (large) or too many (small) clusters could each adversely affect the confirmation rate and the number of hits called. We chose the number of clusters on the basis of power considerations and median cluster size, as described in section 4.1 below.

We also used the computationally simpler Murcko scaffolds [24]. As each molecule is assigned to one Murcko scaffold, these implicitly form the clusters. We did not have control over the number of clusters created, and there were many more, but smaller, clusters compared to the functional class clusters.

3.2. Algorithm to call hits using enriched clusters

We called cluster-supported hits separately using the Murcko scaffold clusters and the Functional Class clusters, because we thought the two sets of descriptors might provide different sets of information. After quality control and filtering, compounds were ranked individually by assay activity level. Compounds ranking above 12% activation (in the top 2% of activity) were called candidate hits, yielding 3079 candidates. The threshold of the top 2% was chosen by considering the distribution of the no-activation control wells. Activity of 12% was considered to be low, which was at approximately the 98.3^th percentile of the no-activation controls (note that the top 4% of activity was at the 95.1^th percentile).

Each cluster was scored for enrichment of candidate hits within the cluster as compared to the remaining compounds outside the cluster, using Fisher’s exact test. The Benjamini-Hochberg method [27] was used to control the false discovery rate (FDR) over the clusters, and the threshold for significance was a q-value of less than 0.05. We computed the FDR adjustment separately for the two kinds of clusters (Murcko or Functional Class). Because enrichment was negatively correlated between clusters, whereas Benjamini-Hochberg requires independence or positive correlation, a permutation test was used to assess FDR control. For both sets of clusters, the permutation test validated the set of selected clusters as statistically significant. Candidate hits contained in a significantly enriched cluster were called as hits, and carried forward to the confirmation screen.

3.3. Data-driven estimation of confirmation rates

It is usual in HTS to both call and confirm hits by comparison with a fixed activity threshold established during the primary screen. The confirmation rate is then calculated as the number of compounds above this threshold in the confirmation screen, divided by the total number of hits carried forward from the primary screen to the confirmation screen. However, in our cluster enrichment strategy we intended to set the activity threshold in the primary screen at a purposefully low value, to identify candidate hits for further data analysis. Thus it may not be appropriate to use the same low threshold for confirming hits in the subsequent screen. Hence we investigated methods of identifying the appropriate confirmation threshold using data from both the primary and confirmation screens.

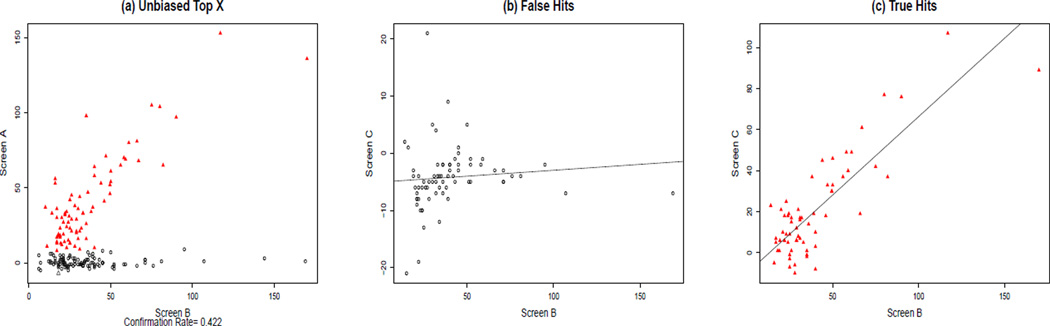
We used the 10,192 compounds with activity data from both the pilot and primary screens (Figure 2) to study how to estimate confirmation rates. We first called 187 hits in Screen B, using as criterion activity more than 3 standard deviations above the mean of all testing compounds on each plate (12% activity threshold). We used the pilot screen as confirmation. Figure 2a) shows a plot of activity level from the ‘confirmation screen’ (Screen A) against the primary screen (Screen B) for these 187 called hits. The figure clearly shows two distinct clusters: a ‘confirmed active’ cluster (red) and a ‘false positive’ cluster (black). We then used a mixture of two linear regression models to classify compounds into confirmed and false positive hits. We constrained the slope for the ‘false positive’ cluster to be zero; when we removed this constraint and estimated the slope instead, it was almost always not statistically different from zero in these data sets. The mixture model was:

$$E[y_i|x_i]=\pi ({\beta }_{01}+{\beta }_{11}{x}_i+{\epsilon }_1)+(1-\pi )({\beta }_{02}+{\epsilon }_2)$$

where y is the activity level in the confirmation screen, x is the activity level in the primary screen, and ${\epsilon }_i~N(0,{\sigma }_i^2)$ for i = 1, 2. An EM algorithm was used to estimate model parameters [28]. A compound was classified into Cluster 1 if π > 0.5, with the exception that if y_i ≤ β₀₂, the estimated mean activity from the false positive cluster, the compound was classified as false positive. This latter was introduced to take care of a few low outliers which were assigned to the true positive class by the model.

Figure 2.

Performance of the data-driven threshold for estimating confirmation rates. 187 hits were selected from among the pilot data (n=10,192) using the top X approach in the primary screen (screen B), and confirmed using screen A. A mixture model applied to data from both screens was used to identify confirmed hits. Screen C was then used to independently assess performance of the mixture model. (a) Activity levels in the primary (Screen B) and ‘confirmation’ screen (Screen A) are plotted for these 187 hits. Confirmed hits (red) and false positives (black) were identified by fitting a mixture model. (b) False positive hits identified by the mixture model and carried forward to screen C showed that these compounds also had low activity in Screen C. (c) Confirmed hits identified by the mixture model in (a) and carried forward to Screen C. Most of the confirmed hits were also independently confirmed in Screen C, establishing that the mixture model gives reasonable estimates of confirmed and false positive hits.

We validated this mixture model approach to estimating the confirmation rate, using available data from screen C. Among the 187 hits selected by the top X approach in screen B, 108 (B+ and A−) compounds were classified as false positives by our mixture model (Figure 2a; black circles); Of these, 71 also had Screen C data. Activities for these compounds were then plotted against screen C and only one among these ‘false positives’ failed to validate, by recording a value above 12% (Figure 2b). This confirms that for the majority of these compounds designated as false positive, an unknown factor associated with Screen B caused them to have high activities in the primary screen, which did not replicate in the other two screens. In addition, the slope in Figure 2b was estimated using a simple linear regression and it was not statistically different from 0 (slope = 0.02; p =0.45), whereas for the confirmed hits in Figure 2c, the estimated slope remained significantly above zero (slope =0.76, p ≪ 0.0001). While some confirmed hits have low activity in the confirmation screen, this is consistent with a mixture model with normally distributed errors, and gave an estimated confirmation rate of 42% for the top X approach, which was consistent with results from the primary and confirmation screens and in line with other HTS studies. Thus we used this data-driven threshold for estimating the confirmation rate, which we felt was more appropriate for our cluster enrichment analysis..

4. Choice of number of clusters k

4.1. Number of clusters k and statistical power

The first important data analysis decision was the criterion to choose the number of clusters k. Table 1 below gives the size distribution of the clusters and the number of cluster-supported hits and that would be selected for various choices of k. Our thinking was that size would influence both power to detect enrichment (larger is better) and the similarity of compounds within the cluster (smaller is better). We speculated that smaller, more similar clusters might have a higher confirmation rate, while larger clusters might have a greater chance of being declared significantly enriched.

Table 1.

The number of Functional Class clusters k v.s. the OR detectable at 90% power

k	25	50	100	200	400	800
# compounds per cluster: Median (Q1, Q3)	1346 (611, 8121)	876 (326, 2964)	409 (212, 1099)	345 (133, 793)	153 (61, 399)	118 (48, 246)
OR w/~ 90% power, at median cluster size	1.34	1.42	1.64	1.69	2.15	2.47
# unadjusted hits called	2063	1573	1544	1233	1202	1270
# of FDR adjusted hits called	1348	1564	1460	1149	1136	1000

Following the literature, we first considered using similarity measures as the criterion for selecting the optimal number of clusters, including the total dissimilarity score [9], the average silhouette width [10], as well as a chemoinformatic entropy score that tests the chemical similarity principle within clusters [2]. However, all these measures continued to change significantly as k increased up to 800 clusters, suggesting that more and smaller clusters were needed. However, we feared that with too many clusters we would pay too large a penalty to control the false discovery rate, and that within small clusters the effect odds ratios would have to be very large in order for the cluster to be called statistically significant, leading to low power. Finally, when ranking clusters, we feared that estimated enrichment odds ratios would be too variable to be be informative if there were many small clusters. These fears appear to have been born out in our analysis of the confirmation screen data on the Murcko clusters (Section 5), which were very numerous and very small.

Having decided against use of information measures in selecting the number of clusters, we investigated power considerations. Given that 2% of compounds were considered candidate hits, we can derive the asymptotic power of Pearsons’s Chi-squared test by considering the asymptotically equivalent approximately normal test statistic

$$z=({\widehat{p}}_c-{\widehat{p}}_r)/{(p_c(1-p_c)/n_c+p_r(1-p_r)/n_r)}^{1/2},$$

where the subscript c refers to the compounds within the cluster and r the remaining compounds, p the proportion of candidate hits, and n the number of compounds. If p_c is small, p_r = 0.02, and n_r is large, this test statistic has mean (p_c − 0.02) and standard deviation approximately $\sqrt{p_c/n_c}$. Using this relation, given a cluster size n we solved for the proportion p_c(n_c) and subsequently the enrichment odds ratio that would give a relative effect size of 2 (that is, the for which the test statistic mean would be approximately 2 standard deviations above zero), considering that this would give adequate asymptotic power. In terms of absolute odds ratios, we thought that enrichment odds ratios of between 1.5 and 2 would represent a reasonable range for meaningful detectable effect sizes; using the relation between p_c(n_c) and n_c, we found a detectable effect size of from 1.5 to 2 corresponded to cluster sizes of 200 to 700. Thus we aimed to have the bulk of our clusters within this range, and from Table 1, k = 200 seemed to best fit this criterion.

Although we did not formally include the loss of power due to the FDR correction with increasing number of clusters, this is clearly seen in Table 1. The number of FDR adjusted hits falls substantially when comparing k = 400 with k = 800. The robustness of the choice of k across a wide range is also seen. In fact, the set of hits selected was fairly stable across the range of 50 ≤ k ≤ 400; thus any k within this range may have been reasonable, although we chose k=200 based on the power considerations above.

4.2. Resulting size distribution of clusters

Functional Class clusters

With the number of clusters set to 200, the median cluster size was 345 compounds, with first and third quartiles 133 and 793, respectively. Thus we were able to obtain a cluster set with about half of the clusters near or within our desired range of cluster sizes. However, eighteen clusters contained more than 2000 compounds and just under half of all compounds (69,565 or 44.8%) resided in one of these large clusters.

Murcko scaffold clusters

We had less control over the size distribution of the Murcko scaffold clusters, and the Murcko clusters were smaller than we desired. Compounds in the primary screen belonged to a total of 43,973 Murcko scaffold clusters, most of which had four or fewer compounds. To reduce loss due to the FDR correction, we restricted our analysis to the 5452 clusters which contained at least 5 compounds. Together these contained the majority (100,040, or 64.4%) of compounds. Consequently, among 3079 candidate hits, only the 1942 (63.1%) residing in these clusters were considered by this approach, clearly demonstrating the loss of power by using clusters that are too numerous and too small.

4.3. Results: significant clusters and called hits

Among the 200 functional clusters, 29 (14.5%) were found to be significantly enhanced. About one-third (1,149 of 3079) of candidate hits were called as hits because they were contained in a significantly enhanced Functional Class cluster. Among the 5425 Murcko scaffold clusters, 62 (1.1%) were significantly enhanced. About one-quarter (496 of 1942) of screened candidates were called as hits, and the total number of contributed hits was much lower, confirming the low power of the scaffold clusters.

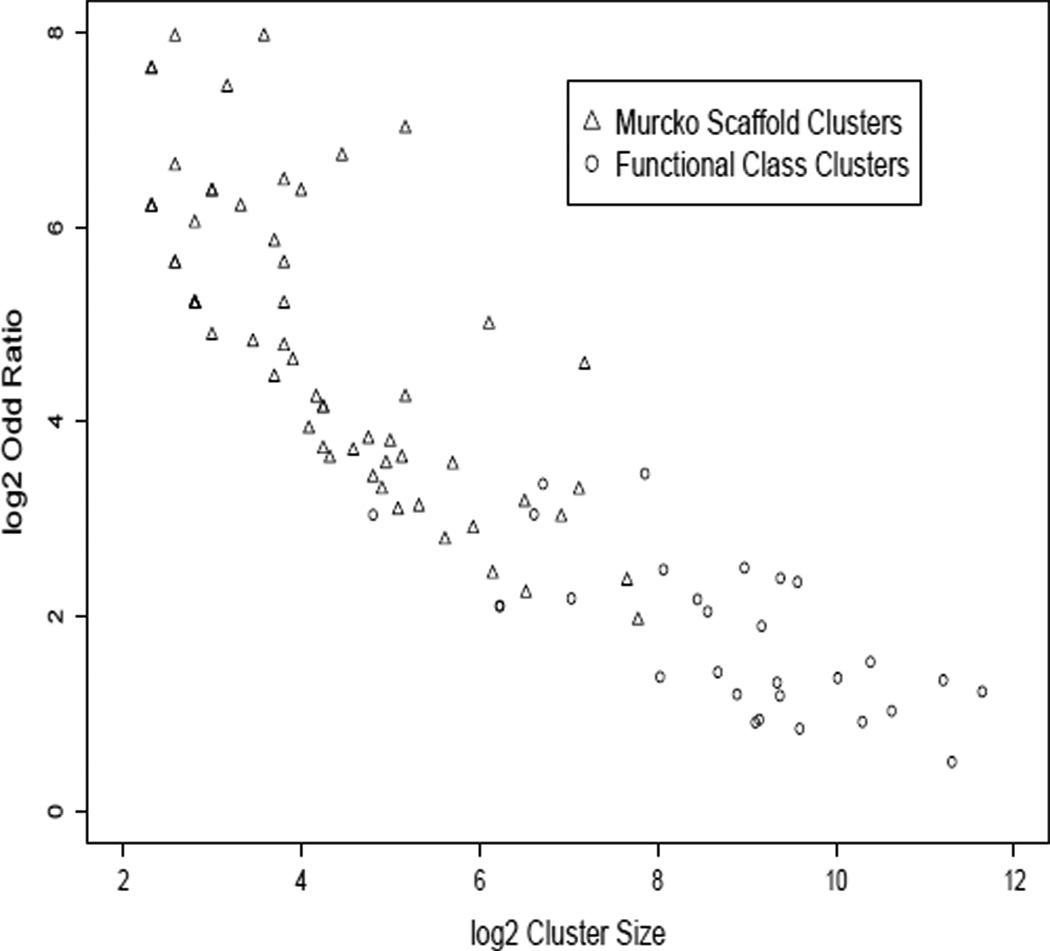
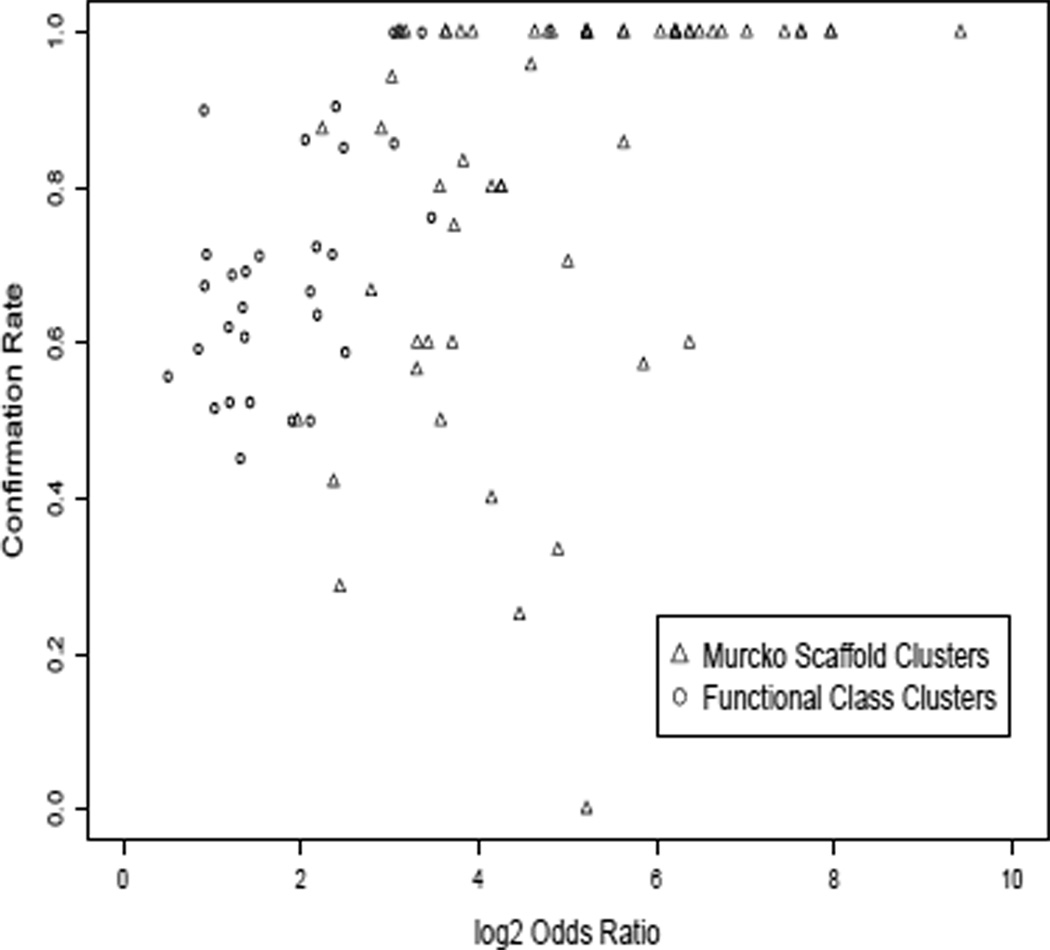
It is possible that the low power of the Murcko classes was because these descriptors simply carry less information. However, Figure 3 confirms the strong negative correlation between cluster size and OR among clusters selected as significant. The Murcko clusters are seen to be generally smaller and with larger enrichment odds ratios, compared to the larger Fingerprint clusters. The large number of Murcko clusters further reduced power by requiring a large FDR correction in order to avoid false positive clusters. There is no apparent difference between cluster types (functional or scaffold) in the relation between cluster size and enrichment odds ratio. Further, all but 106 of the Murcko class hits had already been selected by the Functional Class clusters and and a majority of the significant Murcko class clusters were a subset of a significant Functional class cluster. This supports the interpretation that the information carried by these two sets of descriptors was similar, and that the low power of the Murcko clusters was because they were too numerous and too small.

Figure 3.

Estimated enrichment log odds ratio (OR) vs log cluster size for clusters selected as significantly enriched. For Functional class clusters, we targeted the cluster size as closely as possible to be powered to detect an OR of 1.5 to 2, thinking these would be practically meaningful and robustly estimated effect sizes; Murcko clusters sizes were smaller than we desired. The relation between observed OR and cluster size is consistent with our power calculations and does not appear to differ between the two sets of descriptors, consistent with the interpretation that cluster size was the major difference between them.

An important observation is that our enrichment methods together failed to reach the goal of 2033 hits, selecting only a total of 1255 compounds. To reach the desired number of hits, the top X approach was used to select additional compounds. To avoid auto-fluorescence, we included all compounds with activity between 22% and 120%. Thus, 778 additional compounds were selected using only the individual activity readout.

5. Confirmation rates, and prioritizing the hit list

We carried forward the 2033 selected hits to the confirmation screen. Here we investigate whether the cluster-based methods increased the confirmation rate and the number of confirmed hits selected. We see whether the lower number of selected hits using smaller Murcko clusters was offset by higher confirmation rates. We also investigate how to best prioritize hit selection during analysis of the primary screen. In these analyses, we use our data driven estimates of the confirmation rate, as described in Section 3.3.

5.1. Comparison of confirmation rates and number of confirmed hits

The overall confirmation rate for the 2033 selected hits was 58.4%, which gave us a total of 1187 hits. Figure 4 shows the activity distribution of confirmed hits and false positives separately for the three sets of hits. Compounds supported by Murcko clusters had the highest confirmation rate (83.3%) but also the smallest number of compounds selected (496), for a total of 413 confirmed hits (Figure 4a). The confirmation rate from the Functional Class clusters was lower (67.3%), however a larger number of hits were selected (1149), to arrive at 773 confirmed hits (Figure 4b). A total of 310 compounds were confirmed hits by both the methods. The Top X approach on the remaining data had the lowest confirmation rate, at 40% (Figure 4c), and contributed 311 confirmed hits.

Figure 4.

Estimation of confirmation rates using a mixture model of two linear regressions, which identifies confirmed hits (red) and false positives (black). It is apparent that fewer hits are selected, but with higher confirmation rates, for Murcko clusters. However the total number of confirmed hits (red) is smaller than that of the Functional Class Fingerprints method. Analysis suggests this is a function of the smaller cluster size of the Murcko clusters.

Thus, the cluster based methods were highly successful in increasing the confirmation rate compared to a Top-X approach. The smaller number of confirmed hits selected by the Murcko clusters again is consistent with the cluster size being too small for adequate power, and this was not overcome by its higher confirmation rate. Overall, we would have liked to have been able to call additional hits using either cluster-based approach without sacrificing a high confirmation rate, as we fell short of the goal of 2033 hits. How to best do so is investigated in Section 6.

5.2. Prioritizing the hit list

A fundamental goal in selecting hits from a HTS is to optimize the confirmation rate given the total number of hits selected. The desired number of hits may be dictated by programmatic reasons, which in our case were budgetary and dictated 2033 hits. Our strategy was to first rank the significant clusters according to enrichment OR, as a proxy for the unknown cluster confirmation rate. Then we walked down the list, sequentially adding the supported hits within each cluster, until the desired number of hits was selected. (Because we found too few hits, in fact we used all available clusters.) This strategy should optimize the confirmation rate given the total number of hits selected, provided there is a monotone increasing relationship between OR and confirmation rate.

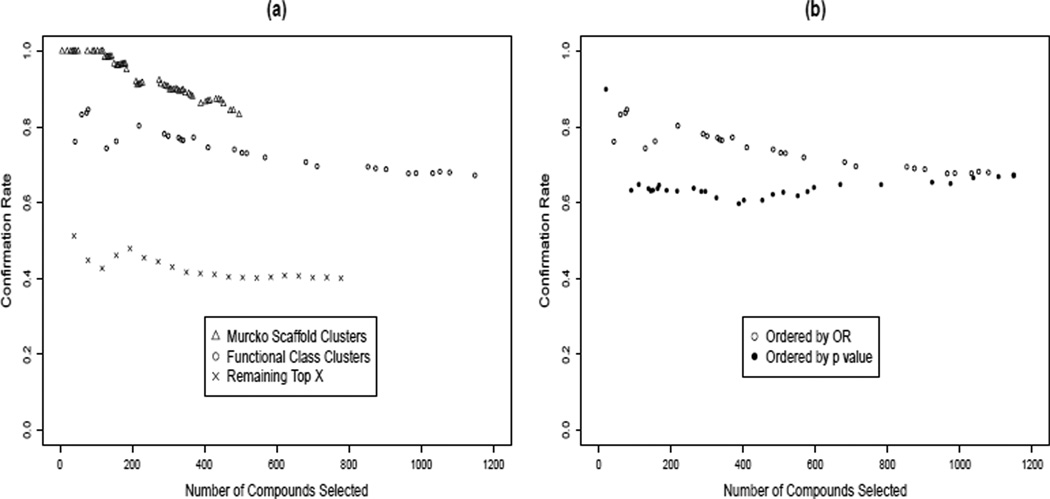
To evaluate this method, Figure 5a shows the cumulative confirmation rate using data from the confirmation screen (C) versus the number of compounds selected, as each additional ranked cluster is called significant and its candidate hits are added to the hit list. To calculate the cumulative confirmation rate for cluster i, all the compounds in clusters 1 to i were included. (Here, for the Top X approach, compounds were sorted in descending order of activity level and grouped into 20 same-sized clusters. ) Thus, the cumulative confirmation rate at a given cluster shows what the confirmation rate and number of selected hits would have been, had the total number of selected clusters stopped at that point. The last data point for each series shows the final number of selected hits and the final confirmation rate for our HTS.

Figure 5.

Ranking of significant clusters. (a) Cumulative confirmation rate versus number of selected hits, among significant clusters as ranked by enrichment odds ratio, for three approaches. Although Murcko clusters have higher confirmation rates, the total number of hits selected is smaller and the confirmation rate declines more rapidly, as compared to Functional Class Clusters. The ‘Top X’ approach has the least satisfactory performance. (b) Confirmation rate versus the number of compounds selected by Functional Class clusters, ordered by either odds ratio (open circles) or cluster p-value (solid circles). P-values are unrelated to confirmation rate, demonstrating that enrichment odds ratio is a better metric by which to rank significant clusters.

In Figure 5a, one can see both the steep decline of the Murcko clusters as additional clusters are called significant and the smaller number of hits called. Extrapolating these trends, should we have continued, the confirmation rate for Murcko clusters would have been below the Functional Class clusters after about 800 hits called. On the other hand, the Functional Class clusters could have apparently continued at about 67% confirmation rate, potentially increasing the overall confirmation rate. This suggests that an effective strategy to increase the number of hits called would have been to lower the significance threshold on the clusters. We investigate this strategy in Section 6 below.

The reason for the steep decline of the cumulative confirmation rate for the Murcko clusters can be seen in Figure 6, which shows the cluster-level confirmation rate plotted against estimated enrichment OR, separately for Murcko clusters and Functional Class clusters. For the Functional Class clusters, as expected the average confirmation rate increases with increasing OR (ρ = 0.34, p = 0.08). This confirms that the cluster ranking strategy to call hits worked well for Functional Class clusters. However, for the Murcko clusters after the first 18 clusters are excluded, there is no longer a relation between enrichment OR and confirmation rate (ρ = −0.08, p = 0.80). Increased variability of the OR for Murcko compared to Functional Class clusters is also apparent in figure 6; this may be due to the small size of the Murcko clusters. Thus, after the first few clusters, ranking the clusters by OR adds no information on the eventual confirmation rate for Murcko clusters.

Figure 6.

Confirmation rate vs the enrichment odds ratio for statistically significant clusters. Triangles: Murcko scaffold fragments; Circles: Clusters made using Scitegic FCFP6 functional class descriptors. The larger functional class clusters show consistent correlation between odds ratio and confirmation rate; the smaller and more variable Murcko clusters do not.

It has been suggested in the literature that ranking clusters by p-value, or by a combination of p-value and activity ratio is an appropriate metric [3]. Note that there was no correlation of confirmation rate with p-value for the Functional Class clusters (Figure 5b). Thus enrichment odds ratio (OR) is an appropriate metric for ranking significant clusters in order to choose hits, but p-value is not.

6. Sensitivity studies using the Pilot Data: choice of the cluster scoring statistic, the threshold for candidate hits, and cluster size

In this section we use the 10,192 compounds with complete data in both pilot and main screens to evaluate the a priori choices that must be made during cluster-based analysis of a HTS. These include the number and size of clusters, the scoring algorithm used to call clusters as significant, and the strategy for ranking clusters and thresholding them for hit selection. Note that these choices must be made prior to observing confirmation data, as was the case in our prospective HTS. Recall that we selected fewer than the optimal number of hits using cluster based methods, and would have liked to have found additional cluster-supported hits.

We used Screen A as the confirmation screen and screen B as the primary screen; thus for these sensitivity studies we have complete confirmation data on all the compounds in a random subset of the primary screen, in contrast to our actual experiment. The compounds were clustered into functional classes using the Functional Class descriptors as input to the R Clara program, or using Murcko fragments, as before.

6.1. Choice of test statistic for scoring clusters

Much attention has been paid in the literature to the choice of test statistic for scoring clusters [3, 5]. While simple and effective, our method has the potential drawback that the threshold for the candidate hits must be specified in advance. Recall that we set this threshold at 12% activation by considering activity levels for the no-activation controls. In this section, we compare this simpler method to using a data-driven threshold for candidate hits which is specific to each cluster [3], similar to gene-ontology analysis.

We clustered the compounds into 25 clusters using the Functional Class descriptors, which gave a median cluster size of 101 compounds. To apply the data-driven method proposed by Yan et al [3], we first ranked all the compounds by activity level in screen B. Let x_(i) represent the activity level from the ith ordered compound. Let p_ij be the hypergeometric p-value assessing enrichment of cluster j with candidate hits, where compounds with activity above x_(i) are considered candidate hits. Finally, let p_j = min_i{p_ij} be the enrichment score assigned to cluster j. Permutation p-values were used to assess the statistical significance of the p_j, with a separate permutation of size 1,000 computed for each cluster, and significance was assessed at the 5% level without an FDR correction. Because we wanted a truly data driven approach, we did not prefilter the compounds we considered to those with activity levels above a threshold, in contrast to the published method [3]. Consequently, we discovered the lowest p-values sometimes fell at very low activity levels, and thus we were selecting for enrichment with inactive compounds rather than active compounds. To remedy this, we considered only p-values which came from activity thresholds within the first 300 compounds. Interestingly, it seems an implicit global candidate activity threshold is required for this method as well.

For our global- threshold method, the top 3% (activity cut-off ≥ 12%, as before) of the compounds were considered to be candidate hits, and each cluster was scored for enrichment using Fisher’s exact test, with significance assessed at the 5% level without an FDR correction. For each test statistic, hits were selected as the candidate hits within significant clusters. We then compared confirmation rates using screen A as the pilot screen.

Using the data-driven method, at 5% significance level 107 compounds were selected and the confirmation rate was 53.3%. Using our global threshold method,111 compounds were selected with a confirmation rate (CR) of 52.3%. Most compounds selected were the same. This pattern repeated if we changed the significance level to 1%: Yan’s method selected 37 compounds with a CR of 78.4% and our fixed threshold method selected 34 compounds with a CR of 79.4%. Again most compounds selected were the same. Thus, for the most reasonable choice of parameters, the two methods were very similar in hits selected, but our method is much simpler.

We then explored the effect of changing the number of clusters and the threshold for candidate hits. Table 2 shows the confirmation rates and number of confirmed hits selected given different choices for the number of clusters, K, and the candidate hit threshold, θ, for both Yan’s method and the fixed threshold method. In implementing Yan’s method, if θ =3%, we only searched for the lowest p-value in the top 3% of the activity-sorted compound list. Clusters were called significant based on unadjusted p-values below 5% significance level, and we estimated confirmation rates using the mixture model approach. Overall, these studies confirm the equivalence of the two test statistics for scoring clusters: they generated equivalent confirmation rates and a similar number of hits, and often selected virtually the same set of compounds.

Table 2.

Confirmation rates^a from Functional Class clusters for various combinations of k (number of k-medoids clusters) and θ (threshold for candidate hits^b). A: Global threshold (our method). B: Cluster-specific thresholds [3].

K	A: Fixed Threshold for candidate hits: θ
	1%	2%	3%	4%	5%	6%
25	13/14 (92.9%)	27/51 (52.9%)	58/111 (52.3%)	43/86 (50%)	79/166 (47.6%)	88/196 (44.9%)
50	17/25 (68%)	41/71 (57.7%)	81/134 (60.4%)	93/161 (57.8%)	106/206 (51.5%)	138/243 (56.8%)
100	27/31 (87.1%)	52/73 (71.2%)	59/90 (65.6%)	80/124 (64.5%)	110/172 (64%)	99/174 (56.9%)
500	19/26 (73%)	35/52 (67.3%)	62/99 (62.6%)	69/112 (61.6%)	91/156 (58.3%)	96/171 (56.1%)
K	B. Yarn’s method: Data driven threshold for candidate hits: θ
	1%	2%	3%	4%	5%	6%
25	7/10 (70%)	40/77 (51.9%)	56/107 (52.3%)	61/123 (49.6%)	63/128 (49.2%)	65/133 (48.9%)
50	9/20 (45%)	37/68 (54.4%)	73/130 (56.2%)	88/152 (57.9%)	114/200 (57%)	125/220 (56.8%)
100	23/34 (67.6%)	46/76 (60.5%)	66/105 (62.9%)	97/151 (64.2%)	116/180 (64.4%)	124/195 (63.6%)
500	25/47 (53.2%)	50/91 (54.9%)	70/123 (56.9%)	85/166 (51.2%)	108/199 (54.3%)	118/221 (53.4%)

^aConfirmation rates were estimated using the mixture model approach.

^bHit selection based on significant clusters at an unadjusted p-value ≤ 0.05.

In summary, in this study there was no advantage seen for the more complex cluster specific threshold method in [3]. A global threshold was in fact still required, and if this threshold was set to a comparable level, virtually the same hit set was selected as by our simpler scoring using Fisher’s exact test against a global threshold.

6.2. Varying the number of clusters k

Table 2 appears to confirm our earlier remarks regarding size and number of clusters. For any given θ ≥ 3%, within a wide range of the number of clusters (50 ≤ K ≤ 500), the confirmation rate and number of confirmed hits appears to be fairly stable. However, if k is too small so that clusters are too large, both the number of confirmed hits and the confirmation rate are lower, and the same is true if k is too large. Thus we recommend choosing the number of clusters based on power considerations as in Section xx.

6.3. Setting the activity threshold for candidate hits and the FDR threshold for significant clusters

Recall that, in retrospect, we would have liked to call additional hits using the cluster enrichment strategy. However, we used all the significant clusters and still fell short of our goal of 2033 hits to carry forward to the confirmation screen. There are two ways we might have increased the number of significant clusters: one might lower the threshold for candidate hits, thereby increasing the number of candidate hits residing within each cluster. Or, one might directly increase the number of significant clusters by relaxing the FDR q-value at which a cluster is declared significant.

Table 2 shows that as the candidate hit threshold θ decreases from 2% to 6%, the confirmation rate appears to be fairly stable, with only a small decrease. However, the absolute number of hits increases. This suggests that lowering the threshold θ is an effective way to increase the number of hits selected while maintaining a high confirmation rate. However, for each new value of θ, the scoring statistic has to be recomputed across all the clusters.

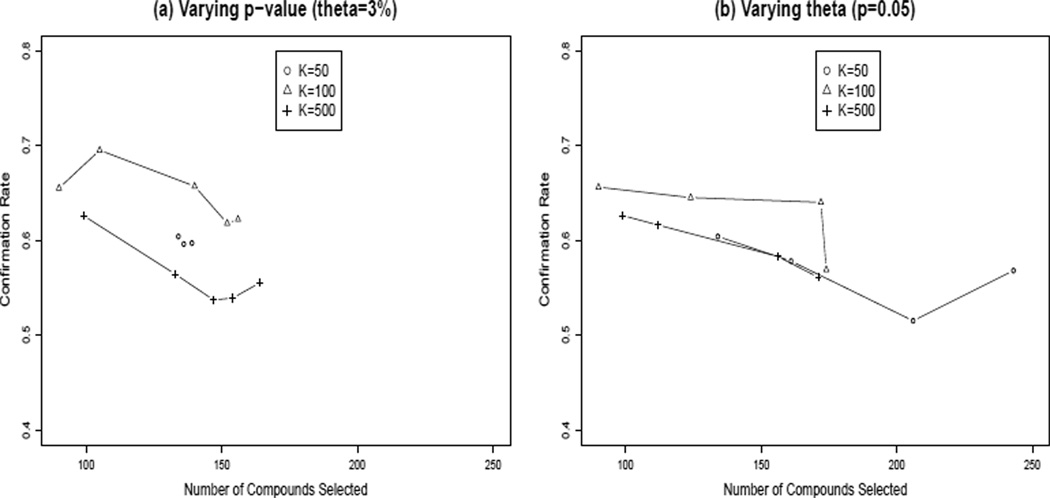
It is computationally simpler to choose a fixed value for θ, to score all the clusters using Fisher’s exact test, and then to relax the significance standard α for calling a cluster significant. We compared these methods using a starting values of α = 0.05 and θ = 3%, for three sets of cluster sizes (k = 50, 100, 500). Results are plotted in Figure 7, where we let α range from 0.05 to 0.25 at θ = 3% and let θ range from 3% to 6% at α = 0.05. It can be seen that the two methods perform similarly in terms of confirmation rate vs number of hits selected. At least in this example, relaxing the candidate hit threshold θ increases the potential total number of hits that might be selected, while relaxing the p-value (or q-value) is more easily done for a given set of scored clusters.

Figure 7.

Confirmation rate vs number of compounds selected when including all significant clusters, by relaxing two different selection criteria: (a) lowering the threshold θ for candidate hits; (b) raising the significance level α for significant clusters. α ranges from 0.05 to 0.25 at θ = 3% and θ ranges from 3% to 6% at α = 0.05. Each method is shown on three different cluster sets. Either method appears to work well for increasing the potential number of hits selected; the significance level is computationally more convenient.

Thus in practice, we recommend choosing the candidate activity threshold θ from intrinsic properties of the assay, and then walking down the clusters in order of enrichment OR until the desired number of hits are called. If this number is insufficient at a reasonable FDR value such as 5% to 20%, then we suggest further relaxing θ. In addition, in practice additional hits may be called for programmatic reasons such as diversity.

7. Discussion

In this paper, we have discussed how to prospectively conduct a cluster-based analysis to identify hits in a high throughput screen, and have demonstrated a resulting improvement in both the confirmation rate and total number of confirmed hits from the screen. Although cluster-based statistics have previously been proposed [2, 3], we aimed to provide a unified evaluation of all the design parameters required in the analysis.

Our studies suggest that the screening library first be clustered into a number of moderate-sized clusters, based on power considerations. Then, a relaxed activity threshold should be chosen, in order to call a large number of candidate hits. The clusters are then scored for enrichment with candidate hits. Clusters that pass an FDR-adjusted significance level are prioritized by enrichment odds ratio, not p-value. One can then walk down the ranked list of candidate hits until the desired number of hits is called. If the desired number of hits is not achieved, either the activity threshold or the FDR level can be further relaxed, and the analysis repeated. Once the selected hits are assayed in the confirmation screen, confirmed hits are identified using a data-driven threshold. By using this strategy, we estimate that we were able to improve the number of confirmed hits by about 31.5%, from 813(= 2033 × 0.4) using the Top X approach to 1187 (see section 5.1) using our cluster-based method, in the HTS presented here.

Importantly, among all design choices, the choice of test statistic to score the clusters appears to be relatively unimportant, despite the attention paid to this aspect in the literature. Comparing our Fisher exact test to a more complex data-driven approach [3], we arrived at nearly identical hit sets. Our approach was similar to Klekota, et al, although more statistically motivated. Our studies suggest that cluster size is the most important parameter, and that this should be chosen based on power considerations.

We used enrichment odds ratios rather than p-values to rank the clusters, however only clusters with a statistically significant FDR adjusted q-value were considered. Figure 5 showed that the cumulative confirmation rate decreased as expected across clusters when ordered by odds ratios, but this was not the case when ordered by p-values. The figure also demonstrates that it is helpful if clusters are large enough to reliably estimate the enrichment odds ratios.

In previous studies [2, 3] the numbers of compounds considered were in the ballpark of our pilot data; thus our application, an order of magnitude larger, is more typical of HTS practice. We used a k-medoids clustering algorithm, suitable for clustering the 160,000 compounds in the primary screen using 1024 variables, and this was feasible and worked well. The choice of number of clusters k was among the most important analysis decisions, as this determined the distribution of cluster sizes. Unlike other published methods, we chose not to discard compounds with very low activities in order to reduce computational burden of clustering, because we wanted to retain an objective estimate of the percentages of active compounds contained within the clusters. We chose the number of clusters k attempting to maximize the number of FDR adjusted hits using a priori power considerations, rather than similarity measures as suggested in the literature. We demonstrated the loss of power if too many, too small clusters are used, as would be the case using similarity measures to determine k.

We used two classes of molecular descriptors to form clusters: Functional Class fingerprints and Murcko scaffold fragments. Although the Functional Class clusters had a lower confirmation rate (67% compared to 83%), a larger number of hits were called, which resulted in more than double the number of confirmed hits. Our analysis suggested that somewhat surprisingly, the information carried by the Murcko scaffolds and the Functional Class clusters was similar, and the reason for the improved performance of the latter was a better size distribution across clusters. Both of the cluster-based approaches greatly improved confirmation rates compared to the standard Top X approach, providing additional evidence that treating each compound individually is not optimal.

In our HTS, we did not achieve our target number of hits using our cluster-based approach, and we supplemented the cluster-supported hits by calling additional top X hits. In retrospect, based on the studies reported here, we could have selected additional cluster-supported hits by either lowering the threshold for a candidate hit or by relaxing the significance level at which a cluster was selected. Our studies using a random subsample of the data with complete screening information suggest that either method would perform about equally well, and that either would outperform Top X; thus we suggest relaxing the significance level to achieve the desired number of hits as it is computationally simpler. If the target number of hits cannot be achieved at reasonable significance levels, then the threshold for a candidate hit can be lowered, and significance levels recomputed.

To identify confirmed hits, we used a novel data-driven method based on fitting a mixture of two linear models to the combined primary and confirmation screening data. We validated this approach using our pilot data: estimated confirmation rates for the Top X approach using our pilot data were within the ballpark of other studies and agreed with the rate seen in the confirmation screen, which was around 40%.

A potential limitation of a cluster-based approach is that it may miss singleton compounds that may be good candidates but which lack related active compounds within a large structural family. This may potentially reduce the chemical or biological diversity of the selected hits. Thus it may be desirable to increase diversity by selecting only a few hits from within each cluster, or by supplementing cluster supported hits with additional hits called using the top X approach, with an eye to increasing compound diversity. The computational burden of clustering may also be a limitation for very large screening libraries. In this case, a top X approach could be used to filter out compounds with very low activity and the remaining compounds could be clustered. In large dedicated HTS facilities, there may be capacity to run large scale confirmatory screens, in which case our method may be of less interest. These methods will be useful in settings, such as our early stage research, where confirmatory screening capacity is limited, and so it is of importance to increase the confirmation rate.

In summary, our cluster-based approach to analyzing the data from a HTS appears to have improved both the confirmation rates and the number of called hits. In our screen, confirmation rates using Murcko fragments were 83.3%, and those using Functional Class clusters were 67.3%. We estimate these methods enabled us to increase the number of confirmed hits by about 31.5%. This project demonstrates the value of applying careful statistical analysis to calling hits from High Throughput Screening assays.