Basic Concepts in Population Modeling, Simulation, and Model-Based Drug Development—Part 2: Introduction to Pharmacokinetic Modeling Methods

Population pharmacokinetic models are used to describe the time course of drug exposure in patients and to investigate sources of variability in patient exposure. They can be used to simulate alternative dose regimens, allowing for informed assessment of dose regimens before study conduct. This paper is the second in a three-part series, providing an introduction into methods for developing and evaluating population pharmacokinetic models. Example model files are available in the Supplementary Data online.

Background

Population pharmacokinetics is the study of pharmacokinetics at the population level, in which data from all individuals in a population are evaluated simultaneously using a nonlinear mixed-effects model. “Nonlinear” refers to the fact that the dependent variable (e.g., concentration) is nonlinearly related to the model parameters and independent variable(s). “Mixed-effects” refers to the parameterization: parameters that do not vary across individuals are referred to as “fixed effects,” parameters that vary across individuals are called “random effects.” There are five major aspects to developing a population pharmacokinetic model: (i) data, (ii) structural model, (iii) statistical model, (iv) covariate models, and (v) modeling software. Structural models describe the typical concentration time course within the population. Statistical models account for “unexplainable” (random) variability in concentration within the population (e.g., between-subject, between-occasion, residual, etc.). Covariate models explain variability predicted by subject characteristics (covariates). Nonlinear mixed effects modeling software brings data and models together, implementing an estimation method for finding parameters for the structural, statistical, and covariate models that describe the data.¹

A primary goal of most population pharmacokinetic modeling evaluations is finding population pharmacokinetic parameters and sources of variability in a population. Other goals include relating observed concentrations to administered doses through identification of predictive covariates in a target population. Population pharmacokinetics does not require “rich” data (many observations/subject), as required for analysis of single-subject data, nor is there a need for structured sampling time schedules. “Sparse” data (few observations/subject), or a combination, can be used.

We examine the fundamentals of five key aspects of population pharmacokinetic modeling together with methods for comparing and evaluating population pharmacokinetic models.

Data Considerations

Generating databases for population analysis is one of the most critical and time-consuming portions of the evaluation.² Data should be scrutinized to ensure accuracy. Graphical assessment of data before modeling can identify potential problems. During data cleaning and initial model evaluations, data records may be identified as erroneous (e.g., a sudden, transient decrease in concentration) and can be commented out if they can be justified as an outlier or error that impairs model development.

All assays have a lower concentration limit below which concentrations cannot be reliably measured that should be reported with the data. The lower limit of quantification (LLOQ) is defined as the lowest standard on the calibration curve with a precision of 20% and accuracy of 80–120%.³ Data below LLOQ are designated below the limit of quantification. Observed data near LLOQ are generally censored if any samples in the data set are below the limit of quantification. One way to understand the influence of censoring is to include LLOQ as a horizontal line on concentration vs. time plots. Investigations^4,5,6,7 into population-modeling strategies and methods to deal with data below the limit of quantification (Supplementary Data online) show that the impact of censoring varies depending on circumstance; however, methods such as imputing below the limit of quantification concentrations as 0 or LLOQ/2 have been shown to be inaccurate. As population-modeling methods are generally more robust to the influence of censoring via LLOQ than noncompartmental analysis methods, censoring may account for differences in the results when applied to the same data set.

It is worthwhile considering what the concentrations reported in the database represent in vivo. Three major considerations of the data are of importance. First, the sampling matrix may influence the pharmacokinetic model and its interpretation. Plasma is the most common matrix, but the extent of distribution of drug into RBC dictates (i) whether whole blood or plasma concentrations are more informative; (ii) whether measured clearance (CL) should be referenced to plasma or blood flow in an eliminating organ; or (iii) may imply hematocrit or RBC binding contributes to differences in observed kinetics between subjects.⁸ Second, whether the data are free (unbound) or total concentrations. When free concentrations are measured, these data can be modeled using conventional techniques (with the understanding that parameters relate to free drug). When free and total concentrations are available, plasma binding can be incorporated into the model.⁹ Third, determining whether the data must be parent drug or an active metabolite is important. If a drug has an active metabolite, describing metabolite formation may be crucial in understanding clinical properties of a drug.

Software and Estimation Methods

Numerous population modeling software packages are available. Choosing a package requires careful consideration including number of users in your location familiar with the package, support for the package, and how well established the package is with regulatory reviewers. For practical reasons, most pharmacometricians are competent in only one or two packages.

Most packages share the concept of parameter estimation based on minimizing an objective function value (OFV), often using maximum likelihood estimation.² The OFV, expressed for convenience as minus twice the log of the likelihood, is a single number that provides an overall summary of how closely the model predictions (given a set of parameter values) match the data (maximum likelihood = lowest OFV = best fit). In population modeling, calculation of the likelihood is more complicated than models with only fixed effects.² When fitting population data, predicted concentrations for each subject depend on the difference between each subject's parameters (P_i) and the population parameters (P_pop) and the difference between each pair of observed (C_obs) and predicted (Ĉ) concentrations. A marginal likelihood needs to be calculated based on both the influence of the fixed effect (P_pop) and the random effect (η). The concept of a marginal likelihood is best illustrated for a model with a single population parameter (Supplementary Data online).

Analytical solutions for the marginal likelihood do not exist; therefore, several methods were implemented approximating the marginal likelihood while searching for the maximum likelihood. How this is done differentiates the many estimation methods available in population modeling software. Older approaches (e.g., FOCE, LAPLACE) approximate the true likelihood with another simplified function.¹⁰ Newer approaches (e.g., SAEM) include stochastic estimation, refining estimates partially by iterative “trial and error.” All estimation methods have advantages and disadvantages (mostly related to speed, robustness to initial parameter estimates, and stability in overparameterized models and parameter precision).^11,12 The only estimation method of concern is the original First Order method in nonlinear mixed-effects model, which can generate biased estimates of random effects. The differences between estimation methods can sometimes be substantial. Trying more than one method during the initial stages of model building (e.g., evaluating goodness of fit with observed or simulated data) is reasonable. Changing default values for optimization settings and convergence criteria should not be considered unless the impact of these changes is understood.

Comparing models

The minimum OFV determined via parameter estimation (OBJ) is important for comparing and ranking models. However, complex models with more parameters are generally better able to describe a given data set (there are more “degrees of freedom,” allowing the model to take different shapes). When comparing several plausible models, it is necessary to compensate for improvements of fit due to increased model complexity. The Akaike information criterion (AIC) and Bayesian information criterion (BIC or Schwarz criterion) are useful for comparing structural models:

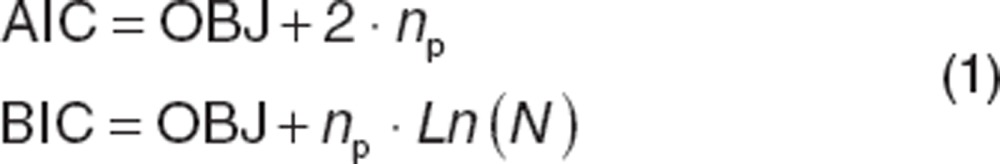where n_p is the total number of parameters in the model, and N is the number of data observations. Both can be used to rank models based on goodness of fit. BIC penalizes the OBJ for model complexity more than AIC, and may be preferable when data are limited. Comparisons of AIC or BIC cannot be given a statistical interpretation. Kass and Raftery¹³ categorized differences in BIC between models of >10 as “very strong” evidence in favor of the model with the lower BIC; 6–10 as “strong” evidence; 2–6 as “positive” evidence; and 0–2 as “weak” evidence. In practice, a drop in AIC or BIC of 2 is often a threshold for considering one model over another.

The likelihood ratio test (LRT) can be used to compare the OBJ of two models (reference and test with more parameters), assigning a probability to the hypothesis that they provide the same description of the data. Unlike AIC and BIC, models must be nested (one model is a subset of another) and have different numbers of parameters. This makes LRT suitable to comparing covariate models to base models (Covariate models section).

As the OBJ depends on the data set and estimation method used, the OBJ and its derivations cannot be compared across data sets or estimation methods. The lowest OBJ is not necessarily the best model. A higher order polynomial can be a near perfect description of a data set with the lowest OBJ, but may be “overfitted” (describing noise rather than the underlying relationship) and of little value. Polynomial parameters cannot be related to biological processes (e.g., drug elimination), and the model will have no predictive utility (either between data points or extrapolating outside the range of the data). Mechanistic plausibility and utility therefore take primacy over OBJ value.

Structural Model Development

The choice of the structural model has implications for covariate selection.¹⁴ Therefore, care should be taken when evaluating structural models.

Systemic models

The structural model (Supplementary Data online) is analogous to a systemic model (describing kinetics after i.v. dosing) and an absorption model (describing the drug uptake into the blood for extravascular dosing). For the former, though physiologically based pharmacokinetic models have a useful and expanding role,^15,16 mammillary compartment models are predominant in the literature. When data are available from only a single site in the body (e.g., venous plasma), concentrations usually show 1, 2, or 3 exponential phases¹⁷ which can be represented using a systemic model with one, two, or three compartments, respectively. Insight into the appropriate compartment numbers can be gained by plotting log concentration vs. time. Each distinct linear phase when log concentrations are declining (or rising to steady state during a constant-rate infusion) will generally need its own compartment. However, the log concentration time course can appear curved when underlying half-lives are similar.

Mammillary compartment models can be parameterized as derived rate constants (e.g., V₁, k₁₂, k₂₁, k₁₀) or preferentially as volumes and CL (e.g., V₁, CL, V₂, Q₁₂ where Q₁₂ is the intercompartmental CL between compartments one and two) and are interconvertible (Supplementary Data online). Rate constants have units of 1/time; intercompartmental CLs (e.g., Q₁₂) have the units of flow (volume/time) and can be directly compared with elimination CL (e.g., CL, expressed as volume/time) and potentially blood flows. Volume and CL parameterization have the advantage of allowing the model to be visualized as a hydraulic analog¹⁸ (Supplementary Data online). Parameters can be expressed in terms of half-lives, but the relationship between the apparent half-lives and model parameters is complex for models with more than one compartment (Supplementary Data online). For drugs with multicompartment kinetics, the time course of the exponential phases in the postinfusion period depends on infusion duration, a phenomenon giving rise to the concept of context sensitive half-time rather than half-life.¹⁹

When choosing the number of compartments for a model, note that models with too few compartments describe the data poorly (higher OBJ), showing bias in plots of residuals vs. time. Models with too many compartments show trivial improvement in OBJ for the addition of extra compartments; parameters for the additional peripheral compartment will converge on values that have minimal influence on the plasma concentrations (e.g., high volume and low intercompartmental CL, or the reverse); or parameters may be estimated with poor precision.

An important consideration is whether assuming first-order elimination is appropriate. In first-order systems, elimination rate is proportional to concentration, and CL is constant. Doubling the dose doubles the concentrations (the principle of superposition).² Conversely, for zero-order systems, the elimination rate is independent of concentration. CL depends on dose; doubling the dose will increase the concentrations more than two-fold. Note that elimination moves progressively from a first-order to a zero-order state as concentrations increase, saturating elimination pathways.

Pharmacokinetic data collected in subjects given a single dose of drug are rarely sufficient to reveal and quantitate saturable elimination, a relatively wide range of doses may be needed. Data from both single- and multidose studies may reveal saturable elimination if steady-state kinetics cannot be predicted from single-dose data. Graphical and/or noncompartmental analysis may show evidence of nonlinearity: dose-normalized concentrations that are not superimposable; dose-normalized area under the curve (AUC) (by trapezoidal integration) that are not independent of dose; multidose AUC_τ or C_ss that is higher than predicted by single-dose AUC and CL.

Classically, saturable elimination is represented using the Michaelis–Menten equation.² For a one-compartment model with predefined dose rate:

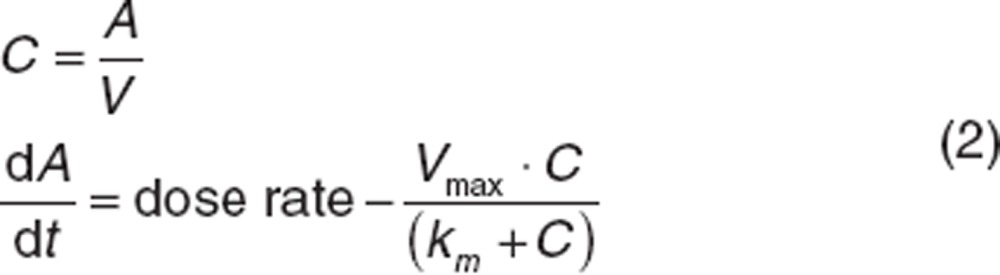where dA/dt is the rate of change of the amount of drug, V_max is maximum elimination rate and k_m is concentration associated with half of V_max. Note that when C << k_m, the rate becomes V_max/k_m·C, where V_max/k_m can be interpreted as the apparent first-order CL. When C >> k_m, rate becomes V_max (apparent zero-order CL). V_max and k_m can be highly correlated, making it difficult to estimate both as random effects parameters (Between-subject variability section). Broadly, k_m can be considered a function of the structure of the drug and the eliminating enzyme (or transporter) whereas V_max can be considered as a function of the available number of eliminating enzymes (or transporters).

The contribution of saturable elimination to plasma concentrations should be considered carefully in the context of the drug, the sites of elimination for the drug, and the route of administration. For drugs with active renal-tubular secretion, saturation of this process will decrease renal CL and increase concentrations above that expected from superposition. For drugs with active tubular re-absorption, saturation of this process will increase renal CL and decrease concentrations below that expected from superposition.

Absorption models

Drugs administered via extravascular routes (e.g., p.o., s.c.) need a structural model component representing drug absorption (Supplementary Data online). The two key processes are overall bioavailability (F) and the time course of the absorption rate (the rate the drug enters the blood stream).

F represents the fraction of the extravascular dose that enters the blood. Functionally, unabsorbed drug does not contribute to the blood concentrations, and the measured concentrations are lower as if the dose was a fraction (F) of the actual dose. The fate of “unabsorbed” dose depends on administration route and the drug, but could include: drug not physically entering the body (e.g., p.o. dose remaining in the gastrointestinal tract), conversion to a metabolite during absorption (e.g., p.o. dose and hepatically cleared drug), precipitation or aggregation at the site of injection (e.g., i.m., s.c.) or a component of absorption that is so slow that it cannot be detected using the study design (e.g., lymphatic uptake of large compounds given s.c.).

Absolute bioavailability can only be estimated when concurrent extravascular and i.v. data are available (assuming the i.v. dose is completely available, F = 100%). Both CL and F are estimated parameters (designated as θ), with F only applying to extravascular data (Supplementary Data online). Although F can range between 0 (no dose absorbed) and 1 (completely absorbed dose), models may be more stable if a logit transform is used to constrain F where LGTF can range between ±infinity.

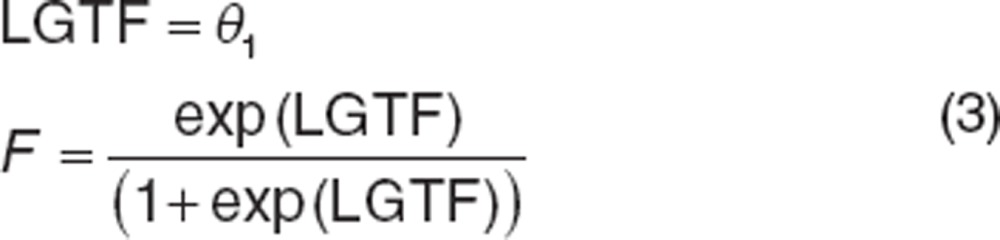In such models, the CL estimated for the i.v. route is the reference CL; the apparent CL for the extravascular route (that would be estimated from the AUC) is calculated as CL_i.v./F.

When only extravascular data are available, it is impossible to estimate true CLs and volumes because F is unknown. For a two compartment model, e.g., estimated parameters are a ratio of the unknown value of F: CL/F, V₁/F, Q/F, and V₂/F (absorption parameters are not adjusted with bioavailability). Although F cannot be estimated, population variability in F can contribute to variability in CLs and volumes making them correlated (Supplementary Data online).

If the process dictating oral bioavailability has an active component in the blood to gut lumen direction, bioavailability may be dose dependent with higher doses associated with higher bioavailability. Conversely, if the active component is in the gut lumen to blood direction, higher doses may be associated with lower bioavailability. If the range of doses is insufficient to estimate parameters for a saturable uptake model (e.g., V_max, k_m) using DOSE or log(DOSE) as a covariate on F may be an expedient alternative. In general, nonlinear uptake affecting bioavailability can be differentiated from nonlinear elimination as the former shows the same half-life across a range of doses, whereas the latter shows changes in half-life across a range of doses.

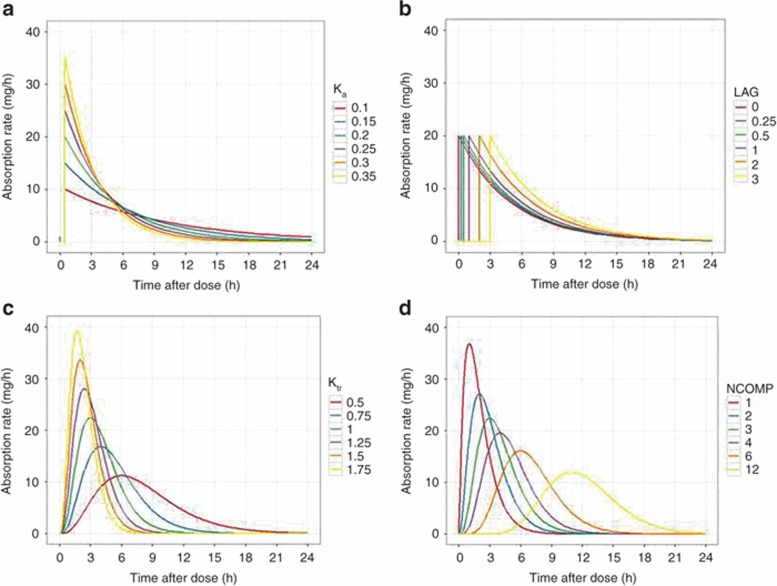
The representation of extravascular absorption is classically a first-order process described using an absorption rate constant (k_a). This represents absorption as a passive process driven by the concentration gradient between the absorption site and blood (Figure 1a). The concentration gradient diminishes with time as drug in the absorption site is depleted in an exponential manner. An extension of this model is to add an absorption lag if the appearance of drug in the blood is delayed (Figure 1b). The delay can represent diverse phenomena from gastric emptying (p.o. route) to diffusion delays (nasal doses). Because lags are discontinuous, numerical instability can arise and transit compartment models may be preferred.²⁰

Figure 1.

Models of extravascular absorption. The time profile of absorption rate for selected absorption models. (a) A first-order absorption model with different values of the absorption rate constant (k_a). Absorption lag was 0.5 h in all cases. (b) A first-order absorption model with different values of the absorption lag (LAG). Absorption rate constant was 0.5/h in all cases. (c) A three-compartment transit chain model with different values of the transit chain rate constant (k_tr). Note that decreasing the rate constant lowers the overall absorption rate and delays the time of its maximum value. (d) Transit chain models with different numbers of transit chain compartments (NCOMP). The transit chain rate constant was 1/h in all cases. Note that increasing the number of compartments introduces a delay before absorption, and functionally acts as a lag. The dose was 100 mg in all cases (hence the area under the curve should be 100 mg for all models).

“Flip-flop” kinetics occurs when absorption is slower than elimination²¹ making terminal concentrations dependent on absorption, which becomes rate limiting. For example, for a one-compartment model, there are two parameter sets that provide identical descriptions of the data, one with fast absorption and slow elimination, the other with slow absorption and fast elimination. Prior knowledge on the relative values of absorption and elimination rates is needed to distinguish between these two possibilities. Drugs with rate-limiting absorption show terminal concentrations after an extravascular dose with a longer half-life than i.v. data suggest. Flip-flop kinetics can be problematic when fitting data if individual values of k_a and k₁₀ (e.g., CL/V) “overlap” in the population. It may be advantageous to constrain k₁₀ to be faster than k_a, (e.g., k₁₀ = k_a +θ₁) where θ₁ is >0 if prior evidence suggests flip-flop absorption.

Although first-order absorption has the advantage of being conceptually and mathematically simple, the time profile of absorption (Figure 1b) has “step” changes in rate that may be unrepresentative of in vivo processes, and this is a “change-point” that presents difficulties for some estimation methods. For oral absorption in particular, transit compartment models may be superior.²⁰ The models represent the absorbed drug as passing through a series of interconnected compartments linked by a common rate constant (k_tr), providing a continuous function that can depict absorption delays. The absorption time profile can be adjusted by altering the number of compartments and the rate constant (Figure 1c,d). As they are coded by differential equations (Supplementary Data online), transit compartment absorption models have longer run times than first-order models, which may outweigh their advantages in some situations. The transit compartment model can be approximated using an analytical solution in some cases.²⁰

Statistical Models

The statistical model describes variability around the structural model. There are two primary sources of variability in any population pharmacokinetic model: between-subject variability (BSV), which is the variance of a parameter across individuals; and residual variability, which is unexplained variability after controlling for other sources of variability. Some databases support estimation of between-occasion variability (BOV), where a drug is administered on two or more occasions in each subject that might be separated by a sufficient interval for the underlying kinetics to vary between occasions. Developing an appropriate statistical model is important for covariate evaluations and to determine the amount of remaining variability in the data, as well as for simulation, an inherent use of models.²

BSV

When describing BSV, parameterization is usually based on the type of data being evaluated. For some parameters that are transformed (e.g., LGTF), the distribution of η values may be normal, and BSV may be appropriately described using an additive function:

where θ₁ is the population bioavailability and η_1i is the deviation from the population value for the ith subject. Taken across all individuals evaluated, the individual η₁ values are assumed to be normally distributed with a mean of 0 and variance ω². This assumption is not always correct, and the ramifications of skewed or kurtotic distributions for η₁ will be described later. The different variances and covariances of η parameters are collected into an “Ω matrix.”

Pharmacokinetic data are often modeled assuming log-normal distributions because parameters must be positive and often right-skewed.^22,23 Therefore, the CL of the ith subject (CL_i) would be written as:

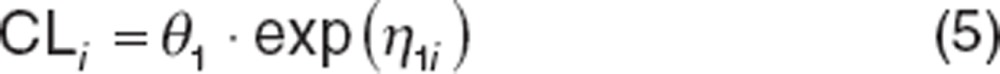where θ₁ is the population CL and η_1i is the deviation from the population value for the ith subject. The log-normal function is a transformation of the distribution of η values, such that the distribution of CL_i values may be log-normally distributed but the distribution of η_1i values is normal.

When parameters are treated as arising from a log-normal distribution, the variance estimate (ω²) is the variance in the log-domain, which does not have the same magnitude as the θ values. The following equation converts the variance to a coefficient of variation (CV) in the original scale. For small ω² (e.g., <30%) the CV% can be approximated as the square root of ω².

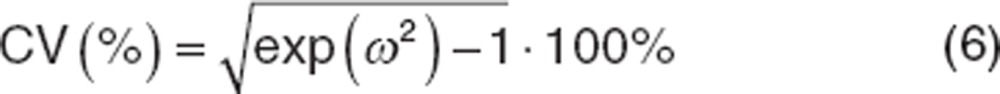The use of OBJ (e.g., LRT) is not applicable for determining appropriateness of including variance components.²⁴ Variance terms cannot be negative, which places the null hypothesis (that the value of the variance term is 0) on the boundary of the parameter space. Under such circumstances, the LRT does not follow a χ² distribution, a necessary assumption for using this test. Using LRT to include or exclude random effects parameters is generally unreliable, as suggested by Wählby et al.²⁵ For this reason, models with different numbers of variance parameters should also not be compared using LRT. Varying approaches to developing the Ω matrix have been recommended. Overall, it is best to include a variance term when the estimated value is neither very small nor very large suggesting sufficient information to appropriately estimate the term. Other diagnostics such as condition number (computed as the square root of the ratio of the largest eigenvalue to the smallest eigenvalue of the correlation matrix) can be calculated to evaluate collinearity which is the case where different variables (CL and V) tend to rise or fall together. A condition number ≤20 suggests that the degree of collinearity between the parameter estimates is acceptable. A condition number ≥100 indicates potential instability due to high collinearity²⁶ because of difficulties with independent estimation of highly collinear parameters.

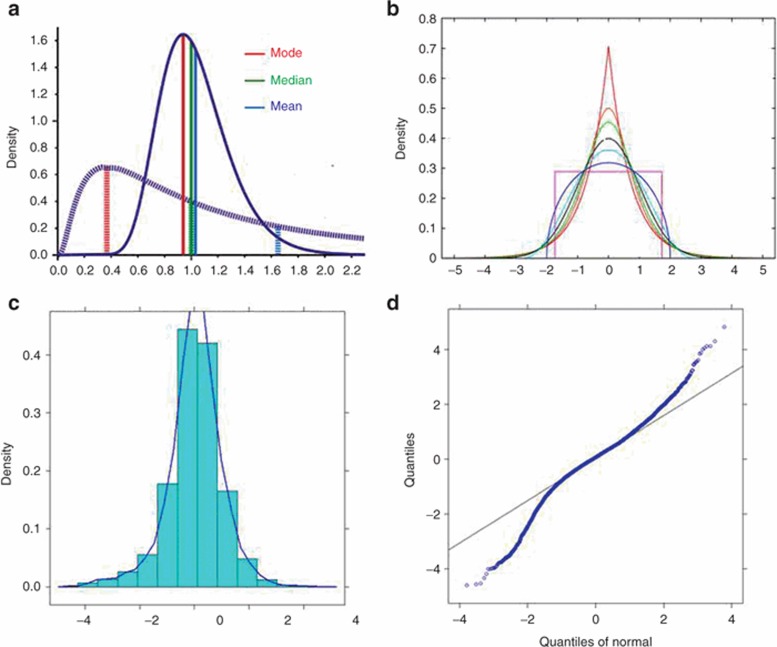
Skewness and kurtosis of the distributions of individual η values should be evaluated. Skewness measures lack of symmetry in a distribution arising from one side of the distribution having a longer tail than the other.²⁷ Kurtosis measures whether the distribution is sharply peaked (leptokurtosis, heavy-tailed) or flat (platykurtosis, light-tailed) relative to a normal distribution. Leptokurtosis is fairly common in population modeling. Representative skewed and kurtotic distributions are shown in Figure 2a,b, respectively. Metrics of skewness and kurtosis can be calculated in any statistical package. Although reference values for these metrics are somewhat dependent on the package, they are mostly defined as 0 for a normal distribution. Very skewed or kurtotic distributions can affect both type I and type II error rates²⁷ making identification of covariates impractical, and can also impact the utility of the model for simulation. Although the assumption of normality is not required during the process of fitting data, it is important during simulation, at which random values of η are drawn from a normal distribution. Therefore, if the distributions of η values are skewed or kurtotic, transformation is necessary to ensure that the η distribution is normal. Numerous transforms are available,²⁸ with the Manly transform²⁹ being particularly useful for distributions that are both skewed and kurtotic. An example implementation is shown below:

Figure 2.

Skewed and kurtotic distributions. (a) Shows distributions with varying degrees of skewness. For a normal distribution, the mode, median, and mean should be (nearly) the same. As skewness becomes more pronounced, these summary metrics differ by increasing degrees. (b) A range of kurtotic distributions. The red line is very leptokurtotic, the pink line is very platykurtotic (a uniform distribution is the extreme of platykurtosis). (c) A frequency histogram of a leptokurtotic distribution. and (d) The quantile–quantile (q–q) plot of that distribution, where the quantiles deviate from the line of unity indicates the heavy tails in the leptokurtotic distribution. For a normal distribution, the quantiles should not deviate from the line of unity.

where “LAM” is a shape parameter and “ET1” is the transformed variance allowing η₁ to be normally distributed.

Initially, variance terms are incorporated such that correlations between parameters are ignored (referred to as a “diagonal Ω matrix”):

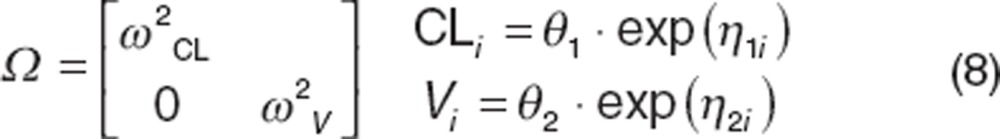where ^ω2_CL is the variance for CL and ω²_v is the variance for distributional volume. Models evaluating random effects parameters on all parameters are frequently tested first, followed by serial reduction by removing poorly estimated parameters. Variance terms should be included on parameters for which information on influential covariates is expected and will be evaluated. When variance terms are not included (e.g., the parameter is a fixed effects parameter), that parameter can be considered to have complete shrinkage because only the median value is estimated (Between-subject variability section). Thus, as with any covariate evaluation when shrinkage is high, the probability of type I and type II errors is high and covariate evaluations should be curtailed with few exceptions (e.g., incorporation of allometric or maturation models).

Within an individual, pharmacokinetic parameters (e.g., CL and volume) are not correlated.³⁰ It is possible, for example, to alter an individual's CL without affecting volume. However, across a patient population, correlation(s) between parameters may be observed when a common covariate affects more than one parameter. Body size has been shown to affect both CL and volume of distribution.³¹ Overall, larger subjects generally have higher CLs as well as larger volumes than smaller subjects. If CL and volume are treated as correlated random effects, then the Ω matrix can be written as shown below:

where ω_CL,V is the covariance between CL and volume of distribution (V). Thus the correlation (defined as r) between CL and V, calculated as follows:

Extensive correlation between variance terms (e.g., an r value ≥ ±0.8) is similar to a high-condition number, in that it indicates that both variance terms cannot be independently estimated. Models with high-condition number or extensive correlation become unstable under evaluations such as bootstrap³² and require alternative parameterizations such as the “shared η approach” shown below:

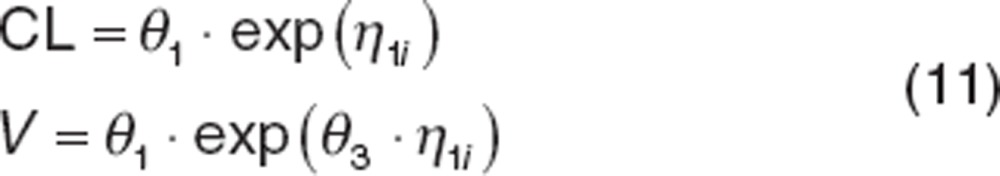where θ₃ is the ratio of the SDs of the distributions for CL and volume (e.g., 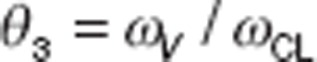) and the variance of V (Var(V)) can be computed as:

The consequence of covariance structure misspecification in mixed-effect population modeling is difficult to predict given the complex way in which random effects enter a nonlinear mixed-effect model. Because population based models are now more commonly used in simulation experiments to explore study designs, attention to the importance of identifying such terms has increased. Under the extended least squares methods, the consequences of a misspecified covariance structure have been reported to result in biased estimates of variance terms.³³ In general, efficient estimation of both fixed parameters and variance terms requires correct specification of both the covariance structure as well as the residual variance structure. However, for any specific case, the degree of resulting bias is difficult to predict. Although misspecification of the variance–covariance relationships can inflate type I and type II error rates (such that important covariates are not identified, or unimportant covariates are identified) specifying the correlations is generally less important than correctly specifying the variance terms themselves. However, failure to include covariance terms can negatively impact simulations because the correlation between parameters that is inherent in the data is not captured in the resulting simulations. Thus, simulations of individuals with high CL and low volumes are likely (a situation unlikely to exist in the original data). Simulated data with inappropriate parameter combinations tend to show increased variability as a wider range of simulated data (referred to as “inflating the variability”). For covariance terms, unlike variance terms, the use of the LRT can be implemented in decision making because covariance terms do not have the same limitations (e.g., covariance terms can be negative).

BOV

Individual pharmacokinetic parameters can change between study occasions (Supplementary Data online). The source of the variability can sometimes be identified (e.g., changing patient status or compliance). Karlsson and Sheiner³⁴ reported bias in both variance and structural parameters when BOV was omitted with the extent of bias being dependent on magnitude of BOV and BSV. Failing to account for BOV can result in a high incidence of statistically significant spurious period effects. Ignoring BOV can lead to a falsely optimistic impression of the potential value of therapeutic drug monitoring. When BOV is high, the benefits of dose adjustment based on previous observations may not translate to improved efficacy or safety.

BOV was first defined as a component of residual unexplained variability (RUV)³⁴ and subsequently cited as a component of BSV.³⁵ BOV should be evaluated and included if appropriate. Parameterization of BOV can be accomplished as follows:

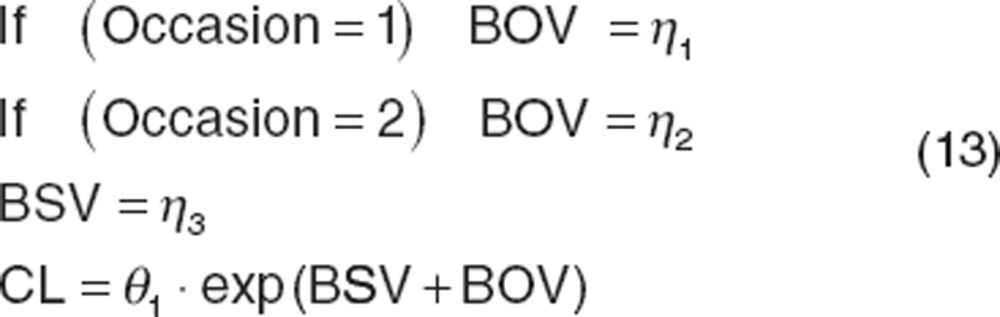Variability between study or treatment arms (such as crossover studies), or between studies (such as when an individual participates in an acute treatment study and then continues into a maintenance study) can be handled using the same approach.

Shrinkage

The mixed-effect parameter estimation method (Software and estimation methods) returns population parameters (and population-predicted concentrations and residuals). Individual-parameter values, individual-predicted concentrations, and residuals are often estimated using a second “Bayes” estimation step using a different objective function (also called the post hoc, empirical Bayes or conditional estimation step). This step is more understandable for a weighted least squares² Bayes objective function³⁶ where for one individual in a population with j observations and a model with k parameters, OFV is represented as follows:

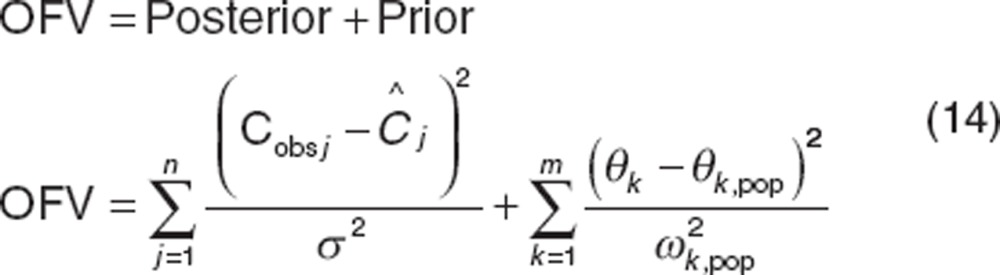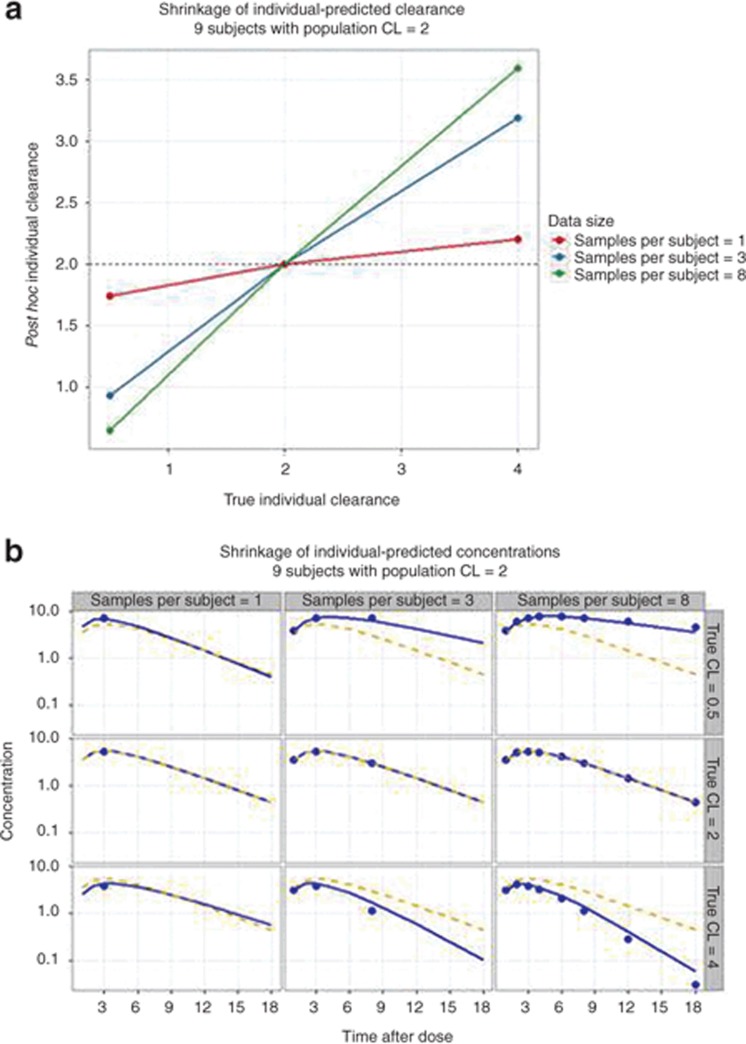
A Bayes objective function can be used to estimate the best model parameters for each individual in the population by balancing the deviation of the individual's model-predicted concentrations (Ĉ ) from observed concentrations (C_obs) and the deviation of the individual's estimated parameter values (θ_k) from the population parameter value (θ_k,pop). Eq. 14 shows that for individuals with little data, the posterior term of the equation is smaller and the estimates of the individual's parameters are weighted more by the population parameters values than the influence of their data. Individual parameters therefore “shrink” toward the population values (Figure 3). The extent of shrinkage has consequences for individual-predicted parameters (and individual-predicted concentrations).

Figure 3.

The concept of shrinkage. A population of nine subjects was created in which kinetics were one compartment with first-order absorption and the population clearance was 2 (Ω was 14% and σ was 0.31 concentration units). The subjects were divided into three groups with true clearances of 0.5, 2, or 4. Each subgroup was further divided into subjects with 1, 3, or 8 pharmacokinetic samples per subject. The individual-clearances and individual-predicted concentrations for each subject were estimated using Bayes estimation in NONMEM (post hoc step). (a) Post hoc individual clearances vs. true clearance. Note that individual-predicted clearances “shrink” towards population values as less data are available per subject and the true clearance is further from the population value. (b) Observed (symbols), population-predicted (dashed line, based on population clearance), and individual-predicted concentrations (solid line, based on individual-predicted clearance). Note also that individual-predicted concentrations “shrink” toward population-predicted concentrations values as less data are available per subject and the true clearance is further from the population value. NONMEM, nonlinear mixed-effects modeling.

When shrinkage is high (e.g., above 20–30%),³⁷ plotting individual-predicted parameters or η values vs. a covariate may obscure true relationships, show a distorted shape, or indicate relationships that do not exist.³⁷ In exposure–response models, individual exposure (e.g., AUC from Dose/CL) may be poorly estimated when shrinkage in CL is high, thereby lowering power to detect an exposure–response relationship. Diagnostic plots based on individual-predicted concentrations or residuals may also be misleading.³⁷ Model comparisons based on OBJ and population predictions are largely unaffected by shrinkage and should dominate model evaluation when shrinkage is high.

Shrinkage should be evaluated in key models. The shrinkage can be summarized as follows:³⁷

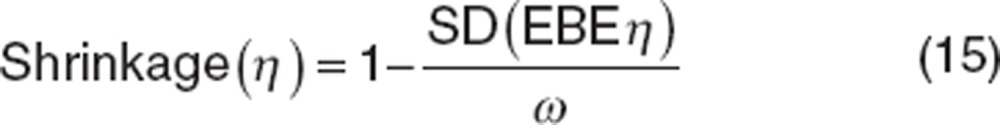where ω is the estimated variability for the population and SD is the SD of the individual values of the empirical Bayesian estimates (EBE) of η.

Residual variability

RUV arises from multiple sources, including assay variability, errors in sample time collection, and model misspecification. Similar to BSV, selection of the RUV model is usually dependent on the type of data being evaluated.

Common functions used to describe RUV are listed in Table 1. For dense pharmacokinetic data, the combined additive and proportional error models are often utilized because it broadly reflects assay variability, whereas for pharmacodynamic data (which often have uniform variability across the range of possible values), an additive residual error may be sufficient. Exponential and proportional models are generally avoided because of the tendency to “overweight” low concentrations. This happens because RUV is proportional to the observation; low values have a correspondingly low error. For small σ², the proportional model is approximately equal to the exponential model.

Table 1. Common forms for residual error models.

Under all these models, the term describing RUV (ε) is assumed to be normally distributed, independent, with a mean of zero, and a variance σ². Collectively, the RUV components (σ²) are referred to as the residual variance or “Σ” matrix. As with BSV, RUV components can be correlated. Furthermore, although ε and η are assumed independent, this is not always the case, leading to an η–ε interaction, (discussed later).

RUV can depend on covariates, such as when assays change between studies, study conduct varies (e.g., outpatient vs. inpatient), or involve different patient populations requiring different RUV models.³⁸ This can be implemented in the residual error using an indicator or “FLAG” variable, FLAG, defined such that every sample is either a 0 or 1, depending on the assignment. In such cases, an exponential residual error can be described for each case as follows:

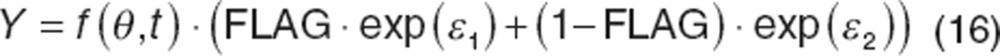Because assay error is often a minor component of RUV, other sources, with different properties should be considered. Karlsson et al.³⁹ proposed alternative RUV models describing serially correlated errors (e.g., autocorrelation), which can arise from structural model misspecification, and time-dependent errors arising from inaccurate sample timing.

As mentioned earlier, η and ε are generally assumed independent, which is often incorrect. For example, with proportional error model, it can be seen that ε is not independent of η:

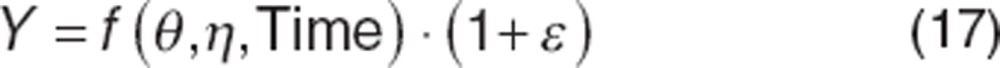With most current software packages, this interaction can be accounted for in the estimation of the likelihood. It should be noted that interaction is not an issue with an additive RUV model, and evaluation of interaction is not feasible with large RUV (e.g., model misspecification) or the amount of data per individual is small (e.g., BSV shrinkage or inability to distinguish RUV from BSV).

As with BSV, it may be appropriate to implement a transform when the residual distribution is not normally distributed, but is kurtotic or right-skewed. Failing to address these issues can result in biased estimates of RUV and simulations that do not reflect observed data. Because RUV is dependent on the data being evaluated, both sides of the equation must be transformed in the same manner. A common transform is the “log transform both sides” (LTBS) approach.

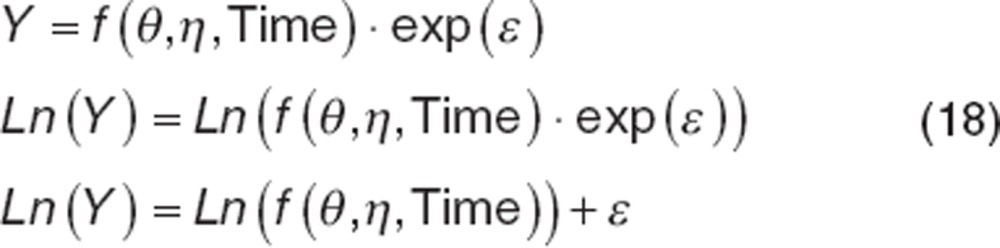Note that the data must be ln-transformed before evaluation and the resulting model-based predictions are also ln-transformed. The parameters, however, are not transformed. Using LTBS, the exponential residual error now enters the model using an additive type residual error function, removing the potential for η–ε interactions. The transform of the exponential error model removes the tendency for the exponential error model to overweight the lowest concentrations as well. If additive or combined exponential and additive errors are needed with LTBS, forms for these models are provided in Table 1.

The use of LTBS has some additional benefits: simulations from models implementing this transform are always positive, which is useful for simulations of pharmacokinetic data over extended periods of time. LTBS can improve numerical stability particularly when the range of observed values is wide. It should be noted that the OBJ from LTBS cannot be compared with OBJ arising from the untransformed data. If the LTBS approach does not adequately address skewness or kurtosis in the residual distribution, then dynamic transforms should be considered.⁴⁰

Covariate Models

Identification of covariates that are predictive of pharmacokinetic variability is important in population pharmacokinetic evaluations. A general approach is outlined below:

1. Selection of potential covariates: This is usually based on known properties of the drug, drug class, or physiology. For example, highly metabolized drugs will frequently include covariates such as weight, liver enzymes, and genotype (if available and relevant).

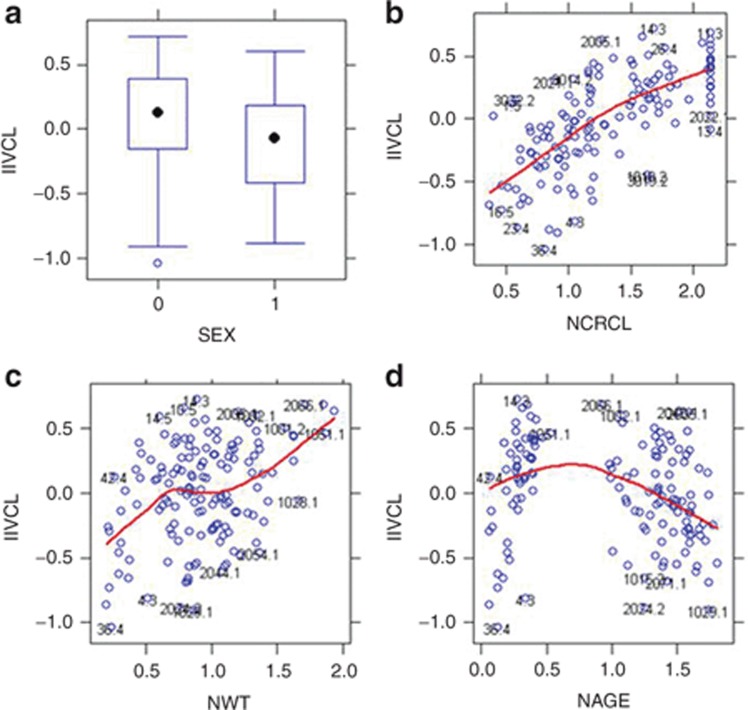
2. Preliminary evaluation of covariates: Because run times can sometimes be extensive, it is often necessary to limit the number of covariates evaluated in the model. Covariate screening using regression-based techniques, generalized additive models, or correlation analysis evaluating the importance of selected covariates can reduce the number of evaluations. Graphical evaluations of data are often utilized under the assumption that if a relationship is significant, it should be visibly evident. Example plots are provided in Figure 4, however, once covariates are included in the model, visual trends should not be present.

3. Build the covariate model: Without covariate screening, covariates are tested separately and all covariates meeting inclusion criteria are included (full model). With screening, only covariates identified during screening are evaluated separately and all relevant covariates are included. Covariate selection is usually based on OBJ using the LRT for nested models. Thus, statistical significance can be attributed to covariate effects and prespecified significance levels (usually P < 0.01 or more) are set prior to model-based evaluations. Covariates are then dropped (backwards deletion) and changes to the model goodness of fit is tested using LRT at stricter OBJ criteria (e.g., P < 0.001) than was used for inclusion (or another approach). This process continues until all covariates have been tested and the reduced or final model cannot be further simplified.

Figure 4.

Graphical evaluations of covariates. Note that the variance term is used to evaluate the effect of the covariate and that normalized covariate values (designated with an “N” preceding the covariate type) are used. For continuous covariates, a Loess smooth (red) line is used to help visualize trends. For discrete covariates, box and whisker plots with the medians designated as a black symbol are used. (a) A box and whisker plot evaluating sex; (b) evaluates the effect of normalized creatinine clearance; (c) evaluates the effect of normalized weight, and (d) evaluates the effect of normalized age. It should be noted that there is a high degree of collinearity in these covariates. CrCL, creatinine clearance; IIVCL, interindividual variability in CL; WT, weight.

Models built using stepwise approaches can suffer from selection bias if only statistically significant covariates are accepted into the model. Such models can also overestimate the importance of retained covariates. Wählby et al.⁴¹ evaluated a generalized additive models based approach vs. forward addition/backwards deletion. The authors reported selection bias in the estimates which was small relative to the overall variability in the estimates.

Evaluating multiple covariates that are moderately or highly correlated (e.g., creatinine CL and weight) may also contribute to selection bias, resulting in a loss of power to find the true covariates. Ribbing and Jonsson⁴² investigated this using simulated data, and showed that selection bias was very high for small databases (≤50 subjects) with weak covariate effects. Under these circumstances, the covariate coefficient was estimated to be more than twice its true value. For the same reason, low-powered covariates may falsely appear to be clinically relevant. They also reported that bias was negligible if statistical significance was a requirement for covariate selection. Thus stepwise selection or significance testing of covariates is not recommended with small databases.

Tunblad et al.⁴³ evaluated clinical relevance (e.g., a change of at least 20% in the parameter value at the extremes of the covariate range) to test for covariate inclusion. This approach resulted in final models containing fewer covariates with a minor loss in predictive power. The use of relevance may be a practical approach because only covariates important for predictive performance are included.

Covariate functions

Covariates are continuous if values are uninterrupted in sequence, substance, or extent. Conversely, covariates are discrete if values constitute individually distinct classes or consist of distinct, unconnected values. Discrete covariates must be handled differently, but it is important for both types of data to ensure that the parameterization of the covariate models returns physiologically reasonable results.

Continuous covariate effects can be introduced into the population model using a variety of functions, including a linear function:

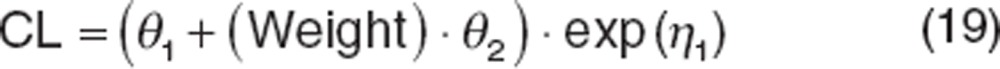This function constitutes a nested model against a base model for CL because θ₂ can be estimated as 0, reducing the covariate model to the base model. However, this parameterization suffers from several shortcomings, the first is that the function assumes a linear relationship between the parameter (e.g., CL) and covariate (e.g., weight) such that when the covariate value is low, the associated parameter is correspondingly low, which rarely exists. Such models have limited utility for extrapolation. The use of functions such as a power function (shown below) or exponential functions are common. Another liability of this parameterization is that the covariate value is not normalized, which can create an “imbalance”: if the parameter being estimated is small (such as CL for drugs with long half-lives) and weight is large, it becomes numerically difficult to estimate covariate effects. Covariates are often centered or normalized as shown below. Centering should be used cautiously; if an individual covariate value is low, the parameter can become negative, compromising the usefulness of the model for extrapolation and can cause numerical difficulties during estimation. Normalizing covariate values avoids these issues. Covariates can be normalized to the mean value in the database, or more commonly to a reference value (such as 70 kg for weight). This parameterization also has the advantage that θ₁ (CL) is the typical value for the reference patient.

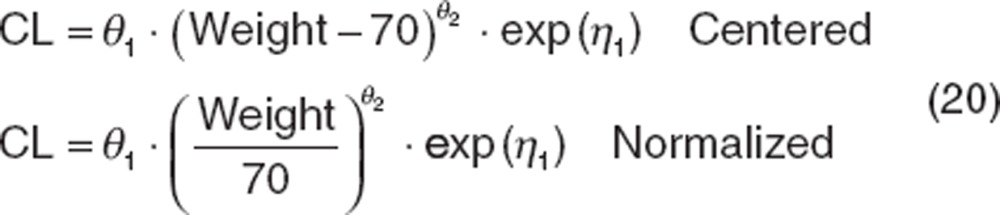Holford³¹ provided rationale for using allometric functions with fixed covariate effects to account for changes in CL in pediatrics as they mature based on weight (the “allometric function”).

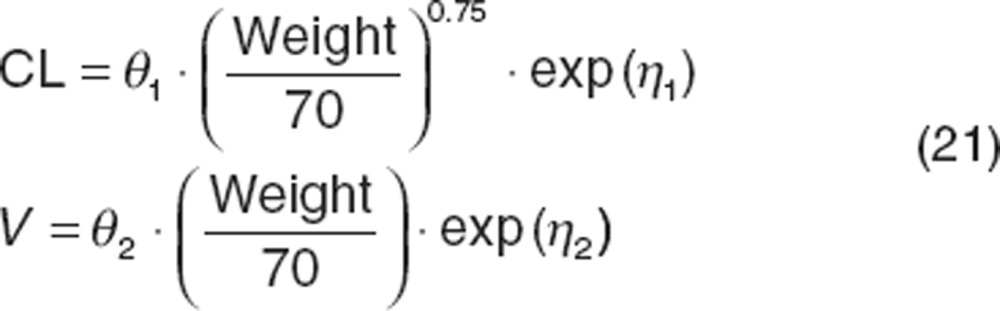Similarly, Tod et al.⁴⁴ identified a maturation function (MF) based on postconception age describing CL changes of acyclovir in infants relative to adults.

For both functions, covariate effects are commonly fixed to published values. This can be valuable if the database being evaluated does not include a large number of very young patients. However, such models are not nested and cannot be compared with other models using LRT; AIC or BIC are more appropriate.

For discrete data, there are two broad classes: dichotomous (e.g., taking one of two possible values such as sex) and polychotomous (e.g., taking one of several possible values such as race or metabolizer status). For dichotomous data, the values of the covariate are usually set to 0 for the reference classification and 1 for the other classification. Common functions used to describe dichotomous covariate effects are shown below:

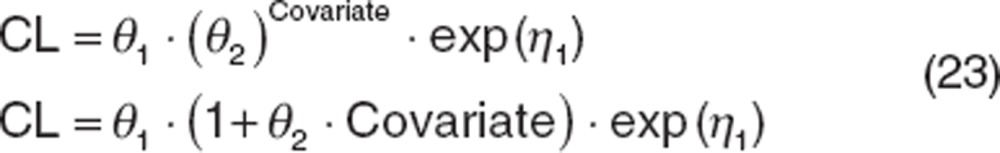Polychotomous covariates such as race (which have no inherent ordering) can be evaluated using a different factor for each classification against a reference value or may be grouped into two categories depending on results of visual examination of the covariates. When polychotomous covariates have an inherent order such as the East Coast Oncology Group (ECOG) status where disease is normal at ECOG = 0 and most severe at ECOG = 4, then alternative functions can be useful:

Model Evaluations

There are many aspects to the evaluation of a population pharmacokinetic model. The OBJ is generally used to discriminate between models during early stages of model development, allowing elimination of unsatisfactory models. In later stages when a few candidate models are being considered for the final model, simulation-based methods such as the visual predictive check (VPC)⁴⁵ may be more useful. For complex models, evaluations (e.g., bootstrap) may be time consuming and are applied only to the final model, if at all. Karlsson and Savic⁴⁶ have provided an excellent critique of model diagnostics. Model evaluations should be selected to ensure the model is appropriate for intended use.

Graphical evaluations

The concept of a residual (RES, C_obs−Ĉ ) is straightforward and fundamental to modeling. However, the magnitude of the residual depends on the magnitude of the data. Weighted residuals (WRES) normalize the residuals so that the SD is 1 allowing informative residual plots. WRES is analogous to a Z-score for the deviation between the model prediction and the data. The method for weighting is complex and depends on the estimation method,⁴⁷ and hence a variety of WRES have been proposed. WRES should be normally distributed, centered around zero, and not biased by explanatory variables (Figure 5), which can be evaluated using histograms and q–q plots of WRES conditioned on key explanatory variables. Plots of WRES against time (Figure 6) should be evenly centered around zero, without systematic bias, and most values within −2 to +2 SDs (marking the ~5th and 95th percentiles of a normal distribution). Systematic deviations may imply deficiencies in the structural model. Plots of WRES against population-predicted concentration (Figure 6) should be evenly centered around zero, without systematic bias, with most values within −2 to +2 SDs. Systematic deviations may imply deficiencies in the RUV model. Plots of observed vs. population and individual-predicted concentration are also shown in Figure 6.

Figure 5.

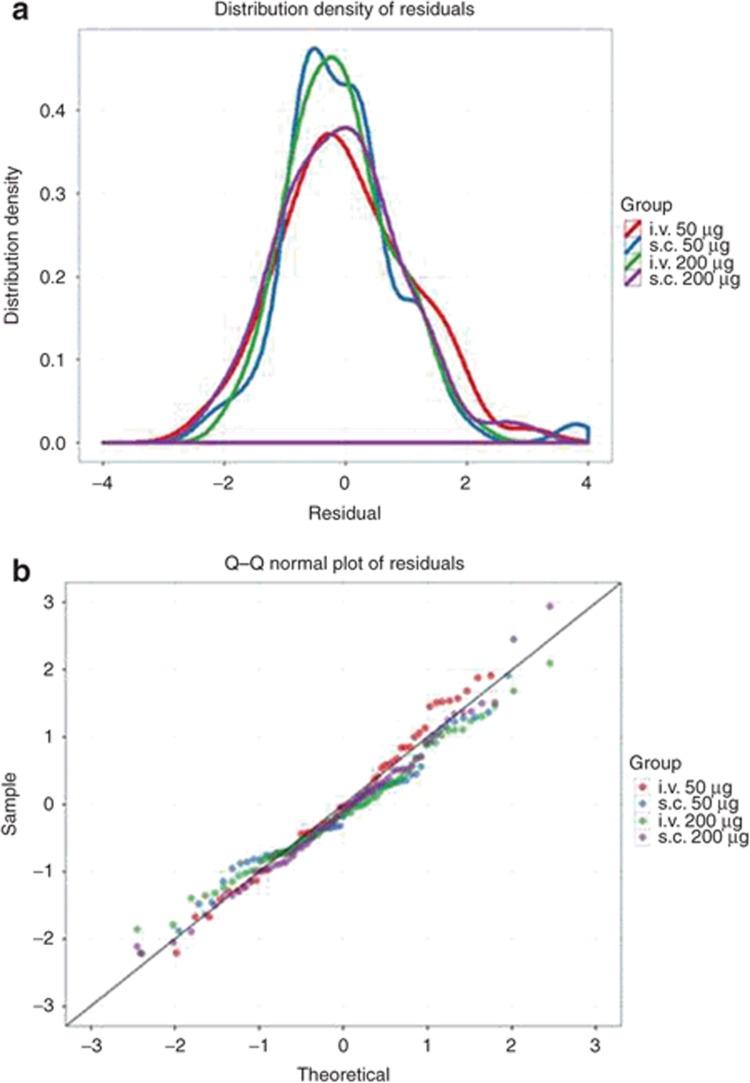
Residual plots. Selected residual plots for an hypothetical model and data set for a fentanyl given by two routes (i.v., s.c.) and two doses (50 and 200 μg) in 20 patients. (a) Distribution density (which can be considered of a continuous histogram) of the conditional weighted residuals (CWRES) conditioned with color on treatment group. The distribution should be approximately normally distributed (symmetrical, centered on zero with most values between −2 and +2). (b) A Q–Q plot of the CWRES conditioned with color on treatment group. These lines should follow the line of identity if the CWRES is normally distributed. In both plots, deviations from the expected behavior may suggest an inappropriate structural model or residual error model. Q–Q, quantile–quantile.

Figure 6.

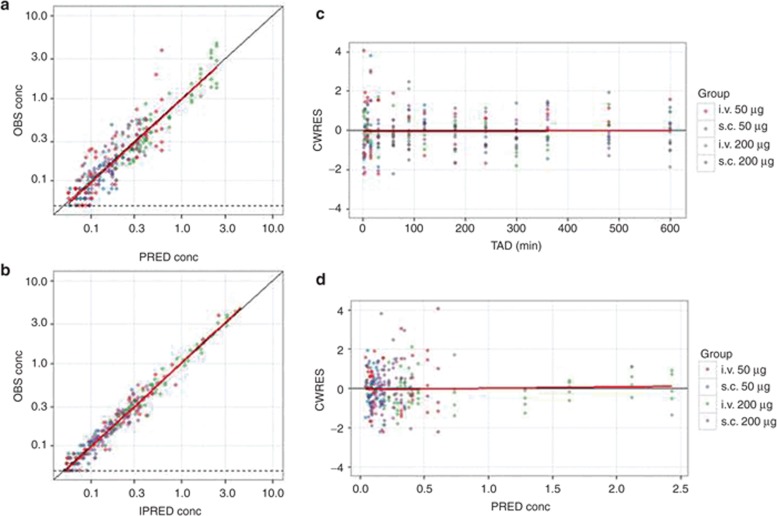
Key diagnostic plots. Key diagnostic plots for an hypothetical data set for fentanyl given by two routes (i.v., s.c.) and two doses (50 and 200 µg) in 20 patients. In each plot, symbols are data points, the solid black line is a line with slope 1 or 0 and the solid red line is a Loess smoothed line. The LLOQ of the assay (0.05 ng/ml) is shown where appropriate by a dashed black line. (a) Observed concentration (OBS) vs. population-predicted concentration (PRED). Data are evenly distributed about the line of identity, indicating no major bias in the population component of the model. (b) OBS vs. individual-predicted concentration. Data are evenly distributed about the line of identity, indicating an appropriate structural model could be found for most individuals. (c) Conditional weighted residuals (CWRES) vs. time after dose (TAD). Data are evenly distributed about zero, indicating no major bias in the structural model. Conditioning the plots with color on group helps detect systematic differences in model fit between the groups (that may require revision to the structural model or a covariate). (d) CWRES vs. population-predicted concentration. Data are evenly distributed about zero, indicating no major bias in the residual error model. CWERS, conditional weighted residuals; IPRED, individual-predicted concentration; LLOQ, lower limit of quantification; OBS, observed; PRED, predicted; TAD, time after dose.

A fundamental plot is a plot of observed, population-predicted and individual-predicted concentrations against time. These plots should be structured using combinations log-scales, faceting, and/or conditioning on explanatory variables to be as informative as possible. Plots of individual subjects may be possible if the number of subjects is low (Figure 7), or subjects may be randomly selected. Individual-predicted concentrations should provide an acceptable representation of the observed data, whereas the population-predicted concentrations should represent the “typical” patient (reflecting the center of pooled observed data).

Figure 7.

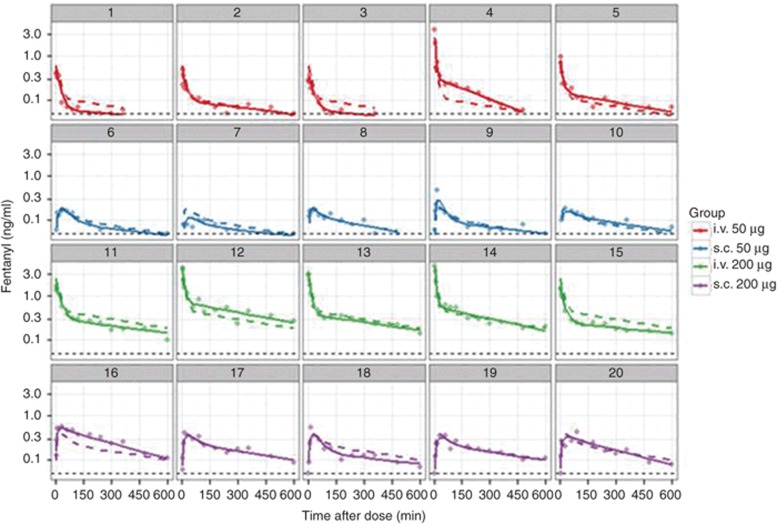
Goodness of fit plots. Goodness of fit plots for an hypothetical data set for fentanyl given by two routes (i.v., s.c.) and two doses (50 and 200 µg) in 20 patients. Each panel is data for one patient. Symbols are observed drug concentrations, solid lines are the individual-predicted drug concentrations and dashed lines are the population-predicted drug concentrations. The LLOQ of the assay (0.05 ng/ml) is shown as a dashed black line. Each data set and model will require careful consideration of the suite of goodness of fit plots that are most informative. When plots are not able to be conditioned on individual subjects, caution is needed in pooling subjects so that information is not obscured and to ensure “like is compared with like”. LLOQ, lower limit of quantification.

Parameters: SE and confidence intervals

Most modeling packages report the precision of parameter estimates, which is derived from the shape of the likelihood surface near the best parameter estimates.² Precision can be expressed as SE or confidence intervals (CI) and are interconvertible:

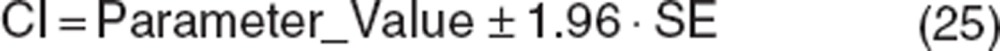Precise parameter estimates are important (models with poor parameter precision are often overparameterized), but the level of precision that is acceptable depends on the size of the database. For most pharmacokinetic databases, <30% SE for fixed effects and <50% SE for random effects are usually achievable (SE for random effects are generally higher than for fixed effects). It is important to quantify the precision of parameters describing covariate effects, as these reflect the precision with which the covariate effect has been estimated. CIs that include the null value for a covariate may imply the estimate of the covariate effect are unreliable.

Bootstrap methods are resampling techniques that provide an alternative for estimating parameter precision.⁴⁸ They are useful to verify the robustness of standard approximations for parameter uncertainty in parametric models.⁴⁹ Although asymptotic normality is a property of large-sample analyses, in population pharmacometrics, the sample size is usually not large enough to justify this assumption. Therefore, CIs based on SE of the parameter estimates sometimes underestimate parameter uncertainty. Bootstrapping avoids parametric assumptions made when computing CIs using other methods.

Bootstrapping involves generating replicate data sets where individuals are randomly drawn from the original database and can be drawn multiple times or not drawn for each replicate. In order to adequately reflect the parameter distributions, many replicates (e.g., ≥1,000) are generated and evaluated using the final model, and replicate parameter estimates are tabulated. The percentile bootstrap CI are constructed by taking the lower 2.5% and the upper 97.5% value of each parameter estimate from runs regardless of convergence status (with exceptions for abnormal terminations), as this interval should cover the true value of the parameter estimate ~ 95% of the time without imposing an assumption of symmetry on the distribution.

Bootstrap replicates can be used to generate the CI for model predictions. For example, when modeling concentrations vs. time in adults and pediatrics, it may be necessary to show precision for average predictions within specific age and weight ranges in pediatrics. In this case, the bootstrap parameters can be used to construct a family of curves representing the likely range of concentrations for patients with a given set of covariates.

VPC

VPCs generally involve simulation of data from the original or new database⁵⁰ and offer benefits over standard diagnostic plots.⁴⁵ The final model is used to simulate new data sets using the selected database design, and prediction intervals (usually 95%) are constructed from simulated concentration time profiles and compared with observed data. VPC can ensure that simulated data are consistent with observed data. VPC plots stratified for relevant covariates (such as age or weight groups), doses, or routes of administration are commonly constructed to demonstrate model performance in these subsets. Numerous VPC approaches are available, including the prediction-corrected VPC⁵¹ or a VPC utilizing adaptive dosing during simulation to reflect clinical study conduct.⁵²

A related evaluation is the numerical predictive check which compares summary metrics from the database (e.g., a peak or trough concentration) with the same metric from simulated output.

Conclusion

There is no “correct” method for developing and evaluating population pharmacokinetic models. We have outlined a framework that may be useful to those new to this area. Population pharmacokinetic modeling can appear complex, but the methodology is easily tested. When initially assessing a method or equation, simplified test runs and plots using test data (whether simulated or subsets of real data) should be considered to ensure the method behaves as expected before use. For formal analyses, a systematic approach to model building, evaluation, and documentation where each component is fully understood maximizes the chances of developing models that are “fit for purpose.”² A good pharmacometrician will see their role as extending beyond developing models for pharmacokinetic data. The model should translate pharmacokinetic data into knowledge about a drug and suggest further evaluations. Population pharmacokinetic models not only provide answers, but should also generate questions.

Conflict of interest

The authors declared no conflict of interest.