A Computational Approach to Detect Gap Junction Plaques and Associate Them with Cells in Fluorescent Images

Abstract

Intercellular signaling is a fundamental requirement for complex biological system function and survival. Communication between adjoining cells is largely achieved via gap junction channels made up of multiple subunits of connexin proteins, each with unique selectivity and regulatory properties. Intercellular communication via gap junction channels facilitates transmission of an array of cellular signals, including ions, macromolecules, and metabolites that coordinate physiological processes throughout tissues and entire organisms. Although current methods used to quantify connexin expression rely on number or area density measurements in a field of view, they lack cellular assignment, distance measurement capabilities (both within the cell and to extracellular structures), and complete automation. We devised an automated computational approach built on a contour expansion algorithm platform that allows connexin protein detection and assignment to specific cells within complex tissues. In addition, parallel implementation of the contour expansion algorithm allows for high-throughput analysis as the complexity of the biological sample increases. This method does not depend specifically on connexin identification and can be applied more widely to the analysis of numerous immunocytochemical markers as well as to identify particles within tissues such as nanoparticles, gene delivery vehicles, or even cellular fragments such as exosomes or microparticles.

Fundamental to understanding how tissues function is understanding how the cells that compose them communicate. In most tissues and organs, cells do not exist as homotypic monolayers but rather coexist as multiple different cell types in close proximity to one another. In some cases, these relationships are random and have no functional significance; others are symbiotic, where the presence and proximity of a neighboring cell are vital to another cell’s quiescence, specification, maturation, function, survival, and so on. Although biochemical, genetic, genomic, and proteomic methods have revealed a wealth of molecules known to participate in cell signaling pathways, many such signaling networks have been established using in vitro systems, and thus it is still unclear how cells within a three-dimensional (3D), functional tissue environment use these pathways.

This question and the increasing importance of 3D microenvironments in cancer (Håkanson et al. 2011) and stem cell biology (Doetsch et al. 1997; Shen et al. 2008; Tavazoie et al. 2008; Kazanis et al. 2010) have stimulated the generation of new methods to quantitatively map protein expression and distribution within intact tissues using automated methods, with the goal of developing models of cell signaling that can further be tested in a tissue-specific context. In many cases, these new methods use automated segmentation and co-localization of immunostaining for specific proteins and factors within tissue sections. However, co-staining with markers to delineate all possible cell types and signaling molecules, as well as further assigning them to particular cells, is not always possible, as methods such as co-localization depend on overlapping or contiguous signals. One such family of proteins that has been difficult to map within 3D microenvironments is gap junctions and their connexin subunits. We are specifically interested in understanding the role that connexin proteins play in defining cellular microenvironments.

Gap junctions consist of plaques of membrane channels, each comprising two connexon hexamers that form at the interface of adjoining cells, allowing for transport of small molecules, ions, and metabolites between coupled cells (Beyer 1993). In addition to mediating cell-cell communication, recent evidence suggests that the connexin proteins that make up the connexon hemichannels serve signaling roles, feeding into growth and survival pathways. There are currently 21 known human connexin proteins, each exhibiting unique selectivity and regulatory properties. Previous studies have demonstrated a critical role for cell-specific connexin protein expression in organ development and function, such as in the cardiovascular system (Brisset et al. 2009). In addition, gap junctional intercellular communication is required to maintain neural stem and progenitor cells in non-differentiated and proliferative states (Cheng et al. 2004; Todorova et al. 2008). Although such cell culture studies have increased our understanding of the role of specific connexin proteins in regulatory processes, our ability to study how multiple connexin proteins collectively coordinate tissue homeostasis, growth, and repair has been limited by our inability to characterize cell-specific connexin protein expression in complex organ microenvironments. Thus, we aimed to devise a strategy to quantify connexin expression in situ.

Automated segmentation of signals localized to well-defined structures, such as the nucleus or other subcellular compartments, can now be performed routinely due to steady development in this area (Lin et al. 2003, 2005, 2007; Al-Kofahi et al. 2010). However, the analysis of some signals, such as connexin expression, still remains a challenge. Connexins are localized in clusters within and on the surface of cells, appearing as puncta in immunohistochemical data. Because of their extremely small size and punctate labeling pattern (Fig. 1, arrows), current methods to quantify connexin expression in fluorescent images involve density measurements of plaque or surface area, volume, and number (Yamanaka et al. 2005; Penuela et al. 2007; Ionta et al. 2009; Romek and Karasinski 2011). Although puncta can be segmented with relative ease, assigning puncta to a specific cell can be challenging. The methods presented here address this problem and complement current cytoplasmic segmentation methods (Al-Kofahi et al. 2010) used when the cytoplasm is not labeled by a fluorescent marker. In this case, fluorescent markers confined to the nuclear surface or its vicinity (Jaiswal et al. 2004; Jablonski et al. 2010) allow assignment of puncta to specific cells.

Figure 1.

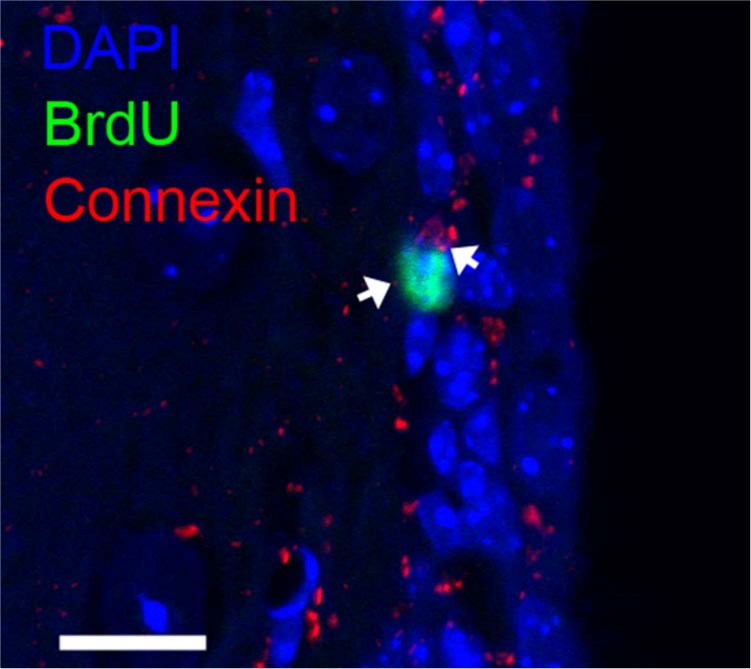
A representative confocal microscope image of connexin 43 expression in the murine subventricular zone (SVZ) (coronal view). BrdU (green) marks a subpopulation of quiescent astrocytic cells that are presumed to be neural stem cells (NSCs) (Shen et al. 2008; Tavazoie et al. 2008; Kazanis et al. 2010). The algorithm described herein allows detection and assignment of connexin expression to BrdU⁺ NSCs (arrows) by performing a nuclear neighborhood search at a pixel-level resolution. Bar = 10 µm.

Here, we present a method to detect connexins while simultaneously associating them with adjacent cells. This method is based on positive connexin expression within a “nuclear neighborhood”, thus establishing a probability for whether expression is associated with the cell’s nucleus. By creating a custom computer program that identifies a cell’s nucleus and implements a simple contour expansion algorithm, we are able to search the immediate vicinity of a nuclear surface at single-pixel resolution to detect and assign connexin expression in fluorescent images to a specific cell type. Although we have directly applied this method to the automated quantitation of connexin expression, it can easily be adapted to detect any punctate signal, including those derived from other protein expression patterns, or even from nanoparticles, gene delivery vehicles, and cellular fragments such as exosomes or microparticles.

Materials and Methods

Animal Use and Tissue Preparation

Two- to 3-month-old CD1 Swiss-Webster mice were used in accordance with Baylor College of Medicine institutional guidelines. BrdU (Sigma; St. Louis, MO) (7.5 mg/ml) was injected intraperitoneally (375 mg/kg) twice daily for 5 days. Mice were sacrificed by cervical dislocation 30 to 40 days after the last injection. Brains were dissected into cold DMEM/F12 and washed in PBS to remove debris. The subventricular zone (SVZ) was microdissected into cold DMEM/F12 and fixed in 4% paraformaldehyde (PFA) in PBS at 4C overnight. Whole brains were fixed in 4% PFA/0.1% Triton X-100 in PBS at 4C overnight, and 70-µm coronal sections were subsequently cut using a Leica VT1000S vibratome (Allendale, NJ).

Immunostaining

Sections used for immunostaining and computational analysis correspond to coordinates (mm) relative to bregma: anterior (A), posterior (P): –0.5, 2. Fixed coronal sections were pretreated with 2 N HCl for 30 min at 37C followed by a 10-min neutralization step in 100 mM sodium tetraborate. Sections were then washed in PBS, treated with 0.5% Triton X-100 in PBS for 10 min, blocked using mouse Ig blocking reagent (Vector Labs; Burlingame, CA) for 6 to 8 hr at room temperature, and incubated with primary antibodies in 0.08% M.O.M protein concentrate diluent (Vector Labs) in PBS for 24 hr at 4C. Tissue was washed in PBS and incubated with appropriate secondary antibodies at room temperature for 2 hr and washed in PBS. DAPI (0.002 mg/ml) (Sigma) was added and tissue was washed in PBS before mounting on a glass slide and coverslipped in MOWIOL (Calbiochem; San Diego, CA). Antibodies used were the following: Connexin 43, rabbit IgG, 1:500 (Abcam; San Francisco, CA); BrdU, mouse IgG, 1:50 (Becton Dickinson; Franklin Lakes, NJ). Primary antibodies were visualized using Alexa Fluor-conjugated (Invitrogen; Carlsbad, CA) secondary antibodies.

Image Acquisition

Coronal sections were imaged using an inverted Zeiss LSM 510 confocal laser scanning microscope (Carl Zeiss; Jena, Germany). Imaged areas were selected at random within the SVZ. The z-stacks were acquired using a Zeiss C-Apochromat 40×/1.2 NA water objective lens. All z-stacks were taken with a zoom factor of 3, at which the lateral pixel resolution was 0.1 µm. The step size between adjacent images in the z-stacks was 1.0 µm. The different fluorescent markers (DAPI, BrdU, and connexin) were excited with 405-nm, 488-nm, and 543-nm lasers, respectively. The z-stacks consisted of images with an area of 512 × 512 pixels and a pixel depth of 8 bits.

Image Analysis

The workflow of our image processing is shown in Fig. 2. Briefly, the main steps in image processing are nuclear segmentation using FARSIGHT (Lin et al. 2003, 2005, 2007; Al-Kofahi et al. 2010) followed by application of the contour expansion algorithm using custom MATLAB programs. The image-processing steps are discussed in detail in the following paragraphs.

Figure 2.

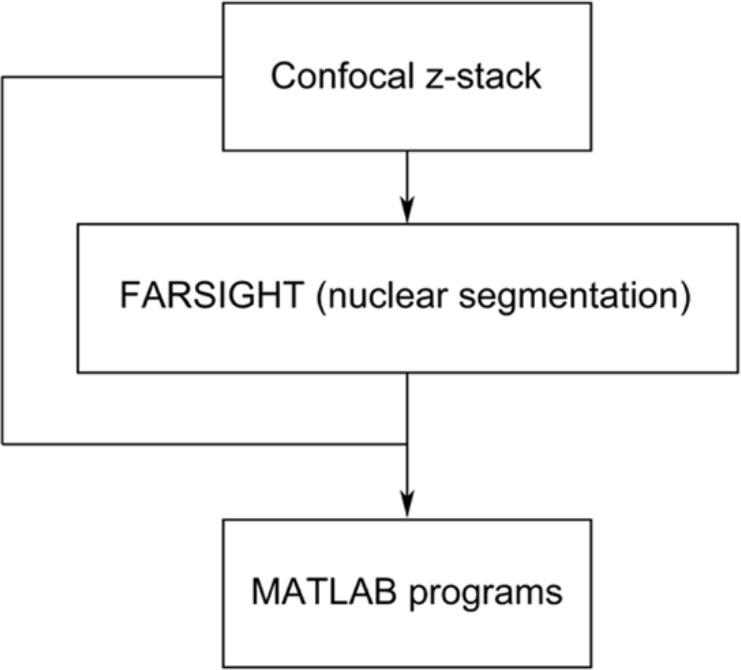
A schematic of the image analysis workflow. Each image in the z-stack is a three-color RGB image. FARSIGHT reads in the confocal z-stack file and segments the nuclear channel of interest (Lin et al. 2003, 2005, 2007; Al-Kofahi et al. 2010). Following segmentation, the confocal z-stack and the FARSIGHT output file, containing the indices of the segmented nuclei, are used as input to the MATLAB programs.

Nuclear Segmentation

The nuclei were segmented using FARSIGHT, followed by index assignment to each cell under investigation. Following segmentation, an output matrix is created that corresponds to the same number of elements as the number of pixels in the z-stack. For a more detailed description, see the Results section.

Contour Expansion Algorithm

The nuclear boundary is obtained from the segmented image using a neighborhood search algorithm. The neighborhood search algorithm is a modification of the connected component analysis commonly used in image analysis (Russ 2002). The serial and parallel programs were written using the MATLAB version R2008a (MathWorks; Natick, MA). The serial MATLAB code was optimized using the profile function available in MATLAB before applying the parallelization scheme. The programs are available from the authors (JSG or TJV) upon request. For a more detailed description, see the Results section.

Results

Image Analysis Workflow

The image analysis workflow used here is shown in Fig. 2. The first step in image analysis uses FARSIGHT to segment the nucleus, which is followed by a nuclear neighborhood search of the nucleus using the contour expansion algorithm. Throughout the segmentation process, indices are assigned to each cell of interest, allowing an output matrix to be built containing equivalent numbers of elements and pixels that are both derived from the original z-stack. In this way, each pixel of every nuclear cross section in each plane of the z-stack is represented by a specific cellular index. The advantage of this type of analysis is that interspatial relationships, between different cell types and structures, are preserved while information is captured in a 3D context.

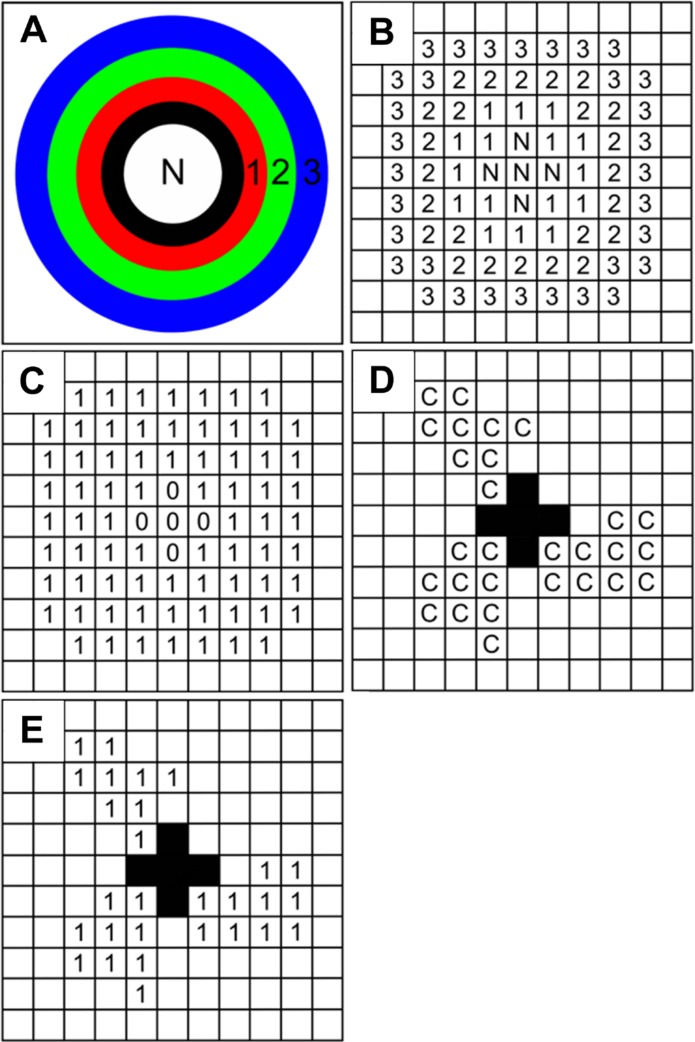
The contour expansion algorithm is then applied to the FARSIGHT-segmented image to extrapolate strength and location of expression. The first nuclear contour (black ring, Fig. 3A) is established after a neighborhood search algorithm identifies the neighborhood pixels of the nuclear boundary; these neighborhood pixels, excluding those within the nucleus, eventually become the contour ring. Thus, the neighborhood is expanded consecutively in a similar fashion, where neighborhood pixels corresponding to the previous nuclear contour are used to form the next contour ring (red, green, and blue rings, Fig. 3A). A pixel-level schematic of the contour expansion approach is illustrated in Fig. 3B. In addition, a contour filter image (Fig. 3C), reflecting the same dimensions as the original fluorescent image, is also constructed from the nuclear neighborhood pixels obtained from the contour expansion. To extract the connexin pixels in a given nuclear neighborhood (Fig. 3E), a pixel-by-pixel dot product of the contour filter image with the binarized connexin channel image (Fig. 3D) was performed. Furthermore, the number of connexin pixels in each loop can be enumerated by summing over the non-zero pixels in the binarized image (Fig. 3E), yielding information about subcellular localization, where differential locations can sometimes lead to distinct functions. For example, connexin 43 predominantly resides at the plasma membrane to facilitate intercellular communication but at times can translocate to the nucleus to regulate gene transcription and growth control (Moorby and Patel 2001; Dang et al. 2003). Therefore, because the contour expansion algorithm is applied to each image of the z-stack, an accurate 3D reconstruction reflecting connexin expression is created that allows for strength, location, and cellular assignment to be determined.

Figure 3.

Illustration of the nuclear neighborhood search algorithm. (A) A schematic of the contour expansion approach in which the nuclear neighborhood is scanned starting at the surface of the nucleus (black ring) and extending to layers (red, green, and blue layers) beyond the surface layer of pixels. Each layer is one pixel wide in an eight-neighborhood sense. (B) The contour expansion approach is illustrated at the pixel level. Pixels labeled as 1, 2, and 3 correspond to different layers starting from the surface of the nucleus. (C) A nuclear neighborhood filter is then constructed from the contour pixels shown in (B). The filter image of the nucleus has the same dimension as the original fluorescent image. (D) The connexin channel in the original fluorescent image is illustrated here. Each pixel in the connexin channel image is then multiplied with the corresponding pixel in the filter image to extract the pixels in the nuclear neighborhood that are occupied by connexins (E).

Program Fidelity

Our goal is to use this method for completely automated feature extraction; therefore, we tested the fidelity of the method using synthetic data. As controls, images of a disk with a concentric ring separated from the disk by an arbitrary set of empty pixels (Suppl. Fig. S1) and a z-stack consisting of two copies of the disk and ring image (Suppl. Fig. S1) were used to evaluate accuracy and consistency of the contour expansion–based pixel detection. The output of the program, when applied to a simple synthetic image of a circular disk, is shown in the supplemental material (Movie 1), where the contours are added concentrically with respect to the disk (Movie 1). Starting at the boundary of the disk, loop extension proceeds outward in increments of one pixel to expand the nuclear neighborhood.

The fidelity of our program was further tested by using a test image consisting of a circle concentric with a disk but separated from the disk by empty pixels (Suppl. Fig. S1). The number of pixels in the ring was enumerated by first applying a simple threshold to binarize the test image, making intensity values below the threshold equal to zero and above the threshold equal to 1, and then the number of pixels with a value of 1 was counted. Subsequently, the disk in the test image was segmented using FARSIGHT, and the MATLAB program was applied to enumerate the number of pixels in the ring surrounding the disk. In the end, the number of pixels that constituted the ring in both cases was the same. A z-stack of the test image was created by adding another copy to the existing image. As expected, application of the algorithm to the z-stack produced an output that was twice the number of pixels in the ring of the test image. Taken together, these results strongly demonstrate consistent fidelity of our MATLAB program.

Performance Analysis

To evaluate the performance of the program, execution times were measured using synthetic images and z-stacks that mimic potential in vivo scenarios commonly encountered during confocal image acquisition. The performance of the custom MATLAB program was assessed by measuring the time it takes to complete the contour expansion for 10 loops using synthetic data. The execution time or duration of the calculations was measured using the tic-toc commands in MATLAB. First we used a z-stack consisting of a different number of images from 1 through 20. Each image in the z-stack consisted of 512 × 512 pixels. In each image of the z-stack, a single circular disk with a diameter of 220 pixels was used as a model for the nuclear cross section of a cell. The durations of the calculations for z-stacks of different thicknesses are presented in Fig. 4A. As a result, the duration of the program scales linearly with the number of images in the z-stack.

Figure 4.

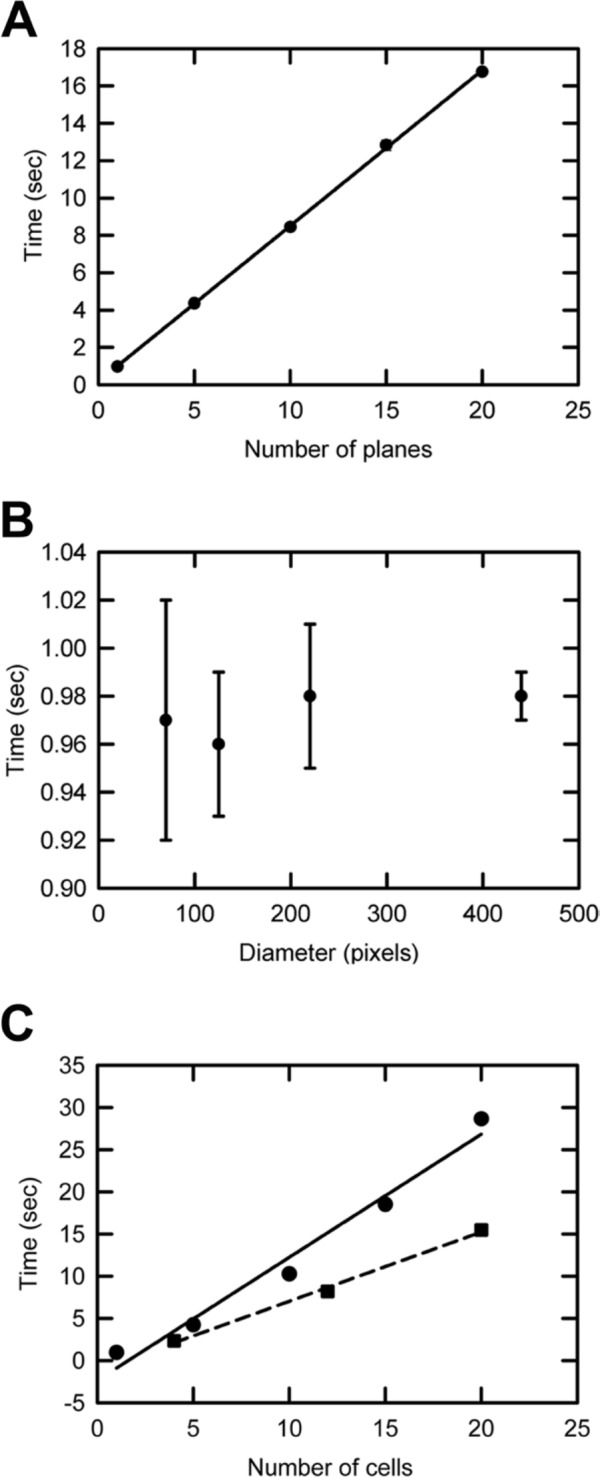
Testing the performance of the MATLAB program using synthetic data. (A) Program execution times were measured when the number of images in the z-stacks varied. Each image in the z-stack consisted of 512 × 512 pixels. A circular disk with a diameter of 220 pixels was used as the test object in each image of the z-stack. The number of contours used in each image in the z-stack was 10. The execution time scales linearly with the number of planes (R ² = 0.99, n=3). The error bars are one unit of standard deviation of the mean values and are smaller than the symbols representing the data points. (B) The mean values of the execution times, to scan 10 contours around circular disks of varying diameters in single-plane images of 512 × 512 pixels each (n=3), were recorded. The error bars are one unit of standard deviations of the mean values. (C, solid line) The durations of the program to perform the loop calculations for varying numbers of circular disks of fixed diameter in single-plane images of 512 × 512 pixels each are illustrated here. The diameter of a single circular disk in these images is 45 pixels. The execution time of the program scales linearly with the number of disks (R ² = 0.98, n=3). (C, dashed line) The dashed line represents the linear scaling of the execution time with the number of disks for the custom-built parallel program (R ² = 0.99, n=3). The parallel program is significantly faster than the serial program (solid line). The error bars are one unit of standard deviations of the mean values and are smaller than the symbols used to represent the data points. The execution times were calculated using the standard MATLAB commands to measure time.

The program is not limited to specific magnifications of objective lens used during image acquisition. To assess the performance of the program in such a scenario, the execution times of the program on images that consist of circular disks of different diameters were measured (Fig. 4B). It is not surprising that execution times are independent of the diameter of the disks because the entire image is scanned when constructing the nuclear neighborhood filter. In practice, at a lower magnification, to scan the same distance covered by 10 loops at a higher magnification, it suffices to decrease loop number because the size of a pixel at a lower magnification is always larger than that at a higher magnification.

Finally, to estimate the scaling of program execution time with the number of cells in an image, we used images with different numbers of circular disks for comparison. The diameter of each disk in these images was 45 pixels. From Fig. 4C, it is clear that the execution time of the program scales linearly with the number of disks, planes, and cells in the image.

Overall, these studies demonstrate consistent and accurate pixel detection under a broad range of user-defined criteria mimicking common imaging scenarios. Regardless of cell diameter, number of planes, or objective magnification used during image acquisition, our contour expansion–based pixel detection method is able to detect and assign positive pixels to a specific cell. This validation of the robustness of the method is the first step in the design of an automated approach that can be applied to high-throughput analysis of complex tissues. We next explored whether these methods could be implemented using a parallel approach to maximize the efficiency when the method is applied to complex tissues with a large number of cells.

Parallel Implementation

A parallel implementation of the image analysis algorithm can be used to expedite calculations when the number of cells in the z-stack is large (Vadakkan and Bassler 2005). This allows distribution of the workload among the cores/processors (e.g., multicore processors, multicore graphics cards, computer arrays in a network) being used. This reduces wait time of program execution that would otherwise be performed sequentially on a single-processor computer. Image analysis using parallel algorithms is possible using a variety of software, such as MATLAB, OpenCV, and Adobe Photoshop. Here, we used the parallel MATLAB Toolbox developed by Dr. Jeremy Kepner (Lincoln Laboratory, MIT, Cambridge, MA) to build a parallel MATLAB program of our algorithm. The toolbox makes use of Message Passing Interface (MPI) to implement MATLAB programs on multiple processors (http://www.ll.mit.edu/mission/isr/pmatlab/pmatlab.html). Although we are using MPI for parallelization, the communication between different processor cores in our parallel implementation is minimal so that the workload arising from communications between the processor cores is very low.

Accordingly, we chose to submit z-stacks (original z-stack from the microscope and the FARSIGHT segmentation file containing the indices of the segmented nuclei) to each processor of an Intel Duo Core processor (1.30 GHz and 4 GB RAM) laptop, with additional information to instruct processor-specific execution on non-overlapping nuclei indices. This ensures that each processor is responsible for analysis of a different data set. Figure 4C (dashed line) illustrates the scaling of the execution time with the number of disks for a custom-built parallel MATLAB program that implements the algorithm discussed above. The same synthetic data used with the serial MATLAB program discussed earlier were used here as well. A significant improvement in the execution times is achieved (dashed line) with the parallel program compared with the serial program (solid line).

In summary, the execution times of the program scale linearly with the number of z-stacks as well as the number of nuclei in the image (Fig. 4A). Similarly, the execution times of the parallel program also scale linearly with the number of nuclei (Fig. 4C); however, the execution times when compared with their serial counterparts are reduced by a factor that is approximately equal to the number of cores in the multicore processor (Fig. 4C, compare between dotted and solid lines). Therefore, it is clear that adding more processors will enhance the execution time, until the number of processors equals the number of cells, but for simple routine use, this approach benefits greatly from a parallel approach available on many commonly used computers and will only improve as personal computers evolve to include even more processors.

Application to the SVZ Reveals Connexin 43 Expression in Adult Neural Stem Cells

After validating the fidelity of the MATLAB program and measuring its performance, we tested its application in the context of neural cell associations and gap junction expression in the adult SVZ. Several reports indicate that connexin 43 is expressed in radial glia, the in vivo precursors to adult neural stem cells, and that it plays an important role in neocortical development. Therefore, we used the program to quantify the expression of connexin 43 in adult neural stem cells residing within the SVZ. We immunostained sections of the SVZ with antibodies against connexin 43 and counterstained the tissue with DAPI to identify cell nuclei. Confocal z-stack images were acquired and subjected to the neighborhood contour expansion algorithm to analyze the distribution of connexin 43–positive puncta within the vicinity of each neural stem cell nucleus. Figure 1 shows a representative image from one such data set.

The z-stacks consisted of 8-bit three-channel images corresponding to connexins and BrdU- and DAPI-stained nuclei. The BrdU-stained nuclei were segmented using FARSIGHT. The confocal z-stack image and the segmentation output file from FARSIGHT were given as input to the MATLAB program. The program created 10 concentric loops starting at the segmented nuclear surface in each plane of the z-stack. The loops created by the program for a representative image in the z-stack are shown in Fig. 5B–D and in Movie 2 (supplemental material). For the imaging parameters used, 10 loops covered a mean distance of 1 µm from the surface of the nucleus to recapitulate reported cross-sectional areas of SVZ neural stem cells (NSCs) (Doetsch et al. 1997). The connexin channel image was binarized by applying an intensity threshold of 100. The nuclear neighborhood filter extracted by the program was used to take a pixel-by-pixel product with the binarized connexin channel image to enumerate the number of connexin-positive pixels in each loop surrounding the nuclear surface. The output from the program for a representative z-stack is summarized in Table 1.

Figure 5.

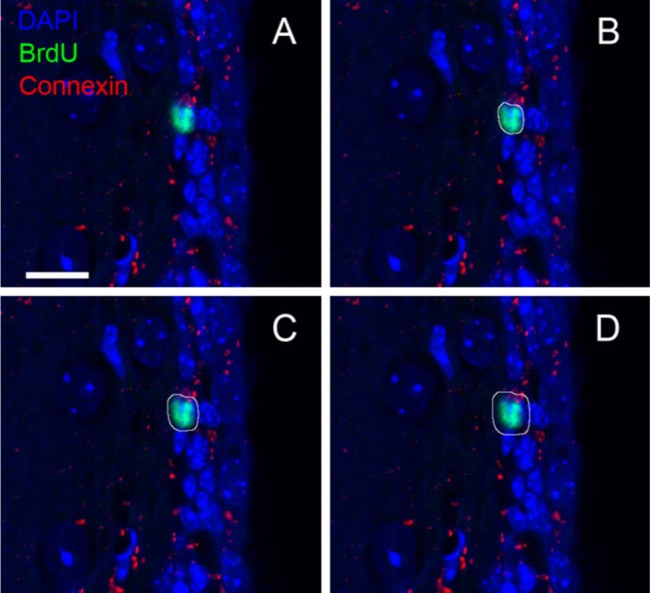
Application of contour expansion algorithm to a representative confocal z-stack image. The z-stack consists of 10 images, and each image consists of 512 × 512 pixels. The x and y pixel scaling is 0.1 µm each, and the axial pixel scaling is 1.0 µm. (B–D) The white loops around the BrdU (green)-stained nucleus (blue) are the contours created by the MATLAB program, labeled as L1, L5, and L10, respectively (Table 1). L1 consists of pixels adjacent to the surface pixels of the nucleus. The surface pixels are obtained following nuclear segmentation using FARSIGHT. The contours sweep the neighborhood of the nucleus starting at the nuclear surface, where each contour is one pixel wide in an eight-neighborhood sense. Similar contours are created with respect to the nuclear surface in all images in the z-stack containing a cross section of the nucleus (Movie 2 [supplemental material]). Bar = 10 µm.

Table 1.

Output from the MATLAB Program for a Representative Confocal z-Stack

	L1	L2	L3	L4	L5	L6	L7	L8	L9	L10
Z1	0	0	0	0	0	0	0	0	0	0
Z2	0	0	0	0	0	0	0	0	0	0
Z3	0	0	0	4	3	0	0	0	0	0
Z4	0	0	0	0	0	0	1	0	0	2
Z5	2	0	0	0	0	0	4	6	7	7
Z6	8	7	3	5	9	7	9	13	13	9
Z7	26	27	24	19	16	14	14	14	11	10
Z8	0	8	11	14	16	21	26	21	20	19
Z9	0	0	0	0	0	0	0	0	0	0
Z10	0	0	0	0	0	0	0	0	0	0

Z1 through Z10 are the labels of images in the confocal z-stack taken within the subventricular zone (Fig. 1). L1 through L10 are the labels of the loops created by the MATLAB program. The entries in the table are the total number of pixels in each loop whose intensity in the connexin channel is above a defined intensity threshold. An intensity threshold of 100 was used to delineate the connexin-positive pixels. The nucleus extends in the z-stack from Z2 through Z8. Even though the nuclear surface starts in Z2, there were no connexin pixels with an intensity greater than 100 in Z2. Therefore, the number of connexin-positive pixels in all loops (L1–L10) in Z1, Z2, Z8, and Z10 is zero. The total duration of the calculations was ~8 sec. Images labeled as Z1, Z2 . . . Z10 correspond to images labeled as Plane 0, Plane 1 . . . Plane 9 in Movie 2 (supplemental material).

The program may be used to classify the nuclei in a confocal z-stack based on their connexin expression (Fig. 6 and Suppl. Fig. S2). Figure 6A is an image from a confocal z-stack consisting of 28 nuclei, where nuclei are stained with DAPI. The red loops around each nucleus are the surface pixels of the nuclei detected by FARSIGHT. We enumerated the number of connexin-positive pixels in the vicinity of each nucleus using the contour expansion algorithm (Fig. 6B). Nuclei (Fig. 6C) were then pseudo-colored based on the number of connexin-positive pixels in their neighborhood. Red nuclei have the maximum number of connexin-positive pixels in their neighborhoods, whereas the nuclei colored in blue have the least number of connexin-positive pixels in their neighborhoods. The program also identified and assigned connexin 43 expression to two astrocytic cell types residing adjacent to one another, confirming previous reports describing connexin 43 in astroglial cells (Pannasch et al. 2011) (Suppl. Fig. S2). These data show that the loop expansion program can be used to detect the unique staining patterns of connexins in fluorescent images and quantify, with subcellular resolution, fluorescent expression to the vicinity of the nuclear surface.

Figure 6.

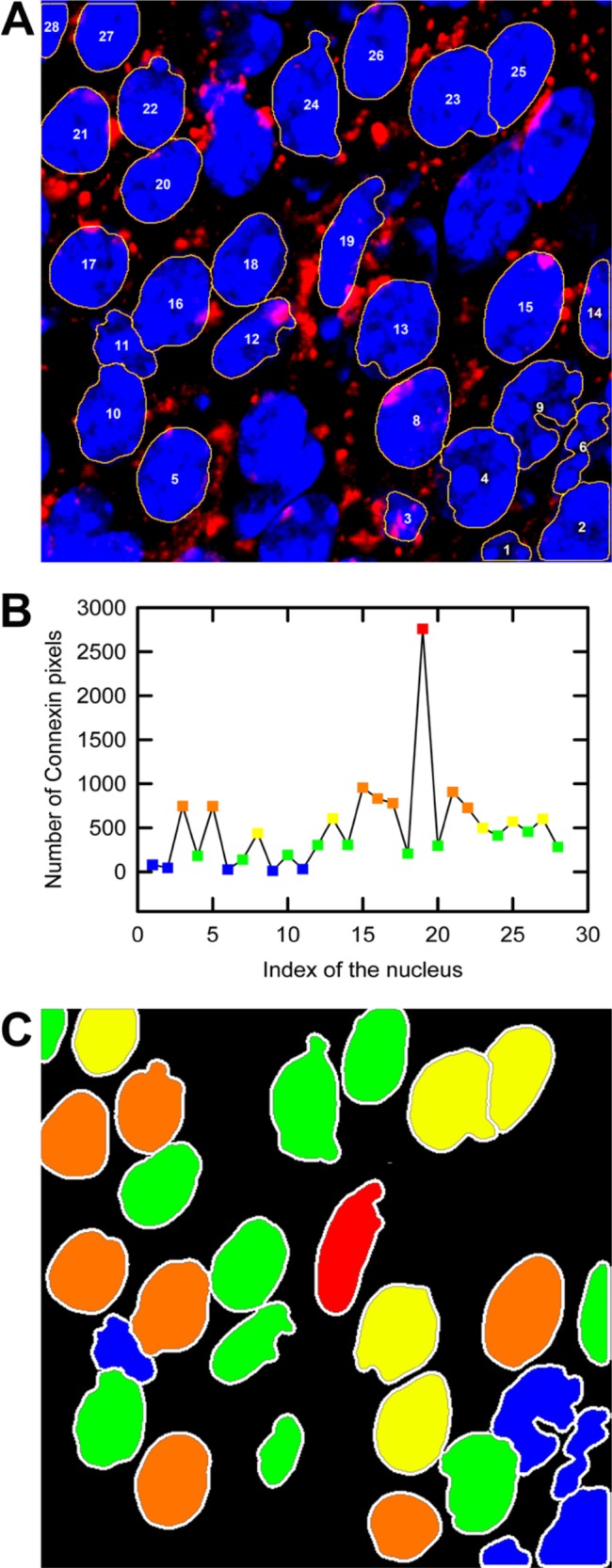
Application of FARSIGHT output to a z-stack consisting of 28 DAPI-stained nuclei. (A) The loops (yellow lines around the nuclei) are the surface pixels of each nucleus. The loop expansion algorithm was applied to the FARSIGHT output data to measure the number of connexin pixels. (B) Histogram depicting the number of connexin pixels detected in 10 loops around each nucleus. (C) The nuclei were then grouped based on the number of connexin pixels and color coded corresponding to pixel number. Blue corresponds to nuclei with the least number of connexin pixels detected, whereas red indicates those with maximum pixel detection.

Discussion

The computational approach presented here allows us to assess connexin expression within cells using an automated quasi-3D nuclear neighborhood scan. The ability to calculate the fraction of connexin-expressing cells in an image and associate them with specific cell types is biologically important as it allows us to monitor how a population of cells reacts to and changes connexin expression under pathological conditions and in normal biological processes. In situations where strength, balance, and location of connexin expression dictate the degree and type of intercellular signal that is propagated, the power to record the minutest change is critical. Toward this goal, the present approach provides a foundation on which computation-based techniques can be used to explore the interaction of particular cell types, as well as their relationship to extracellular structures, and how these may regulate neurogenesis in the SVZ (Shen et al. 2008; Tavazoie et al. 2008; Kazanis et al. 2010).

The adult SVZ represents one of two primary germinal regions in the brain where persistent neurogenesis and regeneration occur. Here, neural stem cells are spatially restricted and give rise to migrating progenitor cells that terminally differentiate into olfactory bulb interneurons. In the current study, we were able to associate BrdU-positive nuclei in the SVZ with connexin expression. Our contour expansion algorithm allowed us to not only detect connexin 43 expression in this rare stem cell population but also quantify the strength and subcellular detection of connexin 43–positive puncta, providing insight into potential functions within the neural stem cell population.

Our contour expansion method enables a thorough interrogation of the image to the full extent of the spatial resolution. We not only can detect connexin expression within a segmented nucleus but, because each pixel is included in the analysis, can also identify positive pixels in the neighborhood of a nuclear boundary and define the precise proximity. Although analysis of each pixel is computationally intensive, we have shown that parallelization can significantly reduce the time burden. Differences in subcellular location may translate to different functions and thus provide a window into the dynamics of neural stem cell behavior. The computational method presented is easily adapted to include differentiated markers, where correlating physiological ranges of connexin 43 puncta to differentiation status remains an attractive possibility.

The algorithm discussed in this article conducts a quasi-3D scan of a nuclear neighborhood where the neighborhood of each nuclear cross section in each plane is searched using the loop expansion algorithm. The program may be easily modified to output the x, y, and z coordinates of the pixels belonging to the connexins to calculate the mean distance of the plaques from the centroid of the nucleus. Significant insights relating to the proximities of cells have been revealed within the subventricular zone, making such measurements important for future studies (Shen et al. 2008; Kazanis et al. 2010). Real 3D analyses could be carried out in a similar manner to what has been proposed here, where the nearest neighbor would now consist of surrounding pixels in all directions; however, this is much more computationally intensive and will not significantly affect the distance measurements over estimates based on the same image stacks that establish the x, y, and z coordinates. Thus, although possible, real 3D analysis would not add much value compared with the quasi-3D analysis described here.

By performing a quasi-3D scan of the nuclear neighborhood, meaning that a series of two-dimensional images from an image stack were analyzed (see Materials and Methods), the program automatically detected and associated gap junction plaques with the nucleus under consideration. The program may be easily modified to output the x, y, and z coordinates of the pixels belonging to the connexins as well. These data can then be used to calculate the mean distance of the plaques from the centroid of the nucleus (Shen et al. 2008; Kazanis et al. 2010).

Here we have described a new approach to define the distribution of connexin 43 within the brain, a complex tissue with densely packed nuclei. Although connexin expression was the primary motivation for this study, several other proteins are also known to have punctate expression patterns—for example, desmin (Isobe et al. 1994) and cadherins (Kuijpers et al. 2007). In addition to protein localization, there is also a growing interest in characterizing the delivery and distribution of nanoparticles and quantum dots within tissues and whole organisms (Minami et al. 2012; Mykhaylyk et al. 2012), as well as the distribution of microparticles and exosomes released by cells and often associated with pathology or the activation of specific signaling pathways (van der Pol et al. 2010). The analysis presented here would also be applicable to images containing these types of particles and thus could be of value to researchers studying a wide range of biological problems. Overall, the ability to quantify changes in the distribution of key proteins or particles within cells is fundamental to being able to further understand their function in complex cellular microenvironments. Success in this area will no doubt require the development of sensitive and robust methods with a high statistical throughput such as the one reported here.