Computation of tightly-focused laser beams in the FDTD method

Abstract

We demonstrate how a tightly-focused coherent TEM_mn laser beam can be computed in the finite-difference time-domain (FDTD) method. The electromagnetic field around the focus is decomposed into a plane-wave spectrum, and approximated by a finite number of plane waves injected into the FDTD grid using the total-field/scattered-field (TF/SF) method. We provide an error analysis, and guidelines for the discrete approximation. We analyze the scattering of the beam from layered spaces and individual scatterers. The described method should be useful for the simulation of confocal microscopy and optical data storage. An implementation of the method can be found in our free and open source FDTD software (“Angora”).

1. Introduction

The finite-difference time-domain (FDTD) numerical electromagnetic method [1] is gaining increasing popularity for solving nano-photonics problems [2–5]. In the FDTD method, the electromagnetic field is defined at a finite number of discrete spatial positions, and calculated at consecutive discrete time instants using an explicit leapfrogging algorithm. The simplest illumination modality in the FDTD method is the plane wave, which is now a standard feature in most FDTD implementations. However, in many optical situations one needs to simulate a more complicated illumination beam. In this paper, we describe how a transverse-electric-magnetic (TEM) laser mode of order (m, n) focused by a lens can be simulated in the FDTD method. The basis of our technique is the decomposition of the beam around the focus into a plane-wave spectrum, and the representation of this infinite sum by a finite number of plane waves with suitable amplitude factors. Each plane wave is introduced into the FDTD computational grid using the total-field/scattered-field (TF/SF) method, which is well-studied in the literature. The traditional TF/SF approach for injecting a plane wave into the FDTD grid, explained in detail in [1], has since been refined by numerous authors. Two notable improvements to the TF/SF method are the matched-numerical-dispersion method [6] and the perfectly-matched plane-wave source method [7].

The approach described in this paper is similar to that followed in our previous work [3], with the following improvements: (i) The range of beams that can be introduced into the FDTD grid is significantly expanded. The results in [3] merely correspond to the (0, 0) mode with f₀ = ∞ within the context of the present paper. (ii) The focused beam is computed in spaces with planar layers and inhomogeneities. A microscopy example is given to demonstrate the possibility for simulating a confocal imaging scenario. (iii) The error analysis performed in the present paper is much more comprehensive and general. (iv) The results described here have been implemented in an open-source FDTD software (Angora), which can be freely downloaded under the GNU Public License.

The rest of the paper is organized as follows. In Section 2, the theory of the focused laser beam is explained. In Section 3, the FDTD computation of the theoretical results in Section 2 are given. In Section 4, a comparative error analysis is presented for various approximation schemes. In Section 5, planar layered spaces and scatterers are discussed, and the capability for simulating confocal microscopy is demonstrated. In Section 6, future directions are discussed. In Section 7, our free, open-source FDTD software (Angora) is briefly introduced. The paper is concluded by final remarks in Section 8.

2. Focusing of laser beams

The transverse-electric-magnetic laser mode of order (m, n) (also called a Hermite-Gaussian mode, or a TEM_mn mode) is a solution of the paraxial wave equation [8], which assumes that the energy in the beam propagates mainly in a single direction along parallel rays. The electric field of a TEM_mn mode at the beam waist, which is assumed to lie in the (x, y) plane, is given by the following expression:

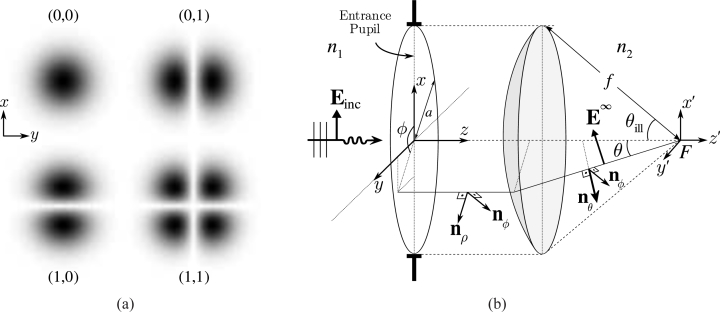
$${\mathbf{E}}_{\text{inc}}\left(x,y;t\right)=\widehat{\mathbf{e}}\psi \left(t\right){\gamma }_{mn}\left(x,y\right)=\widehat{\mathbf{e}}\psi \left(t\right)H_m\left(\sqrt{2}x/w_0\right)H_n\left(\sqrt{2}y/w_0\right)e^{-\left(x^2+y^2\right)/w_0^2},$$ (1)

where ê is the constant transverse unit vector in the (x, y) plane that determines the uniform polarization, ψ(t) is the time waveform of the beam, w₀ is the beam width, and H_n(x) are the n^th-order Hermite polynomials [9]. The first two Hermite polynomials are H₀(x) = 1, H₁(x) = 2x. The intensity maps of the the time-independent parts of the (0, 0), (0, 1), (1, 0), and (1, 1) modes on the beam waist are shown in Fig. 1(a). In real situations, the time dependence ψ(t) is a randomly-fluctuating waveform; which can be assumed statistically stationary in time [8]. This random process will have a wavelength spectrum, which might consist merely of a very narrow wavelength band for a traditional laser, or span a wide range of wavelengths for a su-percontinuum laser. If the entire optical system (including the illuminated object) is linear and time invariant, all second-order coherence properties at the output (e.g., power-spectral density at a point, mutual coherence function between two points, etc.) are completely determined by the second-order coherence properties of the input waveform and the deterministic spectral response of the system [8, 10, 11]. The latter can be obtained by sending a deterministic time pulse with a finite duration and a predefined spectral content through the system. The parameters of a modulated Gaussian waveform, for example, can easily be adjusted to manipulate its spectral content; since the cutoff wavelengths of this waveform are expressible in closed form. This is a suitable approach for a deterministic numerical method such as FDTD that operates directly in time domain.

Fig. 1.

(a) Intensity maps of several TEM_mn modes on the beam waist. (b) The geometry of the incidence and focusing of the beam.

If the maximum appreciable free-space wavelength λ_max present in the spectrum of ψ(t) is much smaller than the beam waist w₀, the paraxial approximation becomes valid, and the rays in the beam stay mostly parallel to the z axis beyond the beam waist for many beam widths [12]. We assume that such a highly-paraxial beam is incident on the entrance pupil of a positive (convergent) optical system, as shown in Fig. 1(b). The focusing system is assumed to be free of spherical aberration and obeying the Abbe sine condition. In other words, all parallel rays entering the entrance pupil are focused at the back focal point F, and a = f sinθ_ill; where a is the radius of the pupil, f is the back focal length of the system, and θ_ill is the illumination aperture angle. A portion of the Gaussian reference sphere around F is shown shaded in Fig. 1(b). The object and image spaces of the focusing system are non-magnetic (μ₁=μ₂=1) with refractive indices n₁ and n₂, respectively. An example ray converging toward F is shown in Fig. 1(b). The ray makes an angle θ with the optical axis at F. In the geometrical optics regime, the electric field E^∞ on the ray is in the form

$${\mathbf{E}}^{\infty }\left(r,\theta ,\varphi ,t\right)=\widehat{\mathbf{a}}\left(\theta ,\varphi \right)E^{\infty }\left(\theta ,\varphi ,t+n_{2}r/c\right)/r,$$ (2)

where â is the unit vector specifying the polarization, and E^∞(θ, ϕ, t) is the strength factor of the ray [13]. The combined electric field around the focus F due to all the incoming rays is given by the Debye-Wolf diffraction integral [13]:

$$\mathbf{E}\left({\mathbf{r}}^{\prime },t\right)=\frac{n_2}{2\pi c}\underset{{\mathrm{\Omega }}_{\text{ill}}}{\iint }\widehat{\mathbf{a}}\left(\theta ,\varphi \right){\dot{E}}^{\infty }\left(\theta ,\varphi ,t-n_2\widehat{\mathbf{s}}\cdot {\mathbf{r}}^{\prime }/c\right)d\mathrm{\Omega },$$ (3)

in which

$$\widehat{\mathbf{s}}=\left(s_x,s_y,s_z\right)=\left(-\text{sin}\theta \text{cos}\varphi ,-\text{sin}\theta \text{sin}\varphi ,\text{cos}\theta \right)$$ (4)

$${\mathbf{r}}^{\prime }=\left(x^{\prime },y^{\prime },z^{\prime }\right)$$ (5)

are the incidence unit vector and the position vector in the image space, Ω_ill is the conical solid angle bounded by θ_ill, and dΩ =sinθdθdϕ =ds_xds_y / cosθ. The dot above E^∞ denotes the derivative with respect to time. The strength factor E^∞(θ, ϕ, t) can be related to the Hermite-Gaussian beam on the entrance pupil using geometrical optics principles [12–14]:

$$E^{\infty }\left(\theta ,\varphi ,t\right)={\left(n_1/n_2\right)}^{1/2}f{\text{cos}}^{1/2}\left(\theta \right)\psi \left(t-t_c\right){\gamma }_{mn}\left(x,y\right),$$ (6)

where γ_mn(x, y) is the Hermite-Gaussian beam profile defined in Eq. (1). The delay t_c in the time waveform ψ(t) represents the time of propagation for any ray from the entrance pupil to F. Since all wavefronts converge at F, this delay is independent of θ and ϕ; so the definition of ψ(t) can be time-advanced to cancel t_c. The relationship between the coordinates (x, y) and (θ, ϕ) in the object and image spaces follows from the Abbe sine condition: (x, y) = (f sinθ cosϕ, f sinθ sinϕ). For small incidence angles at each refracting surface, the angle that â makes with the meridional plane (one defined by the ray and the optical axis) will be the same as that of ê[13, 15]. Therefore we have â · n_θ = ê · n_ρ and â · n_ϕ = ê · n_ϕ, where the unit vectors n_θ, n_ρ, n_ϕ are as shown in Fig. 1(b).

We assume that the entrance pupil of the optical system not overfilled; namely, the beam width w₀ is sufficiently smaller than the pupil radius a so that the beam is contained within the pupil. Following [12], we define the filling factor as the following ratio:

$$f_0=w_0/a=w_0/\left(f\text{sin}{\theta }_{\text{ill}}\right)$$ (7)

In the remainder of this analysis, we assume that the filling factor f₀ is less than 0.6. Increasing f₀ beyond this number causes the focal fields to have a more oscillatory behavior, which makes the approximation methods introduced here less accurate. A more uniform method of approximation that is valid for all values of f₀ is the subject of future study.

The results in Eqs. (1)–(6) express the electromagnetic field around the focus F for a paraxial incoming beam E_inc at the entrance pupil. In the following section, we will show how this formulation can be discretized and adapted to the FDTD numerical method.

3. FDTD implementation using the TF/SF method

Upon inspection, it is seen that the diffraction integral in Eq. (3) is an infinite summation of plane waves, each traveling in a different direction determined by ŝ. Let’s write the integral in Eq. (3) as a Riemann sum over a finite collection of plane waves:

$$\tilde{\mathbf{E}}\left({\mathbf{r}}^{\prime },t\right)=\frac{n_2}{2\pi c}\sum _n{\alpha }_n\widehat{\mathbf{a}}\left({\theta }_n,{\varphi }_n\right){\dot{E}}^{\infty }\left({\theta }_n,{\varphi }_n,t-n_2{\widehat{\mathbf{s}}}_n\cdot {\mathbf{r}}^{\prime }/c\right),$$ (8)

in which the index n is used to enumerate the individual plane waves. The spherical incidence angles are θ_n and ϕ_n, and the incidence directions ŝ_n are

$${\widehat{\mathbf{s}}}_n=\left(s_{x_n},s_{y_n},s_{z_n}\right)=\left(-\text{sin}{\theta }_n\text{cos}{\varphi }_n,-\text{sin}{\theta }_n\text{sin}{\varphi }_n,\text{cos}{\theta }_n\right).$$ (9)

The weight α_n replaces the differential dΩ in Eq. (3). The above form is not necessarily the optimal solution for the approximation of the focal fields, since the choice of ŝ_n and α_n are independent of the image-space position r′ and the time t. However, this arrangement has the advantage that the beam is expressed as a sum of plane waves, each of which can be introduced into the FDTD grid using well-documented approaches such as the scattered-field (SF) or the total-field/scattered-field (TF/SF) methods [1]. We have chosen the TF/SF method for our implementation, mainly because its computational cost is proportional to the surface area of the TF/SF boundary. The cost of the SF method is usually much higher, since it is proportional to the volume of the region over which the beam is calculated.

The Debye-Wolf diffraction integral in Eq. (3) is basically a two-dimensional integral over the direction cosines s_x, s_y inside the unit disk $s_x^2+s_y^2<{\text{sin}}^2{\theta }_{\text{ill}}$. The choice of the incidence directions ŝ_n and the weights α_n in Eq. (8) for the optimal approximation of Debye-Wolf diffraction integral in Eq. (3) is the subject of two-dimensional cubature[17–19]. In this paper, we consider three different approaches to this problem. These are explained in the following subsections.

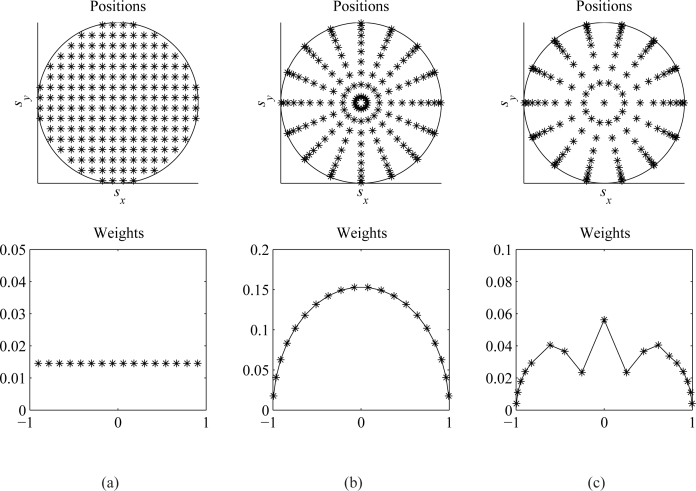
3.1. Equally-spaced s_x, s_y

The most straightforward way of placing the plane wave directions ŝ_n inside the unit disk $s_x^2+s_y^2<{\text{sin}}^2{\theta }_{\text{ill}}$ is an equally-spaced Cartesian arrangement shown in Fig. 2(a). The (s_x, s_y) points are spaced Δs_x and Δs_y apart in the s_x and s_y directions, respectively; with equal cubature weight α_n = Δs_xΔs_y for each point. In addition to the simplicity of this arrangement, useful guidelines can be derived for the spacings Δs_x and Δs_y. These guidelines rely on the Whittaker-Shannon sampling theorem [20]. The principle behind this is best explained if harmonic time dependence exp(−iωt) is assumed in the diffraction integral in Eq. (3):

$$\mathbf{E}\left({\mathbf{r}}^{\prime }\right)=\frac{-i{k}^{\prime }}{2\pi }{\iint }_{-\infty }^{\infty }P\left(s_x,s_y\right)\widehat{\mathbf{a}}\left(\widehat{\mathbf{s}}\right)E^{\infty }\left(\widehat{\mathbf{s}}\right)e^{i{k}^{\prime }\widehat{\mathbf{s}}\cdot {\mathbf{r}}^{\prime }}d{s}_{x}d{s}_y/\text{cos}\theta ,$$ (10)

in which k′ = n₂ω/c is the wavenumber in the object space, and P(s_x, s_y) is equal to 1 for $s_x^2+s_y^2<{\text{sin}}^2{\theta }_{\text{ill}}$, and zero otherwise. For a fixed z′, the observation coordinate r′ depends only on x′ and y′. The integral in Eq. (10) is then in the form of a two-dimensional Fourier transform from the (s_x, s_y) domain to the (x′, y′) domain. Since the center of the beam is usually the region of interest, we can proceed by taking z′ = 0. The Whittaker-Shannon sampling theorem says that, if the integral in Eq. (10) is approximated by a finite sum at a Cartesian grid of (s_x, s_y) points as shown in Fig. 2(a), the result is an infinitely replicated (or aliased) version of E(r′) [20]. Assuming Δs_x=Δs_y=Δ, the period of this replication is given by

$$D=\frac{2\pi }{k^{\prime }\mathrm{\Delta }}$$ (11)

If the fields on the focal plane (z′ = 0) can be contained in a square region of dimensions W₀ × W₀, an overlap can be avoided with D > W₀. From vectorial diffraction theory, we know that the focal fields decay in the lateral direction at a distance scale of d₀ = λ/(n₂f₀ sinθ_ill) around the focus [12]. This holds as long as f₀ is inside our range of interest 0 < f₀ < 0.6. Our extensive numerical experiments suggest that the beam is always well contained within 5d₀ – 6d₀ of the focus. In our implementation, we choose W₀ to be 5.2 d₀. Another length scale to be taken into account is the lateral size of the TF/SF boundary. If the TF/SF boundary is too wide, the beam may be replicated inside the boundary. If the lateral diagonal length of the TF/SF boundary is T₀, D should be larger than T₀ to avoid this replication. In summary, the condition on the spacing Δ is

$$\mathrm{\Delta }<\frac{2\pi }{k^{\prime }\text{max}\left\{W_0,T_0\right\}}.$$ (12)

In the following, we will denote this quadrature scheme by the acronym EQ.

Fig. 2.

Cubature rules for the approximation in Eq. (8) for the 2D integral in Eq. (3). The top graphs show the placement of the quadrature points in the unit disk. The bottom graphs show the weights along s_y=0. (a) 188 points on an equally-spaced Cartesian grid of (s_x, s_y) positions inside the illumination cone. (b) Separation of the 2D integral on the (s_x, s_y) plane into two 1D integrals over the radial coordinates (s, ϕ). The s integral is evaluated using Gauss-Legendre quadrature, and the ϕ integral is evaluated using the midpoint rule. A total of 20×8=160 quadrature points are used. (c) A custom 127-point quadrature rule for the unit disk [16], exact for polynomials $s_x^i{s}_y^j$ where i + j < 25.

3.2. Gauss-Legendre quadrature

The integral in Eq. (3) can be reduced into two nested one-dimensional integrals, and approximated using more familiar quadrature rules. First, the variables are changed from the Cartesian coordinates (s_x, s_y) into the radial coordinates (s, ϕ), where $s={\left(s_x^2+s_y^2\right)}^{1/2}$ and ϕ is the angle between the s_x axis and the vector (s_x, s_y):

$$\mathbf{E}\left({\mathbf{r}}^{\prime },t\right)=\frac{1}{2\pi c}\underset{\varphi =0}{\overset{\pi }{\int }}d\varphi \underset{s=-\text{sin}{\theta }_{\text{ill}}}{\overset{\text{sin}{\theta }_{\text{ill}}}{\int }}\frac{sds}{\sqrt{1-s^2}}\widehat{\mathbf{a}}\left(s,\varphi \right){\dot{E}}^{\infty }\left(s,\varphi ,t-n_2\widehat{\mathbf{s}}\cdot {\mathbf{r}}^{\prime }/c\right)$$ (13)

Note that the limits for the usual radial coordinates are modified such that s ranges from −sinθ_ill to sinθ_ill, and ϕ ranges from 0 to π. In this way, the integral over the unit disk is transformed into an integral over the rectangular region {|s| < sinθ_ill, 0 < ϕ < π} [16]. The integral over s can be approximated using Gauss-Legendre quadrature [21]. The ϕ integral can be approximated trivially by the midpoint rule, since the integrand becomes periodic with period π once the s dependence is integrated out. For periodic functions, the midpoint rule is similar to the Gauss-Legendre quadrature in terms of accuracy [21]. In the following, we will denote this two-dimensional cubature rule by the acronym GL. An example GL quadrature rule with 20×8=160 total points is shown in Fig. 2(b).

3.3. Custom cubature rules

There are more sophisticated alternatives to the approaches in the previous subsections for approximating two-dimensional integrals over special two-dimensional domains. A good review of the known rules tailored for the unit disk can be found in [16]. These rules require fewer cubature points than the EQ and GL rules for the same level of accuracy; thus reducing the number of plane waves in Eq. (8). The downside of these rules is that they have limited availability, with no readily available software for computing them. One has to to resort to tabulated values for the positions and weights for the cubature points, such as R. Cools’ online encyclopedia of cubature formulas [22]. For demonstrating the qualities of these specialized cubature formulas, we have considered the 127-point quadrature rule of degree 25. The degree d of a quadrature rule is the maximum total degree of the two-dimensional polynomials for which the cubature formula is exact. In the following, we will label the results obtained using this cubature rule by the acronym CC. The positions and weights for the 127-point quadrature are shown in Fig. 2(c).

It should be pointed out that the cubature rules in Fig. 2 are given for the standard unit disk $s_x^2+s_y^2<1$. Since the integration domain in Eq. (3) is $s_x^2+s_y^2<{\text{sin}}^2{\theta }_{\text{ill}}$, the coordinates of the cubature points in Fig. 2 should be multiplied by sin θ_ill, and the weights by sin²θ_ill. In the following, we will present an error analysis for the cubature rules shown in Fig. 2.

4. Error analysis

In order to perform an error analysis, the theoretical electric field E_xth (r′, t) around the focus should be computed to a high degree of accuracy. For this purpose, we use previous results from Novotny & Hecht [12, Eq. (3.66)–(3.68)], except a sign change [23] and an extra $\sqrt{2}$ factor for the (1,0) and (0,1) modes due to a difference between their definitions and ours. Suppressing the harmonic time dependence exp(−iωt), E_xth (ρ, ϕ, z,t) is given by

$$\begin{array}{cc}{E}_{x_{\text{th}}}\left(\rho ,\varphi ,z\right)=\frac{-ikf}{2}\sqrt{\frac{n_1}{n_2}}\left(I_{00}+I_{02}\text{cos}2\varphi \right)& \left[\left(0,0\right)\text{mode}\right]\end{array}$$ (14)

$$\begin{array}{cc}{E}_{x_{\text{th}}}\left(\rho ,\varphi ,z\right)=\frac{-ik{f}^2}{\sqrt{2}{w}_0}\sqrt{\frac{n_1}{n_2}}\left(i{I}_{11}\text{cos}\varphi +i{I}_{14}\text{cos}3\varphi \right)& \left[\left(1,0\right)\text{mode}\right]\end{array}$$ (15)

$$\begin{array}{cc}{E}_{x_{\text{th}}}\left(\rho ,\varphi ,z\right)=\frac{-ik{f}^2}{\sqrt{2}{w}_0}\sqrt{\frac{n_1}{n_2}}\left(i\left(I_{11}+2I_{12}\right)\text{sin}\varphi +i{I}_{14}\text{sin}3\varphi \right)& \left[\left(0,1\right)\text{mode}\right]\end{array}$$ (16)

in which E_xth (r′) is expressed in cylindrical coordinates (ρ, ϕ, z). The ρ and z dependencies are contained entirely in the functions I₀₀, I₀₂, I₁₁, I₁₂, and I₁₄; which are given by [12]

$$I_{00}\left(\rho ,z\right)={\int }_0^{{\theta }_{\text{ill}}}{e}^{-\frac{1}{f_0^2}\frac{{\text{sin}}^2\theta }{{\text{sin}}^2{\theta }_{\text{ill}}}}{\text{cos}}^{\frac{1}{2}}\theta \text{sin}\theta \left(1+\text{cos}\theta \right)J_0\left(k\rho \text{sin}\theta \right)e^{ikz\text{cos}\theta }d\theta$$ (17)

$$I_{02}\left(\rho ,z\right)={\int }_0^{{\theta }_{\text{ill}}}{e}^{-\frac{1}{f_0^2}\frac{{\text{sin}}^2\theta }{{\text{sin}}^2{\theta }_{\text{ill}}}}{\text{cos}}^{\frac{1}{2}}\theta \text{sin}\theta \left(1-\text{cos}\theta \right)J_2\left(k\rho \text{sin}\theta \right)e^{ikz\text{cos}\theta }d\theta$$ (18)

$$I_{11}\left(\rho ,z\right)={\int }_0^{{\theta }_{\text{ill}}}{e}^{-\frac{1}{f_0^2}\frac{{\text{sin}}^2\theta }{{\text{sin}}^2{\theta }_{\text{ill}}}}{\text{cos}}^{\frac{1}{2}}\theta {\text{sin}}^2\theta \left(1+3\text{cos}\theta \right)J_1\left(k\rho \text{sin}\theta \right)e^{ikz\text{cos}\theta }d\theta$$ (19)

$$I_{12}\left(\rho ,z\right)={\int }_0^{{\theta }_{\text{ill}}}{e}^{-\frac{1}{f_0^2}\frac{{\text{sin}}^2\theta }{{\text{sin}}^2{\theta }_{\text{ill}}}}{\text{cos}}^{\frac{1}{2}}\theta {\text{sin}}^2\theta \left(1-\text{cos}\theta \right)J_1\left(k\rho \text{sin}\theta \right)e^{ikz\text{cos}\theta }d\theta$$ (20)

$$I_{14}\left(\rho ,z\right)={\int }_0^{{\theta }_{\text{ill}}}{e}^{-\frac{1}{f_0^2}\frac{{\text{sin}}^2\theta }{{\text{sin}}^2{\theta }_{\text{ill}}}}{\text{cos}}^{\frac{1}{2}}\theta {\text{sin}}^2\theta \left(1-\text{cos}\theta \right)J_3\left(k\rho \text{sin}\theta \right)e^{ikz\text{cos}\theta }d\theta .$$ (21)

Here, J_n(·) is the n^th order Bessel function. For the error analysis, these integrals are evaluated with very high accuracy using an adaptive Gauss-Kronrod quadrature rule. A general time dependence in ψ(t) is handled by multiplying Eqs. (14)–(16) by the temporal spectrum of ψ(t), and taking the inverse temporal Fourier transform.

The error in the approximation in Eq. (8) can be quantified in various ways. Here, we consider two measures of error that quantify the difference between the computed focused beam and the theoretical focused beam over a surface A, such as the one shown in Fig. 3:

$${\epsilon }_2=\frac{{\left(\int dt{\iint }_{A}d{\mathbf{r}}^{\prime }{\left|{\tilde{E}}_x\left({\mathbf{r}}^{\prime },t\right)-E_{x_{\text{th}}}\left({\mathbf{r}}^{\prime },t\right)\right|}^2\right)}^{1/2}}{{\left(\int dt{\iint }_{A}d{\mathbf{r}}^{\prime }{\left|E_{x_{\text{th}}}\left({\mathbf{r}}^{\prime },t\right)\right|}^2\right)}^{1/2}}$$ (22)

$${\epsilon }_{\text{inf}}=\frac{{\text{max}}_{A,t}\left|{\tilde{E}}_x\left({\mathbf{r}}^{\prime },t\right)-E_{x_{\text{th}}}\left({\mathbf{r}}^{\prime },t\right)\right|}{{\text{max}}_{A,t}\left|E_{x_{\text{th}}}\left({\mathbf{r}}^{\prime },t\right)\right|}$$ (23)

where r′ is the position variable on the surface A. The normalized Euclidean-norm error ε₂ is a measure of the root-mean-square (rms) average of the error on A compared to the rms average of the theoretical field E_xth (r′, t) on the same surface. The normalized ∞-norm error ε_inf is a measure of the maximum error on A compared to the maximum amplitude of the theoretical field E_xth (r′, t) on the same surface. We assume in the examples to follow that the incident beam is x-polarized [i.e., ê=x̂ in Eq. (1)], and we only compare the dominant (x̂) components Ẽ_x(r′, t) and E_xth (r′, t) of the computed and theoretical electric fields. Our numerical experiments have shown that the comparison of the dominant components provides a very reliable estimate of the accuracy of the entire beam. Furthermore, we have found that the error calculated over any vertical plane of the beam (as long as the beam does not vanish on the plane, e.g., the yz plane for the (1,0) mode) is highly representative of the total error in the beam.

Fig. 3.

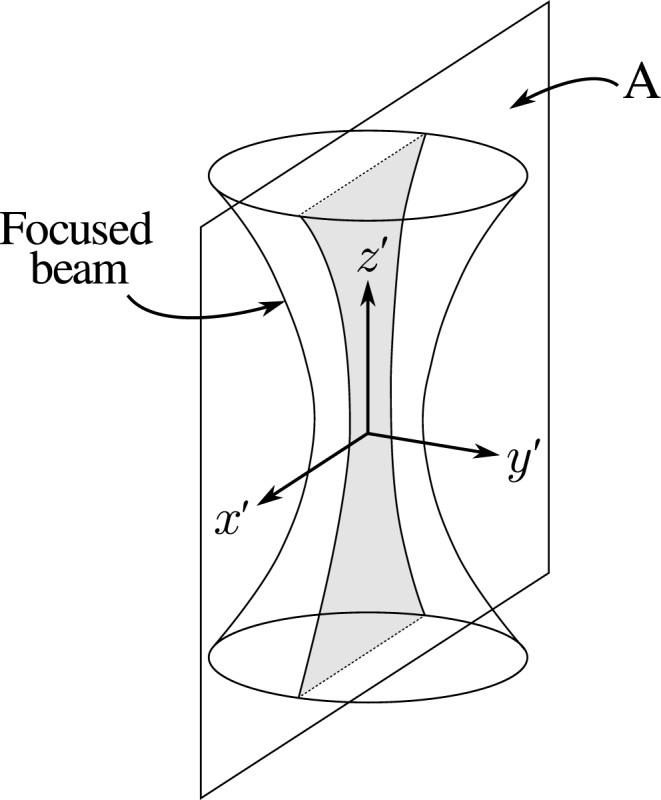
An example surface A over which the computed and theoretical beams are compared. The error ε in Eq. (22) is calculated over this area.

In our simulations, we considered an FDTD grid with the following parameters: grid spacing Δx=Δy=Δz=Δ=6.59 nm, $\mathrm{\Delta }t=\left(0.98/\sqrt{3}\right)\mathrm{\Delta }/c$, grid size 1.713 μm×1.713 μm×3.295 μm, no absorbing boundary. The grid was filled with a lossless, non-dispersive, non-magnetic dielectric material representing immersion oil (n₂ = 1.518). The focused laser beam was assumed to be x-polarized, and propagating in the +z direction. The aperture half angle θ_ill was 68.96°, resulting in a numerical aperture of 1.4. The total-field/scattered-field (TF/SF) surface was located 5 cells away from the grid boundaries. The waveform ψ(t) of the paraxial beam incident on the entrance pupil of the focusing system [see Eq. (1)] was a modulated Gaussian function ψ(t) = sin(2πf₀t) exp(−t²/(2τ²)) with τ =3 fs and f₀=5.889 × 10¹⁴ Hz. This waveform has a Gaussian temporal spectrum that falls to 1% of its maximum amplitude (0.01% of its maximum power) at free-space wavelengths 400 nm and 700 nm. In order to reduce the errors caused by the inherent grid anisotropy and grid dispersion, the grid spacing was chosen to be 1/40^th of the wavelength in the immersion oil at 400 nm. This is much stricter than the usual λ/20-λ/15 rule-of-thumb for the grid spacing. From Eqs. (14)–(21), it follows that the back focal length f of the lens is merely a constant scaling factor in all resulting field values, as long as the filling factor f₀ is kept constant. We have used the somewhat arbitrary value of 0.1 m for the back focal length. The x component of the electric field is shown in Fig. 4 at several time instants for a filling factor of f₀ = 0.4. Figs. 4(a)–4(c) are for the (0, 0), (1, 0), and (2, 0) beams, respectively.

Fig. 4.

Snapshots of the electric field amplitude from FDTD simulations for focused laser beams traveling in the +z direction. The x component of the electric field on the xz plane is plotted linearly in grayscale at 4.975 fs intervals from left to right. The maximum brightness corresponds to 1.059 × 10⁵ V/m. (a) (0, 0) mode. [ Media1 ^{(2.2MB, MOV)} ] (b) (1, 0) mode. [ Media2 ^{(2.2MB, MOV)} ] (c) (2, 0) mode. [ Media3 ^{(2.2MB, MOV)} ]

The surface A in Fig. 3 over which the error is calculated was the xz plane. We recorded the x component of the electric field in the FDTD grid over a rectangular grid on the xz plane, with a spacing of 12 cells in the z dimension and 8 cells in the x dimension. This amounts to a total of 1271 recording points. The normalized errors in Eqs. (22)–(23) were then approximated as a sum over these recording points. The results for a range of filling factors [see Eq. (7)] and for EQ, GL, and CC cubature rules are tabulated in Table 1 and Table 2. Table 1 is for the normalized Euclidean-norm error ε₂, while Table 2 is for the normalized ∞-norm error ε_inf.

Table 1.

Normalized Euclidean-norm error ε₂ [given by Eq. (22)] over the xz plane for the approximation in Eq. (8).

f 0	Cubature rules
	Equally-spaced sx, sy (EQ)		20×8 Gauss-Legendre (GL)		127-point cubature (CC)
	(0,0) mode	(1,0) mode	(0,0) mode	(1,0) mode	(0,0) mode	(1,0) mode
0.4	0.96%	1.07%	3.72%	0.92%	1.62%	3.70%
0.5	1.58%	2.83%	3.01%	1.16%	1.89%	4.02%
0.6	3.38%	5.78%	2.68%	1.86%	2.88%	5.30%

Table 2.

Normalized ∞-norm error ε_inf [given by Eq. (23)] over the xz plane for the approximation in Eq. (8).

f 0	Cubature rules
	Equally-spaced sx, sy (EQ)		20×8 Gauss-Legendre (GL)		127-point cubature (CC)
	(0,0) mode	(1,0) mode	(0,0) mode	(1,0) mode	(0,0) mode	(1,0) mode
0.4	0.91%	1.32%	2.04%	0.83%	3.37%	9.64%
0.5	1.35%	3.17%	1.51%	1.80%	2.80%	7.24%
0.6	2.65%	5.27%	1.73%	3.02%	3.99%	6.90%

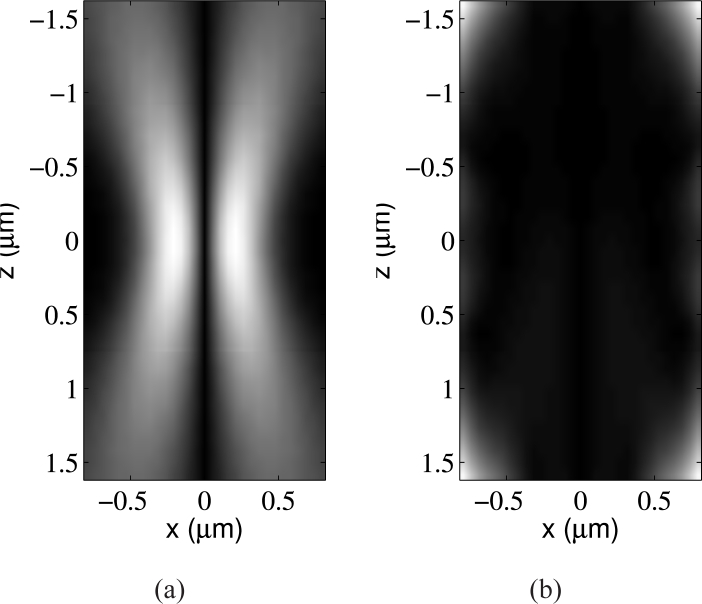
The positions and weights of the cubature points are shown in Fig. 2. The EQ rule has the best performance for small f₀ values, while this performance deteriorates much faster than GL and CC as f₀ increases. The normalized errors are generally higher for the (1, 0) mode, with the exception of the Euclidean error ε₂ for the GL rule. The GL rule is also seen to have superior performance for high f₀. The overall performance of the CC rule is particularly noteworthy. Although it has 30%-40% less number of points than the EQ and GL rules, it results in comparable error for the (0, 0) mode. On the negative side, the performance of the CC rule deteriorates much faster than the others as the focal fields are evaluated farther away from the focus. Controlling the lateral dimensions of the TF/SF boundary is therefore much more important for the CC rule. The normalized ∞-norm error ε_inf resulting from the CC rule is also significantly higher for the (1, 0) mode. A quick comparison of Table 1 and Table 2 shows that the two measures of error in Eqs. (22) and (23) are not drastically different from each other. One notable exception is the significantly increased error in the rightmost column in Table 2. The contribution to this error comes mainly from the corners of the measurement plane, as seen in Fig. 5(b). Although not shown here, it was observed that the error is distributed in a similar way regardless of the cubature rule employed. This reaffirms the importance of the limits of the TF/SF boundary in the approximation in Eq. (8).

Fig. 5.

The distribution of the error on the measurement (xz) plane for the FDTD parameters in the rightmost column of Table 2. (a) The ∞-norm of the theoretical incident field. (b) The ∞-norm of the error. The grayscale upper limit is 1/10^th of that in (a) for accentuation. The error is seen to be concentrated at the corners of the plane.

It was mentioned above that the grid spacing was chosen to be 1/40^th of the wavelength in the immersion oil at 400 nm, which is much stricter than usual. Normally, a grid spacing of ≈ λ/20 would be enough for most purposes [1]. As the grid spacing is made larger, inherent FDTD errors caused by grid anisotropy and grid dispersion become more prominent. These effects are demonstrated in Table 3, in which the normalized Euclidean-norm error (Eq. (22)) is shown for grid spacings ranging from λ/40 to λ/10. The wavelength λ is taken to be 400 nm, which is the lower −40-dB wavelength of the excitation waveform in the immersion oil. Each of the plane waves in Eq. (8) suffer from grid anisotropy and dispersion while propagating from the TF/SF surface toward the center of the grid. If no correction is applied to these plane waves, the errors increase significantly, as seen in the right column of Table 3. In our FDTD implementation (see Section 7), we have used a dispersion-correction algorithm called the matched-numerical-dispersion method [6]. The middle column in Table 3 shows that the error is drastically reduced by this dispersion correction algorithm.

Table 3.

The normalized Euclidean-norm error (Eq. (22)) for different grid spacings. The middle and right columns show the error with and without dispersion correction, respectively.

Grid spacing	Dispersion correction	No dispersion correction
λ/40	0.96%	1.93%
λ/30	1.68%	3.43%
λ/20	3.77%	7.75%
λ/10	15.2%	31.2%

The FDTD simulations were run in parallel on 96 processors on the Quest system (see Acknowledgments). The TF/SF focused beam calculations accounted for 77%, 75%, and 70% of the total simulation times for the EQ, GL, and CC rules, respectively. The additional memory requirements for the focused beams in our FDTD simulations were not significant, thanks to the low storage requirements of TF/SF sources. Because of the low spatial step (λ/40) used, the simulations took much longer than necessary (7–10 minutes). At λ/20, the simulation took about 3 minutes on the same number of processors.

5. Inhomogeneous spaces

Until now, the focused laser beams were computed in homogeneous media. It would be of interest to observe the behavior of the beam when injected into an inhomogeneous medium; considering that almost any simulation will involve some inhomogeneity from which the beam will scatter. We will first consider a planar stratified medium with two layers, and then introduce a scatterer inside one of the layers. We will also show the synthetic microscope images of the scatterer in the latter case.

5.1. Two-layered space

If the beam is incident on an interface between two media, and the beam width is much smaller than the radius of curvature of the interface, the two media can be approximated as infinite half spaces. In our FDTD implementation (see Section 7), a plane wave can be simulated in the presence of arbitrary layered media [24]. Since the focused beam is constructed as a finite combination of plane waves, it can also be injected into layered spaces. As an example, we repeat the simulation for the (0, 0) beam described in Section 4, except the following changes: The lower half space from which the beam is incident is air instead of immersion oil, and the upper half space has a refractive index of 1.5, which could represent glass or resin. The evolution of the electric field is shown in several time instants in Fig. 6. The reflection from the planar interface is seen clearly in the fourth snapshot. The beam is seen to be transmitted into the optically denser upper half space with a smaller wavelength. The TF/SF boundary was deliberately made narrower, to show more clearly the containment of the beam in both half spaces. The absence of leakage outside the TF/SF boundary indicates the accuracy of the plane-wave injection algorithm in the two-layered space.

Fig. 6.

Snapshots of the electric field amplitude for a focused laser beam traveling in the +z direction in a two-layered space. The x component of the electric field on the xz plane is plotted linearly in grayscale at 4.975 fs intervals from left to right. The maximum brightness corresponds to 5 × 10⁴ V/m. [ Media4 ^{(2.1MB, MOV)} ]

5.2. Numerical microscope image of a scatterer

The complexity of the incidence geometry can be further increased by inserting scatterers inside the TF/SF boundary. The scattered electromagnetic field can then be collected outside the TF/SF boundary (e.g. using a near-field-to-far-field transform for multilayered spaces [25]) and processed suitably to yield a wealth of information. In this subsection, we will numerically calculate the microscope image of a scatterer under focused-beam illumination. This could represent one of the scanning positions in a confocal microscopy scenario, wherein a focused beam is scanned over the sample to obtain a complete image. The physical and FDTD parameters of the simulation are the same as those in Section 5.1, except the following changes: Two rectangular blocks of refractive index 1.38 and dimensions 150 nm×600 nm×600 nm are buried symmetrically just above the material interface, and the grid is terminated by a 5-cell thick convolution perfectly-matched layer to absorb the scattered field [26]. The electric field at different time instants is shown in Fig. 7. Using the scattered field outside the TF/SF boundary, and propagating it to the far (Fraunhofer) zone using a multilayer NFFFT [25], a numerical microscope image of the scatterer can be synthesized [27]. In Fig. 8(a), the cross section of the scatterers is shown at z = 300 nm. In Figs. 8(b)–8(c), two microscope images of the scatterers are shown under different microscope modalities. Both images are synthesized at wavelength λ = 509 nm using the light scattered into the lower half space, which amounts to epi (or re-flectance) microscopy. The bright-field microscope image, shown in Fig. 8(b), is obtained by integrating the reflectance spectrum at each pixel over the excitation spectrum. The image is saturated because the grayscale limits are chosen to be the same as in Fig. 8(c), which shows the image obtained when the reflection from the planar interface is removed, leaving only the reflection from the scatterers. This is closely analogous to the procedure followed in dark-field microscopy. As a result of the weak scattering from the two blocks, the image in Fig. 8(c) is much dimmer than the total bright-field image in Fig. 8(b). The overlap of the images of the two blocks is a consequence of the diffraction limit at λ = 509 nm.

Fig. 7.

Snapshots of the electric field amplitude for a focused laser beam traveling in the +z direction in a two-layered space containing rectangular scatterers. The x component of the electric field on the xz plane is plotted linearly in grayscale at 4.975 fs intervals from left to right. The maximum brightness corresponds to 5 × 10⁴ V/m. [ Media5 ^{(2.1MB, MOV)} ]

Fig. 8.

Numerical microscope images of two rectangular scatterers buried inside the upper half space, under focused-beam illumination. (a) Refractive index map of the xy cross section at z = 300 nm. (b) The bright-field image of the structure, dominated by the light reflected from the interface. (c) The image with the reflection from the interface removed. This resembles the procedure followed in dark-field microscopy.

6. Future work

The error analysis presented here is by no means exhaustive. It is only meant to demonstrate the proof-of-concept for the viability of the plane-wave summation method explained in Section 3. Many improvements and innovations could be the subject of future work. For example, reliable guidelines for choosing the number of cubature points for the GL and CC rules for an arbitrary FDTD setting would be very useful. One could also seek alternatives to expressing the Debye-Wolf diffraction integral in Eq. (3) as a fixed sum of plane waves as in Eq. (8). Any method of computing Eq. (3) efficiently and accurately on the TF/SF boundary for an arbitrary ψ(t) in Eq. (1) could be a good alternative to the method described in this paper. The computational cost of such a method would still be inherently proportional to the surface area of the TF/SF boundary, rather than its volume.

7. FDTD implementation: Angora

The focused-beam creation method described in this paper has been incorporated into our free, open-source FDTD software, Angora[28, 29]. Angora is currently available for the GNU/Linux operating system. It supports full parallelization in all three dimensions, allowing it to be run easily on high-performance computing systems. Angora operates by reading a text-based con-figuration file that specifies all details of the simulation. The Angora binaries and configuration files used to generate the results in this paper can be found on the Angora website [30]. Please consult the README file in that directory for details.

8. Summary

In this paper, we described a method to synthesize a laser beam focused tightly into a focal area by an aplanatic converging optical system. The synthesis method is especially geared toward the finite-difference time-domain (FDTD) method. We expressed the focused beam as an infinite summation of plane waves, and used a finite combination of them to approximate the beam. This approach has the advantage that the plane-wave creation methods in FDTD are well researched and documented. For our implementation, we chose the total-field/scattered-field (TF/SF) method for creating a plane wave [1]. We discussed three different methods for approximating the beam as a finite sum of plane waves, and presented a comparative error analysis for these methods. We showed that good accuracy can be obtained with acceptable computational cost. We investigated the behavior of the focused beam in a two-layered space, and computed the numerical microscope images of weakly-scattering objects under focused-beam illumination. We also discussed possibilities for future improvement. Finally, we introduced our free, open-source FDTD software (Angora), which features the method described in this paper. The binaries and configuration files used for the examples in this paper have been made available on the Angora website [30].