Estimating Individualized Treatment Rules Using Outcome Weighted Learning

Abstract

There is increasing interest in discovering individualized treatment rules for patients who have heterogeneous responses to treatment. In particular, one aims to find an optimal individualized treatment rule which is a deterministic function of patient specific characteristics maximizing expected clinical outcome. In this paper, we first show that estimating such an optimal treatment rule is equivalent to a classification problem where each subject is weighted proportional to his or her clinical outcome. We then propose an outcome weighted learning approach based on the support vector machine framework. We show that the resulting estimator of the treatment rule is consistent. We further obtain a finite sample bound for the difference between the expected outcome using the estimated individualized treatment rule and that of the optimal treatment rule. The performance of the proposed approach is demonstrated via simulation studies and an analysis of chronic depression data.

1. INTRODUCTION

In many different diseases, patients can show significant heterogeneity in response to treatments. In some cases, a drug that works for a majority of individuals may not work for a subset of patients with certain characteristics. For example, molecularly targeted cancer drugs are only effective for patients with tumors expressing targets (Grünwald & Hidalgo 2003; Buzdar 2009), and significant heterogeneity exists in responses among patients with different levels of psychiatric symptoms (Piper et al. 1995; Crits-Christoph et al. 1999). Thus significant improvements in public health could potentially result from judiciously treating individuals based on his or her prognostic or genomic data rather than a “one size fits all” approach. Treatments and clinical trials tailored for patients have enjoyed recent popularity in clinical practice and medical research, and, in some cases, have provided high quality recommendations accounting for individual heterogeneity (Sargent et al. 2005; Flume et al. 2007; Insel 2009). These proposals have focused on smaller, specific and well-defined subgroups, sought to provide guidance in clinical decision making based on individual differences, and have attempted to achieve better risk minimization and benefit maximization.

One statistical approach for developing individual-adaptive interventions is to classify subjects into different risk levels estimated by a parametric or semiparametric regression model using prognostic factors, and then to assign therapy according to risk level (Eagle et al. 2004; Marlowe et al. 2007; Cai et al. 2010). However, the parametric or semiparametric model assumptions may not be valid due to the complexity of the disease mechanism and individual heterogeneity. Moreover, these approaches require preknowledge in allocating the optimal treatment to each risk category. There is also a significant literature examining discovery and development of personalized treatment relying on predicting patient responses to optional regimens (Rosenwald et al. 2002; van’t Veer & Bernards 2008), where the optimal decision leads to the best predicted outcome. One recent paper by Qian & Murphy (2011) applies a two-step procedure which first estimates a conditional mean for the response and then estimates the rule maximizing this conditional mean. A rich linear model is used to sufficiently approximate the conditional mean, with the estimated rule derived via l₁ penalized least squares (l₁-PLS). The method includes variable selection to facilitate parsimony and ease of interpretation. The conditional mean approximation requires estimating a prediction model of the relationship between pretreatment prognostic variables, treatments and clinical outcome using a prediction model. Reduction in the mean response is related to the excess prediction error, through which an upper bound can be constructed for the mean reduction of the associated treatment rule. However, by inverting the model to find the optimal treatment rule, this method emphasizes prediction accuracy of the clinical response model instead of directly optimizing the decision rule.

In this paper, we proposed a new method for solving this problem which circumvents the need for conditional mean modeling followed by inversion by directly estimating the decision rule which maximizes clinical response. Specifically, we demonstrate that the optimal treatment rule can be estimated within a weighted classification framework, where the weights are determined from the clinical outcomes. We then alleviate the computational problem by substituting the 0–1 loss in the classification with a convex surrogate loss as is done with the support vector machine (SVM) via the hinge loss (Cortes & Vapnik 1995). The directness of this outcome weighted learning (OWL) approach enables us to better select targeted therapy while making full use of available information.

The remainder of the paper is organized as follows. In Section 2, we provide the mathematical concepts and framework for individualized treatment rules, and then formulate the problem as OWL. The proposed weighted SVM approach for constructing the optimal ITR is then developed in detail. In Section 3, consistency and risk bound results are established for the estimated rules. Faster convergence rates can be achieved with additional marginal assumptions on the data generating distribution. We present simulation studies to evaluate performance of the proposed method in Section 4. The method is then illustrated on the Nefazodone-CBASP data (Keller et al. 2000) in Section 5. In Section 6, we discuss future work. The proofs of theoretical results are given in the Appendix.

2. METHODOLOGY

2.1 Individualized Treatment Rule (ITR)

We assume the data are collected from a two-arm randomized trial. That is, treatment assignments, denoted by A ∈ = {−1, 1}, are independent of any patient’s prognostic variables, which are denoted as a d-dimensional vector X = (X₁, …, X_d)^T ∈ 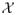. We let R be the observed clinical outcome, also called the “reward,” and assume that R is bounded, with larger values of R being more desirable. Thus an individualized treatment rule (ITR) is a map from the space of prognostic variables, 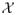, to the space of treatments, 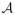. An optimal ITR is a rule that maximizes the expected reward if implemented.

Mathematically, we can quantify the optimal ITR in terms of the relationship among (X, A, R). To see this, denote the distribution of (X, A, R) by P and expectation with respect to the P is denoted by E. For any given ITR 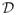, we let 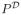denote the distribution of (X, A, R) given that A = 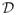(X), i.e., the treatments are chosen according to the rule 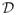; correspondingly, the expectation with respect to 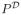is denoted by 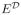. Then under the assumption that P(A = a) > 0 for a = 1 and −1, it is clear that 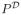is absolutely continuous with respect to P and d 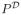/dP = I(a = 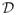(x))/P(A = a), where I(·) is the indicator function. Thus, the expected reward under the ITR 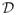is given as

$$E^{\mathcal{D}}(R)=\int {\mathit{RdP}}^{\mathcal{D}}=\int R\frac{d{P}^{\mathcal{D}}}{dP}dP=E\left[\frac{I(A=\mathcal{D}(X))}{A\pi +(1-A)/2}R\right],$$

where π = P(A = 1). This expectation is called the value function associated with 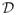and is denoted 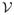( 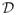). Consequently, an optimal ITR, 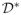, is a rule that maximizes 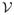( 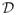), i.e.,

$${\mathcal{D}}^{\ast }\in \underset{\mathcal{D}}{\text{argmax}}E\left[\frac{I(A=\mathcal{D}(X))}{A\pi +(1-A)/2}R\right].$$

Note that 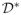does not change if R is replaced by R + c for any constant c. Thus, without loss of generality, we assume that R is nonnegative in the following.

2.2 Outcome Weighted Learning (OWL) for Estimating Optimal ITR

Assume that we observe i.i.d data (X_i, A_i, R_i), i = 1, …, n from the two-arm randomized trial described above. Previous approaches to estimating optimal ITR first estimate E(R|X, A), using the observed data via parametric or semiparametric models, and then estimate the optimal decision rule by comparing the predicted value E(R|X, A = 1) versus E(R|X, A = −1) (Robins 2004; Moodie et al. 2009; Qian & Murphy 2011). As discussed before, these approaches indirectly estimate the optimal ITR, and are likely to produce a suboptimal ITR if the model for R given (X, A) is overfitted. As an alternative, we propose a nonparametric approach which directly maximizes the value function based on an outcome weighted learning method.

To illustrate our approach, we first notice that searching for the optimal ITR, 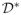, which maximizes 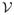( 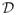), is equivalent to finding 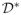that minimizes

$$E[R\mid A=1]+E[R\mid A=-1]-\mathcal{V}(\mathcal{D})=E\left[\frac{I(A\ne \mathcal{D}(X))}{A\pi +(1-A)/2}R\right].$$

The latter can be viewed as a weighted classification error, for which we want to classify A using X but we also weigh each misclassification event by R/(Aπ + (1 − A)/2). Hence, using the observed data, we approximate the weighted classification error by

$$n^{-1}\sum _{i=1}^n\frac{R_i}{A_i\pi +(1-A_i)/2}I(A_i\ne \mathcal{D}(X_i))$$

and seek to minimize this expression to estimate 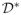. Since 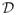(x) can always be represented as sign(f(x)), for some decision function f, minimizing the above expression for 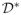is equivalent to minimizing

$$n^{-1}\sum _{i=1}^n\frac{R_i}{A_i\pi +(1-A_i)/2}I(A_i\ne \text{sign}(f(X_i)))$$ (2.1)

to obtain the optimal f^*, and then setting 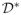(x) = sign(f^*(x)).

The above minimization also has the following interpretation. That is, we intend to find a decision rule which assigns treatments to each subject only based on their prognostic information. For subjects observed to have a large reward, this rule is apt to recommend the same treatment assignments that the subject has actually received; however, for subjects with small rewards, the rule is more likely to give the opposite treatment assignment to what they received. In other words, if we stratify subjects into different strata based on the rewards, we will expect that the optimal ITR misclassifies less subjects in the high reward stratum as compared to the low reward stratum.

In the machine learning literature, (2.1) can be viewed as a weighted summation of 0–1 loss. It is well known that minimizing (2.1) is difficult due to the discontinuity and non-convexity of 0–1 loss. To alleviate this difficulty, one common approach is to find a convex surrogate loss for the 0–1 loss in (2.1) and develop a tractable estimation procedure (Zhang 2004; Lugosi & Vayatis 2004; Steinwart 2005). Among many choices of surrogate loss, one of the most popular is the hinge loss used in the context of the support vector machine (Cortes & Vapnik 1995), which we will adopt in this paper. Furthermore, we penalize the complexity of the decision function in order to avoid overfitting. In other words, instead of minimizing (2.1), we aim to minimize

$$n^{-1}\sum _{i=1}^n\frac{R_i}{A_i\pi +(1-A_i)/2}{(1-A_i(f(X_i)))}^{+}+{\lambda }_n{\left|\right|f\left|\right|}^2,$$ (2.2)

where x⁺ = max(x, 0) and ||f|| is some norm for f. In this way, we cast the problem of estimating the optimal ITR into a weighted classification problem using support vector machine techniques.

2.3 Linear Decision Rule for Optimal ITR

Suppose that the decision function f(x) minimizing (2.2) is a linear function of x, that is, f(x) = 〈β, x〉 + β₀, where 〈·,·〉 denotes the inner product in Euclidean space. Then the corresponding ITR will assign a subject with prognostic value X into treatment 1 if 〈β, X〉 + β₀ > 0 and −1 otherwise.

In (2.2), we define ||f|| as the Euclidean norm of β. Following the usual SVM, we introduce a slack variable ξ_i for subject i to allow a small portion of wrong classification. Denote C > 0 as the classifier margin. Then minimizing (2.2) can be rewritten as

$$\underset{\beta ,{\beta }_0,\left|\right|\beta \left|\right|=1}{max}C\text{subject}\text{to}{A}_i(\langle \beta ,X_i\rangle +{\beta }_0)\ge C(1-{\xi }_i),{\xi }_i\ge 0,\sum \frac{R_i}{{\pi }_i}{\xi }_i<s,$$

where π_i = πI(A_i = 1)+(1 − π)I(A_i = −1) and s is a constant depending on λ_n. This is equivalent to

$$min\frac{1}{2}{\left|\right|\beta \left|\right|}^2\text{subject}\text{to}{A}_i(\langle \beta ,X_i\rangle +{\beta }_0)\ge (1-{\xi }_i),{\xi }_i\ge 0,\sum \frac{R_i}{{\pi }_i}{\xi }_i<s,$$

that is

$$min\frac{1}{2}{\left|\right|\beta \left|\right|}^2+\kappa \sum _{i=1}^n\frac{R_i}{{\pi }_i}{\xi }_i\text{subject}\text{to}{A}_i(\langle \beta ,X_i\rangle +{\beta }_0)\ge (1-{\xi }_i),{\xi }_i\ge 0,$$

where κ > 0 is a tuning parameter and R_i/π_i is the weight for the i^th point. We observe that the main difference compared to standard SVM is that we weigh each slack variable ξ_i with R_i/π_i.

After introducing Lagrange multipliers, the Lagrange function becomes:

$$\frac{1}{2}{\left|\right|\beta \left|\right|}^2+\kappa \sum _{i=1}^n\frac{R_i}{{\pi }_i}{\xi }_i-\sum _{i=1}^n{\alpha }_i\{A_i(X_i^T\beta +{\beta }_0)-(1-{\xi }_i)\}-\sum _{i=1}^n{\mu }_i{\xi }_i,$$

with α_i ≥ 0, μ_i ≥ 0. Taking derivatives with respect to (β, β₀) and ξ_i, we have $\beta ={\sum }_{i=1}^n{\alpha }_i{A}_i{X}_i,0={\sum }_{i=1}^n{\alpha }_i{A}_i$ and α_i = κR_i/π_i − μ_i. Plugging these equations into the Lagrange function, we obtain the dual problem

$$\underset{\alpha }{max}\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{A}_i{A}_j\langle X_i,X_j\rangle$$

subject to 0 ≤ α_i ≤ κR_i/π_i, i = 1, …, n, and ${\sum }_{i=1}^n{\alpha }_i{A}_i=0$. Quadratic programming algorithms from many widely available software packages can be used to solve this dual problem. Finally, we obtain that

$$\widehat{\beta }=\sum _{{\widehat{\alpha }}_i>0}{\widehat{\alpha }}_i{A}_i{X}_i,$$

and β̂₀ can be solved using the margin points (0 < α̂_i, ξ̂_i = 0) subject to the Karush-Kuhn-Tucker conditions (Page 421, Hastie, Tibshirani & Friedman 2009). The decision rule is given by sign{〈β̂, X〉 + β̂₀}. Similar to the traditional SVM, the estimated decision rule is determined by the support vectors with α̂ > 0.

2.4 Nonlinear Decision Rule for Optimal ITR

The previous section targets a linear boundary of prognostic variables. This may not be practically useful since the dimension of the prognostic variables can be quite high and complicated relationships may be involved between the desired treatments and these variables. However, we can easily generalize the previous approach to obtain a nonlinear decision rule for obtaining the optimal ITR.

We let k : 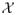× 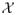→ ℝ, called a kernel function, be continuous, symmetric and positive semidefinite. Given a real-valued kernel function k, we can associate with it a reproducing kernel Hilbert space (RKHS) , which is the completion of the linear span of all functions {k(·, x), x ∈ 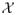}. The norm in , denoted by ||·||_k, is induced by the following inner product,

$${\langle f,g\rangle }_k=\sum _{i=1}^n\sum _{j=1}^m{\alpha }_i{\beta }_{j}k(x_i,x_j),$$

for $f(·){\sum }_{i=1}^n{\alpha }_{i}k(·,x_i)$ and $g(·){\sum }_{j=1}^m{\beta }_{j}k(·,x_j)$.

We note that our decision function f(x) is from equipped with norm ||·||_k. Thus since any function in takes the form ${\sum }_{i=1}^m{\alpha }_{i}k(·,x_i)$, it can be shown that the optimal decision function is given by

$$\sum _{i=1}^n{\widehat{\alpha }}_i{A}_{i}k(X,X_i)+{\widehat{\beta }}_0,$$

where (α̂₁, …, α̂_n) solves

$$\underset{\alpha }{max}\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{A}_i{A}_{j}k(X_i,X_j)$$

subject to 0 ≤ α_i ≤ κR_i/π_i, i = 1, …, n, and ${\sum }_{i=1}^n{\alpha }_i{A}_i=0$. We note that if we choose k(x, y) = 〈x, y〉, then the obtained rule reduces to the previous linear rule.

3. THEORETICAL RESULTS

In this section, we establish consistency of the optimal ITR estimated using OWL. We further obtain a risk bound for the estimated ITR and show how the bound can be improved for certain specific, realistic situations.

3.1 Notation

For any ITR 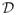(x) = sign(f(x)) associated with decision function f(x), we define

$$\mathcal{R}(f)=E\left[\frac{R}{A\pi +(1-A)/2}I(A\ne \text{sign}(f(X)))\right]$$

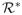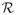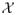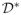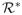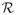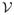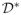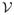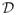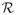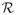and the minimal risk (called Bayes risk in the learning literature) as = inf_f { (f)|f: → ℝ}. Thus, for the optimal ITR (x) = sign(f^*(x)) (called the Bayes classifier in the learning literature), = (f^*). In terms of the value function, we note that ( ) − ( ) = (f) − (f^*).

In the OWL approach, we substitute 0–1 loss I(A ≠ sign(f(X))) by a surrogate loss, φ(Af(X)), where φ(t) = (1 − t)⁺. Thus we define the φ-risk

$${\mathcal{R}}_{\phi }(f)=E\left[\frac{R}{A\pi +(1-A)/2}\phi (Af(X))\right],$$

and, similarly, the minimal φ–risk as ${\mathcal{R}}_{\phi }^{\ast }={inf}_f\{{\mathcal{R}}_{\phi }(f)\mid f:\mathcal{X}\to \mathbb{R}\}$.

Recall that the estimated optimal ITR is given by sign(f̂_n(X)), where

$${\widehat{f}}_n=\underset{f\in {\mathcal{H}}_k}{\text{argmin}}\left\{\frac{1}{n}\sum _{i=1}^n\frac{R_i}{{\pi }_i}{\{1-A_{i}f(X_i)\}}^{+}+{\lambda }_n{\left|\right|f\left|\right|}_k^2\right\}.$$ (3.1)

3.2 Fisher Consistency

We establish Fisher consistency of the decision function based on surrogate loss φ(t). Specifically, the following result holds:

Proposition 3.1

For any measurable function f, if f̃ minimizes R_φ(f), then 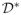(x) = sign(f̃(x)). Proof. First, we note

$${\mathcal{D}}^{\ast }(x)=\text{sign}\{E[R\mid X=x,A=1]-E[R\mid X=x,A=-1]\}.$$

Next, for each x ∈ ,

$$\begin{array}{l}E\left(R\frac{\phi (Af(X))}{A\pi +(1-A)/2}|X=x\right)=E(R\mid A=1,X=x)(1-f(x))+E(R\mid A=-1,X=x)(1+f(x))\\ =((E(R\mid A=-1,X=x)-E(R\mid A=1,X=x))f(x)+E(R\mid A=-1,X=x)+E(R\mid A=1,X=x)).\end{array}$$

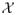Therefore, f̃(x), which minimizes 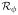(f), should be positive if E(R|A = 1, X = x) > E(R|A = −1, X = x) and negative if E(R|A = 1, X = x) < E(R|A = −1, X = x). That is, f̃(x) has the same sign as 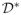(x). The result holds.

The proposition is analogous to results for SVM, for example, Lin (2002). This theorem justifies the validity of using φ(t) as the surrogate loss in OWL.

3.3 Excess Risk for 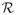(f) and 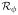(f)

The following result shows that for any decision function f, the excess risk of f under 0–1 loss is no larger than the excess risk of f under the hinge loss. Thus, the loss of the value function due to the ITR associated with f can be bounded by the excess risk under the hinge loss. The proof of the theorem can be found in the Appendix.

Theorem 3.2

For any measurable f: 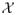→ ℝ and any probability distribution for (X, A, R),

$$\mathcal{R}(f)-{\mathcal{R}}^{\ast }\le {\mathcal{R}}_{\phi }(f)-{\mathcal{R}}_{\phi }^{\ast }.$$ (3.2)

The proof follows the general arguments of Bartlett, Jordan & McAuliffe (2006), in which they bound the risk associated with 0–1 loss in terms of the risk from surrogate loss, utilizing a convexified variational transform of the surrogate loss. In our proof, we extend this concept to our setting by establishing the validity of a weighted version of such a transformation.

3.4 Consistency and Risk Bounds

The purpose of this section is to establish the consistency of f̂_n, and, moreover, to derive the convergence rate of 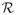(f̂_n) − .

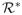First, the following theorem shows that the risk due to f̂_n does converge to 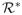, and, equivalently, the value of f̂_n converges to the optimal value function. Results on consistency of the SVM have been shown in current literature, for example, Zhang (2004). Here we apply the empirical process techniques to show that the proposed OWL estimator is consistent. The proof of the theorem is deferred to the Appendix.

Theorem 3.3

Assume that we choose a sequence λ_n > 0 such that λ_n → 0 and λ_nn → ∞. Then for all distributions P, we have that in probability,

$$\underset{n\to \infty }{lim}\left\{{\mathcal{R}}_{\phi }({\widehat{f}}_n)-\underset{f\in {\overline{\mathcal{H}}}_k}{inf}{\mathcal{R}}_{\phi }(f)\right\}=0,$$

where 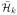denotes the closure of _k. Thus, if f^* belongs to the closure of lim sup_n→∞ , where can potentially depend on n, we have ${lim}_{n\to \infty }{\mathcal{R}}_{\phi }({\widehat{f}}_n)={\mathcal{R}}_{\phi }^{\ast }$ in probability. It then follows that lim_n→∞ 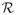(f̂_n) = 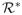in probability.

One special situation where f^* belongs to the limit space of is when we choose to be an RKHS with Gaussian kernel and let the kernel bandwidth decrease to zero as n → ∞. This will be shown in Theorem 3.4 below.

We now wish to derive the convergence rate of 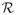(f̂_n) − 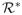under certain regularity conditions on the distribution P. Specifically, we need the following “geometric noise” assumption for P (Steinwart & Scovel 2007): Let

$$\eta (x)=\frac{E[R\mid X=x,A=1]-E[R\mid X=x,A=-1]}{E[R\mid X=x,A=1]+E[R\mid X=x,A=-1]}+1/2,$$ (3.3)

then 2η(x) − 1 is the decision boundary for the optimal ITR. We further define 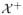= {x ∈ 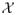: 2η(x) − 1 > 0}, and 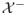= {x ∈ 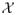: 2η(x) − 1 < 0}. A distance function to the boundary between 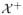and 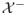is Δ(x) = d̃(x, 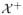) if x ∈ 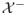, Δ(x) = d̃(x, 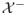) if x ∈ 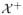and Δ(x) = 0 otherwise, where d̃(x, 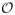) denotes the distance of x to a set 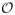with respect to the Euclidean norm. Then the distribution P is said to have geometric noise exponent 0 < q < ∞, if there exists a constant C > 0 such that

$$E\left[exp\left(-\frac{\mathrm{\Delta }{(X)}^2}{t}\right)\mid 2\eta (X)-1\mid \right]\le {Ct}^{qd/2},t>0.$$ (3.4)

In some sense, this geometric noise exponent describes the behavior of the distribution in a neighborhood of the decision boundary. It is affected by how fast the density of the distance Δ(X) decays along the boundary. For example, assume the boundary is linear, in which case Δ(x) = |2η(x)−1|. If for the density of Δ(X), defined as f(u), we have f(u) ~ u^p when u is close to 0, then we can show q = (p + 2)/d. Larger p corresponds to a faster decaying rate of the density, resulting in a larger q accordingly. Another example is distinctly separable data, i.e., when |2η(x) − 1| > δ > 0, for some constant δ, and η is continuous, q can be arbitrarily large.

In addition to this specific assumption for P, we also restrict the choice of RKHS to the space associated with Gaussian Radial Basis Function (RBF) kernels, i.e.,

$$k(x,x^{\prime })=exp(-{\sigma }_n^2{\left|\right|x-x^{\prime }\left|\right|}^2),x,x^{\prime }\in \mathcal{X},$$

where σ_n > 0 is a parameter varying with n. The tuning parameter σ_n is related to approximation properties of Gaussian RBF kernels. When σ_n goes large, only observations in the small neighborhood contribute to the prediction, in which case we obtain a non-linear decision boundary or even non-parametric decision rule. If σ_n does not diverge, then points further away can contribute to the prediction, resulting in a nearly linear boundary. One advantage of using the Gaussian kernel is that we can determine the complexity of in terms of capacity bounds with respect to the empirical L²-norm, defined as

$${\left|\right|f-g\left|\right|}_{L_2(P_n)}={\left(\frac{1}{n}\sum _{i=1}^n{\mid f(X_i)-g(X_i)\mid }^2\right)}^{1/2}.$$

For any ε > 0, the covering number of functional class 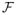with respect to L₂(P_n), N ( 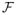, ε, L₂(P_n)), is the smallest number of L₂(P_n) ε-balls needed to cover 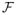, where an L₂(P_n) ε-ball around a function g ∈ 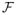is the set {f ∈ 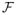: ||f − g||_L2(Pn) < ε}.

Specifically, according to Theorem 2.1 in Steinwart & Scovel (2007), we have that for any ε > 0,

$$\underset{P_n}{sup}logN(B_{{\mathcal{H}}_k},\epsilon ,L_2(P_n))\le c_{\nu ,\delta ,m}{\sigma }_n^{(1-\nu /2)(1+\delta )d}{\epsilon }^{-\nu },$$ (3.5)

where 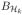is the closed unit ball of , and ν and δ are any numbers satisfying 0 < ν ≤ 2 and δ > 0.

Under the above conditions, we obtain the following theorem:

Theorem 3.4

Let P be a distribution of (X, A, R) satisfying condition (3.4) with noise exponent q > 0. Then for any δ > 0, 0 < ν < 2, there exists a constant C (depending on ν, δ, d and π) such that for all τ ≥ 1 and ${\sigma }_n={\lambda }_n^{-1/(q+1)d}$,

$${Pr}^{\ast }(\mathcal{R}({\widehat{f}}_n)\le {\mathcal{R}}^{\ast }+\epsilon )\ge 1-e^{-\tau },$$

where Pr^* denotes the outer probability for possibly nonmeasurable sets, and

$$\epsilon =C\left[{\left(\frac{1}{{\lambda }_n}\right)}^{\frac{2}{2+\nu }+\frac{(2-\nu )(1+\delta )}{(2+\nu )(1+q)}}{\left(\frac{1}{n}\right)}^{\frac{2}{2+\nu }}+{\left(\frac{1}{{\lambda }_n}\right)}^{\frac{q}{q+1}}\frac{\tau }{n}+{\lambda }_n^{\frac{q}{q+1}}\right].$$

The first two terms bound the stochastic error, which arises from the variability inherent in a finite sample size and which depends on the complexity of in terms of covering numbers, while the third term controls the approximation error due to using , which depends on both σ_n and the noise behavior in the underlying distribution. We expect better approximation properties when the RKHS is more complex, but, conversely, we also expect larger stochastic variability. Using the above expression, an optimal choice of λ_n that balances bias and variance is given by

$${\lambda }_n=n^{-\frac{2(1+q)}{(4+\nu )q+2+(2-\nu )(1+\delta )}},$$

so the optimal rate for the risk is

$$\mathcal{R}({\widehat{f}}_n)-{\mathcal{R}}^{\ast }=O_p\left(n^{-\frac{2q}{(4+\nu )q+2+(2-\nu )(1+\delta )}}\right).$$

In particular, when data are well separated, q can be sufficiently large and we can let (δ, ν) be sufficiently small. Then the convergence rate almost achieves the rate n^−1/2. However, if the marginal distribution of 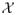has continuous density along the boundary, it can be calculated that q = 2/d. In this case, the convergence rate is approximately n^−2/(d+2). Clearly, the speed of convergence is slower with larger dimension of the prognostic variable space.

To prove Theorem 3.4, we note that according to Theorem 3.2, it suffices to prove the result for the excess φ risk. We also use the fact that

$${\mathcal{R}}_{\phi }({\widehat{f}}_n)-{\mathcal{R}}_{\phi }^{\ast }={\mathcal{R}}_{\phi }({\widehat{f}}_n)-\underset{{\mathcal{H}}_k}{inf}{\mathcal{R}}_{\phi }(f)+\underset{{\mathcal{H}}_k}{inf}{\mathcal{R}}_{\phi }(f)-{\mathcal{R}}_{\phi }^{\ast }.$$

We will then bound the first difference on the right-hand side using the empirical counterpart plus the stochastic variability due to the finite sample approximation. The latter can be controlled using large deviation results from empirical processes and some preliminary bound for ||f̂_n||_k. The second difference on the right-hand side will be bounded by using the approximation property of the RHKS and the geometric noise assumption of the underlying distribution P. The proof is modified based on Vert & Vert (2006) and Steinwart & Scovel (2007), where the weights in the loss function are taken into consideration. The details are provided in the Appendix.

3.5 Improved Rate with Data Completely Separated

In this section, we show that a faster convergence rate can be obtained if the data are completely separated. We assume

• (A1)∀x ∈ 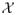, |η(x) − 1/2| ≥ η₀, where η(x) is defined in (3.3), and η is continuous.
• (A2)∀x ∈ 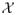, min(η(x), 1 − η(x)) ≥ η₁.

Assumption (A1) can be referred as a “low noise” condition equivalent to |E(R|A = 1, X) − E(R|A = −1, X)| ≥ η₀. Thus, a jump of η (x) at the level of 1/2 requires a gap between the rewards gained from treatment 1 and −1 on the same patient. This assumption is an adaptation of the noise condition used in classical SVM to obtain fast learning rates and it is essentially equivalent to one of the conditions in Blanchard et al. (2008).

Theorem 3.5

Assume that (A1) and (A2) are satisfied. For any ν ∈ (0, 1) and q ∈ (0, ∞), let λ_n = O(n^−1/(ν+1)) and ${\sigma }_n={\lambda }_n^{-1/(q+1)d}$. Then

$$\mathcal{R}({\widehat{f}}_n)-{\mathcal{R}}^{\ast }=O_p\left(n^{-\frac{1}{\nu +1}\frac{q}{q+1}}\right).$$

We can let q go to ∞ and ν go to zero, and this theorem shows that the convergence rate for 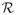(f̂_n) − 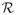(f*) is almost n⁻¹, a much faster rate compared to what was given in Theorem 3.4. This result is similar to results for SVM described in Tsybakov (2004), Steinwart & Scovel (2007), and Blanchard et al. (2008).

To prove Theorem 3.5, we can rewrite the minimization problem in (3.1) as:

$$\underset{S\in {\mathbb{R}}^{+}}{min}\left\{\underset{f:{\left|\right|f\left|\right|}_k\le S}{min}\frac{1}{n}\sum _{i=1}^n\frac{R_i}{{\pi }_i}{\{1-A_{i}f(X_i)\}}^{+}+\lambda S^2\right\}.$$

Thus the problem can be viewed in the model selection framework: a collection of models are balls in , and for each model, we solve the penalized empirical φ-risk minimization to obtain an estimator f̂_n. We can utilize a result for model selection, presented in Theorem 4.3 of Blanchard et al. (2008), to choose the model which yields the minimal penalized empirical φ-risk among all the models. We need to verify the conditions required for the theorem based on the weighted hinge loss and the condition on the covering number of functional class 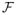with respect to L₂(P_n), i.e., condition (3.5). Proof details are provided in the Appendix.

4. SIMULATION STUDY

We have conducted extensive simulations to assess the small-sample performance of the proposed method. In these simulations, we generate 50-dimensional vectors of prognostic variables X₁, …, X₅₀, consisting of independent U [−1, 1] variates. The treatment A is generated from {−1, 1} independently of X with P(A = 1) = 1/2. The response R is normally distributed with mean Q₀ = 1 + 2X₁ + X₂ + 0.5X₃ + T₀(X, A) and standard deviation 1, where T₀(X, A) reflects the interaction between treatment and prognostic variables and is chosen to vary according to the following four different scenarios:

1. T₀(X, A) = 0.442(1 − X₁ − X₂)A.

2. $T_0(X,A)=(X_2-0.25X_1^2-1)A$.

3. $T_0(X,A)=(0.5-X_1^2-X_2^2)(X_1^2+X_2^2-0.3)A$.

4. $T_0(X,A)=(1-X_1^3+exp(X_3^2+X_5)+0.6X_6-{(X_7+X_8)}^2)A$.

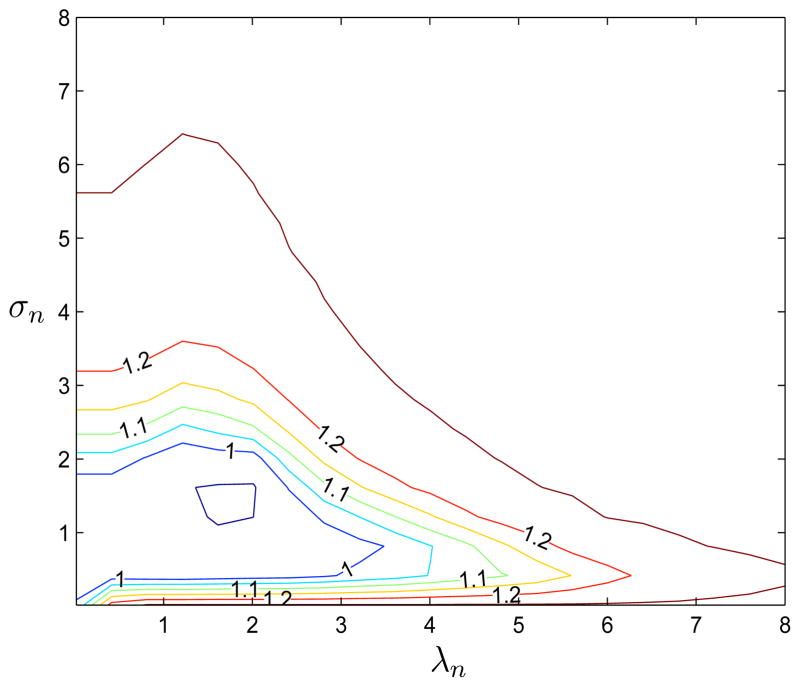
The decision boundaries in the first three scenarios are determined by X₁ and X₂. Scenario 1 corresponds to a linear decision boundary in truth, where the shape of the boundary in Scenario 2 is a parabola. The third is a ring example, where the patients on the ring are assigned to one treatment, and another if inside or outside the ring. The decision boundary in the fourth example is fairly nonlinear in covariates, depending on covariates other than X₁ and X₂. For each scenario, we estimate the optimal ITR by applying OWL. We use the Gaussian kernel in the weighted SVM algorithm. There are two tuning parameters: λ_n, the parameter for penalty, and σ_n, the inverse bandwidth of the kernel. Since λ_n plays a role in controlling the severity of the penalty on the functions and σ_n determines the complexity of the function class utilized, σ_n should be chosen adaptively from the data simultaneously with λ_n. To illustrate this, Figure 1 shows the contours of the value function for the first scenario with different combinations of (λ_n, σ_n) when n = 30. We can see that λ_n interacts with σ_n, with larger λ_n generally coupled with smaller σ_n for equivalent value function levels. In our simulations, we apply a 5-fold cross validation procedure, in which we search over a pre-specified finite set of (λ_n, σ_n) to select the pair maximizing the average of the estimated values from the validation data. In case of tied values for parameter pair choices, we first choose the set of pairs with smallest λ_n and then select the one with largest σ_n.

Figure 1.

Contour Plots of Value Function for Example 1 with λ_n ∈ (0, 10) and σ_n ∈ (0, 10)

Additionally, comparison is made among the following four methods:

• the proposed OWL using Gaussian kernel (OWL-Gaussian)

• the proposed OWL using linear kernel (OWL-Linear)

• the l₁ penalized least squares method (l₁-PLS) developed by Qian & Murphy (2011), which approximates E(R|X, A) using the basis function set (1, X, A, XA) and applies the LASSO method for variable selection, and

• ordinary least squares method (OLS), which estimates the conditional mean response using the same basis function set as in 3 but without variable selection.

We consider the OWL with linear kernel (method 2) mainly to assess the impact of different kernels in the weighted SVM algorithm. In this case, there is only one tuning parameter, λ_n, which can be chosen to maximize the value function in a cross-validation procedure. The selection of the tuning parameters in the l₁-PLS approach follows similarly. The last two approaches estimate the optimal ITR using the sign of the difference between the predicted E(R|X, A = 1) and the predicted E(R|X, A = −1). In the comparisons, the performances of the four methods are assessed by two criteria: the first criterion is to evaluate the value function using the estimated optimal ITR when applying to an independent and large validation data; the second criterion is to evaluate the misclassification rates of the estimated optimal ITR from the true optimal ITR using the validation data. Specifically, a validation set with 10000 observations is simulated to assess the performance of the approaches. The estimated value function using any ITR 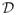is given by ${\mathbb{P}}_n^{\ast }[I(A=\mathcal{D}(X))R/P(A)]/{\mathbb{P}}_n^{\ast }[I(A=\mathcal{D}(X))/P(A)]$ (Murphy et al. 2001), where ${\mathbb{P}}_n^{\ast }$ denotes the empirical average using the validation data and P(A) is the probability of being assigned treatment A.

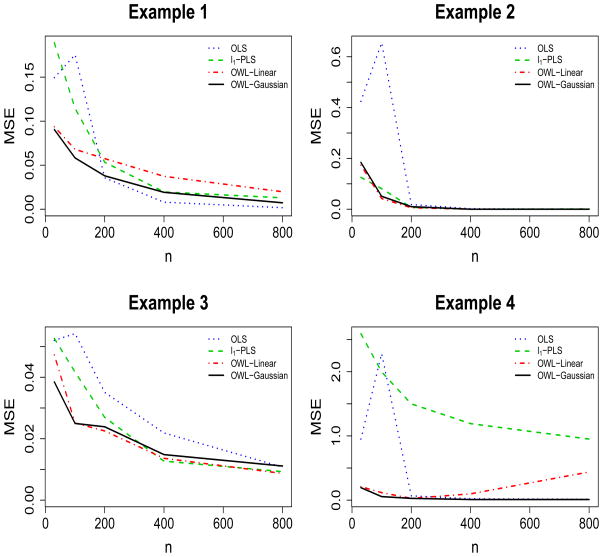
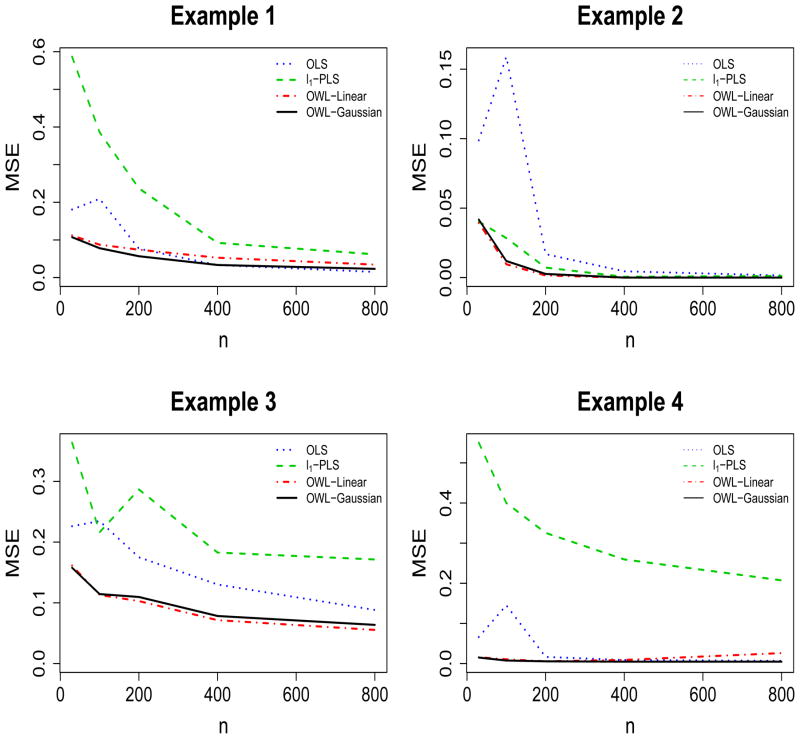
For each scenario, we vary sample sizes for training datasets from 30 to 100, 200, 400 and 800, and repeat the simulation 1,000 times. The simulation results are presented in Figures 2 and 3, where we report the mean square errors (MSE) of both value functions and misclassification rates. Simulations show there are no large differences in the performance if we replace the Gaussian kernel with the linear kernel in the OWL. However, there are examples presenting advantages of the Gaussian kernel, which suggests that under certain circumstances, it is useful to have a flexible nonparametric estimation procedure to identify the optimal ITR for the underlying nonparametric structures. As demonstrated in Figure 2 and Figure 3, the OWL with either Gaussian kernel or linear kernel has better performance, especially for small samples, than the other two methods, from the points of view of producing larger value functions, smaller misclassification rates, and lower variability of the value function estimates. Specifically, when the approximation models used in the l₁-PLS and OLS are correct in the first scenario, the competing methods perform well with large sample size; however, the OWL still provides satisfactory results even if we use a Gaussian kernel. When the optimal ITR is nonlinear in X in the other scenarios, the OWL tends to give higher values and smaller misclassification rates. OLS generally fails unless the sample size is large enough since it encounters severe bias for small sample sizes. This is due to the fact that without variable selection for OLS, there is insufficient data to fit an accurate model with all 50 variables included. We also note that l₁-PLS has comparatively larger MSE, resulted from high variance of the method, which may be explained by the conflicting goals of maximizing the value function and minimizing the prediction error (Qian & Murphy 2011). Note that a richer class of basis functions can be used for fitting the regression models. We have tried a polynomial basis and a wavelet basis to see if they could improve the performance. However, as a larger set of basis functions enters the model, we need to take into account higher dimensional interactions which do not necessarily yield better results. Also, we noted that higher variability is introduced with a richer basis for the approximation space (results not shown).

Figure 2.

MSE for Value Functions of Individualized Treatment Rules

Figure 3.

MSE for Misclassification Rates of Individualized Treatment Rules

Additional simulations are performed by generating binary outcomes from a logit model. It turns out the OWL procedures outperform a traditional logistic regression procedure (results not shown). Finally, using empirical results, we also verify that the cross validation procedure can indeed identify the optimal pairs (λ_n, σ_n) with the order desired by the theoretical results, i.e., ${\sigma }_n={\lambda }_n^{-(q+1)d}$. The numerical results indicate that log₂ σ_n is linear in log₂ λ_n and the ratio between the slopes is close to the reciprocal ratio between the dimensions of the covariate spaces.

5. DATA ANALYSIS

We apply the proposed method to analyze real data from the Nefazodone-CBASP clinical trial (Keller et al. 2000). The study randomized 681 outpatients with non-psychotic chronic major depressive disorder (MDD), in a 1:1:1 ratio to either Nafazodone, Cognitive Behavioral-Analysis System of Psychotherapy (CBASP) or the combination of Nefazodone and CBASP. The score on the 24-item Hamilton Rating Scale for Depression (HRSD) was the primary outcome, where higher scores indicate more severe depression. After excluding some patients with missing observations, we use a subset with 647 patients for analysis. Among them, 216, 220 and 211 patients were assigned to Nafazodone, CBASP and the combined treatment group respectively. Overall comparisons using t-tests show that the combination treatment had significant advantages over the other treatments with respect to HRSD scores obtained at end of the trial, while there are no significant differences between the nefazodone group and the psychotherapy group.

To estimate the optimal ITR, we perform pairwise comparisons between all combinations of two treatment arms, and, for each two-arm comparison, we apply the OWL approach. We only present the results from the Gaussian kernel, since the analysis shows a similarity with that of the linear kernel. Rewards used in the analyses are reversed HRSD scores and the prognostic variables X consist of 50 pretreatment variables. The results based on OWL are compared to results obtained using the l₁-PLS and OLS methods which use (1, X, A, XA) in their regression models. For comparison between methods, we calculate the value function from a cross-validation type analysis. Specifically, the data is partitioned into 5 roughly equal-sized parts. We perform the analysis on 4 parts of the data, and obtain the estimated optimal ITRs using different methods. We then compute the estimated value functions using the remaining fifth part. The value functions calculated this way should better represent expected value functions for future subjects, as compared to calculating value functions based on the training data. The averages of the cross-validation value functions from the three methods are presented in Table 1.

Table 1.

Mean Depression Scores (the Smaller, the Better) from Cross Validation Procedure with Different Methods

	OLS	l1-PLS	OWL
Nefazodone vs CBASP	15.87	15.95	15.74
Combination vs Nefazodone	11.75	11.28	10.71
Combination vs CBASP	12.22	10.97	10.86

From the table, we observe that OLS produces smaller value functions (corresponding to larger HRSD in the table) than the other two methods, possibly because of the high dimensional prognostic variable space. OWL performs similarly to l₁-PLS, but gives a 5% larger value function than l₁-PLS when comparing the Combination arm to the Nefazodone arm. In fact, when comparing combination treatment with nefazodone only, OWL recommends the combination treatment to all the patients in the validation data in each round of the cross validation procedure; the OLS assigns the combination treatment to around 70% of the patients in each validation subset; while the l₁-PLS recommends the combination to all the patients in three out of five validation sets, and 7% and 28% to the patients for the other two, indicating a very large variability. If we need to select treatment between combination and psychotherapy alone, the OWL approach recommends the combination treatment for all patients in the validation process. In contrast, the l₁-PLS chooses psychotherapy for 10 out of 86 patients in one round of validation, and recommends the combination for all patients in the other rounds. The percentages of patients who are recommended the combination treatment range from 66% to 85% across the five validation data sets when applying OLS. When the two single treatments are studied, there are only negligible differences in the estimated value functions from the three methods and the selection results also indicate an insignificant difference between them. Thus OWL not only yields ITRs with the best clinical outcomes, but the ITRs also have lowest variability compared to the other methods.

6. DISCUSSION

The proposed OWL procedure appears to be more effective, across a broad range of possible forms of the interaction between prognostic variables and treatment, compared to previous methods. A two-stage procedure is likely to overfit the regression model, and thus cause troubles for value function approximation. The OWL provides a nonparametric approach which sidesteps the inversion of the predicted model required in other methods and benefits from directly maximizing the value function. The convergence rates for the OWL, aiming to identify the best ITR, nearly reach the optimal for the nonparametric SVM with the same type of assumptions on the separations. The rates, however, are not directly comparable to Qian & Murphy’s (2011), because we allow for complex multivariate interactions and formulate the problem in a nonparametric framework. The proposed estimator will lead to consistency and fast rate results, but not necessarily the most efficient approach. In some cases when we have knowledge of the specific parametric form, a likelihood based method may be more efficient and aid in the improvement of the estimation. Other possible surrogate loss functions, for example, the negative log-likelihood for logistic regression, can also be useful for finding the desired optimal individualized treatment rules.

Several improvements and extensions are important to consider. An important extension we are currently pursuing is to right-censored clinical outcomes. Another extension involves alleviating potential challenges arising from high dimensional prognostic variables. Recall that the proposed OWL is based on a weighted SVM which minimizes the weighted hinge loss function subject to an l₂ penalty. If the dimension of the covariate space is sufficiently large, not all the variables would be essential for optimal ITR construction. By eliminating the unimportant variables from the rule, we could simplify interpretations and reduce health care costs by only requiring collection of a small number of significant prognostic variables. For standard SVM, the l₁ penalty has been shown to be effective in selecting relevant variables via shrinking small coefficients to zero (Bradley & Mangasarian 1998; Zhu et al. 2003). It outperforms the l₂ penalty when there are many noisy variables and sparse models are preferred. Other forms of penalty have been proposed such as the F_∞ norm (Zou & Yuan 2008) and the adaptive l_q penalty (Liu et al. 2007). In the future, we will examine use of these sparse penalties in the OWL method.

In this paper, we only considered binary options for treatment. When there are more than two treatment classes, although we could do a series of pairwise comparisons as done in Section 5 above, this approach may not be optimal in terms of identifying the best rule considering all treatments simultaneously. It would thus be worthwhile to extend the OWL approach to settings involving three or more treatments. The case of multicategory SVM has been studied recently (Lee, Lin & Wahba 2004; Wang & Shen 2006), and a similar generalization may be possible for finding ITRs involving three or more treatments. Another setting to consider is optimal ITR discovery for continuous treatments such as, for example, a continuous range of dose levels. In this situation, we could potentially utilize ideas underlying support vector regression (Vapnik 1995), where the goal is to find a function that has at most ε deviation from the response. Using a similar rationale as the proposed OWL, we could develop corresponding procedures for continuous treatment spaces through weighing each subject by his/her clinical outcome.

Obtaining inference for individualized treatment regimens is also important and challenging. Due to high heterogeneities among individuals, there may be large variations in the estimated treatment rules across different training sets. Laber & Murphy (2011) construct an adaptive confidence interval for the test error under the non-regular framework. Confidence intervals for value functions help us determine whether essential differences exist among different decision rules. Thus an important future research topic is to derive the limiting distribution of 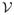( 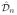) − 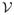( 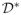) and to derive corresponding sample size formulas to aid in design of personalized medicine clinical trials.

In some complex diseases, dynamic treatment regimes may be more useful than the single-decision treatment rules studied in this paper. Dynamic treatment regimes are customized sequential decision rules for individual patients which can adapt over time to an evolving illness. Recently, this research area has been of great interest in long term management of chronic disease. See, for example, Murphy et al. (2001), Thall, Sung & Estey (2002), Murphy (2003), Robins (2004), Moodie, Richardson & Stephens (2007), Zhao, Zeng, Socinski & Kosorok (2011). Extension of the proposed OWL approach to the dynamic setting would be of great interest.

APPENDIX A. PROOFS

Proof of Theorem 3.2

We consider the case where rewards are discrete. Arguments for the continuous rewards setting follow similarly. Let η_r(x) = p(A = 1|R = r, X = x) and q_r(x) = rp(R = r|X = x). We can write

$$\begin{array}{l}\mathcal{R}(f)=E\left[\sum _{r}rp(R=r\mid X)E\left(\frac{I(A\ne \text{sign}(f(X)))}{A\pi +(1-A)/2}|R=r,X\right)\right]\\ =E\left[\sum _r{q}_r(X)\left(\frac{{\eta }_r(X)}{\pi }I(\text{sign}(f(X))\ne 1)+\frac{1-{\eta }_r(X)}{1-\pi }I(\text{sign}(f(X))\ne -1)\right)\right]\\ =E[c_0(X)(\eta (X)I(\text{sign}(f(X))\ne 1)+(1-\eta (X))I(\text{sign}(f(X))\ne -1))],\end{array}$$ (A.1)

where c₀(x) = Σ_r q_r(x)[ηr(x)/π + (1 − η_r(x))/(1 − π)], and η(x), defined previously in (3.3), is equal to Σ_r q_r(x) η_r(x)/πc₀(x). Similarly,

$${\mathcal{R}}_{\phi }(f)=E[c_0(X)(\eta (X)\phi (f(X))+(1-\eta (X))\phi (-f(X)))].$$

We define C(η, α) = ηφ(α) + (1 − η)φ (−α). Then the optimal φ-risk satisfies

$${\mathcal{R}}_{\phi }^{\ast }=E\left[c_0(X)\underset{\alpha \in \mathbb{R}}{inf}C(\eta (X),\alpha )\right]$$

and

$${\mathcal{R}}_{\phi }-{\mathcal{R}}_{\phi }^{\ast }=E\left[c_0(X)\left(C(\eta (X),f(X))-\underset{\alpha \in \mathbb{R}}{inf}C(\eta (X),\alpha )\right)\right].$$

By a result in Bartlett et al. (2006) for a convexified transform of hinge loss, we have

$$2\eta -1=\underset{\alpha :\alpha (2\eta -1)\le 0}{inf}C(\eta ,\alpha )-\underset{\alpha \in \mathbb{R}}{inf}C(\eta ,\alpha ).$$ (A.2)

Thus, according to (A.1) and (A.2), we have

$$\begin{array}{l}\mathcal{R}(f)-{\mathcal{R}}^{\ast }\le E(I(\text{sign}(f(X))\ne \text{sign}[c_0(X)(\eta (X)-1/2)])\mid c_0(X)(2\eta (X)-1)\mid )\\ =E\left[c_0(X)I(\text{sign}(f(X))\ne \text{sign}[c_0(X)(\eta (X)-1/2)])\left(\underset{\alpha :\alpha (2\eta (X)-1)\le 0}{inf}C(\eta (X),\alpha )-\underset{\alpha \in \mathbb{R}}{inf}C(\eta (X),\alpha )\right)\right]\\ \le E\left[c_0(X)\left(C(\eta (X),f(X))-\underset{\alpha \in \mathbb{R}}{inf}C(\eta (X),\alpha )\right)\right]\\ ={\mathcal{R}}_{\phi }(f)-{\mathcal{R}}_{\phi }^{\ast }.\end{array}$$

The last inequality holds because we always have C(η(x), f(x)) ≥ inf_{α ∈ ℝ} C(η(x), α) on the set where sign(f(x)) = sign[c₀(x)(η(x) − 1/2)] and C(η(x), f (x)) ≥ inf_{α:α(2η (x)−1)≤0} C(η(x), α) when sign(f(x)) ≠ sign[c₀(x)(η(x) − 1/2)].

Proof of Theorem 3.3

Define L_φ(f) = Rφ(Af)/(Aπ + (1 − A)/2). By the definition of f̂_n, we have for any f ∈ ,

$${\mathbb{P}}_n\left(L_{\phi }({\widehat{f}}_n)\right)\le {\mathbb{P}}_n\left(L_{\phi }({\widehat{f}}_n)+{\lambda }_n{\Vert {\widehat{f}}_n\Vert }^2\right)\le {\mathbb{P}}_n\left(L_{\phi }(f)+{\lambda }_n{\left|\right|f\left|\right|}^2\right),$$

where ℙ_n denotes the empirical measure of the observed data. Thus lim sup_n ℙ_n(L_φ(f̂_n)) ≤ ℙ(L_φ(f)). It leads to lim sup_n ℙ_n(L_φ(f̂_n)) ≤ inf_{f ∈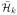} ℙ(L_φ(f)). Theorem 3.3 holds if we can show ℙ_n(L_φ(f̂_n))− ℙ(L_φ(f̂_n)) → 0 in probability.

To this end, we first obtain a bound for ${\left|\right|{\widehat{f}}_n\left|\right|}_k^2$ . Since ${\mathbb{P}}_n(L_{\phi }({\widehat{f}}_n))+{\lambda }_n{\left|\right|{\widehat{f}}_n\left|\right|}^2\le {\mathbb{P}}_n(L_{\phi }(f))+{\lambda }_n{\left|\right|f\left|\right|}_k^2$ for any f ∈ , we can select f = 0 to obtain

$${\left|\right|{\widehat{f}}_n\left|\right|}_k^2\le \frac{1}{{\lambda }_n}\frac{1}{n}\sum \frac{R_i}{{\pi }_i}\phi (0)\le \frac{2}{{\lambda }_n}\frac{E(R)}{min\{\pi ,1-\pi \}}.$$

Let M = 2E(R)/min{π, 1 − π} so that the norm of $\sqrt{{\lambda }_n}{\widehat{f}}_n(X)$ is bounded by $\sqrt{M}$. Note that the class { $\sqrt{{\lambda }_n}f:{\left|\right|\sqrt{{\lambda }_n}f\left|\right|}_k\le \sqrt{M}$} is contained in a Donsker class. Thus, $\{\sqrt{{\lambda }_n}{L}_{\phi }(f),{\left|\right|\sqrt{{\lambda }_n}f\left|\right|}_k\le \sqrt{M}\}$ is also P-Donsker because (1 − Af(X))⁺ is Lipschitz continuous with respect to f. Therefore,

$$\sqrt{n}({\mathbb{P}}_n-\mathbb{P})L_{\phi }({\widehat{f}}_n)=\sqrt{{\lambda }_n^{-1}}\sqrt{n}({\mathbb{P}}_n-\mathbb{P})\left[\frac{R}{A\pi +(1-A)/2}{\left(\sqrt{{\lambda }_n}-A\sqrt{{\lambda }_n}{\widehat{f}}_n(X)\right)}^{+}\right]=O_p\left(\sqrt{{\lambda }_n^{-1}}\right).$$

Consequently, from nλ_n → ∞, ℙ_n(L_φ(f̂_n)) − ℙ(L_φ(f̂_n)) → 0 in probability.

Proof of Theorem 3.4

First, we have

$$\begin{array}{l}{\mathcal{R}}_{\phi }({\widehat{f}}_n)-{\mathcal{R}}_{\phi }^{\ast }\le {\lambda }_n{\left|\right|{\widehat{f}}_n\left|\right|}_k^2+{\mathcal{R}}_{\phi }({\widehat{f}}_n)-{\mathcal{R}}_{\phi }^{\ast }\\ \le \left[{\lambda }_n{\left|\right|{\widehat{f}}_n\left|\right|}_k^2+{\mathcal{R}}_{\phi }({\widehat{f}}_n)-\underset{f\in {\mathcal{H}}_k}{inf}({\lambda }_n{\left|\right|f\left|\right|}_k^2+{\mathcal{R}}_{\phi }(f))\right]+\left[\underset{f\in {\mathcal{H}}_k}{inf}({\lambda }_n{\left|\right|f\left|\right|}_k^2+{\mathcal{R}}_{\phi }(f)-{\mathcal{R}}_{\phi }^{\ast })\right].\end{array}$$ (A.3)

We will bound each term on the right-hand-side separately in the following arguments.

For the second term on the right-hand-side of (A.3), we use Theorem 2.7 in Steinwart & Scovel (2007) to conclude that

$$\underset{f\in {\mathcal{H}}_k}{inf}({\lambda }_n{\left|\right|f\left|\right|}_k^2+{\mathcal{R}}_{\phi }(f)-{\mathcal{R}}_{\phi }^{\ast })=O\left({\lambda }_n^{q/(q+1)}\right),$$ (A.4)

when we set ${\sigma }_n={\lambda }_n^{-1/(q+1)d}$.

Now we proceed to obtain a bound for the first term on the right-hand-side of (A.3). To do this, we need the useful Theorem 5.6 of Steinwart & Scovel (2007) presented below: Theorem 5.6, Steinwart & Scovel (2007). Let 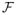be a convex set of bounded measurable functions from Z to ℝ and let L : 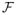× Z → [0, ∞) be a convex and line-continuous loss function. For a probability measure P on Z we define

$$\mathcal{G}:=\{L\circ f-L\circ f_{P,\mathcal{F}}:f\in \mathcal{F}\}.$$

Suppose that there are constants c ≥ 0, 0 < α < 1, δ ≥ 0 and B > 0 with E_P g² ≤ c(E_P g)^α + δ and ||g||_∞ ≤ B for all g ∈ 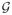. Furthermore, assume that 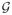is separable with respect to || · ||_∞ and that there are constants a ≥ 1 and 0 < p < 2 with

$$\underset{T\in Z^n}{sup}logN(B^{-1}\mathcal{G},\epsilon ,L_2(T))\le a{\epsilon }^{-p}$$

for all ε > 0. Then there exists a constant c_p > 0 depending only on p such that for all n ≥ 1 and all τ ≥ 1 we have

$${Pr}^{\ast }(T\in Z^n:{\mathcal{R}}_{L,P}(f_{T,\mathcal{F}})>{\mathcal{R}}_{L,P}(f_{P,\mathcal{F}})+c_p\epsilon (n,a,B,c,\delta ,\tau ))\le e^{-\tau },$$

where

$$\epsilon (n,a,B,c,\delta ,x):=B^{2p/(4-2\alpha +\alpha p)}{c}^{(2-p)/(4-2\alpha +\alpha p)}{\left(\frac{a}{n}\right)}^{2/(4-2\alpha +\alpha p)}+B^{p/2}{\delta }^{(2-p)/4}{\left(\frac{a}{n}\right)}^{1/2}+B{\left(\frac{a}{n}\right)}^{2/(2+p)}+\sqrt{\frac{\delta x}{n}}+{\left(\frac{c\tau }{n}\right)}^{1/(2-\alpha )}+\frac{B\tau }{n}.$$

In their paper, 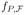∈ 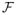is a minimizer of 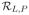(f) = E(L(f, z)), and 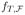is similarly defined when T is an empirical measure. To use this theorem, we define 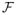, Z, T, 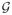, 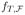and 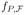according to our setting. It suffices to consider the subspace of , denoted by $B_{{\mathcal{H}}_k}\left(\sqrt{M/{\lambda }_n}\right)$, as the ball of of radius $\sqrt{M/{\lambda }_n}$. Specifically, we let 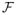be $B_{{\mathcal{H}}_k}\left(\sqrt{M/{\lambda }_n}\right)$ and Z be 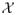. The loss function we consider here is $L_{\phi }(f)+{\lambda }_n{\left|\right|f\left|\right|}_k^2$ and 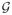is the function class

$${\mathcal{G}}_{\phi ,{\lambda }_n}=\left\{L_{\phi }(f)+{\lambda }_n{\left|\right|f\left|\right|}_k^2-L_{\phi }(f_{\phi ,{\lambda }_n}^{\ast })-{\lambda }_n{\left|\right|f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k^2:f\in B_{{\mathcal{H}}_k}\left(\sqrt{M/{\lambda }_n}\right)\right\},$$

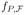where $f_{\phi ,{\lambda }_n}^{\ast }={\text{argmin}}_{f\in B_{{\mathcal{H}}_k}\left(\sqrt{M/{\lambda }_n}\right)}({\lambda }_n{\left|\right|f\left|\right|}_k^2+{\mathcal{R}}_{\phi }(f))$. and 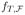correspond to $f_{\phi ,{\lambda }_n}^{\ast }$ and f̂_n, respectively. Therefore, to apply this theorem, we will show that there are constants c ≥ 0 and B > 0, which can possibly depend on n, such that E(g²) ≤ cE(g) and ||g||_∞ ≤ B, ∀g ∈ 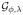. Moreover, there are constants c̃ and 0 < ν < 2 with

$$\underset{P_n}{sup}logN(B^{-1}{\mathcal{G}}_{\phi ,{\lambda }_n},\epsilon ,L_2(P_n))\le \stackrel{\sim }{c}{\epsilon }^{-\nu },$$

for all ε > 0.

Let C_L denote sup{R/min(π, 1 − π)}, which is finite provided that R is bounded. Since the weighted hinge loss is Lipschitz continuous with respect to f, with Lipschitz constant C_L, and since ||f||_∞ ≤ ||f||_k given that k(x, x) ≤ 1, for any g ∈ 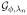, we have

$$\begin{array}{l}\mid g\mid \le \mid L_{\phi }(f)-L_{\phi }(f_{\phi ,{\lambda }_n}^{\ast })\mid +{\lambda }_n\mid {\left|\right|f\left|\right|}_k^2-{\left|\right|f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k^2\mid \\ \le C_L\mid f(x)-f_{\phi ,{\lambda }_n}^{\ast }(x)\mid +M\\ \le 2C_L\sqrt{M}{\lambda }_n^{-1/2}+M.\end{array}$$ (A.5)

Therefore, we can set $B=2C_L\sqrt{M}{\lambda }_n^{-1/2}+M$.

For any g ∈ 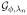, we have

$$\begin{array}{l}g(f)\le \mid L_{\phi }(f)-L_{\phi }(f_{\phi ,{\lambda }_n}^{\ast })\mid +{\lambda }_n\mid {\left|\right|f\left|\right|}_k^2-{\left|\right|f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k^2\mid \\ \le C_L\mid f-f_{\phi ,{\lambda }_n}^{\ast }\mid +{\lambda }_n{\left|\right|f-f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k{\left|\right|f+f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k\\ =\left(C_L+2\sqrt{M{\lambda }_n}\right){\left|\right|f-f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k.\end{array}$$

Squaring both sides and taking expectations yields

$$E(g^2)\le {\left(C_L+2\sqrt{M{\lambda }_n}\right)}^2{\left|\right|f-f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k^2.$$ (A.6)

On the other hand, from the convexity of L_φ, we have

$$\begin{array}{l}\frac{1}{2}(L_{\phi }(f)+{\lambda }_n{\left|\right|f\left|\right|}_k^2+L_{\phi }(f_{\phi ,{\lambda }_n}^{\ast })+{\lambda }_n{\left|\right|f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k^2)\ge L_{\phi }\left(\frac{f+f_{\phi ,{\lambda }_n}^{\ast }}{2}\right)+{\lambda }_n\frac{{\left|\right|f\left|\right|}_k^2+{\left|\right|f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k^2}{2}\\ =L_{\phi }\left(\frac{f+f_{\phi ,{\lambda }_n}^{\ast }}{2}\right)+{\lambda }_n{\Vert \frac{f+f_{\phi ,{\lambda }_n}^{\ast }}{2}\Vert }_k^2+{\lambda }_n{\Vert \frac{f-f_{\phi ,{\lambda }_n}^{\ast }}{2}\Vert }_k^2\\ \ge L_{\phi }(f_{\phi ,{\lambda }_n}^{\ast })+{\lambda }_n{\left|\right|f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k^2+{\lambda }_n{\Vert \frac{f-f_{\phi ,{\lambda }_n}^{\ast }}{2}\Vert }_k^2.\end{array}$$

Taking expectations on both sides leads to $E(g)\ge {\lambda }_n{\left|\right|f-f_{\phi ,{\lambda }_n}^{\ast }\left|\right|}_k^2/2$. Combining this with (A.6), we conclude that E(g²) ≤ cE (g), where

$$c=\frac{2}{{\lambda }_n}{\left(C_L+2\sqrt{M{\lambda }_n}\right)}^2.$$ (A.7)

To estimate the bound for N(B⁻¹ 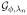, ε, L₂(P_n)), we first have

$$N(B^{-1}{\mathcal{G}}_{\phi ,{\lambda }_n},\epsilon ,L_2(P_n))=N\left(B^{-1}\left\{L_{\phi }(f)+{\lambda }_n{\left|\right|f\left|\right|}_k^2:f\in B_{{\mathcal{H}}_k}\left(\sqrt{M/{\lambda }_n}\right)\right\},\epsilon ,L_2(P_n)\right).$$

From the sub-additivity of the entropy,

$$logN(B^{-1}{\mathcal{G}}_{\phi ,{\lambda }_n},2\epsilon ,L_2(P_n))\le logN\left(B^{-1}\left\{L_{\phi }(f):f\in B_{{\mathcal{H}}_k}\left(\sqrt{M/{\lambda }_n}\right)\right\},\epsilon ,L_2(P_n)\right)+logN\left(\left\{{\lambda }_n{\left|\right|f\left|\right|}_k^2,f\in B_{{\mathcal{H}}_k}\left(\sqrt{M/{\lambda }_n}\right)\right\},\epsilon ,L_2(P_n)\right).$$ (A.8)

Using the Lipschitz-continuity of the weighted hinge loss, we now have that if u, $u^{\prime }\in B^{-1}\{L_{\phi }(f):f\in B_{{\mathcal{H}}_k}(\sqrt{M/{\lambda }_n})\}$with corresponding f, $f^{\prime }\in B_{{\mathcal{H}}_k}(\sqrt{M/{\lambda }_n})$, then ||u − u′||_L2(Pn) ≤ B⁻¹C_L|| f − f′||_L2(Pn), and therefore the first term on the right-hand-side of (A.8) satisfies

$$\begin{array}{l}logN\left(B^{-1}\left\{L_{\phi }(f):f\in B_{{\mathcal{H}}_k}\left(\sqrt{M/{\lambda }_n}\right)\right\},\epsilon ,L_2(P_n)\right)\le logN\left(B_{{\mathcal{H}}_k}\left(\sqrt{M/{\lambda }_n}\right),\frac{B\epsilon }{C_L},L_2(P_n)\right)\\ \le logN\left(B_{{\mathcal{H}}_k},\frac{B\epsilon }{C_L\sqrt{M/{\lambda }_n}},L_2(P_n)\right)\\ \le logN(B_{{\mathcal{H}}_k},2\epsilon ,L_2(P_n)).\end{array}$$

The last inequality follows because $B/C_L\sqrt{M/{\lambda }_n}\ge 2$. It is trivial to see that for the second term on the right hand side of (A.8),

$$logN\left(\left\{{\lambda }_n{\left|\right|f\left|\right|}_k^2,f\in B\left(\sqrt{M/{\lambda }_n}\right)\right\},\epsilon ,L_2(P_n)\right)\le log\left(\frac{M}{B\epsilon }\right).$$

Thus,

$$logN(B^{-1}{\mathcal{G}}_{\phi ,{\lambda }_n},2\epsilon ,L_2(P_n))\le logN(B_{{\mathcal{H}}_k},2\epsilon ,L_2(P_n))+log\left(\frac{M}{B\epsilon }\right).$$

Using (3.5) and a given choice for B, we obtain for all σ_n > 0, 0 < ν < 2, δ > 0, ε > 0,

$$\underset{P_n}{sup}logN(B^{-1}{\mathcal{G}}_{\phi ,{\lambda }_n},\epsilon ,L_2(P_n))\le c_2{\sigma }_n^{(1-\nu /2)(1+\delta )d}{\epsilon }^{-\nu },$$

where c₂ depends on ν, δ and d.

Consequently, from Theorem 5.6 in Steinwart & Scovel (2007), there exists a constant c_ν > 0 depending only on ν such that for all n ≥ 1 and all τ ≥ 1, we have the bound for the first term

$$P^{\ast }\left({\lambda }_n{\left|\right|{\widehat{f}}_n\left|\right|}_k^2+{\mathcal{R}}_{\phi }({\widehat{f}}_n)>\underset{f\in {\mathcal{H}}_k}{inf}({\lambda }_n{\left|\right|f\left|\right|}_k^2+{\mathcal{R}}_{\phi }(f))+c_{\nu }\epsilon (n,\stackrel{\sim }{c},B,c,\tau )\right)\le e^{-\tau },$$

where

$$\epsilon (n,\stackrel{\sim }{c},B,c,\tau )=\left(B+B^{\frac{2\nu }{2+\nu }}{c}^{\frac{2-\nu }{2+\nu }}\right){\left(\frac{\stackrel{\sim }{c}}{n}\right)}^{\frac{2}{2+\nu }}+(B+c)\frac{\tau }{n}.$$

With B and c as defined in (A.5) and (A.7), i.e., $\stackrel{\sim }{c}=c_2{\sigma }_n^{(1-\nu /2)(1+\delta )d}$ and ${\sigma }_n=-{\lambda }_n^{1/(q+1)d}$, we obtain

$$\epsilon (n,\stackrel{\sim }{c},B,c,\tau )=C_1{\left(\frac{1}{{\lambda }_n}\right)}^{\frac{2}{2+\nu }+\frac{(2-\nu )(1+\delta )}{(2+\nu )(1+q)}}{\left(\frac{1}{n}\right)}^{\frac{2}{2+\nu }}+C_2{\left(\frac{1}{{\lambda }_n}\right)}^{\frac{q}{q+1}}\frac{\tau }{n},$$ (A.9)

where C₁ and C₂ are constants depending on ν, δ, d, M and π. We complete the proof of Theorem 3.4 by plugging (A.4) and (A.9) into (A.3).

Proof of Theorem 3.5

We apply Theorem 4.3 in Blanchard et al. (2008) on the scaled loss function L̃_φ(f) = L_φ(f)/C_L to obtain the rates in Theorem 3.5. Without loss of generality, we can assume that the Bayes classifier f^* ∈ , since we can always find g ∈ such that ${\mathcal{R}}_{\phi }(g)={\mathcal{R}}_{\phi }(f^{\ast })={\mathcal{R}}_{\phi }^{\ast }$, provided that is dense in C( 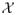). Let 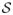be a countable and dense subset of ℝ⁺, and let 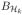(S) denote the ball of of radius S. Then 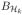(S), S ∈ is a countable collection of classes of functions. We can then use Theorem 4.3 in Blanchard et al. (2008) after we verify the following conditions (H1)–(H4):

• (H1)∀S ∈ , ∀f ∈ 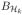(S), ||L̃_φ(f)||_∞ ≤ b_S, b_S = 1+ S;
• (H2)∀f, f′ ∈ , Var(L̃_φ(f) − L̃_φ(f′)) ≤ d²(f, f′), d(f, f′) = ||f − f′||_L2(P);
• (H3)∀S ∈ 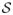, ∀f ∈ 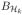(S), d²(f, f^*) ≤ C_S E(L̃_φ(f) − L̃_φ(f^*)), C_S = 2(S/η₀ + 1/η₁);
• (H4)
  Let

  $$\xi (x)={\int }_0^x\sqrt{logN(B_{{\mathcal{H}}_k},\epsilon ,L_2(P_n))}d\epsilon .$$
  We have

  $$E[\underset{\begin{array}{c}f\in B_{{\mathcal{H}}_k}(S)\\ d^2(f,f^{\prime })\le r\end{array}}{sup}(P-P_n)({\stackrel{\sim }{L}}_{\phi }(f)-{\stackrel{\sim }{L}}_{\phi }(f^{\prime }))]\le \underset{\vartheta >0}{inf}\left\{4\vartheta -\frac{12}{\sqrt{n}}\xi (\vartheta )+\frac{12}{\sqrt{n}}\xi \left(\frac{\sqrt{r}}{\sqrt{2}S}\right)\right\}={\psi }_S(r).$$

  ψ_S, S ∈ 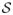, is a sequence of sub-root functions, that is, ψ_S is non-negative, nondecreasing, and ${\psi }_S(r)/\sqrt{r}$ is non-increasing for r > 0. Denote x_* as the solution of the equation $\xi (x)=\sqrt{n}{x}^2$

• . If $r_S^{\ast }$ denotes the solution of ψ_S(r) = r/C_S, then

  $$r_S^{\ast }\le \underset{\vartheta >0}{inf}{C}_S\{4\vartheta -12\xi (\vartheta )/\sqrt{n}\}+c^2{C}_S^2{x}_{\ast }^2.$$

Under these conditions, we define for n ∈ ℕ the following quantity:

$${\gamma }_n=\underset{\vartheta >0}{inf}\left\{4\vartheta -\frac{12}{\sqrt{n}}\xi (\vartheta )+x_{\ast }^2(n)\right\}.$$

Given is associated with the Gaussian kernel, we can show that ξ(x) ⪯ ε^1−ν for any 0 < ν < 2. Thus, γ_n ⪯ max(n^−1/2ν, n^−1/(ν+1)). By the choice of λ_n = O(n^−1/(ν+1)) for any ν ∈ (0, 1), this satisfies

$${\lambda }_n\ge c\left({\gamma }_n+{\eta }_1^{-1}\frac{log({\tau }^{-1}logn)\vee 1}{n}\right).$$

Therefore, according to Theorem 4.3 in Blanchard et al. (2008), the following bound holds with probability at least 1 − τ, where τ > 0 is a fixed real number:

$$E({\stackrel{\sim }{L}}_{\phi }({\widehat{f}}_n))-E({\stackrel{\sim }{L}}_{\phi }(f^{\ast }))\le 2\underset{f\in {\mathcal{H}}_k}{inf}[E({\stackrel{\sim }{L}}_{\phi }(f))-E({\stackrel{\sim }{L}}_{\phi }(f^{\ast }))+2{\lambda }_n{\left|\right|f\left|\right|}_k^2]+4{\lambda }_n(8+c{\eta }_1{\eta }_0^{-1}).$$

The result does not change after we scale back to the original loss L_φ(f). We have shown that ${inf}_{f\in {\mathcal{H}}_k}[{\mathcal{R}}_{\phi }(f)-{\mathcal{R}}_{\phi }(f^{\ast })+2{\lambda }_n{\left|\right|f\left|\right|}_k^2]=O({\lambda }_n^{q/(q+1)})$ in the proof of Theorem 3.4. Thus

$$\mathcal{R}({\widehat{f}}_n)-{\mathcal{R}}^{\ast }=O_p({\lambda }_n^{q/(q+1)})=O_p\left(n^{-\frac{1}{\nu +1}\frac{q}{q+1}}\right).$$

The remainder of the proof is to verify conditions (H1)–(H4).

For condition (H1), ||L̃_φ(f)||_∞ ≤ sup{R/(Aπ + (1 − A)/2)}(1 + S)/C_L ≤ 1 + S, ||f||_k ≤ S.

For condition (H2), let d(f, f′) = ||f − f′||_L2(P). L_φ(f) is a Lipschitz function with respect to f with Lipschitz constant C_L. Then L̃_φ(f) − L̃_φ(f′) ≤ |f(x) − f′(x)|. Hence (H2) is easily satisfied.

For condition (H3), the proof is similar to to Lemma 6.4 of Blanchard et al. (2008) with C_S = 2(S/η₁ + 1/η₀), where η₀ and η₁ are as defined in Assumptions (A1) and (A2) of Section 3.5.

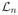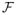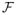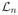
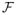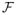
For condition (H4), we introduce the notation for Rademacher averages: let ε₁,…, ε_n be n i.i.d Rademacher random variables, independent of (X_i, A_i, R_i), i = 1, …, n. For any measurable real-valued function f, the Rademacher average is defined as ${\mathcal{L}}_{n}f=n^{-1}{\sum }_{i=1}^n{\epsilon }_{i}f(X_i)$. Also let ( ) be the empirical Rademacher complexity of function class , = sup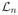_f∈ f.

First we have from Lemma 6.7 of Blanchard et al. (2008) that for f′ ∈ ,

$$E\left[\underset{f\in {\mathcal{H}}_k}{sup}(P-P_n)({\stackrel{\sim }{L}}_{\phi }(f)-{\stackrel{\sim }{L}}_{\phi }(f^{\prime }))\right]\le 4E[{\mathcal{L}}_n\{f-f^{\prime },f\in {\mathcal{H}}_k\}].$$

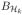Thus for the set {f ∈ : ||f||_k ≤ S, d²(f, f′) ≤ r} and f′ ∈ (S),

$$E\left[\underset{f\in {\mathcal{H}}_k}{sup}(P-P_n)({\stackrel{\sim }{L}}_{\phi }(f)-{\stackrel{\sim }{L}}_{\phi }(f^{\prime }))\right]\le 4E[{\mathcal{L}}_n\{f-f^{\prime },f\in {\mathcal{H}}_k:{\left|\right|f\left|\right|}_k\le S,d^2(f,f^{\prime })\le r\}],$$

the right-hand-side of which is equivalent to $4E\left[{\mathcal{L}}_n\{f,f\in {\mathcal{H}}_k:{\left|\right|f\left|\right|}_k\le 2S,{\left|\right|f\left|\right|}_{L_2(P_n)}^2\le 2r\}\right]$. Now we proceed to show that

$$E{\mathcal{L}}_n\left\{f\in {\mathcal{H}}_k:{\left|\right|f\left|\right|}_k\le 2S,{\left|\right|f\left|\right|}_{L_2(P_n)}^2\le 2r\right\}\le \underset{\vartheta >0}{inf}\left\{4\vartheta +\frac{12}{\sqrt{n}}{\int }_{\vartheta }^{\frac{\sqrt{r}}{\sqrt{2}S}}\sqrt{logN(B_{\mathcal{H}},\epsilon ,L_2(P_n))}d\epsilon \right\}={\psi }_S(r),$$

by slightly modifying the procedure in obtaining Dudley’s Entropy Integral for Rademacher complexity of sets of functions. For j ≥ 0, let $r_j=\sqrt{2r}{2}^{-j}$ and T_j be a r_j-cover of 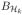(2S) with respect to the L₂(P_n)-norm. For each f ∈ 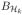(2S), we can find an f̃_j ∈ T_j, such that ||f − f̃_j||_L2(Pn) ≤ r_j. For any N, we express f as $f=f-{\stackrel{\sim }{f}}_N+{\sum }_{j=1}^N({\stackrel{\sim }{f}}_j-{\stackrel{\sim }{f}}_{j-1})$, where f̃₀ = 0. Note f̃₀ = 0 is an r₀-approximation of f. Hence,

$$\begin{array}{l}{\mathcal{L}}_n(B_{{\mathcal{H}}_k}(2S))=E\left[\underset{f\in B_{{\mathcal{H}}_k}(2S)}{sup}\frac{1}{n}\sum _{i=1}^n{\epsilon }_i\left(f(X_i)-{\stackrel{\sim }{f}}_N(X_i)+\sum _{j=1}^N({\stackrel{\sim }{f}}_j(X_i)-{\stackrel{\sim }{f}}_{j-1}(X_i))\right)\right]\\ \le E\left[\underset{f\in B_{{\mathcal{H}}_k}(2S)}{sup}{\left|\right|\epsilon \left|\right|}_{L_2(P_n)}{\Vert f-{\stackrel{\sim }{f}}_N\Vert }_{L_2(P_n)}\right]+\sum _{j=1}^{N}E\left[\underset{f\in B_{{\mathcal{H}}_k}(2S)}{sup}\frac{1}{n}\sum _{i=1}^n\left({\stackrel{\sim }{f}}_j(X_i)-{\stackrel{\sim }{f}}_{j-1}(X_i)\right)\right]\\ \le r_N+\sum _{j=1}^{N}E\left[\underset{f\in B_{{\mathcal{H}}_k}(2S)}{sup}\frac{1}{n}\sum _{i=1}^n\left({\stackrel{\sim }{f}}_j(X_i)-{\stackrel{\sim }{f}}_{j-1}(X_i)\right)\right].\end{array}$$

Note that

$${\Vert {\stackrel{\sim }{f}}_j-{\stackrel{\sim }{f}}_{j-1}\Vert }_{L_2(P_n)}^2\le {\left({\Vert {\stackrel{\sim }{f}}_j-f\Vert }_{L_2(P_n)}+{\Vert f-{\stackrel{\sim }{f}}_{j-1}\Vert }_{L_2(P_n)}\right)}^2\le {(r_j+r_{j-1})}^2=9r_j^2.$$

We therefore have

$$\begin{array}{l}{\mathcal{L}}_n(B_{{\mathcal{H}}_k}(2S))\le r_N+\sum _{j=1}^{N}3r_j\sqrt{\frac{2log(\mid T_j||T_{j-1}\mid )}{n}}\\ \le r_N+12\sum _{j=1}^N(r_j-r_{j+1})\sqrt{\frac{logN(B_{{\mathcal{H}}_k}(2S),r_j,L_2(P_n))}{n}}\\ \le r_N+12{\int }_{r_{N+1}}^{\sqrt{r}/\sqrt{2}S}\sqrt{\frac{logN(B_{{\mathcal{H}}_k},\epsilon ,L_2(P_n))}{n}}d\epsilon .\end{array}$$

For any ϑ > 0, we can choose N = sup{j : r_j > 2ϑ}. Therefore, ϑ < r_N+1 < 2ϑ, and r_N < 4ϑ. We therefore conclude that

$$\begin{array}{l}{\mathcal{L}}_n(B_{{\mathcal{H}}_k}(2S))\le \underset{\vartheta >0}{inf}\left\{4\vartheta +12{\int }_{\vartheta }^{\sqrt{r}/\sqrt{2}S}\sqrt{\frac{logN(B_{{\mathcal{H}}_k},\epsilon ,L_2(P_n))}{n}}d\epsilon \right\}\\ =\underset{\vartheta >0}{inf}\left\{4\vartheta -\frac{12}{\sqrt{n}}\xi (\vartheta )+\frac{12}{\sqrt{n}}\xi \left(\frac{\sqrt{r}}{\sqrt{2}S}\right)\right\}={\psi }_S(r).\end{array}$$

The function ψ_S is sub-root because log N ( 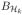, ε, L₂(P_n)) is a decreasing function of ε.

To show the upperbound of r^*, let $t_S^{\ast }=c^2{C}_S^2{x}_{\ast }^2$. Then $\sqrt{t_S^{\ast }}/\sqrt{2}S={cC}_S{x}_{\ast }/\sqrt{2}S$, C_S/S ≥ 1. Assuming that c ≥ 2, we have $\sqrt{t_S^{\ast }}/\sqrt{2}S\ge x_{\ast }$. Since x⁻¹ ξ(x) is a decreasing function, it follows that

$$\xi \left(\frac{\sqrt{t_S^{\ast }}}{\sqrt{2}S}\right)\le c\frac{C_S}{\sqrt{2}S}\xi (x_{\ast })=\frac{\sqrt{n}}{{\mathit{cSC}}_S}{t}_S^{\ast }.$$

Therefore, by selecting an appropriate constant c,

$${\psi }_S(t_S^{\ast })\le \underset{\vartheta >0}{inf}\left\{4\vartheta -\frac{12}{\sqrt{n}}\xi (\vartheta )\right\}+\frac{12}{{\mathit{cSC}}_S}{t}_S^{\ast }\le \frac{C_S{inf}_{\vartheta >0}\{4\vartheta -12/\sqrt{n}\xi (\vartheta )\}+t_S^{\ast }}{C_S}.$$

The desired result follows from the property of sub-root functions, which states that if ψ : [0, ∞) → [0, ∞) is a sub-root function, then the unique positive solution of ψ(r) = r, denoted by r^*, exists, and for all r > 0, r ≥ ψ(r) if and only if r* ≤ r (Bartlett et al. 2005).