Electrostatics Control Actin Filament Nucleation and Elongation Kinetics

Background: pH plays important roles in cellular morphogenesis, but how actin polymer dynamics are affected by pH is not well understood.

Results: Actin filament nucleation and elongation are strongly enhanced at acidic pH due to a reduction of charge repulsion.

Conclusion: Actin filament dynamics in vitro and in vivo are strongly influenced by electrostatics.

Significance: Cellular pH homeostasis will impact directly on actin dynamics.

Abstract

The actin cytoskeleton is a central mediator of cellular morphogenesis, and rapid actin reorganization drives essential processes such as cell migration and cell division. Whereas several actin-binding proteins are known to be regulated by changes in intracellular pH, detailed information regarding the effect of pH on the actin dynamics itself is still lacking. Here, we combine bulk assays, total internal reflection fluorescence microscopy, fluorescence fluctuation spectroscopy techniques, and theory to comprehensively characterize the effect of pH on actin polymerization. We show that both nucleation and elongation are strongly enhanced at acidic pH, with a maximum close to the pI of actin. Monomer association rates are similarly affected by pH at both ends, although dissociation rates are differentially affected. This indicates that electrostatics control the diffusional encounter but not the dissociation rate, which is critical for the establishment of actin filament asymmetry. A generic model of protein-protein interaction, including electrostatics, explains the observed pH sensitivity as a consequence of charge repulsion. The observed pH effect on actin in vitro agrees with measurements of Listeria propulsion in pH-controlled cells. pH regulation should therefore be considered as a modulator of actin dynamics in a cellular environment.

Introduction

The actin cytoskeleton plays a crucial role in many fundamental cellular processes such as adhesion, polarization, migration, division, and differentiation. This pivotal function of actin is largely due to its capacity to self-assemble into linear polymers with a directed polarity, a process that generates local mechanical forces (1–3). Arrays and networks of actin filaments in turn provide cells with a skeleton that determines shape and helps to resist and sense mechanical deformation (4, 5). An essential feature of the actin cytoskeleton is its dynamic nature, known to be regulated by a multitude of signaling pathways. However, one ubiquitous parameter that has been shown to affect actin polymerization (21, 22) has been overlooked in most studies, i.e. pH. The physiological role of increasing pH in actin polymerization has already been observed in early studies on fertilization of sea urchin eggs (6) and on the acrosomal reaction of echinoderm sperms (7). More recently, molecular mechanisms contributing to pH regulation of actin turnover (8) and force generation (9) have been identified. In this respect, the major actin severing and depolymerizing factor cofilin has been shown to be inhibited by low pH (8). Similarly, activity of talin, which links actin to integrins in focal adhesion and helps traction force generation, has been shown to be sensitive to local pH (9). The major regulator of intracellular pH (pH_i) in mammalian cells, the Na/H⁺ exchanger 1 (NHE1),⁴ is localized at the leading edge, where continuous polymerization and turnover of actin occurs during cell migration (10). NHE1 has been shown to directly affect cell migration by locally modulating intracellular pH_i (11, 12). Interestingly, the localization of NHE1 itself is mediated by the actin cytoskeleton (13). pH_i is highly regulated to prevent disruption of basic cell functions such as enzyme activity, membrane permeability, cellular metabolism, ATP maintenance, cell proliferation, and apoptotic mechanisms (14–17). Not surprisingly, dynamic changes in pH are linked to pathogenic conditions, with many cancer cells exhibiting elevated pH_i (18–20). Although there have been intense efforts to understand the molecular basis of how pH_i regulates cellular actin dynamics (20), many fundamental questions remain unresolved.

In contrast to complex cellular actin turnover (6, 7), which depends on many regulatory actin-binding proteins, polymerization of pure actin in vitro is paradoxically increased at acidic pH (21, 22). In general, pH modulates protein electrostatics by altering the protonation state of amino acid side chains, therefore influencing protein-protein interactions (e.g. actin/actin or actin/actin-binding protein). In this way, electrostatics can enhance or retard reaction rates of complex formation that are limited by diffusion (23, 24), such as barbed-end actin filament elongation (25). It was suggested, using Brownian dynamic simulations, that electrostatics could establish the actin filament asymmetry (26), although this prediction has so far not been tested experimentally.

Here, we use biochemical assays, TIRF microscopy (TIRFM), and advanced fluorescence fluctuation methods to explore the effects of electrostatics on actin nucleation and elongation. A generic theoretical model provides a framework for our observations.

EXPERIMENTAL PROCEDURES

Proteins

G-actin was purified from rabbit or chicken skeletal muscle (27, 28) and stored at 4 °C for up to 2 weeks. Myosin was purified and chemically inactivated with N-ethylmaleimide according to Ref. 29. Actin was labeled in random surface lysines with atto488 or atto532, or it was purchased from Hypermol (Bielefeld, Germany).

Bulk Assays

Polymerization of actin was induced by addition of one-tenth of the final volume of 10× KMEI buffer (1× contained the following: 50 mm KCl, 1 mm MgCl₂, 1 mm EGTA, and 10 mm imidazole HCl, pH 7.0) and incubation for >1 h at room temperature. For the polymerization assays, 20% pyrene-labeled actin was used (30, 31). Ca²⁺ to Mg²⁺ exchange was done by adding one-tenth of the final volume of 10× ME buffer (50 μm MgCl₂, 0.2 mm EGTA) for 5 min. Polymerization was promoted by addition of one-tenth of the final volume 10× KMEI buffer. The final volume was 100 μl. Pyrene fluorescence was monitored by excitation at 365 nm and emission at 407 nm with a Cary Varian spectrofluorometer. Lag times were extracted as the intercept from the slope at the inflection point of the polymerization curve. Depolymerization was carried out by diluting 1 μm of 100% pyrene-actin (polymerized for 2 h at RT in the desired pH) in F-buffer, pH 7.1, to 10 nm. Data from Zimmerle and Frieden (22) was digitized using the freely available program grabit in MATLAB.

Circular Dichroism and Electron Microscopy

CD spectra from 195 to 260 nm were acquired with a Jasco J-715 spectropolarimeter (Jasco). A protein concentration of 10 μm in P-buffer at the desired pH value was used. The measurements were performed at a bandwidth of 5 nm, a response time of 2 s, and a scan rate of 0.1 nm·s⁻¹. For electron microscopy, a 3-μl drop of polymerized actin was incubated for 90 s on a copper grid previously plasma-cleaned for 30 s and stained with 3% uracil acetate for 30 s.

Fluorescence Fluctuation Spectroscopy

Photon counting histogram experiments (32) with pulsed interleaved excitation (33) were performed on a homebuilt confocal multiparameter fluorescence detection setup (33). The multiparameter fluorescence detection setup uses a polarizing beam splitter in the detection path to separate fluorescence photons with respect to their polarization, followed by spectral separation. Hence, multicolors can be detected, and the anisotropy can be determined in addition to the fluorescence lifetime information. The system is built about a Nikon TE2000 microscope. As picosecond excitation sources, we used an amplified frequency-doubled diode laser (PicoTA, PicoQuant, Berlin) at 530 nm and a diode laser at 636 nm (LDH-P-C-635b PicoQuant) for fluorophore excitation. The laser was coupled into a single-mode fiber (AMS Technologies, Martinsried, Germany), collimated (Schäfter & Kirchhoff, Hamburg, Germany), and focused on the sample by a ×60 1.2NA water immersion objective (Plan Apo VC ×60 WI, Nikon, Germany). Average excitation powers of 5–10 microwatts were used and measured before the dichroic mirror (DualLine z532/635, AHF Analysentechnik, Munich, Germany) separating excitation and emission beam paths. The collected fluorescence was focused on a 50-μm pinhole (Thorlabs, Dachau, Germany) via the microscope tube lens. A polarizing beam splitter cube (AHF Analysentechnik) separated the two polarization planes followed by two identical emission filters (BrightLine HC 582/75, AHF Analysetechnik, Tübingen, Germany) for each polarization. Fluorescence was collected by two single-photon-counting avalanche photodiodes (×2 SPQR-16, PerkinElmer Life Sciences) and registered by two independent TCSPC data collection cards (SPC-154, Becker&Hickl, Berlin, Germany). The lasers and the data collection cards were synchronized by the laser controller (Sepia, Picoquant, Berlin, Germany). For the measurements, labeled actin was diluted to the designated concentration in G-buffer for nonpolymerizing conditions and F-buffer for polymerizing conditions, respectively, and measured in a Teflon sample holder with a glass coverslip. The photon-counting histogram data (32, 34) were analyzed using a bin width of 37.5 μs in a custom program written in MATLAB. For PCH analysis, 60 nm of atto532-labeled actin monomers were measured either in G- or F-buffer for 30 min. The solutions were preincubated for 60 min before the measurements were started to allow equilibration of the sample.

TIRF Microscopy and Analysis

Flow cells were made as a sandwich of a coverslip (20 × 20 mm), parafilm, and a cover slide. Flow cells were passivated by incubating them with 10% BSA in PBS for 10 min. Flow cells were washed three times with 90 μl of G-buffer. The tethering protein was then applied for 5 min and washed again three times with 90 μl of G-buffer. Actin was incubated for 5 min on ice with one-tenth volume of 10× ME buffer (MgCl₂ and EGTA) to exchange Ca²⁺ for Mg²⁺. Actin-containing solution was then mixed with imaging buffer (catalase, β-mercaptoethanol, glucose oxidase, d-glucose, 0.25% (w/v) methylcellulose, and one-tenth 10× KMEI buffer, with a final pH of 7.1) and introduced into the flow cell. TIRF microcopy was performed using a TILL photonics inverted microscope. Kymographs were made using Metamorph, and further analysis was done in MATLAB.

For length distribution measurements, actin was polymerized for 30 min, stabilized with Alexa488-phalloidin, and diluted 100× for imaging individual filaments on a poly-l-lysine-coated coverslip using an epifluorescence Zeiss microscope. Length measurements were done manually using ImageJ.

Rate Calculations

In general, protein-protein (e.g. A and B) complex formation (AB) is described by Equation 1,

where A·B is the transient complex defined with a separation and orientation close to the native complex but where short range interactions still have to be formed. k_D and k_−D are the diffusion-limited rate constant for transient complex formation and the reverse process, respectively. k_C and k_−C are the rate constants from the transient complex to tight native complex through conformational changes and the reverse process, respectively. The association rate constant, k_on, is then defined as k_Dk_C/k_−D + k_C. The dissociation rate constant, i.e. the off rate, k_off, is given by k_−Dk_C/k_−D + k_C. If the conformational rearrangement is very fast upon transient complex formation, it is said that the reaction is diffusion-limited or diffusion-controlled (i.e. when k_C ≫ k_−D).

To rationalize the experimental trends in the pH and salt concentration dependence of the rate constants, we make use of a simple generic theory. We assume the reaction is completely diffusion-controlled and isotropic, and the two reactive constituents A and B, say, two actin proteins or one dimer and one actin protein, can be effectively modeled as two spheres with size (diameter) σ_i = 2R_i, with i = A, B, where R is equal to 2.5 nm. The reaction size is then given by σ_AB = (σ_A + σ_B)/2. We further assume that the two spheres interact with an isotropic pair potential V_AB(r) for center-to-center distances r > σ_AB. The steady-state result for the diffusion-controlled rate constant k_D is then given by Equation 2 (35, 36),

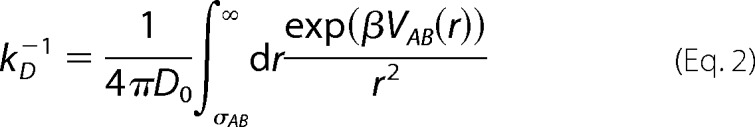where D₀ is the mutual diffusion constant between the reactants and is assumed to be given by Stokes relationship shown in Equation 3,

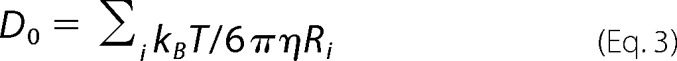in a solvent with viscosity η, and β = k_BT. As the proteins carry a (pH-dependent) net charge, the leading order interaction between the spheres can be modeled by the so-called DLVO potential (37) shown in Equation 4,

which is the sum of attractive dispersion interactions (V_disp) and the repulsive electrostatic double-layer interaction (V_dl). Higher order multipoles are neglected in our approach but can be included in principle in Equation 2 by resolving angular degrees of freedom in the integral. To a good approximation for short distances (r ≪ σ_AB),

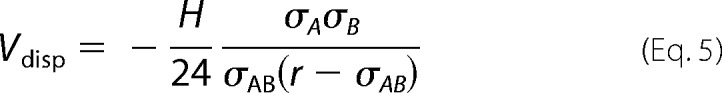where H is a material constant called the Hamaker constant and is typically between 3 and 10 k_BT values for proteins. We used H = 5 k_BT. The double layer interaction between two charged spheres in a solution with salt concentration c is given by Equation 6,

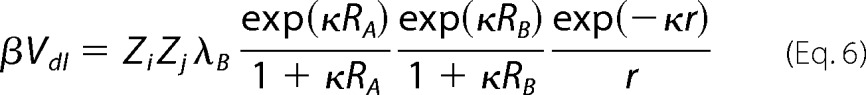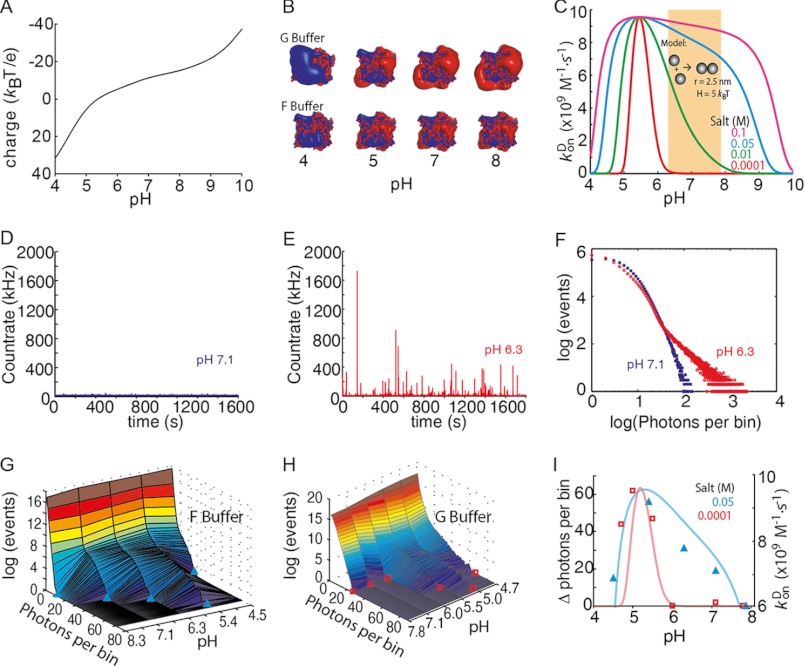
where λ_B = e²/4πϵ0 k_BT = 0.71 nm is the Bjerrum length in water, κ = √ ¯8 πλ_Bc the inverse (Debye-Hückel) screening length, and Z_i the valency of reactant i. In our case, Z_i = n_iz_i (pH), where n_i is the degree of polymerized actin of reactant i, for instance n_i = 2 for a dimer. The actin net charge z_i (pH) has been estimated by the Scripps APBS software for the actin protein structure (Protein Data Bank code 1J6Z) and is shown in Fig. 5. Actin has an isoelectric point at a pH ≃ 5.4. This analysis is very generic, and the trends with pH and salt should hold for every step during polymerization, i.e. dimerization, trimerization, etc., where the reactive size σ_AB has to be effectively adjusted. Quantitatively, the analysis ignores a few details such as anisotropic reactivity (the “patchiness”), hydrodynamic corrections to the diffusion constant, and rotational diffusion. These extensions will only slow down the reaction. Other refinements, such as a more accurate approximation of the dispersion interactions (Equation 3) or inclusion of multipoles, will also not change the calculated trends. At higher salt concentrations (above 0.1 m), nontrivial ion-specific effects may occur (38) as well as a reduction of any favorable electrostatically mediated interactions that stabilize filament formation (39). The observed maximal association rates at a pH of 6.3 (Fig. 5), which are higher than the predicted pI of actin at 5.4, may be due to the anisotropic reactivity of the monomer to a particular filament end.

FIGURE 5.

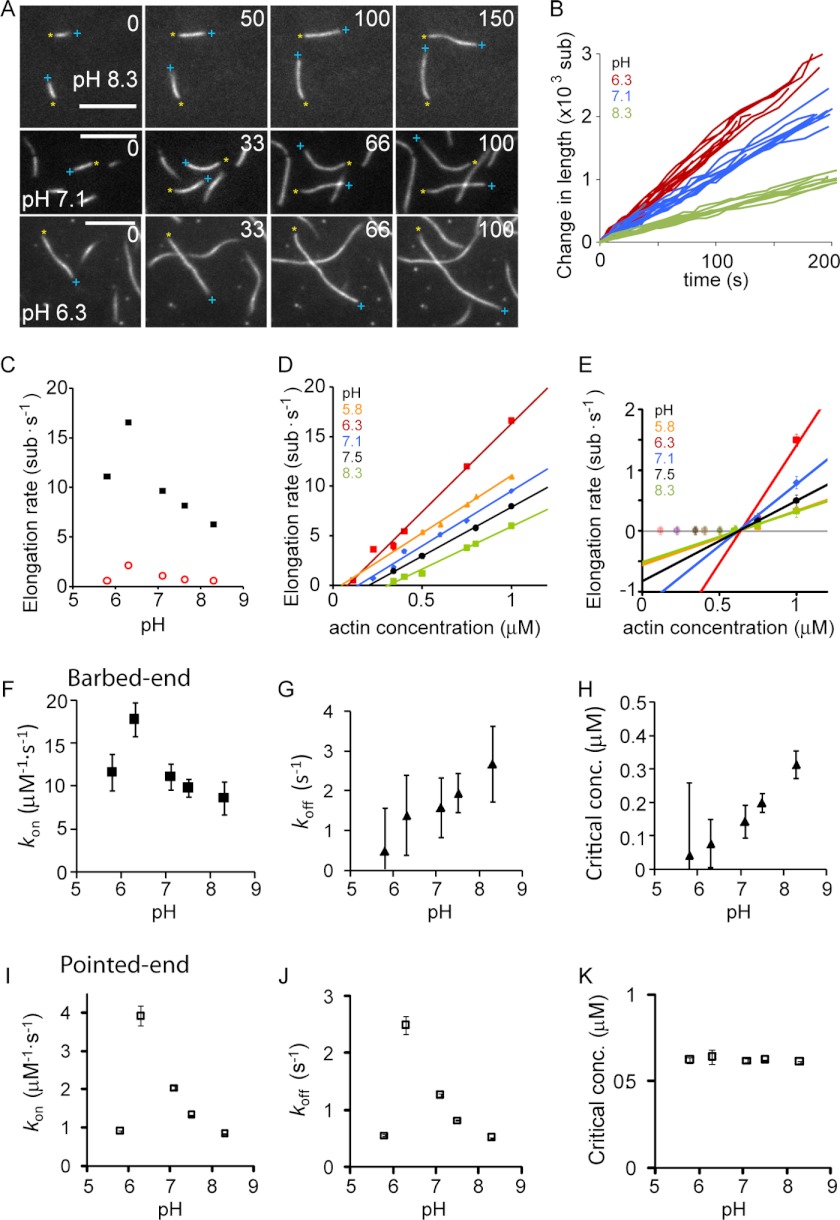
Dependence of actin filament elongation kinetics on pH. A, individual filaments (30% atto488-labeled) monitored with time using TIRFM at pH 8.3, 7.1, and 6.3. Barbed ends are marked by a blue plus sign, and pointed ends are marked by a yellow asterisk. All scale bars are 5 μm. B, change of filament length versus time for different filaments measured at the indicated pH values. C, elongation rate of barbed end and pointed end at 1 μm versus pH. Error bars are S.E. D, barbed-end elongation rate versus actin concentration for various pH values. E, pointed-end elongation rate versus actin concentration for various pH values. Only concentration points above 600 nm were used to estimate rate constants (see supplemental material for fits using all data points). F–H, rate constants of barbed-end elongation versus pH as follows: association rate (F), dissociation rate (G), and critical concentration (H). I–K, rate constants of pointed-end elongation versus pH as follows: association rate (I), dissociation rate (J), and critical concentration (K). F–K, error bars were determined from the propagation of errors from the linear fits of the data presented in D and E. At least 25 filaments were measured per condition.

Cell Line Construction and Listeria Infection

Lentiviral constructs of Lifeact-mEGFP were generated according to the protocol of Untergasser, using the ViraPower^TM II Lentiviral Gateway® expression system (Invitrogen). Cellular pH_i was determined using the fluorescent H⁺-sensitive dye 2,7-biscarboxyethyl-5(6)-carboxyfluorescein (Invitrogen) as described previously (40, 41). Listeria monocytogenes 10403S strain expresses red fluorescent protein (RFP) under the actA promoter (pactA-RFP). Upon entry of the bacteria into the cytosol of the host cell, transcription of RFP is up-regulated 200-fold (42). Hence, the expression of RFP in this strain correlates with entry of bacteria into the cytoplasm. Before infection with L. monocytogenes, cells were plated in MatTek dishes containing an inserted coverslip, maintained in growth medium for 24–48 h, then washed three times with PBS, and incubated with DMEM containing 10% FBS without antibiotics. A culture of L. monocytogenes incubated overnight at 30 °C was diluted 1:100 in PBS, and 5 μl of this dilution was added to the MatTek dishes and incubated for 8–14 h to achieve 90% infection. Just before imaging, the cells were washed two times with PBS and maintained in Hepes buffer (25 mm Hepes, 140 mm NaCl, 5 mm KCl, 10 mm glucose, 1 mm KP_i buffer, 1 mm MgSO₄, 2 mm CaCl₂, pH 7.4) for 2–3 min during imaging.

Imaging and Image Analysis of Listeria Motility

The pH-dependent motility of L. monocytogenes was tested using PSN and E266I fibroblasts cells. Cells were imaged at 37 °C using a ×100 objective on an inverted microscope system (Nikon Eclipse TE2000 Perfect Focus System; Nikon Instruments, Melville, NY), equipped with a spinning disk confocal scanner unit (CSU10; Yokogawa, Newnan, GA), 488-nm solid-state laser (LMM5; Spectral Applied Research, Richmond Hill, Canada), 561-nm solid state laser (MPB VFL-P-series), multipoint stage (MS-2000; Applied Scientific Instruments, Eugene, OR), a CoolSnap HQ2 cooled charge-coupled device (CCD) camera (Photometrics, Tucson, AZ), and camera-triggered electronic shutters controlled with NIS-Elements Imaging Software (Nikon). A single confocal plane of cells was imaged for 3 min, 1 image/s, with an exposure time from 50 to 100 ms for both 488 and 561 nm excitation. Forty six L. monocytogenes trajectories per cell line were tracked by the manual tracking command in the NIS elements software.

RESULTS

pH Affects Actin Polymerization

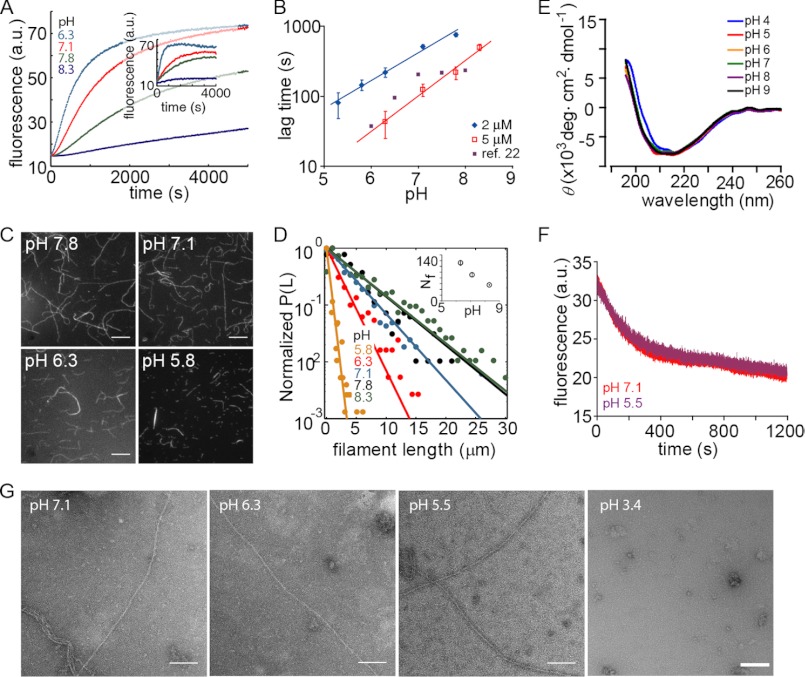
We studied the effect of pH on actin polymerization by measuring the increased fluorescence of pyrene-labeled actin. In agreement with previous reports (21, 22), we found that polymerization kinetics were sensitive to solution pH for both muscle (Fig. 1A) and non-muscle actin (Fig. 1A, inset). The duration of the lag phase under standard polymerization conditions (i.e. 50 mm KCl and 2 mm MgCl₂) exhibited a nonlinear relationship with pH (Fig. 1B), suggesting an effect on nucleation. Previous data in the presence of 2 mm MgCl₂ only (22) showed a similar power law dependence of the lag phase for a narrow pH range (Fig. 1B). The filament length distribution, observed 30 min after the start of polymerization, revealed an increase in number and decrease in length of filaments at lower pH (Fig. 1, C and D, and inset of D). This suggests an effect of pH on nucleation, as faster nucleation would be expected to lead to more and shorter filaments as monomers are consumed faster.

FIGURE 1.

pH dependence of actin polymerization. A, polymerization kinetics of 2 μm muscle actin (20% pyrene-labeled) at different pH values. Inset, non-muscle actin (2 μm total) with 1% muscle actin pyrene-labeled. B, estimated lag time versus pH for 2 and 5 μm actin. Red and black lines are power law fits with exponents 0.9 (black) and 1.1 (red) and comparison for previously reported data (filled squares) (22). The filled squared data points are taken from Zimmerle and Frieden (22) who measured 10 μm actin in 1.8 mm Mg²⁺ and 200 μm Ca²⁺, in contrast to our values of 50 mm KCl and 2 mm MgCl₂. C, individual actin filaments polymerized at the indicated pH value. They were stabilized and labeled with Alexa488-phalloidin after polymerization and visualized on a 0.05% polylysine-coated coverslip. D, normalized probability of filament length for actin polymerized at various pH values (>1000 filaments were measured under each condition). Inset, filament number (N_f) measured as a function of pH. Error bars represent S.E. and are within symbol size. E, far-UV circular dichroism measurements with 5 μm actin in P-buffer with pH values between 4 and 9 (see under “Experimental Procedures”. No significant structural change was observed above pH 5. F, 85% pyrene-labeled muscle actin depolymerized in pH 7 buffer after 2 h of polymerization at pH 7.1 (red) or pH 5.5 (purple). G, electron microscopy of actin filaments polymerized at the indicated pH values. a.u., arbitrary units. Scale bar, 100 nm.

One possible explanation for the observed effects is that low pH, especially at values close to the pI of actin, promotes irreversible actin denaturation and aggregation instead of reversible actin polymerization. However, when varying the pH between 5 and 9, we found no significant effects on the overall fold and secondary structure of monomeric actin as measured by circular dichroism (Fig. 1E). In addition, filaments grown at pH 5 or 7 for 2 h exhibited no significant difference in depolymerization assays (Fig. 1F), suggesting that pH does not induce structural changes during filament formation. Finally, individual actin filaments grown at pH 5–7 did not show obvious differences when visualized by negative stain electron microscopy, whereas acid-unfolded actin did not form any filaments (Fig. 1G). Hence, we concluded that the pH effects on actin polymerization between pH 5 and 9 did not originate from structural changes in actin or actin filaments, and thus we investigated the effects of pH on the reaction kinetics.

Spontaneous Nucleation of Actin Filaments Increases with Decreasing pH

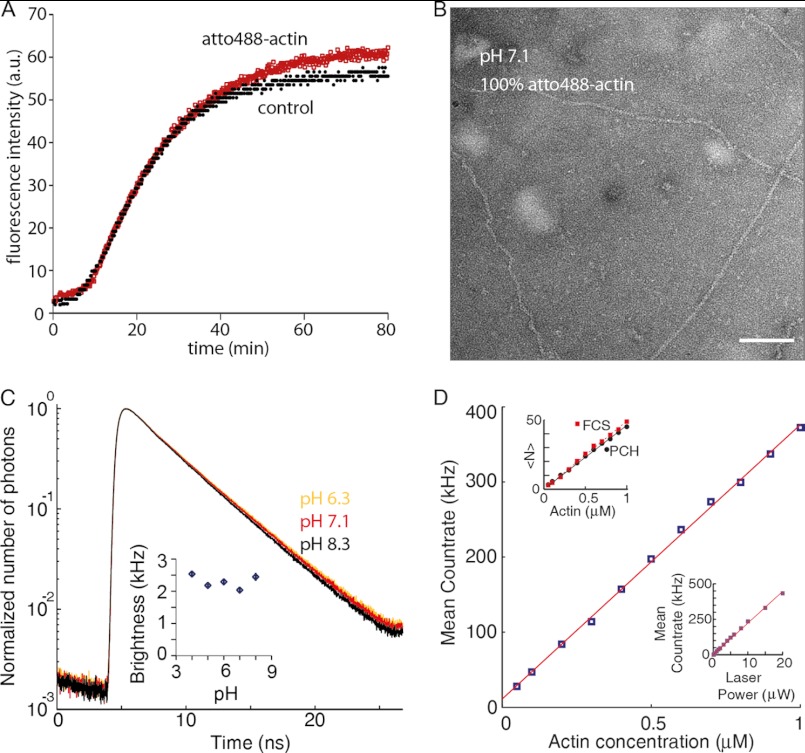
Actin nucleation and its regulation have mostly been studied using bulk assays such as pyrene fluorescence (Fig. 1, A, C, and D), which only provide an indirect measure of polymer mass without resolving individual species. To obtain a more direct readout of actin nucleation, we applied various fluorescence fluctuation spectroscopy (FFS) methodologies. FFS techniques have single molecule sensitivity, high temporal resolution, and can be performed with dyes that, in contrast to pyrene, are pH-insensitive (Fig. 2C) (22). FFS techniques such as fluorescence correlation spectroscopy (FCS) utilize a very small observation volume (∼1 fl in a diffraction-limited focus of a confocal microscope (Fig. 3A)) to detect individual and interacting single molecules (43, 44). A practical limitation in the use of fluorescently labeled actin is its overall lower polymerization capacity when labeled at Cys-375 (45). We therefore used lysine-labeled actin (46). Labeling of the actin did not affect polymerization kinetics or filament structure (Fig. 2, A and B).

FIGURE 2.

Photophysical characterization and polymerization capacity of atto488-labeled actin. A, 2 μm total actin, of which 5% is pyrene-labeled actin, was polymerized under standard conditions in the presence of 95% unlabeled actin (control) or 100% atto488-labeled actin (atto488-actin). B, negative-stain of 100% atto488-actin was polymerized for 1 h and then applied to an EM grid. C, normalized photon count of 400 nm atto488-labeled actin in F-buffer at pH 6.3 (yellow), 7.1 (red), and 8.3 (black). The fluorescence lifetimes are 3.97 ± 0.01, 4.32 ± 0.02, and 4.39 ± 0.02 ns, respectively. Inset, brightness of atto488 measured at 10 microwatts determined using PCH (32). Bars represent S.E. of three independent measurements. D, there is a linear relationship between the actin concentration and the mean count rate; upper inset, the mean number of molecules in the observation volume 〈N〉 (as determined by PCH or FCS) versus actin concentration are shown. Lower inset, the laser power and the mean count rate at 100 nm atto488-actin. a.u., arbitrary units.

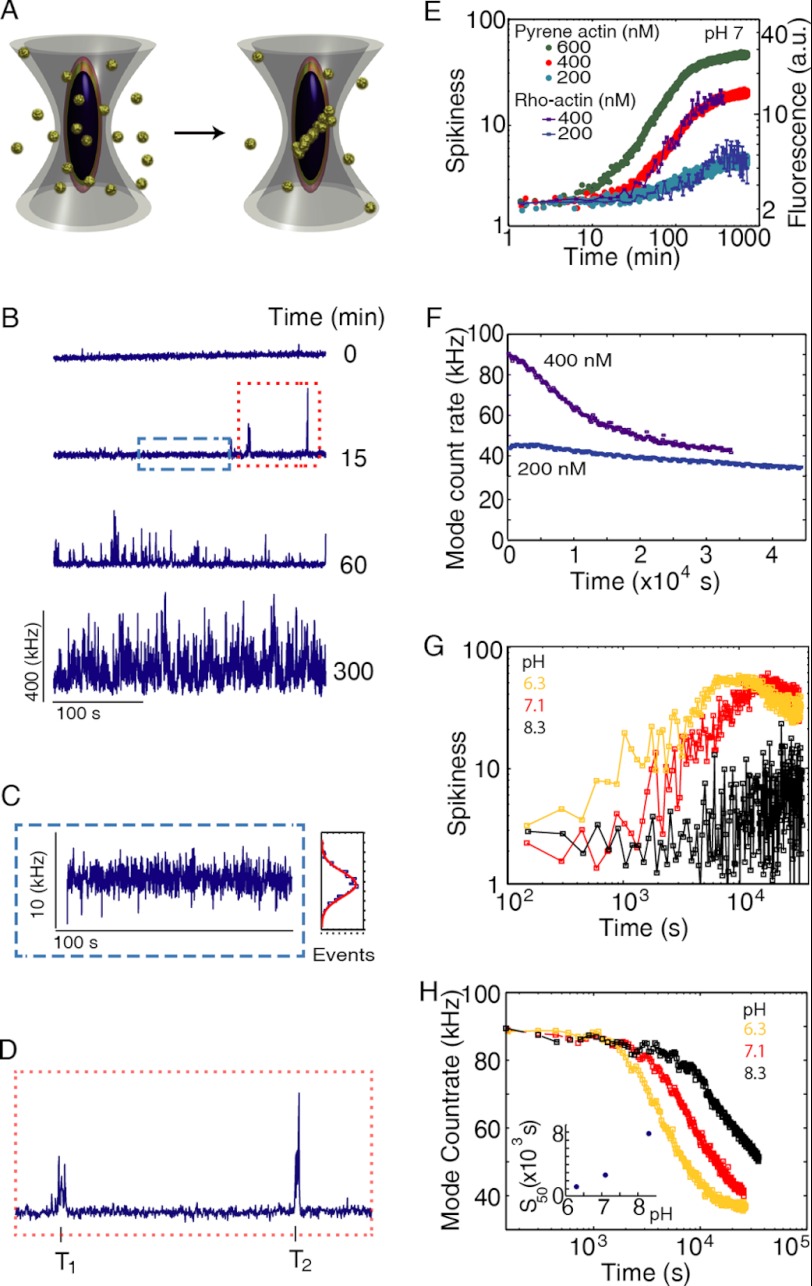
FIGURE 3.

Monitoring actin polymerization dynamics with fluorescence fluctuation spectroscopy. A, schematic of the experiment. Actin molecules, each labeled with a single atto488 fluorophore (i.e. 95% labeled), are free in solution as monomers and filaments. The fluorescence intensity will fluctuate as the particles diffuse through the observation volume. B, fluorescence intensity arising from the sample as a function of time after polymerization. Filaments form as a function of time after the start of polymerization. As filaments contain multiple-labeled actin molecules, they will be observed as a spike in fluorescence intensity. 400 nm atto488-labeled actin was polymerized by the addition of one-tenth volume of 10× KMEI at pH 7.1. C, zoom in of the blue box from B. At 1 s temporal binning, the fluorescence signal is absent of spikes and is well described by a Gaussian distribution of intensities with a standard deviation σ. D, zoom in of the red box from B showing the first two spikes. Each individual spike has associated an arrival time T, a duration time, and a number of photons. E, spikiness (i.e. percentage of counts >3σ) versus time for 200, 400, and 600 nm. Shown on the right axis is the pyrene fluorescence increase for a similar concentration of actin. F, mode of counts versus time showing the decrease in monomer concentration upon filament formation. G, spikiness of polymerization at three different pH values. H, decrease of the mode versus pH (data from supplemental Fig. S1, A–C). Inset, time that has elapsed between beginning of the experiment and appearance of the first 50 spikes in seconds as a function of pH.

The fluorescence of a sample containing 400 nm of atto488-labeled actin was monitored over time after the addition of salts to initiate polymerization (Fig. 3B). After a period of time, spikes appeared due to fluorescently labeled actin filaments diffusing through the focal volume. Without filaments, the fluorescence signal fluctuated due to thermodynamic fluctuations in the number of monomers within the observation volume, which is given by δN (Fig. 3C). For a Poisson distribution, δN is proportional to √N̄, where N̄ is the average number of molecules in the confocal spot (47), and the mode of the count rate is related to the monomer concentration in solution (Fig. 2D). When a filament is diffused through the observation volume, the fluorescence intensity increased well beyond what was observed due to the statistical fluctuations in monomer concentration (Fig. 3C) and was detected as a spike (Fig. 3, B and D). With time, spikes became more frequent and increased in amplitude (Fig. 3B). The initial delay from the start of polymerization to the appearance of the first spikes resembled the lag phase observed in pyrene assays. To compare our results with those from standard pyrene assays, we defined the spikiness of the measurement as the percentage of counts with values higher than three standard deviations beyond the mode of the signal (Fig. 3D). Curves of spikiness over time closely resembled the sigmoidal shape of pyrene assays (Fig. 3E). The beginning of the experiment was spike-free, followed by the appearances of spikes that increased in number and size over time (Fig. 3, B and C), while the mode (i.e. monomer concentration) decreased with time (Fig. 3F). The monomer concentration continued to decrease until it reached the critical concentration, making it possible to directly determine the critical concentration in a single measurement.

Visual inspection of the raw data for several pH values already revealed a strong effect of pH on actin polymerization (supplemental Fig. S1, A–C). There was a faster appearance of spikes at lower pH (Fig. 3G). At pH 6.3, there was practically no lag phase observed while, at pH 8.3, the lag phase lasted for more than an hour (Fig. 3G). Monitoring monomer concentration revealed the existence of lag phase at all pH values measured (Fig. 3H). The duration of the lag phase in monomer concentration was also shorter with lower pH (Fig. 3H). It is interesting to note that the lag phase, as estimated from both polymer mass and monomer concentration, was not devoid of filaments. For example, at pH 7, the first filaments were observed around 500 s, whereas the lag phase lasted for ∼1000 s (Fig. 3, E–H, and supplemental Fig. S1, A–C).

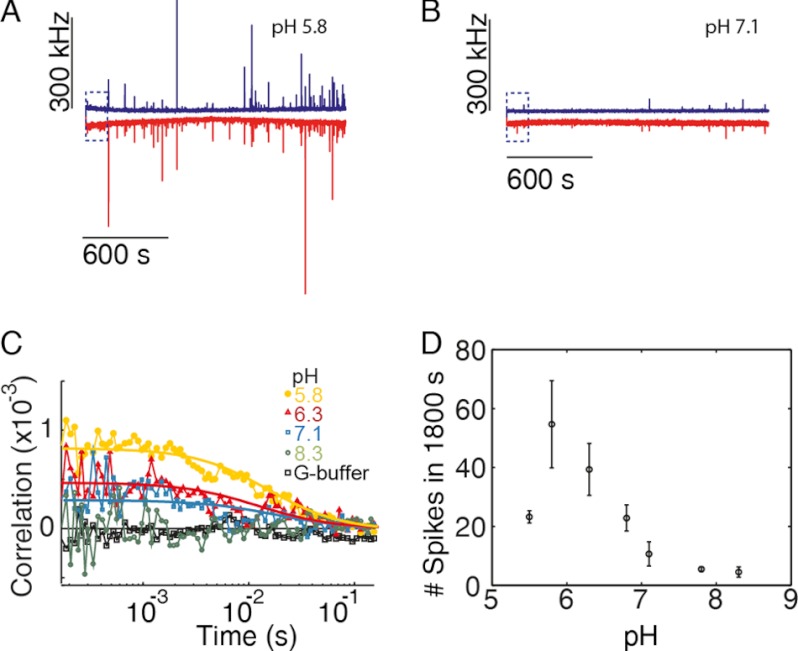
To further investigate the origin of the faster kinetics at lower pH, we performed fluorescence cross-correlation spectroscopy with a mixture of atto488- and atto647-labeled actin. The presence of dual-color-labeled complexes reveals the existence of actin filament nuclei and short oligomers. Measurements were performed at 80 nm of each labeled species of actin (total actin concentration of 160 nm), which is just above the critical concentration of actin at pH 7 (∼150 nm). Spikes appeared coincidently in the two different detection channels as the filaments assembled and incorporated actin monomers with the different labels (Fig. 4). At a pH of 5.8, larger multiple two-color coincident spikes were observed within minutes after the initiation of polymerization (Fig. 4A). In contrast, fewer coincident spikes were observed at pH 7.1 (Fig. 4B). Cross-correlation analysis of the data collected using pulsed-interleaved excitation (33) during the very early times (spike-free) of the lag phase revealed larger amounts of double-labeled complexes prior to filament emergence at lower pH values (Fig. 4C). A rough estimate of the amount of double-labeled complexes suggests that there is at most one complex out of 100 molecules at the highest cross-correlation amplitude observed, at pH 5.8. The amount of filaments formed (i.e. the number of spikes detected) within the first 15 min after the start of polymerization is shown in Fig. 4D as a function of pH and has a maximum at pH 5.8. Therefore, pH modulates the kinetics of nuclei formation, which gives rise to filaments (Fig. 4, A and B).

FIGURE 4.

Actin nucleation is pH-sensitive. 80 nm atto488- and atto647-labeled actin (95 and 50% labeled, respectively) were mixed, and polymerization was started by addition of one-tenth v/v of 10× KMEI buffer. A and B, count rate for the first 1800 s of polymerization at pH 5.8 (A) and 7.1 (B) are shown. Blue indicates the signal from the blue detection channel, and red indicates the signal from the red channel. C, cross-correlation curves from the first 150 s of the above measurements. Solid lines are fits to a single diffusion species in a three-dimensional Gaussian volume to guide the eye. A control sample was measured using G-buffer, where no polymerization occurs. D, number of spikes versus pH during the first 15 min after initiation of polymerization. The error bars are the S.D. from three independent measurements.

Barbed-end and Pointed-end Elongation Rates Are Sensitive to pH

To determine whether pH also affects actin elongation, we visualized individually growing actin filaments by TIRFM. At 1 μm actin and at pH 7.1, we observed that one filament end elongated at ∼11 sub·s⁻¹ whereas the other end grew with a rate of ∼1 sub·s⁻¹. Therefore, we designated the faster growing end as the barbed end and the slower one as the pointed end. We found that pH strongly affected the elongation rates (Fig. 5, A and B). Filaments grew faster at both ends with decreasing pH, until they reached a maximal extension rate at pH 6.3 (Fig. 5C). Below this value, elongation again became slower (Fig. 5 C).

Next, we determined association and dissociation rates at both filament ends by measuring elongation rates at different actin concentrations (Fig. 5, C–E). The slope of the elongation versus concentration curve corresponds to the association rate k_on in sub·μm⁻¹·s⁻¹ (Fig. 5, F and I); the y axis intercept corresponds to k_off in sub·s⁻¹ (Fig. 5, G and J), and the x axis intercept corresponds to the critical concentration (C_c) (Fig. 5, H and K), where there is neither growth nor disassembly. The association rates for barbed ends mimicked the pH dependence of overall elongation (Fig. 5, C and F) with a maximal rate around pH 6.3. In contrast, the dissociation rate increased with pH (Fig. 5G) leading to higher critical concentrations with increasing pH (Fig. 5H).

Interestingly, a close look at the pointed end elongation rates revealed no significant growth or shrinkage at actin concentrations below ∼600 nm (see also Ref. 45). This pausing of depolymerization has been linked to light-induced effects (48), and hence, we decided to exclude data points below 600 nm from our analysis. An analysis including all data points did not yield qualitatively different results and is shown in supplemental Fig. S2 for comparison. At concentrations above 600 nm, both the association (Fig. 5I) and dissociation rates (Fig. 5J) for the pointed end followed the overall elongation rate (Fig. 5C), whereas the critical concentration was pH-independent and remained at 600 nm (Fig. 5K). In summary, our results imply that, in contrast to previous predictions that electrostatics determine filament asymmetry by differentially influencing monomer association at filament ends (26), pH rather exhibits a differential influence on monomer dissociation rates. Electrostatics contribute, but do not determine, actin filament asymmetry.

pH-dependent Electrostatics Control Actin Polymer Formation

Next, we wanted to know whether the sensitivity of monomer association rates to pH is consistent with the general predictions for typical diffusion-controlled reactions. The net charge of a protein is determined directly by the pH of the solution (Fig. 6A). At low salt concentrations (G-buffer), the electrostatic potential reduces monomer-monomer contact formation (Fig. 6B). With increasing salt concentration, the electrostatic potential is better screened, and polymerization is facilitated (Fig. 6B). A generic model of protein-protein association provides a way of rationalizing the observed pH effects. Assuming isoreactive spheres (5 nm in size), an attractive potential of 5 k_BT values, and a homogeneous charge distribution, the diffusion-limited on-rates can be calculated as a function of pH and salt concentration (Fig. 6C). With this simple model, two trends are visible. First, the diffusion-limited k_on has a maximum at the isoelectric point where charge repulsion completely vanishes. Second, as the salt concentration increases, the charge repulsion (Equation 6) is more efficiently screened, and the reaction rate increases considerably even for pH values far from the isoelectric point. At high salt concentrations (c = 0.03 m and above), the pH dependence flattens out, and actin polymerization becomes practically pH-independent. This generic model already reproduces the overall trend observed for monomer association rates as a function of pH (Fig. 5). Also, it predicted that even in the absence of salt, polymerization can occur at pH values close to the pI value of actin.

FIGURE 6.

pH-dependent actin electrostatics control polymer formation. A, protein net charge prediction from the atomic structure of muscle actin (Protein Data Bank code 1J6Z) as a function of pH using the protein calculator (see The Scripts website). B, electrostatic map made with the Adaptative Poisson-Boltzmann Solver visualized with PyMOL. Isosurfaces displayed are 2 kT/e in blue and −2 kT/e in red. C, diffusion-controlled k_on for dimer formation with actin's pH-defined net charge determined using isoreactive spheres as an approximation for the actin interactions. The orange-shaded region indicates the physiological pH range (see text). D, fluorescence intensity trace for 60 nm atto532-actin in F-buffer at pH 7.1. E, fluorescence intensity trace for 60 nm atto532-actin (80% labeled) in F-buffer at pH 6.3. F, photon-counting histogram analysis (with 1-ms bin size) of the traces shown in D and E. G and H, photon counting histogram versus pH in F-buffer (G) and G-buffer (H). I, difference of the maximum number of photons per bin detected during a measurement at given pH with respect to the measurement at pH 8.3. The light solid curves are taken from C for the same salt concentrations for comparison with its association rate axis on the right.

To further explore our model, we performed a PCH (32, 34) analysis of our fluorescence fluctuation spectroscopy data (Fig. 6, D–F). A histogram of photon counts (with 1-ms bin size) directly revealed the effect of pH on the polymerization process (Fig. 6F). The PCH results at pH 6.3 agreed with the data determined from bulk and TIRF measurements (Figs. 1 and 4). However, in contrast to pyrene assays, we could measure at pH values below 6, and in contrast to the surface-restricted polymerization in TIRFM assays (Fig. 5C), maximal polymer mass generation in solution was observable at pH 5.4 (Fig. 6G), close to the calculated pI of actin. In the absence of salts (G-buffer), we did not observe any polymer above pH 5.5 (Fig. 6H). The predicted trend of association rates from our model therefore closely coincided with the observed polymer formed in solution at different salt concentrations (Fig. 6I). In conclusion, our results therefore suggest that polymer formation can be controlled by electrostatics.

pH_i Modulates Actin-driven Pathogen Motility in Vivo

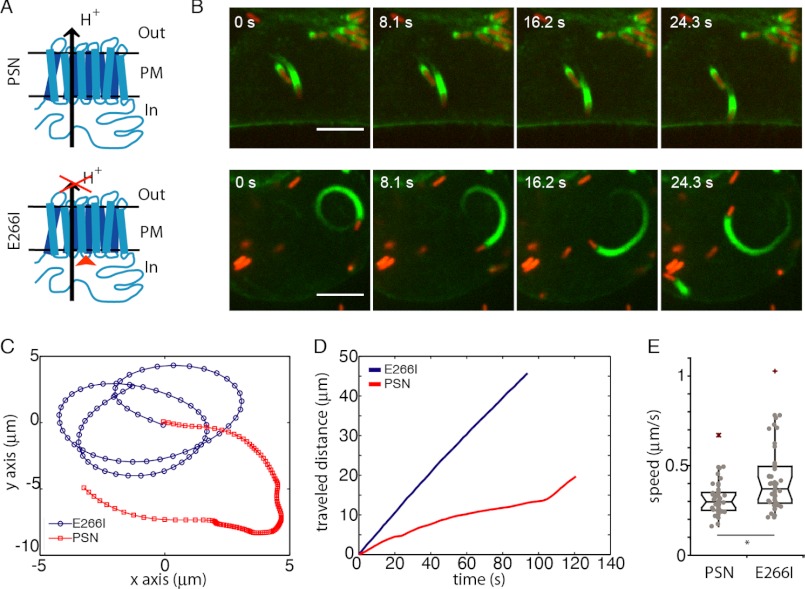
Finally, we asked whether the observed effects in vitro could provide insight into processes observed under more physiological conditions. To this end, we tested the cellular pH dependence of L. monocytogenes motility. Listeria is a bacterial pathogen that hijacks the host actin cytoskeleton to move through the cytoplasm and escapes immune response by spreading from cell to cell without extracellular exposure. Listeria cells express ActA, an activator of the Arp2/3 complex, which then nucleates actin filaments at the surface of the bacteria, resulting in ‘comet tails’ composed of actin filaments that propel the bacteria forward (51). The intracellular speed of Listeria correlates directly with the rate of actin polymerization in cells (3), making it a direct readout of effects on actin polymerization. We determined velocities of moving Listeria in clonal fibroblasts with different pH_i values as follows: NHE1-deficient fibroblasts engineered to stably express either wild-type NHE1 (PSN) with a resulting cytosolic pH of 7.4 or an inactive NHE1 mutant (E266I) resulting in a lower pH_i value of 7.1 (Fig. 7A) (11). In addition, both cell types stably expressed the actin marker Lifeact-GFP (31) for visualization of the Listeria-induced actin comet tails. Listeria internalization was visualized by ActA-RFP expression once they entered the cytosol (Fig. 7B). We measured velocities for individual trajectories in both cell lines (Fig. 7, B–D). The average transport velocities increased from 0.31 ± 0.03 μm·s⁻¹ in PSN control cells to 0.42 ± 0.04 μm·s⁻¹ for E266I cells (mean ± S.E., n = 46 each, p < 0.01, Fig. 7E). This change, of ∼20%, of Listeria actin-driven motility in fibroblasts agrees well with the change in elongation measured in vitro, also of ∼20% (Fig. 5).

FIGURE 7.

Effect of pH_i on actin polymerization-driven motility of L. monocytogenes. A, schematic of NHE1 and the point mutation that blocks ion translocation of NHE1 while maintaining its ability to interact with adaptor proteins through its long cytoplasmic tail and thereby bind to the cytoskeleton. PM refers to the plasma membrane, Out to the extracellular space, and In to the cytosol. B, single bacteria moving in either a PSN cell (red) (upper panels) or an E266I cell (lower panels). Scale bar, 5 μm. C, representative trajectories of bacterial transport in PSN cells and E266I cells (blue). D, traveled distance as a function of time for the trajectories shown in C. E, boxplot of L. monocytogenes speeds in PSN or E266I cells. n = 46 for each condition, *, p = 0.009.

DISCUSSION

We performed an extensive evaluation of the direct pH effects on the polymerization of actin and actin assemblies, independent of actin regulatory proteins. By using a combination of bulk fluorimetric measurements, single filament TIRFM analysis, and FFS methods, we were able to reveal mechanistic details on actin filament nucleation and elongation and explain the observed pH effects with a simple model of electrostatic protein-protein interaction.

Nucleation

Here, we have introduced the use of FFS techniques to study actin nucleation. In its simplest application (i.e. spikiness), FFS data provide an equivalent readout to the established pyrene method with the typical sigmoidal polymerization kinetics. In addition, FFS provides direct information on monomer concentration (i.e. the mode of the count rate) and can be applied over long time scales and a wide range of pH values. Using FFS techniques, we found a strong effect of pH on nucleation. The high sensitivity of FFS clearly showed that short filaments already form during the lag phase of polymerization. This is predicted by the kinetic model for actin polymerization (52, 53) but had not been detected experimentally. The early existence of such rapidly elongating filaments leads to a direct competition with newly forming nuclei, a critical aspect of the nucleation-elongation model (53). Using fluorescence cross-correlation spectroscopy, we were able to detect actin complexes formed prior to filament appearance, suggesting that these species represent the actual polymerization nuclei. Our findings that nuclei are present preceding filament emergence agree with and support the expectations based on pyrene experiments (52, 53). Finally, something that also became obvious from using ultrasensitive FFS techniques (in particular at low molecule concentrations) is that extensive actin polymerization dynamics occur below the critical concentration. Hence, FFS opens up new possibilities for elucidating mechanisms of nucleation.

Elongation

Using TIRFM on single elongating actin filaments, we determined the effect of pH on the association and dissociation rates at both filament ends. Barbed-end elongation is known to be a diffusion-controlled reaction (25). Consistent with this idea, we find that net charge modulation by pH determines barbed-end growth kinetics. In contrast to a previous suggestion that the removal of electrostatic forces would lead to an inversion of filament asymmetry (26), we observe that barbed-end and pointed-end growth kinetics are affected similarly by pH (Fig. 5, F, G, I, and J). This is largely due to effects on monomer association rates, which are strongly regulated by pH (implying a role of surface charge). In contrast, we find that dissociation of monomers is differentially affected by pH. At the barbed end, k_off increases with pH, whereas the dissociation rate at the pointed end follows the overall elongation as a function of pH.

If elongation is faster at lower pH, why then are filaments at pH 6.3 shorter than those at pH 7.8 (Fig. 1, C and D)? To better understand this effect, we performed simulations using our experimentally obtained kinetic parameters (supplemental Fig. S3). At early times, the faster elongation kinetics at low pH dominates and leads to the expected longer filaments. However, monomers are depleted faster. At later time points, once the monomer pool has been depleted, dissociation and fragmentation become relevant, leading to a reduced average filament length (supplemental Fig. S3). Therefore, the observed length distributions (Fig. 1, C and D) reflect the measured trend in dissociation rates and not only the change in nucleation.

Our results indicate that electrostatics do contribute to filament asymmetry but not via monomer association rates as suggested by Sept et al. (26). In addition, we observed very little pointed-end growth or shrinkage at low actin concentrations. This could be due to a “closed” conformation as suggested by a recent structural study (54). Future work will elucidate whether this closed state is due to the presence of lattice-binding proteins, such as N-ethylmaleimide-myosin (29), a light-induced effect (48), or is indeed related to a conformational transition (54). In summary, we find that electrostatics regulates the diffusional encounter to both filament ends, with monomer binding at the pointed end likely involving an extra step (25).

Electrostatics

The strong pH dependence of polymerization suggests an important role of electrostatic forces in filament formation. Consistent with this hypothesis, we found that screening of charges by the addition of salt increased the association rate for actin (Fig. 6). A similar explanation for the effect of salt on actin was proposed more than 50 years ago (55, 56). By using a generic theoretical model, we were now able to quantitatively correlate effects of pH and salt. Hence, polymerization of actin can either occur in the presence of sufficient amounts of screening salts or if the net charge is reduced, i.e. close to the pI of actin. Interestingly, salt has been reported to have a nonmonotonic effect on actin polymerization; at high salt concentrations, the elongation rate decreases monotonically with increasing salt (25). This is possibly due to a reduction of intra-strand contacts that mostly consist of salt bridges (57). Conversely, at low salt concentrations, screening allows inter-strand contacts to be formed, which are largely based on hydrophobic interactions (57). Altogether, our results explain the overall polymerization response to pH within a general framework of electrostatic forces and provide a basis to understand the nonspecific effects of salt on actin polymerization.

Implications within a Cellular Environment

We performed an extensive analysis of pH effects on polymerization of pure actin. However, actin in cells always functions within complex assemblies that are regulated by a vast number of modulating factors. Along this line, we have recently found that the mechanical properties of actin networks cross-linked by either cortexillin or filamin can be tuned by pH (49). Interestingly, the pH sensitivities of various cross-linkers are very different from each other (49). This diversity could help to regulate mechanical properties of local cellular environments such as stress fibers, lamellipodia, or the isotropic actin cortex. In this way, a cell could modulate its mechanical properties and contractility by locally changing its pH_i values (50) in time scales that are only limited by proton diffusion within the cytoplasm. For dynamic processes that are determined by the rate of actin polymerization, such as cell migration or bacteria moving through the cytosol, changes in pH_i could be expected to have a direct effect. Indeed, we found that velocities of Listeria in fibroblast were higher at lower pH_i values (Fig. 7), which agrees with the increased polymerization rates of actin measured in vitro. In contrast, the increased motility and metastatic capacity of cancer cells with an increased pH_i (20) are likely dominated by pH-sensitive actin regulators, such as cofilin (8). Careful evaluation of all involved regulators will therefore be required to fully understand the effects of pH on the complex machinery generating cellular motion and how it is harnessed by cancer cells. So far, our results suggest that actin polymerization-driven cellular processes will be sensitive to the pH_i and suggest that pH modulation can be used to finely tune the intracellular environment to promote and assist the vast variety of cellular behaviors.