The changing landscape of functional brain networks for face processing in typical development

Abstract

Greater expertise for faces in adults than in children may be achieved by a dynamic interplay of functional segregation and integration of brain regions throughout development. The present study examined developmental changes in face network functional connectivity in children (5–12 years) and adults (18–43 years) during face-viewing using a graph-theory approach. A face-specific developmental change involved connectivity of the right occipital face area (ROFA). During childhood, this node increased in strength and within-module clustering based on positive connectivity. These changes reflect an important role of the ROFA in segregation of function during childhood. In addition, strength and diversity of connections within a module that included primary visual areas (left and right calcarine) and limbic regions (left hippocampus and right inferior orbitofrontal cortex) increased from childhood to adulthood, reflecting increased visuo-limbic integration. This integration was pronounced for faces but also emerged for natural objects. Taken together, the primary face-specific developmental changes involved segregation of a posterior visual module during childhood, possibly implicated in early stage perceptual face processing, and greater integration of visuo-limbic connections from childhood to adulthood, which may reflect processing related to development of perceptual expertise for individuation of faces and other visually homogenous categories.

1. Introduction

Infants show a preference for the face versus other stimuli soon after birth (Johnson, 2005) and some aspects of face processing are present in rudimentary form as early as 3 months of age (Hayden et al., 2007). However, face processing improves throughout childhood and adolescence (Ellis et al., 1973). Carey and Diamond (1994) posited a qualitative developmental shift in the processing of faces—from a reliance on featural processing in early childhood to a reliance on configural information later in life and other studies have supported this idea (Carey and Diamond, 1977; Diamond and Carey, 1977; Freire and Lee, 2001; Mondloch et al., 2002; Mondloch et al., 2006; Schwarzer, 2000). However, this issue has been debated more recently based on evidence that even 4-year olds may be as sensitive as adults to configural information in faces (McKone and Boyer, 2006; Pellicano et al., 2006).

Although Carey and Diamond (1977) postulated that the developmental shift from featural to configural processing around age 10 may rely on maturation of the right hemisphere, surprisingly little research has investigated the brain basis of typical face processing development. The “fusiform face area” (Kanwisher et al., 1997) is functional in both adults and older children but not in children younger than 7-to-8 years of age (Gathers et al., 2004; Passarotti et al., 2003; Scherf et al., 2007). Also, there is an increase in the fine tuning of the FFA for faces with development (Aylward et al., 2005b; Golarai et al., 2007; Scherf et al., 2007). Although these studies report changes in the developing brain for face processing, the mechanism for increased specialization has not been addressed.

The Interactive Specialization (IS) account of brain development (Johnson, 2005) suggests that cortical specialization results from activity-dependent interactions among regions, rather than developmental changes only in specific circumscribed regions, which has been the focus of most developmental fMRI studies to date. Functional or effective connectivity analyses are ideal for studying the developing brain, and for testing the IS account in particular, because they emphasize the functional interactions among brain regions. These analyses capture higher-level information about brain activation by exploiting the temporal synchrony among multiple brain regions (Bullmore et al., 2000). This type of information is critical for studying the developing brain in which a high degree of functional and anatomical plasticity is occurring.

Surprisingly, no fMRI functional connectivity analyses of typical development of face processing have been conducted. However, Cohen, Kadosh et al. (2011) conducted a developmental effective connectivity study of face processing using dynamic causal modeling. They showed that connectivity of three regions of the core face network (fusiform, inferior occipital and superior temporal gyri) was modulated by task demands in adults but not in children. In other words, these three regions interact differently for face identification, detection of expression and eye gaze in adults but not in children. Effective connectivity analyses reveal how brain regions may interact and influence each other, but these models are often restricted to just a handful of brain regions. In contrast, functional connectivity analyses, as used in the present study, can examine connectivity within a more extended network. This could then lead to more directed models to be explored with effective connectivity analyses.

Compared to other functional connectivity approaches, a graph theory approach (Rubinov and Sporns, 2010, 2011) to functional connectivity has the advantage of providing both global (i.e., network-wide) and local (i.e., specific node- or edge-based) measures of connectivity. Seed-based functional connectivity, for example, determines which voxels are functionally connected to a particular seed voxel, or a voxel within a functionally significant brain region (e.g., a voxel in the mid-fusiform gyrus might serve as a seed voxel to assess connectivity for face processing; Kleinhans et al., 2008). The resulting connectivity map gives a first-order description of connectivity with respect to only the seed voxel. However, graph theory metrics consider all of the possible connections among the nodes of network (where nodes are brain regions), thereby describing higher order properties of connectivity. For example, a seed-based analysis describes the strength of the connection between a voxel and a seed usually as the correlation coefficient of the two time series. With graph-theory, a particular node’s strength is based on a combination (usually the sum) of the correlation coefficients for all possible connections between that node and other nodes. In addition, some graph theory metrics can characterize the degree of integration and segregation of functional brain modules, which is particularly relevant for understanding brain development (e.g., Fair et al., 2007a).

In the present study, we examined several measures of network connectivity that are suited specifically for functional brain networks, which are described by Rubinov and Sporns (2011) as fully connected networks with connections that are weighted and signed (i.e., have both positive and negative weights). Nodes refer to brain regions and edges refer to the connections between nodes. In the present context, a “connection” refers to the magnitude of the correlation of the time-varying fMRI signal between two regions. The correlation coefficient is the weight of the connection (which can be signed). All of the graph theory metrics used in the present study are derived from a correlation matrix that captures the full connectivity in the network. In other words, connections among all regions are used in computing graph theory measures. To assess degree of segregation and integration over development, we examined several measures: strength, modularity / number of modules, clustering coefficient and diversity coefficient. The strength of a node simply reflects the sum of the weights of the edges for that node. Greater strength implies stronger connectivity with brain regions which may facilitate stronger functional integration (Rubinov and Sporns, 2010). Modules are subsets of regions in which the number or strength of connections within the module is maximized and number or strength of connections with other modules is minimized. Modules can be thought of as sub-networks within a more complex network. Importantly, modules are not imposed on the data, but are derived from the connectivity matrix. Higher modularity or number of modules indicates greater segregation (Rubinov and Sporns, 2010). We also used the clustering coefficient for weighted networks provided by Rubinov and Sporns (2011) as an index of segregation. A node with a high clustering coefficient is strongly connected within a module in that the node has many neighbors that are also neighbors of each other. Finally, we examined the diversity coefficient, which is an index of integration with other nodes. A high diversity coefficient reflects a greater spread of connectivity strength across different modules.

Many complex networks like the functional or anatomical connections in the brain exhibit a small-world architecture, which is characterized by a high degree of clustering or segregation of nodes into modules, with some degree of integration among the modules (Watts and Strogatz, 1998). The overall goal of the present study was to understand whether this type of organization changes during development, particularly in the domain of face processing as that has not been explored with this functional connectivity approach. One hypothesis is that the typical face network in adults is present in rudimentary form in children, but that connectivity strengthens with age. In this account (roughly aligned with a “maturational account” of brain development; see Johnson, 2005; Joseph et al., 2011) there would be minimal reorganization of nodes into different modules, and the primary developmental change would be the addition of more connections or strengthening existing connections either within or between modules, or both. This would predict a general increase in strength with little change in modularity partitioning. Another possibility is that global measures of connectivity remain fairly stable with age but there is significant reorganization of nodes into different modules. This account predicts that nodes will fuse with different modules over the course of development and specific nodes might show greater change than the global network metrics. The reorganization of modules across development is likely achieved by a process of greater integration both within (e.g., reflected in strength) and across modules (e.g. reflected by diversity coefficient) and stronger segregation within modules (e.g. based on clustering coefficient) to achieve functional specialization. This prediction is generally in line with the Interaction Specialization account (Johnson, 2005). Joseph, Gathers and Bhatt (2011) reported that many nodes of the face network in children lose functionality (for face processing) by adulthood. In addition to these regressive changes, nodes of the adult face network are functional in children, but not specialized for face processing. This pattern of regressive and progressive changes suggests a dynamic reorganization throughout childhood; however, Joseph, Gathers and Bhatt did not examine patterns of connectivity among nodes of the face network. Therefore, the present study examines changes in face-network connectivity with development.

The first goal of the present study was to determine changes in functional connectivity patterns during childhood within regions of the adult face network using a graph theory approach. To this end, we examined correlations between age and various graph theory metrics only during childhood. A second goal was to explore how these network metrics differ between children and adults by comparing graph-theory metrics across all age groups (younger children, older children and adults) using ANOVAs. A third goal was to determine the degree to which connectivity patterns are indeed specific for faces. To test this, changes in connectivity patterns were examined not only during face viewing but also during resting state and non-face object-viewing conditions. Graph-theory metrics were then used to test predictions of the maturational and IS accounts of functional brain development.

2. Methods

2.1. Participants

Forty-three right-handed, native English speaking adults (20 males, mean age = 26.4 years) and 47 right-handed, native English speaking children (23 males; 5.5 – 12 years of age) with normal or corrected-to-normal vision and no significant medical histories provided written consent in accordance with University of Kentucky Institutional Review Board guidelines. The data for children and some adults were pooled from prior published studies (Gathers et al., 2004; Joseph et al., 2006) with additional data from adults from unpublished studies. For some analyses (described more below), two age groups of children were determined by a median-split of the larger sample based on age. This produced a younger group (twenty-three 5.5-to-9.7 years of age; 12 males) and an older group (twenty-four 9.8-to-12 years of age; 11 males). The motivation for this split was that others have suggested there is a developmental shift in face processing around 10 years of age (Carey and Diamond, 1977); thus, dividing the present child sample into two age groups allows us to examine this potential shift.

2.2. Design and Procedure

The face localizer task that was used in this study had nine pseudorandomly ordered task blocks (three each of human faces, different categories of natural objects, and different categories of manufactured objects; see Figure 1) and nine fixation blocks (17.8 s each – the fixation blocks were not an even 18 s due to small adjustments in timing needed to synchronize with the scanner). In each task block, 30 randomly-ordered, gray-scale photographs were presented (1000 ms duration followed by a 400 ms fixation cross) and total duration of the task blocks was 42 seconds. Each photograph appeared three times during the experiment. Face photographs were scanned from a high school yearbook and were primarily Caucasian faces (3 faces were Asian or Hispanic). Natural and manufactured object photographs were acquired from various sources. Additional details of the stimuli can be found in Joseph et al (2006). The stimuli were not equated for luminance, complexity or spatial frequency. Although all of these factors could contribute to differences in brain activation for different categories of objects, the present analysis was not concerned with differences in magnitude of brain activation but rather focused on spatial coherence of time-varying fMRI signals in response to a specific category of objects. Moreover, the same stimuli have been used in prior studies (e.g., Gathers et al., 2004) which have reliably isolated brain regions like the FFA that are driven by face processing rather than low-level stimulus attributes (e.g., Kanwisher et al., 1997).

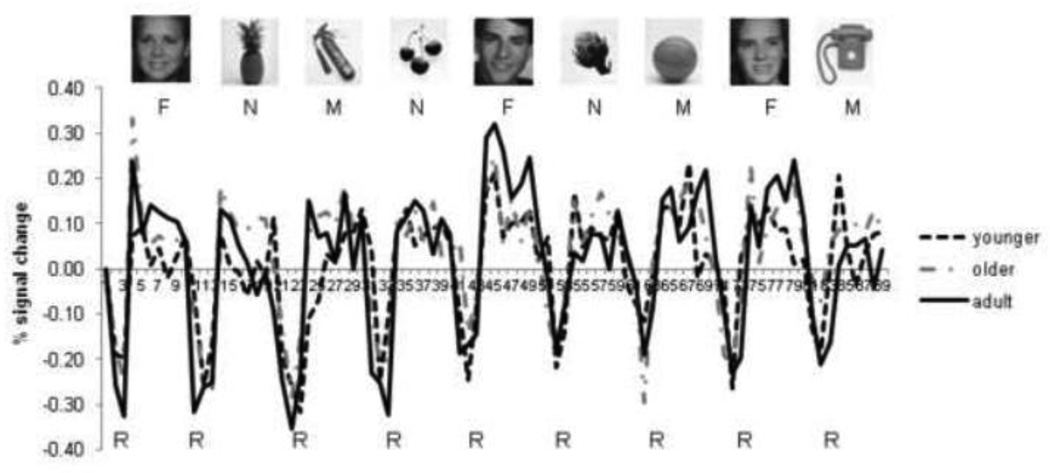
Figure 1.

Average time series for each age group in the right fusiform face area region of interest. F = face blocks, N = natural object blocks, M = manufactured object blocks, R = rest blocks. Intensity values of the time series were converted to percent signal change relative to the first volume so that the time series for the different age groups could be visualized on the same scale. Sample stimuli for each category are shown.

Participants were instructed to press a button with their index finger each time they viewed a stimulus, but not to respond during fixation blocks. Analysis of percent button presses as a function of stimulus type (face, natural, manufactured) and age (adult, older, younger) indicated that younger children (M = 97%, SD = 7%) performed as well as adults (M = 97%, SD = 6%) with older children slightly lower (M = 94%, SD =21%). However, none of the main effects or interactions was significant. Subjects viewed the stimuli (visual angle of 6.74 degrees) through a mirror attached to the head coil.

2.3. fMRI Data Acquisition

Data were collected using a Siemens Vision 1.5 Tesla magnet with a quadrature head coil and T2*-weighted gradient echo sequence (46 axial slices, ascending acquisition, 3.6 mm × 3.6 mm in-plane resolution, TR = 6000 ms, TE = 40 ms, flip angle = 90°, 64 × 64 matrix, FOV = 228 × 228 mm, thickness = 3 mm, gap = 0.6 mm). High-resolution T1-weighted MP-RAGE anatomical scans (150 sagittal slices, 1 mm thick for adults; 76 sagittal slices, 2 mm for the children, FOV = 256 × 256 mm²) were collected for each participant at the end of the experiment.

2.4. fMRI Data Analysis

Using FMRIB’s FSL package (http://www.fmrib.ox.ac.uk/fsl), images in each participant’s time series were motion corrected. Functional runs were discarded when uncorrected head motion exceeded half a voxel (1.7 mm). As reported in the earlier studies from which the present data were pooled, corrected head motion did not differ between adults and children (Gathers et al., 2004; Joseph et al., 2006). Spatial (3D Gaussian kernel; FWHM = 7.5 mm), and temporal (360 s high-pass filter) smoothing were applied. Other kinds of functional connectivity analyses that operate at the voxel level do not use smoothing because smoothing effectively averages the time series of spatially contiguous voxels, which may artificially increase or decrease the connectivity among those voxels. However, the present analysis averaged time series from many voxels within spatially discontinuous regions of interest prior to the functional connectivity analysis. Therefore, smoothing would have little effect on the time series that were submitted to correlations for the present connectivity analysis. Six movement parameters (3 rotation and 3 translation values) were added as covariates of no interest to model the variance in the fMRI signal induced by head motion. Regression model parameters were estimated for each explanatory variable (face, natural or manufactured object blocks) and statistical contrasts of interest (Face v. Natural, Face v. Manufactured, Face v. Fixation) were generated. Contrast maps were normalized into common stereotactic space using an affine 12-parameter model (FLIRT in FSL) before mixed-effects group analyses were performed. The MNI template was used as the common stereotactic space for all age groups for two reasons. First, the analyses used extracted time series in each participant within regions of the adult network. This required that all brain images be normalized to the same standardized space. Second, Kang et al. (2003) did not find appreciable differences in localization using an adult template in children as young as 7 to 8 years of age. To address the concern of fitting brains of children into a common standard space based on adult brains, we examined localization of face-preferential activation in individual participants in both native space and standardized MNI space. In native space, 67% of adults, 30% of older children and 50% of younger children showed face-preferential activation in the right FFA. In standard space, 61% of adults, 39% of older children and 41% of younger children showed activation in the right FFA. The correspondence between detecting activation in the right FFA in standard space and native space was quite high in all three age groups. We conducted a correlation analysis to determine whether a region detected in native space was also present in standard space in children (and, likewise, whether a region not detected in native space was also not detected in MNI space). Phi coefficients for this analysis were high and significant for both older children (phi = .71, p < .05) and younger children (phi = .91, p < .05). This analysis shows that fitting brains of children to an adult template does not systematically bias detection of functional brain regions like the FFA.

Regions-of-interest (ROIs) were determined from the adult group activation map (rather than from group activation maps in younger and older children), so that extraction of time-series data from both groups of children was independent from the definition of the ROIs and would not be biased toward significant activation. We also extracted time series data from adults in the same regions for comparison. To determine the ROIs, the individual contrast maps (Face > Fixation, Face > Manufactured, Face > Natural) were logically combined (Gathers et al., 2004) to yield face-preferential ROIs (Table 1), some of which were then used in the functional connectivity analysis. “Face-preferential” activation was defined as those voxels in which faces elicited more activation than fixation and greater activation than either natural objects or manufactured objects or both. This is similar to how other studies define the FFA using a contrast of Faces > non-face objects (Berman et al., 2010); but see Gathers et al. (2004) and Joseph et al. (2011) for a more detailed discussion of this issue).

Table 1.

Face-preferential Regions-of-interest isolated in adults

Region	Cluster Size	MNI-x			MNI-y		MNI-z
R Fusiform (FFA)		262	44		−60		−22
R Inferior Occipital (OFA)		169	38		−82		−14
R Calcarine / Middle Occipital		202	22		−96		−2
R Inf Frontal Opercular		114	42		2		26
R Inf Frontal Orbital	15	32		28		−16
R Middle Temporal		57	52		−64		8
R Superior Temporal	23	48		−40		14
L Fusiform (FFA)		18	−40		−52		−24
L Fusiform (OFA)		25	−28		−82		−16
L Calcarine / Middle Occipital		325	−22		−98		−2
L Hippocampus		24	−20		−8		−18
L Cerebellum	54	−20		−84		−22
L Thalamus		119	−12		−20		2
Brain Stem		10	16		−10		−4

After logical combination ROIs were defined as clusters of voxels in which parameter estimate values for faces versus fixation differed significantly from zero (p < 0.001, 2-tailed; Table 1). We only considered small face-preferential regions (fewer than 43 voxels in MNI space) if that region was part of the core or extended face network as defined by Haxby et al. (2000a) and Fairhall and Ishai (2007). Because the main data for functional connectivity analyses are the time series of fMRI signal in different ROIs or in single voxels rather than the activation magnitude or extent, the issue of small ROIs in not as critical as in general linear modeling. In fact, in the present dataset size of the ROI was not correlated with the variance of the group-averaged face time series (rho = .13, p = .66, n = 14 ROIs), indicating that time series from larger ROIs are not necessarily less noisy than time series from smaller ROIs.

2.5. Functional Connectivity Analysis

We used a graph-theory based approach to network connectivity (Rubinov and Sporns, 2010, 2011) to explore functional connectivity among face-preferential ROIs. In this approach, the correlation matrices of time series across different regions in the brain are used to explore different functional connections related to face processing. We opted to examine non-directional functional connections rather than test models in which directional paths were postulated because our goal was to explore the full range of network connectivity rather than selecting specific connections or sub-networks a priori.

In functional connectivity analyses such as that used in the present study, the regions that are explored need not meet typical requirements of statistical significance for “activation” studies; in fact, some approaches to functional connectivity (such as Principal Components Analysis; e.g., Andersen et al., 1999) explore temporal synchrony among individual voxels without regard to the magnitude of fMRI signal in those voxels. The present approach was to isolate regions that are implicated in face recognition in adults and overlay those regions as masks for extracting the time series data from both adults and children. These regions need not be functionally activated in children in order for this approach to be valid. In addition, assumptions about the shape of the hemodynamic response, restrictions on the size of regions and requirements for minimum activation magnitude are not relevant when conducting functional connectivity analyses. Nevertheless, Figure 1 shows the average time series for each age group in the right FFA to illustrate that the signal for task conditions versus baseline in children is quite robust, although it may not always be of the same magnitude as adults. As mentioned, we were interested in the temporal synchrony of the time series for different conditions across different regions rather than the magnitude of signal change versus baseline.

In each ROI of the adult face-preferential network (described below) for each subject, the entire time series (as illustrated in Figure 1) was broken into four separate time-series, one for each condition: (1) one series for the face condition, in which only those brain volumes associated with the three face blocks were included (21 timepoints), (2) one series for the natural object condition, in which only those volumes associated with the three natural object blocks were included (21 time points), (3) one series for the manufactured object condition, in which only those brain volumes associated with the three manufactured blocks were included (20 timepoints – this time series had only 20 time points because the last block in the functional run was for manufactured objects and time-shifting caused the last time point to be excluded) and (4) one series for the rest condition, in which only those brain volumes associated with the rest blocks were included (27 timepoints). Each time series was shifted by one TR. Although time-shifting was not necessary, it more closely links the time points with the conditions of interest by accounting for the hemodynamic lag.

Note that these time series are concatenated time series (i.e. segments of the entire times series associated with specific stimulus conditions) as used in other studies (Fair et al., 2007b). One reason for using concatenated time series rather than the entire continuous time series was to be able to test the degree of specificity of the connectivity patterns for different stimulus conditions (faces, natural objects, manufactured objects and rest periods). By having a separate time series for each of these conditions, we were able to test whether a certain measure of connectivity emerged only for faces or if that measure emerged for any condition, thereby reflecting a more generalized phenomenon. A second reason for using concatenated time series was that the correlation matrix would reflect temporal synchrony of the fMRI signal for a given condition of interest (e.g., only for face conditions) and would not be affected by the more robust task versus rest fluctuations in fMRI signal as illustrated in Figure 1. If the entire time series were used, the degree of correlation among regions would be much higher (and this was confirmed by preliminary inspection of the data). By using a concatenated time series, we could isolate the degree of connectivity for faces from the overall task effect.

A third reason for using concatenated time series for the four conditions separately was that the time series in adults would not be completely redundant with the time series used to isolate the ROIs (which were defined in adults based on differences between the fMRI signal for faces versus other conditions). In other words, the correlations among regions for the present functional connectivity analysis were based on the time-varying signal within blocks rather than based on the time-varying signal between blocks, which defined the ROIs. However, one concern about this approach is that the connectivity among regions may be greater in adults than in children due to the fact that the time series used for functional connectivity in adults was somewhat related to the time series used to define the ROIs, rather than reflecting a true developmental effect. This would predict that adults should show higher correlations than both age groups of children. To address this, we examined the average Fisher-z transformed unsigned correlation coefficients across age groups. Adults showed a higher correlation coefficient (M = .327, SE = .01) compared to younger (M = .281, SE = .013; p = .015) but not older children (M = .299, SE = .013, p = .114). Therefore, the stronger correlations in adults more likely reflect a developmental change. In addition, correlation coefficients showed an increase with age in children (Spearman rho = .318, p = .03, n = 47), which provides additional support that the differences in correlation coefficients between younger children and adults or older children reflects a true developmental change. We also examined the variance of the fMRI signal intensity in the face time series by age group to ensure that the time series were not necessarily noisier at one age versus another. The average variance in younger children (M = 5111.1, SE = 566.5), older children (M = 5520.8, SE = 554.7) and adults, (M = 5423.3, SE = 419.2) was not different, F(1,89) = .15, p = .861. In addition, variance did not correlate with age in children, Spearman rho = .154, p = .3, n=47.

Four correlation matrices (one for each condition: face, natural, manufactured, rest) that reflected the intercorrelations of the fourteen regions of the adult face network were computed for each subject and submitted to the Brain Connectivity Toolbox (Rubinov and Sporns, 2010); http://www.brain-connectivity-toolbox.net). We also computed 20 random networks for each subject that preserved the weight and strength properties of the face network (following Rubinov and Sporns, 2011 and Wormald, 1999) in each subject. Metrics from the 20 random networks were then averaged to provide a single metric to compare to the metrics of the face network. The main comparison of interest was whether the face network differed from a random network. Weighted and signed connection weights were used because they filter out the effects of weak or insignificant edges, do not rely on an arbitrarily determined threshold, and are most appropriate for functional networks (Rubinov and Sporns, 2010, 2011).

For each subject and each condition, we computed the following metrics, all of which are described in more detail in Rubinov and Sporns (2011) and are summarized in Table 2: (a) Modularity using two different measures (referred to as Q*, Q⁺, with Q* being the preferred metric according to Rubinov and Sporns (2011). Because the modular structure in a network is usually determined by optimization algorithms, the modularity (Q) gives a sense of the goodness of the partitioning into modules. We explored modularity based both on positive connections only (Q+) and based on a combination of positive and negative connections (Q*). Rubinov and Sporns (2011) suggest that positive and negative connections of a network should have different importance. More specifically, “positive weights associate nodes with modules explicitly, while negative weights associate nodes with module implicitly, by dissociating nodes from other modules.” (p. 2). Therefore, high modularity based on positive connections is more optimal than high modularity based on negative connections. Q* reflects the combined positive and negative connectivity but weights the positive connectivity more than negative connectivity. (b) Number of modules based on the modularity measures in (a), number* and number⁺. (c) From the modularity partitions determined by Q*, we calculated the diversity coefficient for positive and negative weights combined where the contribution of positive weights is greater than negative weights. Diversity coefficient was calculated for each node separately (node-diversity*), averaged over all nodes (network-diversity*) and averaged within modules (module-diversity*) that were associated with the adult group-averaged time series. (d) Within-module weights, both positive (module-weights+) and negative (module-weights−). (e) Within-module clustering coefficient, which yields the proportion of balanced and unbalanced triangles within modules. Balanced triangles are those with three positively weighted edges; unbalanced triangles are those with only two positively weighted edges. The within-module clustering coefficient was averaged over all nodes (network-within-clustering+ and network-within-clustering−), averaged within modules (module-within-clustering+ and module-within-clustering−) that were associated with an adult group-averaged time series, or reported separately for nodes (node-within-clustering+ and node-within-clustering−). (f) Strength*, which combines positive and negative weights, but considers the positive weights to be more important. Strength* reflects connectivity within a module. These strength measures were calculated for each node separately (node-strength*), averaged over all nodes (network-strength*) and averaged within modules associated with the adult group-averaged time series (module-strength*).

Table 2.

Graph theory metrics used in the present study and related results

Metric & Description	Variable name(s)	Effects of age and interactions
Modularity	Q+	no effects
	Q*	alower Q* in adults than children for faces, natural and random conditions
Number of modules	number+	aface-specific decrease during childhood
	number*	no effects
Diversity coefficient	network-diversity*	agreater network diversity in adults than younger children
	module-diversity*	agreater subcortical diversity in adults than younger children;
		agreater visuo-limbic diversity in adults than children for faces and natural objects
	node-diversity*	agreater left calcarine diversity in adults than children
Module weights	module-weights+	no effects
	module-weights−	no effects
Clustering coefficient	network-within-clustering+	btrend for greater clustering in adults than children
	module-within-clustering+	no effects
	node-within-clustering+	bface-specific increase in right occipital face area clustering during childhood;
		bgreater right occipital face area clustering in adults than children for faces;
		bgreater right occipital face area clustering in adults than older children for natural objects
	network-within-clustering−	cnot analyzed
	module-within-clustering−	cnot analyzed
	node-within-clustering−	cnot analyzed
Strength	network-strength*	agreater strength in adults than children
	module-strength*	agreater visuo-limbic strength in adults than younger children for faces;
		agreater visuo-limbic strength in adults than children for natural objects;
		agreater visuo-cerebellar strength in adults than younger children
	node-strength*	bincrease in right occipital face area strength during childhood for faces;
		agreater right occipital face area strength in adults than younger children;
		agreater right fusiform face area strength in adults than children;
		agreater brainstem strength in adults than children

^asignificant at Holm adjusted alpha level;

^bsignificant at uncorrected alpha = .05,

^cthis variable had a significant number of zeros

Spearman rank correlations were conducted between age and each metric in children separately from adults rather than in the sample as a whole to avoid selection bias. The separate correlation analyses allowed us to examine developmental change within the time window of 5 to 12 years of age, so that we could examine developmental changes during childhood. To examine developmental changes that occur at some point between childhood and adulthood, we conducted mixed ANOVAs that included all three age groups (as the between-subjects factor) to determine whether there was a main effect of age and interactions of age with other variables. A difference between adults and older children indicates that some type of developmental change occurred during adolescence (although we did not test an adolescent age group), but no difference between adults and older children indicates that the given metric does not undergo further developmental change during adolescence. To address the issue of potential unequal variances in the age groups due to different sample sizes, we compared age groups when there was a main effect of age using Tamahane’s T2, which is considered a conservative post-hoc comparison method (SPSS statistics 18.0.0, Chicago, IL).

To address the issue of multiple tests using the same dependent variable (i.e., for each dependent variable we conducted 4 ANOVAs for the four different modules and 14 ANOVAs for the 14 different nodes), we used the Holm procedure for multiple tests (Holm, 1979) which bears some similarity to the false discovery rate procedure (Benjamini and Hochberg, 1995). The Holm approach is not as conservative as Bonferroni correction but is more powerful. As an example, when conducting the 14 ANOVAs for a given dependent measure, the alpha level used for the first test is .05/14 = .00357, which is the same as Bonferroni correction. For the next test, however, the alpha level is .05/13 = .00385, etc., and the alpha level for the last test is .05. Essentially, the lowest of the 14 p-values is compared to the alpha level for the first test, which is .00357 and if it is greater than this, then hypothesis testing stops. To visualize developmental change in the face network, an average correlation matrix was determined from the average time series for each age group, then visualized using Gephi software (Bastian et al., 2009). The partitioning into modules was determined using the Q* metric for these average correlation matrices.

2.6. Image similarity analysis

To address the degree of similarity of the images within each category, we followed the approach by Cilibrasi and Vitanyi (2005). This is an information-theoretic, compression-based similarity metric which captures dissimilarity distance, using relationships between the size of compressed files or data strings to fulfill otherwise incomputable values of Kolmogorov complexity. The main metric is the normalized compression distance, defined as:

$$\mathit{\text{NCD }}(x,y)=\frac{C(x,y)-\text{min}\{C(x),C(y)\}}{\text{max}\{C(x),C(y)\}}$$

Where C(x) is the compression (in bytes as computed by gzip supplied with Matlab 2012a) of image x, and C(x,y) is the compression of the concatenation of images x and y. The degree that a joint compression is smaller than the compressions of individual images reflects the visual information shared between images, and has been used for content-based image retrieval (Gondra and Heisterkamp, 2008). This technique has been validated across a wide range of domains including optical character recognition, language trees and genomics and phylogeny.

From all images we compiled a dissimilarity matrix containing these pairwise NCD values, and to more easily quantify and visualize the geometric embedding of data we examined the top 3 eigenvectors of this matrix (similar to a principal components analysis). We also conducted a quadratic discriminant analysis (Krzanowski, 1988) to determine classification accuracy of the images into three categories corresponding to faces, natural objects, and manufactured objects.

3. Results

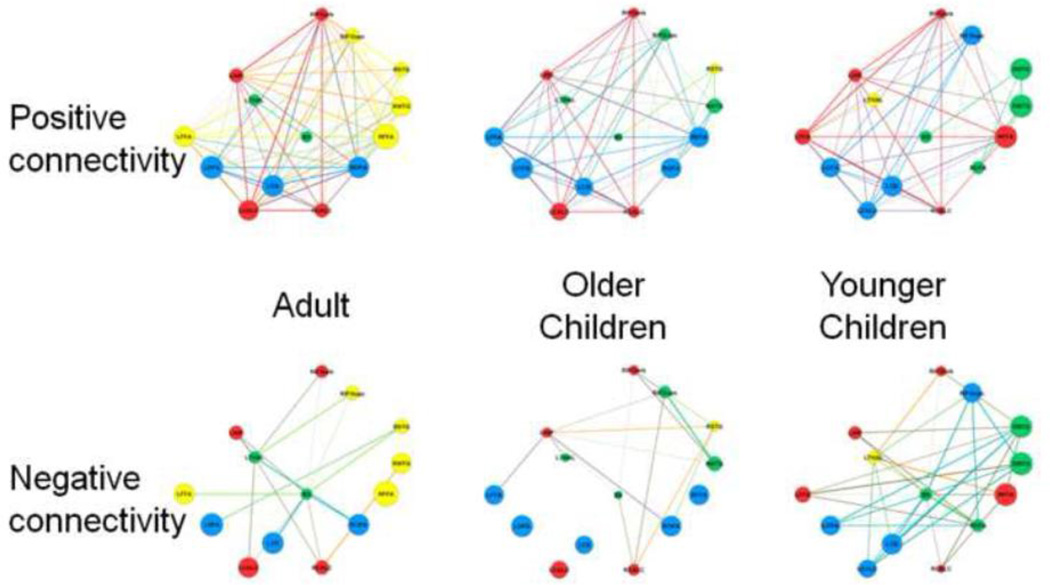
Figure 2 shows the modular structure derived from the average face networks in each age group with different modules coded in different colors. Each age group’s average network consisted of four modules, but module composition changed across age. We refer to the four modules in adults as: (a) a fronto-temporal module consisting of the right fusiform gyrus (RFFA), left fusiform face area (LFFA), right superior temporal gyrus (RSTG), right middle temporal gyrus (RMTC), and right inferior frontal gyrus-opercular portion, (RIFGopc), (b) a visual-limbic module consisting of the right calcarine sulcus (RCALC), left calcarine sulcus (LCALC), left hippocampus (LHIP) and right inferior frontal gyrus-orbital portion (RIFGorb), (c) a visuo-cerebellar module consisting of the right occipital face area (ROFA), left occipital face area (LOFA) and left cerebellum (LCB), and (d) a sub-cortical module, consisting of the left thalamus (LTHAL) and brainstem (BS). The size of each node in Figure 2 reflects its strength, which is scaled to the largest value across all three age groups (i.e. the node with the highest strength has a value of 1 and all other nodes are scaled to that value proportionally). Positive and negative connectivity are shown separately.

Figure 2.

Graphs of the positive and negative connectivity among regions of the typical adult face network at three ages: adults, older children and younger children. Colors represent the assignment of nodes to modules. Size of the nodes represents the strength of each node scaled to the maximum strength across all three age-specific networks. Node labels are described in Table 1.

Prior to conducting the ANOVAs and correlations described below, the distribution of each dependent measure was examined for outliers. Values between 1.5 and 3 times the interquartile range were considered outliers and omitted from analyses. Because each condition (face, natural, manufactured, rest) is treated as a dependent variable in repeated measures analyses (O'Brien and Kaiser, 1985) if a case was an outlier for one condition, the entire case was omitted from the analysis. Examination of the distributions also revealed that the distribution of network-within-clustering−, module-within-clustering−, node-within-clustering− included many zero values; therefore, we omitted this metric from analyses.

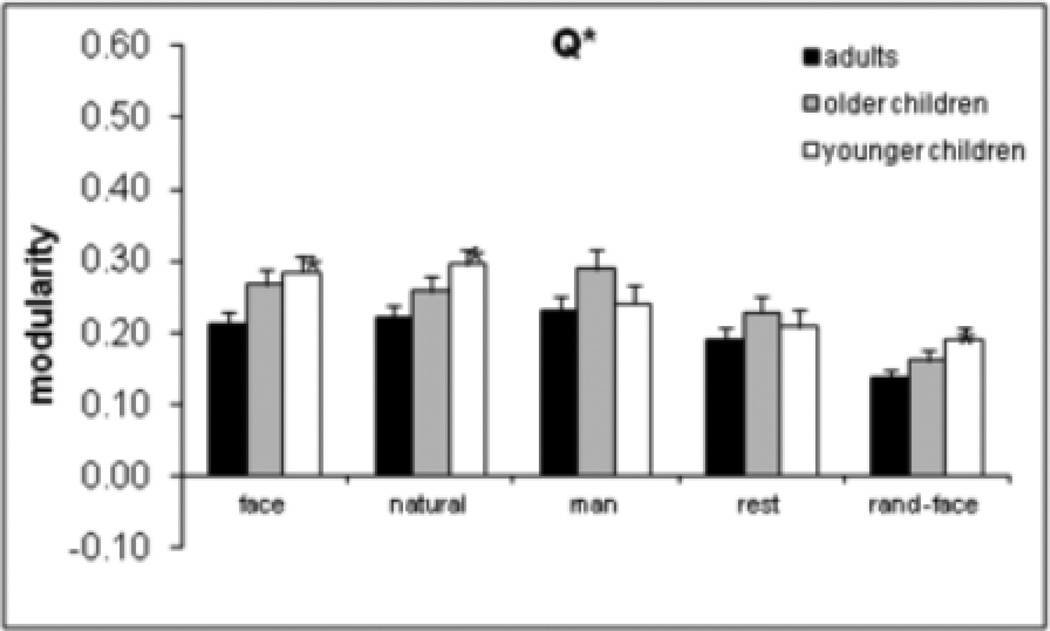
3.1 Modularity

Higher modularity indicates more segregation of nodes into sub-networks. The two modularity measures (Q+ and Q*) were examined as dependent variables in two separate mixed 5 (condition) × 3 (age group) ANOVAs. The main effect of condition was significant for Q+, F(4, 69) = 171.5, p = .0001, and Q*, F(4, 79) = 168.8, p = .0001) as shown in Figure 2 for Q*. Planned comparisons for faces versus random were significant for Q+, F(1, 72) = 376.8, p = .0001, and Q*, F(1, 82) = 370.0, p = .0001, as were the planned comparisons for faces versus rest [for Q+, F(1, 72) = 8.9, p = .004; for Q*, F(1, 82) = 11.6, p = .001. Faces were not different from natural and manufactured objects. The age effect was significant for Q*, F(2, 82) = 4.3, p = .017, as was the Age × Condition interaction, F(8, 160) = 2.2, p = .027. As shown in Figure 3, adults had lower modularity than younger children for faces (p = .029), natural objects (p = .019), and random (p = .025) conditions, according to Tamahane’s T2 test. In other words, adults exhibited less segregation into sub-networks for face and natural object conditions and with respect to the random network. Because the random networks were generated from the network in the face condition, and random networks preserve the weight and strength (but not modularity) properties of the face network, the finding that random networks had lower modularity in adults than younger children is not surprising as it mirrors the finding with the face network.

Figure 3.

Age × Condition interaction for modularity based on Q* partitioning. Asterisks indicate a significant difference from adults for the given condition. Error bars are standard error of the mean.

3.2 Number of modules

More modules indicate greater segregation of the network into sub-networks. Number of modules showed a face-specific decrease with age among children, but only for number⁺ (rho = −.425, p = .008, n = 38). This face-specific finding indicates reduced segregation with age during childhood, based on positive connectivity. Similar to the analysis of modularity, number of modules from the two different modularity measures served as dependent variables in mixed 5 (condition) × 3 (age group) ANOVAs. For both measures (Figure 3), faces had fewer modules than the random network (main effect of condition was significant, F(4, 344) > 2.8, p < .032) and planned comparisons for faces versus random were significant, F(1, 86) > 5.2, p < .025. However, faces were not different from natural, manufactured and rest conditions in terms of number of modules. The age effect was only significant for number⁺, F(1, 86) > 3.7, p < .028. Adults and older children had fewer modules than younger children based on positive connectivity (p < .044), but this was not specific for faces Together, these results indicate developmental changes in functional segregation based on positive connectivity: a face-specific decrease in segregation during childhood (based on the correlation results) and a generalized non-face-specific decrease in segregation from childhood to adulthood (based on the ANOVA results)

3.3 Network-diversity

Higher diversity coefficients reflect greater integration across modules. Network diversity measures this in the network as a whole. The mixed 4 (condition) × 3 (age group) ANOVA revealed a main effect of age, F(2, 86) = 4.5, p = .014, in which adults had greater network-diversity* of connections than younger (p = .033) children. No correlations with age were significant for any of the four conditions. This suggests a generalized increase in functional integration from early childhood to adulthood.

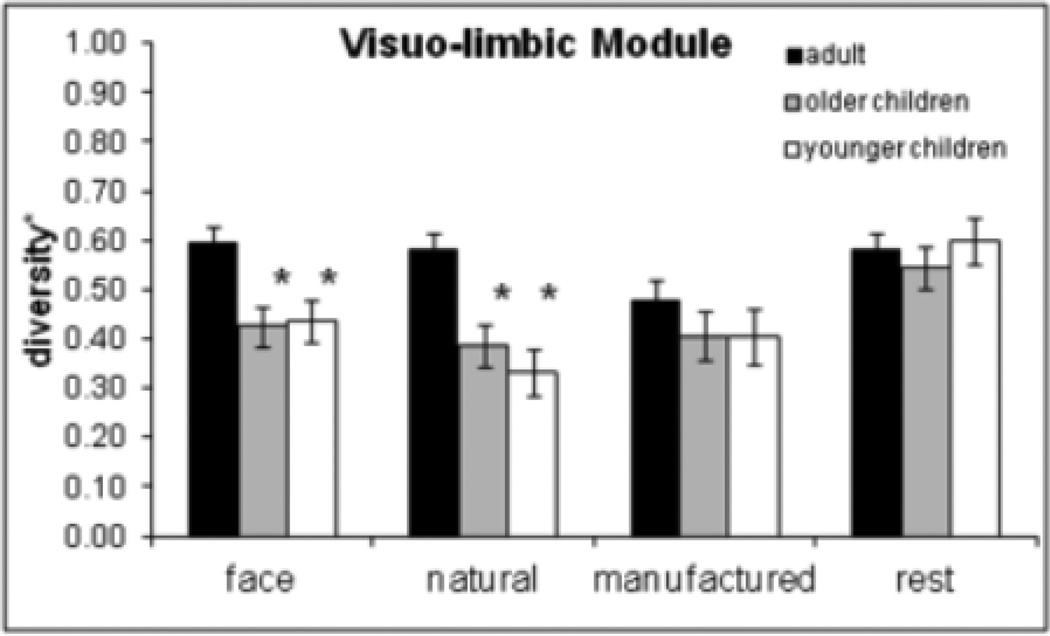
3.4 Module-diversity

Higher module diversity for a specific module reflects more intermodular integration. The mixed 4 (condition) × 3 (age group) ANOVAs conducted for each module separately revealed a main effect of age in the visuo-limbic, F(2, 82) = 7.14, p = .001, and sub-cortical module, F(2, 83) = 5.84, p = .004. Adults had higher module-diversity* than older (p = .002) and younger (p = .002) children in the visuo-limbic module and higher module-diversity* than younger children (p = .002) in the sub-cortical module. The visuo-limbic module also had a significant Age × Condition interaction, F(6, 246) = 2.96, p = .008, indicating that module-diversity* for faces and natural objects was greater for adults than for older (p < .013) and younger children (p < .001), but there was no age effect for manufactured and rest conditions (Figure 4). No correlations with age were significant for any of the four modules. These results indicate greater functional integration in adults than in children. In the sub-cortical module, greater integration in adults (compared to younger) was not specific to faces, but in the visuo-limbic module greater integration in adults was specific for faces and natural objects.

Figure 4.

Diversity* results for the visuo-limbic module. Adults showed higher diversity* in the visuo-limbic module for faces and natural objects but not for manufactured objects and the rest condition. Asterisks indicate a significant difference from adults for the given condition. Error bars are standard error of the mean.

3.5 Node-diversity

Higher node diversity for a specific node reflects more intermodular integration. The mixed 4 (condition) × 3 (age group) ANOVAs conducted separately for each of the 14 nodes revealed that the left calcarine sulcus showed a significant main effect of age, F(2, 76) = 9.74, p = .0001, in which adults showed greater diversity than both older (p = .004) and younger (p = .0001) children, but this did not interact with condition. Hence, this developmental increase in integration reflects a generalized effect, not specific to face.

3.6 Module-weights

No face-specific or age-related effects or correlations emerged.

3.7 Network-within-clustering

Higher within-clustering coefficients in the network as a whole reflect more centrality within modules, as an index of greater segregation. The mixed 4 (condition) × 3 (age group) ANOVA revealed a main effect of age for network-within-clustering+ (F(2, 81) = 3.6, p < .031), but the pair-wise age comparisons were not significant using Tamahane’s T2 test.

3.8 Module-within-clustering

No face-specific or age-related effects or correlations emerged in any of the four modules.

3.9 Node-within-clustering

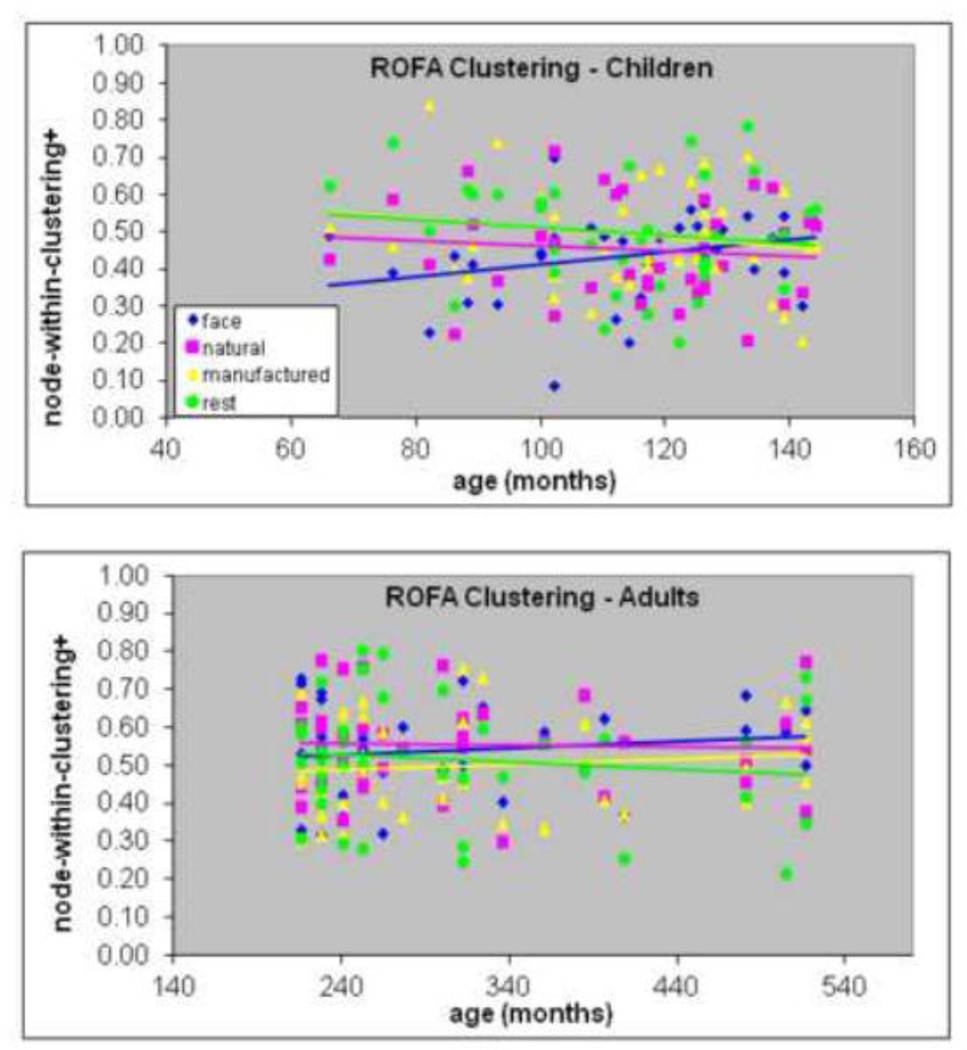
Higher node-within-clustering reflects greater centrality of that node within its module as an index of greater segregation. Although node-within-clustering+ increased with age in children in the right OFA (rho = .327, p = .045, n = 38, Figure 5a) this did not survive the Holm-adjusted alpha level. Nevertheless, this trend suggests increased functional segregation of the right OFA during childhood. The mixed 4 (condition) × 3 (age group) ANOVAs conducted separately for each node revealed that the right OFA showed a main effect of age for node-within-clustering+, F(2, 74) = 6.1, p < .004 (but this fell just short of the corrected alpha-level of .0035). Adults had greater clustering than both older (p = .022) and younger (p = .019) children. The Age × Condition interaction, F(6, 222) = 2.9, p = .011 (which also did not survive the corrected alpha level), indicated that adults showed greater clustering for faces compared with both older (p = .037) and younger (p = .002) children and greater clustering for natural objects compared with older children (p = .001, Figure 5b). The ANOVA results suggest that functional segregation of the right OFA is (a) specific to faces and natural objects and (b) continues to change in the transition from childhood to adulthood.

Figure 5.

Association between age (in months) and within-module clustering coefficient based on positive connections in the right occipital face area (OFA) in children (top) and adults (bottom) for each of the four conditions (faces, natural objects, manufactured objects, rest). The correlation with age was only significant for faces in children.

3.10 Network-strength

Greater network strength reflects stronger connectivity with other nodes in a module based on a combination of positive and negative connections. The mixed 4 (condition) × 3 (age group) ANOVA revealed that adults showed greater network-strength* than both age groups of children (main effect of age: F(2, 77) = 6.7, p = .002; adults > older: p = .027; adults > younger: p = .003) but there were no differences among children. There were no interactions with condition, suggesting a generalized increase in network strength with development.

3.11 Module-strength

Greater module strength reflects stronger connectivity within that module based on a combination of positive and negative connections. The visuo-cerebellar, F(2, 78) = 6.5, p = .002, and visuo-limbic, F(2, 80) = 4.68, p = .012, modules showed an increase in module-strength* with age. For both measures, adults showed greater strength than younger children (p < .014). In the visuo-limbic module the significant Age × Condition interaction, F(6, 240) = 2.5, p = .022, revealed that the age effect was significant for faces (p = .002) and natural objects (p = .0001) but not for manufactured and rest conditions (Figure 6a). Adults showed greater module-strength* for faces compared to younger children (p = .005) but not older children. For natural objects, adults showed greater module-strength* compared to both age groups (p < .012). The ANOVA results suggest that increased connectivity within the visuo-limbic module is (a) specific to faces and natural objects and (b) continues to increase in the transition from childhood to adulthood for natural objects, but (c) appears to increase during childhood for faces.

Figure 6.

(A) Strength* results for the visuo-limbic module. Adults showed higher diversity* in the visuo-limbic module for faces and natural objects but not for manufactured objects and the rest condition. Asterisks indicate a significant difference from adults for the given condition. Error bars are standard error of the mean. (B) Association between age (in months) and strength* in the right occipital face area (OFA) in children and adults for each of the four conditions (faces, natural objects, manufactured objects, rest). The correlation with age was only significant for faces in children.

3.12 Node-strength

Greater node strength reflects stronger connectivity within a module for that node based on a combination of positive and negative connections. Although right OFA node-strength* (r = .407, p = .006, n = 45) increased with age in children for faces (Figure 6b), this did not survive the Holm-adjusted alpha level of .0035. Nevertheless, this trend suggests increased within-module connectivity of the right OFA during childhood. The mixed 4 (condition) × 3 (age group) ANOVA on node-strength* revealed a main effect of age in three nodes: the right FFA, F(2, 85) = 6.9, p = .002, right OFA, F(2, 83) = 7.5, p = .001, and brainstem, F(2, 78) = 5.8, p = .004. In all nodes, adults had greater strength than at least one other age group (right FFA: A > O, p = .003, A > Y, p = .022; right OFA: A > Y, p = .0001; brainstem: A > O, p = .02, A > Y, p = .023), but these effects were not further qualified by condition; therefore, they reflect generalized increases in connectivity with development during childhood and in the transition from childhood to adulthood.

3.13 Image similarity

Some of the results indicated developmental differences in graph-theory metrics for both faces and natural but not manufactured objects. It is possible that faces and natural objects are more visually homogenous stimuli compared to manufactured objects. To address this, we applied the information-theoretic similarity test described in the methods. The similarity metric indicates that when two images are similar, then one image can be succinctly described given the information in the other image. NCD values were used to create a dissimilarity matrix among all stimuli and the top three eigenvectors were used to classify the images into general groups using quadratic discriminant analysis. In Figure 7 (top) we plot all images according to the first (x-axis) and third (y-axis) eigenvector, the two most informative dimensions for image separation. Images that are closer to each other along either axis are more similar than images that are more distant. Classification accuracy was 85.5% for grouping the images into faces, natural and manufactured objects (Figure 7, bottom) based on the two most informative eigenvectors, and 90% using all three eigenvectors.

Figure 7.

(Top) Principal eigenvectors associated with all pairwise NCD values for the images used as stimuli in the experiment. For visualization purposes we display these images along the first and third eigenvectors. Colored labels indicate stimulus type –face (blue), natural (green), or manufactured (cyan) images. (Bottom) Result of a discriminant analysis of the labeled images along these dimensions, with the learned prediction regions colored accordingly. Misclassified stimuli are indicated with a red X. Over 85% are successfully labeled.

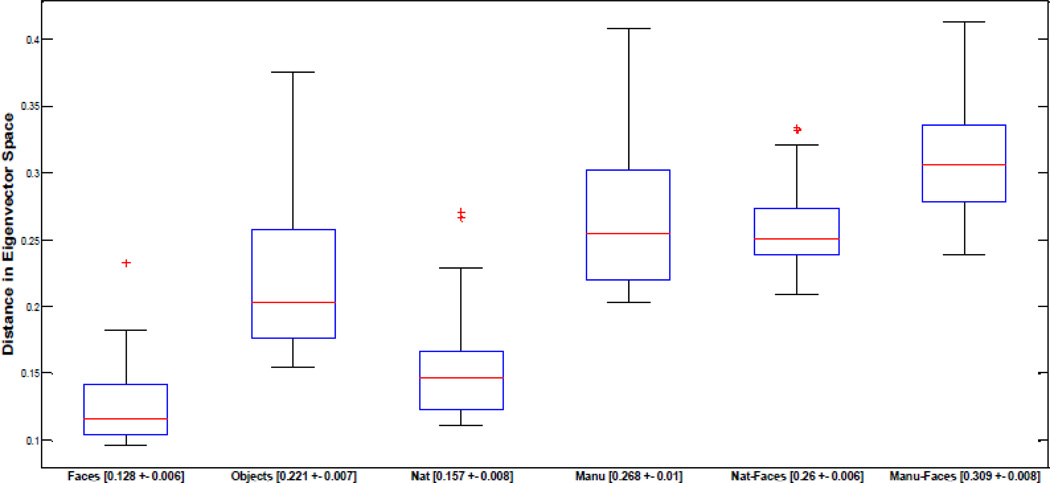
For each image, we used these top three eigenvectors to compute the mean distance for an image relative to all other images within the same category (faces, natural, manufactured objects) as well as between different categories (natural v. faces and manufactured v. faces). Hence, each image had a single value for within and between-category comparisons. As shown in Figure 8, faces were significantly closer to each other than objects, indicating greater similarity within the face category (p<.001), natural objects were more similar than manufactured objects (p<.001), and natural objects were significantly closer to faces than manufactured (p<.001). These findings suggest that faces and natural objects form more visually homogenous categories, in line with other suggestions in the literature (e.g., Bruce & Humphreys, 1994).

Figure 8.

Boxplots displaying medians (red line) and quartiles of the distributions for the distances of individual images to other images within the same class or to those images within another class in eigenvector space. Within-face distances (n=30) are significantly lower than within-object distances (n=60), within-natural distances (n=30) are significantly lower than within-manufactured distances (n=30). Mean distance between natural and face images (n=30) is significantly lower than the mean distance between manufactured and face images (n=30). All p-values are < 0.001. Outliers are indicated as red crosses and mean value and standard error for each condition are given on the x axis.

4. Discussion

Prior studies on the neuro-development of face processing primarily have concentrated on magnitude or extent of activation in specific brain regions, but the current study documents developmental changes in brain connectivity for face processing. We explored two hypotheses concerning developmental changes in functional connectivity of the face network across childhood and in the transition from childhood to adulthood. One hypothesis (associated with the maturational approach to development) was that the basic modular structure among regions of the adult face network is already established in childhood but that the primary developmental change would be an increase in strength of connections with age. An alternative hypothesis (associated with the Interactive Specialization approach) was that modular structure would change throughout development and that significant reorganization would involve both integration and segregation of nodes within and across modules. The evidence is in favor of this latter account.

The maturation account predicts an increase in strength of connections with age, but that these strength increases would largely occur within a developmentally stable modular organization. Although strength increased with age across the entire network, in the visuo-limbic and visuo-cerebellar modules and in the right FFA, right OFA and brainstem, there was also reorganization of the modular structure during development. Therefore, the first result that supports the IS account is that modular structure changed over development, meaning that the nodes of the network are grouped into different sub-networks at different ages (Figure 2). Although this is a qualitative comparison, it is clear that the modular structure is dynamic across development. The modular structure in younger children does not resemble that of adults very closely, whereas there are more similarities between older children and adults, such as the presence of a visuo-limbic module in both age groups.

The second result that supports the IS account is that there was greater integration of positive connectivity and weaker integration of negative connectivity with age (based on the modularity, number of modules and diversity coefficient analyses that included all three age groups). This was especially true for diversity of connections of the visuo-limbic module with respect to faces and natural objects.

The IS account also predicts that segregation would occur; however, the evidence for this property was not as strong as the evidence for integration in that the trends toward significance fell short of the corrected alpha levels for multiple tests. Nevertheless, because this is the first study using graph-theory metrics to examine development of face processing, these trends are worth reporting as they can guide hypotheses for future studies. Adults had higher within-module clustering across the entire network compared with the other two age groups, and the right OFA showed a developmental increase in clustering for faces and natural objects. Therefore, functional connectivity changes from childhood to adulthood involve both integration and segregation of connections, consistent with predictions of the IS account. All of the graph-theory metrics showed some developmental change at one of the spatial scales we examined (network, module or node level) with the exception of module-weights. This measure reflects the proportion of positive or negative weights within a module and does not reflect network properties that are more germane to functional integration and segregation. Apparently, this measure it not as sensitive to developmental changes as are the other metrics.

Interestingly, only two face-specific developmental changes emerged and these changes occurred during childhood rather than in the transition from childhood to adulthood. One of those changes was that number of modules based on positive connectivity (number+) decreased during childhood for faces but not other conditions. Fewer modules were also observed in adults, but not specifically for faces. We presently interpret the finding of fewer modules as an indication of greater integration of regions with development. In other words, regions of the face network are less likely to divide into distinct sub-networks in older children and adults.

Another face-specific developmental change involved the right OFA which increased in within-module strength during childhood for faces (based on the correlation between age and strength* in children) suggesting that weights of positive connections increased but weights of negative connections decreased with age. Although this correlation did not survive alpha-correction, we think these results are suggestive that the ROFA is an important node in the development of an occipito-temporal module (Figure 1b) in the face network during childhood. This module consists of bilateral OFA regions, bilateral FFA regions and the left cerebellum.

In the present study, the right OFA was the only region to show a trend toward face-specific developmental changes in connectivity. Although some developmental changes involved the right FFA, these changes were not face-specific. The present finding that the right OFA plays a role in development of face processing is not surprising given that others consider the right OFA to be a critical and necessary component of face processing in adults (Pitcher et al., 2011; Pitcher et al., 2007; Rossion et al., 2003). Moreover, in another fMRI developmental study of face processing the right OFA showed a greater increase in face specialization with age compared to the right FFA (Joseph et al., 2011); c.f. (Golarai et al., 2007; Joseph et al., 2011; Scherf et al., 2007) and the OFA tends to be activated in younger children whereas the FFA is not activated as strongly (Aylward et al., 2005a; Gathers et al., 2004).

Although the right OFA shows a preference for faces like the FFA, its exact function in face processing has not been determined. Some evidence shows that the right OFA is involved in featural processing of faces (Pitcher et al., 2007) or represents an earlier stage of face processing (Fairhall and Ishai, 2007; Haxby et al., 2000b), whereas the right FFA is more heavily involved in configural and holistic processing (Aylward et al., 2005b; Maurer et al., 2007; Rossion et al., 2007). In the present study, the right FFA and right OFA coalesced into the same module during childhood, but dissociated in adulthood. Although it is difficult to ascribe particular functions to these regions in the present study, as we did not manipulate different types of face processing, we speculate that the reorganization of modular structure involving the right OFA may reflect functional separation of featural and configural processing of faces in adulthood. The visuo-cerebellar module in adults (which includes the bilateral OFA) may be largely associated with analysis of featural information in a face and may, therefore, play a more central role in perceptual processing of faces. Configural information (i.e., the spacing of features) is more relevant for perceiving the changeable aspects of faces and the right superior temporal sulcus (part of the fronto-temporal module in adults) is known for its role in processing dynamic aspects of faces such as changes in facial expression (Furl et al., 2007) and eye gaze (Haxby et al., 2000b). In addition, the right inferior frontal gyrus (also part of the fronto-temporal module in adults) is involved in imitating and empathizing with facial emotions (Morita et al., 2008) which are both important component processes of non-verbal communication and understanding the intentions of others. Therefore, the fronto-temporal module may be more associated with aspects of face processing that are relevant for social cognition.

The visuo-limbic module, which includes early visual areas, the left hippocampus and right inferior frontal (orbital portion) cortex showed increases in diversity with development, but for both faces and natural objects. We speculate that the emergence of visuo-limbic connections with development may relate to the development of perceptual expertise. Faces, natural objects and manufactured objects fall along a continuum of structural similarity, or similarity of form (Arguin, Bub and Dudek, 1996; Bruce & Humphreys, 1994; Damasio, Damasio and Van Hoesen, 1982). Faces represent the extreme end of this similarity scale in that they share the same overall structure of two eyes, two ears, a nose, and a mouth. Natural objects are generally more similar in shape than are manufactured objects. The analysis of image similarity reflected this continuum. As noted by others, faces require perceptual expertise for differentiating members of visually homogenous categories, but perceptual expertise can be demonstrated for categories other than faces (Diamond and Carey, 1986; Gauthier, Behrmann & Tarr, 1999). We suggest that the present findings for increased functional integration with development for both faces and natural objects in the visuo-limbic module may be related to development of perceptual expertise for differentiating items from visually homogenous categories (faces or natural objects). For example, the hippocampus has been implicated in specific face identification (Iidaka et al., 2003) and the connectivity between left hippocampus and right inferior frontal gyrus-orbital portion is stronger for successful than for unsuccessful coding of faces (Takashi and Cabeza, 2011). The early visual cortex (calcarine sulcus) may be recruited for additional perceptual analysis of object categories that are highly similar in shape (Martin et al., 1996). In addition, because face recognition performance improves with development (Carey and Diamond, 1977; Goldstein and Chance, 1964), we suggest that the increased visuo-limbic connectivity from childhood to adulthood may support the capacity to discriminate faces at a more specific or individual level, which is associated with greater perceptual expertise (Gauthier and Nelson, 2001). Apparently, this capacity is not reserved only for faces as the increased visuo-limbic connectivity also emerged for natural objects.

Some of the present findings are consistent with other findings in the literature regarding the development of functional brain networks. For example, Supekar et al. (2009) used resting-state connectivity analyses and reported that sub-cortical areas are more strongly connected with primary sensory areas in children than in adults. In the present study, the brain stem and thalamus were associated with the same module as lateral temporal lobe regions during childhood, but in adulthood, these two sub-cortical structures formed a separate module. In addition, functional integration (diversity*) of the subcortical module and left calcarine sulcus and within-module connectivity (strength*) of the visuo-cerebellar module and brainstem was greater in adults than children. Potentially, these developmental changes could reflect development of a sub-cortical module that is tightly connected only to early sensory areas (e.g. left calcarine) in childhood but becomes more modular (via increased strength*) yet integrated (via increased diversity*) with other brain regions by adulthood.

An important consideration about the present application of graph theory to examine functional connectivity of the face network is that the metrics described by Rubinov and Sporns (2011) are designed to isolate modules within a complex whole-brain network. The present face network was composed of only fourteen regions and may, in fact, already be a sub-network or module within a more complex brain network. One implication of this is that if the face sub-network were to be considered with respect to whole-brain complex networks, developmental changes may reflect greater segregation of the face-network from other brain networks with age as an index of specialized processing of faces. At present, we have demonstrated that partitions within the face sub-network are reorganized during development via changes in integration and segregation. Because this is the first graph-theory based functional connectivity study on development of a face network, the modularity properties and partitions described here would need to be replicated in future studies in order to demonstrate that these modules reliably reflect sub-networks involved in face processing. The interesting question of how the face network itself either dissociates or becomes integrated with other sub-networks of the brain should also be addressed with future studies. Moreover, graph-theory analysis applied to functional imaging data is constantly being refined and re-evaluated (e.g. (Power et al., 2012) and future studies will need to incorporate these refinements.

Another consideration about the present findings of developmental changes in graph theory metrics is that differences in metrics between adults and younger children could be explained by the fact that adults had, on average, higher correlations (or edge weights) than younger children. However, graph-theory metric differences between adults and older children cannot be attributed to higher edge weights in adults because edge weights were not different between adults and older children. We suggest that differences between adults and older children or differences between adults and both age groups of children are more likely due to a developmental change because differences in edge weights cannot fully explain the age group differences. In addition, in the case of right OFA within-clustering and strength, the increase with age during childhood gives more confidence this is a true developmental change and not just due to adults having higher edge weights than younger children. Therefore, we suggest that the collective findings indicate true developmental changes rather than reflecting higher edge weights in adults than younger children.

Other differences between children and adults must be considered as potential explanations for changes in network organization with age. One consideration is that signal amplitude differences between children and adults may drive the present findings of age differences in connectivity. Although connectivity analyses focus on the temporal synchrony of fMRI signal across brain regions (rather than relying on amplitude differences with respect to baseline), we cannot completely rule out the proposal that developmental changes in graph-theory metrics are driven by signal amplitude differences between children and adults. Nevertheless, age differences in signal amplitude and age differences in graph-theory metrics (or other measures of connectivity) could stem from the same underlying developmental process. Therefore, it would not be surprising if these types of measures were correlated. Whether age differences in signal amplitude should be thought of as a confound or indicative of an underlying developmental process will need to be carefully teased apart in future studies.

Another potential explanation for developmental changes in connectivity is that many aspects of cognitive function apart from face processing are not as developed in children as in adults (e.g., attention and executive function). It is possible that these differences drive the developmental changes in network organization observed here. However, children and adults did not differ in terms of button presses to the stimuli, indicating that they were as alert and attentive as adults. Moreover, the present task made minimal cognitive demands, which suggests that the network changes with development were not likely driven by cognitive processing related to the passive viewing task.

Yet some of the present findings that were not category-specific may reflect generalized cognitive differences between children and adults. Developmental changes that were not specific to faces or natural objects included increased functional integration (diversity*) of the subcortical module and left calcarine sulcus and increased within-module connectivity (strength*) of the visuo-cerebellar module and brainstem. In all of these cases, subcortical structures and early visual areas are involved but higher cortical areas are not. As noted, Supekar et al. (2009) found that children showed stronger connectivity between subcortical and primary sensory regions compared to adults. Together with the present findings, we suggested that these regions change from being tightly connected in childhood to more integrated with other brain areas by adulthood. Although subcortical regions are not typically associated with higher level cognitive and executive function, a recent functional connectivity study showed that stronger connectivity within subcortical regions was related to poorer episodic memory performance in elderly adults (Ystad et al., 2010). It is conceivable, then, that reduced diversity of subcortical connections observed in children in the present study is associated with inefficient whole-brain communication, which in turn could influence higher level executive or more generalized cognitive functioning. Future research will need to test this hypothesis directly.

Nevertheless, the present findings are relevant for the IS framework (Johnson, 2005) of brain development and complement prior findings of both regressive and progressive changes in fMRI signal magnitude in face-preferential brain regions with development (Joseph et al., 2011). The IS account characterizes changes in cortical function as competitive interactions among brain regions in order to increase efficiency of specialized processing. This implies functional reorganization based on connectivity patterns, rather than simply the addition of more connections to developmentally stable modules. The present results demonstrate this property through the modular reorganization of brain regions during childhood and in the transition from childhood to adulthood. These developmental changes were marked both by greater integration associated with a visuo-limbic module and greater segregation associated with the ROFA. Future research is needed to characterize whether these different modules subserve different functions in face processing.

In conclusion, the present findings provide one of the first characterizations of developmental changes in functional connectivity patterns of typical face processing networks. Although regions like FFA, OFA, primary visual and frontal cortex are activated at all ages to some degree (Joseph et al., 2011), the novel finding is that the connectivity of these regions and modular organization changes with age. Most of the face-specific changes in connectivity emerged during childhood rather than in the transition from childhood to adulthood. Understanding developmental changes in functional brain connectivity will be critical for determining whether face processing networks in autism and other developmental disorders are best described by long-range underconnectivity (Kleinhans et al., 2008; Koshino et al., 2008), local overconnectivity in sensory areas (Belmonte et al., 2004), adaptive variants of typical networks or atypical organization of face-processing networks (Berl et al., 2006).

Highlights.

Few functional connectivity studies of typical development of face processing exist

Graph-theory based connectivity revealed network changes during childhood

The right occipital face area segregated from the right fusiform face area during childhood

Visuo-limbic connections increased from childhood to adulthood

Increased visuo-limbic connectivity may support development of perceptual expertise