Circuit-level input integration in bacterial gene regulation

Abstract

Gene regulatory circuits can receive multiple simultaneous inputs, which can enter the system through different locations. It is thus necessary to establish how these genetic circuits integrate multiple inputs as a function of their relative entry points. Here, we use the dynamic circuit regulating competence for DNA uptake in Bacillus subtilis as a model system to investigate this issue. Specifically, we map the response of single cells in vivo to a combination of (i) a chemical signal controlling the constitutive expression of key competence genes, and (ii) a genetic perturbation in the form of copy number variation of one of these genes, which mimics the level of stress signals sensed by the bacteria. Quantitative time-lapse fluorescence microscopy shows that a variety of dynamical behaviors can be reached by the combination of the two inputs. Additionally, the integration depends strongly on the relative locations where the two perturbations enter the circuit. Specifically, when the two inputs act upon different circuit elements, their integration generates novel dynamical behavior, whereas inputs affecting the same element do not. An in silico bidimensional bifurcation analysis of a mathematical model of the circuit offers good quantitative agreement with the experimental observations, and sheds light on the dynamical mechanisms leading to the different integrated responses exhibited by the gene regulatory circuit.

Cells are usually subject to multiple simultaneous sources of biochemical and physical signals, which they must integrate to respond adequately to their external environment and internal conditions. Previous efforts addressed at understanding signal integration in gene regulation have mainly concentrated on mapping the combinatorial response of single bacterial promoters to multiple transcription factors (1–5), and on quantifying the combined effect of bacterial cell–cell signaling molecules acting upon a shared phosphorelay pathway (6–8). However, in many instances different inputs operate in a distributed manner, acting upon distinct nodes (genes or proteins) of the gene regulation network. In those cases, it is the network itself, and not a particular promoter or phosphorylation reaction, that has to integrate the information at the system’s level. It thus becomes necessary to understand how the integrated response of gene regulatory networks depends on the specific entry points of the inputs.

Some studies have recently examined the population-level response of complex signaling pathways to ligand combinations (9–12). However, a systematic in vivo study at the single-cell level of the integration of distributed inputs by gene circuits is still lacking. It also remains unclear how these integration maps are related to the underlying regulatory circuitry. Here, we address these issues by means of a combination of time-lapse fluorescence microscopy and mathematical modeling of multiple simultaneous perturbations of the genetic circuit governing competence in the bacterium Bacillus subtilis.

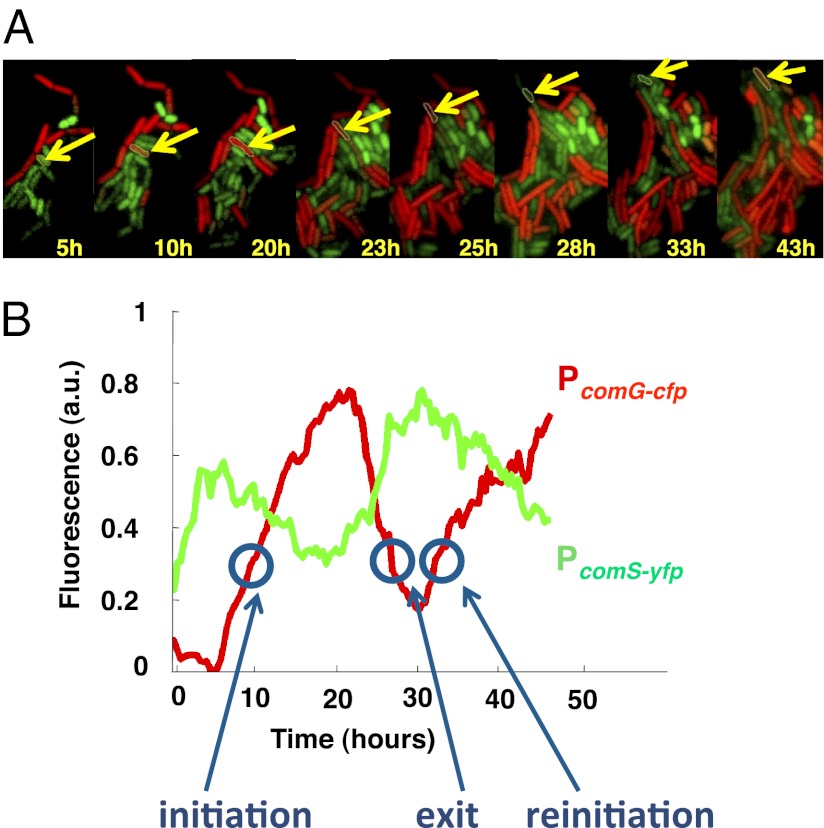
Genetic competence is a well-defined cellular state in bacteria that is triggered by nutrient depletion. This state is distinct from the vegetative state characteristic of exponential growth. In this state, B. subtilis cells cannot divide, and develop the ability to uptake and process extracellular DNA. This is accomplished by the activation of a master transcription factor, ComK, which leads to the expression of over a hundred proteins that bring about the new phenotypical state. Previous studies at the level of single cells (13, 14) have shown that wild-type competence is a transient, noise-driven cellular state, and have identified the gene regulatory circuit that controls it. Fig. 1A shows a sequence of false-color snapshots of a B. subtilis microcolony subject to stress, with the activity of the ComK-regulated P_comG promoter monitored by cyan fluorescent protein (CFP), whose fluorescent emission is represented in red in the figure. The filmstrip shows that a fraction of cells in the colony differentiate into the competent state. In particular, the cell outlined in yellow undergoes two consecutive transient differentiation events in a time window of over 30 h.

Fig. 1.

Dynamical features of genetic competence. (A) Typical filmstrip of a cell undergoing two consecutive competence events, as labeled by the activity of the comG promoter fused to cfp (in red in the figure). The comS promoter activity, fused to yfp, is shown in green. (B) Time traces of comG and comS fluorescence levels for the cell highlighted in A. The conditions for this experiment are those of Fig. 5H below. See Materials and Methods and SI Materials and Methods, Growth Conditions for Microscopy, for details of the microscopy procedures used.

The competence behavior can be quantified by computing the average fluorescence as a function of time, as shown in the red time trace of Fig. 1B. A systematic monitoring of competence along these lines reveals that this process is strongly dynamic, taking the form of pulsed activations of ComK-regulated promoters. These pulses can be analyzed in terms of their probability of initiation, exit, and reinitiation, events indicated in the time trace of Fig. 1B. This statistical characterization represents an advantage of studying dynamic phenotypes over static cellular responses. Fluorescence measurements are not able to provide absolute values of expression levels, unless single molecules are detected (15). Transition probabilities, however, are absolute by definition and are relatively easy to measure.

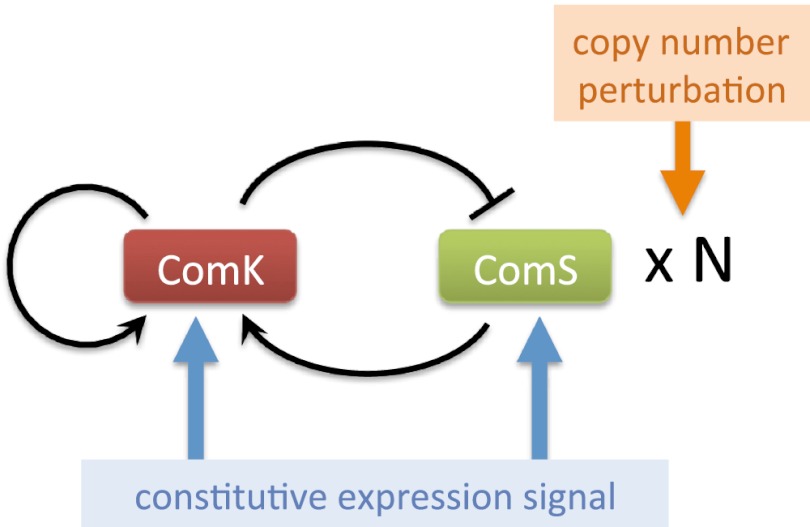
A second advantage that makes competence an ideal model process for signal integration studies is the fact that its underlying gene regulatory circuit is well known and relatively simple. Fig. 2 shows a scheme, with minor simplifications, of the interactions and two main components forming the circuit (13). The master regulator of competence, ComK, is subject to a positive- and a negative-feedback loop. On the one hand, ComK directly activates its own transcription. On the other hand, it negatively regulates the expression of the stress sensor protein ComS, which promotes ComK activation by competitively binding to their common protease MecA (13). This combination of a positive- and a negative-feedback loop gives rise to excitable behavior in the form of noise-driven ComK pulses, which are interpreted as competence events. Previous work has shown that, when this circuit is subject to single-input perturbations acting in isolation, different dynamical regimes such as oscillations arise (14).

Fig. 2.

Scheme of the circuit underlying genetic competence in B. subtilis. The two types of inputs whose integration is considered in this paper are also shown.

Results

Perturbing the Competence Circuit.

Here, we aim to characterize the response of the circuit to pairs of simultaneous perturbations, depending on their relative location within the circuit. We consider two types of inputs (Fig. 2): (i) the constitutive expression level of either of the two main components of the circuit, ComK and ComS; and (ii) the strength of the regulated expression of ComS. The first type of input might represent a context-dependent signal affecting an additional transcription factor acting upon the ComK or ComS promoters, whereas the second input correlates with the level of stress signals acting on the bacteria (16).

To control the constitutive expressions of ComK and ComS, we used strains containing additional copies of the two genes under the control of the isopropyl β-d-1-thiogalactopyranoside (IPTG)-induced hyperspank promoter, P_hyp (see Materials and Methods and SI Materials and Methods, Strain Construction, for a description of the strains used in this paper). The strains also contain a reporter construct in which the P_comG promoter drives the expression of cfp (Hyper-αK and Hyper-αS strains; Table S1). We applied five different IPTG levels in each case, namely 0, 3, 5, 10, and 100 μM. To calibrate the promoter activities triggered by these IPTG values in each of the two strains analyzed, we quantified the amount of fluorescence emitted by cells with a P_hyp-yellow fluorescent protein (yfp) reporter (Control-α strain; Table S1) for the same IPTG levels, and compared the measured values with the average signals obtained from strains containing a P_comS-yfp reporter (V10 strain; Table S1) under stress, and a P_comK-yfp reporter (KG strain; Table S1) in cells not exhibiting competence (Fig. S1). These comparisons allowed us to establish the amounts of constitutive expression from the P_comS and P_comK promoters for increasing IPTG, with respect to the maximum expression level of the P_comS promoter and the basal expression level of the P_comK promoter, respectively (Fig. S1, Table S2 and SI Materials and Methods, Dose–Response and Calibration of P_hypActivity). In what follows, we call these normalized values 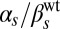and 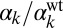, respectively.

As mentioned above, the second input that we consider affects the regulated (native) expression of ComS. Although the natural way in which this expression level is controlled is through the stress signals to which the bacteria are subject (16), using general stress media does not allow for well-controlled experiments because such stress conditions produce systemic changes in the cells that alter their physiology in multiple ways. Therefore, to vary in a controlled way the strength of the regulated ComS expression, we used copy number variations of the gene (but see Discussion for experiments varying the stress conditions). Specifically, we introduced an additional copy of the comS gene (under the control of its native promoter) in one of two plasmids of different characteristic copy numbers (kindly provided by Beth A. Lazazzera, University of California, Los Angeles, CA): pHP13, which has a low and relatively stable copy number of ∼6, and pDG148, with a larger copy number. To calibrate the actual copy number of these plasmids, we compared the fluorescence generated by cells containing the P_comS-cfp reporter in the pHP13 and pDG148 plasmids, with respect to the signal produced by a strain in which a single copy of P_comS-cfp had been integrated chromosomically (Norm-βS strain; Table S1). Quantifying the mean expression levels over long times allowed us to establish the copy numbers of these two plasmids at around 6.5 and 75, respectively (Fig. S2 and SI Materials and Methods, Calibration of P_comSPromoter Activity Triggered by Plasmids). In that way, we were able to apply three different values of the maximum expression level of the P_comS promoter with respect to its wild-type value. We denote this quantity as 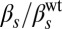below. We then included the multi-ComS plasmids in the Hyper-αK and Hyper-αS strains described above, generating new strains that allowed us to vary the two inputs simultaneously and independently.

Statistical Characterization of Competence Events.

In wild-type conditions, B. subtilis cells activate competence in a probabilistic and sparse manner, with less than 10% of cells in a microcolony exhibiting competence pulses at any given time as a response to stress. As anticipated above, this behavior can be characterized statistically by computing the probabilities of several types of events associated with the pulses, such as their initiation, exit, and reinitiation within a certain time window after exit (Fig. 1B and SI Materials and Methods, Determination of the Probabilities of Initiation, Exit, and Reinitiation). We systematically evaluated these probabilities under a combination of the two inputs described above.

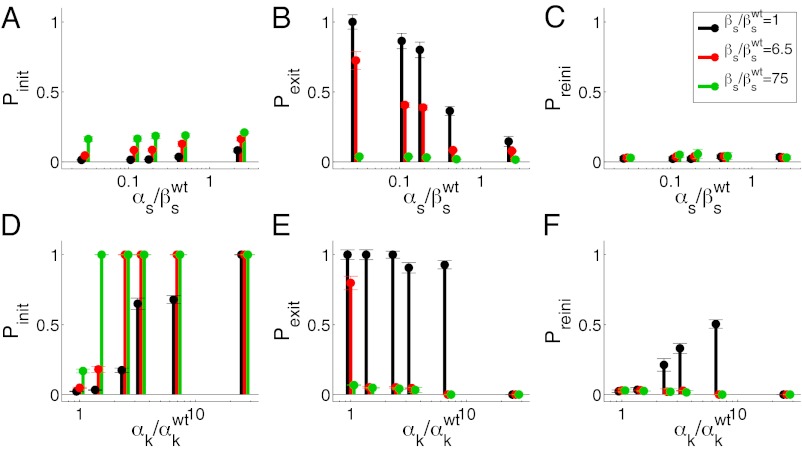
Fig. 3 summarizes our observed statistical characterization of the integrated response of the competence circuit to the pairs of inputs described above (full data in Tables S3–S5). The upper row shows results for the integration of the constitutive expression of ComS, 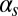, with the copy number of its natural gene, 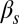, whereas in the lower row the latter is varied together with the constitutive expression of ComK, 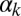. Three statistical observables are computed, namely the probabilities of competence initiation, 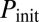, of exit from competence, 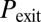, and of competence reinitiation within a defined time window, 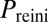. These quantities are computed as described in SI Materials and Methods.

Fig. 3.

Statistical analysis of competence dynamics in the presence of two inputs. The initiation (A, D), exit (B, E), and reinitiation (C, F) probabilities are plotted as the constitutive expressions of ComS (upper row) and ComK (lower row) are varied. Three different copy numbers of the natural ComS gene are considered in both cases: 1 (black), 6.5 (red), and 75 (green). The error bars are calculated via the standard deviation of the means taken in different movies.

This statistical characterization shows distinct integration features depending on the pairs of inputs being applied to the circuit. The probability of initiation, for instance, is small for all 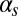levels, with just a minor increase caused by 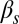(Fig. 3A). For increasing 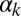, however, 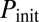increases up to 100% (all cells undergo competence within a cell cycle), but whereas that increase is smooth for low 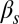, it becomes sharp and occurs earlier for high 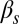(Fig. 3D). The exit probability, in turn, decreases abruptly in all cases for increasing 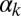(Fig. 3E), whereas the decrease is gradual with respect to 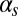(Fig. 3B). Finally, the probability of another competent event arising within one cell cycle after exit is only nonzero for intermediate values of 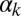and small 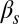(Fig. 3F).

Dynamical Characterization of Competence Events.

We can interpret the results described above in terms of dynamical behavior. For example, low probability of initiation together with high exit probability and no reinitiation [such as what happens for low values of both 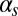and 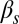(Fig. 3A) and 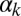and 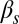(Fig. 3C)] corresponds to a sparse, noise-driven excitable regime such as the one originally identified to occur in this system (13). From that baseline situation, a decrease in the exit probability [e.g., for high values of 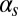(Fig. 3B)] corresponds to the excited state becoming stable, which would amount to bistable behavior. If 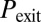becomes very small and the probability of initiation increases strongly [e.g., for high values of 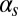and 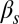(Fig. 3D)], the system becomes monostable, the competent state becoming the only remaining stable state in the circuit. Finally, a nonzero probability of competence reinitiation is an indication of oscillatory behavior [which is what occurs for intermediate values of 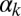and low values of 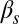(Fig. 3F)]. A summary of these classification criteria is given in Table 1.

Table 1.

Dynamical classification of competence regimes

Dynamical regime	Pinit	Pexit	Preini
Oscillations	Low-medium	High	High
Excitability	Low-medium	High	Low
Bistability (steady)	Low-medium	Low	N/A
Bistability (switching)	High	High	N/A
Monostability	High	Low	N/A

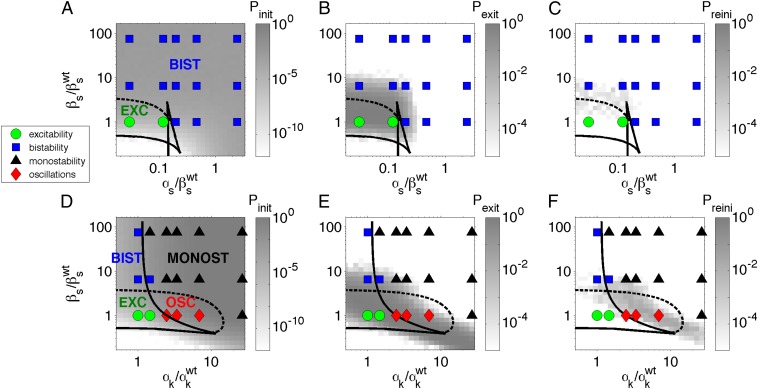
Using these classification criteria, we can represent the different dynamical regimes occurring for varying values of the input pairs, as shown in the phase diagrams of Fig. 4. In those diagrams, the different experimental regimes are represented by means of symbols, for the two types of input-integration experiments performed (Fig. 2). The shape and color of the symbols encode the dynamical regime. The green circles represent the wild-type excitable behavior exhibited by B. subtilis under stress (13). The blue squares correspond to bistability between the vegetative and the competent states. The black triangles denote monostable behavior in which competence is the only cellular state available to the cell. Finally, the red diamonds represent oscillatory behavior. The plots reveal distinct forms of integration in each case, according to the type of dynamical behaviors generated as the two inputs are varied in a coordinated way. In particular, when constitutive expression is varied for the same gene (ComS) that undergoes copy number perturbations (Fig. 4A), no new dynamical regimes arise from the integration of the two inputs: in the two cases, independent increase of the two inputs converts the cells from excitable to bistable, and the same thing happens when the two inputs are varied together. However, when the constitutive expression control is applied to ComK (Fig. 4D), the bifurcation scenario is different between the independent applications of the two inputs, and also with respect to the integrated response. For instance, while the increase of ComS copy number leads to a transition from excitable to bistable behavior, incrementing the constitutive expression of ComK generates oscillatory dynamics. These two scenarios are in turn different from the case of a joint increase of the two inputs, which leads to monostable competence for input levels that, when independently applied, result in either bistability or oscillations. Note that monostability is also the ultimate fate for extremely large levels of ComK constitutive expression, but it is substantially advanced by the joint action of the two inputs.

Fig. 4.

Phase diagrams of the competence circuit. The upper row corresponds to the joint variation of the constitutive expression of ComS, 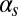, and the ComS copy number, 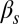, whereas in the lower row, the constitutive expression of ComK, 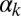, is varied together with 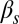. The symbols represent the experimental observations, with green circles corresponding to excitable dynamics (here defined by 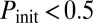and 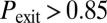), blue squares to bistable behavior ( 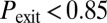if 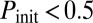: a fraction of the cells turn on competence and stay there, representative of spatial heterogeneity between two stable states; or 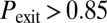if 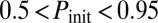: most cells turn on competence and come back, representative of temporal switching between two stable states), black triangles to monostable competence ( 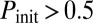and 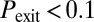), and red diamonds to oscillatory dynamics (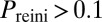). Lines represent bifurcation boundaries of a deterministic mathematical model of the competence circuit (see text), as computed with the numerical continuation software AUTO through XPP; solid lines correspond to saddle-node bifurcations and dashed lines to Hopf bifurcations. The symbols and lines are the same among the three columns, which differ in the quantities plotted in grayscale, obtained from discrete simulations of the competence circuit: 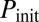(A and D), 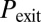(B and E), and 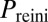(C and F). Parameters of the deterministic model are 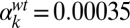, , 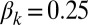, , 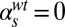, , 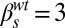, , 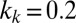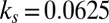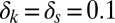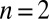and 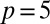. Parameters of the discrete model are given in Table S6.

To understand the different response maps of the circuit for the two input pairs, represented as symbols in the phase diagrams of Fig. 4, we now turn to a mathematical model of the competence circuit. As mentioned in the introduction, one of the advantages of competence is the existence of a good understanding of its underlying gene regulatory circuit, and consequently of a well-defined model of its dynamics. Previous investigations have shown that wild-type competence dynamics (13), and its response to single perturbations of the competence circuit (14), can be adequately described by the following two coupled ordinary differential equations (in dimensionless units):

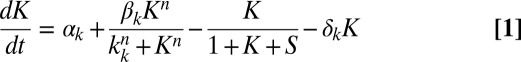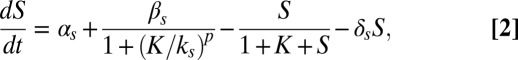where K and S represent the concentrations of ComK and ComS in the cell, respectively. The expression parameters 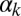, , 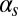and 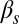have the same meaning as above, whereas 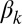represents the maximum rate of regulated expression of ComK. Besides the terms accounting for basal and regulated expression, the model also includes linear and nonlinear degradation terms, the latter corresponding to the competitive degradation of ComK and ComS by the common protease MecA (third term at the right-hand side of each of the two equations) (13).

A stability analysis of the different fixed points exhibited by the system of Eqs. 1 and 2 establishes the various dynamical regimes that the circuit can exhibit, which can then be compared with the experimental results described above. The different regimes are separated by bifurcation points (17), which can be traced in 2D parameter spaces such as the ones shown in Fig. 4 by means of numerical continuation methods. This analysis allows us to establish different regions separated by bifurcation lines. The solid lines in Fig. 4 denote saddle-node bifurcations, in which an unstable and a stable fixed point are created, and the dashed lines correspond to Hopf bifurcations, in which a stable oscillation emerges (17). These lines divide the parameter space into regions with distinct dynamics, labeled in the left panels of Fig. 4. Note that the excitable region in both the upper and lower rows of Fig. 4 is crossed by a saddle-homoclinic bifurcation line, not indicated in the plot, which separates a region of pure excitabilty for lower 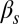, from a regime in which the excitable dynamics coexists with a limit cycle for higher 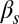. This limit cycle disappears at the Hopf bifurcation denoted by the dashed line. We have not included this bifurcation line in the plots because given the presence of noise, which destabilizes the limit cycle, the two regimes are biologically indistinguishable. This behavior is robust in the presence of noise, as shown by stochastic simulations of the reactions underlying the regulation circuit of Fig. 2 (SI Materials and Methods, Discrete Simulations of the Competence Circuit), for which the resulting event probabilities are plotted in grayscale in the figure. We note that the partition of the parameter space predicted by the model agrees well with the experimental observations represented by the symbols in Fig. 4.

Phenotypic Consequences of Integration.

To establish the biological meaning of the different integration behaviors described above, we now turn to a more detailed analysis of the experimental observations. Fig. 5 shows single-cell data from the competence reporter P_comG-cfp for four selected combinations of each of the two input pairs considered, with the case 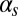- 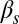being shown in the top two rows and 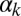- 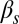in the bottom two rows. In both cases, the copy number increases from bottom to top, and the constitutive expression signal increases from left to right. In each panel, the left plot contains single-cell time traces aligned so that competence turn-on (if it exists) occurs simultaneously in all traces. Cells representing all kinds of dynamical behavior found are included in every case (except for cells that do not turn competence in the excitable regime, represented by green time traces).

Fig. 5.

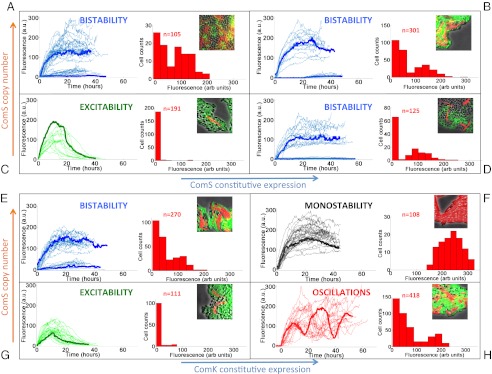
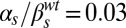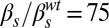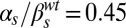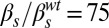Dynamical phenotypes arising from input integration. The four upper panels correspond to joint variation of the ComS copy number (increasing vertically toward the right) and the ComS constitutive expression level (increasing horizontally toward the right): (A) , ; (B) , ; (C) 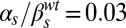, 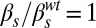; and (D) 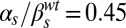, 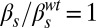. 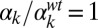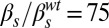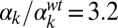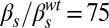The four lower panels correspond to joint variation of the ComS copy number (increasing vertically toward the right) and the ComK constitutive expression level (increasing horizontally toward the right): (E) , ; (F) , ; (G) 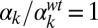, 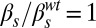; and (H) 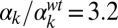, 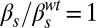. In each panel, the left plot shows a collection of single-cell time traces of CFP levels quantifying P_comG activity, and thus acting as ComK reporter. Color coding corresponds to the one used in Fig. 4, and a particular time trace is highlighted with a thicker line. The right plots show histograms of CFP levels as measured from a typical frame in each movie analyzed, and the Insets display selected snapshots from these movies.

Input conditions for which the system is bistable lead to two types of behaviors, with some cells never entering competence and some others exhibited sustained expression of ComK for up to 40 h, until either the cell dies or the movie ends. A histogram of CFP levels for all measured values at a typical instant of all movies analyzed (right plot in each panel of Fig. 5) reveals a clear bimodality in the bistable regimes (Fig. 5 A, B, D, and E), which contrasts with the extremely weak bimodality of the excitable regimes (Fig. 5 C and G) that is consistent with the low probability of competence of the wild-type cells. From the biological point of view, we note that effective competence requires cells not only to turn on ComK expression, but also to turn it off eventually. Cells in which ComK expression is sustained die without dividing, and therefore without passing on to her progeny any advantage that might have been gained by incorporating exogenous DNA. In that sense, we can say that bistability (and certainly also monostability; Fig. 5F) eliminates functional competence. This does not happen in the oscillatory regime (Fig. 5H) because the cells are able to return to the vegetative state and divide before turning on ComK expression again.

A second phenotypic role of competence is to delay, but not eliminate, sporulation. Sporulation is another cellular differentiation response to stress in which the bacterium becomes dormant and waits for a potential improvement of the environmental conditions before germinating. Sporulation is known to be inhibited by ComK expression (18), and thus when this expression occurs transiently (as in the excitable and oscillatory regimes), that fate is delayed but not eliminated. Similarly, bistability does not prevent sporulation, because in this regime a subpopulation of cells exists that do not express ComK, and are thus able to sporulate. The presence of spores in those regimes (excitability, bistability, and oscillations) is evident in the microcolony snapshots shown as Insets in the right-hand side of the corresponding panels of Fig. 5. In the monostable regime, however, all cells in the population express ComK in a sustained way (see time traces and histograms in Fig. 5F), and as a consequence spores cannot be produced in this case, as is shown in the snapshot displayed in that panel.

Discussion

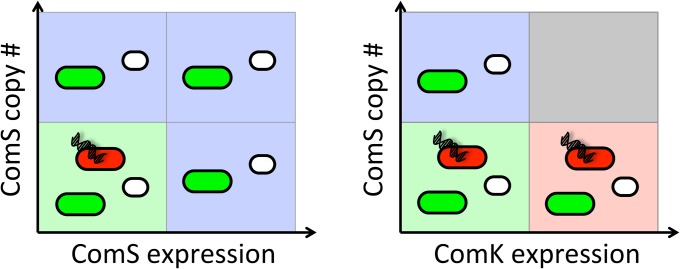
Taken together, these results show that, depending on the nature of the inputs acting together upon the circuit, the phenotypic consequences of the integration vary. In the case of the two inputs acting upon the same circuit element (ComS; Fig. 6, Left), the result of the integration (elimination of effective competence through the appearance of bistability, with no effect on sporulation) is no different from the effect of each input acting independently. However, when the two inputs act upon different circuit elements (ComS and ComK; Fig. 6, Right), the integrated response is functionally very different from the effect of the inputs acting individually. In particular, although no single input prevents sporulation or normal vegetative growth per se, their combination eliminates these two cellular states.

Fig. 6.

Schematic summary of the two integration modes observed experimentally. Background colors have the same meaning as in Figs. 4 and 5. Additionally, green cells denote vegetative cells, red cells represent functional competence, and white cells denote sporulation.

The two inputs considered in this paper have a different nature. One input corresponds to a (continuously controllable) level of constitutive expression of the two fundamental genes of the competence circuit. The other input takes the form of multiple (discrete) copies of one of those two fundamental genes (which retain their native regulation). In a realistic biological setting, the former type of input could correspond to a contextual signal such as those affecting signaling pathways in developing organisms (19). The effect of such contextual signals is beginning to be studied systematically in small developmental networks (20). The second input, however, would correspond to copy number variations such as those being extensively studied in recent years in the human genome (21) and yeast (22, 23), among other organisms. Even though the interplay between these two levels of cellular control is crucial for the correct functioning of cells, little is known about their integration. By systematically probing the integration of genomic and contextual inputs, studies such as the one described here should help shed light on the relationship between structure and function in cellular networks.

Besides the direct interpretation of the copy number variation of ComS as a purely genetic perturbation, we can also understand this input as mimicking realistic stress signals affecting the cells. To verify this assumption, we performed additional experiments integrating the constitutive expression of ComK with an increase in general stress signals, by growing and monitoring the cells in conditioned media, as described in SI Materials and Methods, Growth Conditions for Microscopy. We considered two levels of ComK constitutive expression, namely the wild-type case causing the excitable dynamics shown in Fig. 5G, and an IPTG level leading to the oscillatory dynamics depicted in Fig. 5H. As shown in Fig. S3, the general stress signals contained in conditioned media lead to phenotypes that mirror those produced by a high copy number of the ComS gene: the excitable regime becomes bistable, and the oscillatory regime becomes monostable. Noticeably, the results obtained in the wild-type case might help explain why certain studies identify competence as a bistable phenomenon (24), whereas others interpret it as an excitable dynamics (13): the system responds in one way or the other depending on the specific stress conditions of the medium.

The physiological effects reported here result from changes in the dynamical behavior of our genetic circuit. Functional consequences of dynamics have also been reported in mammalian cells (25, 26). Although recent studies have systematically addressed the effect of individual stimuli on dynamical behavior at the single-cell level (25, 27), here we consider the effects of combining two inputs. In that sense, our study is a dynamical generalization of more “classical” epistasis studies addressing the effect of combinations of genetic perturbations on cell growth (28) or the evolution of resistance under drug interactions (29). In our case, the use of dynamical phenomena (in the form of transient activation of a cellular differentiation program) allows us to define observables that are free from arbitrary factors associated with the measurement process (in our case, fluorescence detection from populations of fluorescent proteins that are not monitored at the single-molecule level). Furthermore, the input signals are quantitatively normalized with respect to appropriate reference strains. These facts allow for an objective comparison with a theoretical model of the competence circuit, which brings us closer to a quantitative understanding of the biology (30) underlying bacterial stress response. This approach could in principle be extended to other gene regulation networks in higher organisms.

Materials and Methods

All strains used in this study, listed in Table S1, were derived from the wild-type strain PY79. Standard transformation protocols were followed to transform the cells with the constructs described in SI Materials and Methods, Strain Construction. B. subtilis microcolonies were grown and imaged with fluorescence time-lapse microscopy as discussed in SI Materials and Methods, Growth Conditions for Microscopy. All procedures are described in detail in the SI Materials and Methods.