Oriented assembly of polyhedral plasmonic nanoparticle clusters

Abstract

Shaped colloids can be used as nanoscale building blocks for the construction of composite, functional materials that are completely assembled from the bottom up. Assemblies of noble metal nanostructures have unique optical properties that depend on key structural features requiring precise control of both position and connectivity spanning nanometer to micrometer length scales. Identifying and optimizing structures that strongly couple to light is important for understanding the behavior of surface plasmons in small nanoparticle clusters, and can result in highly sensitive chemical and biochemical sensors using surface-enhanced Raman spectroscopy (SERS). We use experiment and simulation to examine the local surface plasmon resonances of different arrangements of Ag polyhedral clusters. High-resolution transmission electron microscopy shows that monodisperse, atomically smooth Ag polyhedra can self-assemble into uniform interparticle gaps that result in reproducible SERS enhancement factors from assembly to assembly. We introduce a large-scale, gravity-driven assembly method that can generate arbitrary nanoparticle clusters based on the size and shape of a patterned template. These templates enable the systematic examination of different cluster arrangements and provide a means of constructing scalable and reliable SERS sensors.

The ability to control the arbitrary position, orientation, and connectivity of colloidal building blocks with nanoscale precision is an objective of materials research that is critical for advances in fields including electronics, energy harvesting/conversion, optics, and biosensing (1–4). Additionally, many barriers in our understanding of fundamental nanoscale phenomena are frequently overcome by ever more precise tools to manipulate the processes and organization of matter across extended and multiple-length scales (5, 6). The impact of new tools is particularly apparent in the field of plasmonics, which uses the collective excitations of free electrons in nanoscale metallic structures and periodically structured composites to control and manipulate light at deeply subwavelength scales (7–9). Experiment and simulation show that the subtle differences in the size, geometry, and spacing of metal nanostructures strongly impact their optical properties (10–13). However, to accurately and reproducibly fabricate structures using top–down tools is limited by the challenge of controlling nanoscale materials dimensions that depend on the crystallinity and surface roughness of materials (14–16).

Noble metal nanoparticles can be synthesized in a variety of shapes with exceptional monodispersity (17, 18) and self-assembled into complex, ordered structures (19–21). The outcome of the assembly process depends on particle shape, size, relevant particle interactions, and external driving forces (22). Because their surfaces are atomically smooth, polyhedral nanocrystals can form interparticle gaps with distinct, flat interfaces that are below 2 nm. Reproducible fabrication of such a gap is difficult to achieve with top–down lithographic methods. Nanoscale interparticle gaps between plasmonic antennae localize intense electromagnetic (EM) hotspots (23, 24), which are useful for a host of enhanced nano-optical effects that depend on the intensity and gradient of the local EM field (25, 26). One of the most well-studied nano-optical effects is surface-enhanced Raman spectroscopy (SERS), where the Raman scattering of adsorbed molecules is enhanced by the proximity to intense local fields. Here the SERS enhancement factor (EF) is roughly proportional to the product of the electric field intensities (|E|²) at both excitation and Stokes shifted Raman frequencies (27). Self-assembled Ag nanocube dimers have been studied extensively for SERS-sensing applications (28), but the dispersion of SERS EF values from assembly to assembly depends sensitively on the precise orientation of adjacent nanocube dimers and the size of the interparticle gap, along with the orientation of the structure with respect to the angle and polarization of excitation (29).

In this article, we examine the optical properties and SERS EFs of polyhedral nanoparticle clusters. Comparison of experimental scattering spectra with computed EM models shows that complex multipolar plasmon resonances within the gap dominate the optical properties of nanoparticle dimers, and helps explain observed magnitude of SERS EFs for two standard excitation wavelengths (λ = 633 and 785 nm). The narrow distribution of SERS EFs is attributed to the precise size, shape, and arrangement of particle clusters, in addition to highly uniform nanoscale gaps that were characterized by aberration-corrected high-resolution transmission electron microscopy (TEM). Finally, we describe an inexpensive, scalable method to generate arrays of oriented linear and circular clusters, and interrogate their SERS EFs on a highly parallel scale.

Results and Discussion

Silver (Ag) polyhedra were synthesized by the polyol method to generate facetted particles with exceptional monodispersity in both shape and size (18). Each particle is coated with a film of polyvinylpyrrolidone (PVP; 55,000 MW) polymer that acts as a structure-directing agent during particle synthesis and as a steric stabilizer preventing aggregation (17). In a good solvent, surface-adsorbed PVP can swell up to 20 nm in thickness, counteracting the strong van der Waals (vdW) forces between large facets, which can exceed thousands of kT per particle pair (21). In colloidal systems where particle–substrate interactions are small, solvent drying triggers a phase separation by increasing the interactions between particles because the original solvent is replaced by a poor solvent such as air (30). We assembled Ag octahedra (a = 300 nm) from a dilute solution of ethanol (∼0.05 µg/µL) by dropping it on a clean glass (SiO₂) coverslip that had been passivated with tridecafluoro-1,1,2,2-tetrahydrooctyl-1-trichlorosilane (Materials and Methods). The particles assemble into monomers and a variety of small nanoparticle clusters (Fig. 1A). With confocal Raman microspectroscopy we can measure these different arrangements if they are separated by >1 μm (Fig. 1B). For the SERS measurement, the samples were soaked in 2 mg/mL solution of 4-aminothiophenol (4-AMT) for ∼24 h. The 4-AMT completely exchanged with the PVP, which was confirmed by the absence of PVP peaks in the SERS spectrum. Clusters composed of dimers and trimers of octahedra exhibited dramatically higher SERS signal compared with single, monomer particles (Fig. 1 A and B, arrow). The intensity of the Raman map corresponds to the SERS signal of the a₁ (in plane, in phase) ν(C-S) vibrational mode at 1,079 cm⁻¹ of 4-AMT, which was used for all comparisons of SERS enhancement.

Fig. 1.

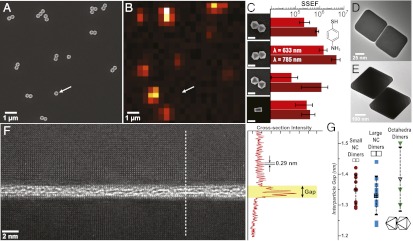
Correlated SEM and Raman micrographs showing assemblies of Ag octahedral nanocrystals (A and B). Dimers and trimers coated with 4-AMT exhibited large SERS signals compared with a monomer (arrow). (C) SSEF values (λ_ex = 633 and 785 nm) for different dimer assemblies: E-E (n = 10), F-F (n = 10), T-T (n = 4), and ncF-F (n = 10). (D and E) TEM images of nanocube and octahedra dimers show nanoscale interparticle gaps. (F) Aberration-corrected TEM image of the gap between two atomically smooth (100) facets of a nanocube dimer. A line profile of F shows the characteristic 0.29 nm spacing between Ag(100) atoms and a gap of 1.3 nm. (G) TEM gap data for two different nanocube dimers (a = 72 nm, n = 8 red circles; a = 122 nm, n = 10, blue squares) and octahedra dimers (a = 300, n = 3, green triangles). The average interparticle gap was 1.3–1.4 nm (black markers) with a SD of ∼0.1–0.2 nm.

We studied the SERS enhancement of isolated dimers of cubes and octahedra using two laser excitation wavelengths (λ_ex = 633 and 785 nm) polarized along the long axis of the particles. Evaporation-assisted assembly of colloidal polyhedra yields a range of symmetrical and asymmetrical dimer arrangements. We limited our study to four symmetrical particle arrangements that could more feasibly be measured and simulated, specifically octahedra face-to-face [F-F; number of dimers measured (n) = 10], edge-to-edge (E-E; n = 10), and tip-to-tip (T-T; n = 4), along with F-F nanocube dimers (ncF-F) for the purpose of comparison (Fig. 1C). The single SERS EF (SSEF) method was used to calculate enhancement in all experiments because it is useful for comparison of different substrates and provides a conservative lower boundary of the EF because it takes into account the entire surface area of the structure instead of the assumed hotspot (Materials and Methods). All particles exhibited an average SSEF between 10⁵ and 10⁶, with F-F octahedra outperforming all other shapes (Fig. 1C). The F-F nanocubes had an SSEF∼10⁵, which is consistent with the average dispersion reported in the literature (29). However, what was most striking about these results was the overall uniformity of SSEF. Dimer particles had a deviation of SSEF less than a factor of 10, which is considered as an extremely narrow dispersion for SERS dimer particles (29). Since dimer particles were many orders of magnitude brighter in SERS intensity than monomer particles—far brighter than can be accounted for simply by a doubling of the surface area—we examined the interparticle gaps carefully to determine their precise dimensions and uniformity.

Fig. 1 D and E shows a bright-field TEM image of F-F nanocube (a = 72 nm) and F-F octahedral (a = 300 nm) dimers. These samples were prepared by dropping a dilute (∼0.1 µg/µL) solution of particles on 15-nm thick silicon nitride (SiN_x) windows. Ag nanocubes are bound by (100) planes, so alignment to the [100] zone axis of one of the cubes ensures parallel viewing of the gap. Additionally, selecting the correct focal depth is critical to avoid the appearance of lattice fringes impinging into the gap (Fig. S1). Fig. 1F shows an atomically resolved view of an interparticle gap between two nanocubes (a = 72). The top particle is aligned along the [100] exact axis showing the cubic symmetry of the (100) plane, whereas the other particle typically had a slight rotational offset that precludes viewing along the same zone axis. The gap would be obscured if the particles were not atomically smooth. A line scan displays the characteristic 0.29 nm spacing between Ag atoms on the [100] direction, with PVP polymer sandwiched in between, stabilizing a gap size of 1.34 nm. We examined the interparticle gaps of populations of these small nanocubes (a = 72 nm; n = 10), along with larger nanocube dimers (a = 122 nm; n = 10) and F-F octahedra dimers (a = 300 nm; n = 3) to see if geometry or larger surface area and thus larger vdW forces affected gap size. All particles selected were in good registry with faces overlapping. The average gap size in all dimers studied was 1.33–1.38 nm, with a SD of 0.1–0.2 nm (Fig. 1F). We also assembled particles on SiO and amorphous carbon membranes, and observed gaps within the same range as those prepared on SiN_x (Fig. S2). Because gap width dominates the SERS EFs of noble metal nanostructures, we deduced that the uniformity in SSEF here was the result of consistent gap sizes.

During assembly, as particles are driven together by evaporation, vdW forces grow rapidly with decreasing distance, and the polymer collapses as solvent is replaced by air. In a poor solvent the collapsing polymer segments will interact more strongly with each other and the Ag surface, and the total force squeezes the polymer on each surface into a monolayer. The dynamic behavior of polymers squeezed into nanoscale gaps in metals is not well studied. However, in clay minerals such as montmorillonite, the collapsed structure of dried, adsorbed PVP is 0.5–0.6 nm for a single layer (31). Since the mutual crystallographic orientations of Ag and silicates should present similar surfaces to PVP (32), our measurements indicate that the interparticle gap is filled with approximately two adjacent PVP polymer monolayers that ultimately control the spacing of the gap. Particles with good registry impose more spatially uniform vdW forces during the final stages of assembly: vdW forces are counteracted by the loss of entropy caused by distorting and flattening the adjacent polymer brushes. Simple calculations show the influence of the substrate should be minimal at these nanoscale separations because vdW forces are very strong between the adjacent metal facet (Fig. S3). As a result, selecting for particle pairs that are aligned (i.e., perfect registry) will naturally lead to consistent SSEF values. Interestingly, generating reproducible gaps at these nanoscale dimensions is a critical step toward understanding the theoretical foundations of classical EM enhancement when interparticle separations approach the quantum mechanical limit of electron tunneling across metal junctions (33). Tuning the interparticle gap at the subnanometer scale could be feasible by introducing other polymers with different monolayer thicknesses.

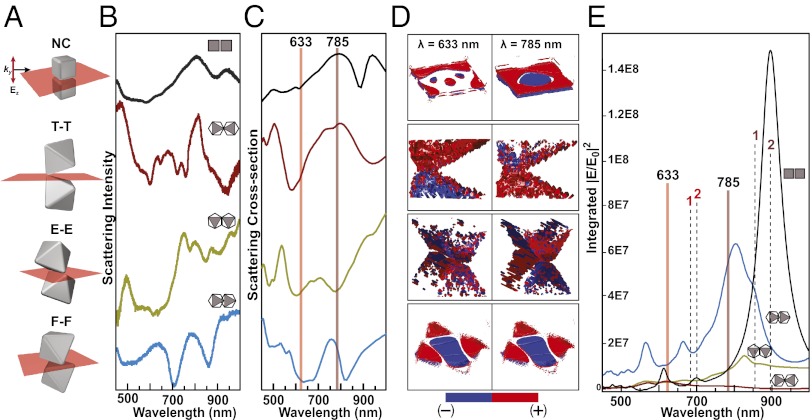
To understand how the structure of dimer nanoparticle clusters affects optical properties and SSEF values, we used experiment and simulation to examine the plasmonic properties of the different dimer clusters. Fig. 2A shows a rendering of each cluster, with a red plane in the gap and normal to the long axis of the dimers. Large metal nanostructures support multipolar plasmon excitations that can depend sensitively on both the direction and polarization of the incident light (34). We designed an experimental dark field optical setup that enabled white-light illumination from a narrow range of excitation directions, while controlling the direction of the electric field using a polarizer. The orientation of the dimers was confirmed afterward with SEM (Materials and Methods). This protocol allowed us to collect dark-field spectrum for each dimer with good optical alignment and showed a complex pattern of peaks and dips (Fig. 2B). Ag nanocubes (a = 122 nm) had the simplest spectra, with two peaks split by a minimum at ∼900 nm. The observed resonance splitting of this spectrum is consistent with the experimental measurements performed by Grillet et al., although our nanocubes are much larger (35). They observed strong plasmon coupling in nanocube dimers, while showing that resonance splitting was caused by edge rounding of the nanoparticle. We modeled each dimer using finite-difference time domain (FDTD) with an interparticle separation of 1.5 nm; each cube (a = 122 nm) had tips and edges with a radius of curvature (R_c) of 10 nm, while each octahedron (a = 300 nm) had tips and edges with a R_c of 20 nm. In the calculation, light is modeled as a plane wave incident parallel to the gap with an electric field normal to the gap. For the octahedral dimers, we used the same excitation scheme and observed multiple peak splitting, and there is excellent agreement between the simulated and experimental spectra (Fig. 2C).

Fig. 2.

Optical properties of polyhedral nanoparticle dimers. (A) Illustrations of the four types of nanoparticle dimers examined, with red planes indicating the interparticle gap. Experimental dark-field spectra (B) and FDTD simulations (C) of the corresponding nanoparticle dimers. (D) 3D charge density maps show the highly polarized, multipolar nature of the interparticle gap at both laser excitation wavelengths in the SERS experiments. (E) The total electric field intensity calculated by integrating over all points within the plane of the interparticle gaps for each nanoparticle dimer. The solid vertical lines indicate the laser excitation wavelengths, and dotted lines indicate the 1,079 cm⁻¹ (1) and 1,590 cm⁻¹ (2) Stokes modes of 4-AMT.

For a flexible SERS sensor that can detect multiple analytes, alignment of the excitation wavelength with strong resonances is essential. We examined the charge distributions that developed within each gap at λ = 633 and 785 nm excitation wavelengths, setting a threshold value for each charge and plotting a 3D isosurface representing the points of constant value within the gap volume (Fig. 2D). Each dimer has charges piled up on opposing sides of the gap, but both cube and octahedral F-F dimers have clearly defined multipolar resonances, while the E-E and T-T octahedra are less easy to interpret but appear to have charges interspersed in a small volume. Since both excitation wavelengths fall in the minima instead of the resonant peaks, it might seem intuitive that the field intensity be smallest at these wavelengths. Strikingly, the integrated total field intensity in the gaps shows that the minima in the scattering spectra correspond to the maximum total field enhancement (Fig. 2E). The positions of the laser excitation wavelengths (λ_ex = 633 nm and 785 nm; solid lines) and two Stokes-shifted frequencies (λ_Stokes) of 4-AMT (1 = 1,079 cm⁻¹ and 2 = 1,590 cm⁻¹) plotted on Fig. 2E show that the F-F dimers are expected to have the highest SSEFs because both excitation and emission overlap with the highest corresponding field intensities.

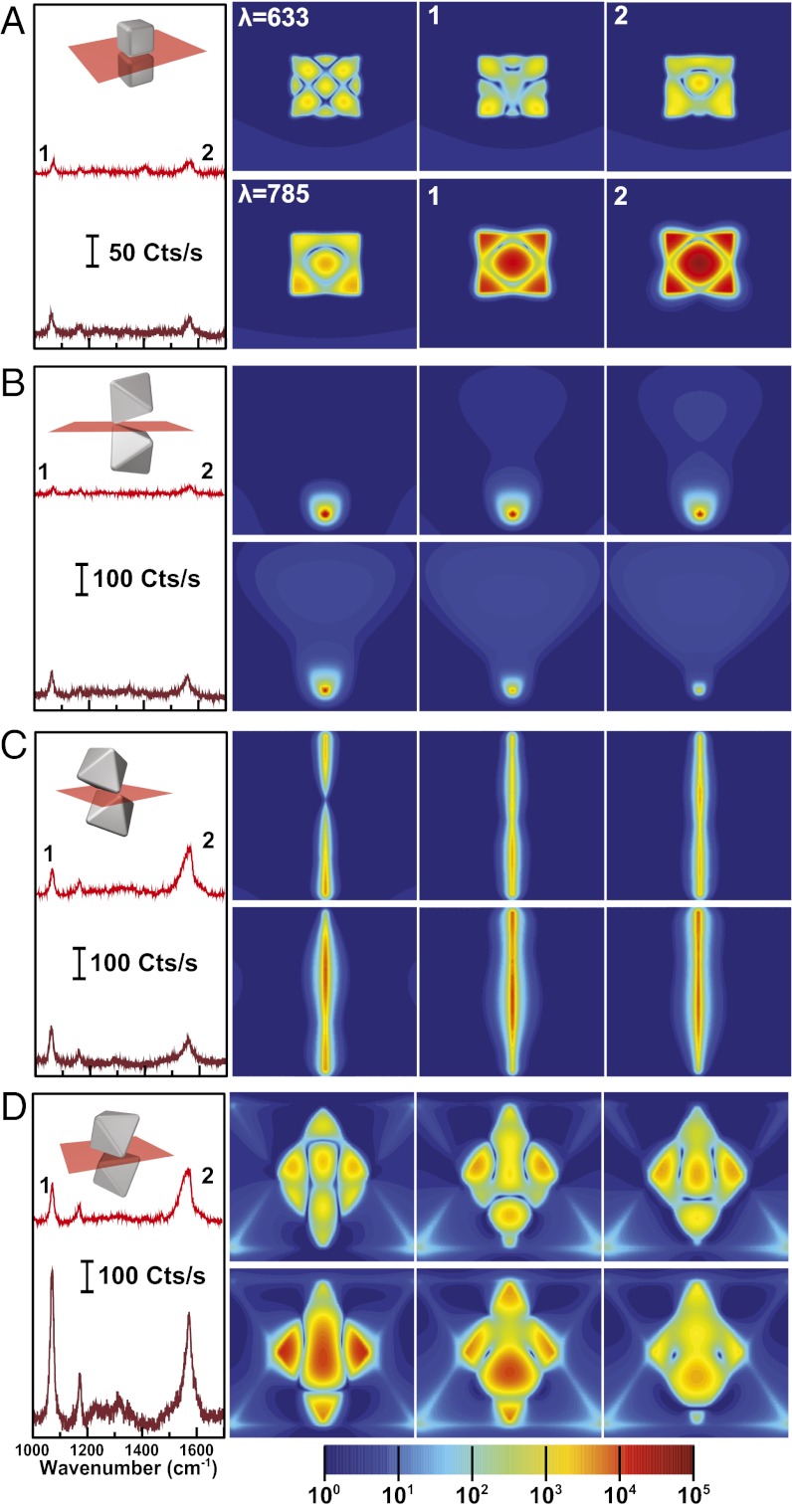
This observation of strong field intensities at minima in the scattering spectra is consistent with the recent discovery of spatially complex near-field properties in heptamer nanosphere clusters (36). Interfering bright and dark plasmon modes yield an overall reduction or “dip” in the scattering cross-section yet produce intense, highly localized fields. And heptamers nanofabricated by electron beam lithography (EBL) have the highest SERS signals when the excitation wavelength (λ_ex) and corresponding Stokes wavelengths (λ_Stokes) of 4-AMT overlap with these minima (37). Fig. 3 shows typical SERS spectra for 4-AMT (Left) for each wavelength and their corresponding field intensity maps (Right). In the experimental spectra, different laser intensities and collection times were used on each dimer to minimize beam damage, but all spectra were normalized to counts per second. The maps for the nanocube dimer show that the field intensities for λ_ex = 633 nm and λ_{Stokes = 1} = 681 nm are less intense than for the octahedra (Fig. 3A). Interestingly, the nanocube dimers exhibit a similar calculated intensity at λ_ex = 785 nm, but its intensity at the Stokes frequency λ_{Stokes = 1} = 858 nm is more than two orders of magnitude brighter. However, such a high intensity at the Stokes frequency will do little to improve the SERS enhancement if light cannot couple into the gap at this excitation wavelength (λ_ex = 785 nm) leading to a lower SSEF for nanocube dimers. Both T-T and E-E dimers have good overlap of λ_ex and λ_Stokes at one of the two wavelengths, but these hotspots are highly localized and have less integrated intensity (Fig. 3 B and C). By comparison, the F-F dimers have large hotspots with high fields at all relevant wavelengths (Fig. 3D). As expected, the highest EM intensities for the F-F dimers are located inside the gap compared with the outside edge of the dimer (Fig. S4). Movies S1–S4 show the electric field intensity maps of all four dimer polyhedra for λ = 450–1,000 nm.

Fig. 3.

SERS properties and near-field enhancement of dimers at different excitation wavelengths. Representative SERS spectra of 4-AMT (Left) and near-field electric field intensity maps corresponding to the SERS excitation wavelengths (λ) and the specified Stokes modes (1, 2) of 4-AMT for the different dimers: (A) nanocube, (B) Octahedra T-T, (C) Octahedral E-E, and (D) Octahedral F-F. All near-field intensity maps use the same color bar below.

Assembly of the dimers relies on drying processes, which are challenging to control due to the harshness of solvation forces and their spatially nonuniform fluctuations (38). A scalable solution for nanoparticle cluster assembly will require better control of cluster size and orientation with respect to the angle of excitation and its polarization. Hierarchical assembly using hard templates and capillary forces can be used to guide particles into the desired arrangements (29, 39, 40). For example, Kraus et al. developed a method reminiscent of gravure printing, where a solution of nanoparticles (the “ink”) is drawn over a patterned surface, and particles are deposited in recessed regions (41). Evaporation at the three-phase contact line of the air/solvent/substrate induces laminar flow, which carries the particles to the assembly zone. This method can produce large-area patterns of spherical metal particles with a low rate of defects, but there are few demonstrations of reproducible, well-defined clusters. Part of the challenge of this hierarchical approach stems from the need to build up a large-particle concentration at the assembly zone. For high-fidelity patterning, every patterned recess gets a particle, so recesses that can accommodate dimer particles clusters would require double the concentration at the assembly zone, and so on. Thus, to achieve a dense particle fluid, uncontrolled nucleation must be prevented by minimizing particle–particle and particle–interfacial interactions. In addition, the final arrangement of particle clusters assembled in templates can depend strongly on capillary forces between the solid particles and the recessed pits (i.e., container), and how these affect the surface deformation at the liquid interface (42, 43). Thus, clusters that do not occupy the whole of the recess will be more likely to rearrange because there is more solvent and they are not stabilized by the boundaries of the container.

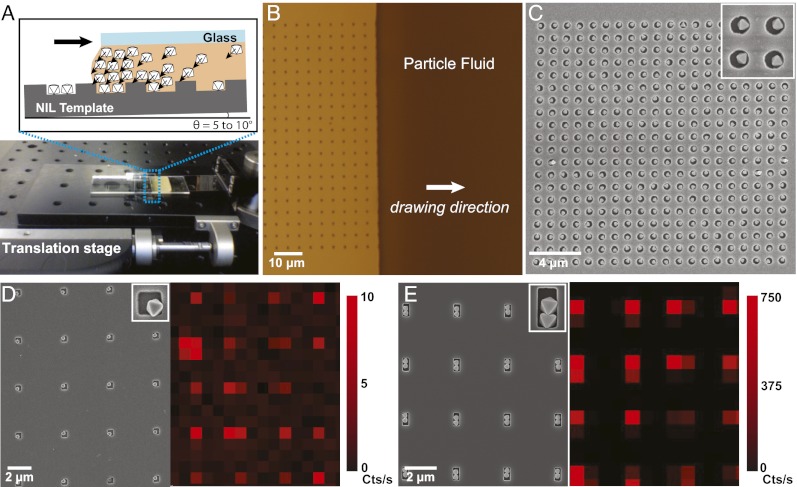
We developed a modified gravure-like method using gravity as a driving force. Fig. 4A shows a photo and illustration of the assembly setup. A template composed of different-sized pits in glass or Si substrates was fabricated by the combination of nanoimprint lithography (NIL) and reactive ion etching (RIE). This pattern was set on a single-axis translation stage, and a drop of particles in solution was drawn across the template using a fixed coverslip. N-N-Dimethylformamide (DMF) was used as the solvent because (i) it has a high boiling point (153 °C) that will minimize convection-driven flow of solvent around the assembly zone. Evaporation at the three-phase contact line can cause spatially nonuniform fluctuations in the density of the particle fluid that makes large-scale uniformity of assembly difficult to control. Minimizing evaporation ensures that gravity can build up a uniform concentration across the assembly zone. And (ii) DMF is an excellent solvent for PVP. PVP-coated Ag polyhedra behave as quasi-hard particles in DMF and can sustain high concentrations without nucleating (21). Particles were driven to the assembly zone by tilting the entire apparatus toward the three-phase contact line, building up net gravitational pressure, and driving the particles into the pits before particle fluid moves beyond the pit (Fig. 4B). Fig. 4C shows near-perfect patterning of 400 monomer octahedra in holes spaced by 400 nm. For analysis of SSEF, we require the particles to be spaced far enough apart to eliminate plasmon coupling and prevent the overlap of signal from individual assemblies. Fig. 4 D and E shows ensembles of monomer and dimer octahedra and their corresponding SERS maps. Light was polarized along the long axis of the dimers, and each map shows uniform SERS intensities within each population. The dimer clusters are expected to be uniform here because they are well aligned in the pits, allowing identical excitation conditions.

Fig. 4.

Oriented assembly of polyhedral plasmonic nanoparticle clusters using gravity-driven nanoparticle printing. (A) Scheme and photo of the assembly setup that was used in an environment with minimal air currents. A solution of particles in DMF is sandwiched between fixed glass coverslip and an NIL template on a single-axis translation stage. The setup is tilted to 5–10°, causing the particles to accumulate at the air/solvent/substrate interface. Once the dense particle fluid has formed, the stage is used to move the NIL template, drawing the nanoparticle fluid across the pattern (B). The high concentration of particles at the interface forces particles inside the recessed pattern, which are left behind once the particle fluid crosses the pattern (C). SEM images and corresponding SERS intensity maps of patterned single octahedra and dimers using 633-nm excitation and monitoring the 1079 cm-1 band of 4-AMT (D and E). Measurements are reported in counts/second. For SERS measurements, particles were assembled in pits spaced 4 μm to ensure each measurement corresponded to a single particle or assembly.

Parallel assembly of oriented clusters enables side-by-side comparison of SSEF under identical excitation conditions. Fig. 5A shows 7 × 6 array pits used to assemble linear trimer octahedra. Arrays of rectangular, 300-nm deep pits in Si with increasing aspect ratio were used to assemble linear arrays of cubes, octahedra, and mildly etched octahedra from single particles up to tetramers (Fig. 5B). These samples allowed us to obtain rapid acquisition of particle clusters of a single shape that are exposed to the analyte under identical conditions and measured using identical excitation conditions (polarization, laser fluence, etc.). These data show that mildly etched particles have high SSEFs for single particles, and SSEFs exceeding ∼10⁸ for dimer particles, but that the EF does not change significantly with increasing length. By comparison, cubes and octahedra continue to increase from dimers to teramers, with SSEFs of ∼10⁶ and 10⁷ for cubes and octahedra, respectively. The SD of each population shows that gravity-driven oriented assembly maintains good control of particle gap dimensions because the SSEF values are very consistent.

Fig. 5.

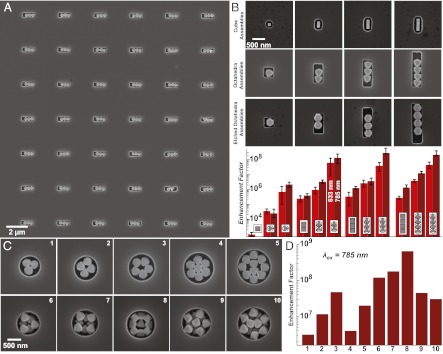
Large-scale assembly of particles into linear and circular templates. (A) SEM image of an array of octahedra trimers in identical-sized pits in Si. Measuring these arrangements side-by-side enables interrogation of SERS enhancement of each trimer under identical excitation conditions. (B) SSEFs at λ_ex = 633 and 785 nm for single particles, dimers, trimers, and tetramers composed of nanocubes (a = 122 nm), octahedra (a = 300 nm), and mildly etched octahedra (a = 270 nm). Light was polarized along the long axis of the particle assembly. Error bars correspond to the SD of each measurement. (C) SEM images of octahedra packed into circular pits of varying diameter with a depth of 300 nm (1–5) and 650 nm (6–10). (D) SERS EFs measured at 785 nm excitation for individual circular single-layer and multilayer octahedral assemblies (1–10).

We can also search for different arrangements and their SSEFs by using varying sizes of circular pits. Octahedra were assembled into arrays of circular pits with varying diameters (450–950 nm with 50-nm steps; Fig. S5). We observed a wide range of unanticipated cluster sizes and symmetries with microscale and nanoscale features relevant to surface plasmons and SERS. Fig. 5C shows the packing of octahedra (a = 300 nm) into circular containers of different diameters (0.85 μm to 1.3 μm) and two different depths (1–5 = 300 nm; 6–10 = 650 nm). We measured the SERS EF of these circular arrangements using circularly polarized light. Two trends are apparent from the data: clusters with F-F arrangements and openings or holes in the structure have the highest SSEFs, and multilayer structures give the highest SSEFs overall. However, there should be a limit to the effectiveness of larger and thicker assemblies because light may be channeled away from the collection optics or absorbed.

Conclusions

Monodisperse Ag polyhedra can be assembled into a variety of arrangements with exceptionally uniform nanoscale interparticle gaps that are resolvable by TEM. The dimensions of these gaps are controlled by the thickness of the PVP polymer brush, which may potentially be controlled by modulating the shrinking–swelling transition of PVP or by using different polymers. Both experiment and simulation show that the optical properties of assembled polyhedral dimer clusters are strongly influenced by the interparticle gap, and the uniformity of the gap size yields consistent SERS enhancement between similar particle clusters. The ability to control the arbitrary size and shape of particle clusters provides a rational path to systematically identify the key structural motifs that focus and concentrate EM fields using surface plasmons. Control at multiple length scales enables the scalable fabrication of uniform plasmonic materials for reliable SERS sensors.

Materials and Methods

Optical Characterization of Nanoparticle Dimers.

Glass coverslips were prepared by sonication in distilled, deionized water followed by ethanol. Then the coverslips were exposed to vapors of tridecafluoro-1,1,2,2-tetrahydrooctyl-1-trichlorosilane under vacuum to form a monolayer of low-surface energy fluoroalkane chains. Unreacted fluoroalkylsilane was washed off with DMF, and then dilute solutions of Ag particles (∼0.1 µg/µL) in ethanol were dried to generate nanoparticle aggregates for use in the DF experiments. Surface plasmon resonances are sensitive to the polarization and wavevector of incident light (34), so great care must be taken to achieve illumination conditions that match the FDTD modeled structures. Linear polarized white light was passed through a dark field condenser (N.A. = 0.92–0.8) that had been equipped with a beam block to eliminate ∼350° of the illumination cone coming from the condenser, leaving the remaining 10° of incident light with a very uniform wavevector (Fig. S6).

Dimers and larger aggregates can be identified optically because of their size and more reddish color. Octahedra dimers have an obvious lobe pattern and can be oriented in the system to achieve illumination along the particle gap (Fig. S7). To take the scattering spectra, light from the particle was collected with an Olympus objective (60×, N.A. = 0.7) and focused into the spectrometer. This scattering spectrum was subtracted from the glass background and divided by the spectrum of the white light source. Afterward, the orientation of the nanoparticle dimers was confirmed using SEM (Fig. S7).

Gravity-Driven Particle Assembly.

Particles were assembled on the patterned Si surfaces using a variation of the gravure printing method. The Si template was affixed to the translation stage. Then Ag particles were suspended in DMF, and 20 µL of this solution was dropped onto the Si template and then sandwiched between a clean, fluorosilanized glass coverslip that functioned as the “doctor blade” in the gravure printing process. The whole setup was tilted by 10° so that the particles moved toward the front of the glass coverslip, and then the template was translated at 1 µm/s, drawing the meniscus of the particle solution across the template and exposing the newly assembled nanoparticle clusters.

Confocal Raman Microspectroscopy and Calculation of the Single SERS Enhancement Factor (SSEF).

Detailed descriptions of the confocal Raman microspectroscopy setup and SSEF calculation are included in the Supporting Information.